Изобретение относится к вычислительной технике и может быть использовано:
1) в высокопроизводительных вычислительных системах, в частности в системах цифровой обработки сигналов, работающих в режиме реального времени,
2) в системах управления скоротечными процессами,
3) в качестве средства повышения производительности персональных компьютеров при решении задач, связанных с упрощением вида матриц систем линейных уравнений (алгебраических и дифференциальных), реализуемого как подсхема в составе арифметического процессора или же в составе отдельного устройства (спецпроцессора).
Известен алгоритм и реализующее его устройство под названием Cordic [1], предназначенное для вычисления тригонометрических функций cos(φ) и sin(φ).
Устройство Cordic осуществляет вычисления по формулам
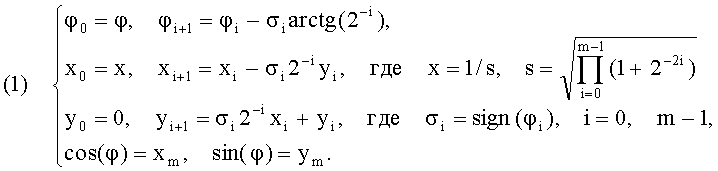
Здесь и далее m - число разрядов, отводимых под числа x и y. Вычисления по формулам (1) носят название «метод Cordic». Следует сказать, что итерационный процесс формул (1) реализует так называемое преобразование псевдовращения, которое наряду с вращением вектора (х,0) на угол φ осуществляет его растяжение на величину
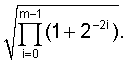
Из формул (1) видно, что исходный вектор (1,0) перед выполнением итерационного процесса нормализуется по формуле
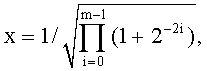
чтобы компенсировать указанное выше растяжение. В результате выполнения алгоритма Cordic на выходе получают вектор (xm,ym), причем 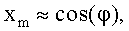
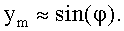 Таким образом, можно считать, что метод Cordic осуществляет ортогональное вращение (поворот) исходного вектора (1,0) на заданный угол φ.
Таким образом, можно считать, что метод Cordic осуществляет ортогональное вращение (поворот) исходного вектора (1,0) на заданный угол φ.
Поскольку исходный вектор (1,0) фиксирован, то в реальном устройстве Cordic вычисления по формуле
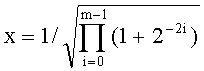
не производятся, и на вход устройства Cordic подаются компоненты вектора (х,0).
Метод Cordic и соответственно устройство Cordic с незначительными изменениями можно использовать для аннулирования одной компоненты двумерного вектора. Пусть теперь (x,y) - произвольный вектор. Нетрудно видеть, что вычисления [2] по формулам
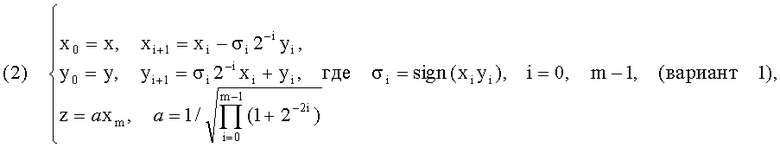
осуществляют поворот вектора (x,y) на угол φ 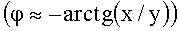 , причем у вектора (xm,ym) вторая компонента ym≈0, а у вектора (z,0) первая компонента
, причем у вектора (xm,ym) вторая компонента ym≈0, а у вектора (z,0) первая компонента 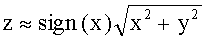 , где
, где
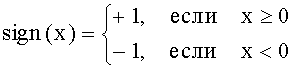 .
.
Кроме этого метод Cordic и соответственно устройство Cordic с незначительными изменениями можно использовать для осуществления ортогонального вращения (поворота) произвольного вектора (u,v) на угол φ≈-arctg(x/y) [2], где x и y - компоненты вектора (x,y)

При осуществлении вычислений по формулам (2, 3) используются произвольные исходные векторы (x,y) и (w,v), поэтому для обеспечения ортогональности преобразования, отображающего их в векторы (z,0) и (s,t) соответственно, невозможно избежать выполнения операции нормировки векторов (формулы
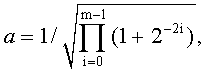
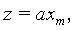
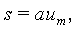
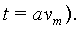
Известно устройство вращения вектора [2], состоящее из блока псевдовращений и блока нормировки, вход которого соединен с выходом блока псевдовращений. Для аппаратной реализации преобразований псевдовращения используется m-каскадный конвейер, в котором вход последующего каскада соединен с выходом предыдущего. Так как число
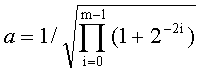
заранее известно, то нормировка в этом устройстве достигается выполнением операции умножения: 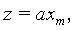
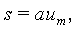
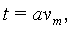 с помощью умножителя(ей) Брауна, входящего(их) в блок нормировки.
с помощью умножителя(ей) Брауна, входящего(их) в блок нормировки.
Наиболее близким по технической сущности к заявляемому устройству является устройство вращения вектора [2], состоящее из блока псевдовращений и блока нормировки, вход которого соединен с выходом блока псевдовращений. Для аппаратной реализации преобразований псевдовращения используется также m-каскадный конвейер, в котором вход последующего каскада соединен с выходом предыдущего.
Используемый в этом устройстве способ нормировки состоит в следующем.
Число 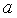 представляют в виде
представляют в виде
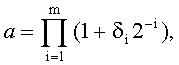
где δi∈{-1,0}, и нормировку осуществляют вычислением по формулам
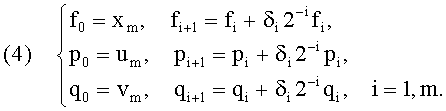
Для аппаратной реализации такой нормировки используется блок нормировки, представляющий собой цепочку(и) из m последовательно соединенных каскадов, в которой вход последующего каскада соединен с выходом предыдущего. В состав каждого каскада входит регистр, схема сдвига и вычитатель, при этом вход регистра является входом каскада, выход регистра соединен с первым входом вычитателя и входом схемы сдвига, выход схемы сдвига соединен со вторым входом вычитателя, а выход вычитателя является выходом каскада. На вход схемы сдвига i-го каскада поступает число fi(pi,qi), а на ее выходе получают δi2-ifi (δi2-ipi,δi2-iqi). Другими словами, указанная схема осуществляет сдвиг числа fi(pi,qi) на i разрядов вправо.
К недостаткам выбранного прототипа можно отнести следующее. Для осуществления нормировки с помощью вычитателей требуется неоправданно большое их количество (m (2m) штук) (соответственно (m+r)m (2(m+r)m) элементарных (двоичных) сумматоров, здесь r - число дополнительных младших разрядов вычитателей, требующихся для обеспечения точности выходных результатов), что увеличивает стоимость и к тому же уменьшает производительность устройства.
Целью изобретения является создание устройства с более низкой, чем прототип, стоимостью за счет снижения числа элементарных сумматоров, требующихся для нормировки, и обладающего при этом более высокой производительностью.
Поставленная цель достигается 1) удалением из блока нормировки каскадов, осуществляющих тождественные преобразования (вычисления по фомулам (4), в которых δi=0, не выполняются), 2) тем, что в состав цепочки каскадов вводятся каскады, содержащие сумматоры, 3) удалением из состава каскадов схем сдвига. Выполнение пунктов 1) и 2) приводит к тому, что число каскадов l в блоке нормировки при m=24 снижается до m/4. Формально работа такого блока нормировки описывается соотношениями
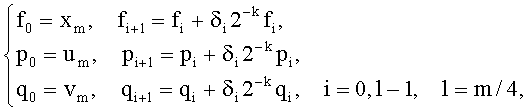
при этом δi∈{-1,1}.
Декларированное выше уменьшение длины цепочки каскадов блока нормировки, в которой вход последующего каскада соединен с выходом предыдущего, обеспечивается за счет специально подобранной последовательности сумматоров-вычитателей и описанного ниже соединения битов их входов. В состав каждого каскада входит регистр и вычитатель (сумматор), при этом вход регистра является входом каскада, выход регистра соединен с первым входом вычитателя (сумматора), выход вычитателя (сумматора) является выходом каскада. В первом каскаде цепочки k-й бит первого входа вычитателя соединен с k+1-м битом второго входа (δ0=-1, k0=1, k=1,m-1), а 1-й бит второго входа устанавливается в ноль. Во втором каскаде k-й бит первого входа сумматора соединен с k+2-м битом второго входа (δ1=1, k1=2, k=1, m-2), а биты второго входа с 1-го по 2-й устанавливаются в ноль. На третьем каскаде цепочки k-й бит первого входа вычитателя соединен с k+5-м битом второго входа (δ2=-1, k2=5, k=1, m-5), а биты второго входа с 1-го по 5-й устанавливаются в ноль. На четвертом каскаде k-й бит первого входа сумматора соединен с k+9-м битом второго входа (δ3=1, k3=9, k=1, m-9), а биты второго входа с 1-го по 9-й устанавливаются в ноль. На пятом каскаде k-й бит первого входа сумматора соединен с k+10-м битом второго входа (δ4=1, k4=10, k=1, m-10), а биты второго входа с 1-го по 10-й устанавливаются в ноль. На шестом каскаде k-й бит первого входа сумматора соединен с k+16-м битом второго входа (δ5=1, k5=16, k=1, m-16), а биты второго входа с 1-го по 16-й устанавливаются в ноль.
Сопоставительный анализ с прототипом показывает, что заявляемое устройство отличается составом: 1) в блоке нормировки используется всего 6 каскадов против 24 у прототипа, 2) в каскадах наряду с вычитателями используются и сумматоры, 3) схемы сдвига отсутствуют.
Таким образом, заявляемое устройство соответствует критерию «новизна».
Сравнение заявляемого технического решения не только с прототипом, но и с другими техническими решениями [2] позволяет сделать вывод о соответствии заявляемого технического решения критерию «существенные отличия».
Изобретение поясняется структурными схемами, где на рис.1 и рис.2 показаны первый и соответственно второй варианты устройства вращения вектора.
Заявляемое устройство выполнено в двух вариантах и состоит из двух блоков: блока псевдовращений и блока нормировки. Первый вариант устройства (рис.1) предназначен для ортогонального аннулирования одной компоненты двумерного вектора. На его вход подаются два числа x и y - компоненты двумерного вектора. На выходе получаются: число
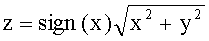 ,
,
где
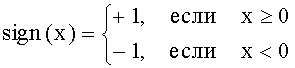 ,
,
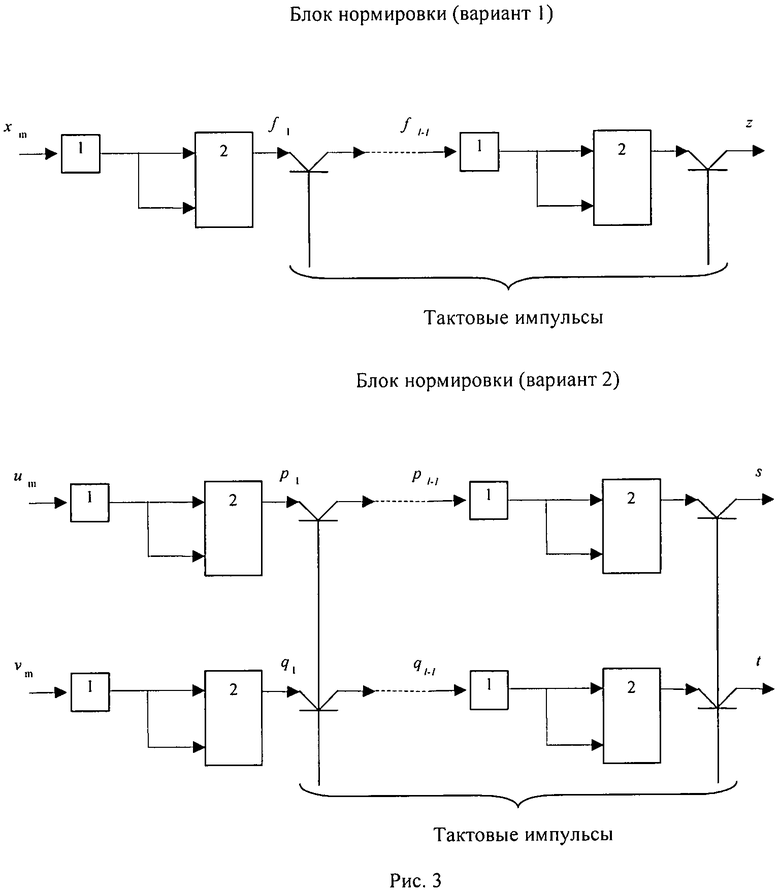
и 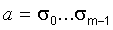 - код угла φ между векторами (x,y) и (z,0). Блок псевдовращений представляет собой m-каскадный конвейер, каждый каскад которого содержит два регистра 1, два сумматора-вычитателя 2, схему 3, устанавливающую сумматоры-вычитатели 2 в режим сложения или вычитания, и две схемы сдвига 4, соединенных как указано на рис.1. Блок нормировки представляет собой цепочку последовательно соединенных каскадов, соединенных как показано на рис.1, при этом каждый каскад содержит сумматор (вычитатель) 2, или же регистр 1 и сумматор (вычитатель) 2, как показано на рис.3, если он выполнен в виде конвейера.
- код угла φ между векторами (x,y) и (z,0). Блок псевдовращений представляет собой m-каскадный конвейер, каждый каскад которого содержит два регистра 1, два сумматора-вычитателя 2, схему 3, устанавливающую сумматоры-вычитатели 2 в режим сложения или вычитания, и две схемы сдвига 4, соединенных как указано на рис.1. Блок нормировки представляет собой цепочку последовательно соединенных каскадов, соединенных как показано на рис.1, при этом каждый каскад содержит сумматор (вычитатель) 2, или же регистр 1 и сумматор (вычитатель) 2, как показано на рис.3, если он выполнен в виде конвейера.
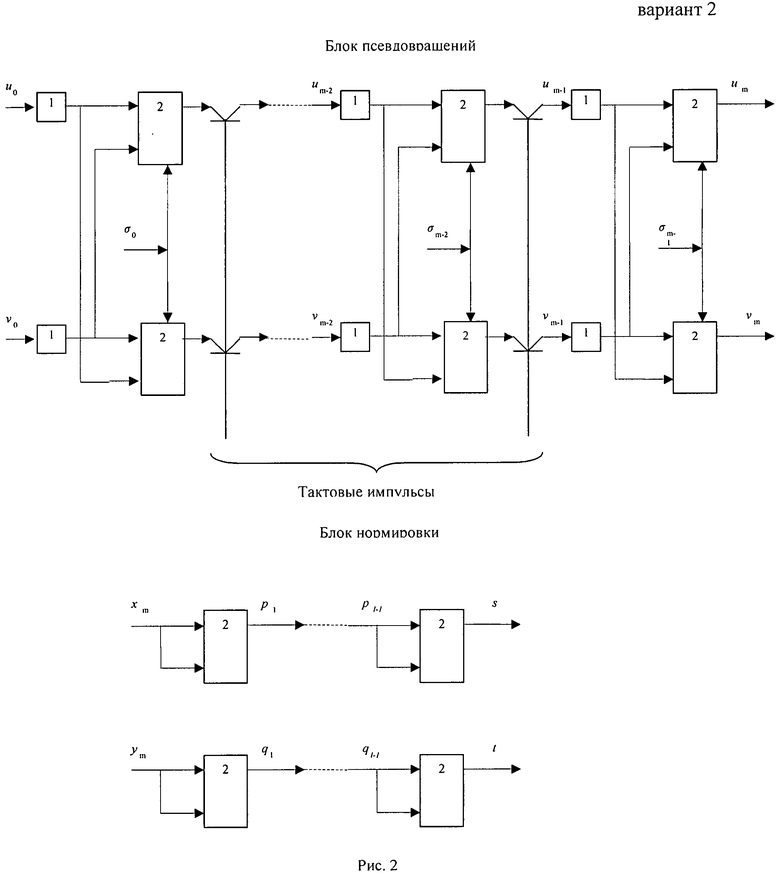
Второй вариант устройства (рис.2) предназначен для вращения произвольного вектора (u,v) на угол φ, код которого α формируется в устройстве первого варианта. На вход устройства второго варианта подаются числа u и v - компоненты двумерного вектора (u,v) и код α угла φ, на который он должен поворачиваться. На выходе получаются числа s и t, связанные с u, v и φ соотношениями:
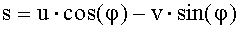 ,
,
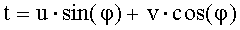 .
.
Блок псевдовращений также представляет собой m-каскадный конвейер, но в отличие от первого варианта не имеет схем 3. Блок нормировки состоит из двух идентичных параллельных шестизвенных цепочек каскадов, соединенных как показано на рис.2, при этом каждый каскад содержит сумматор (вычитатель) 2, или же регистр 1 и сумматор (вычитатель) 2, как показано на рис.3, если он выполнен в виде двух конвейеров.
Оба варианта устройства вращения вектора спроектированы для чисел в формате как с фиксированной, так и плавающей запятой.
В первом случае x, y, u, v, z, s, t - m-разрядные числа (m=24), во втором - тридцатидвухразрядные числа с m-разрядной мантиссой (m=24) и p-разрядным порядком (p=8). В обоих случаях угол поворота представляется (m-2)-разрядным кодом.
Для обеспечения точности выходных величин z, s, t вычисления осуществлялись на (m+r)-разрядных сумматорах. При r=5 погрешность вычисления выходных величин не превышает цены младшего разряда.
Для обеспечения сходимости процесса вычислений понадобилось 54 сумматора (2*24 на псевдовращения и 6 на нормировку (l=6)), соответственно 29*54 элементарных сумматоров в первом варианте. Во втором варианте потребовалось 60 сумматоров (2*24 на псевдовращения и 12 на нормировку), соответственно 29*60 элементарных сумматоров.
Проекты устройств были аппаратно реализованы на программируемых логических интегральных схемах (ПЛИС) семейства АСЕХ1К производства фирмы "Altera": соответственно на "EP1K50QC208-1" для чисел в формате с фиксированной запятой и на "EP1K100FC256-1" для чисел в формате с плавающей запятой.
Стоимость интегральной схемы s зависит от количества вентилей v, содержащихся в ней. Пусть функция s=f(v) описывает эту зависимость. Известно, что f(v) - выпуклая монотонно возрастающая функция.
Заявляемое устройство содержит приблизительно в 1.6  раза меньшее количество вентилей, чем прототип Cordic, следовательно, оно более чем 1.6 раза дешевле второго прототипа.
раза меньшее количество вентилей, чем прототип Cordic, следовательно, оно более чем 1.6 раза дешевле второго прототипа.
Сравним быстродействие заявляемого устройства и рассмотренного прототипа.
Введем обозначения: tп - время задержки сигнала переноса элементарного сумматора, tc - время задержки сигнала суммы элементарного сумматора, tпр, tз - продолжительности тактов прототипа и заявляемого устройства. Конвейер прототипа имеет m каскадов, поэтому время прохождения данных по конвейеру прототипа выразится формулой Тпр=mtпр, заявляемое устройство - 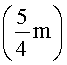 , поэтому время прохождения данных по конвейеру заявляемого устройства выразится формулой
, поэтому время прохождения данных по конвейеру заявляемого устройства выразится формулой
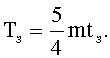
Учитывая, что tпр≈2tз, получим
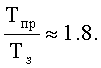
Таким образом, быстродействие заявляемого устройства приблизительно в 1.8 раза выше, чем у рассмотренного прототипа.
Источники информации
1. Попов Б.А., Теслер Г.С. Вычисление функций на ЭВМ. - Киев: Наукова думка, 1984.
2. Сверхбольшие интегральные схемы и современная обработка сигналов. Под ред. С. Гуна, X. Уайтхауса, Т. Кайлата. М.: Радио и связь, 1989, стр.382-391, 287-294.
| название | год | авторы | номер документа |
|---|---|---|---|
| УСТРОЙСТВО НОРМИРОВКИ ВЕКТОРА | 2010 |
|
RU2449354C1 |
| УСТРОЙСТВО НОРМИРОВКИ ВЕКТОРА | 2011 |
|
RU2473961C1 |
| АСИНХРОННОЕ УСТРОЙСТВО ВЕКТОРНОГО ПОВОРОТА | 2017 |
|
RU2683182C1 |
| ЦИФРОВОЙ КОМПЕНСАТОР ПАССИВНЫХ ПОМЕХ | 1994 |
|
RU2087000C1 |
| Устройство для обнаружения и исправления ошибок в интервально-модулярном коде | 1988 |
|
SU1541784A1 |
| УСТРОЙСТВО ДЛЯ ВЫЧИСЛЕНИЯ МОДУЛЯ M-МЕРНОГО ВЕКТОРА | 1992 |
|
RU2029356C1 |
| Устройство для обнаружения и исправления ошибок | 1988 |
|
SU1695512A1 |
| Цифровой функциональный преобразователь | 1980 |
|
SU955082A1 |
| Устройство для сложения чисел в модулярной системе счисления | 1989 |
|
SU1672448A1 |
| УСТРОЙСТВО КОРРЕКЦИИ ОШИБКИ ПРЕОБРАЗОВАТЕЛЕЙ УГЛА В КОД | 2020 |
|
RU2740511C1 |
Изобретения относятся к вычислительной технике и предназначены для использования в высокопроизводительных вычислительных системах, в частности в системах цифровой обработки сигналов, работающих в режиме реального времени, в системах управления скоротечными процессами, в качестве средства повышения производительности персональных компьютеров при решении задач, связанных с упрощением вида матриц систем линейных уравнений (алгебраических и дифференциальных), реализуемого как подсхема в составе арифметического процессора или же в составе отдельного устройства (спецпроцессора). Техническим результатом является уменьшение количества сумматоров, требующихся для нормировки, и повышение производительности. В одном из вариантов устройство содержит блок псевдовращений и блок нормировки, на вход подаются компоненты двумерного вектора, на выходах получают первую (ненулевую) компоненту результирующего вектора и код угла поворота, при этом вход блока нормировки соединен с выходом блока псевдовращений и представляет собой шестизвенную цепочку каскадов, в которой выход предыдущего каскада соединен с входом последующего, при этом в каждый каскад наряду с вычитателем (сумматором) входит регистр, вход регистра является входом каскада, выход регистра соединен с первым входом вычитателя (сумматора), а выход вычитателя (сумматора) является выходом каскада. 2 н.п. ф-лы, 3 ил.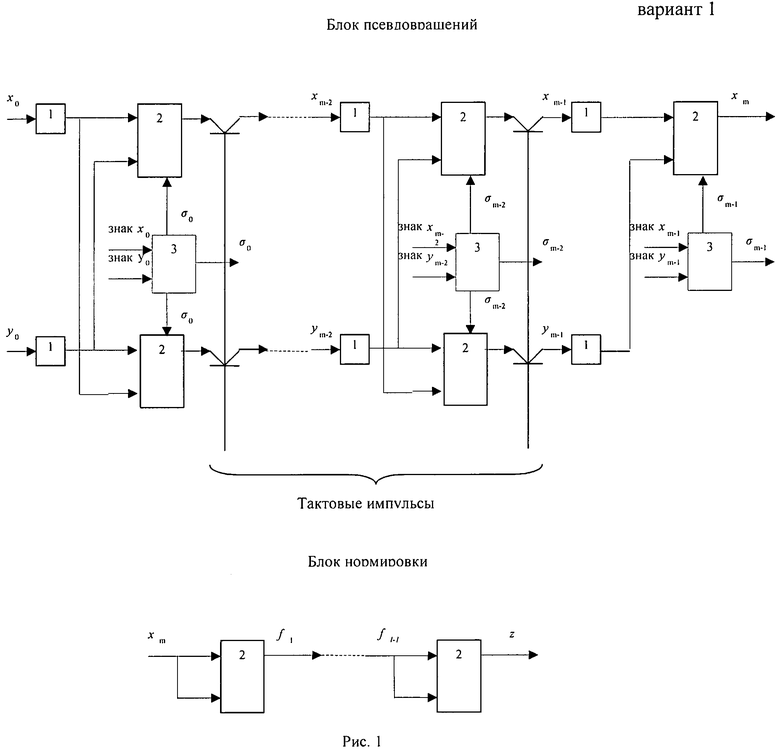
1. Устройство вращения вектора, содержащее блок псевдовращений и блок нормировки, на вход которого подаются компоненты двумерного вектора, на выходах получают: 1) первую (ненулевую) компоненту результирующего вектора (нулевая компонента не выводится), 2) код угла поворота (значения величин σi=sign(xiyi), i=0, m-1, (вариант 1)), при этом вход блока нормировки соединен с выходом блока псевдовращений, отличающееся тем, что в составе цепочки каскадов блока нормировки имеются каскады, содержащие сумматоры наряду с каскадами, содержащими вычитатели, при этом блок нормировки представляет собой шестизвенную цепочку каскадов, в которой выход предыдущего каскада соединен с входом последующего, при этом в каждый каскад наряду с вычитателем (сумматором) входит регистр, причем в каждом каскаде вход регистра является входом каскада, выход регистра соединен с первым входом вычитателя (сумматора), а выход вычитателя (сумматора) является выходом каскада, при этом в первом каскаде цепочки k-й бит первого входа вычитателя соединен с k+1-м битом второго входа (δ0=-1, k0=1, k=1, m-1), а 1-й бит второго входа устанавливается в ноль, во втором каскаде k-й бит первого входа сумматора соединен с k+2-м битом второго входа (δ1=1, k1=2, k=1, m=2), а биты второго входа с 1-го по 2-й устанавливаются в ноль, на третьем каскаде цепочки k-й бит первого входа вычитателя соединен с k+5-м битом второго входа (δ2=-1, k2=5, k=1, m-5), а биты второго входа с 1-го по 5-й устанавливаются в ноль, на четвертом каскаде k-й бит первого входа сумматора соединен с k+9-м битом второго входа (δ3=1, k3=9, k=1, m-9), а биты второго входа с 1-го по 9-й устанавливаются в ноль, на пятом каскаде k-й бит первого входа сумматора соединен с k+10-м битом второго входа (δ4=1, k4=10, k=1, m-10), а биты второго входа с 1-го по 10-й устанавливаются в ноль, на шестом каскаде k-й бит первого входа сумматора соединен с k+16-м битом второго входа (δ5=1, k5=16, k=1, m-16), а биты второго входа с 1-го по 16-й устанавливаются в ноль.
2. Устройство вращения вектора, содержащее блок псевдовращений и блок нормировки, на входы которого подаются компоненты двумерного вектора (первый вход) и код угла поворота (значения величин σi=sign(xiyi), i=0, m-1 (второй вход)), на выходе получают двухкомпонентный вектор - результат поворота входного вектора на угол, код которого поступил на второй вход устройства вращения вектора (вариант 2), при этом вход блока нормировки соединен с выходом блока псевдовращений, отличающееся тем, что в составе цепочек каскадов блока нормировки имеются каскады, содержащие сумматоры наряду с каскадами, содержащими вычитатели, при этом блок нормировки представляет собой две идентичные параллельные шестизвенные цепочки каскадов, в которых выход предыдущего каскада соединен с входом последующего, при этом в каждый каскад наряду с вычитателем (сумматором) входит регистр, причем в каждом каскаде вход регистра является входом каскада, выход регистра соединен с первым входом вычитателя (сумматора), а выход вычитателя (сумматора) является выходом каскада, при этом в первом каскаде цепочки k-й бит первого входа вычитателя соединен с k+1-м битом второго входа (δ0=-1, k0=1, k=1, m-1), а 1-й бит второго входа устанавливается в ноль, во втором каскаде k-й бит первого входа сумматора соединен с k+2-м битом второго входа (δ1=1, k1=2, k=1, m-2), а биты второго входа с 1-го по 2-й устанавливаются в ноль, на третьем каскаде цепочки k-й бит первого входа вычитателя соединен с k+5-м битом второго входа (δ2=-1, k2=5, k=1, m-5), а биты второго входа с 1-го по 5-й устанавливаются в ноль, на четвертом каскаде k-й бит первого входа сумматора соединен с k+9-м битом второго входа (δ3=1, k3=9, k=1, m-9), а биты второго входа с 1-го по 9-й устанавливаются в ноль, на пятом каскаде k-й бит первого входа сумматора соединен с k+10-м битом второго входа (δ4=1, k4=10, k=1, m-10), а биты второго входа с 1-го по 10-й устанавливаются в ноль, на шестом каскаде k-й бит первого входа сумматора соединен с k+16-м битом второго входа (δ5=1, k5=16, k=1, m-16), а биты второго входа с 1-го по 16-й устанавливаются в ноль.
| С.ГУН и др | |||
| Сверхбольшие интегральные схемы и современная обработка сигналов | |||
| - М.: Радио и связь, 1989, с.269-272, 287-294 | |||
| Устройство для поворота вектора с коррекцией | 1980 |
|
SU951299A1 |
| Конвейерное вычислительное устройство | 1987 |
|
SU1432512A1 |
| ИНТЕГРАТОР ТОКА | 1973 |
|
SU453641A1 |
| US 7606852 B2, 20.10.2009. | |||
Авторы
Даты
2013-02-20—Публикация
2010-08-13—Подача