Изобретение относится к вычислительной технике и предназначено для построения быстродействующих параллельно-конвейерных делителей, обрабатывающих массивы положительных целых чисел.
Известен итерационный способ деления целых чисел с плавающей запятой. В этом способе деление сводится к последовательности вычитаний с восстановлением остатка либо без восстановления остатка, которые выполняются последовательно (http.//wwvv.distedu.ru/mirror/_inform/dmivic.chat.ru/inform/div.html) со старших разрядов делимого. Недостаток состоит в том, что, во-первых, при итерационном способе умножения чисел выполняется m-1 операций вычитания, а с учетом последовательного способа переносов в старшие разряды - количество тактов суммирования равно (m-1)·2·m. Во-вторых, процесс формирования суммы является последовательным процессом.
Техническим результатом от использования способа деления целых двоичных чисел без остатка является повышение скорости вычисления за счет замены серии из m-1 арифметических операций вычитания m-разрядных чисел (m-1) операциями подсчета количества единичных бит в разрядных срезах, формируемых из разрядов делителя. На основании анализа и модификации полученных значений сумм количества единиц во всех разрядных срезах выполняется формирование значения двоичного числа, являющегося значением искомого частного. В результате количество тактов, необходимых для формирования значения частного целых двоичных чисел, будет равно 2·(log2m)·m тактов. Таким образом, предлагаемый способ обеспечивает выполнение операции формирования произведения быстрее известного итерационного способа в ((m-1) ·2·m)/((log2m)·2·m)=(m-1)/log2m раз. Например, при m=64 вычисления будут выполняться в 8 раз быстрее.
Описание работы устройства: делитель можно представить в виде последовательности бит A(am, am-1, …, a2, a1), где m - разрядность делителя.
Происходит параллельная запись делителя в ячейки матрицы на элементах памяти, размерность матрицы составляет m столбцов и m строк, где m - разрядность как делителя, так и частного, причем в ячейки с 1 по m первой строки матрицы записывается m-разрядный делитель, в ячейки с 2 по m второй строки матрицы записываются m-1 младших разрядов делителя, …, в ячейки с k по m k-й строки матрицы записывается m-k младших разрядов делителя, …, в m-ю ячейку m-й строки матрицы записывается младший разряд делителя.
Во все остальные ячейки матрицы записываются нули, в общем виде размещение множимого в ячейках матрицы на элементах памяти выглядит следующим образом:

После чего первый разряд частного становится равным сумме по модулю два младшего разряда первого столбца матрицы и первого разряда делимого, остальные разряды частного становятся равными нулю;
затем подсчитывается количество единиц b2 в векторе, равном поразрядному логическому умножению соответствующих разрядов второго столбца матрицы и разрядов частного, при этом второй разряд частного становится равным сумме по модулю два младшего разряда b2 и второго разряда делимого;
затем подсчитывается количество единиц b3 в векторе, который равен поразрядному логическому умножению соответствующих разрядов третьего столбца матрицы и разрядов частного, после чего вычисляется сумма c3 вектора b3 и вектора b2, сдвинутого на один разряд вправо, при этом третий разряд частного становится равным сумме по модулю два младшего разряда c3 и третьего разряда делимого;
и так далее вычисления продолжаются аналогичным образом, подсчитывается количество единиц bk в векторе, который равен поразрядному логическому умножению соответствующих разрядов k-го столбца матрицы и разрядов частного, после чего вычисляется сумма ck вектора bk и вектора ck-1, сдвинутого на один разряд вправо, при этом k-й разряд частного становится равным сумме по модулю два младшего разряда ck и k-го разряда делимого;
затем подсчитывается количество единиц bk+1 в векторе, который равен логическому умножению соответствующих разрядов (k+1)-го столбца матрицы и разрядов частного, после чего вычисляется сумма Ck+1 вектора bk+1 и вектора ck, сдвинутого на один разряд вправо, при этом (k+1)-й разряд частного становится равным сумме по модулю два младшего разряда ck+1 и (k+1)-го разряда делимого;
и так далее вычисления продолжаются аналогичным образом, подсчитывается количество единиц bm в векторе, который равен логическому умножению соответствующих разрядов m-го столбца матрицы и разрядов частного, после чего вычисляется сумма cm вектора bm и вектора cm-1, сдвинутого на один разряд вправо, при этом m-й разряд частного становится равным сумме по модулю два младшего разряда cm и m-го разряда делимого;
в итоге будет сформировано m-разрядное частное исходных чисел.
Пример: необходимо разделить делимое a1=110111 на делитель a2=1011 (m=4). Запишем делитель в виде матрицы размерностью m=4 строк и m=4 столбцов, в ячейки с 1 по m=4 первой строки записывается делитель. В ячейки с 2 по m=4 второй строки записывается m-1=3 младших разрядов делителя. В ячейки с 3 по m-1=4 третьей строки записывается m-2=2 младших разрядов делителя. В четвертую ячейку четвертой строки записывается младший разряд делителя. Во все остальные ячейки матрицы записываются нули:
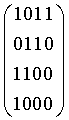
Первый разряд частного d1=l становится равным инверсии суммы по модулю два младшего разряда первого столбца матрицы и первого разряда делимого, остальные разряды частного становятся равными нулю;
затем подсчитывается количество единиц b2=1 в векторе f2=(0011)&(0001)=0001, равном поразрядному логическому умножению соответствующих разрядов второго столбца матрицы и разрядов частного, при этом второй разряд частного d2=l⊕l=0 становится равным сумме по модулю два младшего разряда b2 и второго разряда делимого;
затем подсчитывается количество единиц b3=0 в векторе f3=(0110)&(0001)-0000, который равен поразрядному логическому умножению соответствующих разрядов третьего столбца матрицы и разрядов частного, после чего вычисляется сумма c3=0+0=0 вектора b3=0 и вектора b2=0, сдвинутого на один разряд вправо, при этом третий разряд частного d3=0⊕l=l становится равным сумме по модулю два младшего разряда c3 и третьего разряда делимого;
затем подсчитывается количество единиц b4=10 в векторе f3=(1101)&(0101)-0101, который равен поразрядному логическому умножению соответствующих разрядов четвертого столбца матрицы и разрядов частного, после чего вычисляется сумма С4=10+0=10 вектора b4=10 и вектора c3=0, сдвинутого на один разряд вправо, при этом четвертый разряд частного d4=0⊕0=0 становится равным сумме по модулю два младшего разряда c4 и четвертого разряда делимого.
Таким образом, сформировано частное d=0101.
Если принять за время сложения пары m-разрядных чисел m тактов работы устройства, а за время подсчета единичных бит в m-разрядном векторе log2m тактов, то время вычисления частного в устройстве на базе описанного способа равно 2·p·m тактов, где p=log2m, в то время как время деления итерационным способом равно 2·(m-1)·m тактов. Таким образом, быстродействие устройства на базе описанного способа в (m-1)/log2m раз выше по сравнению с быстродействием устройства на базе известного итерационного способа умножения.
Примером построения устройства на базе способа деления целых двоичных чисел без остатка может служить ее программирование на программируемых логических интегральных схемах (ПЛИС).
На фиг.1 представлен вариант структурной схемы устройства, реализующего операцию вычисления произведения остатков по основанию в общем виде, где 1 - счетчик единичных бит в двоичных векторах, 2 - p-разрядный двухплечевой сумматор, где p=log2n, 3 - сдвиговый p-разрядный регистр, a1-an - m-разрядные информационные входы схемы, s1-Sm - одноразрядные информационные выходы схемы, b1-bm - p-разрядные выходы счетчиков 1, 
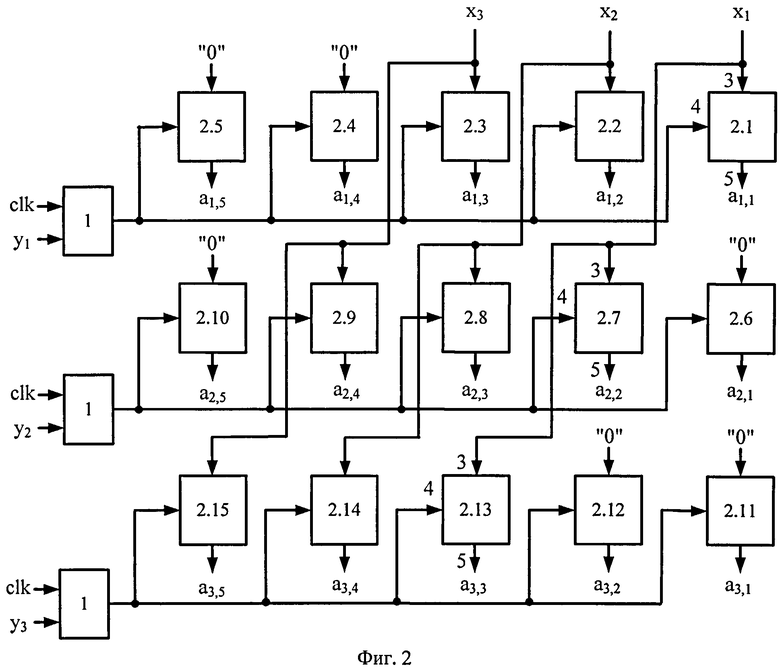
На фиг.2 представлен вариант структурной схемы матрицы на элементах памяти для трехбитного остатка (m=3), где 1 - логический элемент И, 2 - информационный триггер с одним входом данных, одним входом синхронизации и одним выходом данных, 3 - информационный вход триггера, 4 - вход синхронизации триггера, 5 -информационный выход триггера, x1-x3 - входы схемы, на которые подается остаток множимого по трехбитному основанию, yi-y3 - входы схемы, на которые подается остаток множителя по трехбитному основанию, aij - выходы матрицы на элементах памяти.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОРГАНИЗАЦИИ УМНОЖЕНИЯ ЧИСЕЛ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2012 |
|
RU2500018C1 |
| СПОСОБ ОРГАНИЗАЦИИ УМНОЖЕНИЯ ЧИСЕЛ С ПЛАВАЮЩЕЙ ЗАПЯТОЙ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2012 |
|
RU2485574C1 |
| Матричное вычислительное устройство | 1982 |
|
SU1034032A1 |
| Матричное устройство для деления | 1985 |
|
SU1247863A1 |
| Устройство для деления | 1985 |
|
SU1282117A1 |
| Матричное вычислительное устройство | 1988 |
|
SU1541599A1 |
| МАТРИЧНОЕ УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ И ДЕЛЕНИЯ | 1991 |
|
RU2018932C1 |
| Устройство для возведения в квадрат,извлечения квадратного корня,умножения и деления | 1981 |
|
SU1059571A1 |
| Устройство для деления | 1988 |
|
SU1681303A1 |
| Многофункциональное вычислительное устройство | 1985 |
|
SU1293727A1 |
Изобретение относится к вычислительной технике и предназначено для построения быстродействующих параллельно-конвейерных делителей, обрабатывающих массивы положительных целых чисел. Техническим результатом является повышение скорости вычисления. Способ содержит этапы, на которых происходит параллельная запись делителя в ячейки матрицы на элементах памяти, первый разряд частного становится равным сумме по модулю два младшего разряда первого столбца матрицы и первого разряда делимого, остальные разряды частного становятся равными нулю; подсчитывается количество единиц b2 в векторе, равном поразрядному логическому умножению соответствующих разрядов второго столбца матрицы и разрядов частного, при этом второй разряд частного становится равным сумме по модулю два младшего разряда b2 и второго разряда делимого; аналогично подсчитывается количество единиц bi в векторе, который равен поразрядному логическому умножению соответствующих разрядов i-го столбца матрицы и разрядов частного, после чего вычисляется сумма ci вектора bi и вектора bi-1, сдвинутого на один разряд вправо, при этом i-й разряд частного становится равным сумме по модулю два младшего разряда сi и i-го разряда делимого, в итоге будет сформировано m-разрядное частное исходных чисел. 2 ил.
Способ деления целых двоичных чисел без остатка, начиная с младших разрядов, заключающийся в том, что в умножающем устройстве:
происходит параллельная запись делителя в ячейки матрицы на элементах памяти, размерность матрицы составляет m столбцов и m строк, где m - разрядность как делителя, так и частного, причем
в ячейки с 1 по m первой строки матрицы записывается m-разрядный делитель,
в ячейки с 2 по m второй строки матрицы записываются m-1 младших разрядов делителя, …, в ячейки с k по m k-й строки матрицы записывается m-k младших разрядов делителя, …, в m-ю ячейку m-й строки матрицы записывается младший разряд делителя, во все остальные ячейки матрицы записываются нули; затем первый разряд частного становится равным сумме по модулю два младшего разряда первого столбца матрицы и первого разряда делимого, остальные разряды частного становятся равными нулю;
затем подсчитывается количество единиц b2 в векторе, равном поразрядному логическому умножению соответствующих разрядов второго столбца матрицы и разрядов частного, при этом второй разряд частного становится равным сумме по модулю два младшего разряда b2 и второго разряда делимого;
затем подсчитывается количество единиц b3 в векторе, который равен поразрядному логическому умножению соответствующих разрядов третьего столбца матрицы и разрядов частного, после чего вычисляется сумма c3 вектора b3 и вектора b2, сдвинутого на один разряд вправо, при этом третий разряд частного становится равным сумме по модулю два младшего разряда с3 и третьего разряда делимого;
и так далее вычисления продолжаются аналогичным образом, подсчитывается количество единиц bk в векторе, который равен поразрядному логическому умножению соответствующих разрядов k-го столбца матрицы и разрядов частного, после чего вычисляется сумма ck вектора bk и вектора ck-1, сдвинутого на один разряд вправо, при этом k-й разряд частного становится равным сумме по модулю два младшего разряда ck и k-го разряда делимого;
затем подсчитывается количество единиц bk+1 в векторе, который равен логическому умножению соответствующих разрядов (k+1)-го столбца матрицы и разрядов частного, после чего вычисляется сумма ck+1 вектора bk+1 и вектора ck, сдвинутого на один разряд вправо, при этом (k+1)-й разряд частного становится равным сумме по модулю два младшего разряда ck+1 и (k+1)-го разряда делимого;
и так далее вычисления продолжаются аналогичным образом, подсчитывается количество единиц bm в векторе, который равен логическому умножению соответствующих разрядов m-го столбца матрицы и разрядов частного, после чего вычисляется сумма cm вектора bm и вектора cm-1, сдвинутого на один разряд вправо, при этом m-й разряд частного становится равным сумме по модулю два младшего разряда cm и m-го разряда делимого;
в итоге будет сформировано m-разрядное частное исходных чисел.
| RU 2006143196 A, 20.06.2008 | |||
| МАТРИЧНОЕ УСТРОЙСТВО ДЛЯ УМНОЖЕНИЯ И ДЕЛЕНИЯ | 1991 |
|
RU2018932C1 |
| Матричное устройство для деления | 1985 |
|
SU1247863A1 |
| Устройство для подсчета количества единиц в двоичном числе | 1990 |
|
SU1751749A1 |
| Блок предсказания четности результата арифметико-логического устройства | 1977 |
|
SU684548A1 |
| СУЖАЮЩЕЕСЯ АБСОРБИРУЮЩЕЕ ИЗДЕЛИЕ С БОКОВЫМИ ТЕЛАМИ | 2001 |
|
RU2270648C2 |
| US 6625633 B1, 23.09.2003. | |||
Авторы
Даты
2013-11-10—Публикация
2012-07-27—Подача