Текст описания приведен в факсимильном виде.











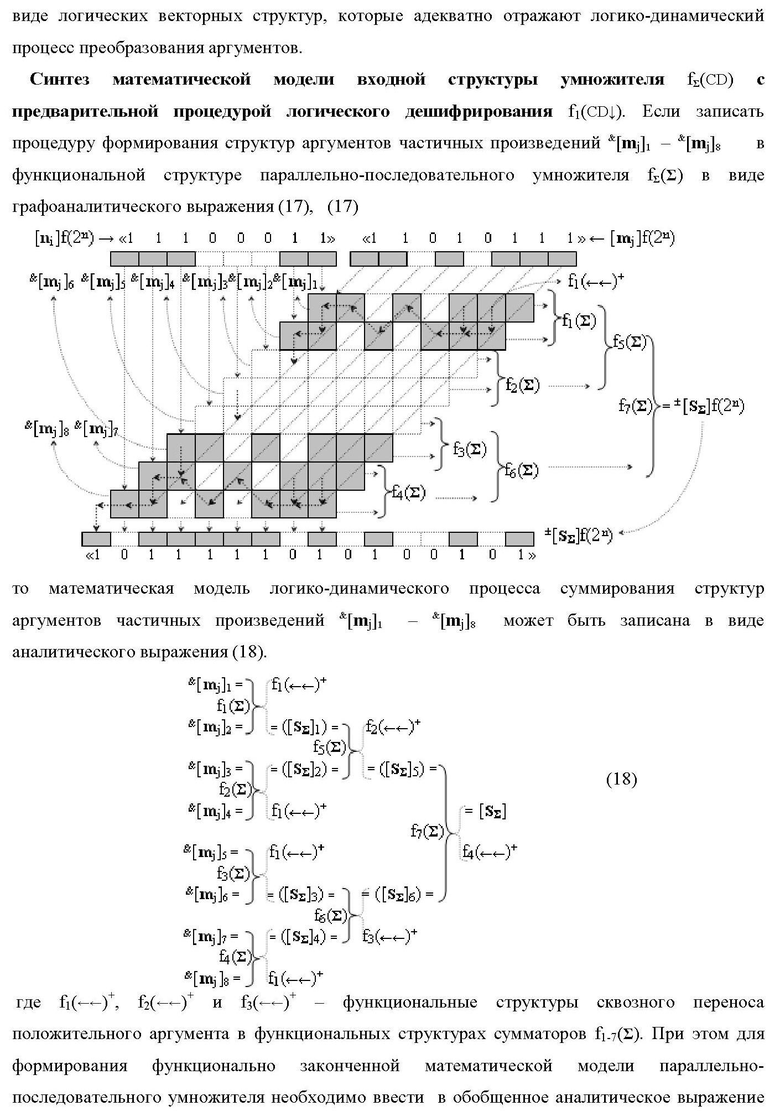



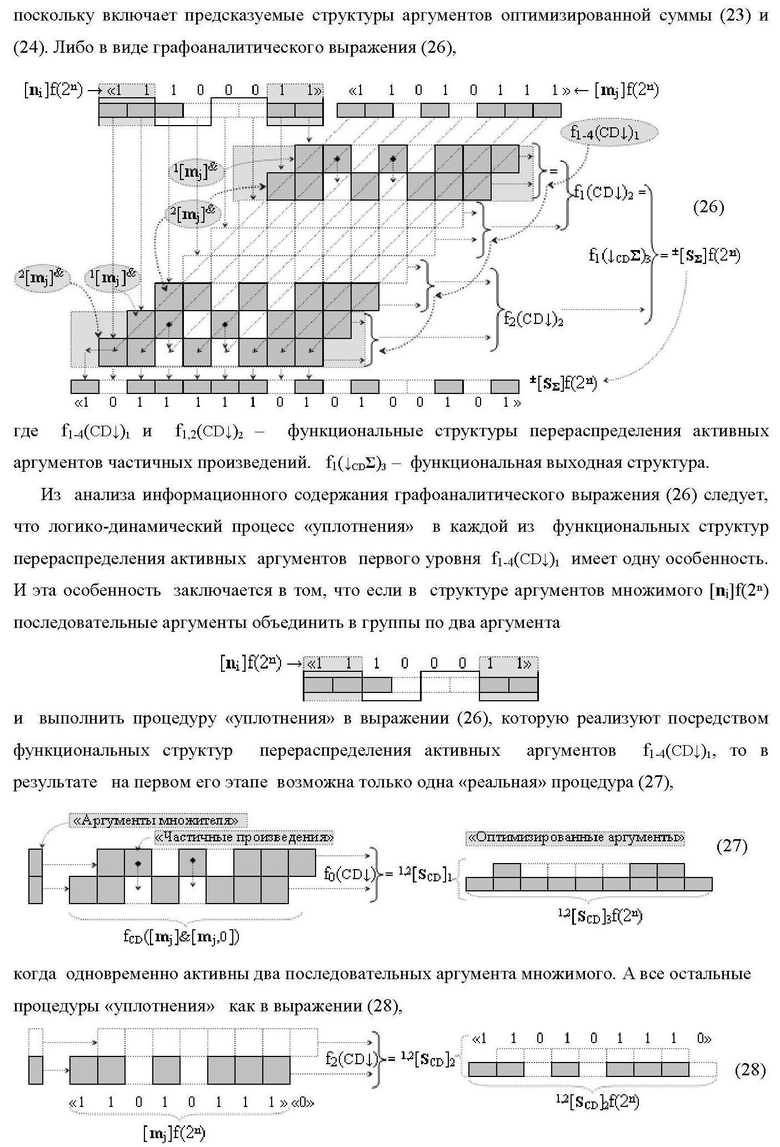












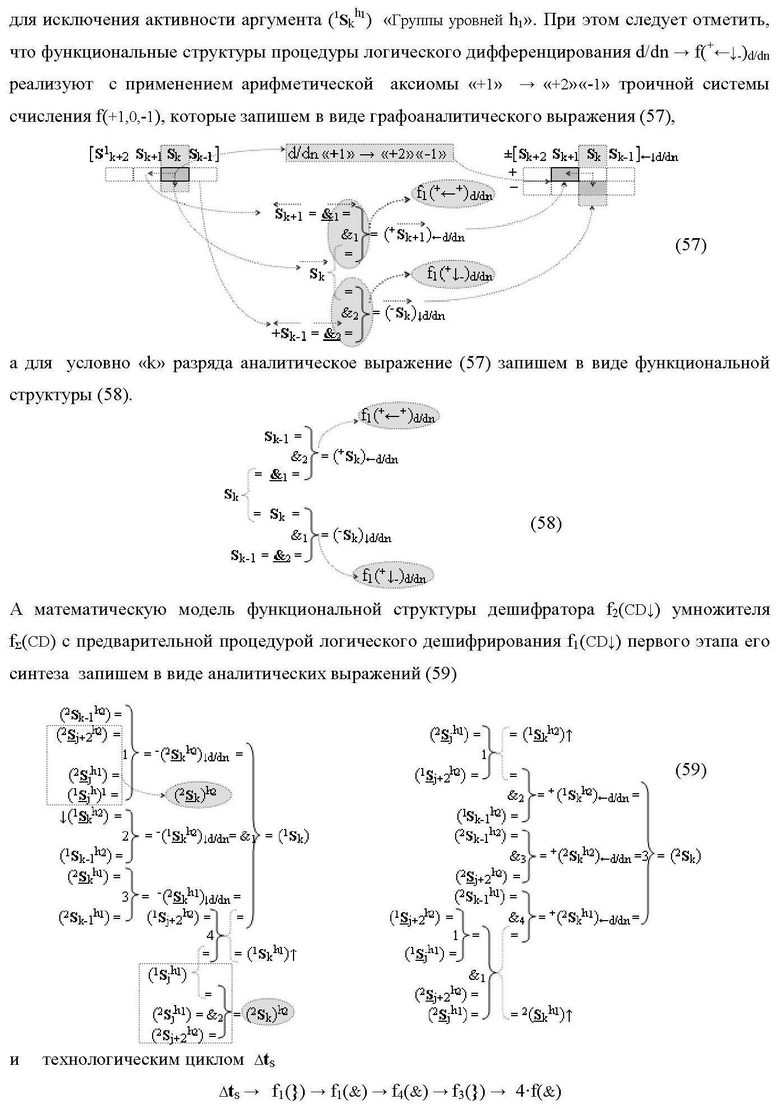
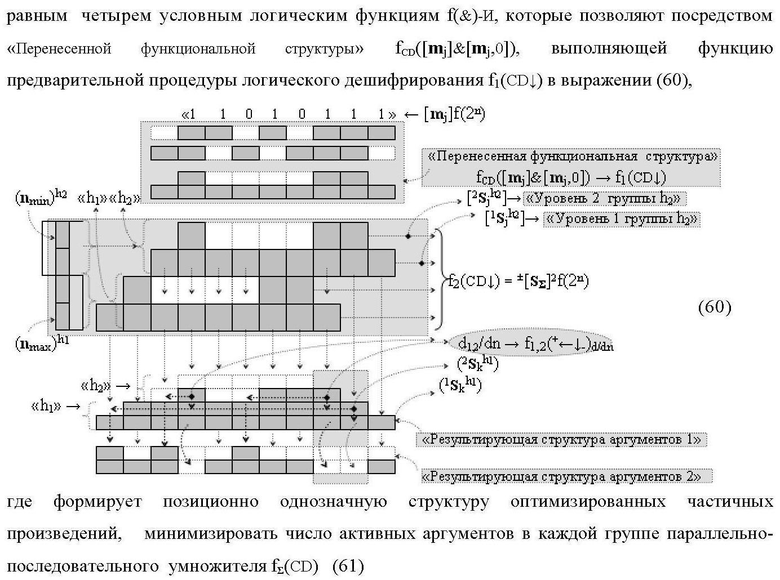

























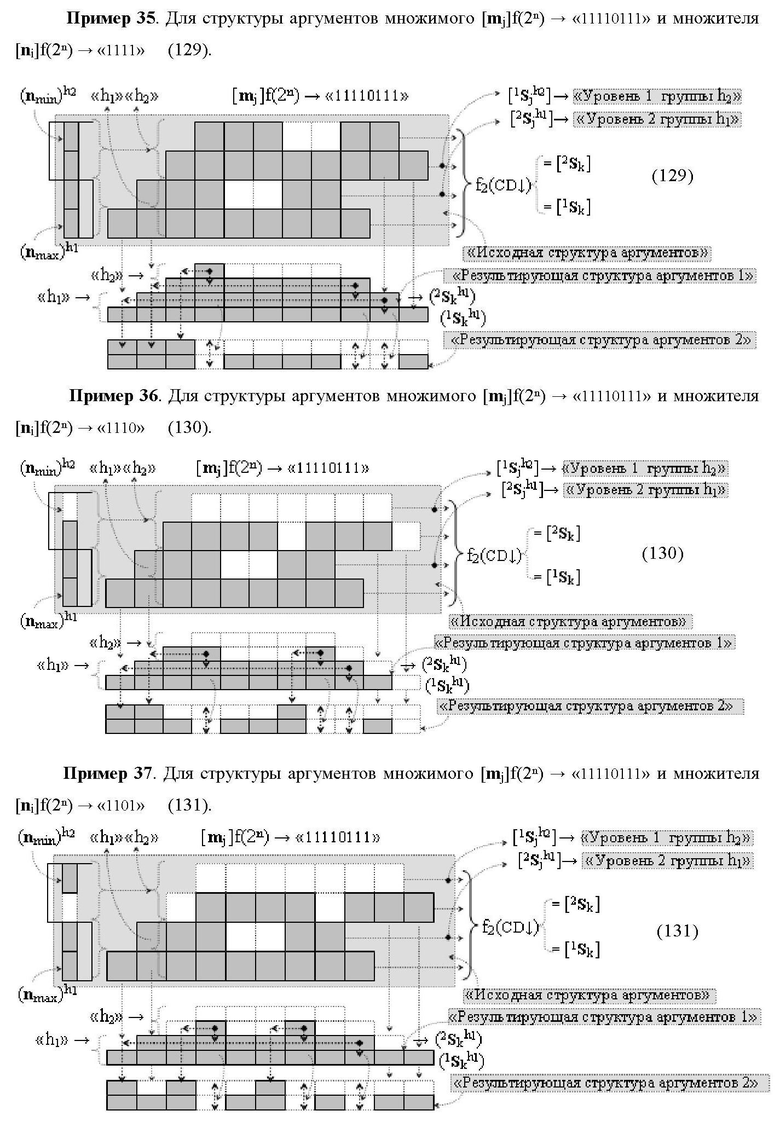














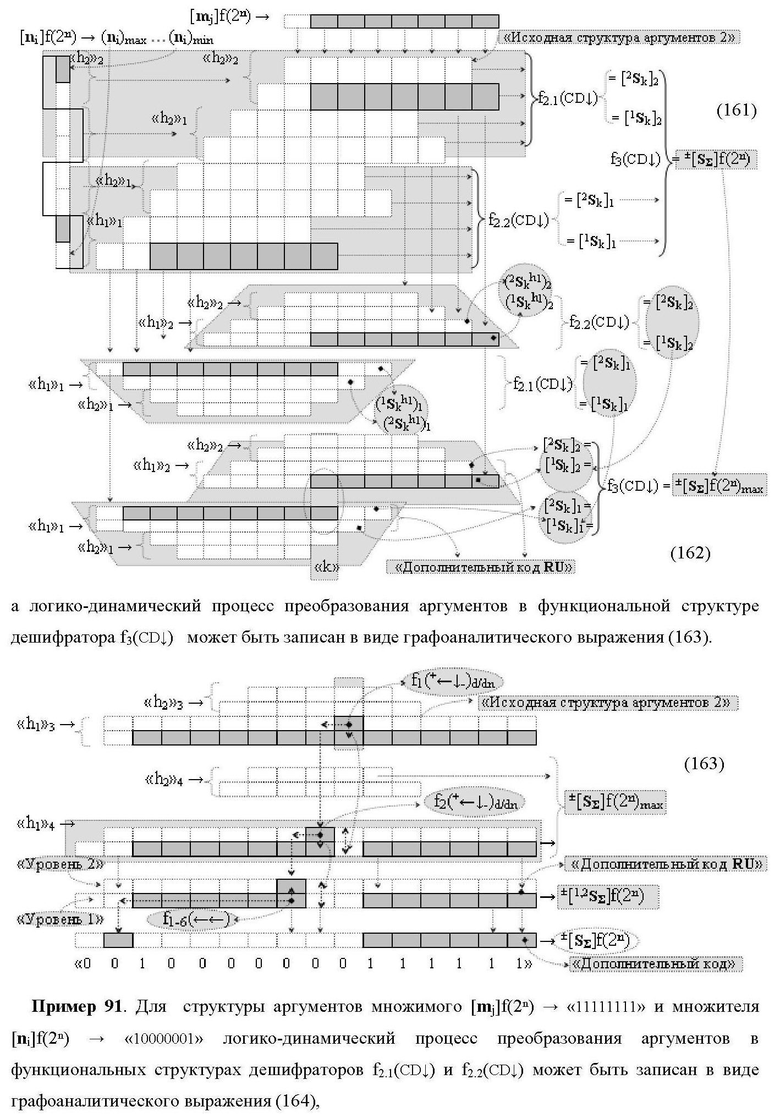


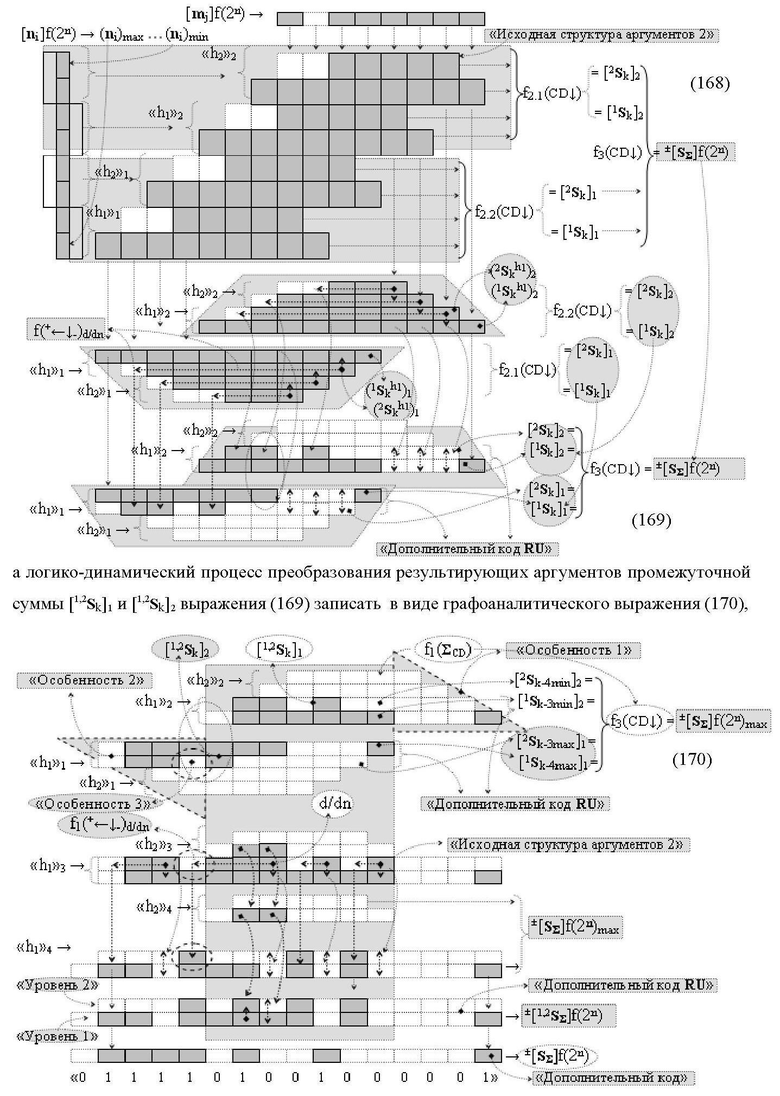

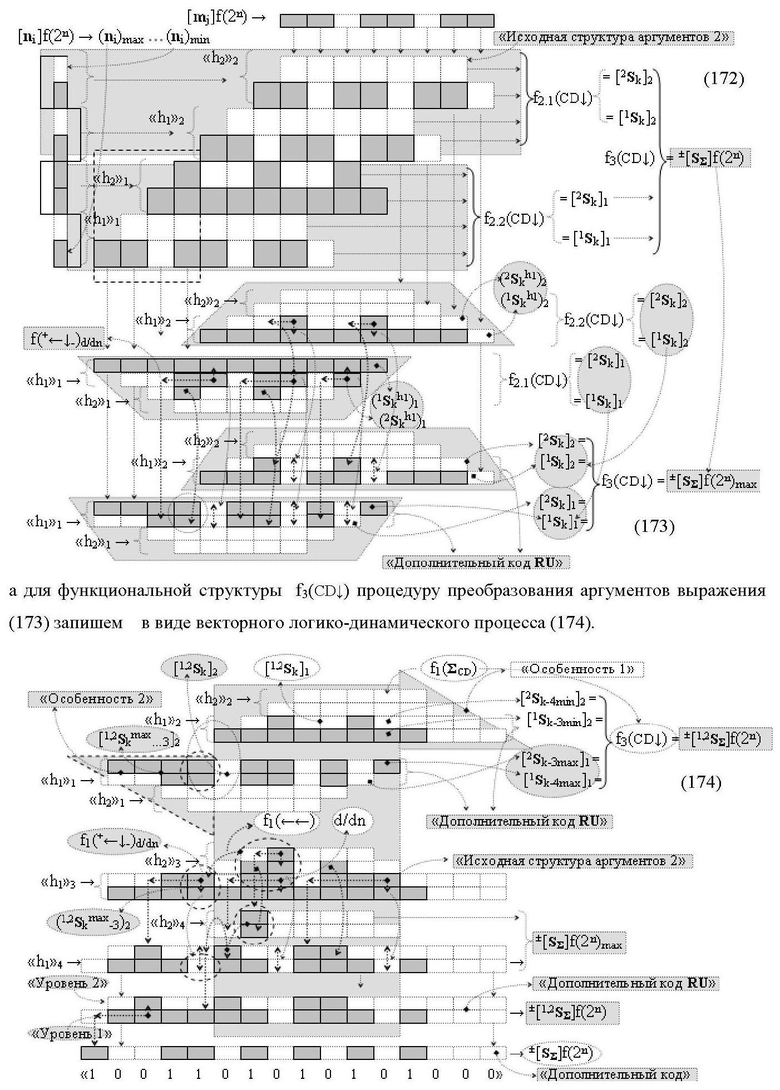






































Изобретения относятся к вычислительной технике и могут быть использованы при реализации арифметических устройств параллельно-последовательного умножителя. Техническим результатом является повышение быстродействия. В одном из вариантов функциональная структура реализована с использованием логических элементов И, ИЛИ. 2 н.п. ф-лы.
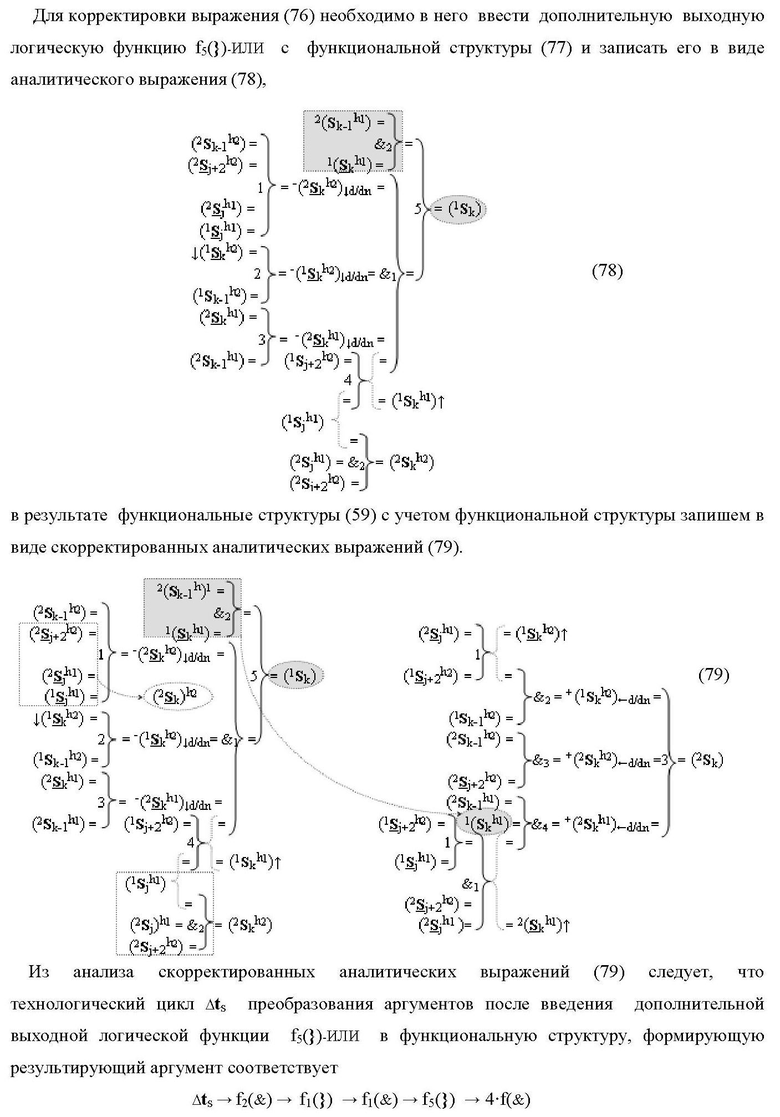
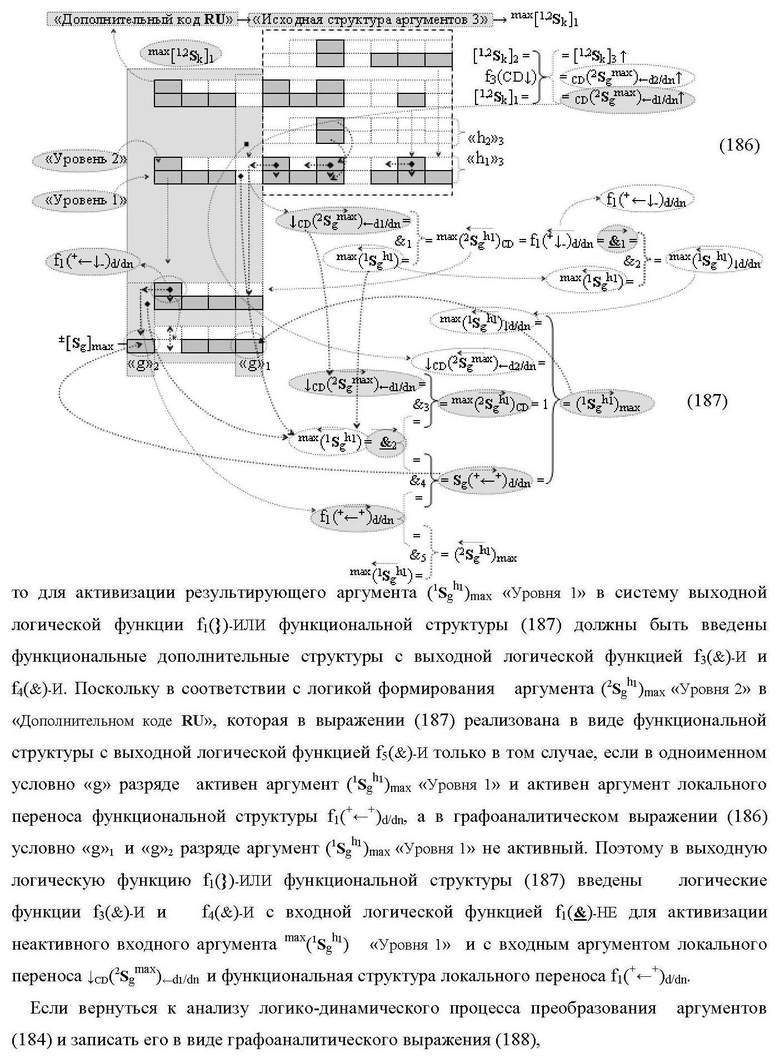
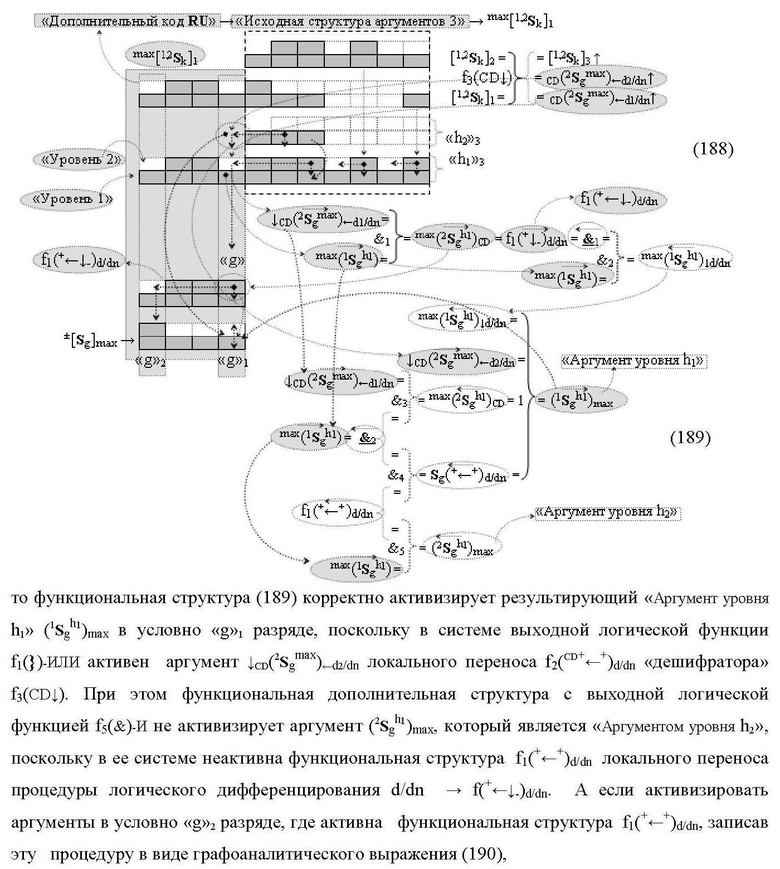
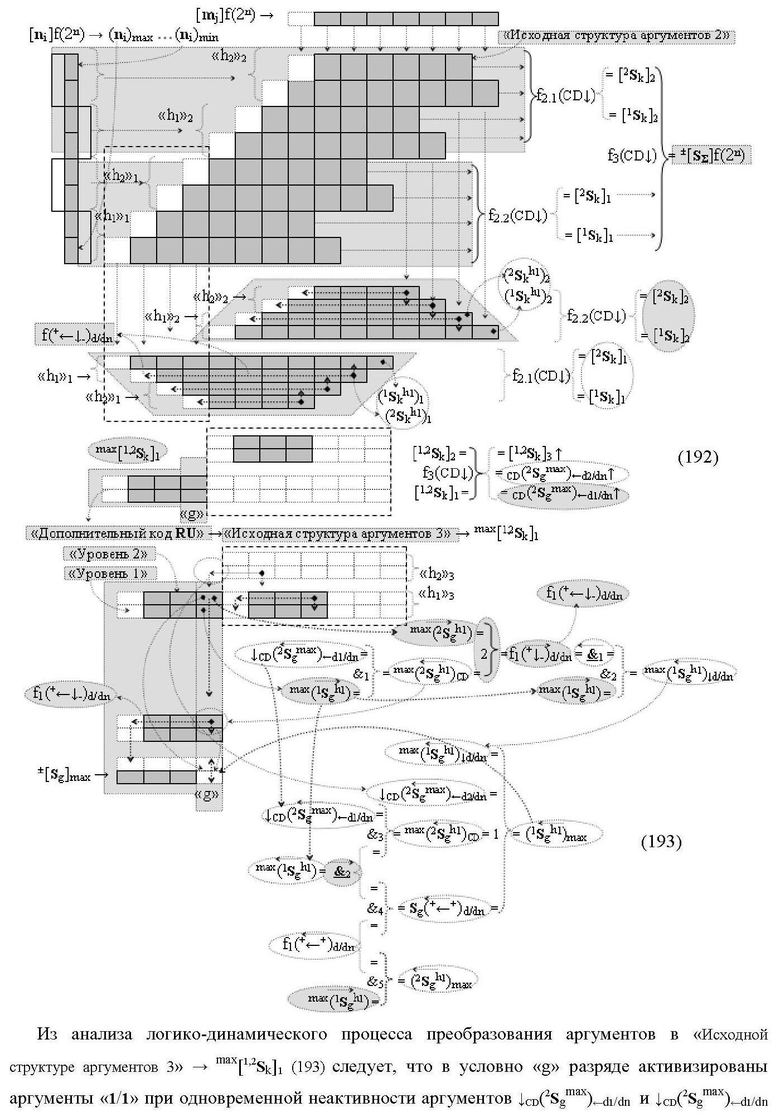
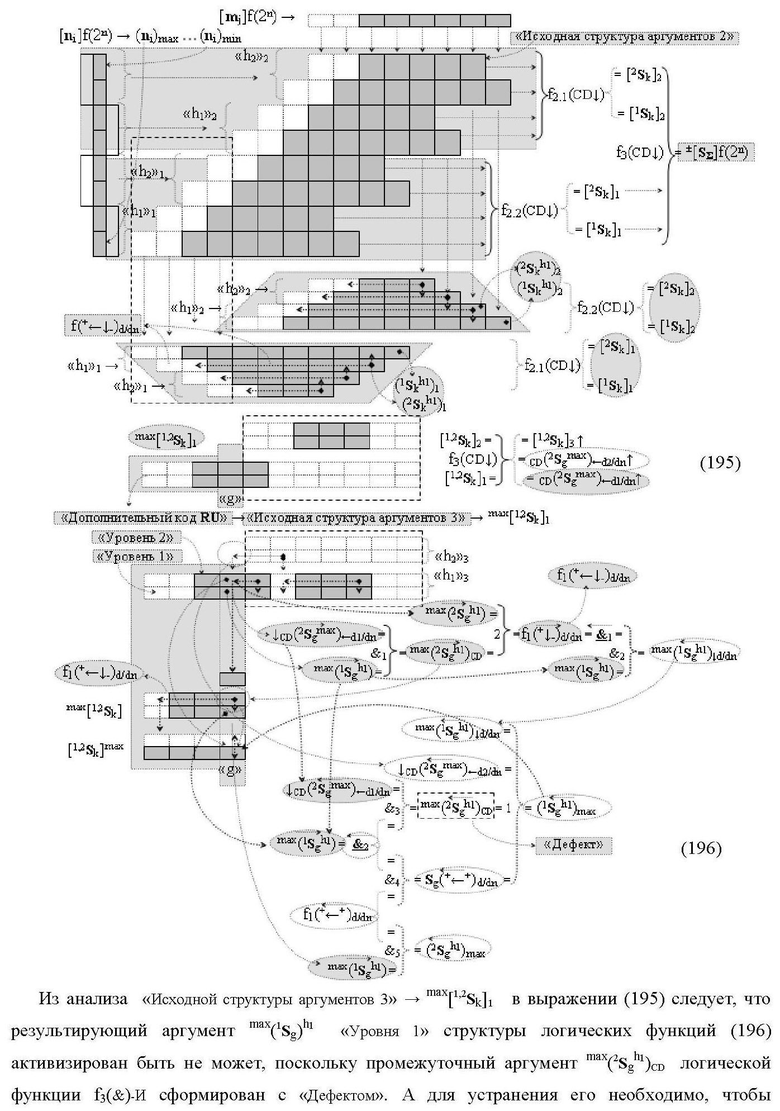
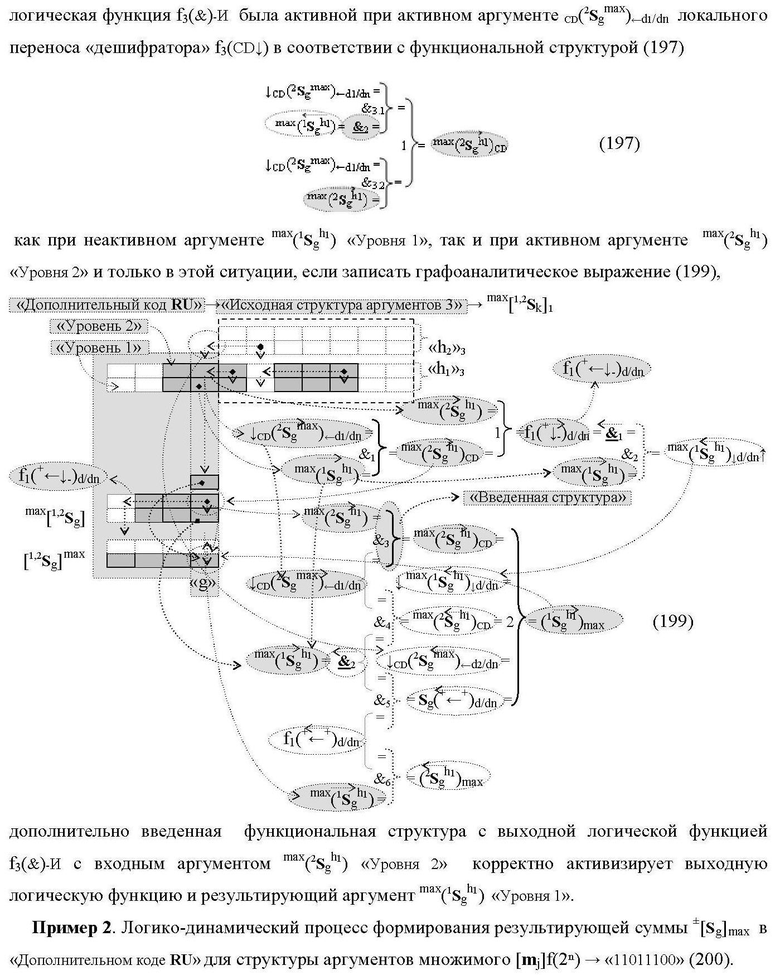
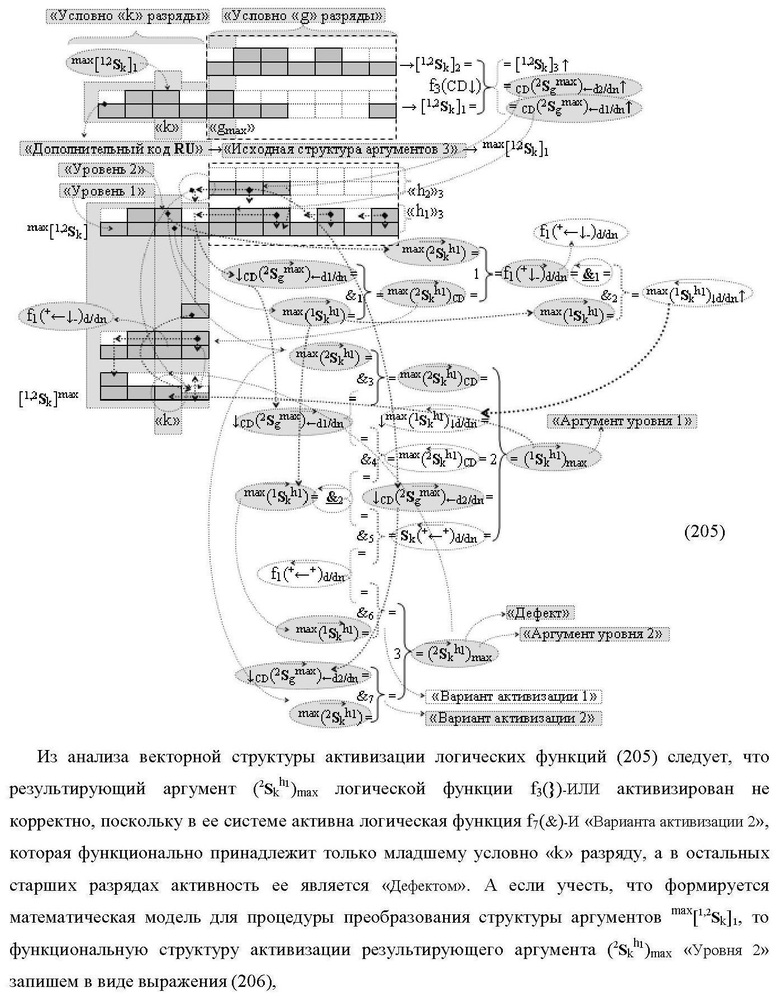
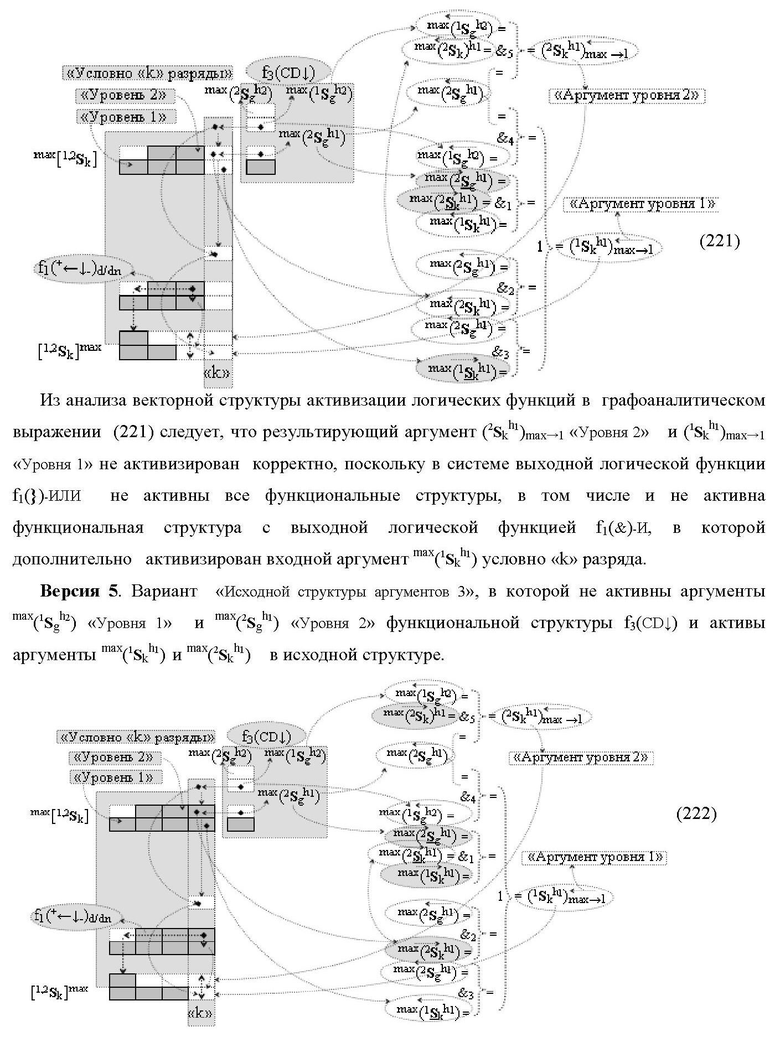
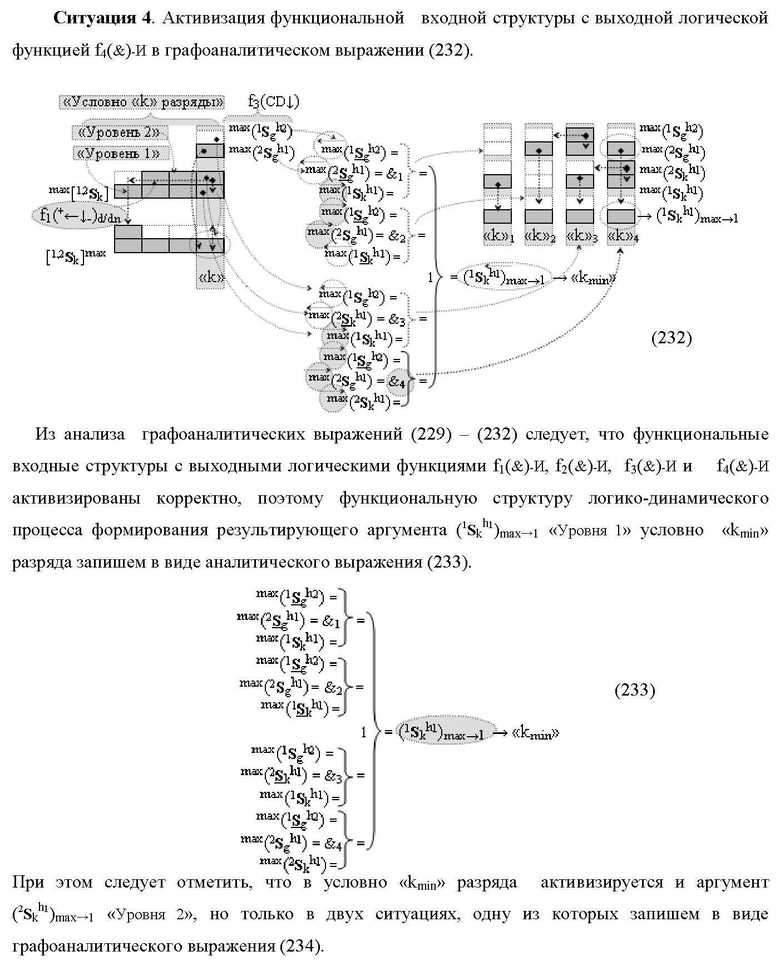
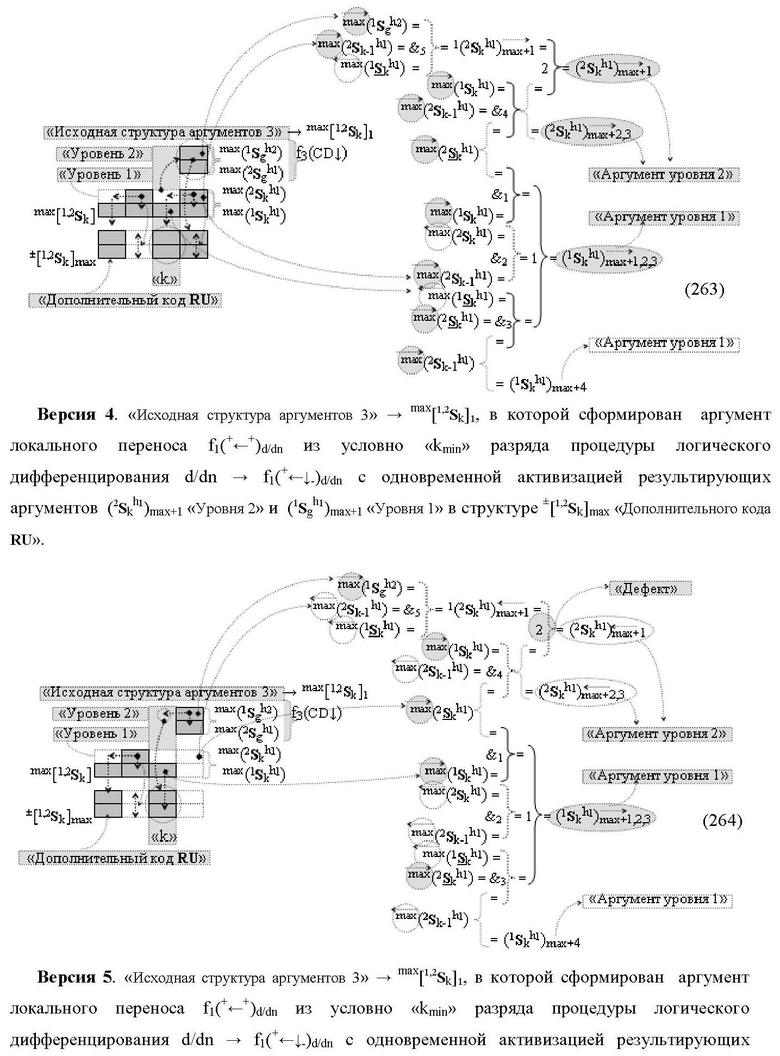
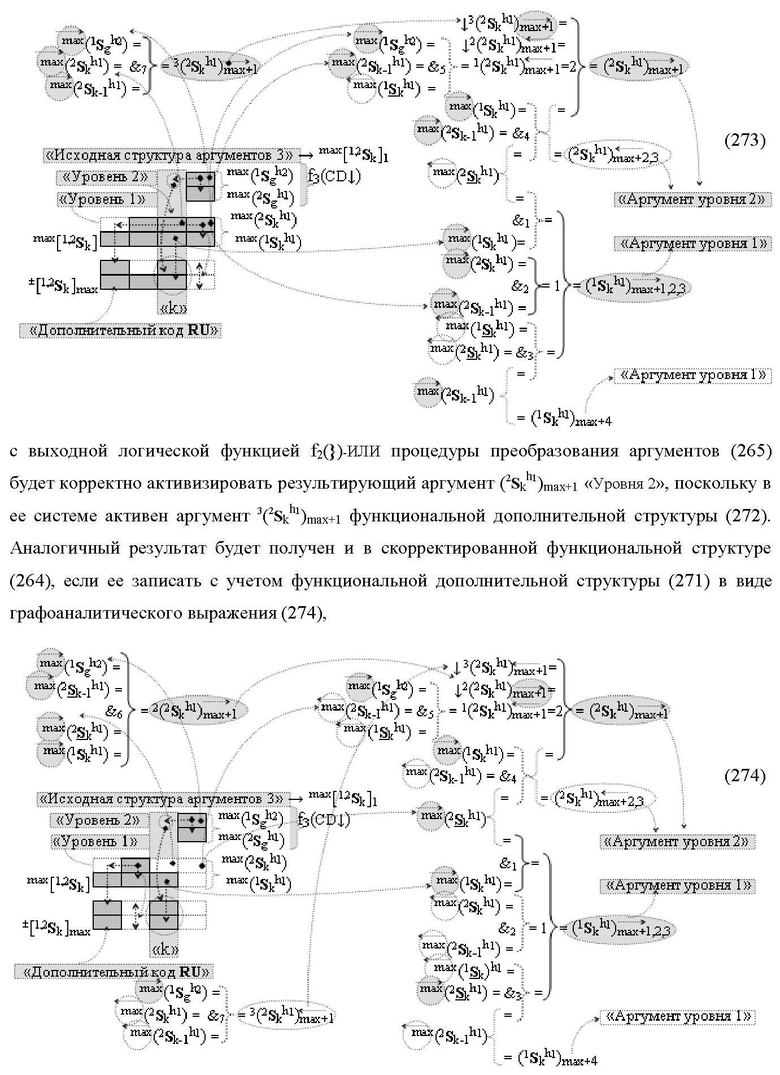
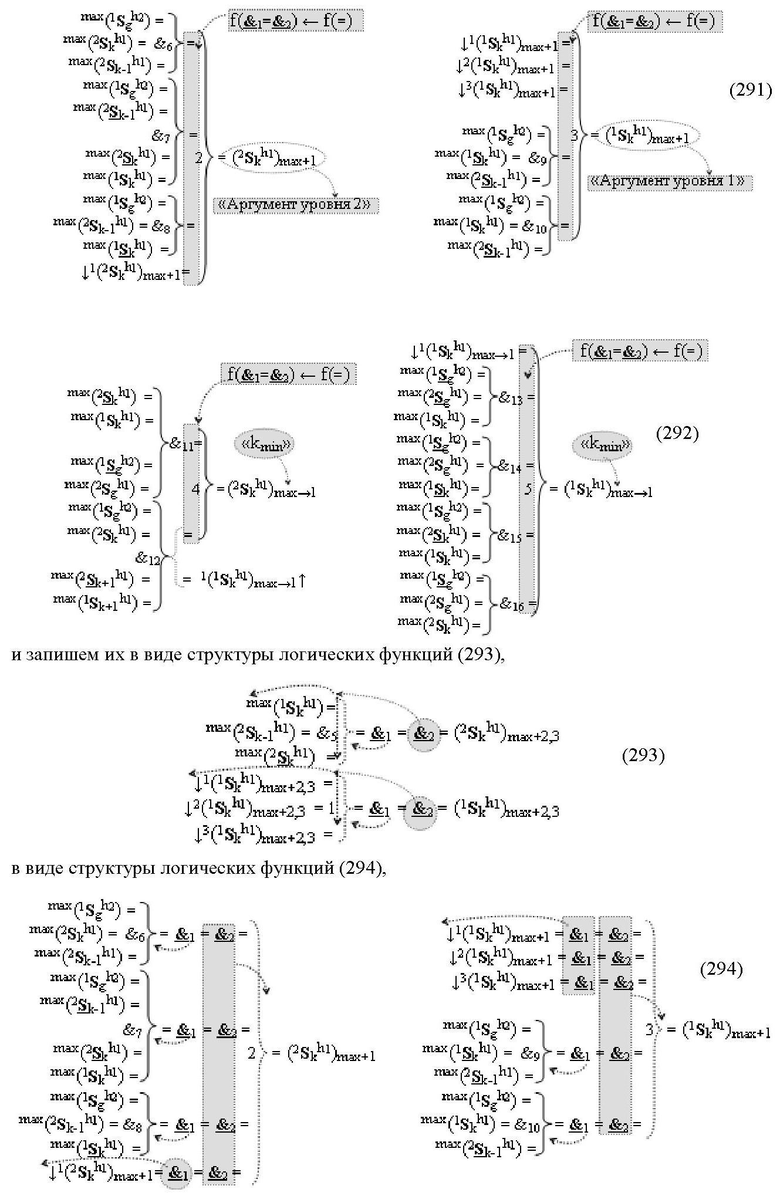
1. Функциональная структура сумматора f3(ΣCD)max старших условно «k» разрядов параллельно-последовательного умножителя fΣ(ΣCD), реализующая процедуру «дешифрирования» аргументов слагаемых [1,2Sg h1] и [1,2Sg h2] в «Дополнительном коде RU» посредством арифметических аксиом троичной системы счисления f(+1,0,-1) и логического дифференцирования d1/dn → f1(+←↓-)d/dn, выполненная в виде последовательных старшего разряда «kmin+4» с формированием результирующего аргумента (1Sk h1)max+4 «Уровня 1», средних разрядов «kmin+2,3» с формированием результирующего аргумента ((1Sk h1)max+2 и (1Sk h1)max+3) → (1Sk h1)max+2,3 «Уровня 1» и двух младших разрядов «kmin+1» и «kmin→1» с формированием результирующего аргумента (1Sk h1)max+1 и (1Sk h1)max→1 «Уровня 1» соответственно, которые включают логическую функцию f1(})-ИЛИ, f3(})-ИЛИ, f5(})-ИЛИ и f2(&)-И, f8(&)-И, f14(&)-И, и логическую функцию f1(&)-И и f9(&)-И, в которой функциональная входная связь является функциональной входной связью функциональной структуры для приема аргумента max(1Sk h1) «Уровня 1» структуры аргументов слагаемых [1Sg h1] и логическую функцию f15(&)-И, в которой функциональная входная связь является функциональной входной связью функциональной структуры для приема аргумента max(2Sk h1) «Уровня 1» структуры аргументов слагаемых [2Sg h1], отличающаяся тем, что функциональные структуры средних разрядов «kmin+2,3» выполнены с формированием дополнительного результирующего аргумента (2Sk h1)max+2,3 «Уровня 2» и в них введены дополнительные логические функции f3(&)-И и f4(&)-И, при этом функциональные связи логических функций выполнены в соответствии с математической моделью вида
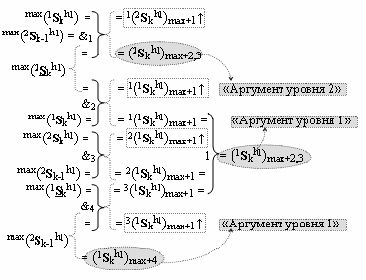
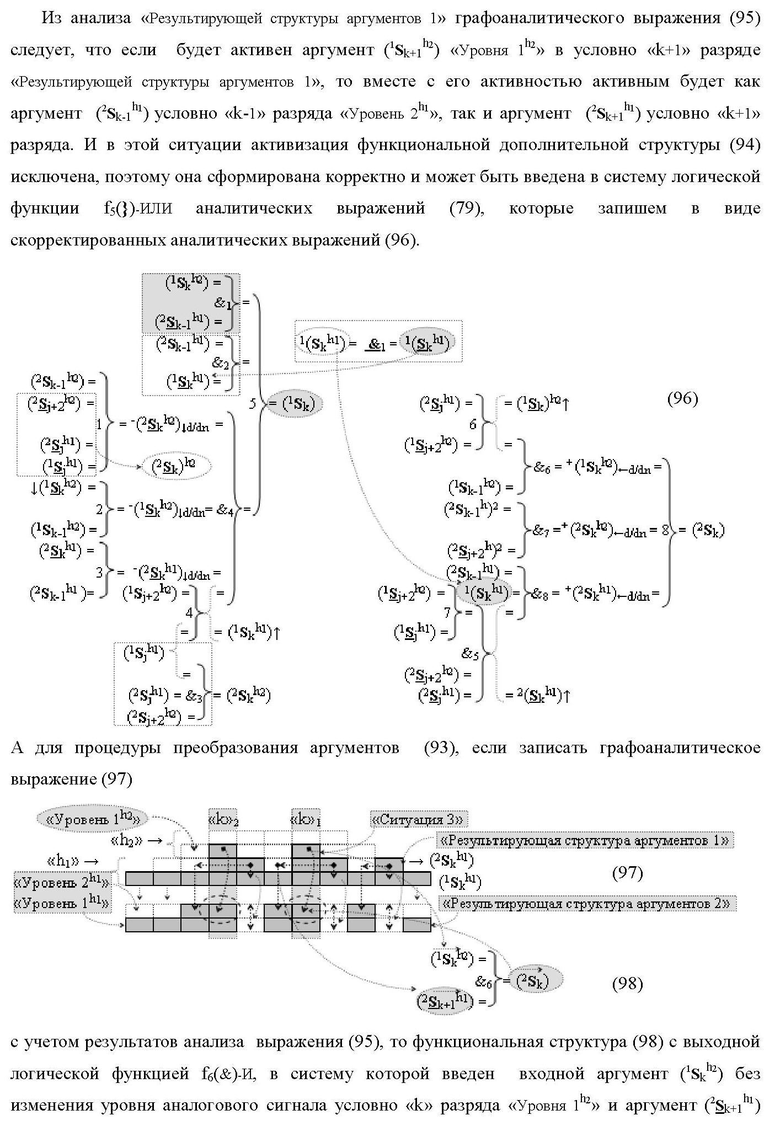
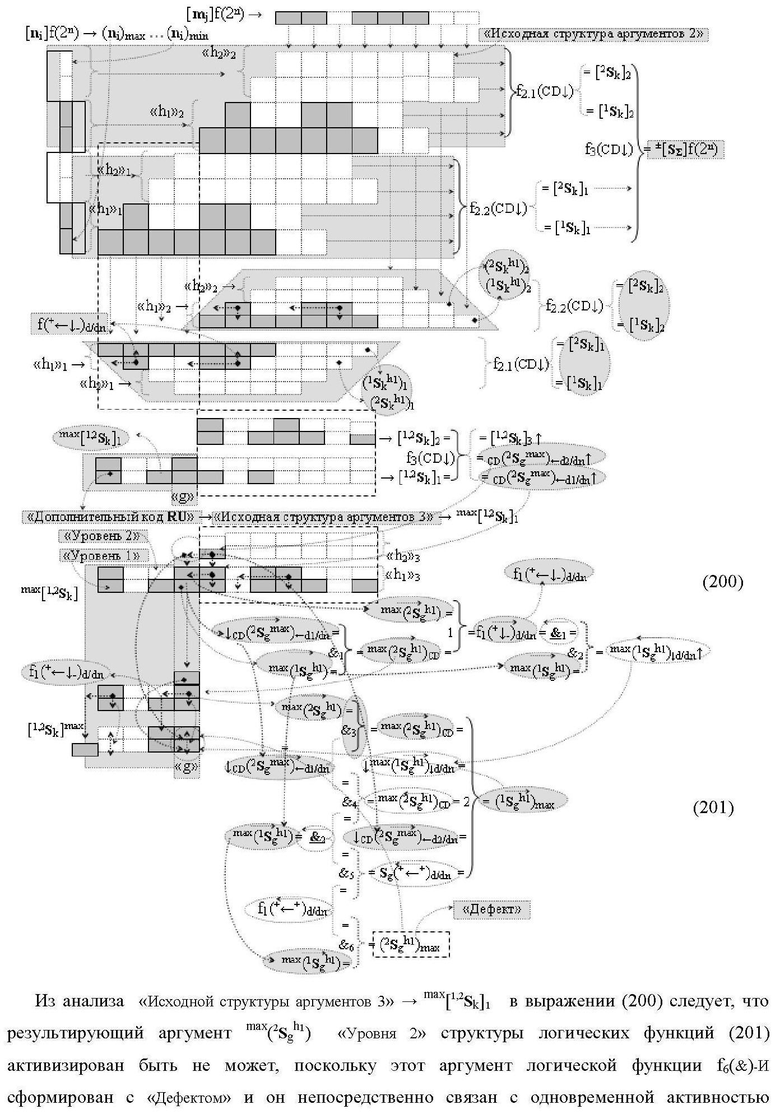
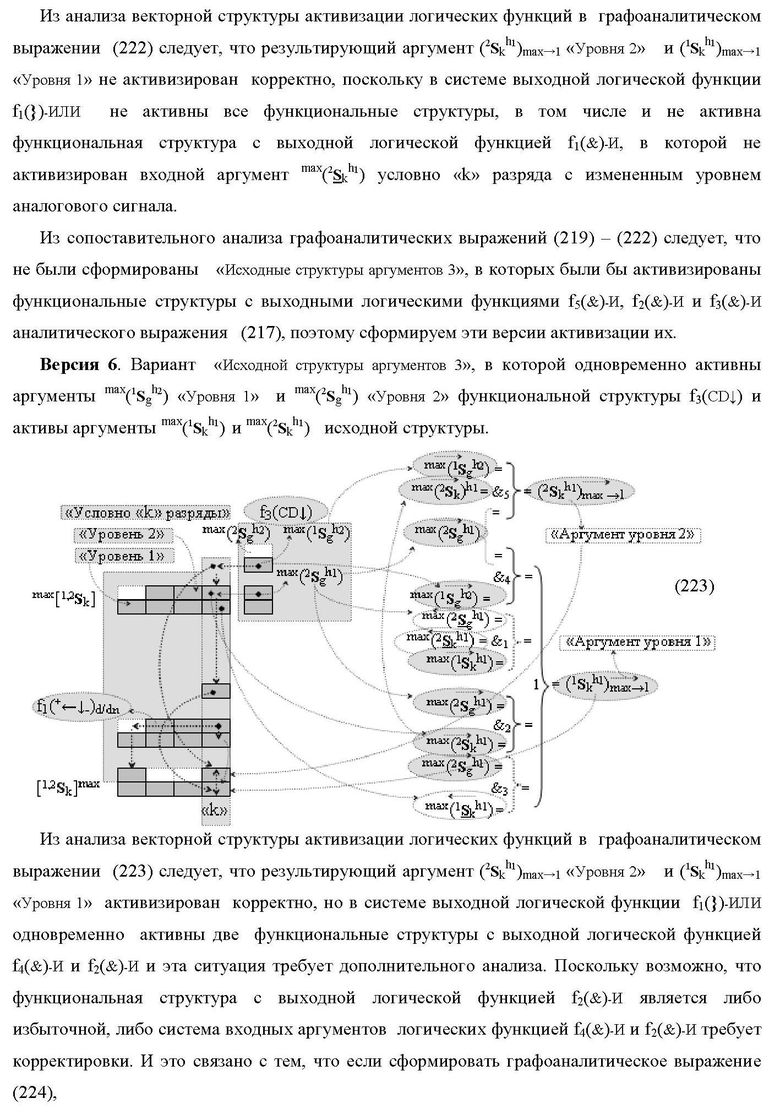
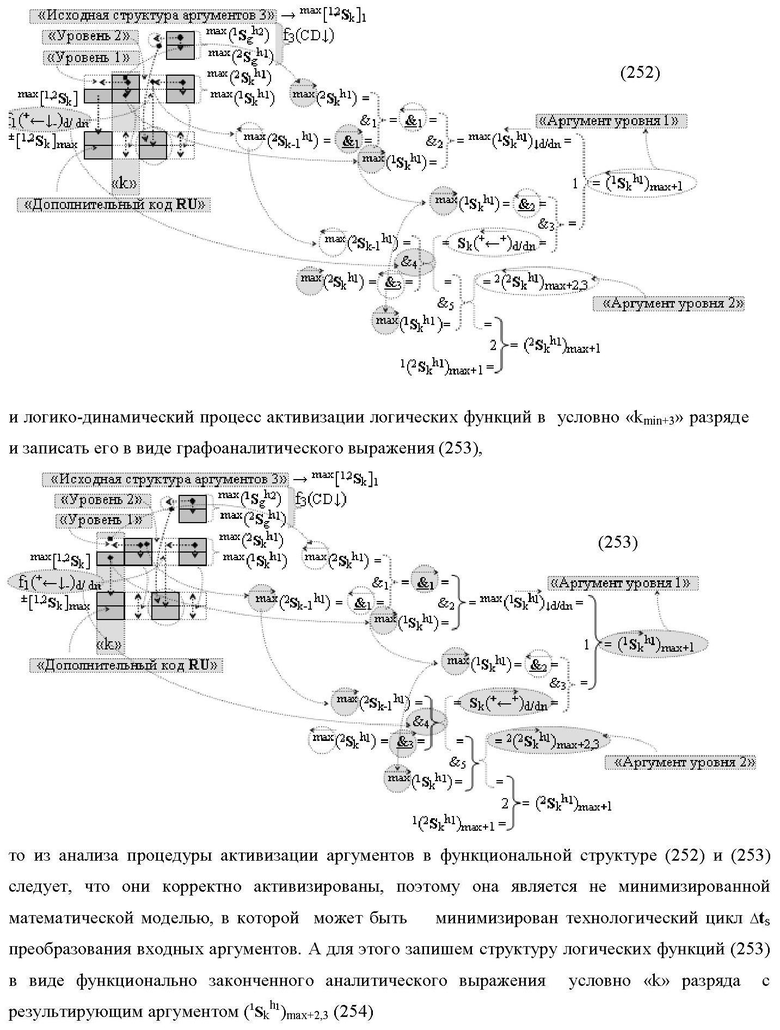
где 1(2Sk h1)max+1↑, 1(1Sk h1)max+1↑, 2(1Sk h1)max+1↑ и 3(1Sk h1)max+1↑ - преобразованные аргументы без изменения уровня аналогового сигнала, которые являются входными аргументами функциональной структуры второго младшего «kmin+1» разряда, которая также выполнена с формированием дополнительного результирующего аргумента (2Sk h1)max+1 «Уровня 2» и в нее введены дополнительные логические функции f5(&)-И, f6(&)-И, f7(&)-И и f2(})-ИЛИ, при этом функциональные связи логических функций выполнены в соответствии с математической моделью

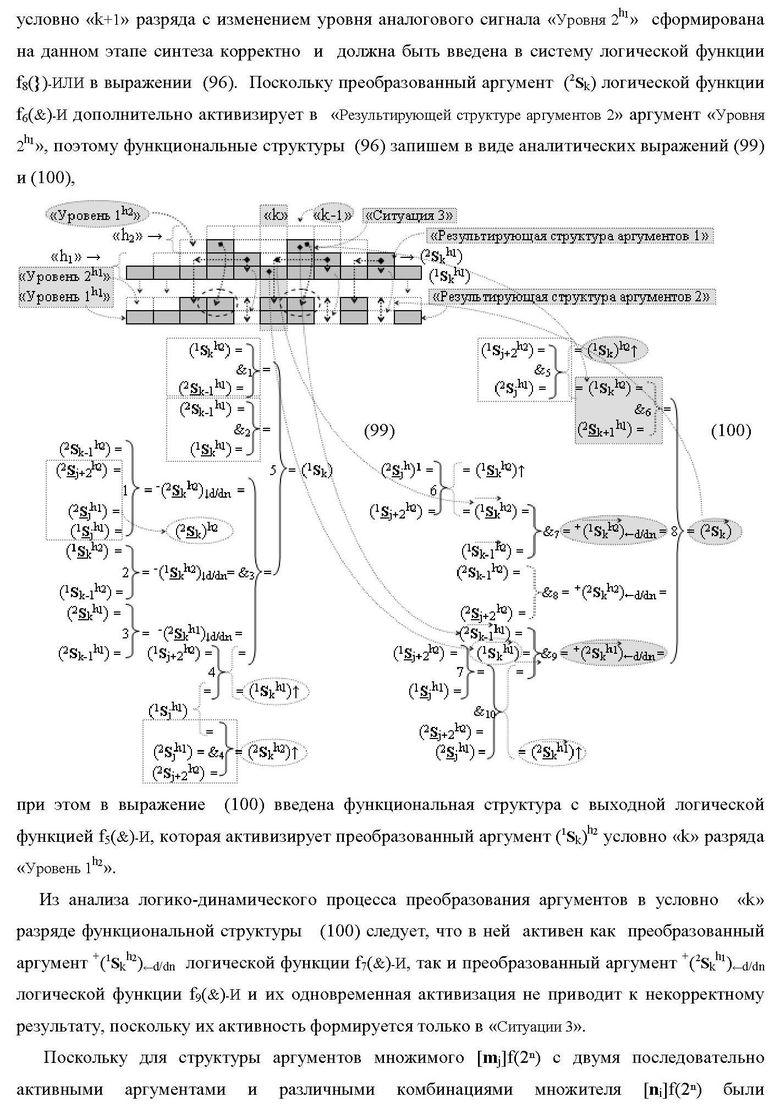
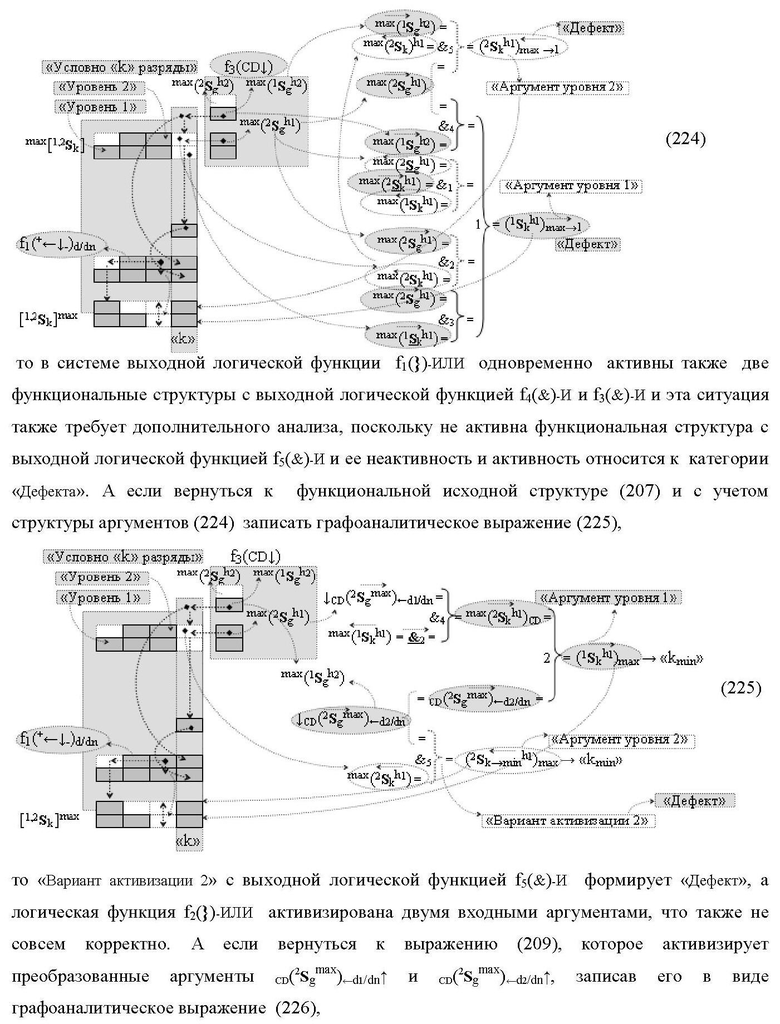
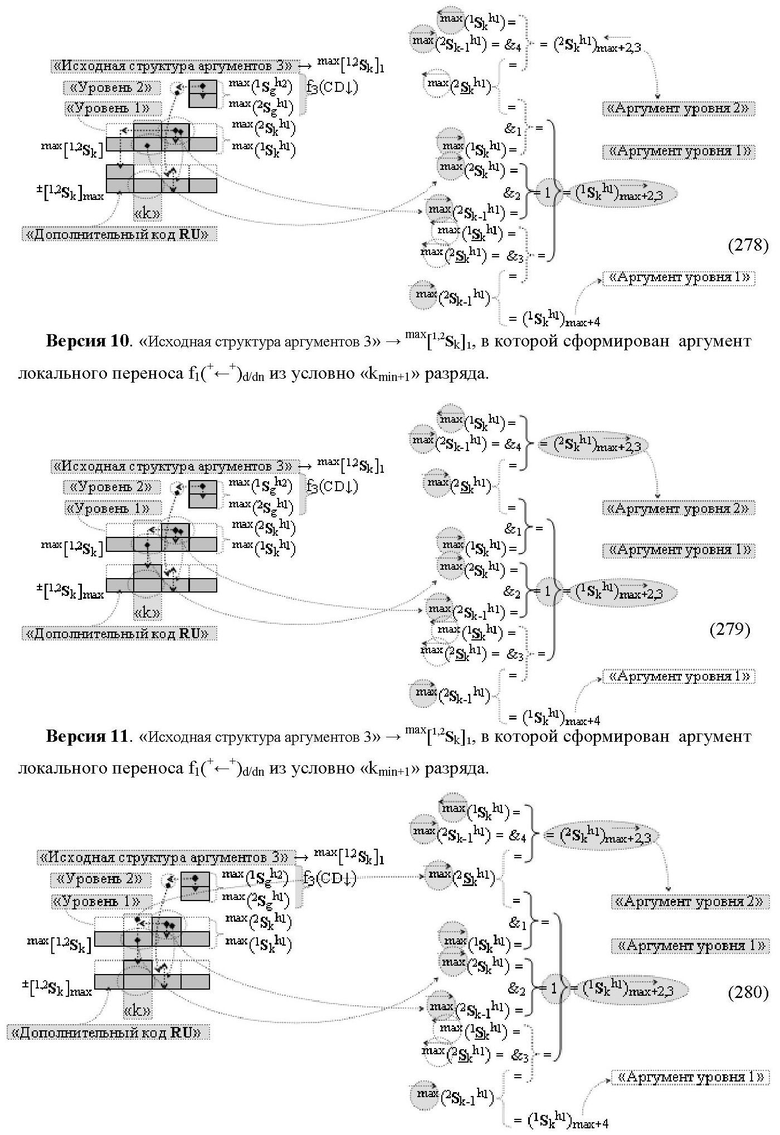
а функциональная структура первого младшего «kmin→1» разряда также выполнена с формированием дополнительного результирующего аргумента (2Sk h1)max→1 «Уровня 2» и в нее введены дополнительные логические функции f10(&)-И, f11(&)-И, f12(&)-И, f13(&)-И и f4(})-ИЛИ, при этом функциональные связи логических функций выполнены в соответствии с математической моделью вида
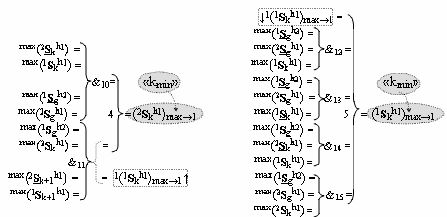
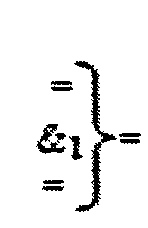 - логическая функция f1(&)-И;
- логическая функция f1(&)-И;  - логическая функция f1(})-ИЛИ.
- логическая функция f1(})-ИЛИ.
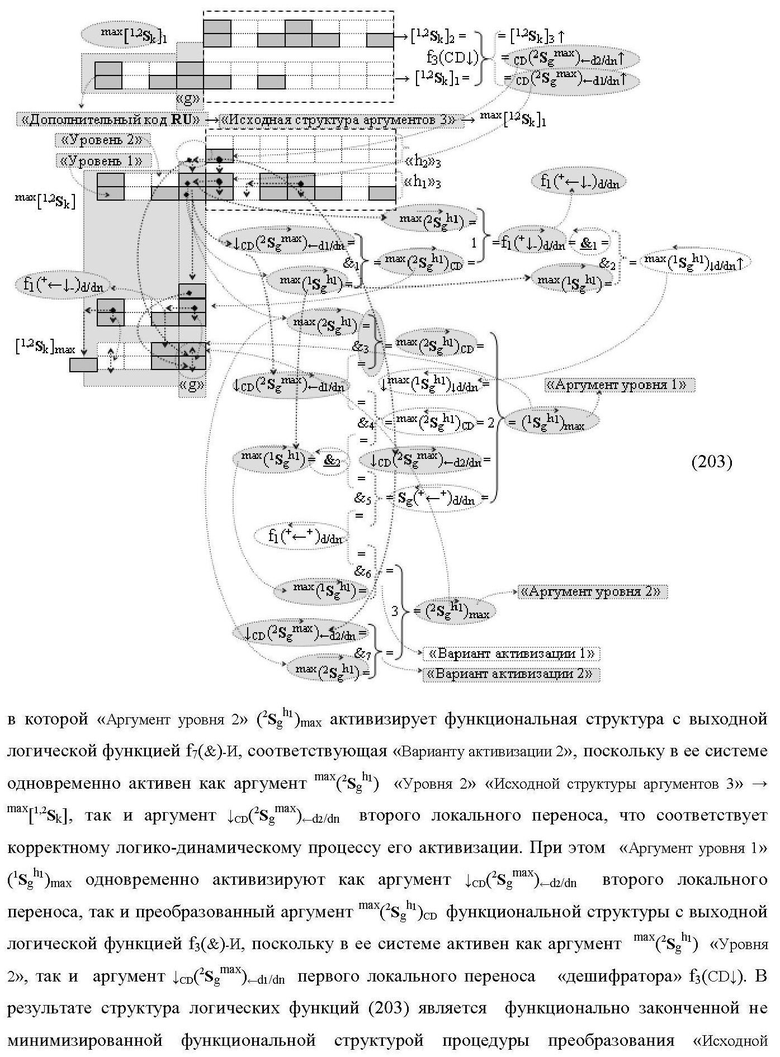
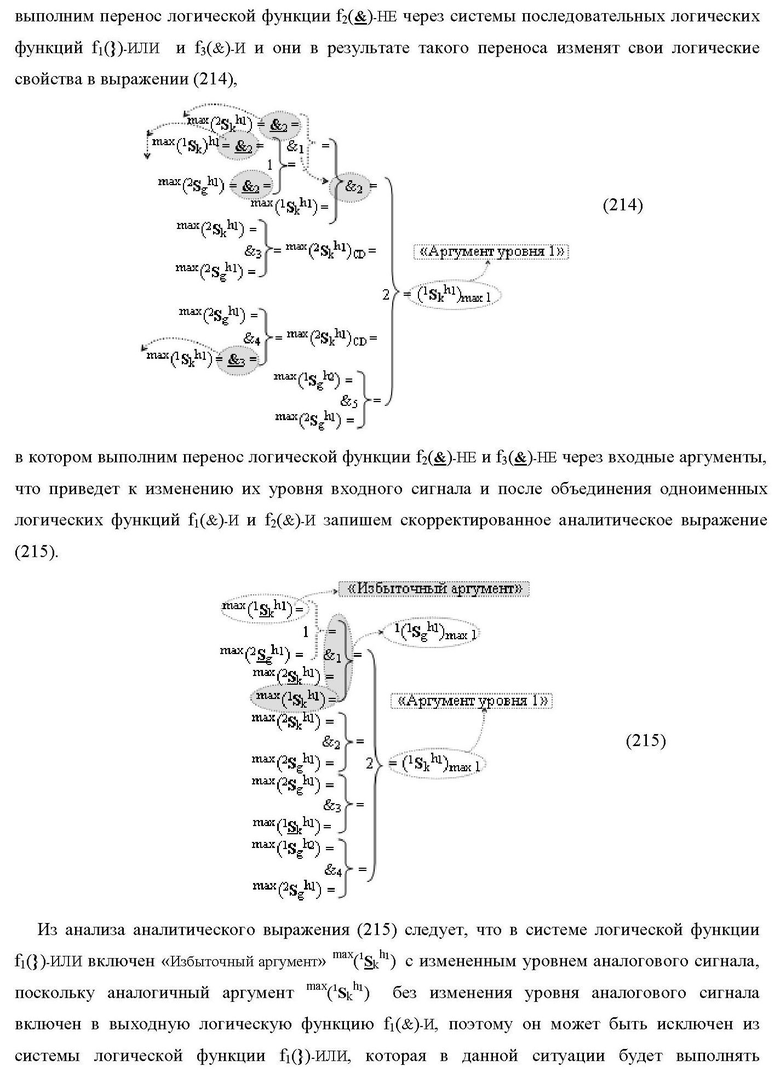
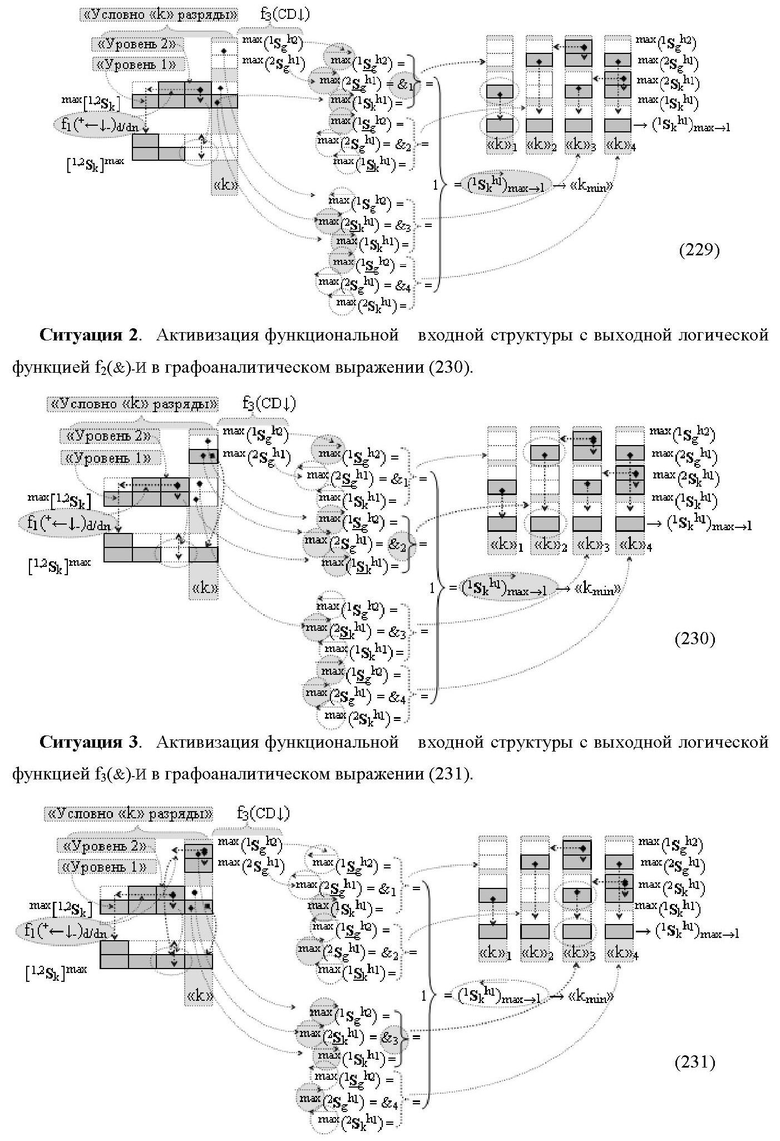
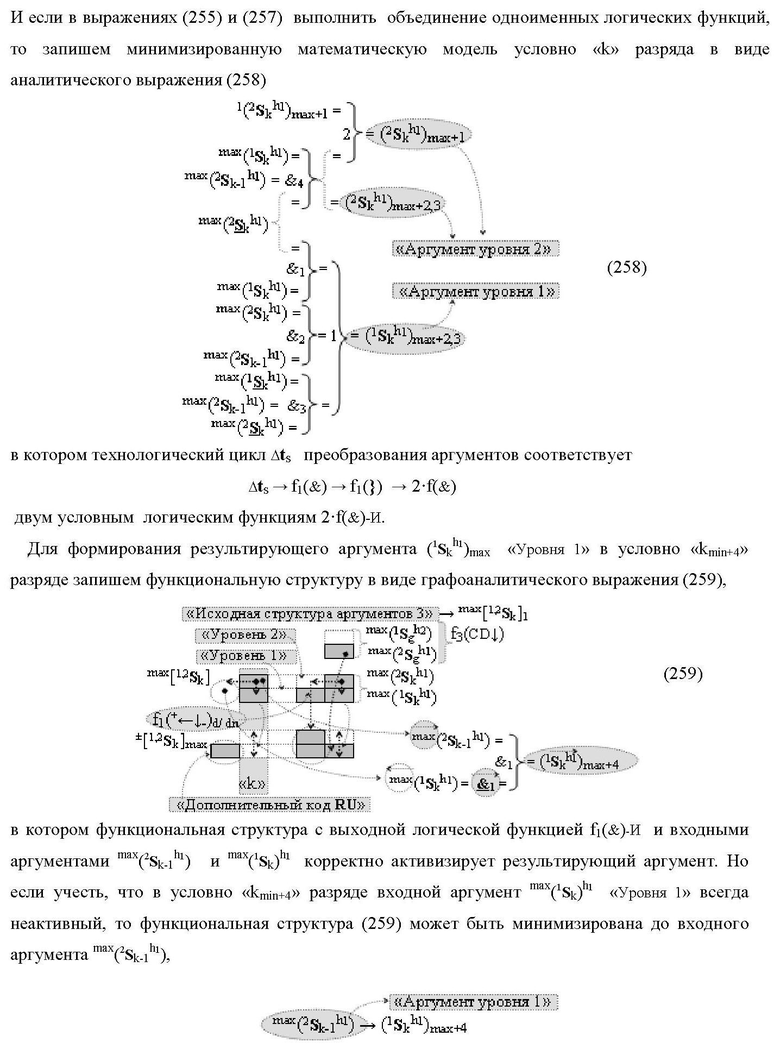
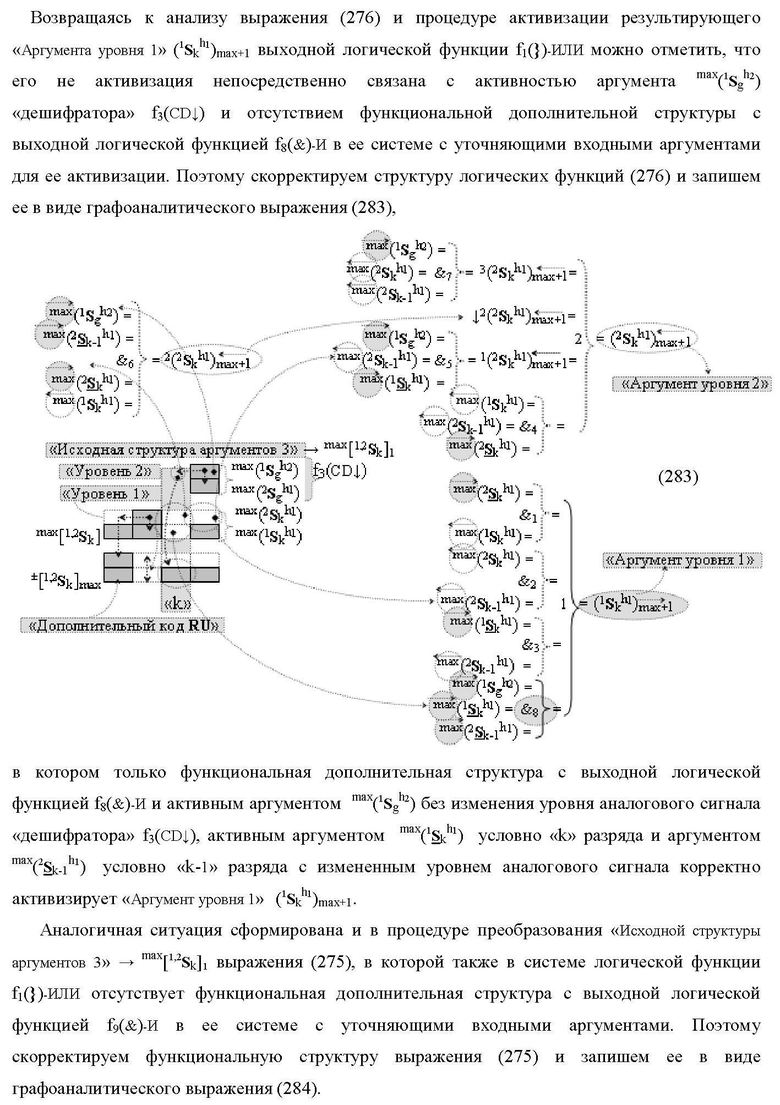
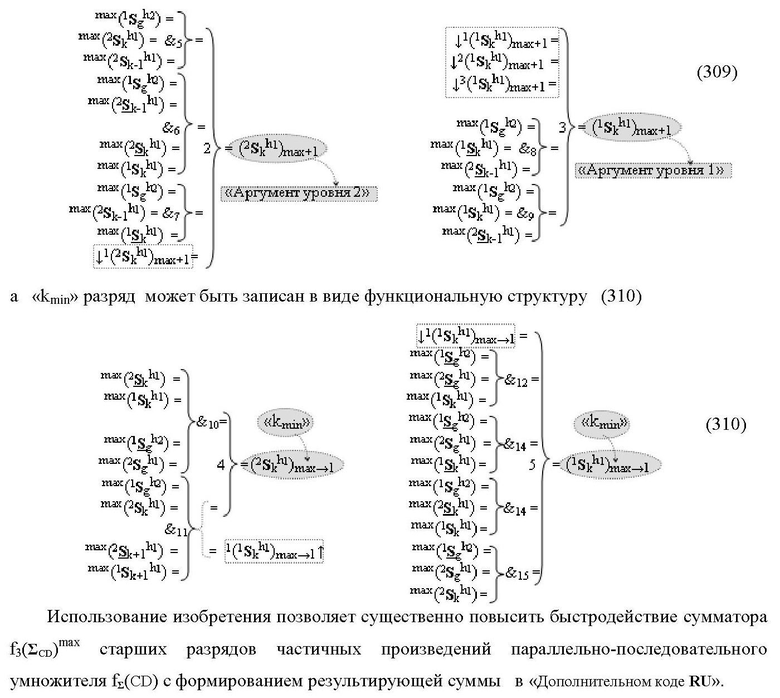
2. Функциональная структура сумматора fΣ(ΣCD)max старших условно «k» разрядов параллельно-последовательного умножителя fΣ(ΣCD), реализующая процедуру «дешифрирования» аргументов слагаемых [1,2Sg h1] и [1,2Sg h2] в «Дополнительном коде RU» посредством арифметических аксиом троичной системы счисления f(+1,0,-1) и логического дифференцирования d1/dn → f1(+←↓-)d/dn, выполненная в виде последовательных разрядов старшего разряда «kmin+4» с формированием результирующего аргумента (1Sk h1)max+4 «Уровня 1», функциональных структур средних разрядов «kmin+2,3» с формированием результирующего аргумента ((1Sk h1)max+2 и (1Sk h1)max+3) → (1Sk h1)max+2,3 «Уровня 1» и двух младших разрядов «kmin+1» и «kmin→1» с формированием результирующего аргумента (1Sk h1)max+1 и (1Sk h1)max→1 «Уровня 1» и двух младших разрядов «kmin+1» и «kmin→1» с формированием результирующего аргумента (1Sk h1)max+1 и (1Sk h1)max→1 «Уровня 1» соответственно, отличающаяся тем, что функциональные структуры средних разрядов «kmin+2,3» выполнены с формированием дополнительного результирующего аргумента (2Sk h1)max+2,3 «Уровня 2» и в них введены дополнительные логические функции f1(}&)-ИЛИ-НЕ, f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ и f4(&)-И-НЕ, при этом функциональные связи логических функций выполнены в соответствии с математической моделью вида
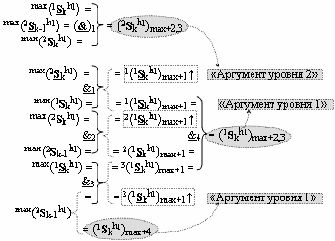
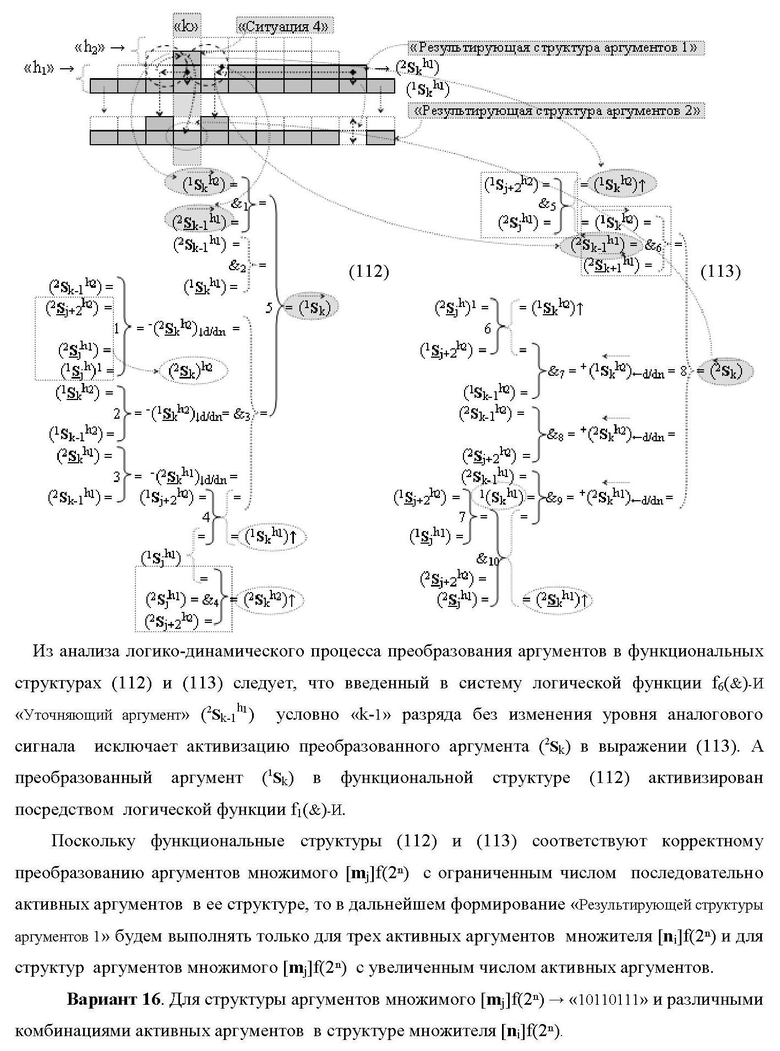
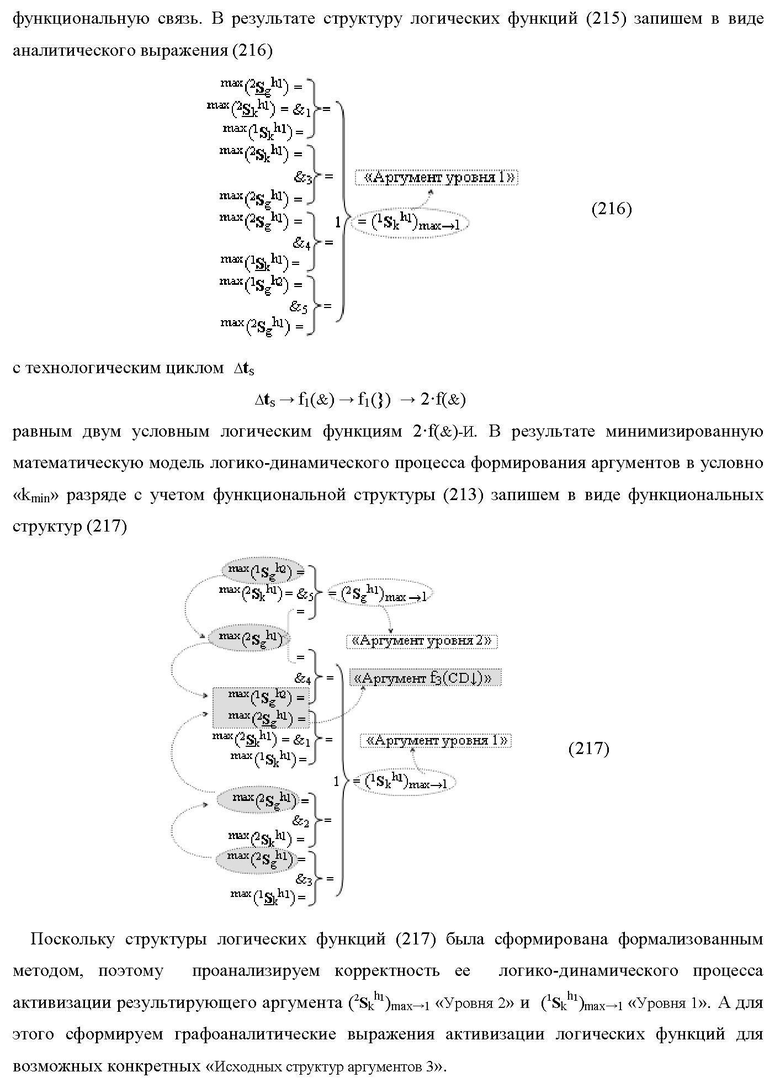
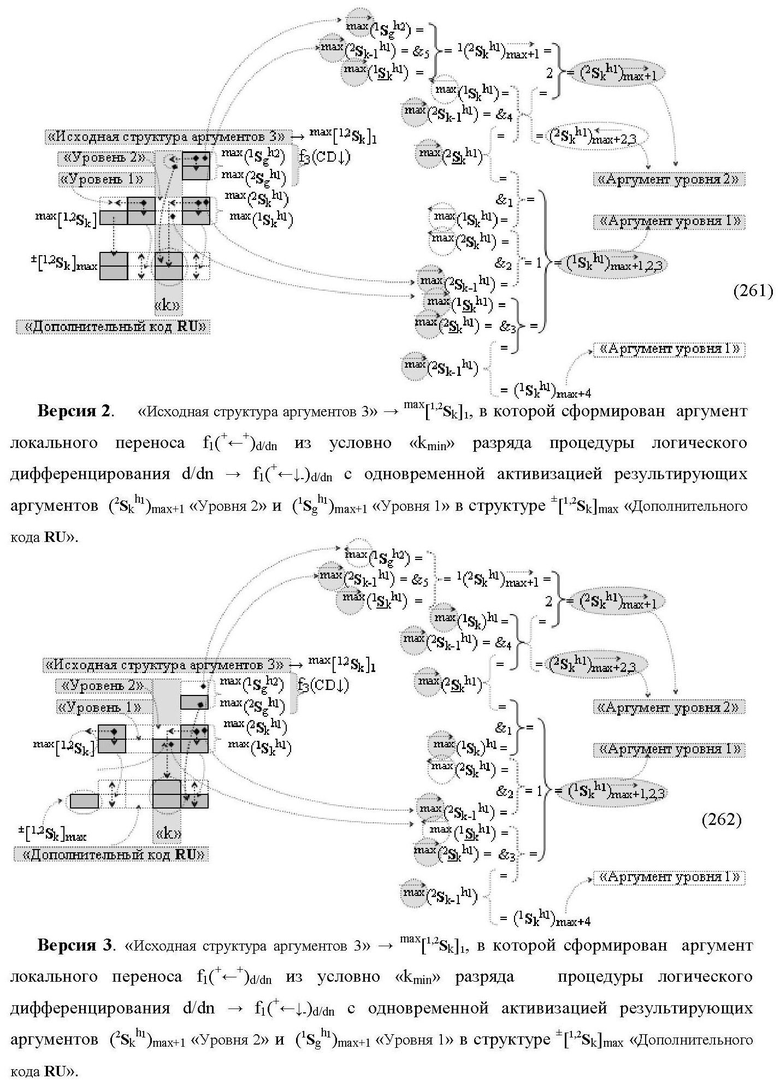
где 1(1Sk h1)max+1↑, 2(1Sk h1)max+1↑ и 3(1Sk h1)max+1↑ - преобразованные аргументы с измененным уровнем аналогового сигнала, которые являются входными аргументами функциональной структуры второго младшего «kmin+1» разряда, которая также выполнена с формированием дополнительного результирующего аргумента (2Sk h1)max+1 «Уровня 2» и в нее введены дополнительные логические функции f5(&)-И-НЕ, f6(&)-И-НЕ, f7(&)-И-НЕ, f8(&)-И-НЕ, f9(&)-И-НЕ, f10(&)-И-НЕ, f11(&)-И-НЕ и f12(&)-И-НЕ, при этом функциональные связи логических функций выполнены в соответствии с математической моделью вида

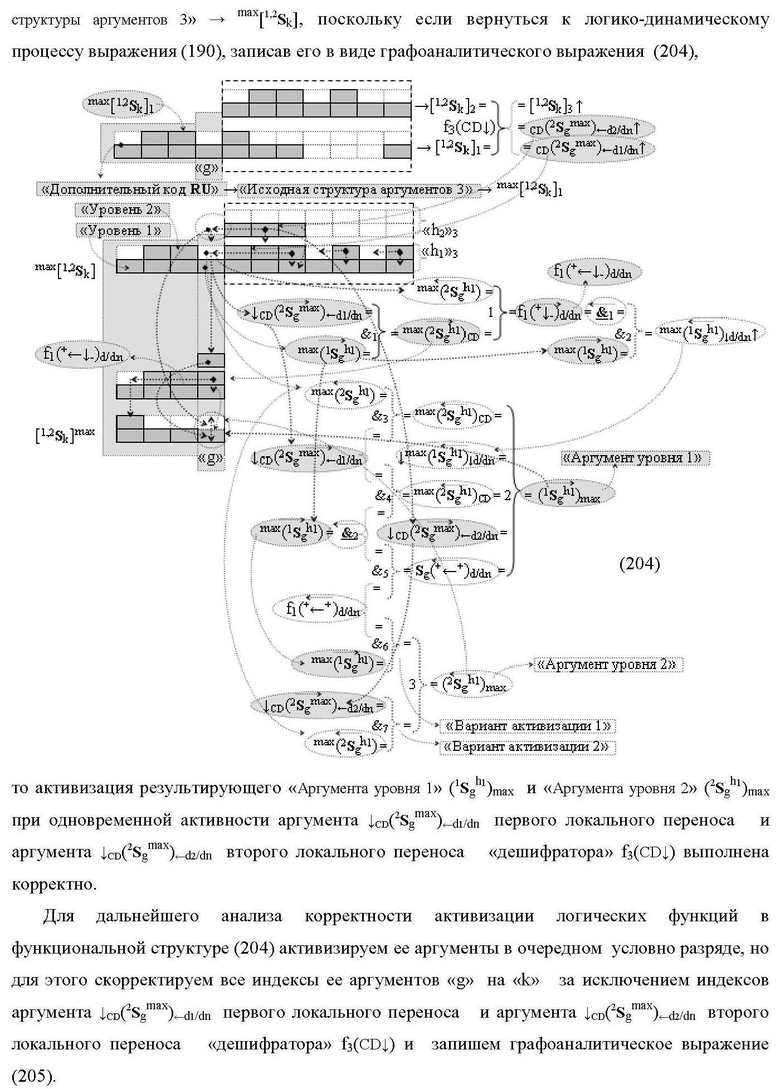
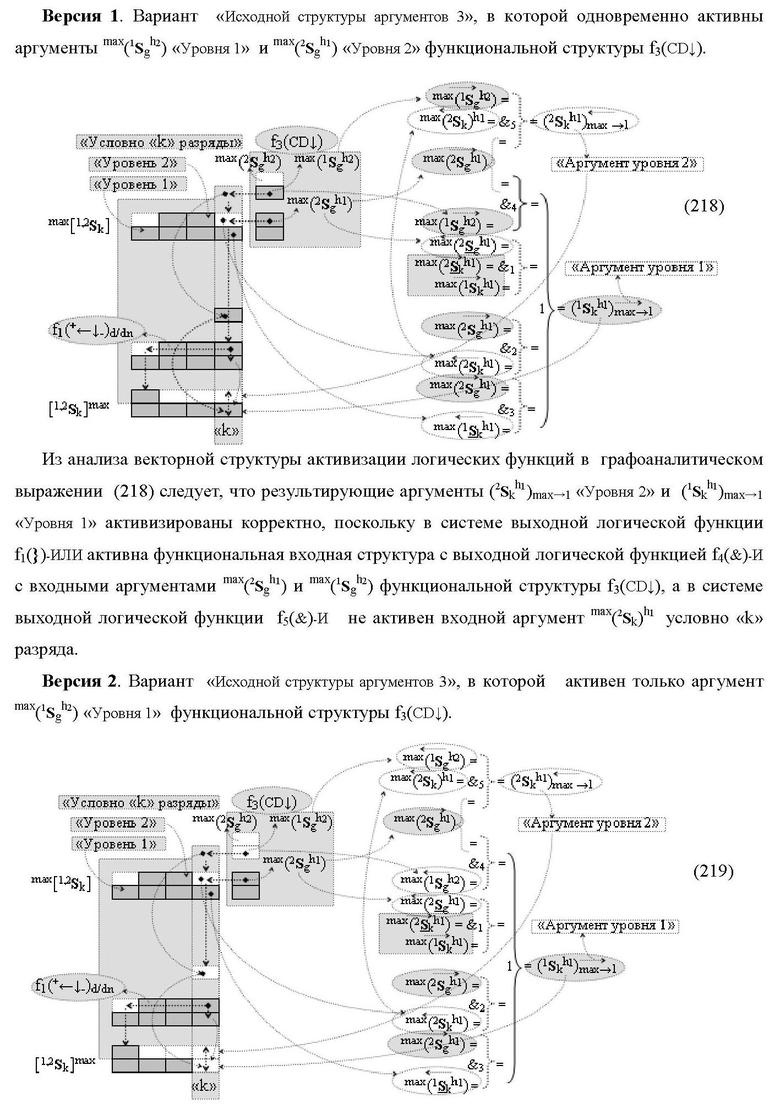
а функциональная структура первого младшего «kmin→1» разряда также выполнена с формированием дополнительного результирующего аргумента (2Sk h1)max→1 «Уровня 2» и в нее введены дополнительные логические функции f13(&)-И-НЕ, f14(&)-И-НЕ, f15(&)-И-НЕ, f16(&)-И-НЕ, f17(&)-И-НЕ, f18(&)-И-НЕ, f19(&)-И-НЕ и f20(&)-И-НЕ, при этом функциональные связи логических функций выполнены в соответствии с математической моделью вида
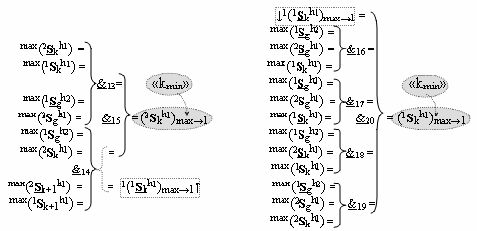
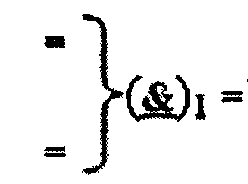 - логическая функция f1(}&)-ИЛИ-НЕ;
- логическая функция f1(}&)-ИЛИ-НЕ; 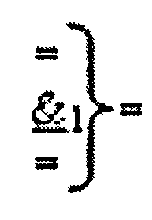 - логическая функция f1(&)-И-НЕ.
- логическая функция f1(&)-И-НЕ.
| УЭЙКЕРЛИ Дж | |||
| Проектирование цифровых устройств | |||
| - М.: ПОСТМАРКЕТ, 2002, с.508 | |||
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПРЕДВАРИТЕЛЬНОГО СУММАТОРА f([n]&[n,0]) УСЛОВНО "i" И "i+1" РАЗРЯДОВ "k" ГРУППЫ ПАРАЛЛЕЛЬНО-ПОСЛЕДОВАТЕЛЬНОГО УМНОЖИТЕЛЯ f(Σ) ДЛЯ ПОЗИЦИОННЫХ АРГУМЕНТОВ МНОЖИМОГО [n]f(2) С ПРИМЕНЕНИЕМ АРИФМЕТИЧЕСКИХ АКСИОМ ТРОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+1,0,-1) (ВАРИАНТЫ РУССКОЙ ЛОГИКИ) | 2010 |
|
RU2439658C1 |
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНОГО СУММАТОРА ДЛЯ УМНОЖИТЕЛЯ, В КОТОРОМ АРГУМЕНТЫ СЛАГАЕМЫХ ЧАСТИЧНЫХ ПРОИЗВЕДЕНИЙ ЯВЛЯЮТСЯ АРГУМЕНТАМИ ТРОИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ f(+1, 0, -1) В ПОЗИЦИОННО-ЗНАКОВОМ ЕЕ ФОРМАТЕ f(+/-) (ВАРИАНТЫ) | 2008 |
|
RU2386162C2 |
| JP 2005326914 A, 24.11.2055 | |||
| JP 2002014804 A, 18.01.2002. | |||
Авторы
Даты
2013-02-27—Публикация
2012-02-13—Подача