Текст описания приведен в факсимильном виде.















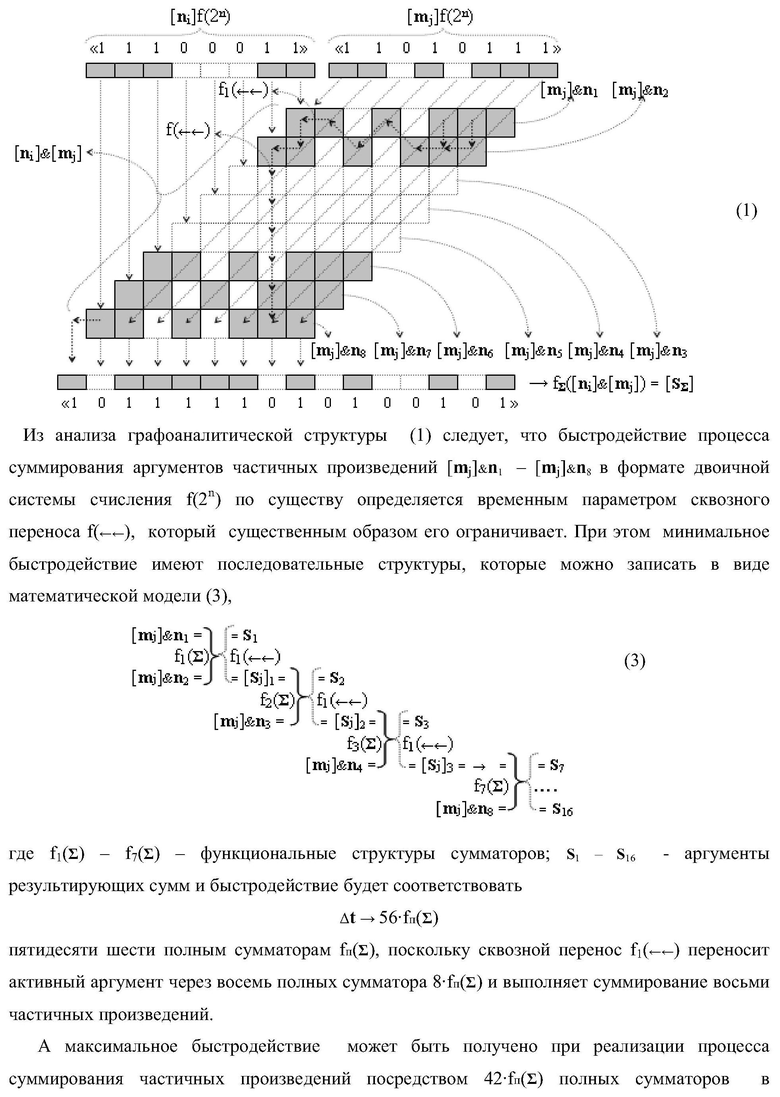








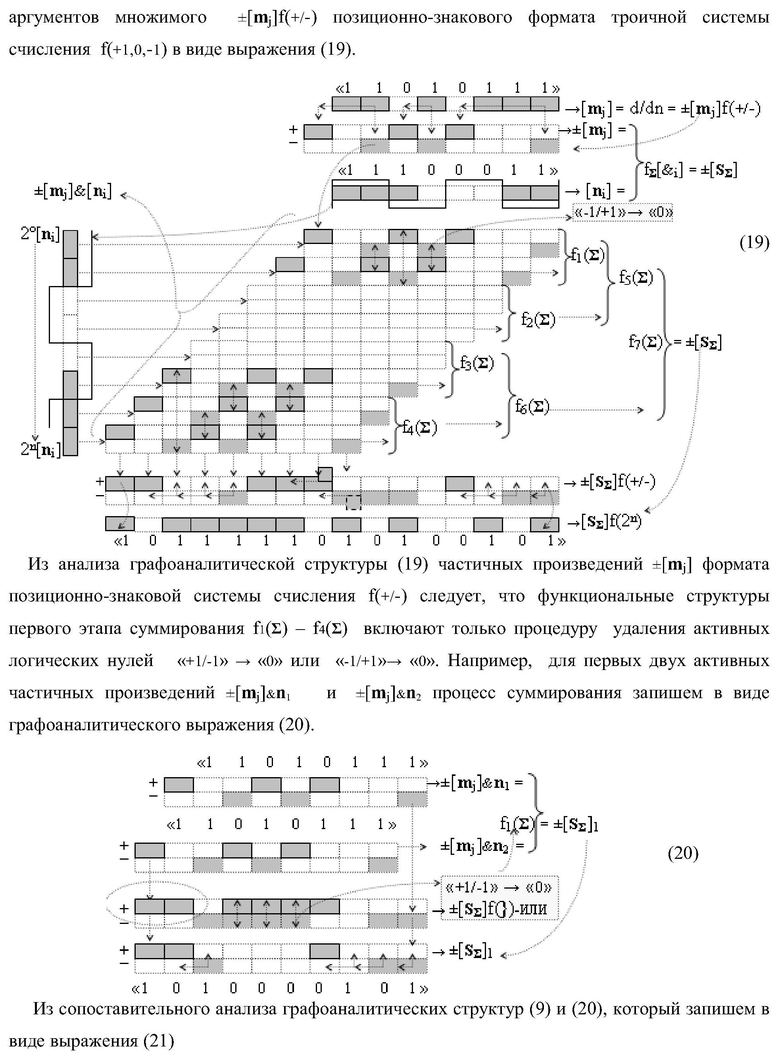


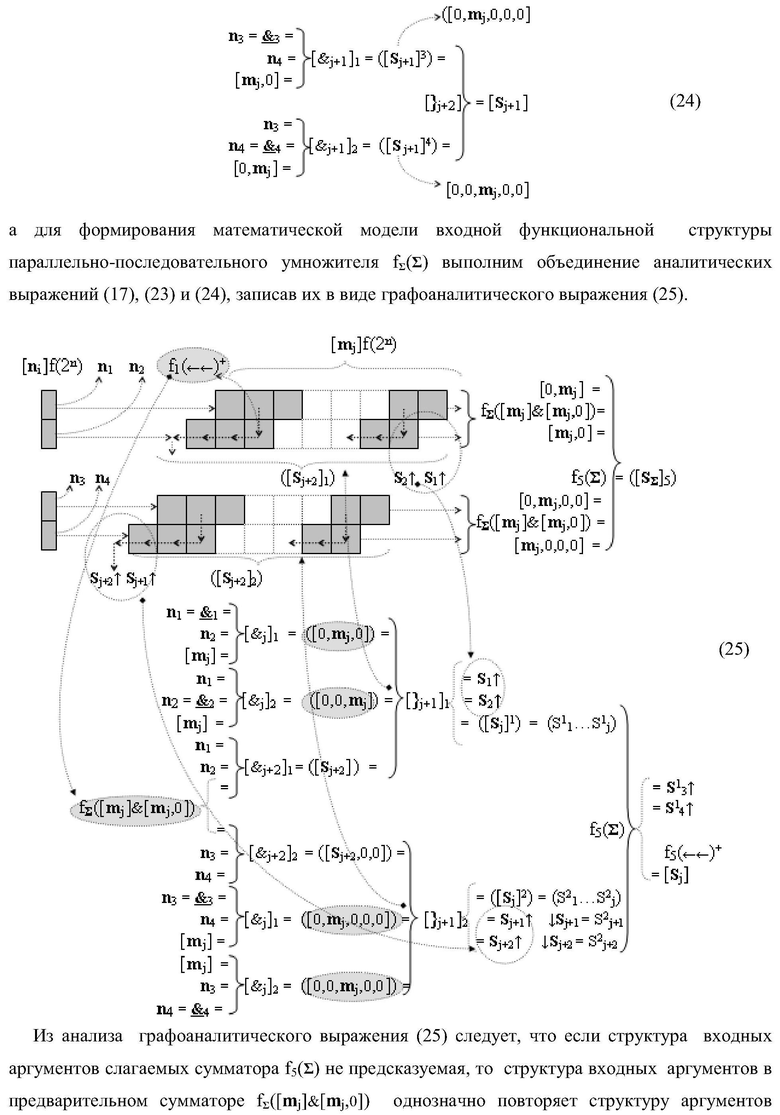

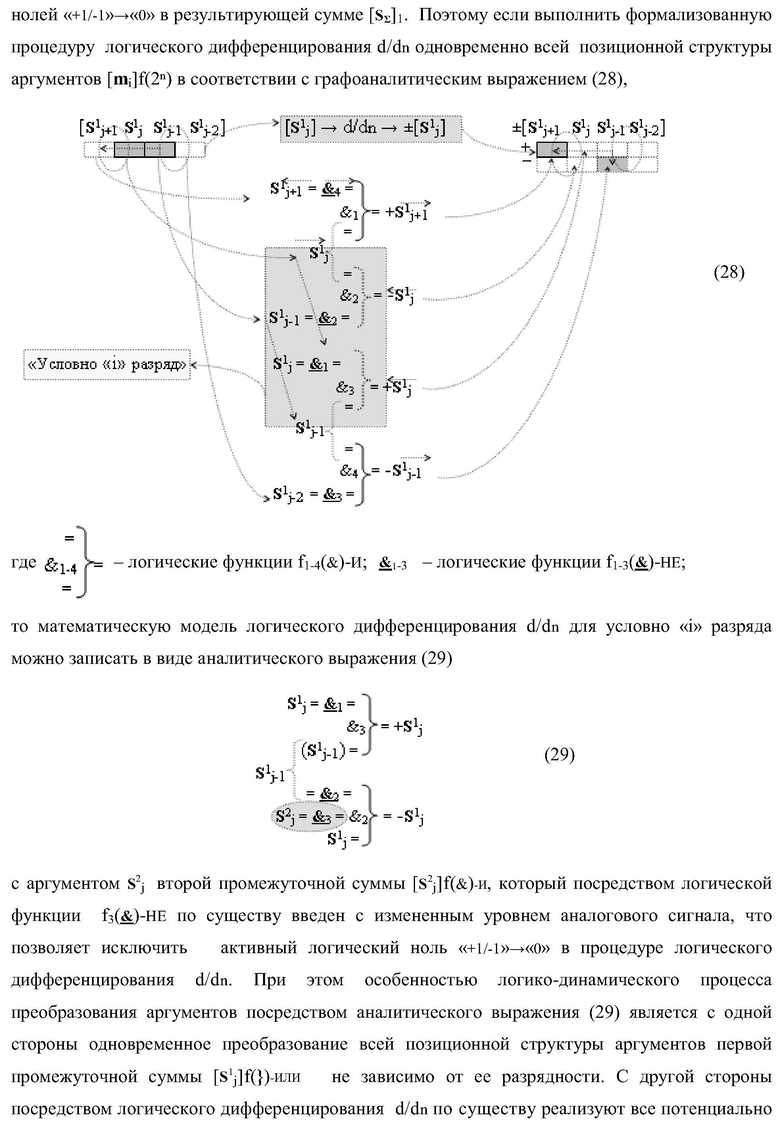

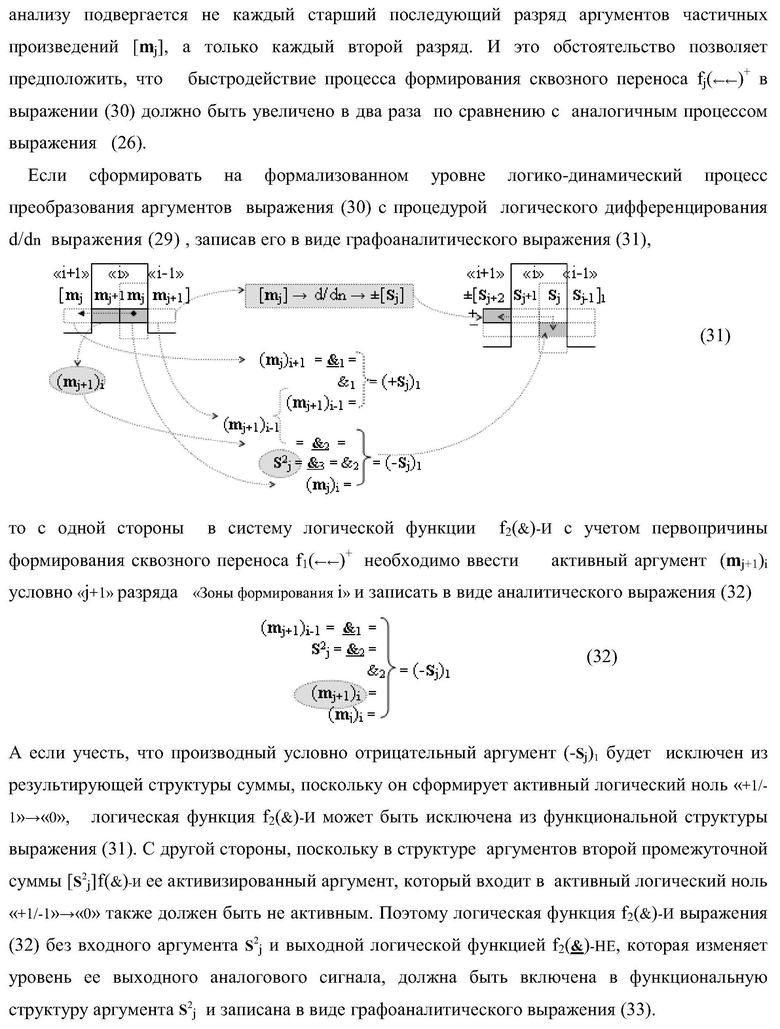








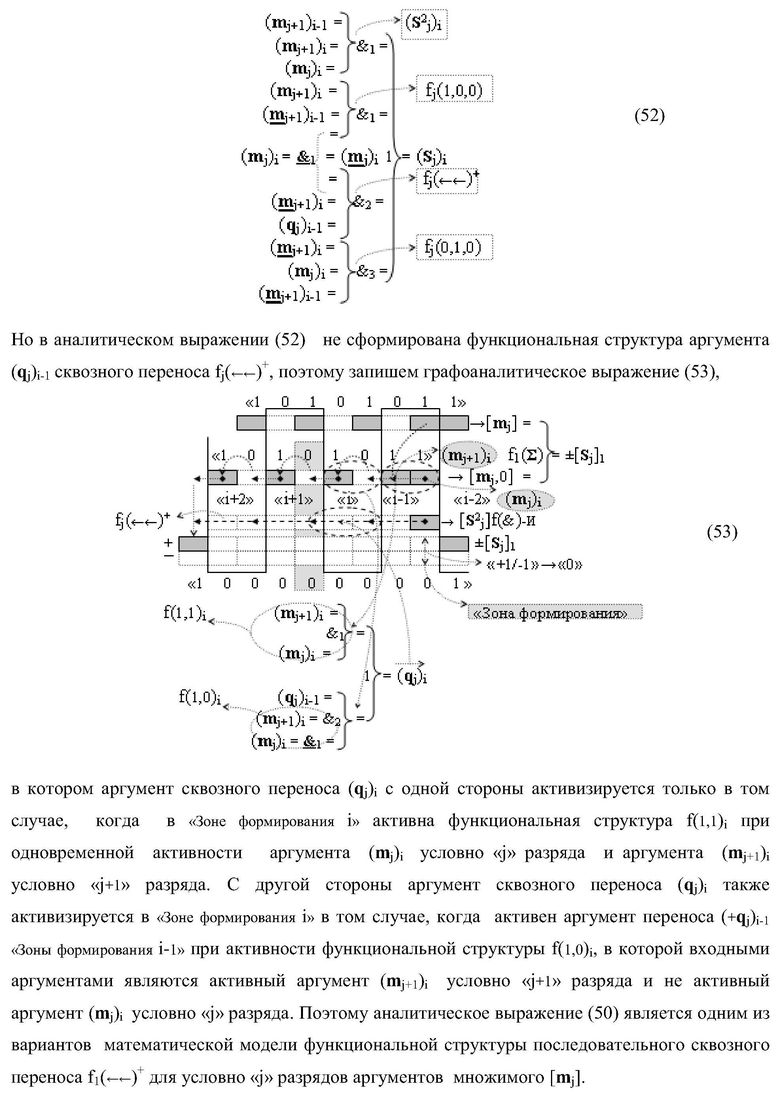




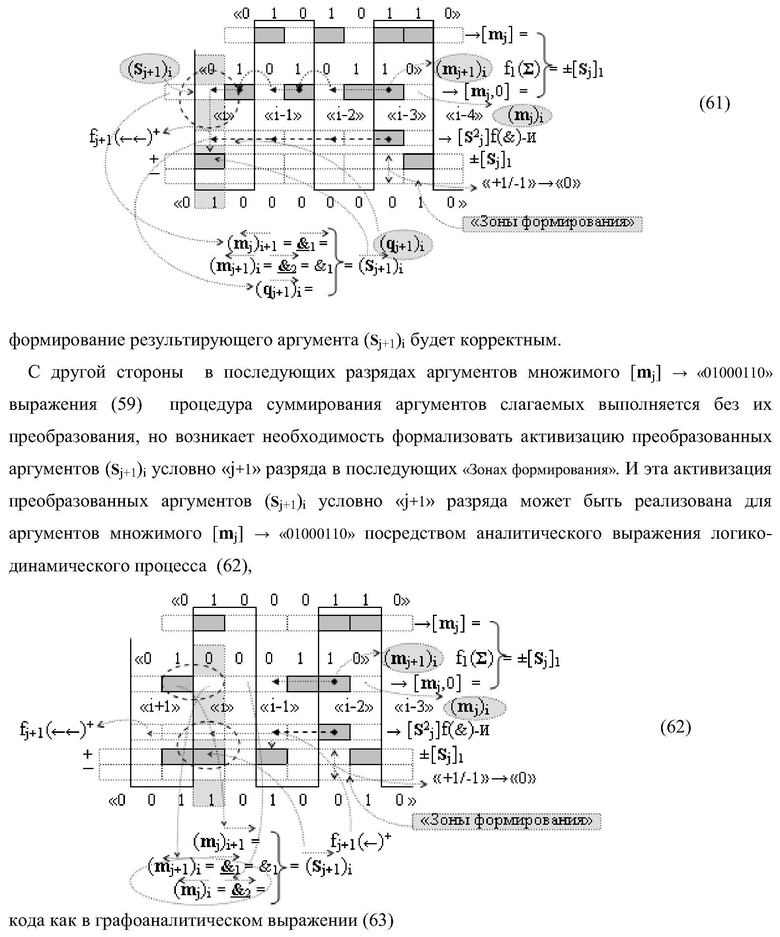












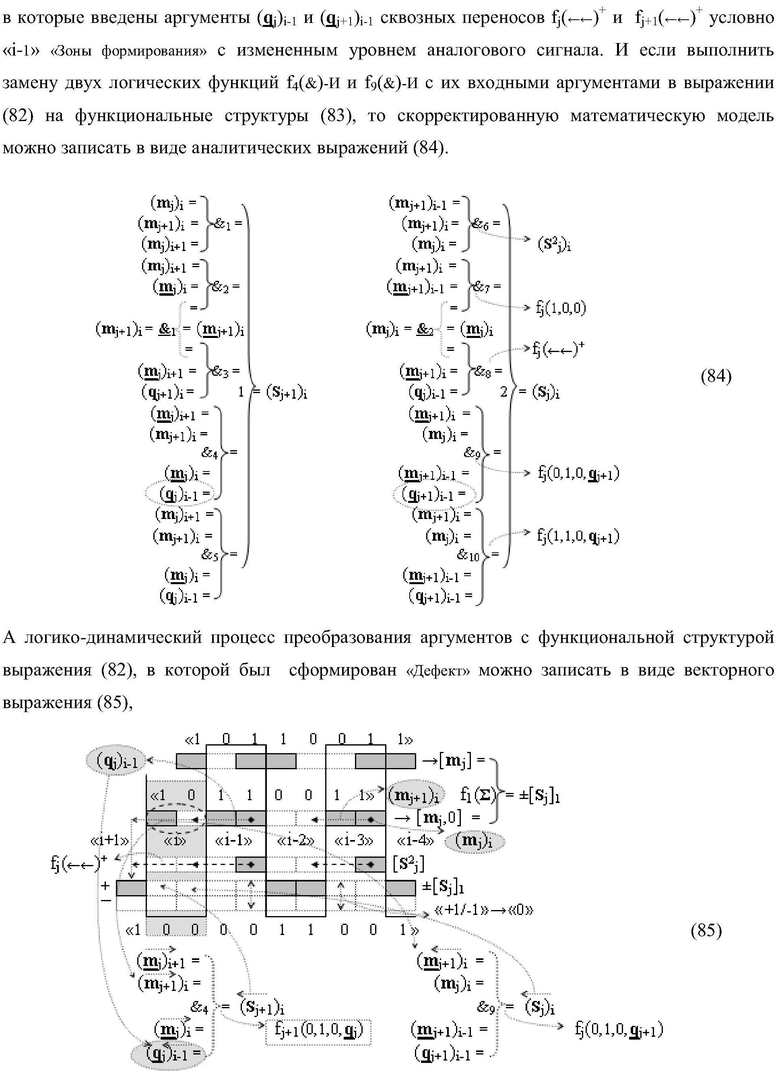
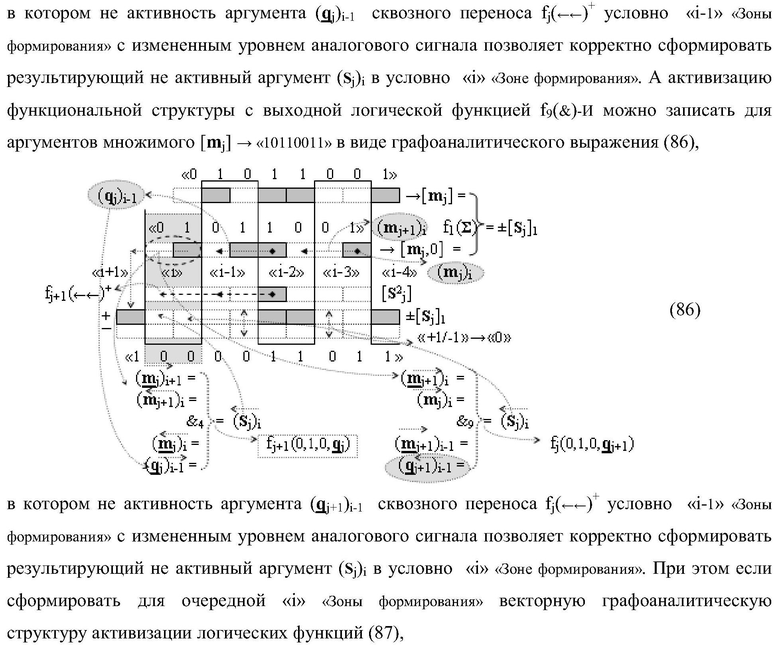
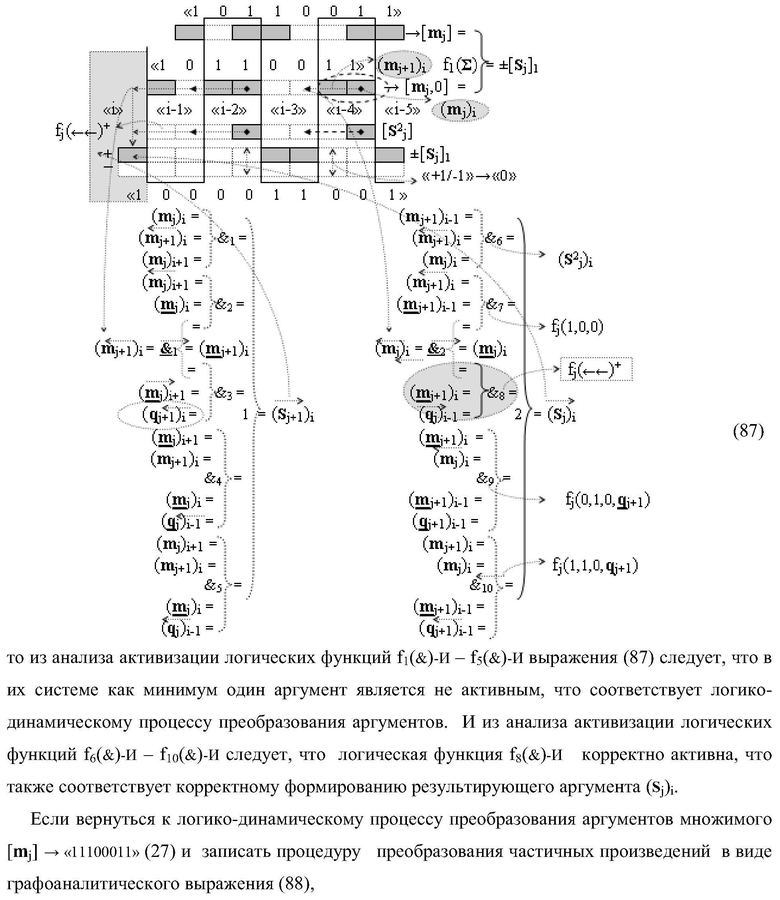







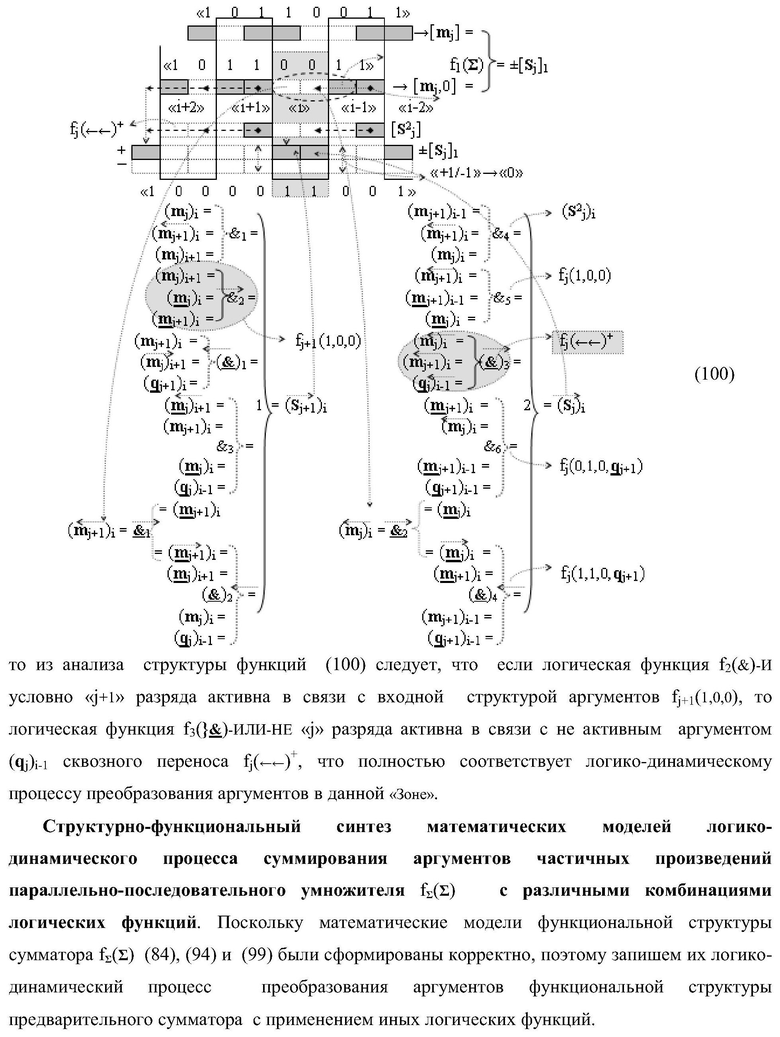














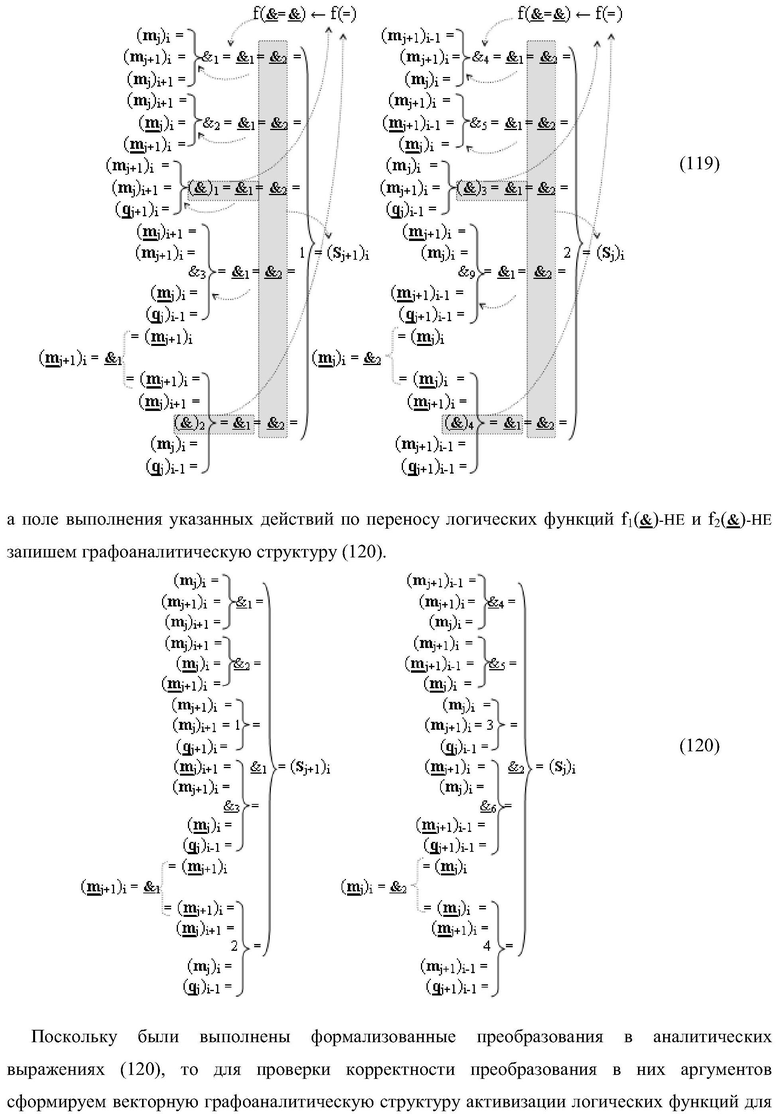

Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств и выполнения арифметических операций суммирования частичных произведений. Техническим результатом является повышение быстродействия процесса предварительного суммирования в параллельно-последовательном умножителе. В одном варианте функциональная структура выполнена в виде двух эквивалентных логических структур условно «j+1»-го и «j»-го разряда с использованием элементов, реализующих логические функции И, ИЛИ и НЕ для формирования выходных аргументов суммы (Sj+1)i и (Sj)i соответственно. 14 н.п. ф-лы.
1. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате, выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(})-ИЛИ и f2(})-ИЛИ, а также логические функции f1(&)-И, f3(&)-И и f6(&)-И, f8(&)-И, при этом вторые функциональные связи логических функций f1(&)-И и f6(&)-И являются функциональными входными связями соответствующих разрядов для приема входного аргумента (m
j+1)i и (m
j)i условно «i» «Зоны формирования», структура «j+1» разряда и «j» разряда также включает логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, в которых функциональная выходная связь является второй функциональной связью логической функции f3(&)-И и логической функции f8(&)-И соответственно, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f2(&)-И, f4(&)-И и f5(&)-И, а в структуру «j» разряда дополнительно введены логические функции f7(&)-И, f9(&)-И и f10(&)-И, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

где 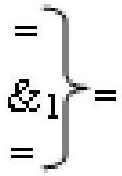 - логическая функция f1(&)-И;
- логическая функция f1(&)-И; 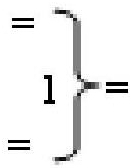 - логическая функция f1(})-ИЛИ;
- логическая функция f1(})-ИЛИ;
«=&
1=» - логическая функция f1(
&
)-НЕ изменения активности входных аналоговых сигналов.
2. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(})-ИЛИ и f2(})-ИЛИ, а также логические функции f1(&)-И, f3(&)-И и f5(&)-И, f7(&)-И, при этом вторые функциональные связи логических функций f1(&)-И и f5(&)-И являются функциональными входными связями для приема входного аргумента (m
j+1)i и (m
j)i соответствующего разряда условно «i» «Зоны формирования», структура «j+1» разряда и «j» разряда также включает логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, в которых функциональная выходная связь является второй функциональной связью соответственно логической функции f3(&)-И и логической функции f7(&)-И, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f2(&)-И, f1(}&
)-ИЛИ-НЕ и f4(&)-И, а в структуру «j» разряда дополнительно введены логические функции f6(&)-И, f2(}&
)-ИЛИ-НЕ и f8(&)-И, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

где 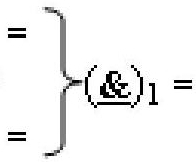 - логическая функция f1(}&
)-ИЛИ-НЕ.
- логическая функция f1(}&
)-ИЛИ-НЕ.
3. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(})-ИЛИ и f2(})-ИЛИ, а также логические функции f1(&)-И, f2(&)-И и f4(&)-И, f5(&)-И, при этом вторые функциональные связи логических функций f1(&)-И и f4(&)-И являются функциональными входными связями для приема входного аргумента (m
j+1)i и (m
j)i соответствующего разряда условно «i» «Зоны формирования», структура «j+1» разряда и «j» разряда также включает логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, в которых функциональная выходная связь является второй функциональной связью соответственно логической функции f2(&)-И и логической функции f5(&)-И, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f1(}&
)-ИЛИ-НЕ, f3(&)-И и f2(}&
)-ИЛИ-НЕ, а в структуру «j» разряда дополнительно введены логические функции f3(}&
)-ИЛИ-НЕ, f6(&)-И и f4(}&
)-ИЛИ-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида
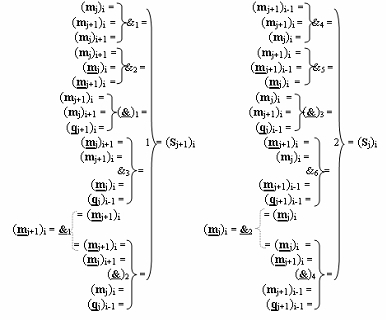
4. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(})-ИЛИ и f2(})-ИЛИ, а также логические функции f1(&)-И, f3(&)-И и f6(&)-И, f8(&)-И, при этом вторые функциональные связи логических функций f1(&)-И и f6(&)-И являются функциональными входными связями соответствующих разрядов для приема входного аргумента (m
j+1)i и (m
j)i соответствующего разряда условно «i» «Зоны формирования», структура «j+1» разряда и «j» разряда также включает логические функции f1(
&
)-НЕ и f3(
&
)-НЕ, в которых функциональная выходная связь является второй функциональной связью соответственно логической функции f3(&)-И и логической функции f8(&)-И, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f2(
&
)-НЕ, f2(&)-И, f4(&)-И и f5(&)-И, а в структуру «j» разряда дополнительно введены логические функции f4(
&
)-НЕ, f7(&)-И, f9(&)-И и f10(&)-И, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

5. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ, f4(&)-И-НЕ, f5(&)-И-НЕ и f6(&)-И-НЕ, а в структуру «j» разряда дополнительно введены логические функции f7(&)-И-НЕ, f8(&)-И-НЕ, f9(&)-И-НЕ, f10(&)-И-НЕ, f11(&)-И-НЕ и f12(&)-И-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

где 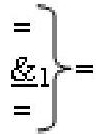 - логическая функция f1(&)-И-НЕ.
- логическая функция f1(&)-И-НЕ.
6. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(
&
)-НЕ и f3(
&
)-НЕ, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f2(
&
)-НЕ, f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ, f4(&)-И-НЕ, f5(&)-И-НЕ и f6(&)-И-НЕ, а в структуру «j» разряда дополнительно введены логические функции f4(
&
)-НЕ, f7(&)-И-НЕ, f8(&)-И-НЕ, f9(&)-И-НЕ, f10(&)-И-НЕ, f11(&)-И-НЕ и f12(&)-И-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида
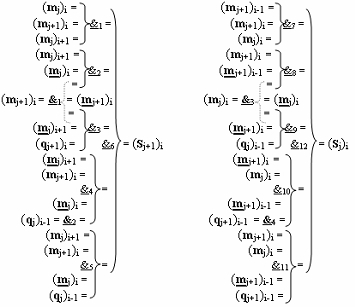
7. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, а также логические функции f3(})-ИЛИ и f8(})-ИЛИ, в которых первая функциональная входная связь является функциональной связью в соответствующих разрядах для приема входного аргумента (m
j+1)i и (m
j)i условно «i» «Зоны формирования», отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f1(})-ИЛИ, f2(})-ИЛИ, f4(})-ИЛИ, f5(})-ИЛИ и f1(&)-И-НЕ, а в структуру «j» разряда дополнительно введены логические функции f6(})-ИЛИ, f7(})-ИЛИ, f9(})-ИЛИ, f10(})-ИЛИ и f2(&)-И-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

8. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(
&
)-НЕ и f3(
&
)-НЕ, а также логические функции f3(})-ИЛИ и f8(})-ИЛИ, в которых первая функциональная входная связь является функциональной связью в соответствующих разрядах для приема входного аргумента (m
j+1)i и (m
j)i условно «i» «Зоны формирования», отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f2(
&
)-НЕ, f1(})-ИЛИ, f2(})-ИЛИ, f4(})-ИЛИ, f5(})-ИЛИ и f1(&)-И-НЕ, а в структуру «j» разряда дополнительно введены логические функции f4(
&
)-НЕ, f6(})-ИЛИ, f7(})-ИЛИ, f9(})-ИЛИ, f10(})-ИЛИ и f2(&)-И-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

9. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(
&
)-НЕ и f3(
&
)-НЕ, а также логические функции f3(})-ИЛИ и f8(})-ИЛИ, в которых первая функциональная входная связь является первой функциональной связью в соответствующих разрядов для приема входного аргумента (m
j+1)i и (m
j)i соответствующего разряда условно «i» «Зоны формирования», отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f2(
&
)-НЕ, f1(})-ИЛИ, f2(})-ИЛИ, f4(})-ИЛИ, f5(})-ИЛИ и f1(&)-И-НЕ, а в структуру «j» разряда дополнительно введены логические функции f4(
&
)-НЕ, f6(})-ИЛИ, f7(})-ИЛИ, f9(})-ИЛИ, f10(})-ИЛИ и f2(&)-И-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

10. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, а также логические функции f1(})-ИЛИ и f2(})-ИЛИ, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f1(}&
)-ИЛИ-НЕ, f2(}&
)-ИЛИ-НЕ, f3(}&
)-ИЛИ-НЕ, f4(}&
)-ИЛИ-НЕ и f5(}&
)-ИЛИ-НЕ, а в структуру «j» разряда дополнительно введены логические функции f6(}&
)-ИЛИ-НЕ, f7(}&
)-ИЛИ-НЕ, f8(}&
)-ИЛИ-НЕ, f9(}&
)-ИЛИ-НЕ и f10(}&
)-ИЛИ-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

11. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(
&
)-НЕ и f3(
&
)-НЕ, а также логические функции f1(})-ИЛИ и f2(})-ИЛИ, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f2(
&
)-НЕ, f1(}&
)-ИЛИ-НЕ, f2(}&
)-ИЛИ-НЕ, f3(}&
)-ИЛИ-НЕ, f4(}&
)-ИЛИ-НЕ и f5(}&
)-ИЛИ-НЕ, а в структуру «j» разряда дополнительно введены логические функции f4(
&
)-НЕ, f6(}&
)-ИЛИ-НЕ, f7(}&
)-ИЛИ-НЕ, f8(}&
)-ИЛИ-НЕ, f9(}&
)-ИЛИ-НЕ и f10(}&
)-ИЛИ-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

12. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f2(
&
)-НЕ и f4(
&
)-НЕ, а также логические функции f1(})-ИЛИ и f2(})-ИЛИ, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f1(
&
)-НЕ, f1(}&
)-ИЛИ-НЕ, f2(}&
)-ИЛИ-НЕ, f3(}&
)-ИЛИ-НЕ, f4(}&
)-ИЛИ-НЕ и f5(}&
)-ИЛИ-НЕ, а в структуру «j» разряда дополнительно введены логические функции f3(
&
)-НЕ, f6(}&
)-ИЛИ-НЕ, f7(}&
)-ИЛИ-НЕ, f8(}&
)-ИЛИ-НЕ, f9(}&
)-ИЛИ-НЕ и f10(}&
)-ИЛИ-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

13. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f2(
&
)-НЕ и f4(
&
)-НЕ, а также логические функции f1(})-ИЛИ и f2(})-ИЛИ, отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ, f4(&)-И-НЕ и f5(&)-И-НЕ, а в структуру «j» разряда дополнительно введены логические функции f6(&)-И-НЕ, f7(&)-И-НЕ, f8(&)-И-НЕ, f9(&)-И-НЕ и f10(&)-И-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

14. Функциональная структура предварительного сумматора параллельно-последовательного умножителя fΣ(Σ) с аргументами множимого [m
j]f(2n) и множителя [n
i]f(2n) в позиционном формате выполнена в виде двух эквивалентных по структуре логических функций условно «j+1» разряд и «j» разряд, которые включают соответственно логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, а также логические функции f1(})-ИЛИ и f3(})-ИЛИ, в которых первые функциональные связи являются функциональными входными связями разрядов для приема входного аргумента (m
j+1)i и (m
j)i условно «i» «Зоны формирования», отличающаяся тем, что в структуру «j+1» разряда дополнительно введены логические функции f2(})-ИЛИ, f1(&)-И-НЕ, f2(&)-И-НЕ и f3(&)-И-НЕ, а в структуру «j» разряда дополнительно введены логические функции f4(})-ИЛИ, f4(&)-И-НЕ, f5(&)-И-НЕ и f6(&)-И-НЕ, при этом функциональные связи логических функций в структуре предварительного сумматора выполнены в соответствии с математической моделью вида

| ДЖ.УЭЙКЕРЛИ | |||
| Проектирование цифровых устройств, т.1 | |||
| - М.: Постмаркет, 2002, с.508 | |||
| ФУНКЦИОНАЛЬНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНОГО СУММАТОРА С ПРЕДВАРИТЕЛЬНО ВВОДИМЫМИ ПЕРЕНОСАМИ (ВАРИАНТЫ) | 2008 |
|
RU2381545C2 |
| ВХОДНАЯ СТРУКТУРА ПАРАЛЛЕЛЬНОГО СУММАТОРА В ПОЗИЦИОННО-ЗНАКОВЫХ КОДАХ f(+/-) (ВАРИАНТЫ) | 2007 |
|
RU2378682C2 |
| Аппарат для отделения сатурационной грязи от сахарного сока | 1929 |
|
SU23363A1 |
| JP 1304532 A, 08.12.1989 | |||
| JP 63197227 A, 16.08.1988. | |||
Авторы
Даты
2011-06-27—Публикация
2010-03-04—Подача