Текст описания приведен в факсимильном виде. 
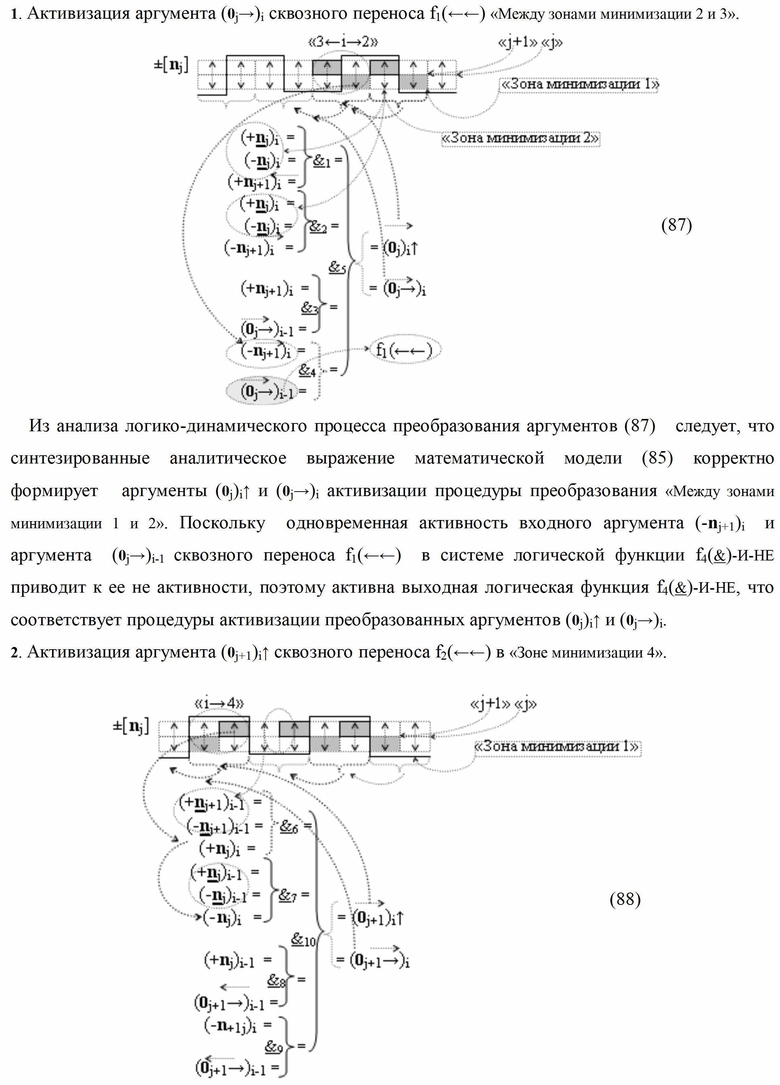
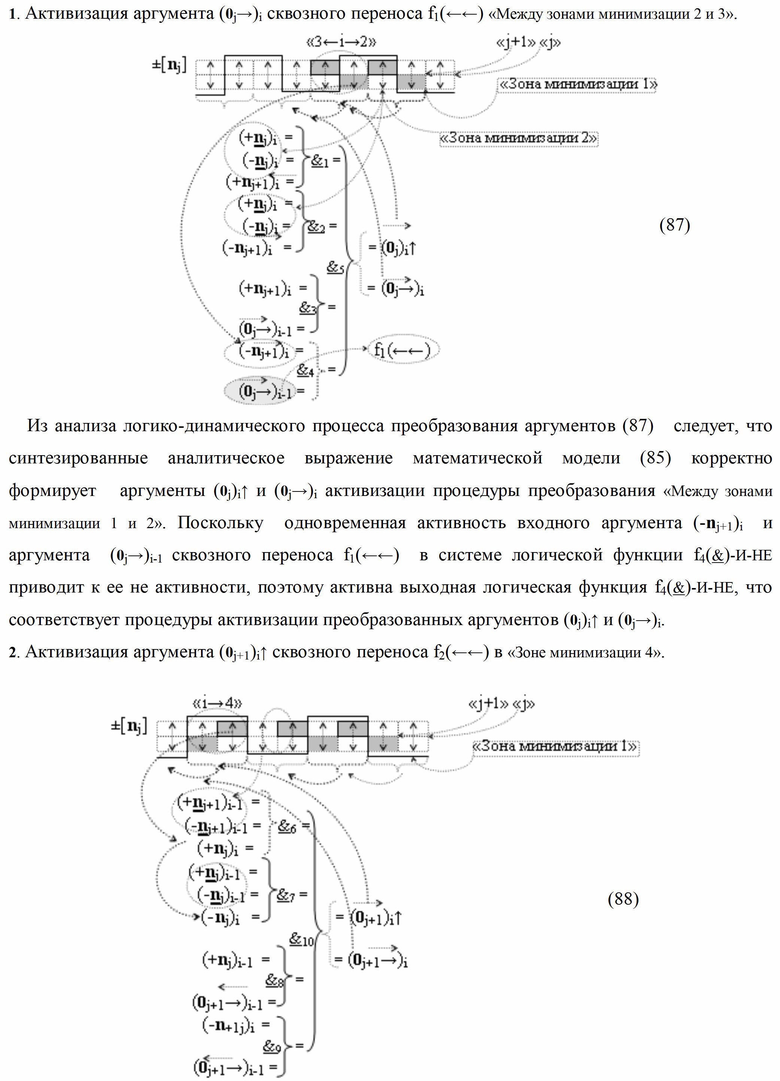
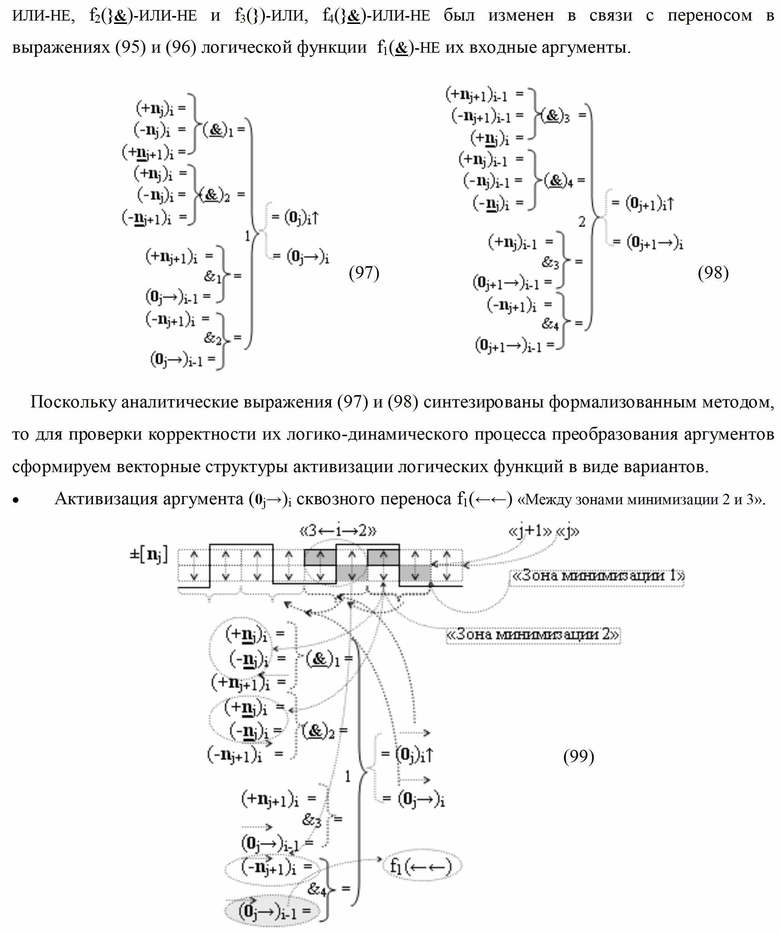
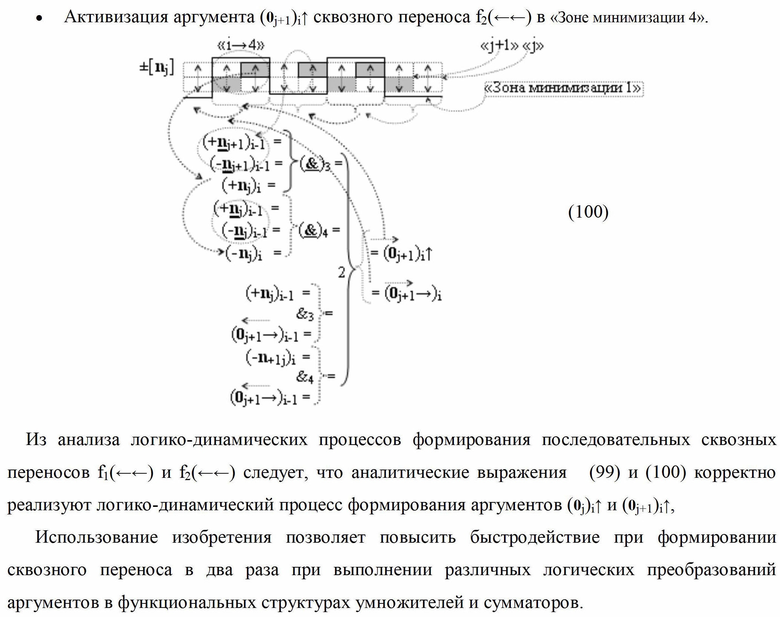
Изобретение относится к вычислительной технике и может быть использовано при построении арифметических устройств и выполнении арифметических операций суммирования и вычитания. Техническим результатом является повышение быстродействия процесса преобразования аргументов при формировании сквозного последовательного переноса f(←←). В одном варианте функциональная структура выполнена с использованием элементов, реализующих логические функции И, ИЛИ и НЕ. При этом функциональная структура выполнена для условно «j»-го и «j+1»-го разрядов в виде структур функций f1,2(←←00), в которых формируют аргументы переноса (0j→)i, (0j+1→)i, и структур функций f1,2(←←11), в которых формируют аргументы переноса (-0j→)i, (-0j+1→)i. 5 н.п. ф-лы.
1. Способ формирования сквозного последовательного переноса в процедуре логического дифференцирования d/dn позиционных аргументов [m
j]f(2n) с учетом их знака и с целью формирования позиционно-знаковой структуры ±[m
j]f(+/-)min с минимизированным числом активных в ней аргументов включает анализ в условной «i» зоне минимизации на логическом уровне как одновременную активность группы аргументов аналоговых сигналов, так и их возможную комбинацию с аргументом локального переноса (0
j→)i-1 предыдущей зоны минимизации и формируют аргументы (1
j)i и (1
j+1)i условно «j» разряда и условно «j+1» разряда «i» зоны минимизации и аргументы переноса (0
j→)i и (0
j+1→)i в очередную зону минимизации, отличающийся тем, что в условной «i» зоне минимизации выполняют анализ позиционных аргументов [m
j]f(2n) и аргументов переноса (0
j→)i и (0
j+1→)i посредством функциональных логических структур f1,2(←←00) и f1,2(←←11), при этом функциональные логические структуры f1,2(←←00) формируют как аргумент аналогового сигнала (1
j)i и аргумент переноса и (0
j→)i условно «j» разряда и аргумента аналогового сигнала (1
j+1)i и аргумент переноса (0
j+1→)i условно «j+1» разряда для активизации активного аргумента позиционной структуры [m
j]f(2n), а функциональные логические структуры f1,2(←←11) формируют как два аргумента аналогового сигнала (±1
j↓)i, (±1
j↓→)i условно «j» разряда и два аргумента (±1
j+1↓)i и (±1
j+1↓→)i условно «j+1» разряда, активизирующие неактивный аргумент условного логического нуля «0» → «+1/-1», так и формируют переносы (-0
j→)i и (-0
j+1→)i соответственно, при этом в функциональных логических структурах f1,2(←←00) анализируют на логическом уровне как активность аргумента (m
j)i и неактивность аргументов (m
j+1)i, «i» зоны минимизации, (m
j+1)i-1 и (m
j)i-1 «i-1» зоны минимизации, так и активность аргумента (m
j+1)i-1 «i-1» зоны минимизации и неактивность аргументов (m
j)i+1 «i+1» зоны минимизации, (m
j)i «i» зоны минимизации и (m
j+1)i-1 «i-1» зоны минимизации соответственно, при этом для активизации аргументов переноса (0
j→)i и (0
j+1→)i дополнительно логически анализируют аргумент переноса (0
j→)i-1 и (0
j+1→)i-1 «i-1» зоны минимизации совместно с активным аргументом (m
j)i неактивным аргументом (m
j+1)i и с активным аргументом (m
j+1)i «i» зоны минимизации и неактивным аргументом (m
j)i+1 «i+1» зоны минимизации соответственно, при этом в функциональных логических структурах f1,2(←←11) для преобразования неактивного аргумента логического нуля «0» → «+1/-1» позиционной структуры [m
j]f(2n) в положительный и условно отрицательный активные аргументы аналогового сигнала (±1
j↓)i и (±1
j↓→)i в условно «j» разряде и активные аргументы сигнала (±1
j+1↓)i и (±1
j+1↓→)i условно «j+1» разряда анализируют на логическом уровне активность аргумента (m
j+1)i «i» зоны минимизации (m
j+1)i-2, (m
j)i-2 «i-2» зоны минимизации и неактивность аргумента (m
j)i «i» зоны минимизации, так и активность аргументов (m
j)i+1 «i+1» зоны минимизации, (m
j)i «i» зоны минимизации, (m
j+1)i-1 «i-1» зоны минимизации и неактивность аргумента (m
j+1)i «i» зоны минимизации соответственно, при этом для активизации аргументов переноса (-0
j→)i и (-0
j+1→)i дополнительно логически анализируют активный аргумент переноса (-0
j→)i-1 и (-0
j+1→)i-1 «i-1» зоны минимизации совместно с активным аргументом (m
j+1)i, неактивным аргументом (m
j)i «i» зоны минимизации и с активным аргументом (m
j)i+1 «i+1» зоны минимизации, неактивным аргументом (m
j+1)i «i» зоны минимизации соответственно, при этом логико-динамический процесс преобразования аргументов аналоговых сигналов для последовательно неактивных позиционных аргументов [m
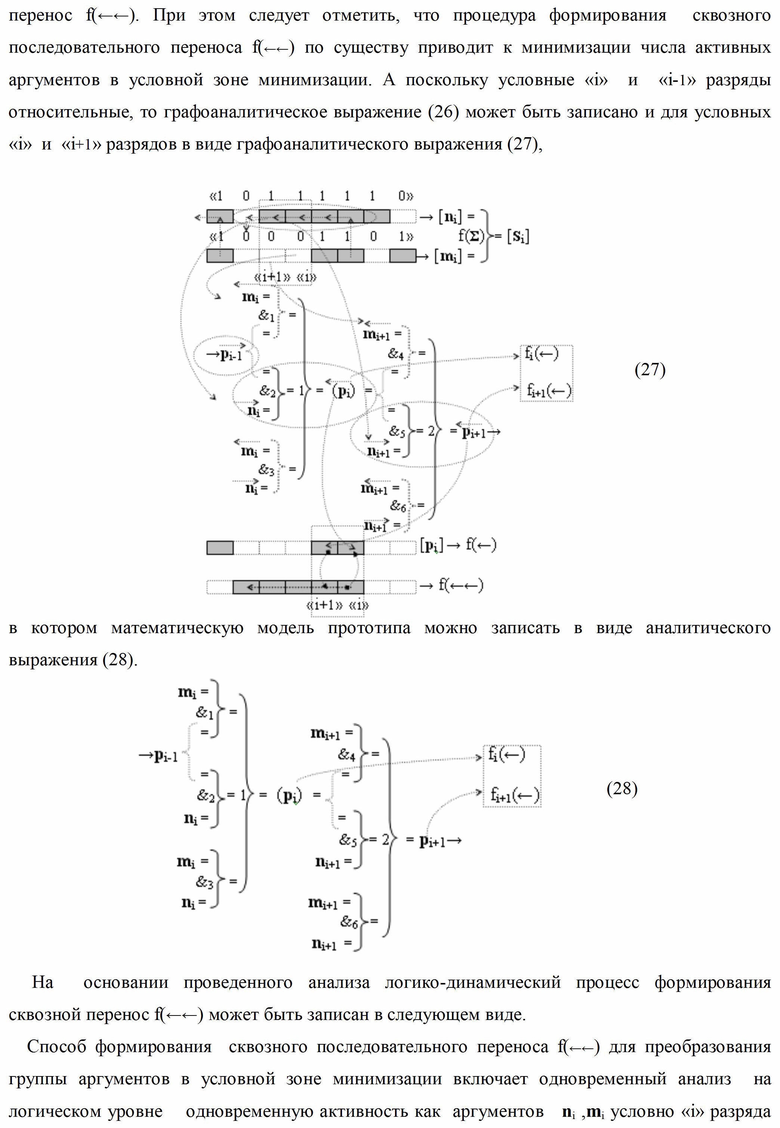
j]f(2n) в зоне минимизации соответствует графоаналитической модели вида
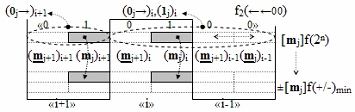
для последовательно неактивных позиционных аргументов [m
j]f(2n) между зонами минимизации соответствует графоаналитической модели вида
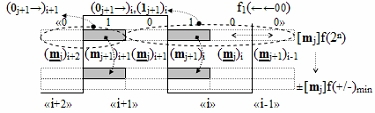
для последовательно активных позиционных аргументов [m
j]f(2n) в зоне минимизации соответствует графоаналитической модели вида
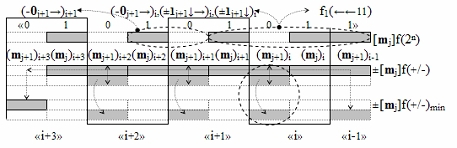
для последовательно активных позиционных аргументов [m
j]f(2n) между зонами минимизации соответствует графоаналитической модели вида
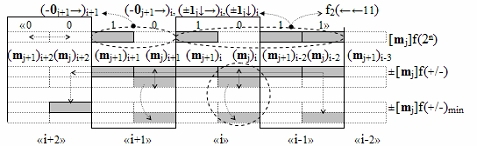
где ±[m
j]f(+/-) - промежуточная позиционно-знаковая структура промежуточных аргументов, которая подвергается логическому дифференцированию.
2. Функциональная структура сквозного последовательного переноса процедуры логического дифференцирования d/dn позиционных аргументов [m
j]f(2n) с учетом их знака с целью формирования позиционно-знаковой структуры ±[m
j]f(+/-)min с минимизированным числом активных в ней аргументов, которая включает логические функции f1(})-ИЛИ и f3(})-ИЛИ, в которых функциональные выходные связи являются функциональными выходными связями структуры условной «i» зоны минимизации для формирования аргумента переноса (0
j+1→)i и (0
j→)i, в которых две функциональные входные связи являются функциональными выходными связями логических функций f1(&)-И, f2(&)-И и f5(&)-И, f6(&)-И, при этом функциональная входная связь логической функции f2(&)-И является функциональной входной связью структуры для приема аргумента (0
j+1→)i-1 условной «i-1» зоны минимизации, структура также включает логические функции f3(&)-И и f8(&)-И, в которых функциональная входная связь является функциональной входной связью структуры для приема входных аргументов (m
j)i и (m
j+1)i соответственно, отличающаяся тем, что функциональная структура выполнена для условно «j» и «j+1» разряда в виде двух структур функций f1,2(←←00) и f1,2(←←11), в которых формируют как аргументы переноса (0
j→)i, (0
j+1→)i для активизации активного аргумента позиционной структуры [m
j]f(2n) и аргументы переноса (-0
j→)i, (-0
j+1→)i активизирующие неактивный аргумент условного логического нуля «0» → «+1/-1» позиционной структуры [m
j]f(2n), так и дополнительные аргументы (1
j)i, (1
j→)i условно «j» разряда и (1
j+1)i, (1
j+1→)i условно «j+1» разряда для корректировки позиционной структуры [m
j]f(2n) перед логическим дифференцированием и дополнительные аргументы (±1
j↓)i, (±1
j↓→)i условно «j» разряда и дополнительные аргументы (±1
j+1↓)i и (±1
j+1↓→)i условно «j+1» разряда для активизации неактивного аргумента условного логического нуля «0» → «+1/-1» в позиционной структуре [m
j]f(2n), а для этого в структуру функций f1,2(←←00) условно «j» и «j+1» разряд введены дополнительные логические функции f1(
&
)-НЕ и f2(
&
)-НЕ, а в структуру функций f1,2(←←11) условно «j» и «j+1» разряд введены дополнительные логические функции f4(&)-И, f2(})-ИЛИ и f7(&)-И, f4(})-ИЛИ соответственно, при этом функциональные связи в функциональной структуре сквозного последовательного переноса f1,2(←←00) выполнены в соответствии с математической моделью вида
и переноса f1,2(←←11) выполнены в соответствии с математической моделью вида
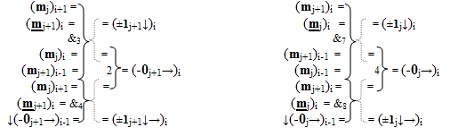
где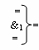 
- логическая функция f1(&)-И; 
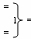- логическая функция f1(})-ИЛИ.
3. Функциональная структура сквозного последовательного переноса процедуры логического дифференцирования d/dn позиционных аргументов [m
j]f(2n) с учетом их знака с целью формирования позиционно-знаковой структуры ±[m
j]f(+/-)min с минимизированным числом активных в ней аргументов, отличающаяся тем, что функциональная структура выполнена для условно «j» и «j+1» разряда в виде двух структур функций f1,2(←←00) и f1,2(←←11), в которых формируют как аргументы переноса (0
j→)i, (0
j+1→)i для активизации активного аргумента позиционной структуры [m
j]f(2n) и аргументы переноса (-0
j→)i, (-0
j+1→)i, активизирующие неактивный аргумент условного логического нуля «0» → «+1/-1» позиционной структуры [m
j]f(2n), так и дополнительные аргументы (1
j)i, (1
j→)i условно «j» разряда и (1
j+1)i, (1
j+1→)i условно «j+1» разряда для корректировки позиционной структуры [m
j]f(2n) перед логическим дифференцированием и дополнительные аргументы (±1
j↓)i, (±1
j↓→)i условно «j» разряда и дополнительные аргументы (±1
j+1↓)i и (±1
j+1↓→)i условно «j+1» разряда для активизации неактивного аргумента условного логического нуля «0» → «+1/-1» в позиционной структуре [m
j]f(2n), а для этого в структуру функций f1,2(←←00) условно «j» и «j+1» разрядов введены дополнительные логические функции f1(
&
)-НЕ, f2(
&
)-НЕ, f3(
&
)-НЕ, f1(&)-И-НЕ, f2(&)-И-НЕ, f3(&)-И-НЕ и f4(
&
)-НЕ, f5(
&
)-НЕ, f6(
&
)-НЕ, f4(&)-И-НЕ, f5(&)-И-НЕ, f6(&)-И-НЕ соответственно, а в структуру функций f1,2(←←11) условно «j» и «j+1» разрядов введены дополнительные логические функции f7(
&
)-НЕ, f8(
&
)-НЕ, f7(&)-И-НЕ, f8(&)-И-НЕ, f9(&)-И-НЕ и f9(
&
)-НЕ, f10(
&
)-НЕ, f10(&)-И-НЕ, f11(&)-И-НЕ и f12(&)-И-НЕ соответственно, при этом функциональные связи в функциональной структуре сквозного последовательного переноса f1,2(←←00) выполнены в соответствии с математической моделью вида
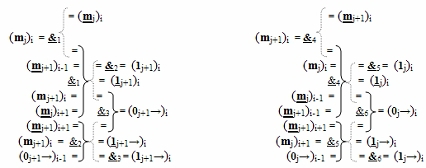
и переноса f1,2(←←11) выполнены в соответствии с математической моделью вида
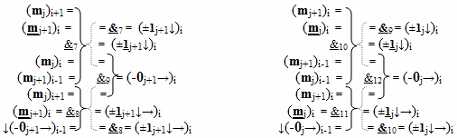
где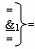 
- логическая функция f1(&)-И-НЕ.
4. Функциональная структура сквозного последовательного переноса процедуры логического дифференцирования d/dn позиционных аргументов [m
j]f(2n) с учетом их знака с целью формирования позиционно-знаковой структуры ±[m
j]f(+/-)min с минимизированным числом активных в ней аргументов, которая включает логические функции f1(})-ИЛИ, f3(})-ИЛИ, f1(&)-И, f2(&)-И, f3(&)-И и f4(&)-И, отличающаяся тем, что функциональная структура выполнена для условно «j» и «j+1» разрядов в виде двух структур функций f1,2(←←00) и f1,2(←←11), в которых формируют как аргументы переноса (0
j→)i, (0
j+1→)i для активизации активного аргумента позиционной структуры [m
j]f(2n) и аргументы переноса (-0
j→)i, (-0
j+1→)i, активизирующие неактивный аргумент условного логического нуля «0» → «+1/-1» позиционной структуры [m
j]f(2n), так и дополнительные аргументы (1
j)i, (1
j→)i условно «j» разряда и (1
j+1)i, (1
j+1→)i условно «j+1» разряда для корректировки позиционной структуры [m
j]f(2n) перед логическим дифференцированием и дополнительные аргументы (±1
j↓)i, (±1
j↓→)i условно «j» разряда и дополнительные аргументы (±1
j+1↓)i и (±1
j+1↓→)i условно «j+1» разряда для активизации неактивного аргумента условного логического нуля «0» → «+1/-1» в позиционной структуре [m
j]f(2n), а для этого в структуру функций f1,2(←←00) условно «j» и «j+1» разрядов введены дополнительные логические функции f1(
&
)-НЕ, f2(
&
)-НЕ, f3(
&
)-НЕ, f2(})-ИЛИ и f4(
&
)-НЕ, f5(
&
)-НЕ, f6(
&
)-НЕ и f4(})-ИЛИ соответственно, а в структуру функций f1,2(←←11) условно «j» и «j+1» разрядов введены дополнительные логические функции f7(
&
)-НЕ, f8(
&
)-НЕ, f5(})-ИЛИ, f6(})-ИЛИ и f9(
&
)-НЕ, f10(
&
)-НЕ, f7(})-ИЛИ, f8(})-ИЛИ соответственно, при этом функциональные связи в функциональной структуре сквозного последовательного переноса f1,2(←←00) выполнены в соответствии с математической моделью вида
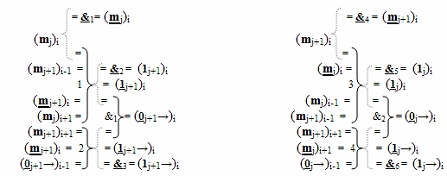
и переноса f1,2(←←11) выполнены в соответствии с математической моделью вида
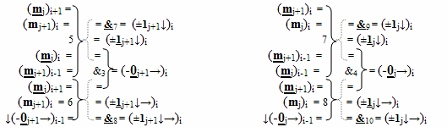
5. Функциональная структура сквозного последовательного переноса процедуры логического дифференцирования d/dn позиционных аргументов [m
j]f(2n) с учетом их знака с целью формирования позиционно-знаковой структуры ±[m
j]f(+/-)min с минимизированным числом активных в ней аргументов, отличающаяся тем, что функциональная структура выполнена для условно «j» и «j+1» разрядов в виде двух структур функций f1,2(←←00) и f1,2(←←11), в которых формируют как аргументы переноса (0
j→)i, (0
j+1→)i для активизации активного аргумента позиционной структуры [m
j]f(2n) и аргументы переноса (-0
j→)i, (-0
j+1→)i, активизирующие неактивный аргумент условного логического нуля «0» → «+1/-1» позиционной структуры [m
j]f(2n), так и дополнительные аргументы (1
j)i, (1
j→)i условно «j» разряда и (1
j+1)i, (1
j+1→)i условно «j+1» разряда для корректировки позиционной структуры [m
j]f(2n) перед логическим дифференцированием и дополнительные аргументы (±1
j↓)i, (±1
j↓→)i условно «j» разряда и дополнительные аргументы (±1
j+1↓)i и (±1
j+1↓→)i условно «j+1» разряда для активизации неактивного аргумента условного логического нуля «0» → «+1/-1» в позиционной структуре [m
j]f(2n), а для этого в структуру функций f1,2(←←00) условно «j» и «j+1» разрядов введены дополнительные логические функции f1(
&
)-НЕ, f1(}&
)-ИЛИ-НЕ, f2(}&
)-ИЛИ-НЕ, f3(}&
)-ИЛИ-НЕ и f2(
&
)-НЕ, f4(}&
)-ИЛИ-НЕ, f5(}&
)-ИЛИ-НЕ, f6(}&
)-ИЛИ-НЕ соответственно, а в структуру функций f1,2(←←11) условно «j» и «j+1» разрядов введены дополнительные логические функции f6(}&
)-ИЛИ-НЕ, f7(}&
)-ИЛИ-НЕ, f8(}&
)-ИЛИ-НЕ и f9(}&
)-ИЛИ-НЕ, f10(}&
)-ИЛИ-НЕ, f11(}&
)-ИЛИ-НЕ соответственно, при этом функциональные связи в функциональной структуре сквозного последовательного переноса f1,2(←←00) выполнены в соответствии с математической моделью вида
и переноса f1,2(←←11) выполнены в соответствии с математической моделью вида
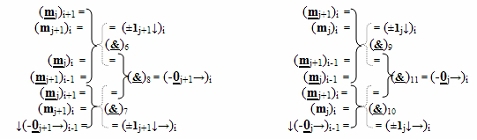
где 
- логическая функция f1(}&
)-ИЛИ-НЕ.
| УЭЙКЕРЛИ Д | |||
| Проектирование цифровых устройств | |||
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| - М.: «Постмаркет», 2002, с.502, рис.5.86 | |||
| Блок формирования сквозного переноса в сумматоре | 1984 |
|
SU1196852A1 |
| Устройство для формирования сигнала переноса при суммировании многофазных кодов | 1989 |
|
SU1633393A1 |
| RU 2007146288 A, 27.06.2009 | |||
| JP 2002312160 A, 25.10.2002 | |||
| US 5600583 A, 04.02.1997. | |||
