Патентон — пантеон патентов

(19)

RU

(11)

2 534 499

(13)

C2

(51)

МПК

G06F11/08(2006-01-01)

G11C29/42(2006-01-01)

H03M13/11(2006-01-01)

(21) (22)

Заявка

2013112828/08, 2013-03-25

(24)

Дата начала отсчета патента

2013-03-25

(22)

дата подачи заявки

2013-03-25

(45)

опубликовано

2014-11-27

(72)

авторы

Борисов Константин ЮрьевичПавлов Александр АлексеевичЦарьков Алексей НиколаевичХоруженко Олег ВладимировичГусев Александр Викторович

(73)

патентообладатели

Межрегиональное Общественное Учреждение Инженерной Физики"Федеральное Государственное Научное Учреждение Информатизации Образования" Российская Академия Образования

(56)

Документы, цитированные в отчете о поиске

US 5933436 A, 03.08.1999JP 58041499 A, 10.03.1983KR 930011573 B1, 11.12.1993

УСТРОЙСТВО ХРАНЕНИЯ И ПЕРЕДАЧИ ДАННЫХ С ИСПРАВЛЕНИЕМ ОШИБОК В ДВУХ БАЙТАХ ИНФОРМАЦИИ Российский патент 2014 года по МПК G06F11/08 G11C29/42 H03M13/11 

Описание патента на изобретение RU2534499C2

Изобретение относится к вычислительной технике и может быть использовано для повышения достоверности функционирования запоминающих устройств.

Известно самокорректирующееся устройство [1], использующее корректирующий код (наиболее часто используется код Хемминга, корректирующий одиночную ошибку и обнаруживающий двойную ошибку).

Недостатком устройства является низкая обнаруживающая способность кода, так как обнаруживаются только двойные ошибки.

Наиболее близким по техническому решению является устройство хранения и передачи данных с исправлением ошибок в байте информации и обнаружением ошибок в байтах информации [2], содержащее узел памяти, входной блок кодирования, выходной блок кодирования, блок вычисления синдрома ошибки, дешифратор, коммутатор, блок коммутаторов, корректор, блок корректоров, первый блок элементов ИЛИ, второй блок элементов ИЛИ, инвертор, элемент И, блок элементов И, вход установки устройства в нулевое состояние, вход записи, вход считывания, адресные входы, двадцатичетырехразрядные информационные входы, вход синхронизации, информационные выходы, выход сигнала «ошибка», вход установки в нулевое состояние, вход записи, вход считывания, адресные входы подключены соответственно к первому, второму, третьему и четвертому входам узла памяти, вход синхронизации подключен к пятому входу узла памяти и к первому входу блока элементов И, информационные входы подключены к шестым входам узла памяти и к входам входного блока кодирования, который формирует значения контрольных разрядов r1 r2, r3, r4, r5, r6, r7, r8 путем сложения по модулю 2 информационных символов x1, x2 x3, z1 z2 z3, a1 a2 a3, c1 c2 c3, e1 e2 e3, f1 f2 f3, g1 g2 g3, h1 h2 h3, поступающих на входы входного блока кодирования, в соответствии с правилом: r1x1⊕z1⊕a1⊕c1⊕e1⊕f1⊕g1⊕h1; r2=x2⊕z2⊕a2⊕c2⊕e2⊕f2⊕g2⊕h2; r3=x3⊕z3⊕a3⊕c3⊕e3⊕f3⊕g3⊕h3; r4=x1⊕z3⊕a2⊕c2⊕e1⊕e3⊕f1⊕f2⊕g1⊕g2⊕g3; r5=x2⊕x3⊕z1⊕a3⊕c1⊕c3⊕e1⊕e2⊕f2⊕g1⊕g2⊕g3; r6=x3⊕z2⊕z3⊕a1⊕c1⊕c2⊕e2⊕f1⊕f3⊕g1⊕g2⊕g3; r7=x3⊕z3⊕a1⊕a3⊕c2⊕e1⊕f2⊕g1⊕g2⊕g3; r8=x1⊕x2⊕z2⊕a2⊕a3⊕c3⊕e3⊕f2⊕f3⊕g1⊕g2⊕g3, которые поступают на седьмые входы узла памяти, информационные выходы узла памяти подключены соответственно к первым входам корректора, блока корректоров и к входам выходного блока кодирования, который формирует значения проверочных контрольных разрядов r1П, r2П, r3П, r4П, r5П, r6П r7П r8П путем сложения по модулю 2 информационных символов x1Пx2Пx3П, z1Пz2Пz3П, a1Пa2Пa3П, c1Пc2Пc3П, e1Пe2Пe3П, f1Пf2Пf3П, g1Пg2Пg3П, h1Пh2Пh3П, поступающих на входы входного блока кодирования с информационных выходов узла памяти, в соответствии с правилом:: r1П=x1П⊕z1П⊕a1П⊕c1П⊕e1П⊕f1П⊕g1П⊕h1П; r2П=x2П⊕z2П⊕a2П⊕c2П⊕e2П⊕f2П⊕g2П⊕h2П; r3П=x3П⊕z3П⊕a3П⊕c3П⊕e3П⊕f3П⊕g3П⊕h3П; r4П=x1П⊕z3П⊕a2П⊕a3П⊕c2П⊕e1П⊕e3П⊕f1П⊕f2П⊕g1П⊕g2П⊕g3П; r5П=x2П⊕x3П⊕z1П⊕a3П⊕c1П⊕c3П⊕e1П⊕e2П⊕f2П⊕g1П⊕g2П⊕g3П; r6П=x3П⊕z2П⊕z3П⊕a1П⊕c1П⊕c2П⊕e2П⊕f1П⊕f3П⊕g1П⊕g2П⊕g3П; r7П=x3П⊕z3П⊕a1П⊕a3П⊕c2П⊕e1П⊕f2П⊕g1П⊕g2П⊕g3П; r8П=x1П⊕x2П⊕z2П⊕a2П⊕a3П⊕c3П⊕e3П⊕f2П⊕f3П⊕g1П⊕g2П⊕g3П, выходы выходного блока кодирования подключены к первым входам блока вычисления синдрома ошибки, к вторым входам которого подключены выходы контрольных разрядов узла памяти, первые выходы блока вычисления синдрома ошибки подключены к первым входам дешифратора, к первым входам коммутатора, к входам первого блока элементов ИЛИ и к первым входам блока коммутаторов, вторые выходы блока вычисления синдрома ошибки подключены к вторым входам дешифратора и к вторым входам первого блока элементов ИЛИ, выходы дешифратора подключены к входам второго блока элементов ИЛИ, при этом первый выход дешифратора подключен к второму входу коммутатора, а вторые выходы подключены к вторым входам блока коммутаторов, выход второго блока элементов ИЛИ через инвертор подключен к первому входу элемента И, второй вход которого подключен к выходу первого блока элементов ИЛИ, выход элемента И является выходом сигнала «ошибка», выходы коммутатора подключены к вторым входам корректора, выходы блока коммутаторов подключены к вторым входам блока корректоров, выходы корректора и блока корректоров подключены к вторым входам блока элементов И, выходы которого являются информационными выходами устройства.

Недостатком устройства является низкая корректирующая способность ошибок, так как корректируются только одиночные байты ошибок.

Целью изобретения является повышение отказоустойчивости устройства за счет коррекции ошибок в двух байтах информации.

Поставленная цель достигается тем, что устройство, содержащие узел памяти, входной блок кодирования, выходной блок кодирования, блок вычисления синдрома ошибки, дешифратор, корректор, блок элементов И, вход установки устройства в нулевое состояние, вход записи, вход считывания, адресные входы, информационные входы, вход синхронизации, информационные выходы, отличающееся тем, что дополнительно содержит блок хранения векторов ошибок, вход установки в нулевое состояние, вход записи, вход считывания, адресные входы подключены соответственно к первому, второму, третьему и четвертому входам узла памяти, вход синхронизации подключен к пятому входу узла памяти и к первому входу блока элементов И, информационные входы подключены к шестым входам узла памяти и к входам входного блока кодирования, который формирует значения контрольных разрядов 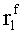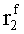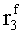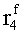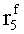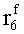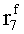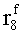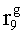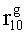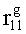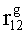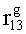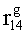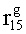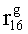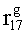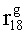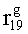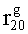r 1 f , r 2 f , r 3 f , r 4 f , r 5 f , r 6 f , r 7 f , r 8 f , r 9 g , r 10 g , r 11 g , r 12 g , r 13 g , r 14 g , r 15 g , r 16 g , r 17 g , r 18 g , r 19 g , r 20 g , путем сложения по модулю 2 информационных символов a0a1a2a3, b0b1b32b3, c0c1c2c3, d0d1d2d3, e0e1e2e3, f0f1f2f3, g0g1g2g3, h0h1h2h3, i0i1i2i3, j0j1j2j3, k0k1k2k3, l0l1l2l3, m0m1m2m3, n0n1n2n3, o0o1o2o3, p0p1p2p3, поступающих на входы входного блока кодирования, в соответствии с правилом:

r 1 f = a 0 ⊕ b 0 ⊕ c 0 ⊕ d 0 ⊕ e 0 ⊕ f 0 ⊕ g 0 ⊕ h 0 ⊕ i 0 ⊕ j 0 ⊕ k 0 ⊕ l 0 ⊕ m 0 ⊕ n 0 ⊕ o 0 ;

r 2 f = a 1 ⊕ b 1 ⊕ c 1 ⊕ d 1 ⊕ e 1 ⊕ f 1 ⊕ g 1 ⊕ h 1 ⊕ i 1 ⊕ j 1 ⊕ k 1 ⊕ l 1 ⊕ m 1 ⊕ n 1 ⊕ o 1 ;

r 3 f = a 2 ⊕ b 2 ⊕ c 2 ⊕ d 2 ⊕ e 2 ⊕ f 2 ⊕ g 2 ⊕ h 2 ⊕ i 2 ⊕ j 2 ⊕ k 2 ⊕ l 2 ⊕ m 2 ⊕ n 2 ⊕ o 2 ;

r 4 f = a 3 ⊕ b 3 ⊕ c 3 ⊕ d 3 ⊕ e 3 ⊕ f 3 ⊕ g 3 ⊕ h 3 ⊕ i 3 ⊕ j 3 ⊕ k 3 ⊕ l 3 ⊕ m 3 ⊕ n 3 ⊕ o 3 ;

r 5 f = b 0 ⊕ c 0 ⊕ d 0 ⊕ e 0 ⊕ f 0 ⊕ g 0 ⊕ h 0 ⊕ i 0 ⊕ j 0 ⊕ k 0 ⊕ l 0 ⊕ m 0 ⊕ n 0 ⊕ o 0 ⊕ p 0 ;

r 6 f = b 1 ⊕ c 1 ⊕ d 1 ⊕ e 1 ⊕ f 1 ⊕ g 1 ⊕ h 1 ⊕ i 1 ⊕ j 1 ⊕ k 1 ⊕ l 1 ⊕ m 1 ⊕ n 1 ⊕ o 1 ⊕ p 1 ;

r 7 f = b 2 ⊕ c 2 ⊕ d 2 ⊕ e 2 ⊕ f 2 ⊕ g 2 ⊕ h 2 ⊕ i 2 ⊕ j 2 ⊕ k 2 ⊕ l 2 ⊕ m 2 ⊕ n 2 ⊕ o 2 ⊕ p 2 ;

r 8 f = b 3 ⊕ c 3 ⊕ d 3 ⊕ e 3 ⊕ f 3 ⊕ g 3 ⊕ h 3 ⊕ i 3 ⊕ j 3 ⊕ k 3 ⊕ l 3 ⊕ m 3 ⊕ n 3 ⊕ o 3 ⊕ p 3 ;

r 9 g = a 2 ⊕ a 3 ⊕ b 2 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ e 1 ⊕ e 3 ⊕ f 1 ⊕ f 2 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ i 0 ⊕ i 3 ⊕ j 0 ⊕ j 2 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 0 ⊕ l 1 ⊕ m 0 ⊕ m 1 ⊕ m 3 ⊕ n 0 ⊕ n 1 ⊕ n 2 ⊕ o 0 ⊕ o 1 ⊕ o 3

r 10 g = a 2 ⊕ b 3 ⊕ c 1 ⊕ d 1 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 1 ⊕ f 2 ⊕ f 3 ⊕ g 0 ⊕ g 3 ⊕ h 0 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 2 ⊕ j 3 ⊕ k 0 ⊕ k 1 ⊕ l 1 ⊕ l 3 ⊕ m 0 ⊕ m 1 ⊕ m 2 ⊕ n 0 ⊕ n 1 ⊕ n 3 ⊕ p 3 ;

r 11 g = a 1 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ c 1 ⊕ c 2 ⊕ d 1 ⊕ d 2 ⊕ e 0 ⊕ f 0 ⊕ f 3 ⊕ g 0 ⊕ g 2 ⊕ h 0 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 1 ⊕ j 0 ⊕ j 1 ⊕ j 3 ⊕ k 1 ⊕ k 2 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ m 3 ⊕ n 3 ⊕ o 2 ⊕ p 2 ⊕ p 3 ;

r 12 g = a 0 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ d 0 ⊕ d 2 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ e 3 ⊕ f 0 ⊕ f 1 ⊕ f 3 ⊕ g 0 ⊕ g 1 ⊕ g 2 ⊕ h 0 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 2 ⊕ l 3 ⊕ m 1 ⊕ n 1 ⊕ n 3 ⊕ ⊕ o 1 ⊕ o 2 ⊕ p 1 ⊕ p 2 ⊕ p 3 ;

r 13 g = a 0 ⊕ b 2 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 0 ⊕ f 2 ⊕ g 0 ⊕ g 1 ⊕ h 0 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 1 ⊕ j 1 ⊕ j 2 ⊕ k 1 ⊕ l 0 ⊕ l 2 ⊕ m 1 ⊕ m 2 ⊕ m 3 ⊕ n 0 ⊕ n 2 ⊕ n 3 ⊕ ⊕ o 0 ⊕ o 1 ⊕ o 3 ⊕ p 0 ⊕ p 1 ⊕ p 2 ;

r 14 g = a 2 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 3 ⊕ d 1 ⊕ d 2 ⊕ e 3 ⊕ f 2 ⊕ g 3 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 1 ⊕ j 3 ⊕ k 2 ⊕ k 3 ⊕ l 1 ⊕ l 2 ⊕ l 3 ⊕ m 1 ⊕ m 3 ⊕ n 0 ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ p 0 ⊕ p 2 ⊕ p 3 ;

r 15 g = a 0 ⊕ a 1 ⊕ a 2 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ e 0 ⊕ e 1 ⊕ e 2 ⊕ f 2 ⊕ f 3 ⊕ g 1 ⊕ g 3 ⊕ h 0 ⊕ i 0 ⊕ i 3 ⊕ j 0 ⊕ j 2 ⊕ k 1 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ m 0 ⊕ m 1 ⊕ n 0 ⊕ n 1 ⊕ n 3 ⊕ ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ o 3 ⊕ p 3 ;

r 16 g = a 0 ⊕ a 3 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ c 0 ⊕ c 1 ⊕ c 2 ⊕ d 3 ⊕ e 2 ⊕ e 3 ⊕ f 0 ⊕ f 2 ⊕ f 3 ⊕ g 2 ⊕ g 3 ⊕ h 1 ⊕ i 0 ⊕ i 2 ⊕ i 3 ⊕ j 1 ⊕ j 2 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ l 0 ⊕ l 1 ⊕ m 0 ⊕ m 3 ⊕ n 3 ⊕ o 0 ⊕ o 2 ⊕ p 1 ⊕ p 2 ;

r 17 g = a 0 ⊕ a 1 ⊕ a 2 ⊕ c 0 ⊕ c 1 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ e 3 ⊕ f 1 ⊕ f 2 ⊕ g 0 ⊕ g 1 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ h 1 ⊕ i 0 ⊕ i 1 ⊕ i 2 ⊕ j 1 ⊕ j 2 ⊕ j 3 ⊕ k 2 ⊕ l 1 ⊕ l 3 ⊕ m 0 ⊕ n 1 ⊕ n 2 ⊕ n 3 ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ p 0 ⊕ p 1 ⊕ p 3 ;

r 18 g = a 0 ⊕ a 2 ⊕ a 3 ⊕ b 2 ⊕ b 3 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 3 ⊕ g 2 ⊕ h 1 ⊕ i 1 ⊕ i 2 ⊕ i 3 ⊕ j 1 ⊕ j 2 ⊕ k 0 ⊕ k 1 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ l 3 ⊕ n 1 ⊕ n 3 ⊕ o 0 ⊕ o 1 ⊕ p 0 ⊕ p 1 ⊕ p 2 ;

r 19 g = a 0 ⊕ a 1 ⊕ a 3 ⊕ b 1 ⊕ b 3 ⊕ c 0 ⊕ d 0 ⊕ d 2 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ f 0 ⊕ f 2 ⊕ g 1 ⊕ g 2 ⊕ g 3 ⊕ h 1 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ l 1 ⊕ m 0 ⊕ m 1 ⊕ m 2 ⊕ n 0 ⊕ n 1 ⊕ o 0 ⊕ o 2 ⊕ o 3 ⊕ p 0 ⊕ p 2 ⊕ p 3 ;

r 20 g = a 1 ⊕ a 2 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 1 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 2 ⊕ e 3 ⊕ f 2 ⊕ f 3 ⊕ g 0 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ h 2 ⊕ h 3 ⊕ i 1 ⊕ i 3 ⊕ j 1 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 0 ⊕ l 2 ⊕ m 0 ⊕ m 3 ⊕ n 0 ⊕ n 3 ⊕ o 0 ⊕ o 3 ⊕ p 0 ⊕ p 1 ⊕ p 3 ,

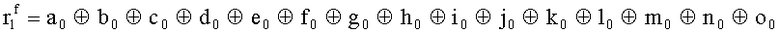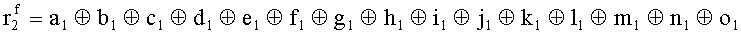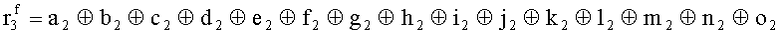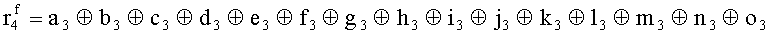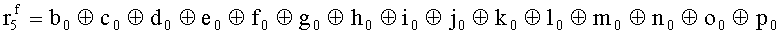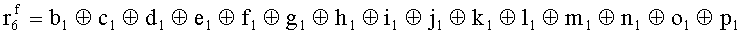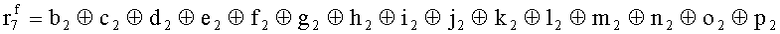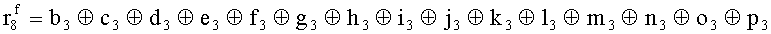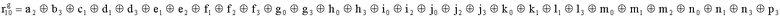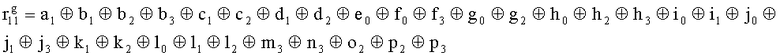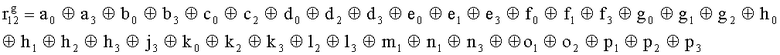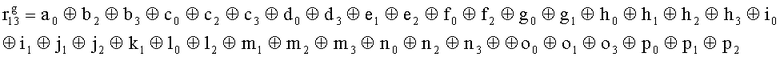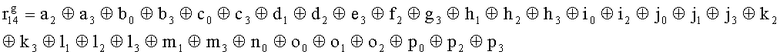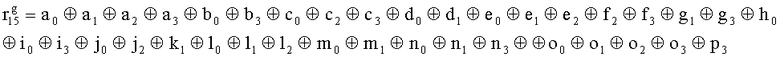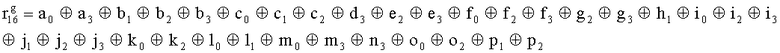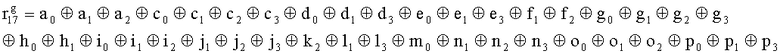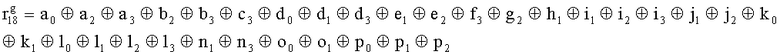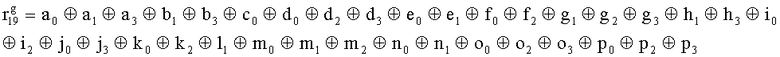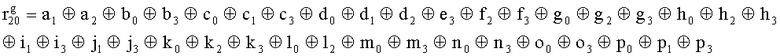выходы входного блока кодирования подключены к седьмым входам узла памяти, информационные выходы узла памяти подключены соответственно к первым входам корректора и к входам выходного блока кодирования, который формирует значения проверочных контрольных разрядов 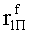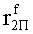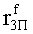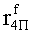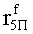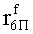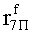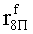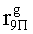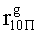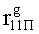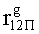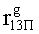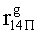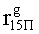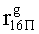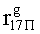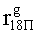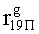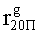r 1 П f , r 2 П f , r 3 П f , r 4 П f , r 5 П f , r 6 П f , r 7 П f , r 8 П f , r 9 П g , r 10 П g , r 11 П g , r 12 П g , r 13 П g , r 14 П g , r 15 П g , r 16 П g , r 17 П g , r 18 П g , r 19 П g , r 20 П g , путем сложения по модулю 2 информационных символов a0Пa1Пa2Пa3П, b0Пb1Пb2Пb3П, c0Пc1Пc2Пc3П, d0Пd1Пd2Пd3П, e0Пe1Пe2Пe3П, f0Пf1Пf2Пf3П, g0Пg1Пg2Пg3П, h0Пh1Пh2Пh3П, i0Пi1Пi2Пi3П, j0Пj1Пj2Пj3П, k0Пk1Пk2Пk3П, l0Пl1Пl2Пl3П, m0Пm1Пm2Пm3П, n0Пn1Пn2Пn3П, o0Пo1Пo2Пo3П, p0Пp1Пp2Пp3П, поступающих на входы входного блока кодирования с информационных выходов узла памяти, в соответствии с правилом:

r 1 П f = a 0 П ⊕ b 0 П ⊕ c 0 П ⊕ d 0 П ⊕ e 0 П ⊕ f 0 П ⊕ g 0 П ⊕ h 0 П ⊕ i 0 П ⊕ j 0 П ⊕ k 0 П ⊕ l 0 П ⊕ m 0 П ⊕ n 0 П ⊕ o 0 П ;

r 2 П f = a 1 П ⊕ b 1 П ⊕ c 1 П ⊕ d 1 П ⊕ e 1 П ⊕ f 1 П ⊕ g 1 П ⊕ h 1 П ⊕ i 1 П ⊕ j 1 П ⊕ k 1 П ⊕ l 1 П ⊕ m 1 П ⊕ n 1 П ⊕ o 1 П ;

r 3 П f = a 2 П ⊕ b 2 П ⊕ c 2 П ⊕ d 2 П ⊕ e 2 П ⊕ f 2 П ⊕ g 2 П ⊕ h 2 П ⊕ i 2 П ⊕ j 2 П ⊕ k 2 П ⊕ l 2 П ⊕ m 2 П ⊕ n 2 П ⊕ o 2 П ;

r 4 П f = a 3 П ⊕ b 3 П ⊕ c 3 П ⊕ d 3 П ⊕ e 3 П ⊕ f 3 П ⊕ g 3 П ⊕ h 3 П ⊕ i 3 П ⊕ j 3 П ⊕ k 3 П ⊕ l 3 П ⊕ m 3 П ⊕ n 3 П ⊕ o 3 П ;

r 5 П f = b 0 П ⊕ c 0 П ⊕ d 0 П ⊕ e 0 П ⊕ f 0 П ⊕ g 0 П ⊕ h 0 П ⊕ i 0 П ⊕ j 0 П ⊕ k 0 П ⊕ l 0 П ⊕ m 0 П ⊕ n 0 П ⊕ o 0 П ⊕ p 0 П ;

r 6 П f = b 1 П ⊕ c 1 П ⊕ d 1 П ⊕ e 1 П ⊕ f 1 П ⊕ g 1 П ⊕ h 1 П ⊕ i 1 П ⊕ j 1 П ⊕ k 1 П ⊕ l 1 П ⊕ m 1 П ⊕ n 1 П ⊕ o 1 П ⊕ p 1 П ;

r 7 П f = b 2 П ⊕ c 2 П ⊕ d 2 П ⊕ e 2 П ⊕ f 2 П ⊕ g 2 П ⊕ h 2 П ⊕ i 2 П ⊕ j 2 П ⊕ k 2 П ⊕ l 2 П ⊕ m 2 П ⊕ n 2 П ⊕ o 2 П ⊕ p 2 П ;

r 8 П f = b 3 П ⊕ c 3 П ⊕ d 3 П ⊕ e 3 П ⊕ f 3 П ⊕ g 3 П ⊕ h 3 П ⊕ i 3 П ⊕ j 3 П ⊕ k 3 П ⊕ l 3 П ⊕ m 3 П ⊕ n 3 П ⊕ o 3 П ⊕ p 3 П ;

r 9 П g = a 2 П ⊕ a 3 П ⊕ b 2 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ e 1 П ⊕ e 3 П ⊕ f 1 П ⊕ f 2 П ⊕ g 2 П ⊕ g 3 П ⊕ h 0 П ⊕ i 0 П ⊕ i 3 П ⊕ j 0 П ⊕ j 2 П ⊕ k 0 П ⊕ k 2 П ⊕ k 3 П ⊕ l 0 П ⊕ l 1 П ⊕ m 0 П ⊕ m 1 П ⊕ m 3 П ⊕ n 0 П ⊕ n 1 п ⊕ n 2 П ⊕ o 0 П ⊕ o 1 П ⊕ o 3 П ;

r 10 П g = a 2 П ⊕ b 3 П ⊕ c 1 П ⊕ d 1 П ⊕ d 3 П ⊕ e 1 П ⊕ e 2 П ⊕ f 1 П ⊕ f 2 П ⊕ f 3 П ⊕ g 0 П ⊕ g 3 П ⊕ h 0 П ⊕ h 3 П ⊕ i 0 П ⊕ i 2 П ⊕ j 0 П ⊕ j 2 П ⊕ j 3 П ⊕ k 0 П ⊕ k 1 П ⊕ l 1 П ⊕ l 3 П ⊕ m 0 П ⊕ m 1 П ⊕ m 2 П ⊕ n 0 П ⊕ n 1 П ⊕ n 3 П ⊕ p 3 П ;

r 11 П g = a 1 П ⊕ b 1 П ⊕ b 2 П ⊕ b 3 П ⊕ c 1 П ⊕ c 2 П ⊕ d 1 П ⊕ d 2 П ⊕ e 0 П ⊕ f 0 П ⊕ f 3 П ⊕ g 0 П ⊕ g 2 П ⊕ h 0 П ⊕ h 2 П ⊕ h 3 П ⊕ i 0 П ⊕ i 1 П ⊕ j 0 П ⊕ j 1 П ⊕ j 3 П ⊕ k 1 П ⊕ k 2 П ⊕ l 0 П ⊕ l 1 П ⊕ l 2 П ⊕ m 3 П ⊕ n 3 П ⊕ o 2 П ⊕ p 2 П ⊕ p 3 П ;

r 12 П g = a 0 П ⊕ a 3 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 2 П ⊕ d 0 П ⊕ d 2 П ⊕ d 3 П ⊕ e 0 П ⊕ e 1 П ⊕ e 3 П ⊕ f 0 П ⊕ f 1 П ⊕ f 3 П ⊕ g 0 П ⊕ g 1 П ⊕ g 2 П ⊕ h 0 П ⊕ h 1 П ⊕ h 2 П ⊕ h 3 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ k 3 П ⊕ l 2 П ⊕ l 3 П ⊕ m 1 П ⊕ n 1 П ⊕ n 3 П ⊕ o 1 П ⊕ o 2 П ⊕ p 1 П ⊕ p 2 П ⊕ p 3 П ;

r 13 П g = a 0 П ⊕ b 2 П ⊕ b 3 П ⊕ c 0 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 3 П ⊕ e 1 П ⊕ e 2 П ⊕ f 0 П ⊕ f 2 П ⊕ g 0 П ⊕ g 1 П ⊕ h 0 П ⊕ h 1 П ⊕ h 2 П ⊕ h 3 П ⊕ i 0 П ⊕ i 1 П ⊕ j 1 П ⊕ j 2 П ⊕ k 1 П ⊕ l 0 П ⊕ l 2 П ⊕ m 1 П ⊕ m 2 П ⊕ m 3 П ⊕ n 0 П ⊕ n 2 П ⊕ n 3 П ⊕ o 0 П ⊕ o 1 П ⊕ o 3 П ⊕ p 0 П ⊕ p 1 П ⊕ p 2 П ;

r 14 П g = a 2 П ⊕ a 3 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 3 П ⊕ d П 1 ⊕ d 2 П ⊕ e 3 П ⊕ f 2 П ⊕ g 3 П ⊕ h 1 П ⊕ h 2 П ⊕ h 3 П ⊕ i 0 П ⊕ i 2 П ⊕ j 0 П ⊕ j 1 П ⊕ j 3 П ⊕ k 2 П ⊕ k 3 П ⊕ l 1 П ⊕ l 2 П ⊕ l 3 П ⊕ m 1 П ⊕ m 3 П ⊕ n 0 П ⊕ o 0 П ⊕ o 1 П ⊕ o 2 П ⊕ p 0 П ⊕ p 2 П ⊕ p 3 П ;

r 15 П g = a 0 П ⊕ a 1 П ⊕ a 2 П ⊕ a 3 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ e 0 П ⊕ e 1 П ⊕ e 2 П ⊕ f 2 П ⊕ f 3 П ⊕ g 1 П ⊕ g 3 П ⊕ h 0 П ⊕ i 0 П ⊕ i 3 П ⊕ j 0 П ⊕ j 2 П ⊕ k 1 П ⊕ l 0 П ⊕ l 1 П ⊕ l 2 П ⊕ m 0 П ⊕ m 1 П ⊕ n 0 П ⊕ n 1 П ⊕ n 3 П ⊕ o 0 П ⊕ o 1 П ⊕ o 2 П ⊕ o 3 П ⊕ p 3 П ;

r 16 П g = a 0 П ⊕ a 3 П ⊕ b 1 П ⊕ b 2 П ⊕ b 3 П ⊕ c 0 П ⊕ c 1 П ⊕ c 2 П ⊕ d 3 П ⊕ e 2 П ⊕ e 3 П ⊕ f 0 П ⊕ f 2 П ⊕ f 3 П ⊕ g 2 П ⊕ g 3 П ⊕ h 1 П ⊕ i 0 П ⊕ i 2 П ⊕ i 3 П ⊕ j 1 П ⊕ j 2 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ l 0 П ⊕ l 1 П ⊕ m 0 П ⊕ m 3 П ⊕ n 3 П ⊕ o 0 П ⊕ o 2 П ⊕ p 1 П ⊕ p 2 П ;

r 17 П g = a 0 П ⊕ a 1 П ⊕ a 2 П ⊕ c 0 П ⊕ c 1 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ d 3 П ⊕ e 0 П ⊕ e 1 П ⊕ e 3 П ⊕ f 1 П ⊕ f 2 П ⊕ g 0 П ⊕ g 1 П ⊕ g 2 П ⊕ g 3 П ⊕ h 0 П ⊕ h 1 П ⊕ i 0 П ⊕ i 1 П ⊕ i 2 П ⊕ j 1 П ⊕ j 2 П ⊕ j 3 П ⊕ k 2 П ⊕ l 1 П ⊕ l 3 П ⊕ m 0 П ⊕ n 1 П ⊕ n 2 П ⊕ n 3 П ⊕ o 0 П ⊕ o П 1 ⊕ o 2 П ⊕ p 0 П ⊕ p 1 П ⊕ p 3 П ;

r 18 П g = a 0 П ⊕ a 2 П ⊕ a 3 П ⊕ b 2 П ⊕ b 3 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ d 3 П ⊕ e 1 П ⊕ e 2 П ⊕ f 3 П ⊕ g 2 П ⊕ h 1 П ⊕ i 1 П ⊕ i 2 П ⊕ i 3 П ⊕ j 1 П ⊕ j 2 П ⊕ k 0 П ⊕ k 1 П ⊕ l 0 П ⊕ l 1 П ⊕ l 2 П ⊕ l 3 П ⊕ n 1 П ⊕ n 3 П ⊕ o 0 П ⊕ o 1 П ⊕ p 0 П ⊕ p 1 П ⊕ p 2 П ;

r 19 П g = a 0 П ⊕ a 1 П ⊕ a 3 П ⊕ b 1 П ⊕ b 3 П ⊕ c 0 П ⊕ d 0 П ⊕ d 2 П ⊕ d 3 П ⊕ e 0 П ⊕ e 1 П ⊕ f 0 П ⊕ f 2 П ⊕ g 1 П ⊕ g 2 П ⊕ g 3 П ⊕ h 1 П ⊕ h 3 П ⊕ i 0 П ⊕ i 2 П ⊕ j 0 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ l 1 П ⊕ m 0 П ⊕ m 1 П ⊕ m 2 П ⊕ n 0 П ⊕ n 1 П ⊕ o 0 П ⊕ o 2 П ⊕ o 3 П ⊕ p 0 П ⊕ p 2 П ⊕ p 3 П ;

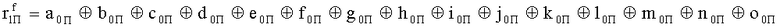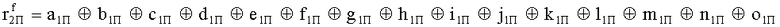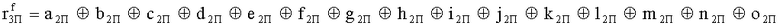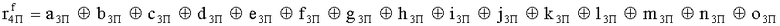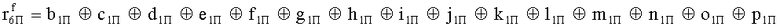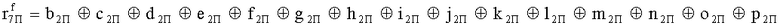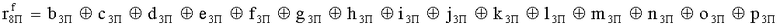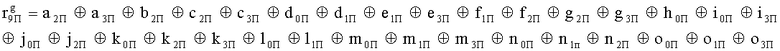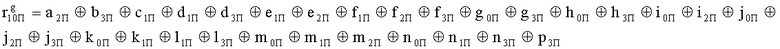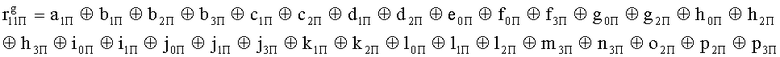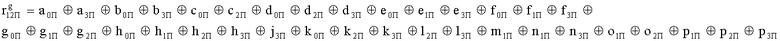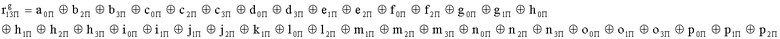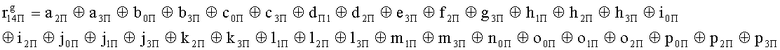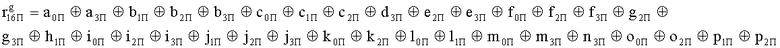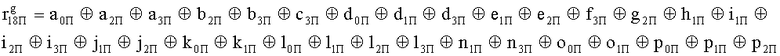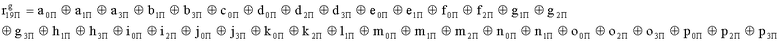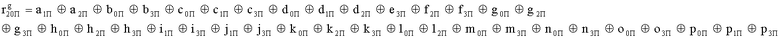r 20 П g = a 1 П ⊕ a 2 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 1 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ d 2 П ⊕ e 3 П ⊕ f 2 П ⊕ f 3 П ⊕ g 0 П ⊕ g 2 П ⊕ g 3 П ⊕ h 0 П ⊕ h 2 П ⊕ h 3 П ⊕ i 1 П ⊕ i 3 П ⊕ j 1 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ k 3 П ⊕ l 0 П ⊕ l 2 П ⊕ m 0 П ⊕ m 3 П ⊕ n 0 П ⊕ n 3 П ⊕ o 0 П ⊕ o 3 П ⊕ p 0 П ⊕ p 1 П ⊕ p 3 П , выходы выходного блока кодирования подключены к первым входам блока вычисления синдрома ошибки, к вторым входам которого подключены выходы контрольных разрядов узла памяти, выходы блока вычисления синдрома ошибки подключены к входам дешифратора, выходы которого подключены к входам блока хранения векторов ошибок, выходы блока хранения векторов ошибок подключены к вторым входам корректора, выходы которого подключены к вторым входам блока элементов И, выходы блока элементов И являются выходами устройства.

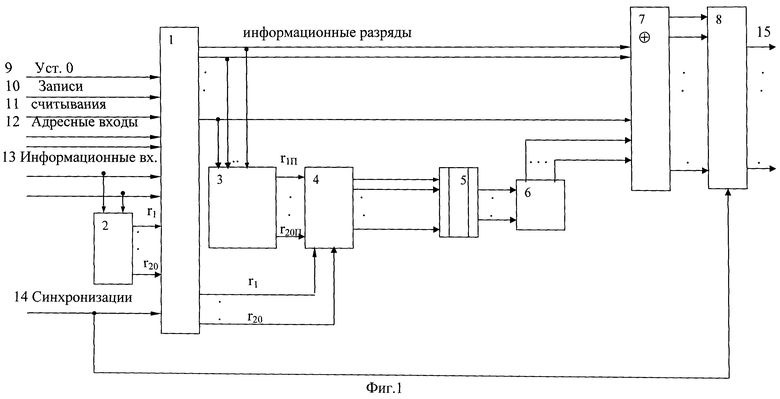
На фиг.1 представлена блок-схема устройства. Устройство хранения и передачи данных с исправлением ошибок в двух байтах информации содержит: узел 1 памяти, входной блок 2 кодирования, выходной блок 3 кодирования, блок 4 вычисления синдрома ошибки, дешифратор 5, блок 6 хранения векторов ошибок, корректор 7, блок 8 элементов И, вход 9 установки в нулевое состояние, вход 10 записи, вход 11 считывания, адресные входы 12, информационные входы 13, вход 14 синхронизации, информационные выходы 15.

Вход 9 установки в нулевое состояние, вход 10 записи, вход 11 считывания, адресные входы 12 подключены соответственно к первому, второму, третьему и четвертому входам узла 1 памяти, вход 14 синхронизации подключен к пятому входу узла 1 памяти и к первому входу блока 8 элементов И, информационные входы 13 подключены к шестым входам узла 1 памяти и к входам входного блока 2 кодирования, который формирует значения контрольных разрядов 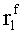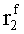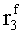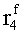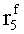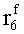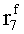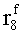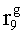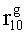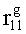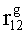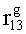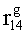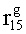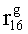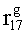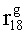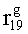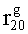r 1 f , r 2 f , r 3 f , r 4 f , r 5 f , r 6 f , r 7 f , r 8 f , r 9 g , r 10 g , r 11 g , r 12 g , r 13 g , r 14 g , r 15 g , r 16 g , r 17 g , r 18 g , r 19 g , r 20 g , путем сложения по модулю 2 информационных символов a0a1a2a3, b0b1b32b3, c0c1c2c3, d0d1d2d3, e0e1e2e3, f0f1f2f3, g0g1g2g3, h0h1h2h3, i0i1i2i3, j0j1j2j3, k0k1k2k3, l0l1l2l3, m0m1m2m3, n0n1n2n3, o0o1o2o3, p0p1p2p3, поступающих на входы входного блока 2 кодирования, в соответствии с правилом:

r 1 f = a 0 ⊕ b 0 ⊕ c 0 ⊕ d 0 ⊕ e 0 ⊕ f 0 ⊕ g 0 ⊕ h 0 ⊕ i 0 ⊕ j 0 ⊕ k 0 ⊕ l 0 ⊕ m 0 ⊕ n 0 ⊕ o 0 ;

r 2 f = a 1 ⊕ b 1 ⊕ c 1 ⊕ d 1 ⊕ e 1 ⊕ f 1 ⊕ g 1 ⊕ h 1 ⊕ i 1 ⊕ j 1 ⊕ k 1 ⊕ l 1 ⊕ m 1 ⊕ n 1 ⊕ o 1 ;

r 3 f = a 2 ⊕ b 2 ⊕ c 2 ⊕ d 2 ⊕ e 2 ⊕ f 2 ⊕ g 2 ⊕ h 2 ⊕ i 2 ⊕ j 2 ⊕ k 2 ⊕ l 2 ⊕ m 2 ⊕ n 2 ⊕ o 2 ;

r 4 f = a 3 ⊕ b 3 ⊕ c 3 ⊕ d 3 ⊕ e 3 ⊕ f 3 ⊕ g 3 ⊕ h 3 ⊕ i 3 ⊕ j 3 ⊕ k 3 ⊕ l 3 ⊕ m 3 ⊕ n 3 ⊕ o 3 ;

r 5 f = b 0 ⊕ c 0 ⊕ d 0 ⊕ e 0 ⊕ f 0 ⊕ g 0 ⊕ h 0 ⊕ i 0 ⊕ j 0 ⊕ k 0 ⊕ l 0 ⊕ m 0 ⊕ n 0 ⊕ o 0 ⊕ p 0 ;

r 6 f = b 1 ⊕ c 1 ⊕ d 1 ⊕ e 1 ⊕ f 1 ⊕ g 1 ⊕ h 1 ⊕ i 1 ⊕ j 1 ⊕ k 1 ⊕ l 1 ⊕ m 1 ⊕ n 1 ⊕ o 1 ⊕ p 1 ;

r 7 f = b 2 ⊕ c 2 ⊕ d 2 ⊕ e 2 ⊕ f 2 ⊕ g 2 ⊕ h 2 ⊕ i 2 ⊕ j 2 ⊕ k 2 ⊕ l 2 ⊕ m 2 ⊕ n 2 ⊕ o 2 ⊕ p 2 ;

r 8 f = b 3 ⊕ c 3 ⊕ d 3 ⊕ e 3 ⊕ f 3 ⊕ g 3 ⊕ h 3 ⊕ i 3 ⊕ j 3 ⊕ k 3 ⊕ l 3 ⊕ m 3 ⊕ n 3 ⊕ o 3 ⊕ p 3 ;

r 9 g = a 2 ⊕ a 3 ⊕ b 2 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ e 1 ⊕ e 3 ⊕ f 1 ⊕ f 2 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ i 0 ⊕ i 3 ⊕ j 0 ⊕ j 2 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 0 ⊕ l 1 ⊕ m 0 ⊕ m 1 ⊕ m 3 ⊕ n 0 ⊕ n 1 ⊕ n 2 ⊕ o 0 ⊕ o 1 ⊕ o 3

r 10 g = a 2 ⊕ b 3 ⊕ c 1 ⊕ d 1 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 1 ⊕ f 2 ⊕ f 3 ⊕ g 0 ⊕ g 3 ⊕ h 0 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 2 ⊕ j 3 ⊕ k 0 ⊕ k 1 ⊕ l 1 ⊕ l 3 ⊕ m 0 ⊕ m 1 ⊕ m 2 ⊕ n 0 ⊕ n 1 ⊕ n 3 ⊕ p 3 ;

r 11 g = a 1 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ c 1 ⊕ c 2 ⊕ d 1 ⊕ d 2 ⊕ e 0 ⊕ f 0 ⊕ f 3 ⊕ g 0 ⊕ g 2 ⊕ h 0 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 1 ⊕ j 0 ⊕ j 1 ⊕ j 3 ⊕ k 1 ⊕ k 2 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ m 3 ⊕ n 3 ⊕ o 2 ⊕ p 2 ⊕ p 3 ;

r 12 g = a 0 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ d 0 ⊕ d 2 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ e 3 ⊕ f 0 ⊕ f 1 ⊕ f 3 ⊕ g 0 ⊕ g 1 ⊕ g 2 ⊕ h 0 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 2 ⊕ l 3 ⊕ m 1 ⊕ n 1 ⊕ n 3 ⊕ ⊕ o 1 ⊕ o 2 ⊕ p 1 ⊕ p 2 ⊕ p 3 ;

r 13 g = a 0 ⊕ b 2 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 0 ⊕ f 2 ⊕ g 0 ⊕ g 1 ⊕ h 0 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 1 ⊕ j 1 ⊕ j 2 ⊕ k 1 ⊕ l 0 ⊕ l 2 ⊕ m 1 ⊕ m 2 ⊕ m 3 ⊕ n 0 ⊕ n 2 ⊕ n 3 ⊕ ⊕ o 0 ⊕ o 1 ⊕ o 3 ⊕ p 0 ⊕ p 1 ⊕ p 2 ;

r 14 g = a 2 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 3 ⊕ d 1 ⊕ d 2 ⊕ e 3 ⊕ f 2 ⊕ g 3 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 1 ⊕ j 3 ⊕ k 2 ⊕ k 3 ⊕ l 1 ⊕ l 2 ⊕ l 3 ⊕ m 1 ⊕ m 3 ⊕ n 0 ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ p 0 ⊕ p 2 ⊕ p 3 ;

r 15 g = a 0 ⊕ a 1 ⊕ a 2 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ e 0 ⊕ e 1 ⊕ e 2 ⊕ f 2 ⊕ f 3 ⊕ g 1 ⊕ g 3 ⊕ h 0 ⊕ i 0 ⊕ i 3 ⊕ j 0 ⊕ j 2 ⊕ k 1 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ m 0 ⊕ m 1 ⊕ n 0 ⊕ n 1 ⊕ n 3 ⊕ ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ o 3 ⊕ p 3 ;

r 16 g = a 0 ⊕ a 3 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ c 0 ⊕ c 1 ⊕ c 2 ⊕ d 3 ⊕ e 2 ⊕ e 3 ⊕ f 0 ⊕ f 2 ⊕ f 3 ⊕ g 2 ⊕ g 3 ⊕ h 1 ⊕ i 0 ⊕ i 2 ⊕ i 3 ⊕ j 1 ⊕ j 2 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ l 0 ⊕ l 1 ⊕ m 0 ⊕ m 3 ⊕ n 3 ⊕ o 0 ⊕ o 2 ⊕ p 1 ⊕ p 2 ;

r 17 g = a 0 ⊕ a 1 ⊕ a 2 ⊕ c 0 ⊕ c 1 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ e 3 ⊕ f 1 ⊕ f 2 ⊕ g 0 ⊕ g 1 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ h 1 ⊕ i 0 ⊕ i 1 ⊕ i 2 ⊕ j 1 ⊕ j 2 ⊕ j 3 ⊕ k 2 ⊕ l 1 ⊕ l 3 ⊕ m 0 ⊕ n 1 ⊕ n 2 ⊕ n 3 ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ p 0 ⊕ p 1 ⊕ p 3 ;

r 18 g = a 0 ⊕ a 2 ⊕ a 3 ⊕ b 2 ⊕ b 3 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 3 ⊕ g 2 ⊕ h 1 ⊕ i 1 ⊕ i 2 ⊕ i 3 ⊕ j 1 ⊕ j 2 ⊕ k 0 ⊕ k 1 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ l 3 ⊕ n 1 ⊕ n 3 ⊕ o 0 ⊕ o 1 ⊕ p 0 ⊕ p 1 ⊕ p 2 ;

r 19 g = a 0 ⊕ a 1 ⊕ a 3 ⊕ b 1 ⊕ b 3 ⊕ c 0 ⊕ d 0 ⊕ d 2 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ f 0 ⊕ f 2 ⊕ g 1 ⊕ g 2 ⊕ g 3 ⊕ h 1 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ l 1 ⊕ m 0 ⊕ m 1 ⊕ m 2 ⊕ n 0 ⊕ n 1 ⊕ o 0 ⊕ o 2 ⊕ o 3 ⊕ p 0 ⊕ p 2 ⊕ p 3 ;

r 20 g = a 1 ⊕ a 2 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 1 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 2 ⊕ e 3 ⊕ f 2 ⊕ f 3 ⊕ g 0 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ h 2 ⊕ h 3 ⊕ i 1 ⊕ i 3 ⊕ j 1 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 0 ⊕ l 2 ⊕ m 0 ⊕ m 3 ⊕ n 0 ⊕ n 3 ⊕ o 0 ⊕ o 3 ⊕ p 0 ⊕ p 1 ⊕ p 3 .,

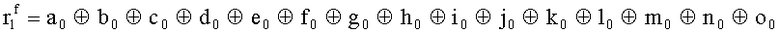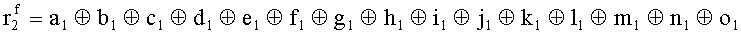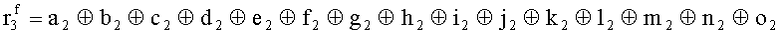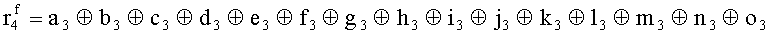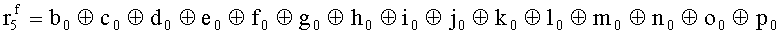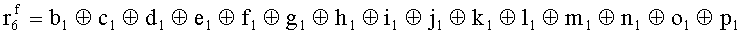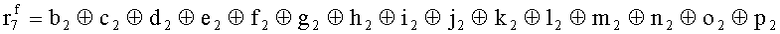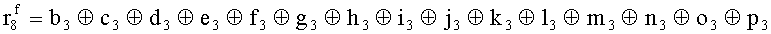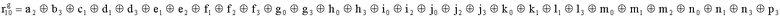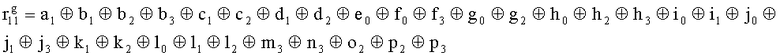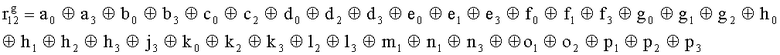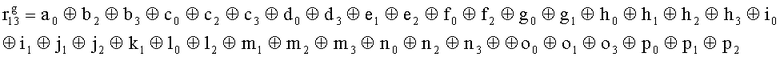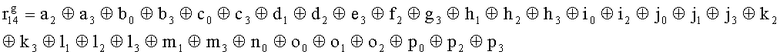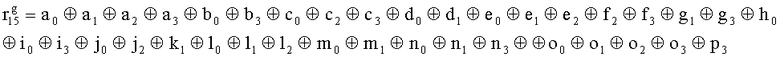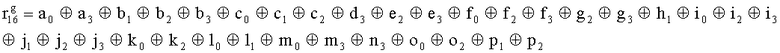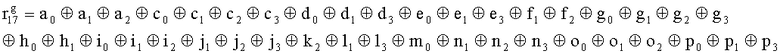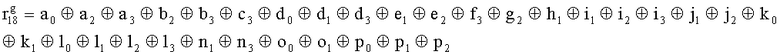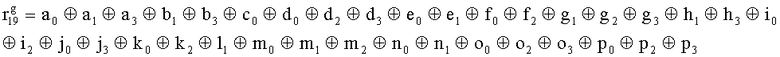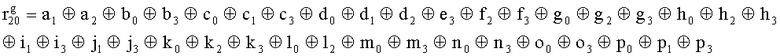выходы входного блока 2 кодирования подключены к седьмым входам узла 1 памяти, информационные выходы узла 1 памяти подключены соответственно к первым входам корректора 7 и к входам выходного блока 3 кодирования, который формирует значения проверочных контрольных разрядов 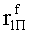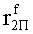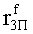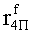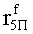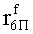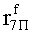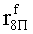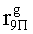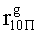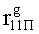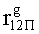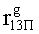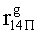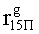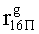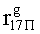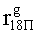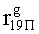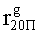r 1 П f , r 2 П f , r 3 П f , r 4 П f , r 5 П f , r 6 П f , r 7 П f , r 8 П f , r 9 П g , r 10 П g , r 11 П g , r 12 П g , r 13 П g , r 14 П g , r 15 П g , r 16 П g , r 17 П g , r 18 П g , r 19 П g , r 20 П g , путем сложения по модулю 2 информационных символов a0Пa1Пa2Пa3П, b0Пb1Пb2Пb3П, c0Пc1Пc2Пc3П, d0Пd1Пd2Пd3П, e0Пe1Пe2Пe3П, f0Пf1Пf2Пf3П, g0Пg1Пg2Пg3П, h0Пh1Пh2Пh3П, i0Пi1Пi2Пi3П, j0Пj1Пj2Пj3П, k0Пk1Пk2Пk3П, l0Пl1Пl2Пl3П, m0Пm1Пm2Пm3П, n0Пn1Пn2Пn3П, o0Пo1Пo2Пo3П, p0Пp1Пp2Пp3П, поступающих на входы входного блока 3 кодирования с информационных выходов узла 1 памяти, в соответствии с правилом:

r 1 П f = a 0 П ⊕ b 0 П ⊕ c 0 П ⊕ d 0 П ⊕ e 0 П ⊕ f 0 П ⊕ g 0 П ⊕ h 0 П ⊕ i 0 П ⊕ j 0 П ⊕ k 0 П ⊕ l 0 П ⊕ m 0 П ⊕ n 0 П ⊕ o 0 П ;

r 2 П f = a 1 П ⊕ b 1 П ⊕ c 1 П ⊕ d 1 П ⊕ e 1 П ⊕ f 1 П ⊕ g 1 П ⊕ h 1 П ⊕ i 1 П ⊕ j 1 П ⊕ k 1 П ⊕ l 1 П ⊕ m 1 П ⊕ n 1 П ⊕ o 1 П ;

r 3 П f = a 2 П ⊕ b 2 П ⊕ c 2 П ⊕ d 2 П ⊕ e 2 П ⊕ f 2 П ⊕ g 2 П ⊕ h 2 П ⊕ i 2 П ⊕ j 2 П ⊕ k 2 П ⊕ l 2 П ⊕ m 2 П ⊕ n 2 П ⊕ o 2 П ;

r 4 П f = a 3 П ⊕ b 3 П ⊕ c 3 П ⊕ d 3 П ⊕ e 3 П ⊕ f 3 П ⊕ g 3 П ⊕ h 3 П ⊕ i 3 П ⊕ j 3 П ⊕ k 3 П ⊕ l 3 П ⊕ m 3 П ⊕ n 3 П ⊕ o 3 П ;

r 5 П f = b 0 П ⊕ c 0 П ⊕ d 0 П ⊕ e 0 П ⊕ f 0 П ⊕ g 0 П ⊕ h 0 П ⊕ i 0 П ⊕ j 0 П ⊕ k 0 П ⊕ l 0 П ⊕ m 0 П ⊕ n 0 П ⊕ o 0 П ⊕ p 0 П ;

r 6 П f = b 1 П ⊕ c 1 П ⊕ d 1 П ⊕ e 1 П ⊕ f 1 П ⊕ g 1 П ⊕ h 1 П ⊕ i 1 П ⊕ j 1 П ⊕ k 1 П ⊕ l 1 П ⊕ m 1 П ⊕ n 1 П ⊕ o 1 П ⊕ p 1 П ;

r 7 П f = b 2 П ⊕ c 2 П ⊕ d 2 П ⊕ e 2 П ⊕ f 2 П ⊕ g 2 П ⊕ h 2 П ⊕ i 2 П ⊕ j 2 П ⊕ k 2 П ⊕ l 2 П ⊕ m 2 П ⊕ n 2 П ⊕ o 2 П ⊕ p 2 П ;

r 8 П f = b 3 П ⊕ c 3 П ⊕ d 3 П ⊕ e 3 П ⊕ f 3 П ⊕ g 3 П ⊕ h 3 П ⊕ i 3 П ⊕ j 3 П ⊕ k 3 П ⊕ l 3 П ⊕ m 3 П ⊕ n 3 П ⊕ o 3 П ⊕ p 3 П ;

r 9 П g = a 2 П ⊕ a 3 П ⊕ b 2 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ e 1 П ⊕ e 3 П ⊕ f 1 П ⊕ f 2 П ⊕ g 2 П ⊕ g 3 П ⊕ h 0 П ⊕ i 0 П ⊕ i 3 П ⊕ j 0 П ⊕ j 2 П ⊕ k 0 П ⊕ k 2 П ⊕ k 3 П ⊕ l 0 П ⊕ l 1 П ⊕ m 0 П ⊕ m 1 П ⊕ m 3 П ⊕ n 0 П ⊕ n 1 п ⊕ n 2 П ⊕ o 0 П ⊕ o 1 П ⊕ o 3 П ;

r 10 П g = a 2 П ⊕ b 3 П ⊕ c 1 П ⊕ d 1 П ⊕ d 3 П ⊕ e 1 П ⊕ e 2 П ⊕ f 1 П ⊕ f 2 П ⊕ f 3 П ⊕ g 0 П ⊕ g 3 П ⊕ h 0 П ⊕ h 3 П ⊕ i 0 П ⊕ i 2 П ⊕ j 0 П ⊕ j 2 П ⊕ j 3 П ⊕ k 0 П ⊕ k 1 П ⊕ l 1 П ⊕ l 3 П ⊕ m 0 П ⊕ m 1 П ⊕ m 2 П ⊕ n 0 П ⊕ n 1 П ⊕ n 3 П ⊕ p 3 П ;

r 11 П g = a 1 П ⊕ b 1 П ⊕ b 2 П ⊕ b 3 П ⊕ c 1 П ⊕ c 2 П ⊕ d 1 П ⊕ d 2 П ⊕ e 0 П ⊕ f 0 П ⊕ f 3 П ⊕ g 0 П ⊕ g 2 П ⊕ h 0 П ⊕ h 2 П ⊕ h 3 П ⊕ i 0 П ⊕ i 1 П ⊕ j 0 П ⊕ j 1 П ⊕ j 3 П ⊕ k 1 П ⊕ k 2 П ⊕ l 0 П ⊕ l 1 П ⊕ l 2 П ⊕ m 3 П ⊕ n 3 П ⊕ o 2 П ⊕ p 2 П ⊕ p 3 П ;

r 12 П g = a 0 П ⊕ a 3 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 2 П ⊕ d 0 П ⊕ d 2 П ⊕ d 3 П ⊕ e 0 П ⊕ e 1 П ⊕ e 3 П ⊕ f 0 П ⊕ f 1 П ⊕ f 3 П ⊕ g 0 П ⊕ g 1 П ⊕ g 2 П ⊕ h 0 П ⊕ h 1 П ⊕ h 2 П ⊕ h 3 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ k 3 П ⊕ l 2 П ⊕ l 3 П ⊕ m 1 П ⊕ n 1 П ⊕ n 3 П ⊕ o 1 П ⊕ o 2 П ⊕ p 1 П ⊕ p 2 П ⊕ p 3 П ;

r 13 П g = a 0 П ⊕ b 2 П ⊕ b 3 П ⊕ c 0 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 3 П ⊕ e 1 П ⊕ e 2 П ⊕ f 0 П ⊕ f 2 П ⊕ g 0 П ⊕ g 1 П ⊕ h 0 П ⊕ h 1 П ⊕ h 2 П ⊕ h 3 П ⊕ i 0 П ⊕ i 1 П ⊕ j 1 П ⊕ j 2 П ⊕ k 1 П ⊕ l 0 П ⊕ l 2 П ⊕ m 1 П ⊕ m 2 П ⊕ m 3 П ⊕ n 0 П ⊕ n 2 П ⊕ n 3 П ⊕ o 0 П ⊕ o 1 П ⊕ o 3 П ⊕ p 0 П ⊕ p 1 П ⊕ p 2 П ;

r 14 П g = a 2 П ⊕ a 3 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 3 П ⊕ d П 1 ⊕ d 2 П ⊕ e 3 П ⊕ f 2 П ⊕ g 3 П ⊕ h 1 П ⊕ h 2 П ⊕ h 3 П ⊕ i 0 П ⊕ i 2 П ⊕ j 0 П ⊕ j 1 П ⊕ j 3 П ⊕ k 2 П ⊕ k 3 П ⊕ l 1 П ⊕ l 2 П ⊕ l 3 П ⊕ m 1 П ⊕ m 3 П ⊕ n 0 П ⊕ o 0 П ⊕ o 1 П ⊕ o 2 П ⊕ p 0 П ⊕ p 2 П ⊕ p 3 П ;

r 15 П g = a 0 П ⊕ a 1 П ⊕ a 2 П ⊕ a 3 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ e 0 П ⊕ e 1 П ⊕ e 2 П ⊕ f 2 П ⊕ f 3 П ⊕ g 1 П ⊕ g 3 П ⊕ h 0 П ⊕ i 0 П ⊕ i 3 П ⊕ j 0 П ⊕ j 2 П ⊕ k 1 П ⊕ l 0 П ⊕ l 1 П ⊕ l 2 П ⊕ m 0 П ⊕ m 1 П ⊕ n 0 П ⊕ n 1 П ⊕ n 3 П ⊕ o 0 П ⊕ o 1 П ⊕ o 2 П ⊕ o 3 П ⊕ p 3 П ;

r 16 П g = a 0 П ⊕ a 3 П ⊕ b 1 П ⊕ b 2 П ⊕ b 3 П ⊕ c 0 П ⊕ c 1 П ⊕ c 2 П ⊕ d 3 П ⊕ e 2 П ⊕ e 3 П ⊕ f 0 П ⊕ f 2 П ⊕ f 3 П ⊕ g 2 П ⊕ g 3 П ⊕ h 1 П ⊕ i 0 П ⊕ i 2 П ⊕ i 3 П ⊕ j 1 П ⊕ j 2 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ l 0 П ⊕ l 1 П ⊕ m 0 П ⊕ m 3 П ⊕ n 3 П ⊕ o 0 П ⊕ o 2 П ⊕ p 1 П ⊕ p 2 П ;

r 17 П g = a 0 П ⊕ a 1 П ⊕ a 2 П ⊕ c 0 П ⊕ c 1 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ d 3 П ⊕ e 0 П ⊕ e 1 П ⊕ e 3 П ⊕ f 1 П ⊕ f 2 П ⊕ g 0 П ⊕ g 1 П ⊕ g 2 П ⊕ g 3 П ⊕ h 0 П ⊕ h 1 П ⊕ i 0 П ⊕ i 1 П ⊕ i 2 П ⊕ j 1 П ⊕ j 2 П ⊕ j 3 П ⊕ k 2 П ⊕ l 1 П ⊕ l 3 П ⊕ m 0 П ⊕ n 1 П ⊕ n 2 П ⊕ n 3 П ⊕ o 0 П ⊕ o П 1 ⊕ o 2 П ⊕ p 0 П ⊕ p 1 П ⊕ p 3 П ;

r 18 П g = a 0 П ⊕ a 2 П ⊕ a 3 П ⊕ b 2 П ⊕ b 3 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ d 3 П ⊕ e 1 П ⊕ e 2 П ⊕ f 3 П ⊕ g 2 П ⊕ h 1 П ⊕ i 1 П ⊕ i 2 П ⊕ i 3 П ⊕ j 1 П ⊕ j 2 П ⊕ k 0 П ⊕ k 1 П ⊕ l 0 П ⊕ l 1 П ⊕ l 2 П ⊕ l 3 П ⊕ n 1 П ⊕ n 3 П ⊕ o 0 П ⊕ o 1 П ⊕ p 0 П ⊕ p 1 П ⊕ p 2 П ;

r 19 П g = a 0 П ⊕ a 1 П ⊕ a 3 П ⊕ b 1 П ⊕ b 3 П ⊕ c 0 П ⊕ d 0 П ⊕ d 2 П ⊕ d 3 П ⊕ e 0 П ⊕ e 1 П ⊕ f 0 П ⊕ f 2 П ⊕ g 1 П ⊕ g 2 П ⊕ g 3 П ⊕ h 1 П ⊕ h 3 П ⊕ i 0 П ⊕ i 2 П ⊕ j 0 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ l 1 П ⊕ m 0 П ⊕ m 1 П ⊕ m 2 П ⊕ n 0 П ⊕ n 1 П ⊕ o 0 П ⊕ o 2 П ⊕ o 3 П ⊕ p 0 П ⊕ p 2 П ⊕ p 3 П ;

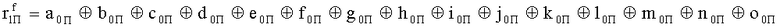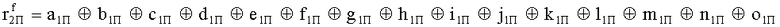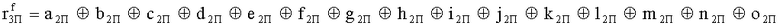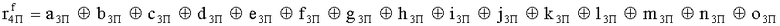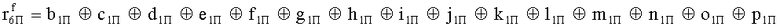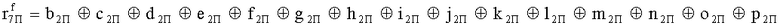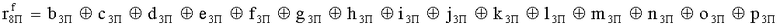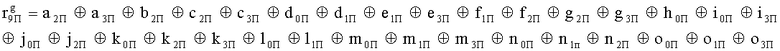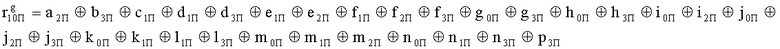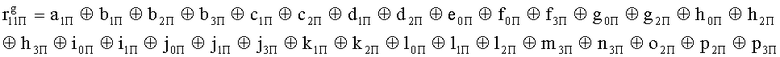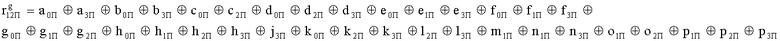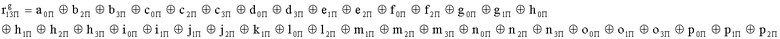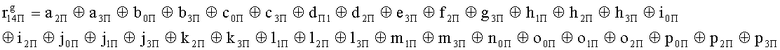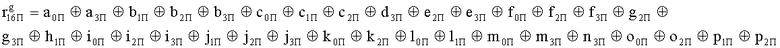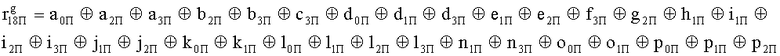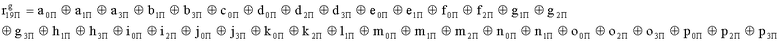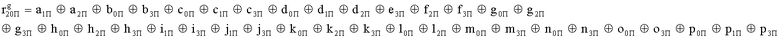r 20 П g = a 1 П ⊕ a 2 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 1 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ d 2 П ⊕ e 3 П ⊕ f 2 П ⊕ f 3 П ⊕ g 0 П ⊕ g 2 П ⊕ g 3 П ⊕ h 0 П ⊕ h 2 П ⊕ h 3 П ⊕ i 1 П ⊕ i 3 П ⊕ j 1 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ k 3 П ⊕ l 0 П ⊕ l 2 П ⊕ m 0 П ⊕ m 3 П ⊕ n 0 П ⊕ n 3 П ⊕ o 0 П ⊕ o 3 П ⊕ p 0 П ⊕ p 1 П ⊕ p 3 П , выходы выходного блока 3 кодирования подключены к первым входам блока 4 вычисления синдрома ошибки, к вторым входам которого подключены выходы контрольных разрядов узла 1 памяти, выходы блока 4 вычисления синдрома ошибки подключены к входам дешифратора 5, выходы которого подключены к входам блока 6 хранения векторов ошибок, выходы блока 6 хранения векторов ошибок подключены к вторым входам корректора 7, выходы которого подключены к вторым входам блока 8 элементов И, выходы блока 8 элементов И являются выходами 15 устройства.

Узел 1 памяти, в данном случае, представляет собой статическое полупроводниковое оперативное устройство памяти и предназначен для хранения кодовых наборов: Ук= a0a1a2a3, b0b1b32b3, c0c1c2c3, d0d1d2d3, e0e1e2e3, f0f1f2f3, g0g1g2g3, h0h1h2h3, i0i1i2i3, j0j1j2j3, k0k1k2k3, l0l1l2l3, m0m1m2m3, n0n1n2n3, o0o1o2o3, p0p1p2p3, 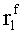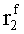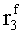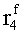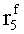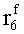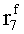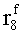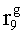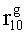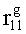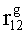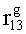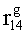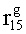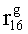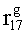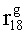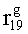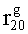r 1 f , r 2 f , r 3 f , r 4 f , r 5 f , r 6 f , r 7 f , r 8 f , r 9 g , r 10 g , r 11 g , r 12 g , r 13 g , r 14 g , r 15 g , r 16 g , r 17 g , r 18 g , r 19 g , r 20 g , полученных при кодировании исходных шестидесяти четырех разрядных двоичных наборов.

Входной блок 2 кодирования предназначен для формирования значений контрольных разрядов 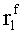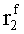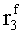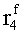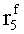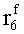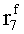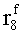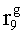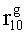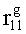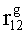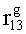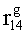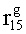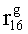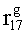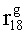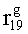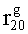r 1 f , r 2 f , r 3 f , r 4 f , r 5 f , r 6 f , r 7 f , r 8 f , r 9 g , r 10 g , r 11 g , r 12 g , r 13 g , r 14 g , r 15 g , r 16 g , r 17 g , r 18 g , r 19 g , r 20 g , путем сложения по mod2 информационных символов в соответствии с правилом:

r 1 f = a 0 ⊕ b 0 ⊕ c 0 ⊕ d 0 ⊕ e 0 ⊕ f 0 ⊕ g 0 ⊕ h 0 ⊕ i 0 ⊕ j 0 ⊕ k 0 ⊕ l 0 ⊕ m 0 ⊕ n 0 ⊕ o 0 ;

r 2 f = a 1 ⊕ b 1 ⊕ c 1 ⊕ d 1 ⊕ e 1 ⊕ f 1 ⊕ g 1 ⊕ h 1 ⊕ i 1 ⊕ j 1 ⊕ k 1 ⊕ l 1 ⊕ m 1 ⊕ n 1 ⊕ o 1 ;

r 3 f = a 2 ⊕ b 2 ⊕ c 2 ⊕ d 2 ⊕ e 2 ⊕ f 2 ⊕ g 2 ⊕ h 2 ⊕ i 2 ⊕ j 2 ⊕ k 2 ⊕ l 2 ⊕ m 2 ⊕ n 2 ⊕ o 2 ;

r 4 f = a 3 ⊕ b 3 ⊕ c 3 ⊕ d 3 ⊕ e 3 ⊕ f 3 ⊕ g 3 ⊕ h 3 ⊕ i 3 ⊕ j 3 ⊕ k 3 ⊕ l 3 ⊕ m 3 ⊕ n 3 ⊕ o 3 ;

r 5 f = b 0 ⊕ c 0 ⊕ d 0 ⊕ e 0 ⊕ f 0 ⊕ g 0 ⊕ h 0 ⊕ i 0 ⊕ j 0 ⊕ k 0 ⊕ l 0 ⊕ m 0 ⊕ n 0 ⊕ o 0 ⊕ p 0 ;

r 6 f = b 1 ⊕ c 1 ⊕ d 1 ⊕ e 1 ⊕ f 1 ⊕ g 1 ⊕ h 1 ⊕ i 1 ⊕ j 1 ⊕ k 1 ⊕ l 1 ⊕ m 1 ⊕ n 1 ⊕ o 1 ⊕ p 1 ;

r 7 f = b 2 ⊕ c 2 ⊕ d 2 ⊕ e 2 ⊕ f 2 ⊕ g 2 ⊕ h 2 ⊕ i 2 ⊕ j 2 ⊕ k 2 ⊕ l 2 ⊕ m 2 ⊕ n 2 ⊕ o 2 ⊕ p 2 ;

r 8 f = b 3 ⊕ c 3 ⊕ d 3 ⊕ e 3 ⊕ f 3 ⊕ g 3 ⊕ h 3 ⊕ i 3 ⊕ j 3 ⊕ k 3 ⊕ l 3 ⊕ m 3 ⊕ n 3 ⊕ o 3 ⊕ p 3 ;

r 9 g = a 2 ⊕ a 3 ⊕ b 2 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ e 1 ⊕ e 3 ⊕ f 1 ⊕ f 2 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ i 0 ⊕ i 3 ⊕ j 0 ⊕ j 2 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 0 ⊕ l 1 ⊕ m 0 ⊕ m 1 ⊕ m 3 ⊕ n 0 ⊕ n 1 ⊕ n 2 ⊕ o 0 ⊕ o 1 ⊕ o 3

r 10 g = a 2 ⊕ b 3 ⊕ c 1 ⊕ d 1 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 1 ⊕ f 2 ⊕ f 3 ⊕ g 0 ⊕ g 3 ⊕ h 0 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 2 ⊕ j 3 ⊕ k 0 ⊕ k 1 ⊕ l 1 ⊕ l 3 ⊕ m 0 ⊕ m 1 ⊕ m 2 ⊕ n 0 ⊕ n 1 ⊕ n 3 ⊕ p 3 ;

r 11 g = a 1 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ c 1 ⊕ c 2 ⊕ d 1 ⊕ d 2 ⊕ e 0 ⊕ f 0 ⊕ f 3 ⊕ g 0 ⊕ g 2 ⊕ h 0 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 1 ⊕ j 0 ⊕ j 1 ⊕ j 3 ⊕ k 1 ⊕ k 2 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ m 3 ⊕ n 3 ⊕ o 2 ⊕ p 2 ⊕ p 3 ;

r 12 g = a 0 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ d 0 ⊕ d 2 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ e 3 ⊕ f 0 ⊕ f 1 ⊕ f 3 ⊕ g 0 ⊕ g 1 ⊕ g 2 ⊕ h 0 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 2 ⊕ l 3 ⊕ m 1 ⊕ n 1 ⊕ n 3 ⊕ ⊕ o 1 ⊕ o 2 ⊕ p 1 ⊕ p 2 ⊕ p 3 ;

r 13 g = a 0 ⊕ b 2 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 0 ⊕ f 2 ⊕ g 0 ⊕ g 1 ⊕ h 0 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 1 ⊕ j 1 ⊕ j 2 ⊕ k 1 ⊕ l 0 ⊕ l 2 ⊕ m 1 ⊕ m 2 ⊕ m 3 ⊕ n 0 ⊕ n 2 ⊕ n 3 ⊕ ⊕ o 0 ⊕ o 1 ⊕ o 3 ⊕ p 0 ⊕ p 1 ⊕ p 2 ;

r 14 g = a 2 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 3 ⊕ d 1 ⊕ d 2 ⊕ e 3 ⊕ f 2 ⊕ g 3 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 1 ⊕ j 3 ⊕ k 2 ⊕ k 3 ⊕ l 1 ⊕ l 2 ⊕ l 3 ⊕ m 1 ⊕ m 3 ⊕ n 0 ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ p 0 ⊕ p 2 ⊕ p 3 ;

r 15 g = a 0 ⊕ a 1 ⊕ a 2 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ e 0 ⊕ e 1 ⊕ e 2 ⊕ f 2 ⊕ f 3 ⊕ g 1 ⊕ g 3 ⊕ h 0 ⊕ i 0 ⊕ i 3 ⊕ j 0 ⊕ j 2 ⊕ k 1 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ m 0 ⊕ m 1 ⊕ n 0 ⊕ n 1 ⊕ n 3 ⊕ ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ o 3 ⊕ p 3 ;

r 16 g = a 0 ⊕ a 3 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ c 0 ⊕ c 1 ⊕ c 2 ⊕ d 3 ⊕ e 2 ⊕ e 3 ⊕ f 0 ⊕ f 2 ⊕ f 3 ⊕ g 2 ⊕ g 3 ⊕ h 1 ⊕ i 0 ⊕ i 2 ⊕ i 3 ⊕ j 1 ⊕ j 2 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ l 0 ⊕ l 1 ⊕ m 0 ⊕ m 3 ⊕ n 3 ⊕ o 0 ⊕ o 2 ⊕ p 1 ⊕ p 2 ;

r 17 g = a 0 ⊕ a 1 ⊕ a 2 ⊕ c 0 ⊕ c 1 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ e 3 ⊕ f 1 ⊕ f 2 ⊕ g 0 ⊕ g 1 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ h 1 ⊕ i 0 ⊕ i 1 ⊕ i 2 ⊕ j 1 ⊕ j 2 ⊕ j 3 ⊕ k 2 ⊕ l 1 ⊕ l 3 ⊕ m 0 ⊕ n 1 ⊕ n 2 ⊕ n 3 ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ p 0 ⊕ p 1 ⊕ p 3 ;

r 18 g = a 0 ⊕ a 2 ⊕ a 3 ⊕ b 2 ⊕ b 3 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 3 ⊕ g 2 ⊕ h 1 ⊕ i 1 ⊕ i 2 ⊕ i 3 ⊕ j 1 ⊕ j 2 ⊕ k 0 ⊕ k 1 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ l 3 ⊕ n 1 ⊕ n 3 ⊕ o 0 ⊕ o 1 ⊕ p 0 ⊕ p 1 ⊕ p 2 ;

r 19 g = a 0 ⊕ a 1 ⊕ a 3 ⊕ b 1 ⊕ b 3 ⊕ c 0 ⊕ d 0 ⊕ d 2 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ f 0 ⊕ f 2 ⊕ g 1 ⊕ g 2 ⊕ g 3 ⊕ h 1 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ l 1 ⊕ m 0 ⊕ m 1 ⊕ m 2 ⊕ n 0 ⊕ n 1 ⊕ o 0 ⊕ o 2 ⊕ o 3 ⊕ p 0 ⊕ p 2 ⊕ p 3 ;

r 20 g = a 1 ⊕ a 2 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 1 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 2 ⊕ e 3 ⊕ f 2 ⊕ f 3 ⊕ g 0 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ h 2 ⊕ h 3 ⊕ i 1 ⊕ i 3 ⊕ j 1 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 0 ⊕ l 2 ⊕ m 0 ⊕ m 3 ⊕ n 0 ⊕ n 3 ⊕ o 0 ⊕ o 3 ⊕ p 0 ⊕ p 1 ⊕ p 3 .

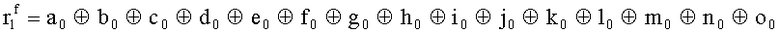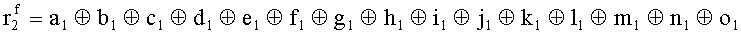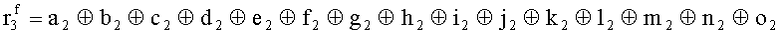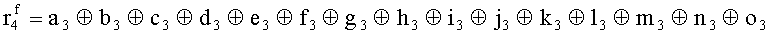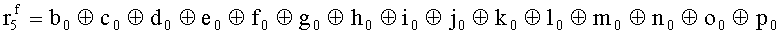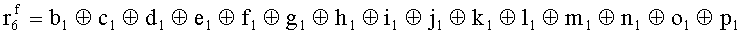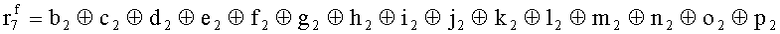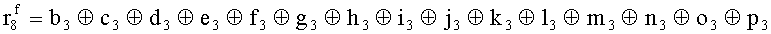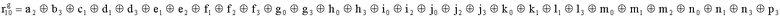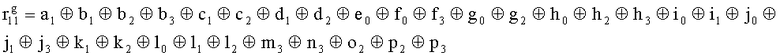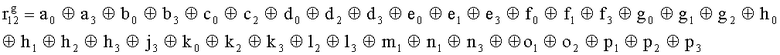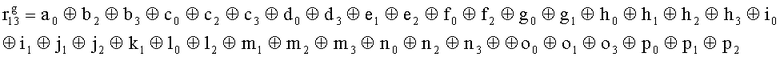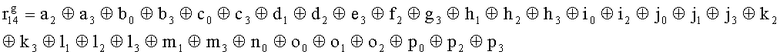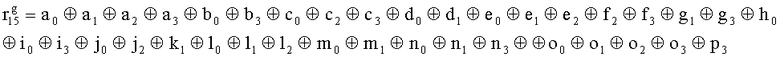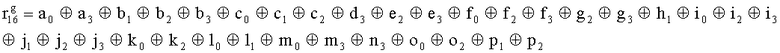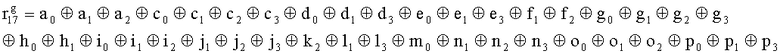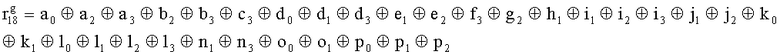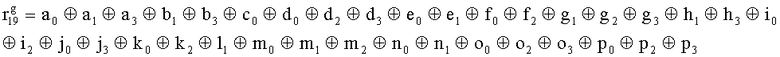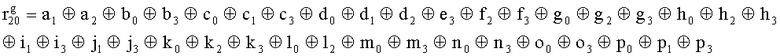Выходной блок 3 кодирования предназначен для формирования значений проверочных контрольных разрядов 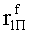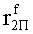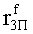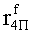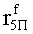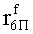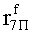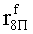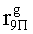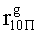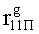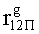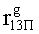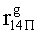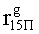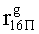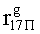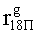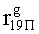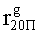r 1 П f , r 2 П f , r 3 П f , r 4 П f , r 5 П f , r 6 П f , r 7 П f , r 8 П f , r 9 П g , r 10 П g , r 11 П g , r 12 П g , r 13 П g , r 14 П g , r 15 П g , r 16 П g , r 17 П g , r 18 П g , r 19 П g , r 20 П g , путем сложения по модулю 2 информационных символов a0Пa1Пa2Пa3П, b0Пb1Пb2Пb3П, c0Пc1Пc2Пc3П, d0Пd1Пd2Пd3П, e0Пe1Пe2Пe3П, f0Пf1Пf2Пf3П, g0Пg1Пg2Пg3П, h0Пh1Пh2Пh3П, i0Пi1Пi2Пi3П, j0Пj1Пj2Пj3П, k0Пk1Пk2Пk3П, l0Пl1Пl2Пl3П, m0Пm1Пm2Пm3П, n0Пn1Пn2Пn3П, o0Пo1Пo2Пo3П, p0Пp1Пp2Пp3П, поступающих на входы входного блока 3 кодирования с информационных выходов узла 1 памяти, в соответствии с правилом:

r 1 П f = a 0 П ⊕ b 0 П ⊕ c 0 П ⊕ d 0 П ⊕ e 0 П ⊕ f 0 П ⊕ g 0 П ⊕ h 0 П ⊕ i 0 П ⊕ j 0 П ⊕ k 0 П ⊕ l 0 П ⊕ m 0 П ⊕ n 0 П ⊕ o 0 П ;

r 2 П f = a 1 П ⊕ b 1 П ⊕ c 1 П ⊕ d 1 П ⊕ e 1 П ⊕ f 1 П ⊕ g 1 П ⊕ h 1 П ⊕ i 1 П ⊕ j 1 П ⊕ k 1 П ⊕ l 1 П ⊕ m 1 П ⊕ n 1 П ⊕ o 1 П ;

r 3 П f = a 2 П ⊕ b 2 П ⊕ c 2 П ⊕ d 2 П ⊕ e 2 П ⊕ f 2 П ⊕ g 2 П ⊕ h 2 П ⊕ i 2 П ⊕ j 2 П ⊕ k 2 П ⊕ l 2 П ⊕ m 2 П ⊕ n 2 П ⊕ o 2 П ;

r 4 П f = a 3 П ⊕ b 3 П ⊕ c 3 П ⊕ d 3 П ⊕ e 3 П ⊕ f 3 П ⊕ g 3 П ⊕ h 3 П ⊕ i 3 П ⊕ j 3 П ⊕ k 3 П ⊕ l 3 П ⊕ m 3 П ⊕ n 3 П ⊕ o 3 П ;

r 5 П f = b 0 П ⊕ c 0 П ⊕ d 0 П ⊕ e 0 П ⊕ f 0 П ⊕ g 0 П ⊕ h 0 П ⊕ i 0 П ⊕ j 0 П ⊕ k 0 П ⊕ l 0 П ⊕ m 0 П ⊕ n 0 П ⊕ o 0 П ⊕ p 0 П ;

r 6 П f = b 1 П ⊕ c 1 П ⊕ d 1 П ⊕ e 1 П ⊕ f 1 П ⊕ g 1 П ⊕ h 1 П ⊕ i 1 П ⊕ j 1 П ⊕ k 1 П ⊕ l 1 П ⊕ m 1 П ⊕ n 1 П ⊕ o 1 П ⊕ p 1 П ;

r 7 П f = b 2 П ⊕ c 2 П ⊕ d 2 П ⊕ e 2 П ⊕ f 2 П ⊕ g 2 П ⊕ h 2 П ⊕ i 2 П ⊕ j 2 П ⊕ k 2 П ⊕ l 2 П ⊕ m 2 П ⊕ n 2 П ⊕ o 2 П ⊕ p 2 П ;

r 8 П f = b 3 П ⊕ c 3 П ⊕ d 3 П ⊕ e 3 П ⊕ f 3 П ⊕ g 3 П ⊕ h 3 П ⊕ i 3 П ⊕ j 3 П ⊕ k 3 П ⊕ l 3 П ⊕ m 3 П ⊕ n 3 П ⊕ o 3 П ⊕ p 3 П ;

r 9 П g = a 2 П ⊕ a 3 П ⊕ b 2 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ e 1 П ⊕ e 3 П ⊕ f 1 П ⊕ f 2 П ⊕ g 2 П ⊕ g 3 П ⊕ h 0 П ⊕ i 0 П ⊕ i 3 П ⊕ j 0 П ⊕ j 2 П ⊕ k 0 П ⊕ k 2 П ⊕ k 3 П ⊕ l 0 П ⊕ l 1 П ⊕ m 0 П ⊕ m 1 П ⊕ m 3 П ⊕ n 0 П ⊕ n 1 п ⊕ n 2 П ⊕ o 0 П ⊕ o 1 П ⊕ o 3 П ;

r 10 П g = a 2 П ⊕ b 3 П ⊕ c 1 П ⊕ d 1 П ⊕ d 3 П ⊕ e 1 П ⊕ e 2 П ⊕ f 1 П ⊕ f 2 П ⊕ f 3 П ⊕ g 0 П ⊕ g 3 П ⊕ h 0 П ⊕ h 3 П ⊕ i 0 П ⊕ i 2 П ⊕ j 0 П ⊕ j 2 П ⊕ j 3 П ⊕ k 0 П ⊕ k 1 П ⊕ l 1 П ⊕ l 3 П ⊕ m 0 П ⊕ m 1 П ⊕ m 2 П ⊕ n 0 П ⊕ n 1 П ⊕ n 3 П ⊕ p 3 П ;

r 11 П g = a 1 П ⊕ b 1 П ⊕ b 2 П ⊕ b 3 П ⊕ c 1 П ⊕ c 2 П ⊕ d 1 П ⊕ d 2 П ⊕ e 0 П ⊕ f 0 П ⊕ f 3 П ⊕ g 0 П ⊕ g 2 П ⊕ h 0 П ⊕ h 2 П ⊕ h 3 П ⊕ i 0 П ⊕ i 1 П ⊕ j 0 П ⊕ j 1 П ⊕ j 3 П ⊕ k 1 П ⊕ k 2 П ⊕ l 0 П ⊕ l 1 П ⊕ l 2 П ⊕ m 3 П ⊕ n 3 П ⊕ o 2 П ⊕ p 2 П ⊕ p 3 П ;

r 12 П g = a 0 П ⊕ a 3 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 2 П ⊕ d 0 П ⊕ d 2 П ⊕ d 3 П ⊕ e 0 П ⊕ e 1 П ⊕ e 3 П ⊕ f 0 П ⊕ f 1 П ⊕ f 3 П ⊕ g 0 П ⊕ g 1 П ⊕ g 2 П ⊕ h 0 П ⊕ h 1 П ⊕ h 2 П ⊕ h 3 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ k 3 П ⊕ l 2 П ⊕ l 3 П ⊕ m 1 П ⊕ n 1 П ⊕ n 3 П ⊕ o 1 П ⊕ o 2 П ⊕ p 1 П ⊕ p 2 П ⊕ p 3 П ;

r 13 П g = a 0 П ⊕ b 2 П ⊕ b 3 П ⊕ c 0 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 3 П ⊕ e 1 П ⊕ e 2 П ⊕ f 0 П ⊕ f 2 П ⊕ g 0 П ⊕ g 1 П ⊕ h 0 П ⊕ h 1 П ⊕ h 2 П ⊕ h 3 П ⊕ i 0 П ⊕ i 1 П ⊕ j 1 П ⊕ j 2 П ⊕ k 1 П ⊕ l 0 П ⊕ l 2 П ⊕ m 1 П ⊕ m 2 П ⊕ m 3 П ⊕ n 0 П ⊕ n 2 П ⊕ n 3 П ⊕ o 0 П ⊕ o 1 П ⊕ o 3 П ⊕ p 0 П ⊕ p 1 П ⊕ p 2 П ;

r 14 П g = a 2 П ⊕ a 3 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 3 П ⊕ d П 1 ⊕ d 2 П ⊕ e 3 П ⊕ f 2 П ⊕ g 3 П ⊕ h 1 П ⊕ h 2 П ⊕ h 3 П ⊕ i 0 П ⊕ i 2 П ⊕ j 0 П ⊕ j 1 П ⊕ j 3 П ⊕ k 2 П ⊕ k 3 П ⊕ l 1 П ⊕ l 2 П ⊕ l 3 П ⊕ m 1 П ⊕ m 3 П ⊕ n 0 П ⊕ o 0 П ⊕ o 1 П ⊕ o 2 П ⊕ p 0 П ⊕ p 2 П ⊕ p 3 П ;

r 15 П g = a 0 П ⊕ a 1 П ⊕ a 2 П ⊕ a 3 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ e 0 П ⊕ e 1 П ⊕ e 2 П ⊕ f 2 П ⊕ f 3 П ⊕ g 1 П ⊕ g 3 П ⊕ h 0 П ⊕ i 0 П ⊕ i 3 П ⊕ j 0 П ⊕ j 2 П ⊕ k 1 П ⊕ l 0 П ⊕ l 1 П ⊕ l 2 П ⊕ m 0 П ⊕ m 1 П ⊕ n 0 П ⊕ n 1 П ⊕ n 3 П ⊕ o 0 П ⊕ o 1 П ⊕ o 2 П ⊕ o 3 П ⊕ p 3 П ;

r 16 П g = a 0 П ⊕ a 3 П ⊕ b 1 П ⊕ b 2 П ⊕ b 3 П ⊕ c 0 П ⊕ c 1 П ⊕ c 2 П ⊕ d 3 П ⊕ e 2 П ⊕ e 3 П ⊕ f 0 П ⊕ f 2 П ⊕ f 3 П ⊕ g 2 П ⊕ g 3 П ⊕ h 1 П ⊕ i 0 П ⊕ i 2 П ⊕ i 3 П ⊕ j 1 П ⊕ j 2 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ l 0 П ⊕ l 1 П ⊕ m 0 П ⊕ m 3 П ⊕ n 3 П ⊕ o 0 П ⊕ o 2 П ⊕ p 1 П ⊕ p 2 П ;

r 17 П g = a 0 П ⊕ a 1 П ⊕ a 2 П ⊕ c 0 П ⊕ c 1 П ⊕ c 2 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ d 3 П ⊕ e 0 П ⊕ e 1 П ⊕ e 3 П ⊕ f 1 П ⊕ f 2 П ⊕ g 0 П ⊕ g 1 П ⊕ g 2 П ⊕ g 3 П ⊕ h 0 П ⊕ h 1 П ⊕ i 0 П ⊕ i 1 П ⊕ i 2 П ⊕ j 1 П ⊕ j 2 П ⊕ j 3 П ⊕ k 2 П ⊕ l 1 П ⊕ l 3 П ⊕ m 0 П ⊕ n 1 П ⊕ n 2 П ⊕ n 3 П ⊕ o 0 П ⊕ o П 1 ⊕ o 2 П ⊕ p 0 П ⊕ p 1 П ⊕ p 3 П ;

r 18 П g = a 0 П ⊕ a 2 П ⊕ a 3 П ⊕ b 2 П ⊕ b 3 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ d 3 П ⊕ e 1 П ⊕ e 2 П ⊕ f 3 П ⊕ g 2 П ⊕ h 1 П ⊕ i 1 П ⊕ i 2 П ⊕ i 3 П ⊕ j 1 П ⊕ j 2 П ⊕ k 0 П ⊕ k 1 П ⊕ l 0 П ⊕ l 1 П ⊕ l 2 П ⊕ l 3 П ⊕ n 1 П ⊕ n 3 П ⊕ o 0 П ⊕ o 1 П ⊕ p 0 П ⊕ p 1 П ⊕ p 2 П ;

r 19 П g = a 0 П ⊕ a 1 П ⊕ a 3 П ⊕ b 1 П ⊕ b 3 П ⊕ c 0 П ⊕ d 0 П ⊕ d 2 П ⊕ d 3 П ⊕ e 0 П ⊕ e 1 П ⊕ f 0 П ⊕ f 2 П ⊕ g 1 П ⊕ g 2 П ⊕ g 3 П ⊕ h 1 П ⊕ h 3 П ⊕ i 0 П ⊕ i 2 П ⊕ j 0 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ l 1 П ⊕ m 0 П ⊕ m 1 П ⊕ m 2 П ⊕ n 0 П ⊕ n 1 П ⊕ o 0 П ⊕ o 2 П ⊕ o 3 П ⊕ p 0 П ⊕ p 2 П ⊕ p 3 П ;

r 20 П g = a 1 П ⊕ a 2 П ⊕ b 0 П ⊕ b 3 П ⊕ c 0 П ⊕ c 1 П ⊕ c 3 П ⊕ d 0 П ⊕ d 1 П ⊕ d 2 П ⊕ e 3 П ⊕ f 2 П ⊕ f 3 П ⊕ g 0 П ⊕ g 2 П ⊕ g 3 П ⊕ h 0 П ⊕ h 2 П ⊕ h 3 П ⊕ i 1 П ⊕ i 3 П ⊕ j 1 П ⊕ j 3 П ⊕ k 0 П ⊕ k 2 П ⊕ k 3 П ⊕ l 0 П ⊕ l 2 П ⊕ m 0 П ⊕ m 3 П ⊕ n 0 П ⊕ n 3 П ⊕ o 0 П ⊕ o 3 П ⊕ p 0 П ⊕ p 1 П ⊕ p 3 П .

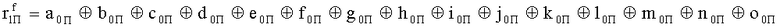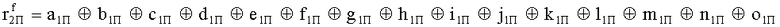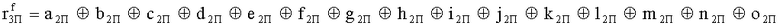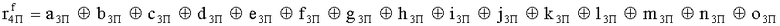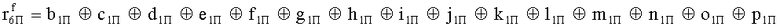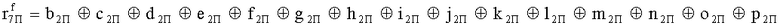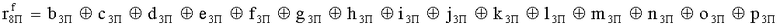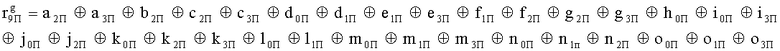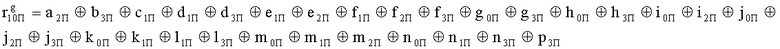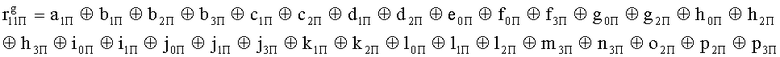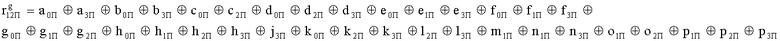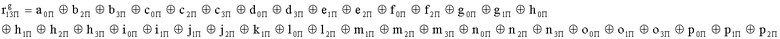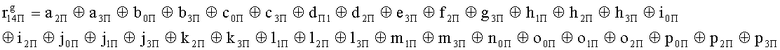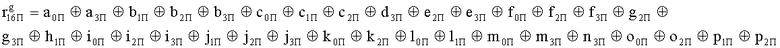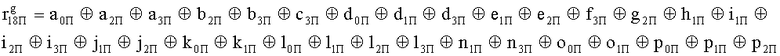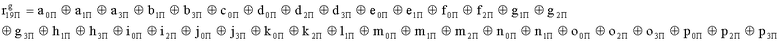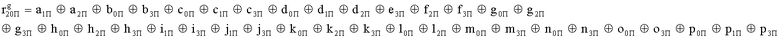Блок 4 вычисления синдрома ошибки предназначен для обнаружения ошибки в кодовом наборе при считывании информации с узла 1 памяти путем сложения no mod2 значений контрольных разрядов 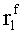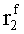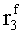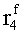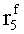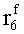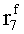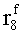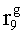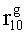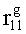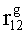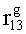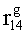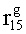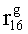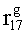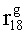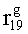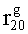r 1 f , r 2 f , r 3 f , r 4 f , r 5 f , r 6 f , r 7 f , r 8 f , r 9 g , r 10 g , r 11 g , r 12 g , r 13 g , r 14 g , r 15 g , r 16 g , r 17 g , r 18 g , r 19 g , r 20 g , считываемых с вторых выходов узла 1 памяти, соответственно с значениями контрольных разрядов 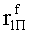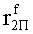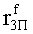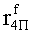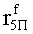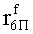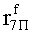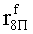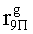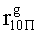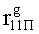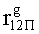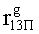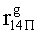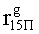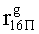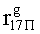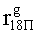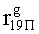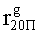r 1 П f , r 2 П f , r 3 П f , r 4 П f , r 5 П f , r 6 П f , r 7 П f , r 8 П f , r 9 П g , r 10 П g , r 11 П g , r 12 П g , r 13 П g , r 14 П g , r 15 П g , r 16 П g , r 17 П g , r 18 П g , r 19 П g , r 20 П g , сформированных на выходах выходного блока 3 кодирования.

Результат поразрядного сложения:

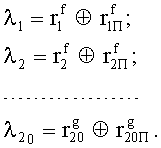
λ 1 = r 1 f ⊕ r 1 П f ; λ 2 = r 2 f ⊕ r 2 П f ; … … … … … … λ 2 0 = r 20 g ⊕ r 20 П g .

Нулевой результат суммы свидетельствует об отсутствии ошибки и ее наличии в противном случае.

Дешифратор 5 формирует единичное значение сигнала на одном из своих выходов в соответствии с значением синдрома ошибки (формирует адрес вектора ошибки в блоке 6 хранения векторов ошибок).

В таблице 1 представлена часть значений синдромов ошибок для кода 84,20.

Примечание: В табл.1 значения информационных разрядов, контрольных разрядов и значения ошибки в байтах информации представлены в шестнадцатеричной системе счисления, а значения синдрома ошибки - в двоичной.

Таблица 1 Значения синдромов ошибок для кода (84,20) Информационные разряды контр. разр. Ошибка в байте Синдром ошибки 0000000000000000 00000 0000 00000000000000000000 0000000000000000 00000 0001 00000001011101101011 0000000000000000 00000 0002 00000010001111010110 0000000000000000 00000 0003 00000011010010111101 0000000000000000 00000 0004 00000100000110011101 0000000000000000 00000 0005 00000101011011110110 0000000000000000 00000 0006 00000110001001001011 0000000000000000 00000 0007 00000111010100100000 0000000000000000 00000 0008 00001000000011001111 0000000000000000 00000 0009 00001001011110100100 0000000000000000 00000 000A 00001010001100011001 0000000000000000 00000 000B 00001011010001110010 0000000000000000 00000 000C 00001100000101010010 0000000000000000 00000 000D 00001101011000111001 0000000000000000 00000 000E 00001110001010000100 0000000000000000 00000 000F 00001111010111101111 0000000000000000 00000 0010 00010000100010100011 0000000000000000 00000 0011 00010001111111001000 0000000000000000 00000 0012 00010010101101110101 0000000000000000 00000 0013 00010011110000011110 0000000000000000 00000 0014 00010100100100111110 0000000000000000 00000 0015 00010101111001010101 0000000000000000 00000 0016 00010110101011101000 0000000000000000 00000 0017 00010111110110000011 0000000000000000 00000 0018 00011000100001101100 0000000000000000 00000 0019 00011001111100000111 0000000000000000 00000 001A 00011010101110111010 0000000000000000 00000 001B 00011011110011010001 0000000000000000 00000 001C 00011100100111110001 0000000000000000 00000 001D 00011101111010011010 0000000000000000 00000 001E 00011110101000100111

0000000000000000 00000 001F 00011111110101001100 0000000000000000 00000 0020 00100000001101111010 0000000000000000 00000 0021 00100001010000010001 0000000000000000 00000 0022 00100010000010101100 0000000000000000 00000 0023 00100011011111000111 0000000000000000 00000 0024 00100100001011100111 0000000000000000 00000 0025 00100101010110001100 0000000000000000 00000 0026 00100110000100110001 0000000000000000 00000 0027 00100111011001011010 0000000000000000 00000 0028 00101000001110110101 0000000000000000 00000 0029 00101001010011011110 0000000000000000 00000 002A 00101010000001100011 0000000000000000 00000 002B 00101011011100001000 0000000000000000 00000 002C 00101100001000101000 0000000000000000 00000 002D 00101101010101000011 0000000000000000 00000 002E 00101110000111111110 0000000000000000 00000 002F 00101111011010010101 0000000000000000 00000 0030 00110000101111011001 0000000000000000 00000 0031 00110001110010110010 0000000000000000 00000 0032 00110010100000001111 0000000000000000 00000 0033 00110011111101100100 0000000000000000 00000 0034 00110100101001000100 0000000000000000 00000 0035 00110101110100101111 0000000000000000 00000 0036 00110110100110010010 0000000000000000 00000 0037 00110111111011111001 0000000000000000 00000 0038 00111000101100010110 0000000000000000 00000 0039 00111001110001111101 0000000000000000 00000 003A 00111010100011000000 0000000000000000 00000 003B 00111011111110101011 0000000000000000 00000 003C 00111100101010001011 0000000000000000 00000 003D 00111101110111100000 0000000000000000 00000 003E 00111110100101011101 0000000000000000 00000 003F 00111111111000110110 0000000000000000 00000 0040 01000000100111101100 0000000000000000 00000 0041 01000001111010000111 0000000000000000 00000 0042 01000010101000111010 0000000000000000 00000 0043 01000011110101010001 0000000000000000 00000 0044 01000100100001110001 0000000000000000 00000 0045 01000101111100011010 0000000000000000 00000 0046 01000110101110100111 0000000000000000 00000 0047 01000111110011001100 0000000000000000 00000 0048 01001000100100100011 0000000000000000 00000 0049 01001001111001001000 0000000000000000 00000 004A 01001010101011110101 0000000000000000 00000 004B 01001011110110011110 0000000000000000 00000 004C 01001100100010111110 0000000000000000 00000 004D 01001101111111010101 0000000000000000 00000 004E 01001110101101101000 0000000000000000 00000 004F 01001111110000000011 0000000000000000 00000 0050 01010000000101001111 0000000000000000 00000 0051 01010001011000100100 0000000000000000 00000 0052 01010010001010011001 0000000000000000 00000 0053 01010011010111110010 0000000000000000 00000 0054 01010100000011010010 0000000000000000 00000 0055 01010101011110111001 0000000000000000 00000 0056 01010110001100000100 0000000000000000 00000 0057 01010111010001101111

0000000000000000 00000 0058 01011000000110000000 0000000000000000 00000 0059 01011001011011101011 0000000000000000 00000 005A 01011010001001010110 0000000000000000 00000 005B 01011011010100111101 0000000000000000 00000 005C 01011100000000011101 0000000000000000 00000 005D 01011101011101110110 0000000000000000 00000 005E 01011110001111001011 0000000000000000 00000 005F 01011111010010100000 0000000000000000 00000 0060 01100000101010010110 0000000000000000 00000 0061 01100001110111111101 0000000000000000 00000 0062 01100010100101000000 0000000000000000 00000 0063 01100011111000101011 0000000000000000 00000 0064 01100100101100001011 0000000000000000 00000 0065 01100101110001100000 0000000000000000 00000 0066 01100110100011011101 0000000000000000 00000 0067 01100111111110110110 0000000000000000 00000 0068 01101000101001011001 0000000000000000 00000 0069 01101001110100110010 0000000000000000 00000 006A 01101010100110001111 0000000000000000 00000 006B 01101011111011100100 0000000000000000 00000 006C 01101100101111000100 0000000000000000 00000 006D 01101101110010101111 0000000000000000 00000 006E 01101110100000010010 0000000000000000 00000 006F 01101111111101111001 0000000000000000 00000 0070 01110000001000110101 0000000000000000 00000 0071 01110001010101011110 0000000000000000 00000 0072 01110010000111100011 0000000000000000 00000 0073 01110011011010001000 0000000000000000 00000 0074 01110100001110101000 0000000000000000 00000 0075 01110101010011000011 0000000000000000 00000 0076 01110110000001111110 0000000000000000 00000 0077 01110111011100010101 0000000000000000 00000 0078 01111000001011111010 0000000000000000 00000 0079 01111001010110010001 0000000000000000 00000 007A 01111010000100101100 0000000000000000 00000 007B 01111011011001000111 0000000000000000 00000 007C 01111100001101100111 0000000000000000 00000 007D 01111101010000001100 0000000000000000 00000 007E 01111110000010110001 0000000000000000 00000 007F 01111111011111011010 0000000000000000 00000 0080 10000000100011111111 0000000000000000 00000 0081 10000001111110010100 0000000000000000 00000 0082 10000010101100101001 0000000000000000 00000 0083 10000011110001000010 0000000000000000 00000 0084 10000100100101100010 0000000000000000 00000 0085 10000101111000001001 0000000000000000 00000 0086 10000110101010110100 0000000000000000 00000 0087 10000111110111011111 0000000000000000 00000 0088 10001000100000110000 0000000000000000 00000 0089 10001001111101011011 0000000000000000 00000 008A 10001010101111100110 0000000000000000 00000 008B 10001011110010001101 0000000000000000 00000 008C 10001100100110101101 0000000000000000 00000 008D 10001101111011000110 0000000000000000 00000 008E 10001110101001111011 0000000000000000 00000 008F 10001111110100010000 0000000000000000 00000 0090 10010000000001011100

0000000000000000 00000 0091 10010001011100110111 0000000000000000 00000 0092 10010010001110001010 0000000000000000 00000 0093 10010011010011100001 0000000000000000 00000 0094 10010100000111000001 0000000000000000 00000 0095 10010101011010101010 0000000000000000 00000 0096 10010110001000010111 0000000000000000 00000 0097 10010111010101111100 0000000000000000 00000 0098 10011000000010010011 0000000000000000 00000 0099 10011001011111111000 0000000000000000 00000 009A 10011010001101000101 0000000000000000 00000 009B 10011011010000101110 0000000000000000 00000 009C 10011100000100001110 0000000000000000 00000 009D 10011101011001100101 0000000000000000 00000 009E 10011110001011011000 0000000000000000 00000 009F 10011111010110110011 0000000000000000 00000 00A0 10100000101110000101 0000000000000000 00000 00A1 10100001110011101110 0000000000000000 00000 00A2 10100010100001010011 0000000000000000 00000 00A3 10100011111100111000 0000000000000000 00000 00A4 10100100101000011000 0000000000000000 00000 00A5 10100101110101110011 0000000000000000 00000 00A6 10100110100111001110 0000000000000000 00000 00A7 10100111111010100101 0000000000000000 00000 00A8 10101000101101001010 0000000000000000 00000 00A9 10101001110000100001 0000000000000000 00000 00AA 10101010100010011100 0000000000000000 00000 00AB 10101011111111110111 0000000000000000 00000 00AC 10101100101011010111 0000000000000000 00000 00AD 10101101110110111100 0000000000000000 00000 00AE 10101110100100000001 0000000000000000 00000 00AF 10101111111001101010 0000000000000000 00000 00B0 10110000001100100110 0000000000000000 00000 00B1 10110001010001001101 0000000000000000 00000 00B2 10110010000011110000 0000000000000000 00000 00B3 10110011011110011011

Блок 6 хранения векторов ошибок предназначен для хранения значений векторов ошибок в соответствии с значениями синдромов ошибок (вектор ошибки имеет единичные значения сигналов в тех разрядах кодового набора, в которых произошла ошибка).

Корректор 7 предназначен для исправления корректируемой ошибки, путем сложения по mod2 одноименных разрядов блока информации, имеющего ошибку с значением вектора ошибки.

Устройство работает следующим образом. Перед началом работы устройства на вход 9 "установки в нулевое состояние" подается единичный сигнал, который переводит устройство в нулевое состояние.

При записи информации в узел 1 памяти, подаются единичные сигналы на вход 14 синхронизации, вход 10 записи, адресные входы 112 и информационные входы 13.

Устройство работает следующим образом: допустим, необходимо закодировать двоичный набор:

У = A 0000 B 0000 C 0000 D 0000 E 0000 F 0000 G 0000 H 0000 I 0000 J 0000 K 0000 L 0000 M 0000 N 0000 O 0000 P 0000 .

Тогда значения контрольных разрядов, сформированных относительно полученного набора входным блоком 2 кодирования, имеют нулевые значения, т.е. имеем кодовый набор:

УК=0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000.

При отсутствии ошибки, значение кодового набора, записанного в узле 1 памяти, равно считанному (переданному кодовому набору):

УКП=0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000 0000.

В этом случае на выходе блока 4 вычисления синдрома ошибки имеем нулевые значения сигналов.

Пусть произошла одиночная ошибка в четвертом разряде шестнадцатого блока информации (P=0001*), тогда выходной блок 3 кодирования сформирует относительно полученного кодового набора значения контрольных разрядов:

r1П=0, r2П=0, r3П=0, r4П=0, r5П=0, r6П=0, r7П=0, r8П=1, r9П=0,. r10П=1, r11П=1, r12П=1, r13П=0, r14П=1, r15П=1, r16П=0, r17П=1, r18П=0, r19П=1, r20П=1.

В блоке 4 вычисления синдрома ошибки складываются переданные контрольные разряды с контрольными разрядами, сформированными относительно полученного кодового набора, в результате получим синдром ошибки S:

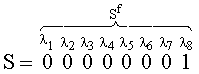
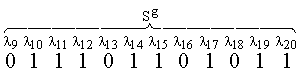
S = 0 λ 1 0 λ 2 0 λ 3 0 λ 4 0 λ 5 0 λ 6 0 λ 7 1 λ 8 ︷ S f 0 λ 9 1 λ 10 1 λ 11 1 λ 12 0 λ 13 1 λ 14 1 λ 15 0 λ 16 1 λ 17 0 λ 18 1 λ 19 1 λ 20 ︷ S g

В этом случае, синдром ошибки указывает четвертый ошибочный разряд блока P (вторая строка табл.1).

На выходе дешифратора 5 появится единичное значение сигнала, которое формирует адрес для считывания значения вектора ошибки из блока 6 хранения векторов ошибок в соответствии с значением синдрома ошибки.

В этом случае, значение вектора ошибки поступает на входы корректора 7 где складывается по mod2 с значениями информационных разрядов. В результате имеем правильное значение информации.

Аналогичным образом корректируются ошибки, возникающие в других одиночных и двойных байтах информации.

ИСТОЧНИКИ ИНФОРМАЦИИ

1. Щербаков Н.С. Достоверность работы цифровых устройств. М.: Машиностроение, 1989, с.82, рис.39, 224 с.

2. Патент РФ на изобретение №2448359 "Устройство хранения и передачи данных с исправлением ошибок в байте информации и обнаружением ошибок в байтах информации”/Борисов К.Ю., Малофеев Ю.Г., Осипенко П.Н., Павлов А.А., Павлов А.А., Павлов П.А. Царьков А.Н., Хоруженко О.В. Дата выдачи: 20.04.2012 г.

Приложение к заявке на изобретение: «Устройство хранения и передачи данных с исправлением ошибок в двух байтах информации »

1.Введение и постановка задачи

Во многих случаях для обнаружения и исправления ошибок используются коды с обнаружением и исправлением байтов ошибок (в этом случае, под байтом ошибок понимаются ошибки, кратность которых не превышает число разрядов b блока информации).

К таким кодам следует отнести коды [1]:

- исправляющие одиночные ошибки и обнаруживающие одиночные байты ошибок;

- коды, исправляющие одиночные ошибки, обнаруживающие двойные независимые ошибки и обнаруживающие одиночные байты ошибок;

- коды, исправляющие одиночные байты ошибок;

- коды, исправляющие одиночные и обнаруживающие двойные байты ошибок.

Широкое распространение получили коды Рида-Соломона, обладающие циклическими свойствами и имеющие наибольшую обнаруживающую и корректирующую способность.

Код Рида-Соломона (PC) - это блочный код (w, N), позволяющий обнаруживать и исправлять ошибки в байтах. Входным словом для него является блок из w байтов, выходным - кодовое слово из N байтов, состоящее из w исходных и N-w проверочных байтов. При этом гарантировано, что при декодировании в кодовом слове будут обнаружены и исправлены t=(N-w)/2 байтов независимо от их расположения внутри кодового слова. Кодирующее устройство PC реализуется на основе регистра сдвига с 2t байтовыми элементами памяти и обратными связями. Процесс кодирования и декодирования сводится к операциям сложения и умножения по модулю.

Использование данных кодов связано с большими временными затратами, что является существенным недостатком при их использовании для систем, работающих в реальном масштабе времени, поэтому существует необходимость в разработке более простой линейной процедуры построения корректирующих кодов, решающих данную задачу.

2. Разработка линейного корректирующего кода с исправлением ошибок в двух байтах информации

Предлагается метод построения корректирующего кода, исправляющего ошибки в двух байтах информации, реализующий линейную процедуру построения корректирующего кода с синдромным декодированием.

Правила кодирования информации

Правило 2.1 Двоичный набор Y, содержащий k информационных символов, разбивается на w=k/b байтов информации (под байтом информации понимается число информационных разрядов, не превышающих значение b, и пусть b кратно k).

Под байтом ошибок понимаются ошибки, кратность которых не превышает число разрядов b блока информации.

В результате двоичный набор может быть представлен в виде:

Y = x 1 x 2 … x b 1 , y 1 y 2 … y b 2 , … … … , z 1 z z … z b w .                                                                                                                 ( 2.1 )

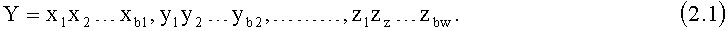
Определение 2.1 Вектор ошибки, полученный относительно сложения одноименных разрядов переданных и полученных байтов информации будем называть аддитивным вектором ошибки.

Правило 2.2 Для формирования первого аддитивного вектора ошибки осуществим сложение по mod2 одноименных разрядов байтов информации начиная с первого по (b-1) - блок информации, а для формирования второго аддитивного вектора ошибки осуществим сложение по mod2 одноименных разрядов байтов информации начиная с второго по b - блок информации (осуществим операцию перемежения) и результат суммирования добавим к двоичному набору Y.

В результате получим кодовый набор YK1:

YK1=x1x2…xb, y1y2…yb,…, z1zz…zb, p1p2…pb, x1x2…xb1 y1y2…yb1

⊕ … … …   …                       … … … … … ( 2.2 )

z 1 z z … z b ( w − 1 ) r 1 f r 2 f … r b f p 1 p z … p b w r b + 1 f r b + 2 f … r 2 b f

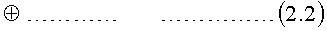
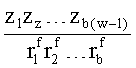
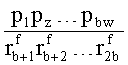
Для исправления ошибочных разрядов информации, возникает необходимость формирования совокупности проверок (разработки правила кодирования информации), позволяющих определить блок (байт) информации, содержащий ошибку.

С этой целью осуществим кодирование блоков информации, используя w матриц кодирования.

Свойство 2.1 Каждая матрица кодирования содержит gH=[log2(k+1)] сток при нечетном значении b и gЧ=[log2(k+1)]+1 - при четном значении b.

Свойство 2.2 Каждая строка матрицы кодирования содержит b разрядов.

Примечание: Квадратные скобки означают округление результата в большую сторону.

Правило 2.3 Представим одноименные строки матриц кодирования двоичным набором, соответствующим одному из значений множества {2b} таким образом, чтобы результат проверки на четность строк матрицы кодирования в двоичном наборе образовывал номер ui, принадлежащий множеству {2 gH} при нечетном значении b и множеству {2 gЧ} - при четном значении b и при этом для полученных значений номеров выполнялось условие ui--ui≥2t.

Правило 2.4 Значения контрольных проверок (значений контрольных разрядов) матрицы кодирования формируются сложением по mod2 элементов строк матрицы, имеющих единичные значения.

Свойство 2.3 Для исключения совпадения синдромов ошибок (при k=b2b) для второй части синдромов ошибок требуется rgч=[log2(2b2b)+1] - контрольных разрядов при четном значении b, и rgH=log2(2b2b) - при нечетном.

В этом случае, число дополнительных контрольных разрядов (строк матрицы кодирования) составит rДОПЧ=[log2(2b2b)+1-b] при четном значении b, и rДОПЧН=[log2(2b2b)-b] - при нечетном.

Граница числа контрольных разрядов для кода, корректирующего ошибки в двух байтах информации с формированием аддитивного вектора ошибки, оценивается выражением:

r=3b+rДОПi.

Правило 2.5 Объединяя по mod2 одноименные контрольные проверки для всех матриц кодирования, получим значения второй части контрольных разрядов

r 1 O = r 1 1 ⊕ r 1 2 ⊕ r 1 3 ⊕ … … … ⊕ r 1 w ;

r 2 O = r 2 1 ⊕ r 2 2 ⊕ r 2 3 ⊕ … … … ⊕ r 2 w ;

………………………………………………

r g O = r g 1 ⊕ r g 2 ⊕ r g 3 ⊕ … … … ⊕ r g w .

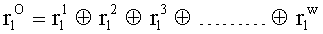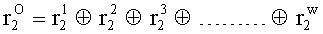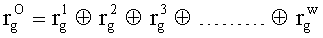Таким образом, имеем регулярную процедуру построения кодового набора с аддитивным формированием вектора ошибки:

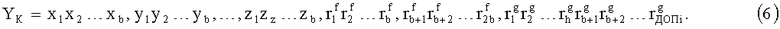
Y К = x 1 x 2 … x b , y 1 y 2 … y b , … , z 1 z z … z b , r 1 f r 2 f … r b f , r b + 1 f r b + 2 f … r 2 b f , r 1 g r 2 g … r h g r b + 1 g r b + 2 g … r Д О П i g .                                       ( 6 )

Результат сложения по mod2 переданных значений контрольных разрядов 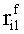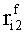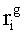r i 1 f , r i 2 f , r i g и контрольных разрядов 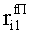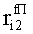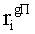r i 1 f П , r i 2 f П , r i g П , сформированных относительно полученных информационных разрядов, даст значение синдрома ошибки, включающего две части:

r 1 f r 2 f … … r b f r b + 1 f r b + 2 f … … r 2 b f r 1 g r 2 g … … r Д О П i g

⊕ r 1 f п r 2 f п … … r b f п   r b + 1 f п r b + 2 f п … … r 2 b f п   r 1 g п r 2 g п … … r Д О П i g п S = s 1 0 s 2 0 … s b 0 ︸ S 1 f   s b + 1 0 s b + 2 0 … … s 2 b 0 ︸ S 2 f   s 1 1 s 2 1 … … … s Д О П i g ︸ S g                                         ( 2.5 )

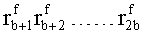
Значение синдрома ошибки 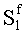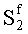S 1 f , S 2 f представляет собой аддитивные векторы ошибки (указывают ошибочные разряды в блоках информации), а значение синдрома ошибки Sg определяет номера ошибочных блоков (байтов) информации.

Свойство 2.4 Возникновение ошибок в соседних байтах информации приводит к искажениям векторов ошибок.

Следствие 2.1 При возникновении ошибок в соседних байтах вектора ошибок формируются в соответствии с синдромом ошибок.

Правило 2.6 декодирования включает следующую стратегию:

1. 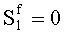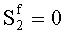S 1 f = 0 ; S 2 f = 0 ; Sg=0. Ошибок нет.

2. 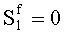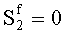S 1 f = 0 ; S 2 f = 0 ; Sg≠0. Произошла ошибка в контрольных разрядах

3. S 1 f g ≠ 0 ; S 2 f = 0 ; Sg≠0,

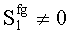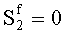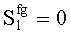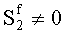( S 1 f g = 0 ; S 2 f ≠ 0 ;Sg≠0). Произошла ошибка в одном байте информации.

4. 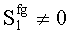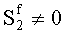S 1 f g ≠ 0 ; S 2 f ≠ 0 ; Sg≠0. Произошла ошибка в двух байтах информации, корректируемая аддитивными векторами ошибок или вектором ошибок, сформированным в соответствии с синдромом, или некорректируемая ошибка (обнаруживаемая).

Аналогичным образом строится код, корректирующий ошибки в заданном n - числе байтов информации (n≤b).

Граница числа контрольных разрядов корректирующего кода, исправляющего ошибки в заданном числе байтов информации (при нечетном значении b), оценивается выражением:

r = ( n + 1 ) b + log 2 ( n b 2 b ) .                                                                                                                                                                                                                 ( 2.2 )

При четном значении b, к данному выражению прибавляется единица.

Таким образом, предлагаемый метод коррекции ошибок в заданном числе байтов информации с аддитивным формированием вектора ошибки имеет регулярную и относительно простую процедуру матричного кодирования. Позволяет сократить временные затраты на кодирование и декодирование информации (исключить циклическую процедуру кодирования).

По отношению к коду Рида-Соломона позволяет исключить временные затраты на нахождения корней полинома локаторов ошибок. Так, для решения ключевого уравнения кода PC (78,8) по алгоритму Евклида потребуется 96 тактов работы декодирующего устройства.

Временные затраты на кодирование информации предлагаемым методом сопоставимы с временными затратами при контроле информации на четность (требующим минимальных временных затрат), что дает возможность обеспечить работу канала передачи данных в реальном масштабе времени.

Предлагаемый метод позволяет сократить аппаратурные затраты на построение декодирующего устройства, т.к. в большинстве случаев не требует аппаратурных затрат на вычисление вектора ошибки.

Использование предлагаемого метода позволяет повысить достоверность передаваемой информации за счет обнаружения некорректируемых ошибок. В отличие кодов PC, использующих для коррекции полином ошибок наименьшей степени (при реализации декодирования по методу «максимума-правдоподобия»), что в некоторых случаях приводит к ошибочной коррекции.

Пример 2. Допустим, требуется осуществить коррекцию ошибок в двух байтах информации кратности 4, в двоичном наборе, содержащем 64 информационных разряда, т.е. построить код (84,20).

Используя полученные правила, построим матрицы кодирования информации для формирования второй части контрольных разрядов:- 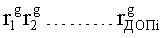r 1 g r 2 g … … … r Д О П i g (табл.2.1).

Таблица 2.1 Матрицы кодирования № п/п 0 1 2 3 4 5 6 7 A B C D E F G H 0 0,0,1,1, 0,0,1,0, 0,0,1,1, 1,1,0,0, 0,1,0,1, 0,1,1,0, 0,0,1,1, 1,0,0,0, 1 0,0,1,0, 0,0,0,1, 0,1,0,0, 0,1,0,1, 0,1,1,0, 0,1,1,1, 1,0,0,1, 1,0,0,1, 2 0,1,0,0, 0,1,1,1, 0,1,1,0, 0,1,1,0, 1,0,0,0, 1,0,0,1, 1,0,1,0, 1,0,1,1, 3 1,0,0,1, 1,0,0,1, 1,0,1,0, 1,0,1,1, 1,1,0,1, 1,1,0,1, 1,1,1,0, 1,1,1,1, 4 1,0,0,0, 0,0,1,1, 1,0,1,1, 1,0,0,1, 0,1,1,0, 1,0,1,0, 1,1,0,0, 1,1,1,1, 5 0,0,1,1, 1,0,0,1, 1,0,0,1, 0,1,1,0, 0,0,0,1, 0,0,1,0, 0,0,0,1, 0,1,1,1, 6 1,1,1,1, 1,0,0,1, 1,0,1,1, 1,1,0,0, 1,1,1,0, 0,0,1,1, 0,1,0,1, 1,0,0,0, 7 1,0,0,1, 0,1,1,1, 1,1,1,0, 0,0,0,1, 0,0,1,1, 1,0,1,1, 0,0,1,1, 0,1,0,0, 8 1,1,1,0, 0,0,0,0, 1,1,1,1, 1,1,0,1, 1,1,0,1, 0,1,1,0, 1,1,1,1, 1,1,0,0, 9 1,0,1,1, 0,0,1,1, 0,0,0,1, 1,1,0,1, 0,1,1,0, 0,0,0,1, 0,0,1,0, 0,1,0,0, 10 1,1,0,1, 0,1,0,1, 1,0,0,0, 1,0,1,1, 1,1,0,0, 1,0,1,0, 0,1,1,1, 0,1,0,1, 11 0,1,1,0, 1,0,0,1, 1,1,0,1, 1,1,1,0, 0,0,0,1, 0,0,1,1, 1,0,1,1, 1,0,1,1,

Продолжение таблицы 2.1

№п/п 8 9 10 11 12 13 14 15 I J K L M N O P 0 1,0,0,1, 1,0,1,0, 1,0,1,1, 1,1,0,0, 1,1,0,1, 1,1,1,0, 1,1,0,1, 0,0,0,0, 1 1,0,1,0, 1,0,1,1, 1,1,0,0, 0,1,0,1, 1,1,1,0, 1,1,0,1, 0,0,0,0, 0,0,0,1, 2 1,1,0,0, 1,1,0,1, 0,1,1,0, 1,1,1,0, 0,0,0,1, 0,0,0,1, 0,0,1,0, 0,0,1,1, 3 0,0,0,0, 0,0,0,1, 1,0,1,1, 0,0,1,1, 0,1,0,0, 0,1,0,1, 0,1,1,0, 0,1,1,1, 4 1,1,0,0, 0,1,1,0, 0,1,0,0, 1,0,1,0, 0,1,1,1, 1,0,1,1, 1,1,0,1, 1,1,1,0, 5 1,0,1,0, 1,1,0,1, 0,0,1,1, 0,1,1,1, 0,1,0,1, 1,0,0,0, 1,1,1,0, 1,0,1,1, 6 1,0,0,1, 1,0,1,0, 0,1,0,0, 1,1,1,0, 1,1,0,0, 1,1,0,1, 1,1,1,1, 0,0,0,1, 7 1,0,1,1, 0,1,1,1, 1,0,1,0, 1,1,0,0, 1,0,0,1, 0,0,0,1, 1,0,1,0, 0,1,1,0, 8 1,1,1,0, 0,1,1,1, ОД 1,0, 0,1,0,1, 1,0,0,0, 0,1,1,1, 1,1,1,0, 1,1,0,1, 9 0,1,1,1, 0,1,1,0, 1,1,0,0, 1,1,1,1, 0,0,0,0, 0,1,0,1, 1,1,0,0, 1,1,1,0, 10 1,0,1,0, 1,0,0,1, 1,0,1,0, 0,1,0,0, 1,1,1,0, 1,1,0,0, 1,0,1,1, 1,0,1,1, 11 0,1,0,1, 0,1,0,1, 1,0,1,1, 1,0,1,0, 1,0,0,1, 1,0,0,1, 1,0,0,1, 1,1,0,1

Контрольные проверки (значения второй части контрольных разрядов), полученные относительно полученных матриц, кодирования имеют вид:

r 0 g = a 2 ⊕ a 3 ⊕ b 2 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ e 1 ⊕ e 3 ⊕ f 1 ⊕ f 2 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ i 0 ⊕ i 3 ⊕ j 0 ⊕ j 2 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 0 ⊕ l 1 ⊕ m 0 ⊕ m 1 ⊕ m 3 ⊕ n 0 ⊕ n 1 ⊕ n 2 ⊕ o 0 ⊕ o 1 ⊕ o 3

r 1 g = a 2 ⊕ b 3 ⊕ c 1 ⊕ d 1 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 1 ⊕ f 2 ⊕ f 3 ⊕ g 0 ⊕ g 3 ⊕ h 0 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 2 ⊕ j 3 ⊕ k 0 ⊕ k 1 ⊕ l 1 ⊕ l 3 ⊕ m 0 ⊕ m 1 ⊕ m 2 ⊕ n 0 ⊕ n 1 ⊕ n 3 ⊕ p 3 ;

r 2 g = a 1 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ c 1 ⊕ c 2 ⊕ d 1 ⊕ d 2 ⊕ e 0 ⊕ f 0 ⊕ f 3 ⊕ g 0 ⊕ g 2 ⊕ h 0 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 1 ⊕ j 0 ⊕ j 1 ⊕ j 3 ⊕ k 1 ⊕ k 2 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ m 3 ⊕ n 3 ⊕ o 2 ⊕ p 2 ⊕ p 3 ;

r 3 g = a 0 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ d 0 ⊕ d 2 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ e 3 ⊕ f 0 ⊕ f 1 ⊕ f 3 ⊕ g 0 ⊕ g 1 ⊕ g 2 ⊕ h 0 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 2 ⊕ l 3 ⊕ m 1 ⊕ n 1 ⊕ n 3 ⊕ ⊕ o 1 ⊕ o 2 ⊕ p 1 ⊕ p 2 ⊕ p 3 ;

r 4 g = a 0 ⊕ b 2 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 0 ⊕ f 2 ⊕ g 0 ⊕ g 1 ⊕ h 0 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 1 ⊕ j 1 ⊕ j 2 ⊕ k 1 ⊕ l 0 ⊕ l 2 ⊕ m 1 ⊕ m 2 ⊕ m 3 ⊕ n 0 ⊕ n 2 ⊕ n 3 ⊕ ⊕ o 0 ⊕ o 1 ⊕ o 3 ⊕ p 0 ⊕ p 1 ⊕ p 2 ;

r 5 g = a 2 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 3 ⊕ d 1 ⊕ d 2 ⊕ e 3 ⊕ f 2 ⊕ g 3 ⊕ h 1 ⊕ h 2 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 1 ⊕ j 3 ⊕ k 2 ⊕ k 3 ⊕ l 1 ⊕ l 2 ⊕ l 3 ⊕ m 1 ⊕ m 3 ⊕ n 0 ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ p 0 ⊕ p 2 ⊕ p 3 ;

r 6 g = a 0 ⊕ a 1 ⊕ a 2 ⊕ a 3 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ e 0 ⊕ e 1 ⊕ e 2 ⊕ f 2 ⊕ f 3 ⊕ g 1 ⊕ g 3 ⊕ h 0 ⊕ i 0 ⊕ i 3 ⊕ j 0 ⊕ j 2 ⊕ k 1 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ m 0 ⊕ m 1 ⊕ n 0 ⊕ n 1 ⊕ n 3 ⊕ ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ o 3 ⊕ p 3 ;

r 7 g = a 0 ⊕ a 3 ⊕ b 1 ⊕ b 2 ⊕ b 3 ⊕ c 0 ⊕ c 1 ⊕ c 2 ⊕ d 3 ⊕ e 2 ⊕ e 3 ⊕ f 0 ⊕ f 2 ⊕ f 3 ⊕ g 2 ⊕ g 3 ⊕ h 1 ⊕ i 0 ⊕ i 2 ⊕ i 3 ⊕ j 1 ⊕ j 2 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ l 0 ⊕ l 1 ⊕ m 0 ⊕ m 3 ⊕ n 3 ⊕ o 0 ⊕ o 2 ⊕ p 1 ⊕ p 2 ;

r 8 g = a 0 ⊕ a 1 ⊕ a 2 ⊕ c 0 ⊕ c 1 ⊕ c 2 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ e 3 ⊕ f 1 ⊕ f 2 ⊕ g 0 ⊕ g 1 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ h 1 ⊕ i 0 ⊕ i 1 ⊕ i 2 ⊕ j 1 ⊕ j 2 ⊕ j 3 ⊕ k 2 ⊕ l 1 ⊕ l 3 ⊕ m 0 ⊕ n 1 ⊕ n 2 ⊕ n 3 ⊕ o 0 ⊕ o 1 ⊕ o 2 ⊕ p 0 ⊕ p 1 ⊕ p 3 ;

r 9 g = a 0 ⊕ a 2 ⊕ a 3 ⊕ b 2 ⊕ b 3 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 3 ⊕ e 1 ⊕ e 2 ⊕ f 3 ⊕ g 2 ⊕ h 1 ⊕ i 1 ⊕ i 2 ⊕ i 3 ⊕ j 1 ⊕ j 2 ⊕ k 0 ⊕ k 1 ⊕ l 0 ⊕ l 1 ⊕ l 2 ⊕ l 3 ⊕ n 1 ⊕ n 3 ⊕ o 0 ⊕ o 1 ⊕ p 0 ⊕ p 1 ⊕ p 2 ;

r 10 g = a 0 ⊕ a 1 ⊕ a 3 ⊕ b 1 ⊕ b 3 ⊕ c 0 ⊕ d 0 ⊕ d 2 ⊕ d 3 ⊕ e 0 ⊕ e 1 ⊕ f 0 ⊕ f 2 ⊕ g 1 ⊕ g 2 ⊕ g 3 ⊕ h 1 ⊕ h 3 ⊕ i 0 ⊕ i 2 ⊕ j 0 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ l 1 ⊕ m 0 ⊕ m 1 ⊕ m 2 ⊕ n 0 ⊕ n 1 ⊕ o 0 ⊕ o 2 ⊕ o 3 ⊕ p 0 ⊕ p 2 ⊕ p 3 ;

r 11 g = a 1 ⊕ a 2 ⊕ b 0 ⊕ b 3 ⊕ c 0 ⊕ c 1 ⊕ c 3 ⊕ d 0 ⊕ d 1 ⊕ d 2 ⊕ e 3 ⊕ f 2 ⊕ f 3 ⊕ g 0 ⊕ g 2 ⊕ g 3 ⊕ h 0 ⊕ h 2 ⊕ h 3 ⊕ i 1 ⊕ i 3 ⊕ j 1 ⊕ j 3 ⊕ k 0 ⊕ k 2 ⊕ k 3 ⊕ l 0 ⊕ l 2 ⊕ m 0 ⊕ m 3 ⊕ n 0 ⊕ n 3 ⊕ o 0 ⊕ o 3 ⊕ p 0 ⊕ p 1 ⊕ p 3 .

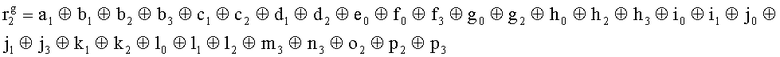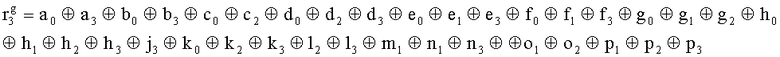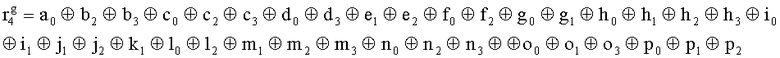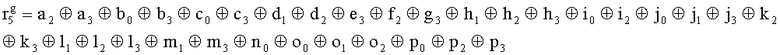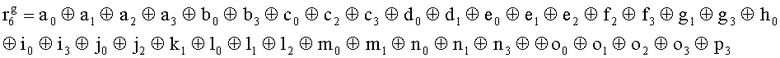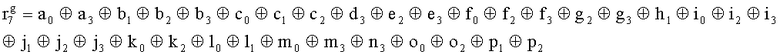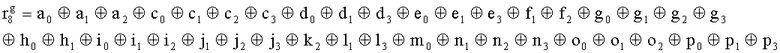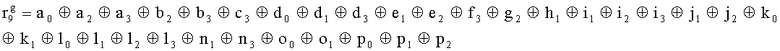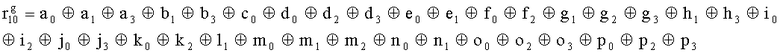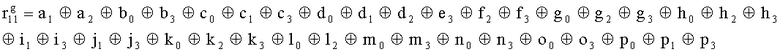В табл.2.2 представлена часть значений синдромов ошибок для кода 84,20.

Примечание: В табл.2.2 значения информационных разрядов, контрольных разрядов и значения ошибки в байтах информации представлены в шестнадцатеричной системе счисления, а значения синдрома ошибки - в двоичной.

Таблица 2.2 Значения синдромов ошибок для кода (84,20) Информационные разряды контр. разр. Ошибка в байте Синдром ошибки 0000000000000000 00000 0000 00000000000000000000 0000000000000000 00000 0001 00000001011101101011 0000000000000000 00000 0002 00000010001111010110 0000000000000000 00000 0003 00000011010010111101 0000000000000000 00000 0004 00000100000110011101 0000000000000000 00000 0005 00000101011011110110 0000000000000000 00000 0006 00000110001001001011 0000000000000000 00000 0007 00000111010100100000 0000000000000000 00000 0008 00001000000011001111 0000000000000000 00000 0009 00001001011110100100 0000000000000000 00000 000A 00001010001100011001 0000000000000000 00000 000B 00001011010001110010 0000000000000000 00000 000C 00001100000101010010 0000000000000000 00000 000D 00001101011000111001 0000000000000000 00000 000E 00001110001010000100 0000000000000000 00000 000F 00001111010111101111 0000000000000000 00000 0010 00010000100010100011 0000000000000000 00000 0011 00010001111111001000 0000000000000000 00000 0012 00010010101101110101 0000000000000000 00000 0013 00010011110000011110 0000000000000000 00000 0014 00010100100100111110 0000000000000000 00000 0015 00010101111001010101 0000000000000000 00000 0016 00010110101011101000 0000000000000000 00000 0017 00010111110110000011 0000000000000000 00000 0018 00011000100001101100 0000000000000000 00000 0019 00011001111100000111 0000000000000000 00000 001A 00011010101110111010 0000000000000000 00000 001B 00011011110011010001 0000000000000000 00000 001C 00011100100111110001 0000000000000000 00000 001D 00011101111010011010

0000000000000000 00000 001E 00011110101000100111 0000000000000000 00000 001F 00011111110101001100 0000000000000000 00000 0020 00100000001101111010 0000000000000000 00000 0021 00100001010000010001 0000000000000000 00000 0022 00100010000010101100 0000000000000000 00000 0023 00100011011111000111 0000000000000000 00000 0024 00100100001011100111 0000000000000000 00000 0025 00100101010110001100 0000000000000000 00000 0026 00100110000100110001 0000000000000000 00000 0027 00100111011001011010 0000000000000000 00000 0028 00101000001110110101 0000000000000000 00000 0029 00101001010011011110 0000000000000000 00000 002A 00101010000001100011 0000000000000000 00000 002B 00101011011100001000 0000000000000000 00000 002C 00101100001000101000 0000000000000000 00000 002D 00101101010101000011 0000000000000000 00000 002E 00101110000111111110 0000000000000000 00000 002F 00101111011010010101 0000000000000000 00000 0030 00110000101111011001 0000000000000000 00000 0031 00110001110010110010 0000000000000000 00000 0032 00110010100000001111 0000000000000000 00000 0033 00110011111101100100 0000000000000000 00000 0034 00110100101001000100 0000000000000000 00000 0035 00110101110100101111 0000000000000000 00000 0036 00110110100110010010 0000000000000000 00000 0037 00110111111011111001 0000000000000000 00000 0038 00111000101100010110 0000000000000000 00000 0039 00111001110001111101 0000000000000000 00000 003A 00111010100011000000 0000000000000000 00000 003B 00111011111110101011 0000000000000000 00000 003C 00111100101010001011 0000000000000000 00000 003D 00111101110111100000 0000000000000000 00000 003E 00111110100101011101 0000000000000000 00000 003F 00111111111000110110 0000000000000000 00000 0040 01000000100111101100 0000000000000000 00000 0041 01000001111010000111 0000000000000000 00000 0042 01000010101000111010 0000000000000000 00000 0043 01000011110101010001 0000000000000000 00000 0044 01000100100001110001 0000000000000000 00000 0045 01000101111100011010 0000000000000000 00000 0046 01000110101110100111 0000000000000000 00000 0047 01000111110011001100 0000000000000000 00000 0048 01001000100100100011 0000000000000000 00000 0049 01001001111001001000 0000000000000000 00000 004A 01001010101011110101 0000000000000000 00000 004B 01001011110110011110 0000000000000000 00000 004C 01001100100010111110 0000000000000000 00000 004D 01001101111111010101 0000000000000000 00000 004E 01001110101101101000 0000000000000000 00000 004F 01001111110000000011 0000000000000000 00000 0050 01010000000101001111 0000000000000000 00000 0051 01010001011000100100 0000000000000000 00000 0052 01010010001010011001 0000000000000000 00000 0053 01010011010111110010 0000000000000000 00000 0054 01010100000011010010 0000000000000000 00000 0055 01010101011110111001 0000000000000000 00000 0056 01010110001100000100

0000000000000000 00000 0057 01010111010001101111 0000000000000000 00000 0058 01011000000110000000 0000000000000000 00000 0059 01011001011011101011 0000000000000000 00000 005A 01011010001001010110 0000000000000000 00000 005B 01011011010100111101 0000000000000000 00000 005C 01011100000000011101 0000000000000000 00000 005D 01011101011101110110 0000000000000000 00000 005E 01011110001111001011 0000000000000000 00000 005F 01011111010010100000 0000000000000000 00000 0060 01100000101010010110 0000000000000000 00000 0061 01100001110111111101 0000000000000000 00000 0062 01100010100101000000 0000000000000000 00000 0063 01100011111000101011 0000000000000000 00000 0064 01100100101100001011 0000000000000000 00000 0065 01100101110001100000 0000000000000000 00000 0066 01100110100011011101 0000000000000000 00000 0067 01100111111110110110 0000000000000000 00000 0068 01101000101001011001 0000000000000000 00000 0069 01101001110100110010 0000000000000000 00000 006A 01101010100110001111 0000000000000000 00000 006B 01101011111011100100 0000000000000000 00000 006C 01101100101111000100 0000000000000000 00000 006D 01101101110010101111 0000000000000000 00000 006E 01101110100000010010 0000000000000000 00000 006F 01101111111101111001 0000000000000000 00000 0070 01110000001000110101 0000000000000000 00000 0071 01110001010101011110 0000000000000000 00000 0072 01110010000111100011 0000000000000000 00000 0073 01110011011010001000 0000000000000000 00000 0074 01110100001110101000 0000000000000000 00000 0075 01110101010011000011 0000000000000000 00000 0076 01110110000001111110 0000000000000000 00000 0077 01110111011100010101 0000000000000000 00000 0078 01111000001011111010 0000000000000000 00000 0079 01111001010110010001 0000000000000000 00000 007A 01111010000100101100 0000000000000000 00000 007B 01111011011001000111 0000000000000000 00000 007C 01111100001101100111 0000000000000000 00000 007D 01111101010000001100 0000000000000000 00000 007E 01111110000010110001 0000000000000000 00000 007F 01111111011111011010 0000000000000000 00000 0080 10000000100011111111 0000000000000000 00000 0081 10000001111110010100 0000000000000000 00000 0082 10000010101100101001 0000000000000000 00000 0083 10000011110001000010 0000000000000000 00000 0084 10000100100101100010 0000000000000000 00000 0085 10000101111000001001 0000000000000000 00000 0086 10000110101010110100 0000000000000000 00000 0087 10000111110111011111 0000000000000000 00000 0088 10001000100000110000 0000000000000000 00000 0089 10001001111101011011 0000000000000000 00000 008A 10001010101111100110 0000000000000000 00000 008B 10001011110010001101 0000000000000000 00000 008C 10001100100110101101 0000000000000000 00000 008D 10001101111011000110 0000000000000000 00000 008E 10001110101001111011 0000000000000000 00000 008F 10001111110100010000

0000000000000000 00000 0090 10010000000001011100 0000000000000000 00000 0091 10010001011100110111 0000000000000000 00000 0092 10010010001110001010 0000000000000000 00000 0093 10010011010011100001 0000000000000000 00000 0094 10010100000111000001 0000000000000000 00000 0095 10010101011010101010 0000000000000000 00000 0096 10010110001000010111 0000000000000000 00000 0097 10010111010101111100 0000000000000000 00000 0098 10011000000010010011 0000000000000000 00000 0099 10011001011111111000 0000000000000000 00000 009A 10011010001101000101 0000000000000000 00000 009B 10011011010000101110 0000000000000000 00000 009C 10011100000100001110 0000000000000000 00000 009D 10011101011001100101 0000000000000000 00000 009E 10011110001011011000 0000000000000000 00000 009F 10011111010110110011 0000000000000000 00000 00A0 10100000101110000101 0000000000000000 00000 00A1 10100001110011101110 0000000000000000 00000 00A2 10100010100001010011 0000000000000000 00000 00A3 10100011111100111000 0000000000000000 00000 00A4 10100100101000011000 0000000000000000 00000 00A5 10100101110101110011 0000000000000000 00000 00A6 10100110100111001110 0000000000000000 00000 00A7 10100111111010100101 0000000000000000 00000 00A8 10101000101101001010 0000000000000000 00000 00A9 10101001110000100001 0000000000000000 00000 00AA 10101010100010011100 0000000000000000 00000 00AB 10101011111111110111 0000000000000000 00000 00AC 10101100101011010111 0000000000000000 00000 00AD 10101101110110111100 0000000000000000 00000 00AE 10101110100100000001 0000000000000000 00000 00AF 10101111111001101010 0000000000000000 00000 00B0 10110000001100100110 0000000000000000 00000 00B1 10110001010001001101 0000000000000000 00000 00B2 10110010000011110000 0000000000000000 00000 00B3 10110011011110011011

Анализ таблицы показывает, что 94% синдромов ошибок имеют разные значения, т.е. не корректируется 6% ошибок в двух блоках информации.

Введение дополнительных контрольных разрядов позволяет осуществить коррекцию до 100% ошибок, однако это ведет к значительному росту аппаратурных затрат, поэтому целесообразно ограничиться коррекцией данного числа ошибок.

Таким образом, разработанный метод коррекции ошибок в двух байтах информации отличается от существующих тем, что позволяет:

- осуществлять коррекцию ошибок с алгебраически-синдромным декодированием (исключить циклическую процедуру кодирования и декодирования информации);

- имеет регулярную и относительно простую процедуру кодирования информации;

- сократить временные затраты на кодирование и декодирование информации и обеспечить работу канала передачи данных в реальном масштабе времени.

Литература:

1. Щербаков Н.С. Достоверность работы цифровых устройств. М.: Машиностроение, 1989, с.122, рис.45., 224 с.

Похожие патенты RU2534499C2

название год авторы номер документа
Сумматор по модулю пятнадцать 1989
  • Музыченко Олег Николаевич
 SU1603375A1
СПОСОБ АМПЛИТУДНОЙ, ФАЗОВОЙ И ЧАСТОТНОЙ МОДУЛЯЦИИ ВЫСОКОЧАСТОТНЫХ СИГНАЛОВ И МНОГОФУНКЦИОНАЛЬНОЕ УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ 2011
  • Головков Александр Афанасьевич
  • Дедов Сергей Владимирович
  • Малютина Ирина Александровна
 RU2490780C2
СПОСОБ ФОРМИРОВАНИЯ КВАЗИСТРУКТУРИРОВАННЫХ МОДЕЛЕЙ ФАКТОГРАФИЧЕСКОГО ИНФОРМАЦИОННОГО НАПОЛНЕНИЯ ДОКУМЕНТОВ 2012
  • Полищук Юрий Владимирович
 RU2517428C2
Способ определения резонансной моды Ми высокого порядка при суперрезонансе в сферической диэлектрической однородной частице 2023
  • Минин Игорь Владиленович
  • Минин Олег Владиленович
 RU2821162C1
СПОСОБ ДЕМОДУЛЯЦИИ И ФИЛЬТРАЦИИ ФАЗОМОДУЛИРОВАННЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ 2011
  • Головков Александр Афанасьевич
  • Головков Владимир Александрович
  • Бегян Елена Андронниковна
 RU2491711C2
СПОСОБ ДЕМОДУЛЯЦИИ И ФИЛЬТРАЦИИ ФАЗОМОДУЛИРОВАННЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ 2011
  • Головков Александр Афанасьевич
  • Малютина Ирина Александровна
  • Бегян Елена Андронниковна
 RU2486662C2
СПОСОБ ДЕМОДУЛЯЦИИ И ФИЛЬТРАЦИИ ФАЗОМОДУЛИРОВАННЫХ СИГНАЛОВ И УСТРОЙСТВО ЕГО РЕАЛИЗАЦИИ 2011
  • Головков Александр Афанасьевич
  • Малютина Ирина Александровна
  • Бегян Елена Андронниковна
 RU2488949C2
СПОСОБ ИСПЫТАНИЙ ПОЛУПРОВОДНИКОВЫХ БИС ТЕХНОЛОГИИ КМОП/КНД НА СТОЙКОСТЬ К ЭФФЕКТАМ ЕДИНИЧНЫХ СБОЕВ ОТ ВОЗДЕЙСТВИЯ ТЯЖЕЛЫХ ЗАРЯЖЕННЫХ ЧАСТИЦ КОСМИЧЕСКОГО ПРОСТРАНСТВА 2011
  • Качемцев Александр Николаевич
  • Киселев Владимир Константинович
  • Торохов Сергей Леонидович
 RU2495446C2
СПОСОБ ШИФРОВАНИЯ С ЗАЩИТОЙ ОТ КВАНТОВЫХ АТАК НА ОСНОВЕ ЦИКЛОВ ФУНКЦИЙ ВЕБЕРА 2013
  • Ростовцев Александр Григорьевич
 RU2541938C1
СПОСОБ АВТОНОМНОГО ОПРЕДЕЛЕНИЯ ОРБИТЫ И ОРИЕНТАЦИИ КОРПУСА КОСМИЧЕСКОГО АППАРАТА В ПРОСТРАНСТВЕ ПРИ ОТСУТСТВИИ АПРИОРНОЙ ИНФОРМАЦИИ 2013
  • Кузнецов Владислав Иванович
  • Данилова Тамара Валентиновна
  • Косулин Дмитрий Михайлович
  • Архипова Марина Александровна
 RU2542599C2

Реферат патента 2014 года УСТРОЙСТВО ХРАНЕНИЯ И ПЕРЕДАЧИ ДАННЫХ С ИСПРАВЛЕНИЕМ ОШИБОК В ДВУХ БАЙТАХ ИНФОРМАЦИИ

Изобретение относится к области телемеханики, автоматики и вычислительной техники и может быть использовано в устройствах хранения и передачи информации. Техническим результатом является повышение отказоустойчивости устройства за счет коррекции ошибок в двух байтах информации. Устройство содержит узел памяти, входной блок кодирования, выходной блок кодирования, блок вычисления синдрома ошибки, дешифратор, блок хранения векторов ошибок, корректор, блок элементов И. 1 ил., 1 табл., 1 прилож.

Формула изобретения RU 2 534 499 C2

Устройство хранения и передачи данных с исправлением ошибок в двух байтах информации, содержащее узел памяти, входной блок кодирования, выходной блок кодирования, блок вычисления синдрома ошибки, дешифратор, корректор, блок элементов И, вход установки устройства в нулевое состояние, вход записи, вход считывания, адресные входы, информационные входы, вход синхронизации, информационные выходы, отличающееся тем, что дополнительно содержит блок хранения векторов ошибок, вход установки в нулевое состояние, вход записи, вход считывания, адресные входы подключены соответственно к первому, второму, третьему и четвертому входам узла памяти, вход синхронизации подключен к пятому входу узла памяти и к первому входу блока элементов И, информационные входы подключены к шестым входам узла памяти и к входам входного блока кодирования, который формирует значения контрольных разрядов , , , , , , , , , , , , , , , , , , , , 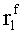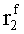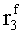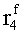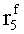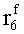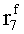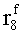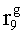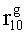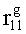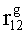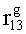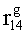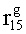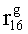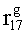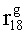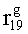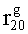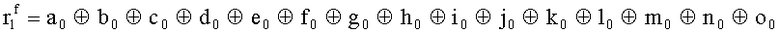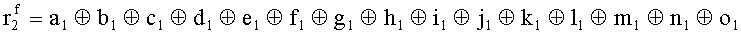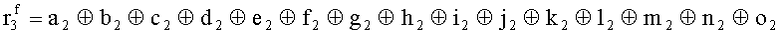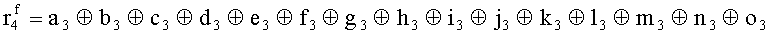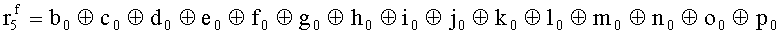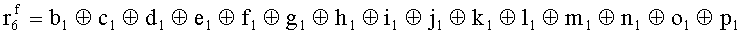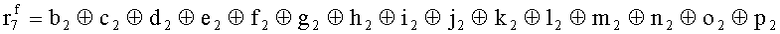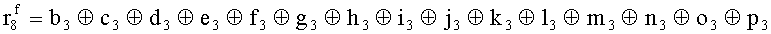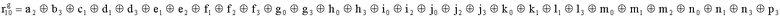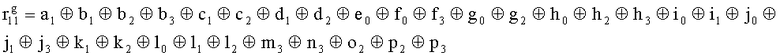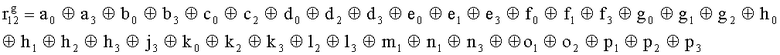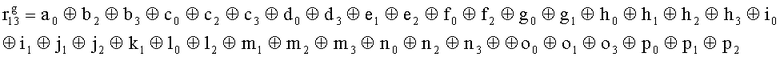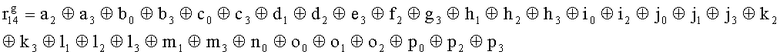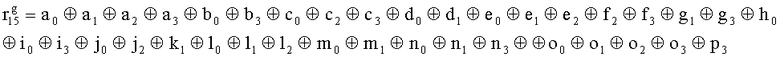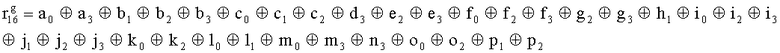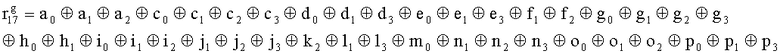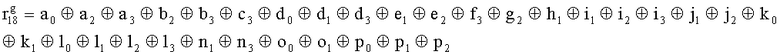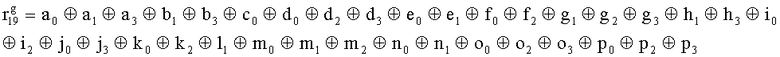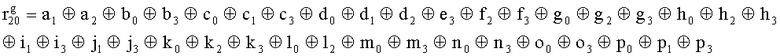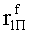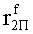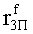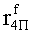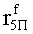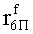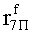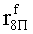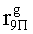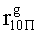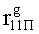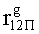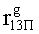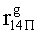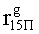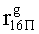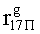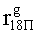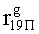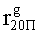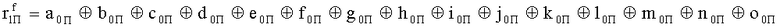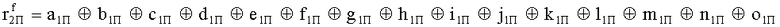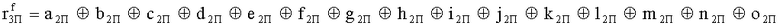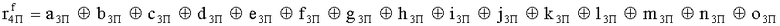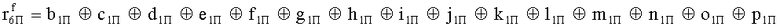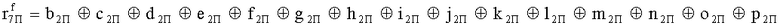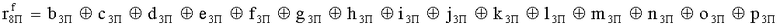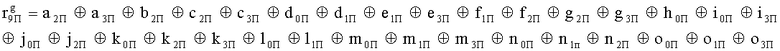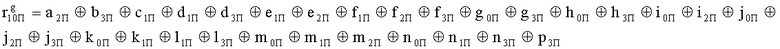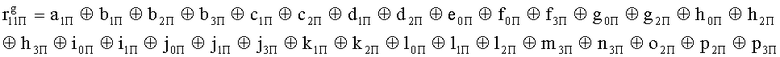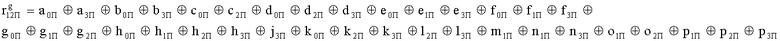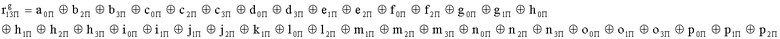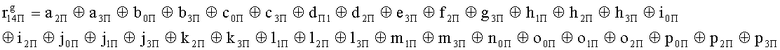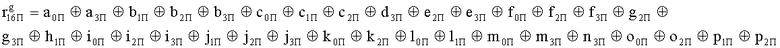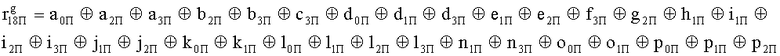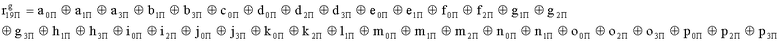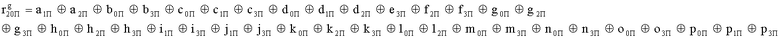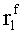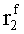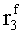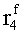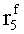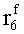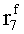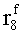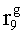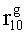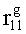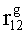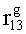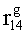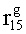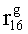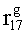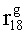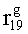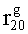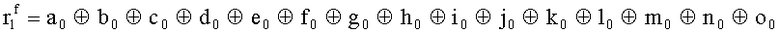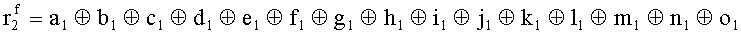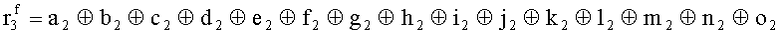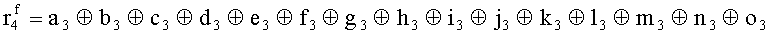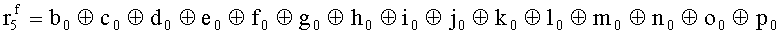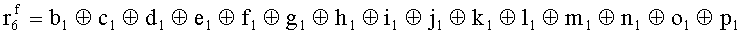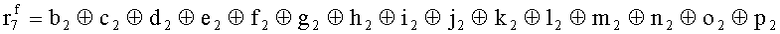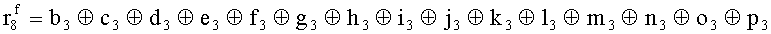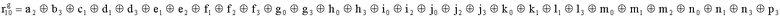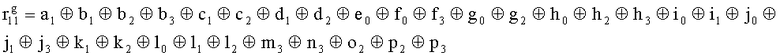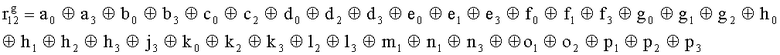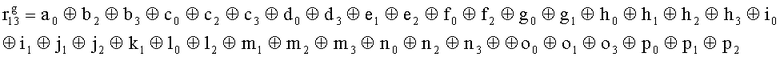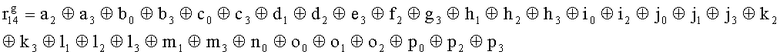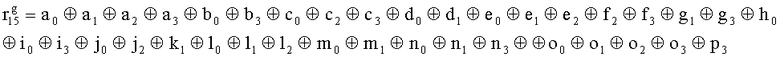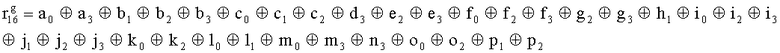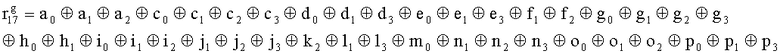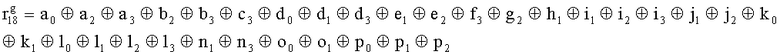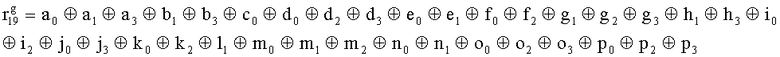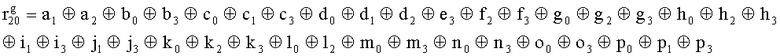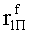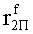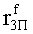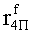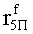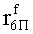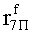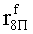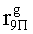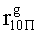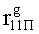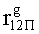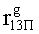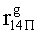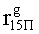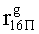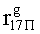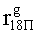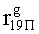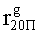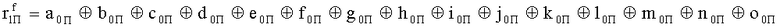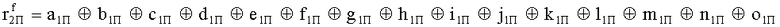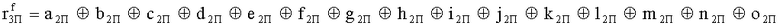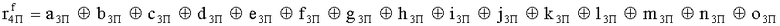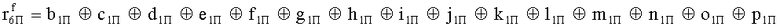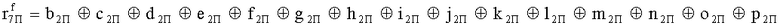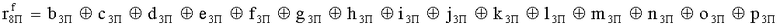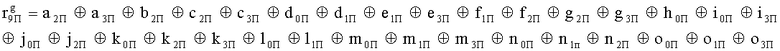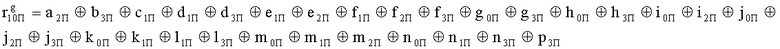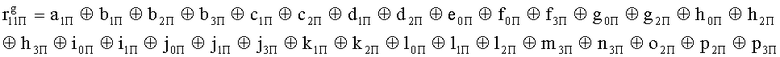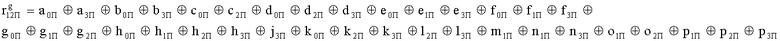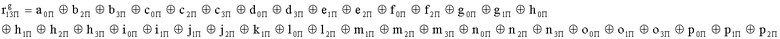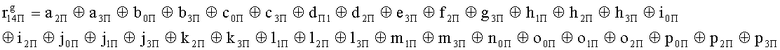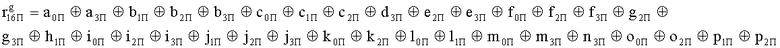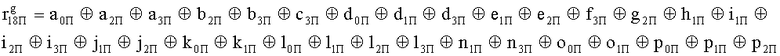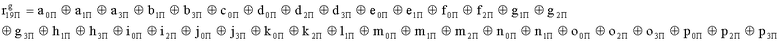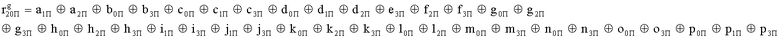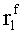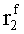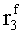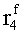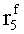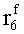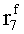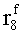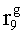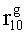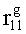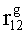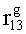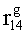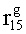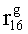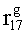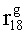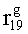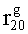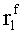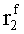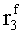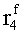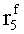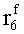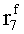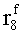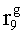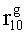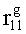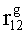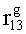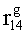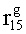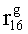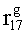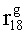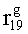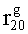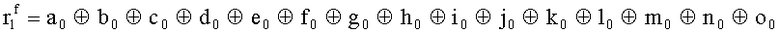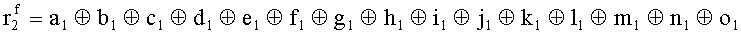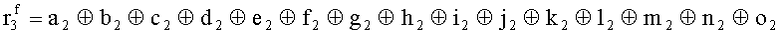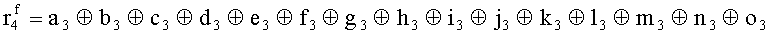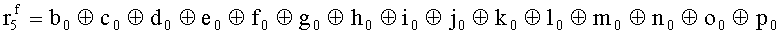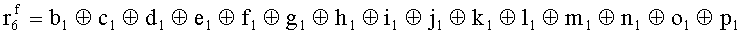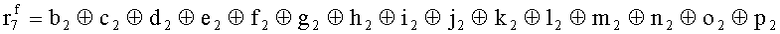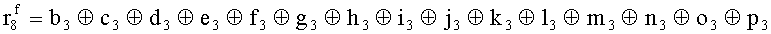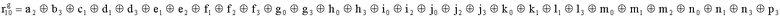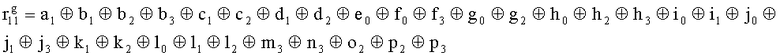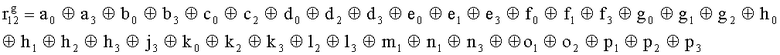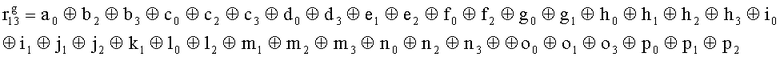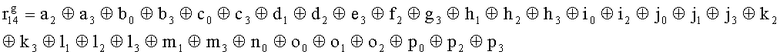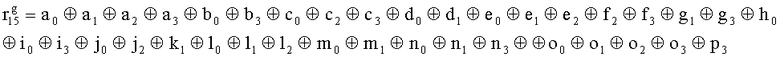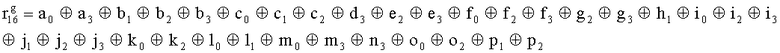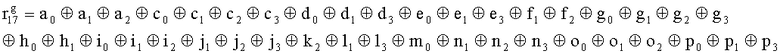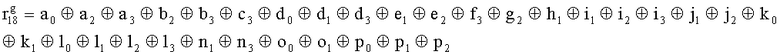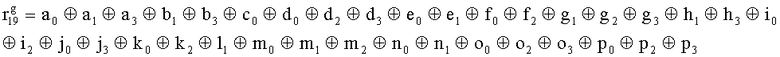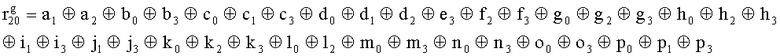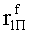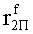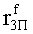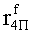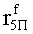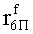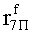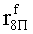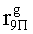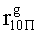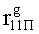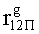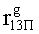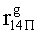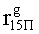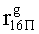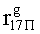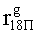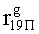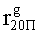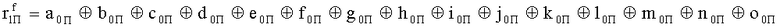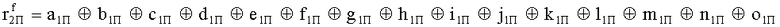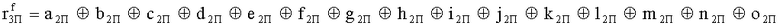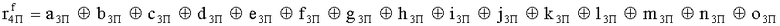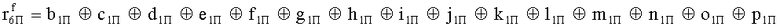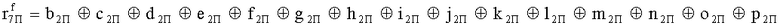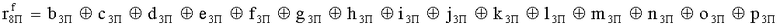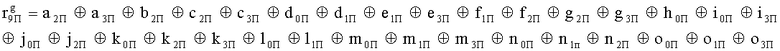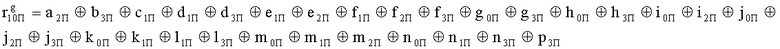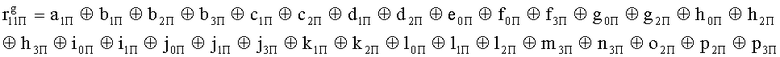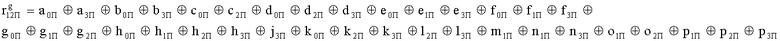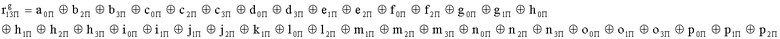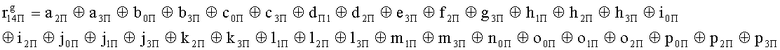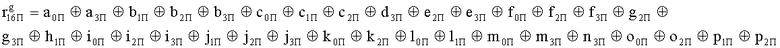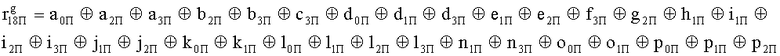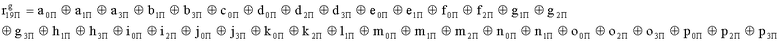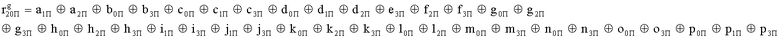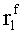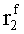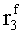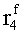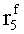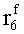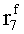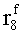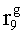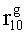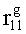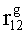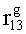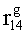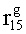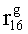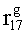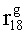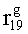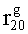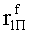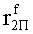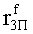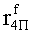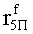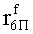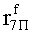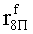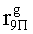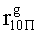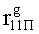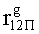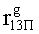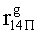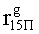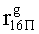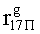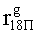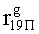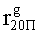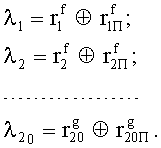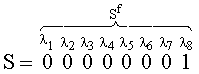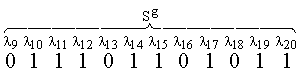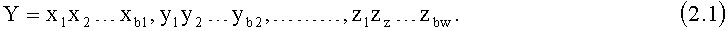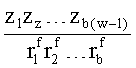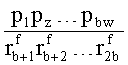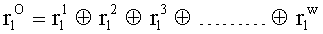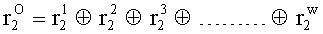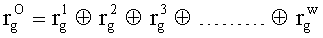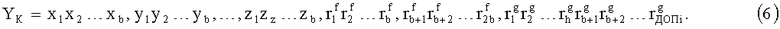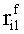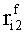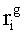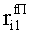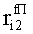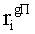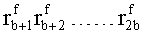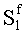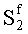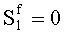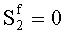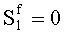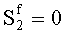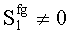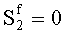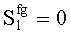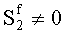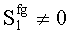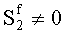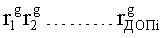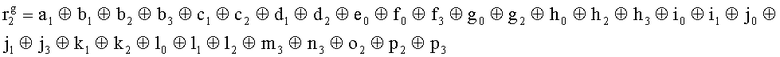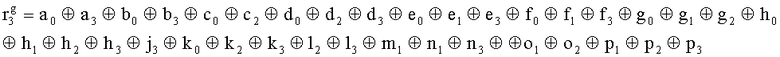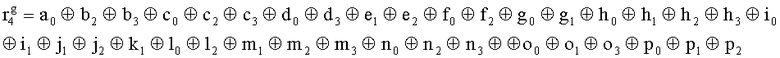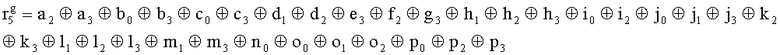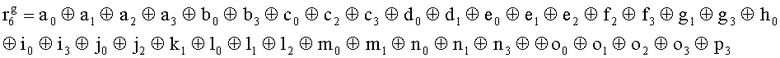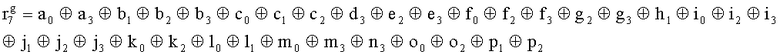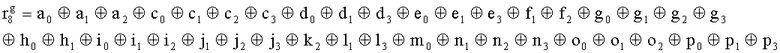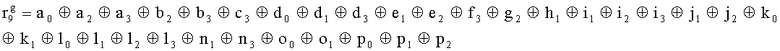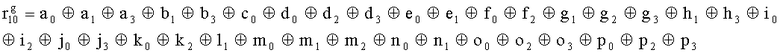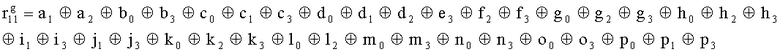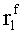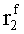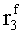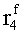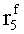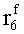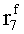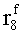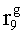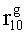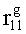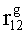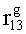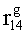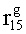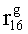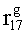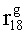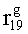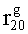путем сложения по модулю 2 информационных символов a0a1a2a3, b0b1b32b3, c0c1c2c3, d0d1d2d3, e0e1e2e3, f0f1f2f3, g0g1g2g3, h0h1h2h3, i0i1i2i3, j0j1j2j3, k0k1k2k3, l0l1l2l3, m0m1m2m3, n0n1n2n3, o0o1o2o3, p0p1p2p3, поступающих на входы входного блока кодирования, в соответствии с правилом:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.,
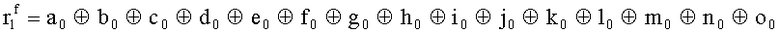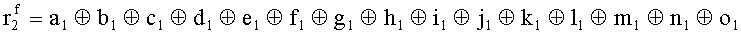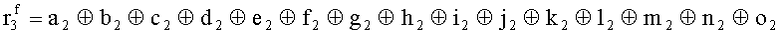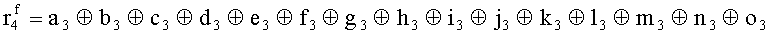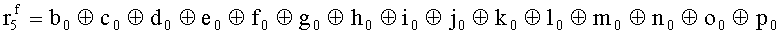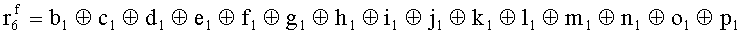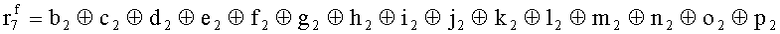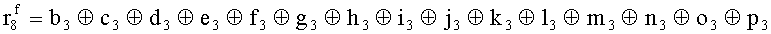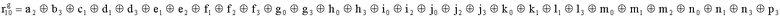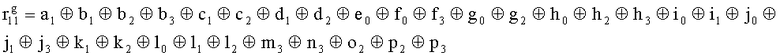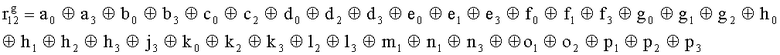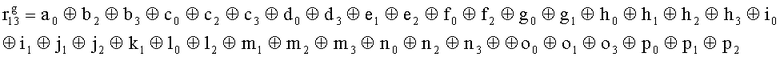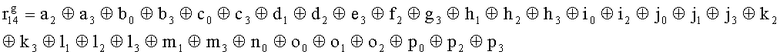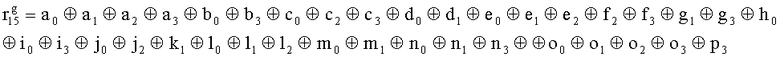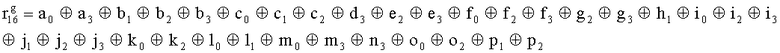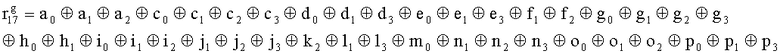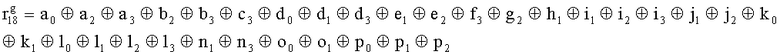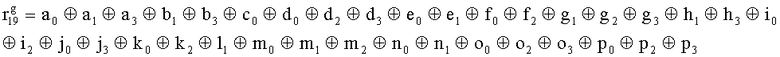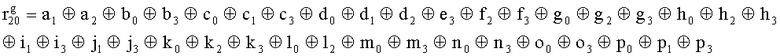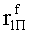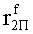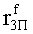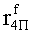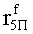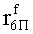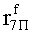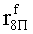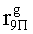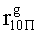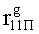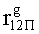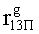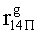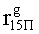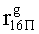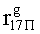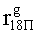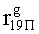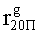выходы входного блока кодирования подключены к седьмым входам узла памяти, информационные выходы узла памяти подключены соответственно к первым входам корректора и к входам выходного блока кодирования, который формирует значения проверочных контрольных разрядов , , , , , , , , , , , , , , , , , , , , путем сложения по модулю 2 информационных символов a0Пa1Пa2Пa3П, b0Пb1Пb2Пb3П, c0Пc1Пc2Пc3П, d0Пd1Пd2Пd3П, e0Пe1Пe2Пe3П, f0Пf1Пf2Пf3П, g0Пg1Пg2Пg3П, h0Пh1Пh2Пh3П, i0Пi1Пi2Пi3П, j0Пj1Пj2Пj3П, k0Пk1Пk2Пk3П, l0Пl1Пl2Пl3П, m0Пm1Пm2Пm3П, n0Пn1Пn2Пn3П, o0Пo1Пo2Пo3П, p0Пp1Пp2Пp3П, поступающих на входы входного блока кодирования с информационных выходов узла памяти, в соответствии с правилом:
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
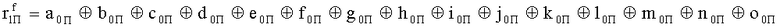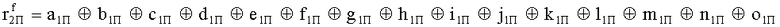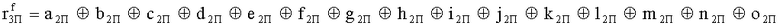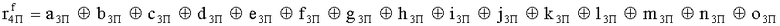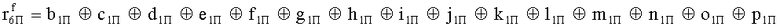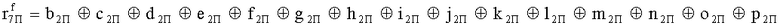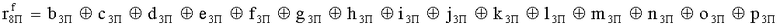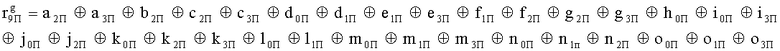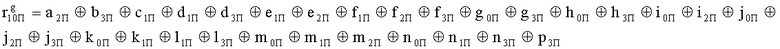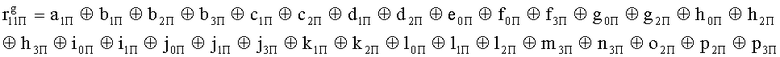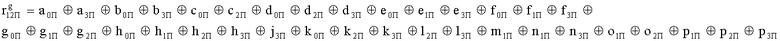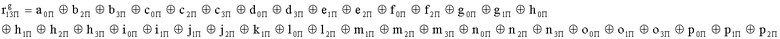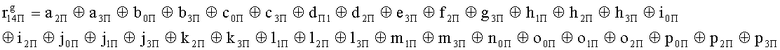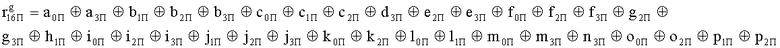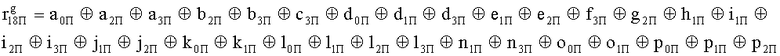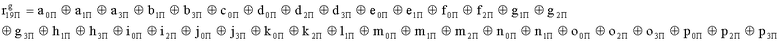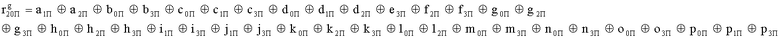, выходы выходного блока кодирования подключены к первым входам блока вычисления синдрома ошибки, к вторым входам которого подключены выходы контрольных разрядов узла памяти, выходы блока вычисления синдрома ошибки подключены к входам дешифратора, выходы которого подключены к входам блока хранения векторов ошибок, выходы блока хранения векторов ошибок подключены к вторым входам корректора, выходы которого подключены к вторым входам блока элементов И, выходы блока элементов И являются выходами устройства.

Документы, цитированные в отчете о поиске Патент 2014 года RU2534499C2

УСТРОЙСТВО ХРАНЕНИЯ И ПЕРЕДАЧИ ДАННЫХ С ИСПРАВЛЕНИЕМ ОШИБОК В БАЙТЕ ИНФОРМАЦИИ И ОБНАРУЖЕНИЕМ ОШИБОК В БАЙТАХ ИНФОРМАЦИИ 2011
  • Борисов Константин Юрьевич
  • Малофеев Юрий Георгиевич
  • Осипенко Павел Николаевич
  • Павлов Алексей Александрович
  • Павлов Павел Александрович
  • Павлов Александр Алексеевич
  • Хоруженко Олег Владимирович
  • Царьков Алексей Николаевич
 RU2448359C1
УСТРОЙСТВО ХРАНЕНИЯ И ПЕРЕДАЧИ ДАННЫХ С ИСПРАВЛЕНИЕМ ОДИНОЧНЫХ ОШИБОК В БАЙТЕ ИНФОРМАЦИИ И ОБНАРУЖЕНИЕМ ПРОИЗВОЛЬНЫХ ОШИБОК В БАЙТАХ ИНФОРМАЦИИ 2011
  • Борисов Константин Юрьевич
  • Малофеев Юрий Георгиевич
  • Осипенко Павел Николаевич
  • Павлов Алексей Александрович
  • Павлов Павел Александрович
  • Павлов Александр Алексеевич
  • Хоруженко Олег Владимирович
  • Царьков Алексей Николаевич
 RU2450331C1
УСТРОЙСТВО ХРАНЕНИЯ И ПЕРЕДАЧИ ИНФОРМАЦИИ С ОБНАРУЖЕНИЕМ ДВОЙНЫХ ОШИБОК 2009
  • Царьков Алексей Николаевич
  • Аряшев Сергей Иванович
  • Бобков Сергей Генадьевич
  • Бородай Владимир Эрнестович
  • Василегин Борис Владимирович
  • Нагаев Константин Дмитриевич
  • Осипенко Павел Николаевич
  • Павлов Александр Алексеевич
  • Хоруженко Олег Владимирович
 RU2403615C2
Устройство для контроля информации на четность 1985
  • Белков Михаил Семенович
  • Братальский Евгений Аврельевич
  • Смирнов Александр Павлович
 SU1339898A1
US 5933436 A, 03.08.1999
JP 58041499 A, 10.03.1983
KR 930011573 B1, 11.12.1993
Способ определения неисправного усилительного участка на магистрали связи с частотным разделением каналов 1974
  • Бычковский Эдуард Кириллович
 SU527025A1

RU 2 534 499 C2

Авторы

Борисов Константин Юрьевич

Павлов Александр Алексеевич

Царьков Алексей Николаевич

Хоруженко Олег Владимирович

Гусев Александр Викторович

Даты

2014-11-27—Публикация

2013-03-25—Подача

download Скачать PDF read Похожие патенты