Предлагаемый способ измерения нечеткой информации требует предварительных пояснений понятий «нечеткая информация» и «измерение нечеткой информации».
Вначале коснемся понятия «информация».
Достаточно полное и общее определение сути информации дано в классической работе К. Шеннона [1]. Согласно этой работе информация - последовательность сообщений, она может представляться буквами, набором функций, которые могут быть достаточно точно определены статистическим (вероятностным) методом.
В [2] можно найти конкретизацию понятия информации по ее характеру: детерминистской и вероятностной. Первая - причинно-обусловленная, она априори может быть определена. Вероятностная информация позволяет судить о статистических характеристиках исследуемых объектов, т.е. здесь имеется в виду случай многократных испытаний (измерений). Эта информация исследователем рассматривается в трех аспектах: практическом - с точки зрения достижения конкретных целей, семантическом - с точки зрения смыслового содержания и правильного ее использования, синтаксическом (технологическом) - с точки зрения способа, техники передачи информации. Наиболее общий из указанных - первый аспект.
Известно и другое определение информации - как разность энтропий законов распределения случайной величины до измерения и после измерения.
Последнее предполагает наличие в основе статистических данных, т.е. измерений исследуемых величин и на их основе - косвенных измерений (вычислений) информации.
В соответствии с [3] (п.5.18) имеем определение: «Измерительная информация - информация о значениях физических величин».
Анализируя это определение, можно увидеть, что измерительная (четкая) информация определяется значениями физических величин, т.е. измерительная информация и значения физических величин - это синонимы: получить значение физической величины и означает получить информацию о физической величине.
Данное совмещение и позволяет использовать словосочетание - измерение (оценивание) информации (значений физических величин).
Нечеткая информация как объект изучения (измерения) широко использовалась ранее и используется в настоящее время [4, 5].
Рассмотрим отличие нечеткой информации от четкой.
В изложенном выше смысле нечеткую информацию истолковать достаточно трудно с учетом ее особенностей. Эти особенности выражаются специфическим представлением нечеткой информации: функциями принадлежности значений физических величин нечетким множествам.
В них по определению находят отражение особенности задания лингвистических переменных: наименование, множество значений (термов), синтаксические и семантические процедуры, позволяющие формировать синтагмы определенного смысла.
Таким образом, нечеткая информация представляется набором нечетких значений физических величин, выраженных в виде функций принадлежности этих значений (элементов) нечетким множествам. Таким образом, в качестве указанных элементов могут быть значения физических величин - параметров исследуемых, эксплуатируемых объектов (устройств) в трудно контролируемых или трудно управляемых условиях, где обычные измерения затруднены или невозможны, или ограничены по объему.
Из данного пояснения следует, что нечеткая информация - набор нечетких чисел, значений измеряемых параметров исследуемых объектов (процессов), представленных набором функций принадлежности.
«Оценить (измерить) нечеткую информацию» означает вначале измерить в ограниченном объеме известным образом в соответствии с понятием «измерение» [3] значение параметра (физической величины), или оценить его значение экспертным путем, а затем определить (оценить) функцию принадлежности. Полученные таким образом значения функций принадлежности по всем параметрам необходимо сравнить с условными шкалами нечетких параметров с использованием алгебраических операций. Результаты сравнения и будут означать результаты оценивания (измерения) нечеткой информации. Полученная таким образом нечеткая информация может быть использована при диагностировании (прогнозировании) состояния объектов, характеризуемых соответствующими условиями, обстоятельствами применения, эксплуатации, хранения и т.д.
Мы ввели в обращение понятие «условные шкалы нечетких параметров», которое можно распространить на «условные шкалы нечетких ситуаций». Само понятие условной шкалы дается в [3], а нечеткой ситуация приводим: нечеткая ситуация - набор значений параметров и им соответствующих значений функций принадлежности на определенный момент времени. В частном случае ситуация может характеризоваться значением одного параметра и соответствующим значением функции принадлежности.
Поясним их расхождение с известными шкалами [3]: наименований, порядка, интервалов, отношений.
Первая классифицирует размеры по признакам или эквивалентности, или тождества, или равенства. Ее суть представляется наборами знаков: «=» или «≠».
Вторая ранжирует размеры параметров по возрастающей (по убывающей) степени, при этом размеры характеризуются качественно: «больше» или «меньше». Суть шкалы выражает набор знаков: «=», «≠», «<», «>».
Последние две (из перечня, указанного выше) - шкалы интервалов и отношений - метрологические. Измерения на их основе связаны со сравнением измеряемой физической величины с мерой (единицей физической величины).
Все перечисленные шкалы предполагают то или иное сравнение подобных друг другу объектов (по параметрам, характеристикам и т.д.).
Для нечеткой информации такое сравнение осуществить затруднительно (практически невозможно). Поэтому и предлагается использовать условные шкалы, в основе которых предлагается использовать упорядоченный набор (множества) термов на базовых множествах значений параметров (характеристик), которые математизируются с помощью указанных шкал.
Для того чтобы можно было оперировать с нечеткой информацией, условные шкалы должны быть переведены в новый вид - в алгебры-шкалы, которые и будут использоваться в качестве меры нечеткой информации.
Далее приведем подробные пояснения к формуле изобретения.
Экспертным путем (эвристически) назначается число термов и их типовые представители на базовом множестве. Базовое множество может задаваться границами контролируемого (измеряемого) параметра на предметной шкале, например [0; Хб], где Хб - верхнее значение базового множества, 0 - нижнее значение, или на универсальной шкале так: [0; l], где нечеткие значения оцениваются как отношение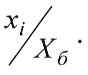 Нижнее нулевое значение получается путем элементарного преобразования: путем вычитания нижнего предметного значения из текущих предметных значений параметра.
Нижнее нулевое значение получается путем элементарного преобразования: путем вычитания нижнего предметного значения из текущих предметных значений параметра.
После этой операции выбирается идентифицированное выражение функции принадлежности, которое учитывало бы все параметры, позволяющие адаптировать их к изменяющейся семантике.
Для этих целей можно использовать различные выражения. Например, авторы предлагают использовать следующее выражение функций принадлежности элементов (значений параметров) нечеткому множеству
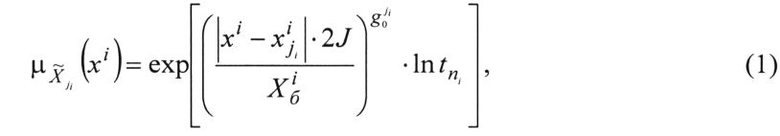
где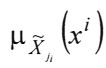 - функция принадлежности значений xi нечеткому множеству
- функция принадлежности значений xi нечеткому множеству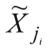 ;
;
i - номер измеряемого (исследуемого) параметра;
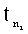
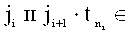
ji - номер терма на базовом множестве 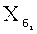
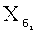
Ji - число термов, выбранных на базовом множестве 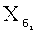
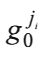 - параметр функции принадлежности, соответствующий степени нарушения комплементарности нечетких множеств
- параметр функции принадлежности, соответствующий степени нарушения комплементарности нечетких множеств 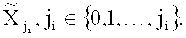
При изменении семантики термов выражение (1) адаптируется путем использования соответствующих функций отображения, которые смещают внутренние термы на базовом множестве в сторону меньших или больших значений.
Первое смещение связано, например, с ужесточением требований к параметру: то, что было «средним», стало «большим», и наоборот. Во втором случае «среднее» стало «малым».
Приведем пример для пояснения: [0;100] - базовое множество значений температуры; используются термы «низкая», «средняя», «высокая» температура с типовыми значениями 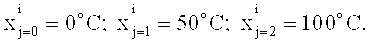
Изменились обстоятельства, для которых «средняя» температура, равная 50°C, стала «низкой», и ее значение изменили на 65°C. Тогда функция принадлежности термам тоже изменится. При переходе к универсальной шкале (от х к δ) функция принадлежности при линейной предметной шкале (как указано в начале примера) примет иной вид
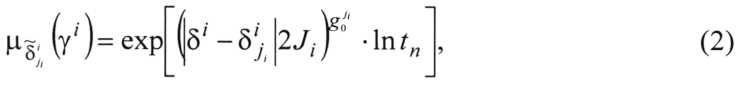
где 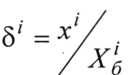 - линейная функция отображения: осуществляет переход к универсальной шкале без ее деформации;
- линейная функция отображения: осуществляет переход к универсальной шкале без ее деформации;
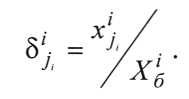
Для того чтобы осуществить адаптацию шкалы температур к новым требованиям, ее необходимо преобразовать при помощи функции отображения. Для снижения требований средний терм смещается в сторону больших их значений, указанных в примере. Следовательно, можно использовать функцию отображения вида

где γi - значение i-го параметра на адаптированной универсальной шкале;
δi - значение i-го параметра на не адаптированной (линейной) универсальной шкале;
k=ln(γi)/ln(δi) - параметр функции отображения, который определяет ее выпуклость (вогнутость), соответствующую смещению среднего терма. В нашем примере смещение на 15%. Это будет соответствовать 50°C+15°C=65°C на предметной адаптированной шкале, на универсальной адаптированной шкале: 0,5+0,15=0,65.
При tn=0,6 и 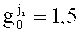
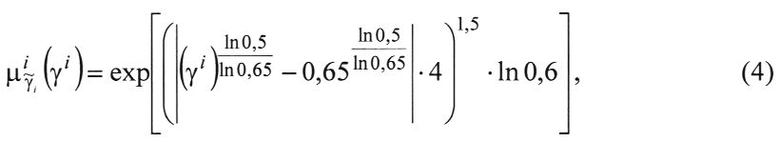
где 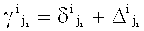
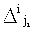
В нашем примере 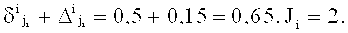
Далее, используя результаты фаззификации, значения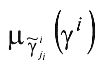 всех параметров и всех термов параметров, для получения требуемой точности нечеткой информации вводятся логические операции, позволяющие сравнить фактические ситуации с эталонными. К числу таких операций относятся:
всех параметров и всех термов параметров, для получения требуемой точности нечеткой информации вводятся логические операции, позволяющие сравнить фактические ситуации с эталонными. К числу таких операций относятся:
- нечеткое включение нечетких ситуаций
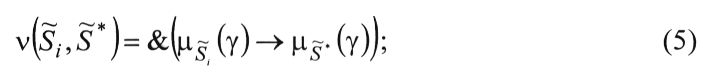
- нечеткое равенство нечетких ситуаций (объектов)
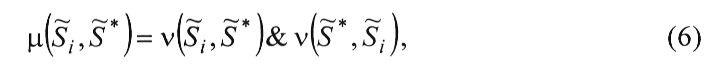
где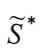 - типовой (эталонный) объект (ситуация, мера);
- типовой (эталонный) объект (ситуация, мера);
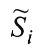 - нечеткий текущий объект (ситуация);
- нечеткий текущий объект (ситуация);
→ - импликация;
& - конъюнкция.
Для детализации этих операций используются частные операции, выраженные через функции принадлежности (для иллюстрации выразим их в общем виде: через функции принадлежности на предметной шкале).
- отрицания (дополнения) нечеткого множества 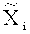
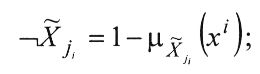
- конъюнкции 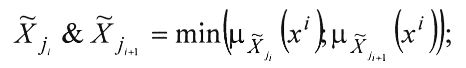
- дизъюнкции 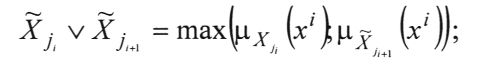
- импликации 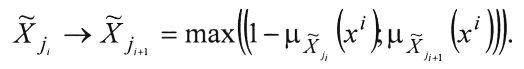
Их использование при оценивании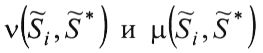 с учетом адаптации (перехода на шкалы δ или γ) вполне очевидно.
с учетом адаптации (перехода на шкалы δ или γ) вполне очевидно.
Таким образом выражаются операции на шкалах, отражающих множества нечетких объектов (элементов) через функции принадлежности этих элементов нечетким множествам, которые носят конкретный характер или (2), или (4) и позволяют реализовать способ измерения - сравнение нечеткого объекта (ситуации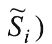 с мерой - с типовыми объектами (нечеткими ситуациями
с мерой - с типовыми объектами (нечеткими ситуациями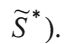
После определения всех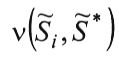 или
или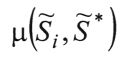 измеряемый объект (параметр, ситуация) приравнивают той
измеряемый объект (параметр, ситуация) приравнивают той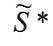 , при которой
, при которой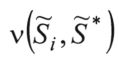 или
или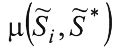 оказались max. Так, косвенным путем получают предварительный результат измерения нечеткой информации.
оказались max. Так, косвенным путем получают предварительный результат измерения нечеткой информации.
Для того чтобы повысить точность предварительного результата измерения нечеткой информации, вводят в них поправки путем использования операции дефаззификации, используя правило
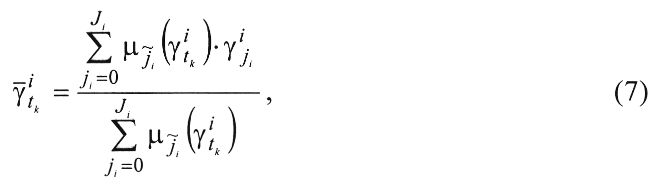
где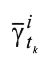 - уточненное значение параметра, соответствующее моменту времени tk
- уточненное значение параметра, соответствующее моменту времени tk
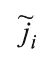 - более краткое обозначение нечеткого множества
- более краткое обозначение нечеткого множества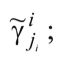
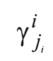 - типовое значение ji-го терма i-го параметра.
- типовое значение ji-го терма i-го параметра.
Отношение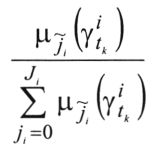 выражает вес (значимость) нечеткой информации в каждом терме условной шкалы, т.е. шкалирует нечеткую информацию в каждом терме путем оценивания ее веса.
выражает вес (значимость) нечеткой информации в каждом терме условной шкалы, т.е. шкалирует нечеткую информацию в каждом терме путем оценивания ее веса.
Таким образом, правило (7) осуществляет свертку всей нечеткой информации во всех термах об исследуемом (измеряемом) параметре γi, соответствующей моменту времени tk, и тем самым вводят поправку в 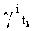
Используя уточненную нечеткую информацию, далее определяют повторно уточненную измерительную информацию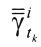 , выполняя процедуры правила свертки (7).
, выполняя процедуры правила свертки (7).
Критерием остановки этого процесса являются неравенства вида

где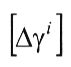 - допустимое значение погрешности оценивания параметра γi (назначается);
- допустимое значение погрешности оценивания параметра γi (назначается);
0<α<1 - коэффициент понижения допустимой погрешности. В выражении (8) учтены, как пример, первое и второе уточнения. Аналогично учитывается, например, m и (m+1) уточнения.
Литература
1. Шеннон К. Работы по теории информации и кибернетике. М.: Иностранная литература. 1963. 829 с.
2. Математика и кибернетика в экономике. Словарь-справочник. М.: Экономика. 1975. 699 с.
3. РМГ 29-99. Метрология. Основные термины и определения.
4. Круглое В.В., Дли И.И., Голунов Р.Ю. Нечеткая логика и искусственные нейронные сети. М.: Физматгиз. 2001. 225 с.
5. Мелихов А.Н., Бернштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой. М.: Наука. 1990. 272 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ПОЛИСОСТАВА ГАЗОВЫХ СРЕД | 2011 |
|
RU2504760C2 |
| СПОСОБ СУШКИ КЕРАМИЧЕСКИХ ИЗДЕЛИЙ | 2020 |
|
RU2751325C1 |
| СПОСОБ СУШКИ КЕРАМИЧЕСКИХ ИЗДЕЛИЙ | 2020 |
|
RU2743979C1 |
| СПОСОБ РЕЗЕРВИРОВАНИЯ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ МЕТОДОВ НЕЧЕТКОЙ ЛОГИКИ | 2014 |
|
RU2565417C1 |
| СПОСОБ КОНТРОЛЯ И РЕМОНТА ИЗОЛЯЦИИ ПРОВОДОВ | 2020 |
|
RU2745432C1 |
| СПОСОБ КОНТРОЛЯ СОСТОЯНИЯ СЕТИ ПЕРЕДАЧИ ДАННЫХ | 2015 |
|
RU2610287C1 |
| СПОСОБ РАСПРЕДЕЛЕНИЯ НАГРУЗКИ МЕЖДУ ТЕХНОЛОГИЧЕСКИМИ ЛИНИЯМИ ЦЕХА ОСУШКИ ГАЗА ГАЗОДОБЫВАЮЩЕГО КОМПЛЕКСА | 2011 |
|
RU2497574C2 |
| Способ оперативной идентификации морских целей по их информационным полям на базе нейро-нечетких моделей | 2021 |
|
RU2763125C1 |
| СПОСОБ ФОРМИРОВАНИЯ ТЕХНОЛОГИЧЕСКОЙ ЦЕПОЧКИ ФОТОГРАММЕТРИЧЕСКОЙ ОБРАБОТКИ КОСМИЧЕСКИХ ИЗОБРАЖЕНИЙ МЕСТНОСТИ | 2018 |
|
RU2711003C1 |
| УСТРОЙСТВО ДЛЯ РАСПОЗНАВАНИЯ СИТУАЦИЙ | 1991 |
|
RU2012057C1 |
Изобретение относится к области метрологии и может быть использовано для измерения и обработки нечеткой информации. Техническим результатом является повышение точности. Способ состоит в следующем: для измерения нечеткой информации формируют условную шкалу нечетких эталонных объектов - термов на базовом множестве путем назначения типовых представителей и в последующем фаззифицируют все значения базового множества путем использования функций принадлежности с семантикой исходной неполной измерительной информации; затем на основе этой условной шкалы фаззифицируют неполную измерительную информацию, которую используют для предварительного измерения нечеткой информации путем определения ее нечеткого включения в типовые термы; при этом терм с наибольшим включением считают предварительным результатом измерения нечеткой информации; в предварительный результат вводят поправки, используя операции его дефаззификации с учетом значений функций принадлежности во всех термах шкалы и всех ее типовых значений; вторичную поправку вводят путем повторной фаззификации уточненной исходной информации и ее последующей дефаззификации.
Способ измерения нечеткой информации включает использование шкал (интервалов, отношений) для получения неполной измерительной информации на базовом множестве, отличающийся тем, что для измерения нечеткой информации формируют условную шкалу нечетких эталонных объектов - термов на базовом множестве путем назначения типовых представителей и в последующем фаззифицируют все значения базового множества путем использования функций, принадлежности с семантикой исходной неполной измерительной информации; затем на основе этой условной шкалы фаззифицируют неполную измерительную информацию, которую используют для предварительного измерения нечеткой информации путем определения ее нечеткого включения в типовые термы; при этом терм с наибольшим включением считают предварительным результатом измерения нечеткой информации; в предварительный результат вводят поправки, для этого используют операции его дефаззификации с учетом значений функций принадлежности во всех термах шкалы и всех ее типовых значений; вторичную поправку вводят путем повторной фаззификации уточненной исходной информации и ее последующей дефаззификации.
| В.В | |||
| РЫЖАКОВ и др | |||
| "ОЦЕНИВАНИЕ НЕЧЕТКОЙ ИНФОРМАЦИИ НА ОСНОВЕ УСЛОВНЫХ ШКАЛ" | |||
| В: "МЕТРОЛОГИЯ", 2009, N 8, с | |||
| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| НЕЧЕТКИЙ РЕГУЛЯТОР С ЛИНГВИСТИЧЕСКОЙ ОБРАТНОЙ СВЯЗЬЮ ДЛЯ УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ | 2006 |
|
RU2309443C1 |
| Устройство для обработки нечеткой информации | 1990 |
|
SU1758642A1 |
| US 5778149 A, 07.07.1998 | |||
| Устройство для подготовки информации на перфоленте | 1977 |
|
SU684549A1 |
| US 2004047289 A1, 11.03.2004 | |||
Авторы
Даты
2015-10-20—Публикация
2012-08-15—Подача