Изобретение относится к системам наведения зенитных управляемых ракет (ЗУР). Рассматриваемая ЗУР относится к классу ракет средней дальности с активной радиолокационной головкой самонаведения. Для таких ракет известен способ наведения [1, стр.28], основанный на выработке команд управления пропорционально рассогласованию между положением равносигнального направления антенны пеленгационного устройства и направлением на цель. Согласно этому способу [1] антенна головки самонаведения ЗУР направлена на воздушную цель (направление на цель совпадает с равносигнальным направлением антенны), а при отклонении цели от равносигнального направления антенны, в силу собственного движения и движения ЗУР, на выходе пеленгационного устройства появляется напряжение UД(t), зависящее от величины и знака этого отклонения. Напряжение UД(t) далее фильтруется, усиливается и передается на исполнительное устройство, для выработки команд управления полетом ЗУР, при этом исполнительное устройство изменяет положение антенны так, что равносигнальное направление смещается в пространстве и исходное угловое рассогласование между ним и направлением на цель уменьшается.
К недостаткам способа следует отнести незащищенность его от негативного влияния угловых шумов цели в случае наведения на групповую сосредоточенную цель (ГСЦ). ГСЦ - это групповая цель, элементы которой находятся в одном импульсном объеме следящего пеленгатора. В случае наведения ЗУР на групповую цель, состоящую из двух и более самолетов, кажущийся центр вторичного излучения всегда находится за пределами реальных объектов локации, а при изменении ракурса групповой цели относительно точки наблюдения этот центр будет блуждать [2].
Возникновение ошибок пеленга, обусловленных протяженностью цели, приводит к тому, что вероятность вывода ЗУР в трубку промаха существенно снижается. Максимальное снижение вероятности наблюдается при дистанции 150-200 м, характерной для сомкнутых боевых порядков.
Задачей изобретения является разработка способа управления ЗУР средней дальности с активной головкой самонаведения при наведении на ГСЦ, адаптивного к интенсивным угловым шумам, с целью повышения точности наведения ЗУР на один из элементов ГСЦ.
Для решения задачи изобретения предлагается структура системы управления зенитной управляемой ракеты, изображенная на фиг. 1. На чертеже обозначены: 1 - устройство оценки поперечного размера цели, 2 - пороговое устройство, 3 - пеленгационное устройство с антенной, 4 - фильтр низкой частоты, 5 - цифровой α-β-γ фильтр, 6 - усилитель, 7 - исполнительное устройство. Предлагаемая структурная схема отличается от исходной, реализующей способ-прототип, наличием дополнительных элементов 1, 2 и 5, наличием связи 4-5 и 5-6, кроме того, отсутствием связи 4-6.
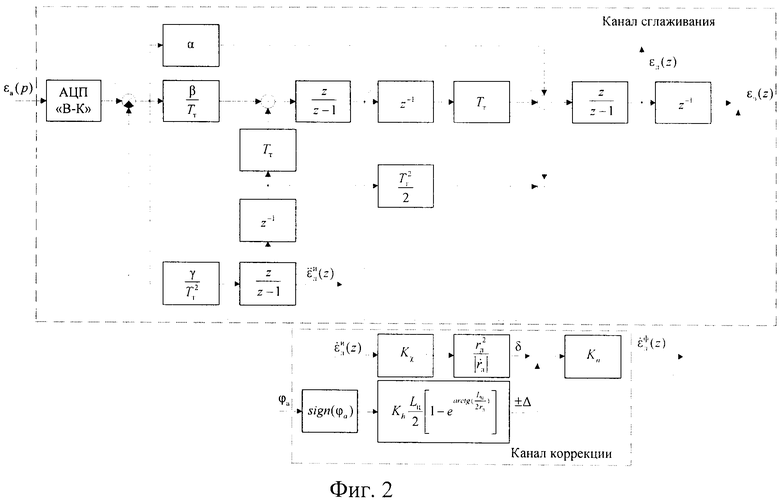
Сущность предлагаемого способа заключается в том, что, в отличие от известного способа [1], для повышения точности наведения зенитной управляемой ракеты на групповую сосредоточенную цель принятый антенной пеленгационного устройства сигнал от цели параллельно поступает в устройство оценки поперечного размера цели. Это устройство, оценив поперечный размер цели двухмоментным способом [3], формирует индекс слежения, пропорциональный поперечному размеру цели, и выдает его на пороговое устройство. В пороговом устройстве, в случае превышения значением индекса слежения порогового значения признака групповой цели, формируется команда на включение рекурсивного цифрового α-β-γ фильтра (канал сглаживания). Напряжение UД(t), пропорциональное величине отклонения направления на цель от равно-сигнального направления антенны εл, с выхода фильтра низкой частоты поступает в рекурсивный цифровой α-β-γ фильтр (фиг.2), где аналого-цифровой преобразователь преобразует напряжение UД(t) в цифровой код, который с помощью передаточных функций α-β-γ фильтра с определенными коэффициентами обрабатывается для получения сглаженного значения текущих координат цели с компенсированной флюктуационной составляющей.
Необходимость получения оценок координат цели и параметров ее движения εл, 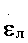

εи[n]=εэ[n]+αΔε[n]; εи[0]=ε0;

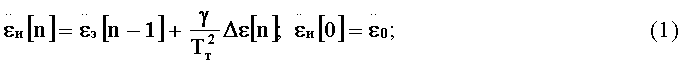


где εи[n] - измеренное значение текущей угловой координаты линии визирования цели;
εэ[n] - экстраполированное на n-й такт значение угловой координаты линии визирования цели
Тт - тактовый период ЦВМ ЗУР;

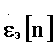
α, β, γ - коэффициенты корректирующего устройства.
Уравнения (1) отображают работу рекурсивного цифрового α-β-γ фильтра и описывают процедуру формирования измеренных значений εл, 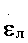



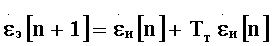
Уравнение рассогласования на линейном участке дискриминационной характеристики может быть представлено в виде:
Δε[n]=ε[n]-εэ[n],
Структурная схема рекурсивного цифрового α-β-γ фильтра (фиг. 2) подразумевает z-преобразование выражений (1):
Δε(z)=ε(z)-εэ(z);



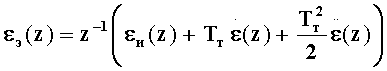

и приведение их к виду:

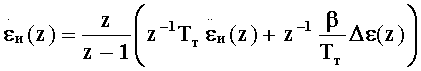
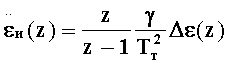
Из уравнений (2) получают передаточные функции замкнутой следящей системы с рекурсивным цифровым α-β-γ фильтром:



где B=3-α-β-0,5γ, С=3-2α-β+0,5γ, D=1-α.
Условия устойчивости следящей системы по угловым координатам выводятся на основе анализа коэффициентов характеристического полинома:
Λ(z)=λmzm+λm-1zm-1+…+λ1z+λ0,
Для полинома третьей степени (m=3) условия устойчивости фильтра имеют вид [4]:
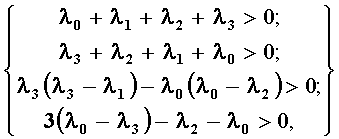
где λ3=1, λ2=-B, λ1=С, λ0=-D
Дальнейшие вычисления дают
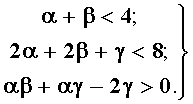
Помимо этого, из принципа физической реализуемости следует, что коэффициенты должны отвечать условию [4]: α>0, β≥0, γ≥0.
При определении установившейся динамической ошибки необходимо учесть, что следящая система обладает астатизмом третьего порядка, следовательно, в качестве простейшего стандартного входного воздействия 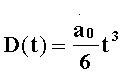
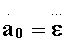
После проведения z-преобразования, входное воздействие имеет вид:

Дискретная передаточная функция по ошибке описывается выражением:

Установившаяся динамическая ошибка принимает вид:

Уменьшение динамической ошибки достигается путем увеличения коэффициентов α и γ, при условии, что α<1.
Флюктуационная ошибка определяется по аналогичной методике. Выражения, описывающие дисперсии ошибок измерений, имеют вид:
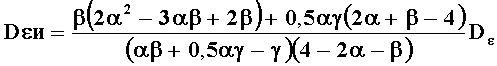
Основное противоречие состоит в том, что для снижения флюктуационных ошибок следует уменьшать указанные коэффициенты α, β, γ, однако, при нарушении условий устойчивости, значения дисперсий ошибок измерения становятся бесконечно большими или отрицательными.
Оптимальные значения коэффициентов α0, β0, γ0 должны удовлетворять следующей системе уравнений [4]:

В данной системе уравнений I - индекс слежения, характеризующий интенсивность углового шума групповой цели, описываемый выражением:

где Dц - дальность до цели;
М - коэффициент, характеризующий класс цели;
Lц - оценка поперечного размера цели.
Результаты численного решения системы уравнений (3) позволяют выбрать оптимальные значения коэффициентов рекурсивного цифрового α-β-γ фильтра для конкретных условий работы следящей системы (фиг. 3).
Матрица дисперсий, характеризующая погрешности работы следящей системы с фильтром, имеет вид:
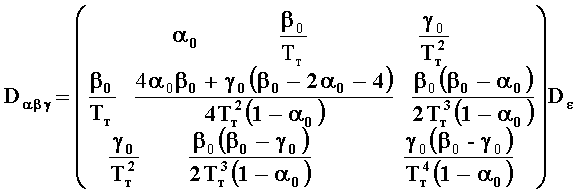
Диагональные элементы матрицы характеризуют дисперсии ошибок измерения угловых координат, угловой скорости вращения линии визирования цели и углового ускорения, а остальные элементы - корреляционные моменты связи. Для среднеквадратических ошибок измерений будут корректны выражения:
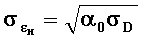
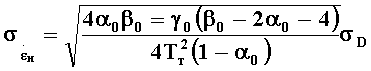

где 
В канале коррекции, по данным, полученным после измерения размера ГСЦ, формируется сигнал поправки, пропорциональный размеру цели. Величина поправки на истинное положение цели выбирается равной
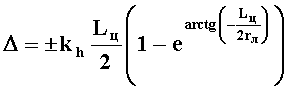
где kh=0,337 1/м, а знак поправки определяется знаком ошибки слежения координатора и положением объекта наведения относительно КЦ.
С целью проверки работоспособности предложенного способа было проведено математическое моделирование с использованием имитационной математической модели системы управления зенитной управляемой ракеты с радиолокационной головкой самонаведения [5] и математических моделей реальных воздушных целей [4]. Результаты моделирования показали, что применение данного способа позволяет повысить точность наведения зенитной управляемой ракеты при стрельбе по групповой цели на 50-60 % (фиг.4). На фиг.4 показано уменьшение величины промаха ЗУР с α-β-γ фильтром при стрельбе по ГСЦ очередью из двух ракет по первой и второй цели (а - первой ракетой, б - второй ракетой).
Таким образом, предложенный способ дал возможность получить сглаженные значения угловых координат групповой сосредоточенной цели, снизив негативное влияние угловых шумов.
Источники информации
1. Первачев С.В. Радиоавтоматика. М.: Радио и связь, 1982. 175 с.
2. Островитянов Р.В., Басалов Ф.А. Статистическая теория радиолокации протяженных целей. М., Радио и связь, 1982. - 232 с.
3. Чертков Е.В. Анализ точностных характеристик двухмоментного способа оценки геометрических размеров воздушных объектов. Деп. рукопись в ЦСИФ. М.: ЦВНИ МО РФ, сер. Б, вып. 59, 2002. - 11 с.
4. Жарков С.В. Использование адаптивных цифровых фильтров в следящих пеленгаторах зенитных комплексов. // Науч. тр. академии. Смоленск, 1996. Вып. 5. С.63-69.
5. Свидетельство об официальной регистрации программы для ЭВМ. М., ОФЭРНиО № 16972. 2011. Система управления зенитной управляемой ракеты средней дальности / Жарков С.В., Кадученко И.В.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОМБИНИРОВАННОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА | 2014 |
|
RU2586399C2 |
| СПОСОБ ЗАЩИТЫ РАДИОЛОКАЦИОННОЙ СТАНЦИИ ОТ ПРОТИВОРАДИОЛОКАЦИОННОЙ РАКЕТЫ НА ОСНОВЕ ИСПОЛЬЗОВАНИЯ ДОПОЛНИТЕЛЬНОГО ИСТОЧНИКА ИЗЛУЧЕНИЯ ПОДЪЕМНОГО ТИПА | 2005 |
|
RU2287168C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАКЛОННОЙ ДАЛЬНОСТИ ВОЗДУШНОЙ ЦЕЛИ ПО ЕЕ УСТАНОВЛЕННОЙ СКОРОСТИ | 2013 |
|
RU2558407C2 |
| Способ распознавания варианта наведения подвижного объекта на один из летательных аппаратов группы | 2019 |
|
RU2713212C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ ФАКТА НАВЕДЕНИЯ САМОНАВОДЯЩЕГОСЯ ПО РАДИОИЗЛУЧЕНИЮ ОРУЖИЯ НА РАДИОЭЛЕКТРОННОЕ СРЕДСТВО, ЗАЩИЩЕННОЕ ОТВЛЕКАЮЩИМ УСТРОЙСТВОМ | 2012 |
|
RU2510481C2 |
| СПОСОБ ФОРМИРОВАНИЯ СИГНАЛА УПРАВЛЕНИЯ ИСТРЕБИТЕЛЕМ В ГОРИЗОНТАЛЬНОЙ ПЛОСКОСТИ ПРИ ЕГО БЛИЖНЕМ НАВЕДЕНИИ НА ГРУППОВУЮ ВОЗДУШНУЮ ЦЕЛЬ | 2015 |
|
RU2593911C1 |
| Пространственная имитационная модель системы управления автоматическим маневренным летательным аппаратом | 2019 |
|
RU2735418C2 |
| МОБИЛЬНЫЙ ЗЕНИТНЫЙ РАКЕТНЫЙ КОМПЛЕКС | 2003 |
|
RU2253820C2 |
| ЗЕНИТНАЯ САМОХОДНАЯ УСТАНОВКА | 2007 |
|
RU2348890C2 |
| Способ измерения дальности и радиальной скорости в РЛС с зондирующим составным псевдослучайным ЛЧМ импульсом | 2017 |
|
RU2688921C2 |



Изобретение относится к области противовоздушной обороны. Способ управления зенитной управляемой ракетой средней дальности с активной головкой самонаведения при наведении на групповую сосредоточенную цель (ГСЦ) основан на использовании зависимости статистических характеристик угловых шумов радиолокационной цели от ее линейных размеров. Сущность способа состоит в том, что значения угловых координат цели подвергаются адаптивной фильтрации методом α-β-γ сглаживания и алгоритму коррекции. Полученные таким образом значения будут соответствовать угловым координатам реальной цели из состава групповой, а не кажущемуся центру, который может находиться за пределами геометрических размеров объектов локации. Технический результат заключается в повышении точности наведения ракеты в условиях негативного воздействия угловых шумов. 4 ил.
Способ управления зенитной управляемой ракетой средней дальности с активной головкой самонаведения при наведении на групповую сосредоточенную цель (ГСЦ), заключающийся в том, что антенна головки самонаведения зенитной управляемой ракеты направлена на групповую сосредоточенную цель (направление на цель совпадает с равносигнальным направлением антенны), а при отклонении цели от равносигнального направления антенны (в силу собственного движения и движения зенитной управляемой ракеты), на выходе пеленгационного устройства появляется напряжение UД(t), зависящее от величины и знака этого отклонения, напряжение UД(t) фильтруется, усиливается и передается на исполнительное устройство, для выработки команд управления полетом зенитной управляемой ракеты, при этом исполнительное устройство изменяет положение антенны так, что равносигнальное направление смещается в пространстве и исходное угловое рассогласование между ним и направлением на цель уменьшается,
отличающийся тем, что принятый антенной пеленгационного устройства сигнал от цели параллельно поступает в устройство оценки поперечного размера цели, где двухмоментным способом осуществляется оценка поперечного размера цели и формируется индекс слежения (пропорциональный поперечному размеру цели), индекс слежения поступает на пороговое устройство, в котором, в случае превышения значения индекса слежения порогового значения признака групповой цели, формируется команда на включение рекурсивного цифрового α-β-γ фильтра (канал сглаживания), значение UД(t) после фильтра низкой частоты поступает в рекурсивный цифровой α-β-γ фильтр, где аналого-цифровой преобразователь преобразует напряжение UД(t) в цифровой код, который с помощью передаточных функций фильтра с оптимальными коэффициентами обрабатывается для получения сглаженного значения текущих координат цели с компенсированной флюктуационной составляющей, в канале коррекции, по данным, полученным после измерения размера ГСЦ, формируется сигнал поправки, пропорциональный размеру цели, полученные значения через цифро-аналоговый преобразователь подаются в исполнительное устройство для выработки команд управления зенитной управляемой ракетой и поворота антенны.
| С.В | |||
| Жарков, И.В | |||
| Кадученко "ОСОБЕННОСТИ УПРАВЛЕНИЯ ЗЕНИТНОЙ УПРАВЛЯЕМОЙ РАКЕТОЙ С РАДИОЛОКАЦИОННОЙ ГОЛОВКОЙ CАМОНАВЕДЕНИЯ ПРИ НАВЕДЕНИИ НА ГРУППОВУЮ СОСРЕДОТОЧЕННУЮ ЦЕЛЬ", Математическая морфология | |||
| Электронный математический и медико-биологический журнал, Том 10, вып | |||
| Переносная печь для варки пищи и отопления в окопах, походных помещениях и т.п. | 1921 |
|
SU3A1 |
| Способ приготовления лака | 1924 |
|
SU2011A1 |
| СПОСОБ ИЗМЕРЕНИЯ ПОПЕРЕЧНЫХ РАЗМЕРОВ РАДИОЛОКАЦИОННЫХ ОБЪЕКТОВ РЛС В РЕАЛЬНОМ МАСШТАБЕ ВРЕМЕНИ | 1999 |
|
RU2150714C1 |
| US 5669581 A1, 23.09.1997 | |||
| US 4115776 A1, 19.09.1978 | |||
| US 4522356 A1, 11.06.1985. | |||
Авторы
Даты
2015-12-10—Публикация
2012-03-23—Подача