Изобретение относится к области техники связи, а именно к системам передачи информации с помехоустойчивым кодированием и может быть использовано в канальных кодеках систем передачи информации.
Известен способ декодирования линейных блочных кодов (Скляр Б. Цифровая связь. Теоретические основы и практическое применение – М.: Издательский дом «Вильяме», 2003. – 1104 с. – С. 366-367), заключающийся в том, что из канала связи принимают кодовые комбинации, закодированные коротким кодом, состоящие из двоичных информационных символов вместе с избыточными символами кода, для каждой кодовой комбинации преобразуют избыточные символы кода в символы синдрома, на основе полученного синдрома локализуют вектор ошибки, осуществляют сложение по модулю 2 локализованного вектора ошибки и принятой кодовой комбинации, что приводит к устранению ошибки.
Наиболее близким по технической сущности и выполняемым функциям аналогом (прототипом) к заявляемому изобретению является способ декодирования циклического кода (патент RU № 2340088 (27.11.2008), класс H03M 13/00), заключающийся в том, что для каждой принятой кодовой комбинации вычисляют расширенный синдром и, используя расширенную проверочную матрицу, определяют те наборы строк, которые являются линейными комбинациями вычисленного синдрома, причем каждой линейной комбинации однозначно соответствует вектор ошибки и для каждого вектора ошибки вычисляют метрику, а для исправления наиболее вероятных ошибок в качестве вектора коррекции при декодировании с «жестким» решением выбирают вектор ошибки, который имеет минимальную метрику (вектор ошибки минимального веса), и при декодировании с «мягким» решением выбирают вектор ошибки, который имеет максимальную модифицированную метрику. Затем инвертируют элементы в систематической части кодового слова, номера которых соответствуют позициям ненулевых элементов вектора коррекции.
В данной области техники существует техническая проблема, заключающаяся в том, что описанные в рассмотренных способах модели источников сообщений и ошибок применимы для идеального гауссовского канала связи, что приводит к снижению достоверности декодирования, так как большинство реальных каналов связи обладают свойством пакетирования ошибок.
Техническая проблема решается разработкой способа декодирования блочных помехоустойчивых кодов, обеспечивающего при его реализации возможность повышения достоверности декодирования вследствие учёта свойств реального канала связи, отличных от статистических свойств идеального гауссовского. Для этого на передающей стороне формируют тестовую последовательность и передают ее по каналу связи. На приемной стороне складывают принятую тестовую последовательность по модулю 2 с эталонной и рассчитывают условные вероятности символов источника ошибок дискретного канала связи с пакетированием ошибок. Далее канал связи переключают в режим приема информационных блоков и осуществляют прием двоичных кодовых комбинаций, закодированных одним из известных блочных помехоустойчивых кодов. На основе принятой кодовой комбинации формируют множество возможных векторов ошибок, затем на основе сведений о вероятностных характеристиках канала связи и источника сообщений рассчитывают распределение вероятностей двоичных векторов ошибок и разрешенных кодовых комбинаций. После этого из рассчитанного распределения выбирают соответствующее значение вероятности для каждого вектора ошибки и разрешенной кодовой комбинации. Далее для заданной длины вектора кода вычисляют матрицу потерь, выступающую в качестве функции потерь, и производят расчет средних рисков относительно каждой разрешенной кодовой комбинации, при этом для выбора вектора ошибки определяют минимальный из рассчитанных средних рисков. После этого осуществляется инвертирование двоичных символов принятой кодовой комбинации на позициях, соответствующих ненулевым символам вектора ошибки.
Перечисленная новая совокупность существенных признаков обеспечивает возможность повышения достоверности декодирования.
Проведенный анализ уровня техники позволил установить, что аналоги, характеризующиеся совокупностью признаков, тождественных всем признакам заявленного технического решения, отсутствуют, что указывает на соответствие заявленного способа условию патентоспособности «новизна».
Результаты поиска известных решений в данной и смежных областях техники с целью выявления признаков, совпадающих с отличительными от прототипа признаками заявленного объекта, показали, что они не следуют явным образом из уровня техники. Из уровня техники также не выявлена известность отличительных существенных признаков, обусловливающих тот же технический результат, который достигнут в заявляемом способе. Следовательно, заявленное изобретение соответствует условию патентоспособности «изобретательский уровень».
Заявленный способ поясняется чертежами, на которых показаны:
фиг. 1 - функциональная схема способа декодирования блочных помехоустойчивых кодов по критерию минимального среднего риска;
фиг. 2 - блок-схема связанного алгоритма формирования множества двоичных векторов ошибок;
фиг. 3 - пример заполнения «массива группированных комбинаций» при формировании распределения вероятностей двоичных векторов источника ошибок и сообщений длины 
фиг. 4 - блок-схема алгоритма формирования распределений финальных вероятностей двоичных векторов источников сообщений и ошибок дискретного канала связи с пакетированием ошибок;
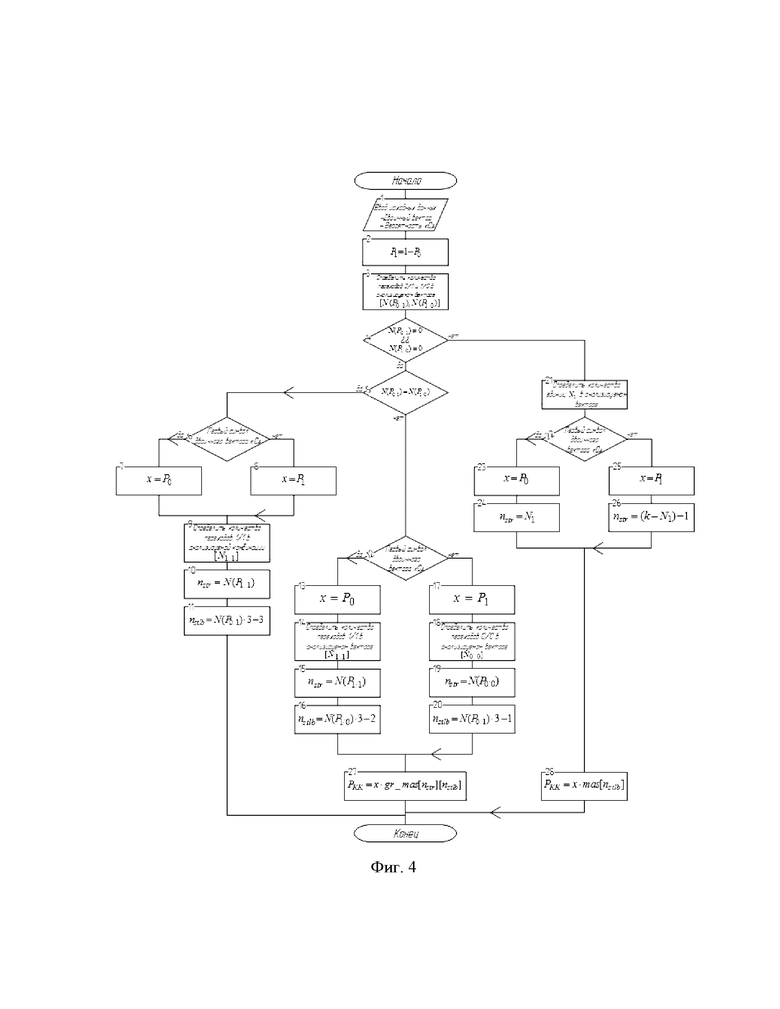
фиг. 5 - графическая зависимость вероятности ошибочного декодирования от выбранного способа декодирования.
Реализация заявленного способа декодирования помехоустойчивых кодов поясняется на фиг.1:
Блок №1 – на вход блока поступает тестовая последовательность 

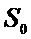

Результаты сложения указанных последовательностей позволяют выделить ошибочные биты тестовой последовательности 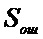


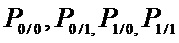

Блок №2 – в блоке №2 осуществляют хранение множества разрешенных кодовых комбинаций выбранного блокового помехоустойчивого кода [Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. – М.: Техносфера, 2005. – 320 с]. Разрешенные кодовые комбинации с выхода блока №2 подают на входы блоков №3 и №4.
Блок №3 – на вход блока № 3 поступает двоичная кодовая комбинация, закодированная одним из известных блочных помехоустойчивых кодов [Морелос-Сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. – М.: Техносфера, 2005. – 320 с]. Затем на основании принятой кодовой комбинации формируют множество возможных векторов ошибок. С целью описания процедуры формирования множества векторов ошибок вводят следующие обозначения:
информационный подвектор - комбинация информационных символов кодовой комбинации, закодированных одним из известных блочных помехоустойчивых кодов;
проверочный подвектор - комбинация проверочных символов кодовой комбинации.
Множества двоичных векторов ошибок источника ошибок дискретного канала связи с пакетированием ошибок формируют в несколько этапов:
1. Производят декомпозицию кодовой комбинации, принятой из канала связи, на информационный и проверочный подвекторы;
2. Формируют множество информационных подвекторов векторов ошибок;
3. Формируют множество проверочных подвекторов векторов ошибок путем сложения по модулю 2 проверочных символов кодовой комбинации, принятой из канала связи, с проверочными символами разрешенных кодовых комбинаций;
4. Выполняют конкатенацию проверочных и информационных подвекторов векторов ошибок, полученных в результате выполнения этапов 2 и 3.
В общем случае формирование множества двоичных векторов ошибок относительно принятой двоичной кодовой комбинации осуществляют путем сложения по модулю 2 кодовой комбинации, принятой из канала связи, с каждой из разрешенных кодовых комбинаций выбранного помехоустойчивого кода. Анализ множеств двоичных векторов ошибок различной размерности позволил выявить взаимные корреляционные связи двоичных векторов ошибок во множестве между собой. Учет взаимных корреляционных связей между двоичными векторами предоставляет возможность формировать информационные подвекторы векторов ошибок (этап №2) с применением минимального количества элементарных вычислительных операций. Суть разработанного подхода заключается в интерпретации связей между векторами ошибок путем представления множества информационных подвекторов в виде групп, в которые объединяются двоичные векторы, имеющие одинаковые значения символов старших 

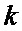

В качестве основы связанного алгоритма формирования множества информационных подвекторов используют группу № 1.1, формируемую на первой итерации, в которую включают подвекторы, полученные в результате сложения по модулю 2 информационного подвектора кодовой комбинации, принятой из канала связи, и информационных подвекторов разрешенных кодовых комбинаций, имеющих индексы от 0 до 3 в десятичном представлении. В соответствии с проведенным анализом двоичных векторов ошибок выявили следующую последовательность операций формирования групп информационных подвекторов. По окончании процедуры формирования группы № 1.1 инвертируют один символ каждого информационного подвектора, рассчитанного на одной из более ранних итераций, номер выполняемой итерации определяют в качестве позиции инвертируемого символа. Таким образом, для того, чтобы сформировать группу № 2.1, инвертируют символ во втором разряде каждого информационного подвектора, отнесенного к группе № 1.1. Количество групп, формируемых на каждой следующей итерации алгоритма, равно суммарному количеству групп, сформированных на предыдущих итерациях. На третьей итерации формируют группы №№ 3.1–3.2, которые образуют путем инверсии символов в третьем разряде информационных подвекторов групп №№ 1.1 и 2.1 соответственно. Последующие группы векторов формируют таким же образом, при этом расчет векторов, отнесенных к группам, имеющим большее значение индекса, производят на основании уже рассчитанных векторов путем инверсии одного бита информационного подвектора кодовой комбинации. Блок-схема связанного алгоритма представлена на фиг. 2. В результате реализации связанного алгоритма исключена необходимость последовательного сложения всех символов двоичной кодовой комбинации, принятой из канала связи, со всеми символами разрешенных кодовых комбинаций кода, что значительно снижает временные и вычислительные затраты при декодировании. Сформированные векторы ошибок с выхода блока № 3 вводят на вход блока № 4.
Блок №4 - в основе блока №4 лежит подход, учитывающий свойство группирования вероятностей двоичных векторов источника сообщений и ошибок дискретного канала связи с пакетированием ошибок, согласно которому часть двоичных комбинаций источников сообщений и ошибок дискретного канала связи с пакетированием ошибок имеет одинаковые значения произведения переходных вероятностей символов [Конышев М. Ю., Двилянский А.А., Барабашов А.Ю., Петров К.Е. «Формирование распределений вероятностей двоичных векторов источника ошибок марковского дискретного канала связи с памятью с применением метода "группирования вероятностей" векторов ошибок». «Промышленные АСУ и контроллеры», №3. – 2018 г. М: НАУЧТЕХЛИТИЗДАТ, – с. 42–52]. Указанное свойство позволяет сгруппировать двоичные векторы с одинаковыми значениями произведения переходных вероятностей символов. В качестве исходных данных для выполнения вычислений в блоке №4 используют значения переходных вероятностей двоичных бит, поступившие с выхода блока № 1.
Общее количество групп вероятностей двоичных векторов источников сообщений и ошибок дискретного канала связи с пакетированием ошибок на длинах вектора кодовой комбинации 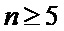
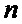
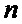
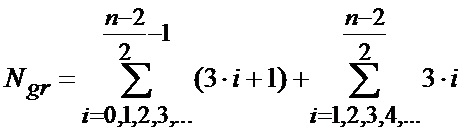

Общее количество двоичных векторов, не входящих в группы, определяется выражением:

где 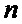
Учет описанного свойства определяет отсутствие необходимости в расчете вероятности для каждого двоичного вектора в отдельности. Достаточно рассчитать 
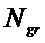
Для полного описания всех возможных значений вероятностей двоичных векторов источников ошибок и сообщений дискретного канала связи с пакетированием ошибок необходимо сформировать 2 массива:
1. «Массив группированных комбинаций» – массив вероятностей двоичных векторов источников ошибок и сообщений дискретного канала связи с пакетированием ошибок, объединенных в группы с учетом одинаковых значений произведения переходных вероятностей символов. Каждый элемент «массива группирования комбинаций» содержит в себе значение вероятности для одной из групп двоичных векторов;
2. «Массив одиночных вероятностей» - массив вероятностей двоичных векторов, не входящих ни в одну из групп «массива группирования комбинаций». Каждый элемент «массива одиночных вероятностей» содержит вероятность одного двоичного вектора источника ошибок или сообщений дискретного канала связи с пакетированием ошибок.
«Массив группирования комбинаций» представляет собой двумерный массив, общее количество строк которого определяется выражением

где 
Общее количество столбцов «массива группирования комбинаций» двоичных векторов длины 
1) Если 

2) Если 

где 
Для заполнения «массива группированных комбинаций» выполняют следующую последовательность действий:
1. Производят расчет вероятностей «базовых» групп, являющихся основой для расчета вероятностей остальных групп распределения:
1.1 Рассчитывают вероятность группы с индексом [0][0], записываемой в строку № 0 столбца № 0 «массива группированных комбинаций» в соответствии с выражением

где 
1.2 Рассчитывают вероятность группы с индексом [0][1], записываемой в строку № 0 столбца № 1 «массива группированных комбинаций» в соответствии с выражением
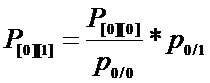
1.3 Рассчитывают вероятность группы с индексом [0][2], записываемой в строку № 0 столбца № 2 «массива группированных комбинаций» в соответствии с выражением

где 
1.4 Производят расчет вероятностей групп комбинаций, записываемых в «массив группированных комбинаций», на основе значений, полученных в шаге № 1.
Результатом выполнения представленной последовательности действий является заполненный «массив группированных комбинаций» размерностью
В качестве примера на фиг. 3 представлена процедура заполнения «массива группированных комбинаций» при формировании распределения вероятностей двоичных векторов источников ошибок и сообщений дискретного канала связи с пакетированием ошибок длины 
Двоичные векторы, вероятности которых относятся к «массиву одиночных вероятностей», также обладают рядом свойств, учет которых позволяет значительно сократить количество вычислительных операций их расчета.
Основное отличие комбинаций, отнесенных к «массиву одиночных вероятностей», заключается в том, что, исходя из структуры двоичного вектора, в расчете вероятностей указанных комбинаций не используется либо вероятность появления символа «0» после «1» (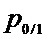
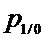
В общем случае, «массив одиночных вероятностей» является одномерным массивом размерностью (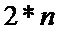

1. Производят расчет вероятностей «базовых» комбинаций, являющихся основой для расчета вероятностей остальных комбинаций «массива одиночных вероятностей»:
1.1 Рассчитывают значение вероятности, записываемое в элемент массива с индексом 
где 
1.2 Рассчитывают значение вероятности, записываемое в элемент «массива одиночных вероятностей» с индексом 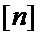

где 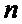
2. Производят заполнение элементов «массива одиночных вероятностей» с индексами от [1] до 

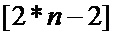
2.1 Заполнение элементов «массива одиночных вероятностей» с индексами от [1] до 

2.2 Заполнение элементов «массива одиночных вероятностей» с индексами от 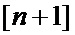
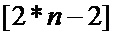
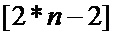

3.1. Производят заполнение элементов «массива одиночных вероятностей» с индексами [0] и 
3.1 Заполнение элемента «массива одиночных вероятностей» с индексом [0] производят в соответствии с выражением:

3.2 Заполнение элемента «массива одиночных вероятностей» с индексом 
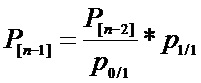
В результате произведенных расчетов в элементах «массива группированных комбинаций» и «массива одиночных вероятностей» будет записана полная группа событий, описывающая произведения переходных вероятностей символов двоичных векторов источников ошибок и сообщений дискретного канала связи с пакетированием ошибок. По окончании процедуры формирования множества вероятностей двоичных векторов источников ошибок и источника сообщений дискретного канала связи с пакетированием ошибок в блоке № 4 производят поиск значения вероятности в «массиве группированных комбинаций» и «массиве одиночных вероятностей» для двоичных векторов ошибок 

С целью определения правила, согласно которому двоичные векторы источников ошибок и сообщений дискретного канала связи с пакетированием ошибок относятся к той или иной группе «массива группированных комбинаций» или к тому или иному элементу «массива одиночных вероятностей» провели анализ, согласно которому выявили, что основным признаком группирования двоичных векторов источников дискретного канала связи с пакетированием ошибок является количество переходов с символа «0» на символ «1» в двоичном векторе (далее «0/1») и, наоборот, – с символа «1» на символ «0» (далее «1/0») [Конышев М.Ю., Барабашов А.Ю., Петров К.Е. Формирование распределений финальных вероятностей двоичных векторов источника ошибок марковского дискретного канала связи с памятью. «Вестник Казанского государственного технического университета им. А. Н. Туполева» №1 – 2018 г. М: ФГБОУ ВПО «КНИТУ им. А. Н. Туполева - КАИ», – с. 106-112]. Вторым параметром, определяющим принадлежность двоичного вектора к той или иной группе, является первый символ – «0» или «1». Третьим признаком, необходимым для анализа, является количество переходов с символа «0» на символ «0» (далее «0/0») и с символа «1» на символ «1» (далее «1/1»). Четвертый анализируемый параметр – количество символов "0" и "1" в двоичном векторе. В результате учета указанных свойств сформулировали следующее правило поиска значения вероятности вектора в «массиве группированных комбинаций» и «массиве одиночных вероятностей»:
1. Если в двоичном векторе существуют переходы «0/1» и «1/0» и их количество равно друг другу, то значение вероятности анализируемого двоичного вектора записано в ячейке одного из столбцов с №№ 0,3,6,9 и т.д. «массива группированных комбинаций». Количество переходов «1/0» определяет столбец, а количество переходов «1/1» – строку «массива группированных комбинаций»;
2. Если в двоичном векторе существуют переходы «0/1» и «1/0» и их количество не равно друг другу, то возможны следующие варианты действий:
2.1 В случае, если первым символом двоичного вектора является символ «0», то значение вероятности анализируемого вектора записано в ячейке одного из столбцов с №№ 1,4,7,10 и т.д. «массива группированных комбинаций». Количество переходов «1/0» определяет искомый столбец, а количество переходов «1/1» – строку «массива группированных комбинаций».
2.2 В случае, если первым символом двоичного вектора является символ «1», то значение вероятности анализируемого вектора записано в ячейке одного из столбцов с №№ 2,5,8,11 и т.д. «массива группированных комбинаций». Количество переходов «0/1» определяет искомый столбец, а количество переходов «0/0» – строку «массива группированных комбинаций».
3. Если в двоичном векторе отсутствует либо переход «0/1», либо «1/0», либо оба перехода, то значение вероятности анализируемого вектора записано в «массиве одиночных вероятностей» и для определения соответствующего значения вероятности возможны следующие варианты действий:
3.1 В случае, если первым символом двоичного вектора является символ «0», то строка «массива одиночных вероятностей», содержащая значение вероятности анализируемого вектора, определяется количеством символов «1» в этом векторе;
3.2 В случае, если первым символом двоичного вектора является символ «1», то строка «массива одиночных вероятностей», содержащая значение вероятности анализируемого вектора, определяется количеством символов «1» в этом векторе и длиной двоичного вектора.
На фиг. 4 представлена блок-схема алгоритма формирования распределений финальных вероятностей двоичных векторов источников ошибок и сообщений дискретного канала связи с пакетированием ошибок.
По результатам выполнения указанных действий для каждого поступившего на вход блока № 4 двоичного вектора определяют соответствующее ему значение произведения переходных вероятностей символов, после чего производят умножение полученного значения на абсолютную вероятность первого символа анализируемого двоичного вектора. Результатом работы блока № 4 является множество финальных вероятностей двоичных векторов источника ошибок и сообщений дискретного канала связи с пакетированием ошибок. Полученные значения вероятностей векторов ошибок 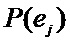
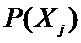
Блок № 5 – в блоке № 5 формируют матрицу потерь 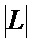
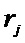




Если критерием достоверности декодирования является вероятность ошибки на бит, то лучшим будет считаться декодер, обеспечивающий минимальное расстояние Хэмминга между информационными частями переданной кодовой комбинации и кодовой комбинации, в пользу которой принято решение. При этом 

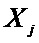

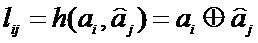
где 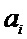



Таким образом, количество искаженных бит на выходе декодера является численной мерой потерь. Правильному декодированию будет соответствовать нулевая потеря. При неправильном декодировании величина потери численно равна весу кодовой комбинации, полученной в результате сложения по модулю 2 разрешённой кодовой комбинации 
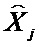
Для произвольного блокового помехоустойчивого 

Элементы 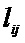
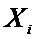



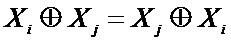



Блок № 6 – в блоке № 6 производят расчет среднего риска относительно каждой разрешенной кодовой комбинации по отношению к принятой кодовой комбинации 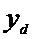

В процессе вычисления средних рисков в блоке № 6 на каждой итерации производят сравнение рассчитанного риска с минимальным, после чего меньшее значение записывают в элемент памяти и принимают за минимальный риск. Средний риск, имеющий большее значение по результатам сравнения, отбрасывают. По окончании расчета средних рисков для каждой кодовой комбинации с выхода блока № 6 на вход блока № 3 поступает индекс 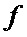
Блок № 7 – на вход блока № 7 подают вектор ошибки, который выбирают в блоке № 3 на основании индекса 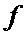



Информационную часть 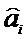

Промышленная применимость изобретения обусловлена тем, что устройство, реализующее предложенный способ, может быть осуществлено с помощью современной элементной базы с достижением указанного в изобретении назначения.
Правомерность теоретических предпосылок проверялась с помощью математического моделирования способа-прототипа и заявленного способа декодирования помехоустойчивых кодов.
Показателем эффективности способа декодирования помехоустойчивых кодов по критерию минимального среднего риска является повышение достоверности декодирования блоковых помехоустойчивых кодов.
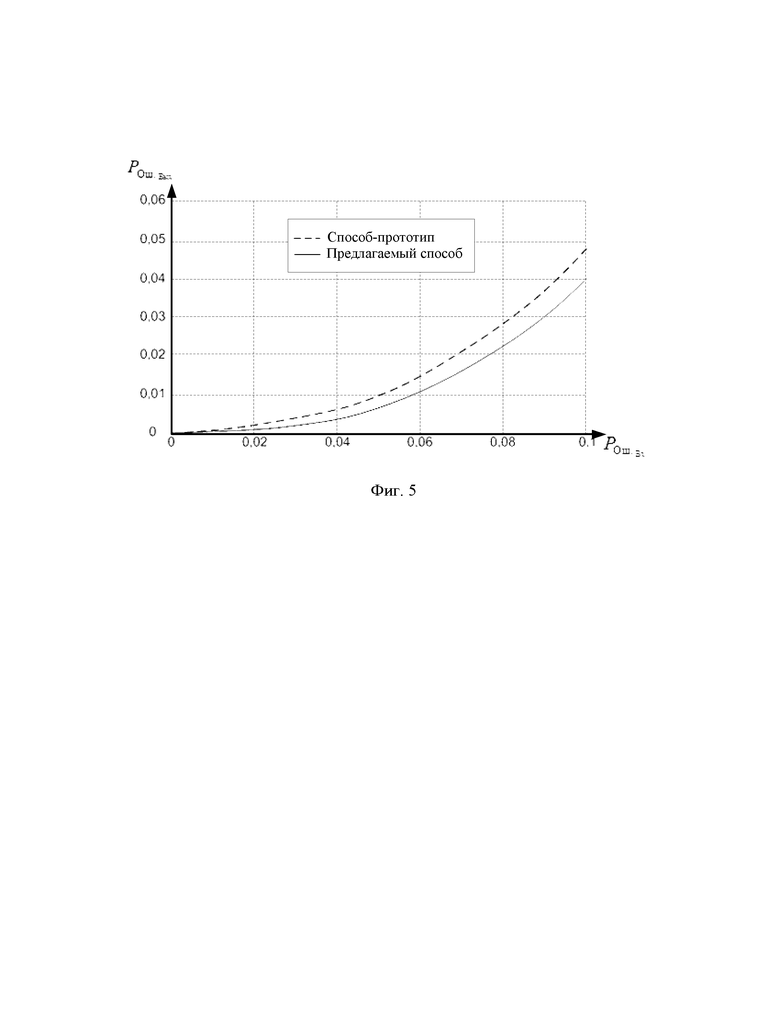
Положительный эффект предложенного способа декодирования помехоустойчивых кодов по критерию минимального среднего риска определяли следующим образом. Произвели математическое моделирование по оцениванию BER (BER – Bit Error Rate) на входе (BERBX) и выходе (ВЕRВЫХ) декодера, функционирующего согласно способа-прототипа и настоящего изобретения. Помехоустойчивому кодированию кодом Хемминга (7, 4) и декодированию подвергались 100 файлов, содержащих текст на русском языке со средним значением энтропии 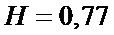

Результаты оценки положительного эффекта показаны на фиг. 5. В зависимости от условий и характера распространения сигнала средний выигрыш составил около 6%.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2011 |
|
RU2450436C1 |
| СПОСОБ КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ | 2007 |
|
RU2342796C1 |
| СПОСОБ И УСТРОЙСТВО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ ДАННЫХ В СКРУЧЕННОМ ПОЛЯРНОМ КОДЕ | 2014 |
|
RU2571587C2 |
| Способ кодовой цикловой синхронизации для каскадного кода Рида-Соломона и Боуза-Чоудхури-Хоквингема [РС(32,16,17), БЧХ(31,16,7)] при одновременном применении жестких и мягких решений | 2020 |
|
RU2747623C1 |
| СПОСОБ ДЕКОДИРОВАНИЯ БЛОКОВЫХ КОДОВ СО СТИРАНИЯМИ ЭЛЕМЕНТОВ | 2006 |
|
RU2327297C2 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ С ЖЕСТКИМИ И МЯГКИМИ РЕШЕНИЯМИ ДЛЯ ДВУХСТУПЕНЧАТОГО КАСКАДНОГО КОДА И МОДУЛЯЦИИ ПО ТИПУ СТЫКА С1-ФЛ | 2024 |
|
RU2834891C1 |
| СПОСОБ ФОРМИРОВАНИЯ КЛЮЧА ШИФРОВАНИЯ / ДЕШИФРОВАНИЯ | 2020 |
|
RU2749016C1 |
| УСТРОЙСТВО КОДОВОЙ ЦИКЛОВОЙ СИНХРОНИЗАЦИИ С МЯГКИМИ РЕШЕНИЯМИ | 2010 |
|
RU2428801C1 |
| УСТРОЙСТВО ДЕКОДИРОВАНИЯ С МЯГКИМИ РЕШЕНИЯМИ ДЛЯ ДВУХСТУПЕНЧАТОГО КАСКАДНОГО КОДА | 2012 |
|
RU2485683C1 |
| Помехоустойчивый кодек для передачи дискретных сообщений | 1990 |
|
SU1727201A2 |



Изобретение относится к области техники связи, а именно к системам передачи информации с помехоустойчивым кодированием, и может быть использовано в канальных кодерах систем передачи информации, в которых передача информационных сообщений осуществляется посредством радиоволн. Технический результат заключается в повышении достоверности декодирования вследствие учета свойств реального канала связи, отличных от статистических свойств идеального гауссовского. Из канала связи принимают кодовые комбинации, состоящие из двоичных информационных символов вместе с избыточными символами кода. Выбирают вектор ошибки. Инвертируют элементы в систематической части кодового слова, номера которых соответствуют позициям ненулевых элементов вектора ошибки. Выделяют систематическую часть в откорректированном кодовом слове. Дополнительно на передающей стороне формируют тестовую последовательность и передают ее по каналу связи. На приемной стороне складывают принятую тестовую последовательность по модулю 2 с эталонной. На основе результата их сложения рассчитывают условные вероятности двоичных символов источника ошибок дискретного канала связи. Рассчитывают распределение вероятностей двоичных векторов ошибок и разрешенных кодовых комбинаций. 5 ил.
Способ декодирования помехоустойчивых кодов по критерию минимального среднего риска, заключающийся в том, что из канала связи принимают кодовые комбинации, состоящие из двоичных информационных символов вместе с избыточными символами кода, выбирают вектор ошибки, затем инвертируют элементы в систематической части кодового слова, номера которых соответствуют позициям ненулевых элементов вектора ошибки, после чего выделяют систематическую часть в откорректированном кодовом слове, отличающийся тем, что дополнительно на передающей стороне формируют тестовую последовательность и передают ее по каналу связи, на приемной стороне складывают принятую тестовую последовательность по модулю 2 с эталонной, далее на основе результата их сложения рассчитывают условные вероятности двоичных символов источника ошибок дискретного канала связи, затем рассчитывают распределение вероятностей двоичных векторов ошибок и разрешенных кодовых комбинаций, после чего переключают декодер в режим приема двоичных кодовых комбинаций, после приема кодовой комбинации из канала связи формируют множество возможных векторов ошибок относительно поступившей на вход декодера кодовой комбинации, далее выбирают из рассчитанных распределений вероятностей соответствующее значение вероятности для каждого вектора ошибки и разрешенной кодовой комбинации, после чего вычисляют матрицу потерь для данного помехоустойчивого кода, затем вычисляют средние риски относительно каждой разрешенной кодовой комбинации, при этом для выбора вектора ошибки определяют минимальный из рассчитанных средних рисков, после чего осуществляется инвертирование двоичных символов принятой кодовой комбинации на позициях, соответствующих ненулевым символам вектора ошибки, и выделение систематической части кодового слова.
| СПОСОБ СИНДРОМНОГО ДЕКОДИРОВАНИЯ ЦИКЛИЧЕСКОГО КОДА (ВАРИАНТЫ) | 2006 |
|
RU2340088C2 |
| КОДЕК ЦИКЛИЧЕСКОГО ПОМЕХОУСТОЙЧИВОГО КОДА | 2002 |
|
RU2212101C1 |
| СПОСОБ ПОМЕХОУСТОЙЧИВОГО КОДИРОВАНИЯ И ДЕКОДИРОВАНИЯ | 2003 |
|
RU2214678C1 |
| JP 3801211 B2, 26.07.2006 | |||
| EP 728390 B1, 28.04.2004. | |||
Авторы
Даты
2019-11-14—Публикация
2019-01-25—Подача