Предлагаемое изобретение относится к области контроля сложными стохастическими системами, и может быть использовано в энергетике, медицине, пищевой, химической, металлургической и других отраслях промышленности, повышении надежности контроля в социально-экономических системах. Целью изобретения является повышение эффективности контроля состояния сложной стохастической системы.
Системы контроля стохастического распределения широко распространены в практических промышленных процессах, цель которых состоит в отслеживании трека вероятности выхода для негауссовых систем [1, 2, 3]. Существуют различные технические приложения, в которых требуются контроль над треком вероятности выходного параметра системы при наличии случайных возмущений. Примерами процессов контроля вероятностного распределения являются: контроль распределением частиц по размерам в химическом машиностроении, контроль распределением пламени в энергетических установках, контроль распределения биологических параметров в медицине, производство пленки, микротехнологии, контроль доменной структуры веществ, контроль распределения параметров для различных отраслей промышленности [4]. На современном этапе развития контроль неопределенности распределения системы строится на основе контроля моментов ответа стохастической системы [1, 2].
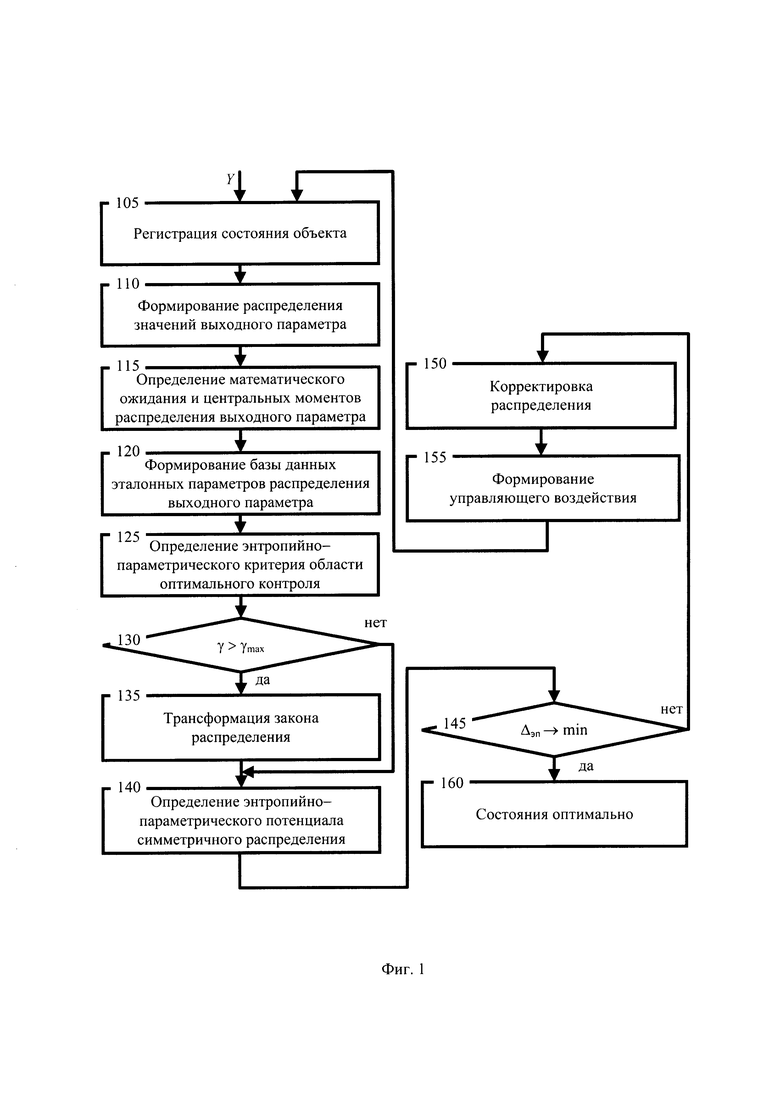
Наиболее близким к предлагаемому изобретению является способ контроля и управления динамической системы [5], заключающийся в том, что осуществляется регистрация состояния объекта, формирование выборки yi значений выходного параметра y(t), определение математического ожидания M и центральных моментов второго μ2 и четвертого μ4 порядка, формирование базы данных эталонных параметров закона распределения выходного параметра, проверку состояния объекта принадлежности области оптимального состояния, трансформация закона распределения управляемого параметра за счет изменения настроек параметра регулятора, минимизацию энтропийно-параметрического потенциала, корректировку закона распределения и формирование управляющего воздействия.
Как следует из формулы изобретения, в известном способе контроля и управления динамической системой осуществляется определение контрэксцесса и коэффициента энтропии симметричного распределения; определение энтропийно-параметрического критерия области оптимального состояния; минимизация величины энтропийно-параметрического потенциала динамической системы и корректировка реального параметра закона распределения выходного параметра.
В качестве недостатков данного способа контроля и управления динамической системой следует отметить: ограничение моделей поведения системы только набором симметричных форм распределений выходного параметра; отсутствие анализа состояния неопределенности при несимметричном распределении выходного параметра системы; отсутствие возможности анализа формы и масштаба несимметричного распределения, что не обеспечивает контроль над состоянием системы по совпадению распределения выходного параметра и целевого распределения с известными параметрами.
Краткое описание чертежей
На фигуре 1 приведена схема процесса, реализующего известный способ контроля и управления динамической системой.
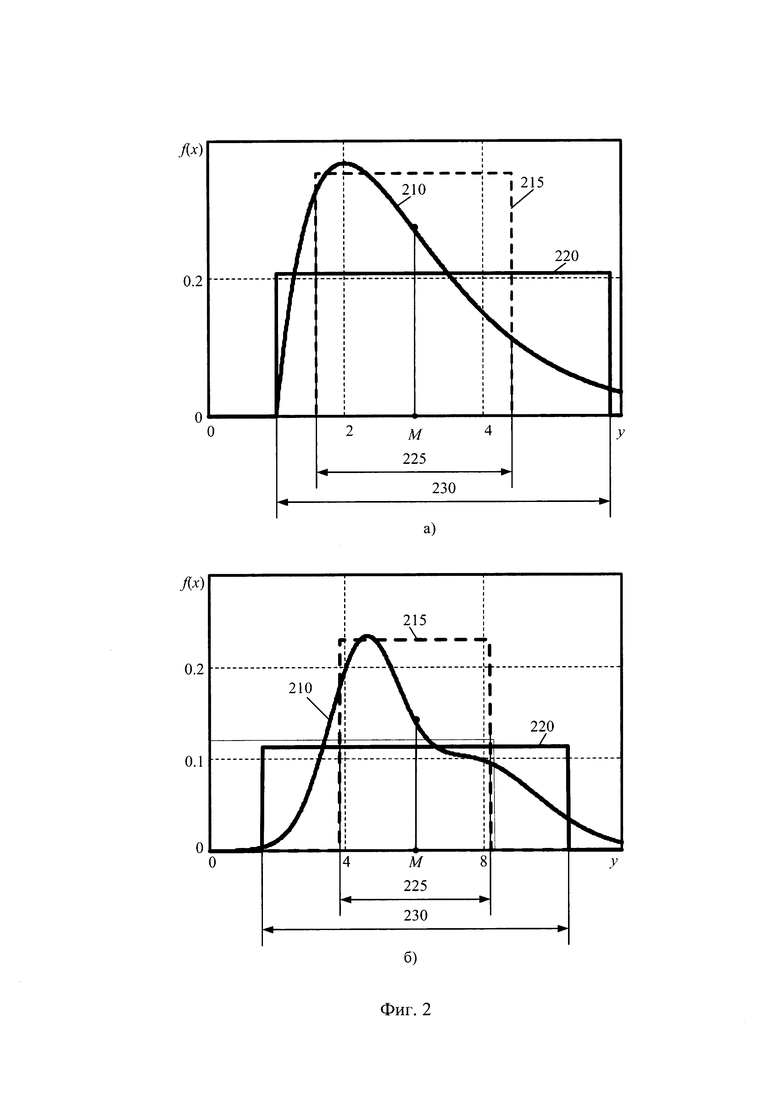
На фигуре 2 приведены чертежи неопределенностей для распределения
а) чертежи неопределенностей для несимметричного гамма распределения;
б) чертежи неопределенностей для несимметричной смеси распределений.
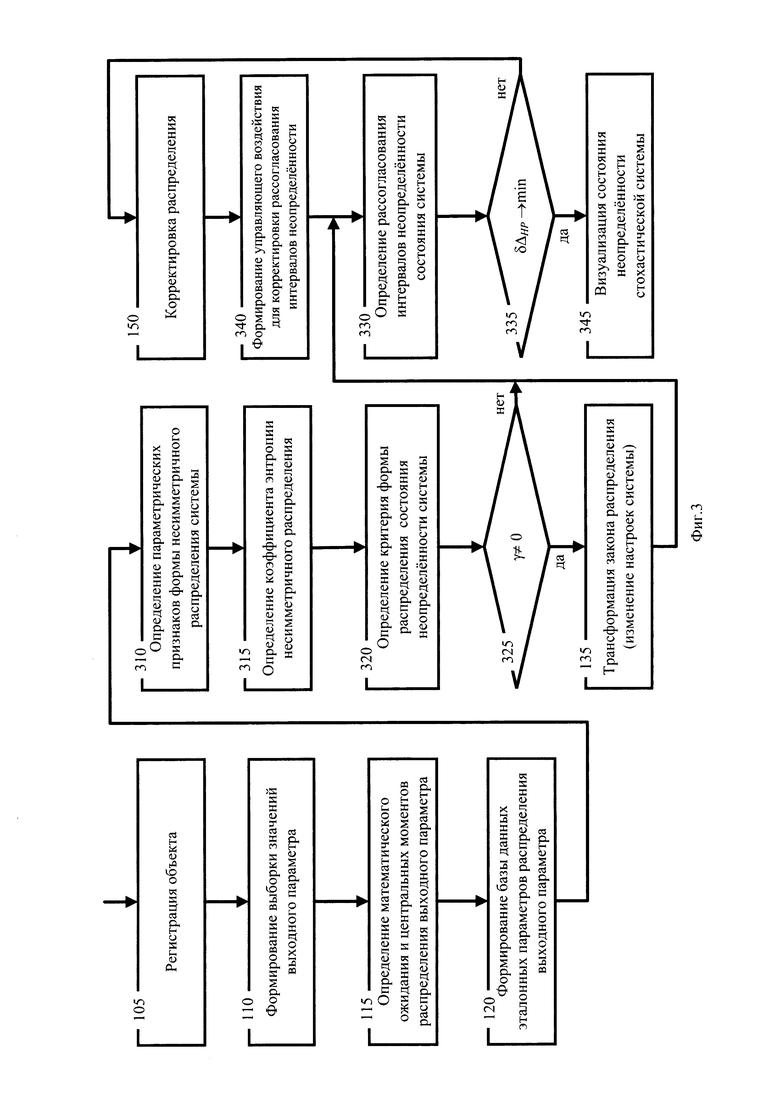
На фигуре 3 приведена схема процесса, реализующего предлагаемый способ контроля состояния стохастической системы.
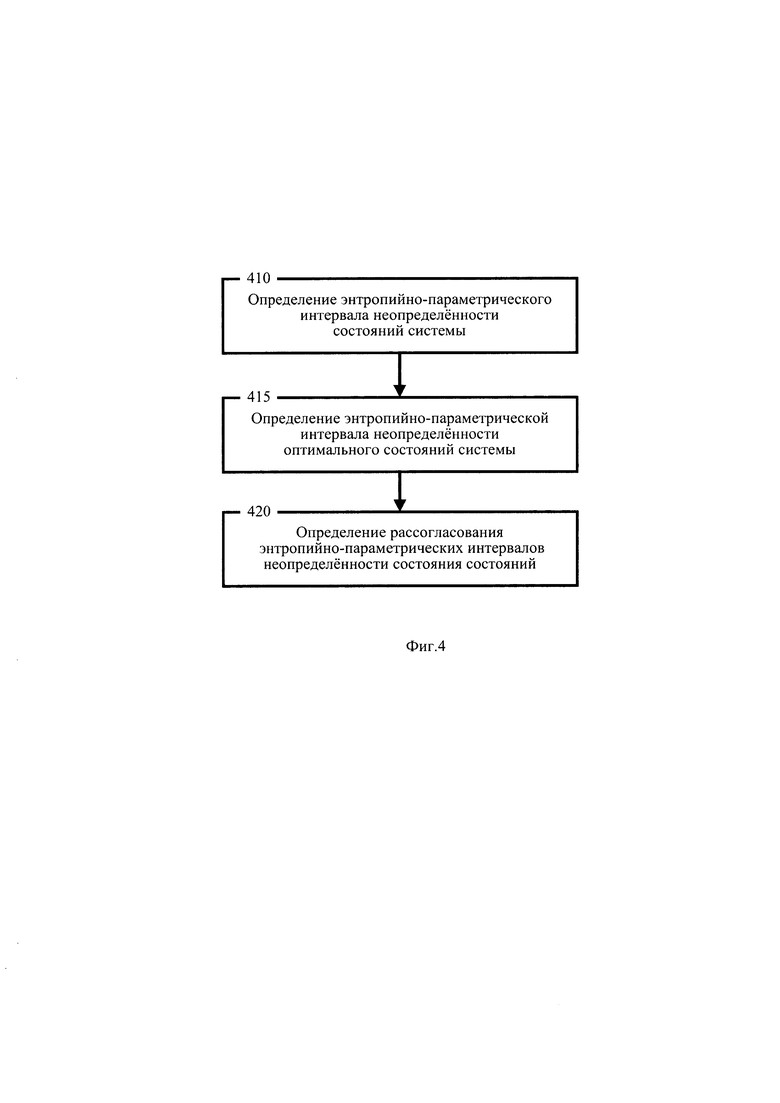
На фигуре 4 приведена схема процесса определения рассогласования неопределенности состояния системы.
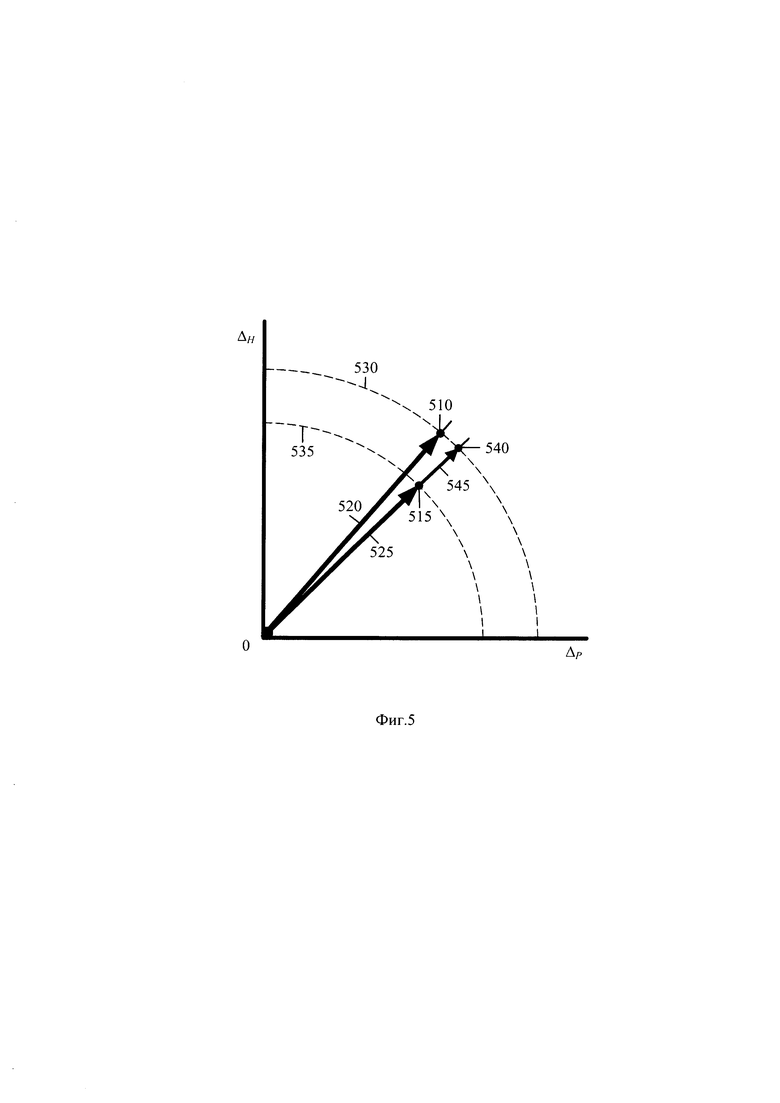
На фигуре 5 приведена диаграмма пространства энтропийной и параметрической неопределенностей состояния системы.
Материал подробного описания содержит пояснения вариантов осуществления изобретения со ссылками на чертежи, где аналогичные ссылочные позиции представляют одинаковые или подобные элементы.
Классические схемы контроля состояния неопределенности системы при известном распределении выходного параметра построены на оценке рассогласований математического ожидания, дисперсии или среднего квадратического разброса стохастического выходного параметра системы при условии, что выходной параметр распределен по нормальному закону [6].
Недостаток классических схем контроля состоит в том, что для стохастических систем характерны асимметричные не Гауссовы плотности распределения. Задача отслеживания плотности распределения для негауссовых систем может быть решена на основе контроля набора статистической информации, характеризующей рассогласование состояния системы относительно заданного целевого распределения. Контроль направлен на то, чтобы статистические параметры распределения выходного параметра системы соответствовали статистическим параметрам целевого распределения.
Известен способ контроля и управления динамической системой, основанный на минимизации энтропийно-параметрического потенциала симметричного распределения выходного параметра в пространстве признаков коэффициента энтропии и контрэксцесса.
Схема процесса на фигуре 1 иллюстрирует этапы для известного способа контроля и управления динамической системой заключающегося в том, что осуществляется регистрация состояния объекта на этапе 105; формирование выборки значений выходного параметра y(t) на этапе 110; определение параметров распределения - математического ожидания, второго и четвертого центральных моментов - на этапе 115; формирование базы данных эталонных параметров распределений выходного параметра на этапе 120; определение энтропийно-параметрического критерия области оптимального управления на этапе 125; проверку состояния объекта принадлежности области оптимального управления на этапе 130; трансформацию закона распределения на этапе 135; определение величины энтропийно-параметрического потенциала на этапе 140; минимизация величины энтропийно-параметрического потенциала на этапе 145; корректировка реальных параметров закона распределения выходного параметра на этапе 155; формирование управляющего воздействия на этапе 155; информирование об оптимальности состояния на этапе 160.
Известного способа контроля динамической системы имеет следующие недостатки.
1. Отсутствует анализа асимметрии распределения, что ограничивает возможность контроля в пространстве коэффициента энтропии и контрэксцесса только симметричных форм плотности распределения выходного параметра системы.
2. Отсутствует контроля масштаба неопределенности несимметричного распределения выходного параметра системы, так как минимизация энтропийно-параметрического потенциала направлена на уменьшение разброса среднего значения распределения выходного параметра.
3. Отсутствует возможность отслеживание и оптимизация трека распределения выходного параметра по отношению к треку целевого распределения.
Основной недостаток известного способа контроля состоит в том, что уменьшение состояния неопределенности системы путем минимизации энтропийно-параметрического потенциала реализует процесс минимизации рассогласования центра распределения в независимости от его формы и положения. При этом одинаковое положение центра распределения возможно при различных значениях формы и масштаба распределения.
Таким образом, известный способ контроля и управления, построенный на основе минимизации энтропийно-параметрического потенциала, не обеспечивает контроль формы и масштаба состояния неопределенности системы и целенаправленное изменение распределения выходного параметра к целевому распределению.
Предлагаемое изобретение направлено на обеспечение контроля состояния неопределенности стохастической системы путем контроля рассогласования интервалов энтропийной и параметрической неопределенностей несимметричного распределения выходного параметра.
По мнению автора предполагаемого изобретения, для обеспечения отслеживания распределения для негауссовых систем относительно эталонного распределения возможно посредством оценки интервалов неопределенности распределения выходного параметра, характеризующих состояние стохастической системы. Дистанции интервалов информационных и параметрических неопределенностей распределений случайных параметров пропорциональны параметру масштаба распределения. Отношение дистанций интервалов неопределенностей содержит дополнительную информацию о форме распределения. Следовательно, контроль интервалов информационных и параметрических неопределенностей распределения позволяет оценивать форму и масштаб распределения. Сравнение интервалов неопределенностей и признаков, полученных на их основе, с эталонными значениями целевого распределения позволяют контролировать и целенаправленно изменять форму и масштаб распределения выходного параметра системы для обеспечения отслеживания эталонного распределения.
Способ контроля состоянием стохастической системы основан на анализе состояния неопределенности и целенаправленном изменении распределения выходного параметра к целевому распределению стохастической системы, при котором осуществляют регистрацию выходные параметры; формирование массива значений выходного параметра yi; определение математического ожидания M, второго μ2, четвертого μ4 центральных моментов распределения выходного параметра; трансформацию закона распределения выходного параметра посредством изменения настроек системы; отличающийся тем, что осуществляют определение параметрических признаков формы асимметрии Sk, эксцесса Ex для несимметричного распределения выходного параметра системы по формулам;

где μ2, μ3, μ4 - второй, третий и четвертый центральные моменты для распределения выходного параметра определены по формуле:

здесь N - число значений в выборке выходного параметра; k - порядок центрального момента; M - математическое ожидание выходного параметра:

определение коэффициента энтропии KH для несимметричной плотности распределения входного параметра системы по формулам;

где ΔP и ΔH параметрический и энтропийный интервалы неопределенности системы:

где H(Y) - информационная энтропия массива значений выходного параметра Y, равная математическому ожиданию логарифма вероятности для массива значений Y:

определение критерия формы для области контроля состояния неопределенности стохастической системы при несимметричном распределении выходного параметра
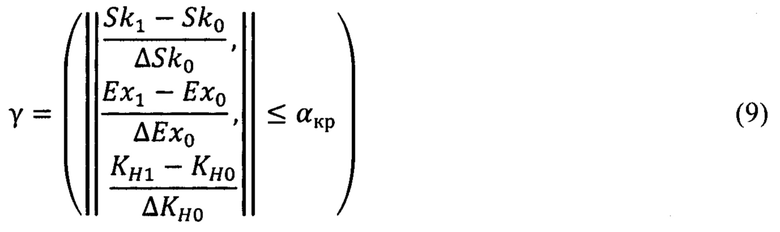
где Sk0, Ex0, KH0 - оптимальные признаки формы асимметрии, эксцесса и коэффициента энтропии для оптимального состояния неопределенности системы; ΔSk0, ΔEx0, ΔKH0 - разбросы признаков формы асимметрии, эксцесса и коэффициента энтропии относительно их оптимальных значений; αкр - критическое значение формы;
проверку принадлежности формы распределения области оптимального состояния системы, и если неравенство (3) верно при γ≠0, то выполняют трансформацию закона распределения выходного параметра посредством изменения настроек системы; и если неравенство (3) ложно при γ=0, то проводят определение рассогласования интервала неопределенности состояния системы путем
- определения энтропийно-параметрического интервала неопределенности 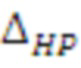 состояния системы по формуле
состояния системы по формуле

- определения энтропийно-параметрического интервала неопределенности ΔHP0 оптимального состояния стохастической системы по выражению

где ΔH0 и ΔP0 - энтропийный и параметрический интервалы неопределенности оптимального состояния;
- определения рассогласования энтропийно-параметрического интервала неопределенности стохастический системы по формуле

минимизацию рассогласования энтропийно-параметрического интервала неопределенности δΔHP стохастической системы; формирование управляющего воздействия для коррекции параметров масштабирования состояния неопределенности стохастической системы за счет изменение настроек регулятора, визуализацию состояния неопределенности стохастической системы.
Введенные действия с их связями проявляют новые свойства, расширяют функциональные возможности известного способа и позволяют обеспечить контроль состоянием неопределенности стохастической системы путем
- целенаправленного изменение распределения выходного параметра к целевому эталонному распределению системы;
- проверки формы несимметричного распределения выходного параметра;
- оценки интервалов информационных и параметрических неопределенностей для определения соответствия масштаба и формы распределения выходного параметра относительно целевого эталонного распределения;
- отслеживания рассогласования энтропийно-параметрического интервала неопределенности распределения выходного параметра относительно энтропийно-параметрического интервала неопределенности целевого распределения.
Свойства стохастической системы определены вероятностью образования множества случайных состояний. Изменение свойств системы связано с изменением вероятности наблюдаемых состояний. Состояние системы контролируют по неопределенности значений выходного параметра, для которого форма и масштаб распределения содержат информацию о состоянии системы.
Положение интервалов информационной и параметрической неопределенностей при несимметричном распределении выходного параметра иллюстрирует фигуре 2.
На фигуре 2, а несимметричное распределение выходного параметра 210 задано смещенным Гамма распределением. На фигуре 2, б несимметричное распределение выходного параметра 210 задано смесью распределений. На фигуре 2, а и на фигуре 2, б одинаковые объекты имеют одинаковые обозначения: 210 - несимметричное распределение выходного параметра; 215 и 220 - модели интервалов параметрической и энтропийной неопределенности; 225 и 230 - дистанцияи интервалов параметрической и информационной неопределенности, соответственно.
Дистанции 225 и 230 моделей параметрической 215 и информативной 220 неопределенностей независимо характеризуют состояние неопределенности стохастической системы при несимметричном распределении выходного распределения 210. Так как обе модели неопределенности зависят от масштаба распределения, то для характеристики масштаба использован энтропийно-параметрический интервал неопределенности.
В работе [5] показано, что несимметричные несмещенные распределения характеризует коэффициент энтропии несмещенного распределения, равный интервалу энтропийной неопределенности несимметричного распределения, отнесенному к корню квадратному второго начального момента несмещенного распределения. Дистанция 230 интервала энтропийной неопределенности откладывается от начала ненулевой плотности несимметричного распределения, так как квадрат дистанции 230 пропорционален второму начальному моменту несмещенного несимметричного распределения. Дистанция интервала энтропийной неопределенности для несимметричного распределения пропорциональна среднему квадратическому значению разниц значений параметра yi и смещения распределения λ. Особенность интервала энтропийной неопределенности несимметричного распределения в том, что его величина не зависит от смещения несимметричного распределения и пропорциональна масштабу распределения.
Для контроля масштаба несимметричных распределений выгодно использовать дистанцию энтропийно-параметрической неопределенности как признак масштаба распределения. Тогда оценка рассогласование масштабов распределения выходного параметра состояния системы будет пропорциональна рассогласованию интервалов энтропийно-параметрических неопределенностей этих состояний.
Таким образом, для контроля состояния неопределенности стохастической системы при несимметричном распределении выходного параметра достаточно осуществить контроль формы распределения посредством контроля признаков формы распределения и контроль масштаба распределения посредством контроля рассогласования энтропийно-параметрических интервалов.
Схемы процесса на фигуре 3 иллюстрируют новые возможности и особенности предлагаемого способа контроля состоянием неопределенности стохастической системы. Для реализации новых возможностей в предполагаемом изобретении проводятся следующие действия, иллюстрируемые в виде этапов 310, 315, 320, 325, 330, 335, 340, 345 на фигуре 3 схемы процесса контроля состояния неопределенности стохастической системы: этапа 310 определения параметрических признаков формы для несимметричного распределения этапа 315 определения коэффициента энтропии несимметричного распределения, этапа 320 определения критерия формы распределения состояния неопределенности системы, этапа 325 проверки принадлежности формы распределения области оптимального состояния, этапа 330 определения рассогласования интервала неопределенности стохастической системы, этапа 335 минимизации рассогласования интервала неопределенности стохастической системы, этапа 340 формирования управляющего воздействия для корректировки рассогласования интервала неопределенности, этапа 345 визуализации состояния неопределенности стохастической системы.
Определение параметрических признаков формы для несимметричного распределения выходного параметра системы
Первое отличительно действие, иллюстрируемое этапом 310 схемы процесса на фигуре 3, состоит в определении параметрических признаков формы несимметричного распределения системы по формулам (1) и (2), соответственно. Признаки асимметрии и эксцесса принято называть первым и вторым признаками формы вероятностных распределений, характеризующими асимметричность и островершинность распределения.
Признаки формы асимметрии и эксцесса представляют собой эффективный инструмент контроля асимметрии и островершинности как отдельных смещенных несимметричных распределений, так и различных смесей симметричных и несимметричных распределений, которые образуются в сложных стохастических системах.
Определение коэффициента энтропии для несимметричной плотности распределения выходного параметра системы.
Отношение дистанций 225 и 230 интервалов параметрической и информационной неопределенности представляют коэффициент энтропии несимметричной плотности распределения. По этой причине на этапе 315 схемы процесса на фигуре 3 проводится определение коэффициента энтропии несимметричного распределения.
Определение критерия формы распределения для области контроля состояния неопределенности стохастической системы
Отличительное действие, иллюстрируемое этапом 320 схемы процесса на фигуре 3, состоит в определении критерия формы распределения состояния неопределенности стохастической системы по формуле (3). Критерий формы, построенный на основе признаков формы асимметрии и эксцесса для несимметричной плотности распределения выходного параметра, позволяет из всего многообразия возможных несимметричных форм состояний неопределенности системы выделить формы несимметричного распределения выходного параметра, соответствующие оптимальному состоянию неопределенности системы. Критерий записан как нераверство между нормой вектора и критического значения формы αкр, выраженное Булево соотношение (9).
Значения признаков формы асимметрии Sk0, эксцесса Ex0 и значение коэффициента энтропии KH0 для оптимального состояния неопределенности системы, разбросы ΔSk0, ΔEx0 и KH0 признаков асимметрии, эксцесса и коэффициента энтропии априорно определены на основе усреднения многократного эксперимента или методом Монте-Карло для модели стохастической системы. Разброс признаков формы обусловлен как внешними случайными воздействиями, так и множеством случайно образующихся стохастических связей системы.
Проверка принадлежности формы распределения области оптимального состояния системы.
Этап 325 схемы процесса на фигуре 3 иллюстрирует проверку принадлежности формы распределения области оптимального состояния. Если критерий формы γ превышает свое максимальное значение γmax, то проводят трансформацию закона распределения выходного параметра системы посредством изменения настроек системы и ее параметров.
Определение рассогласования интервалов неопределенности состояния системы
Следующее отличительное действие, иллюстрируемое этапом 330 фигуры 3, состоит в определении рассогласования интервалов неопределенности стохастической системы. Развернутая схема процесса определения рассогласования интервалов неопределенностей состояния стохастической системы дана на фигуре 4, из которой следует, что на этапе 410 происходит определение интервалов энтропийно-параметрической неопределенности состояния системы по формулам (10). На следующем этапе 415 определяют энтропийно-параметрический интервал неопределенности оптимального состояния системы по формуле (11). Затем, на этапе 420, определение рассогласование интервалов энтропийно-параметрических неопределенностей состояний системы.
Минимизация рассогласования энтропийно-параметрического интервала неопределенности стохастической системы
Этап 335 схемы процесса на фигуре 3 иллюстрирует минимизацию рассогласования неопределенности стохастической системы путем корректироваки распределения на этапе 150 и формирования управляющего воздействия на этапе 340 для корректировки рассогласования интервалов неопределенностей системы за счет изменения настроек регулятор. Этап 345 иллюстрирует визуализацию состояния неопределенности стохастической системы посредством сигнальных индикаторов или схемы на экране дисплея.
Процесс минимизации рассогласования интервалов информационной ΔH и параметрической ΔP неопределенностей иллюстрирует диаграмма пространства энтропийной и параметрической неопределенностей состояния системы на фигуре 5, где даны следующие обозначения: 510 и 515 – положения оптимального и реального состояний неопределенностей системы; 520 и 525 – дистанции энтропийно-параметрического интервалов неопределенности оптимального и реального состояний системы; 530 и 535 – эквипотенциалы энтропийно-параметрических интервалов неопределенностей оптимального и реального состояний системы 540 - положение системы после коррекции рассогласования масштаба неопределенности; 545 - дистанция, равная рассогласованию неопределенности системы.
Положение оптимального состояний неопределенностей системы 510 определено эталонной моделью выходного параметра системы, для которого значения интервалов энтропийной и параметрической неопределенностей хранятся в базе данных эталонных параметров. Коэффициент энтропии для эталонной форма модели определяет наклон дистанции 520 энтропийно-параметрического интервала оптимального состояния. Положение 515 реального состояний неопределенностей системы определено значениями энтропийного ΔH и параметрического ΔP=(μ2)-0,5 интервалов, рассчитанных по массиву Y выборочных данных выходного параметра. Наклон дистанции 515 энтропийно-параметрического интервала неопределенности реального состояний системы определен коэффициентом энтропии реального состояния системы, который равен отношению неопределенностей (5).
Вследствие воздействия влияющих факторов положение 515 реального состояния отлично от положения 510 оптимального состояния. Дистанция 545 характеризует рассогласование интервалов энтропийно-параметрических неопределенностей оптимального и реального состояний системы. Пунктирные линии иллюстрируют эквипотенциали 530 и 535, точки которых имеют одинаковые значения энтропийно-параметрических интервалов неопределенности оптимального и реального состояний системы. Переход системы из положения 515 реального состояния в положение 540 состояние системы после коррекции рассогласования масштаба неопределенности иллюстрирует минимизацию рассогласования неопределенности стохастической системы, выполняемую на этапе 345 схемы процесса на фигуре 3. Сохранившееся рассогласование после коррекции системы, иллюстрируемое положениями 510 и 540 состояния системы, можно достичь только за счет коррекции формы системы.
В большинстве случаев состояние неопределенности стохастической системы образовано вследствие действия нескольких как независимых, так и коррелирующих причин. При влиянии различных воздействий распределение выходного параметра характеризуется смесью симметричных и несимметричных распределений.
Таким образом, проводимые действия позволяют обеспечить контроль состоянием неопределенности стохастической системы путем коррекции формы и масштаба состояния неопределенности системы и целенаправленного изменение распределения выходного параметра к целевому распределения, принятому в качестве эталона.
Литература
1. Jian-Qiao Sun, 2006, Stochastic Dynamics and Control. Monograph Series on Nonlinear Science and Complexity / Elsevier B.V. 2006. - 410 p.
2. Wang, H., 2003, Control of conditional output probability density functions for general nonlinear and non-Gaussian dynamic stochastic systems. IEE Proceedings: Control Theory and Applications 150, P. 55-60.
3. Пухликов А.В. Задачи управления распределениями в динамических системах // Автоматика и телемеханика. - 1995. - №4. - С. 77-87.
4. Пухликов А.В. Задачи управления распределениями // Нелинейная динамика и управление. ФИЗМАТЛИТ - №2, - 2010.
5. Пат. 2565367 Российская Федерация. Способ контроля и управления динамической системой / Полосин В.Г., Бодин О.Н. - заявка №2014111833/08; заявлен 27.03.2014; опубл. 20.10.15 Бюл. №29.
6. Лукас В.А. Теория управления техническими системами. - Издательство Уральского государственного горного университета. Екатеринбург. - 2005 г. - 676 с.
7. Polosin V.G., 2020, Mapping distributions in the entropy-parametric space / Journal of Physics: Conf. Ser., 1515 032044, doi:10.1088/1742-6596/1515/3/032044.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения выходного параметра | 2021 |
|
RU2758638C1 |
| Способ контроля неопределённости стохастической системы при условной оценке центра плотности распределения | 2020 |
|
RU2746904C1 |
| СПОСОБ И УСТРОЙСТВО ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЯ ПРИ ОКАЗАНИИ ЭКСТРЕННОЙ КАРДИОЛОГИЧЕСКОЙ ПОМОЩИ | 2020 |
|
RU2737860C1 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2014 |
|
RU2565367C1 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2016 |
|
RU2615286C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ АВ-БЛОКАДЫ I, II И III СТЕПЕНИ | 2015 |
|
RU2591839C1 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2005 |
|
RU2296356C1 |
| СПОСОБ ИССЛЕДОВАНИЯ ЭЛЕКТРОЭНЦЕФАЛОГРАММЫ ЧЕЛОВЕКА И ЖИВОТНЫХ | 2012 |
|
RU2543275C2 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ СОСТОЯНИЕМ НЕОПРЕДЕЛЕННОСТИ СИСТЕМЫ | 2007 |
|
RU2334262C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ | 1999 |
|
RU2168763C2 |
Изобретение относится к способам организации контроля стохастической системы и может быть использовано в системах контроля в различных отраслях промышленности. Технический результат изобретения заключается в расширении функциональных возможностей способа контроля состояния стохастической системы. Способ контроля состояния системы состоит в обеспечении отслеживания эталонного распределения за счет сравнения интервалов неопределенностей и признаков распределения с эталонными значениями целевого распределения, что позволяет контролировать и целенаправленно изменять форму и масштаб распределения выходного параметра системы. Результат достигается за счет того, что при организации контроля для зарегистрированного массива значений выходного параметра системы проводят проверку формы несимметрично распределенной смеси массива и минимизируют рассогласования энтропийно-параметрической неопределенности состояния системы путем коррекции параметров масштабирования состояния неопределенности изменением настроечных параметров регулятора. 5 ил.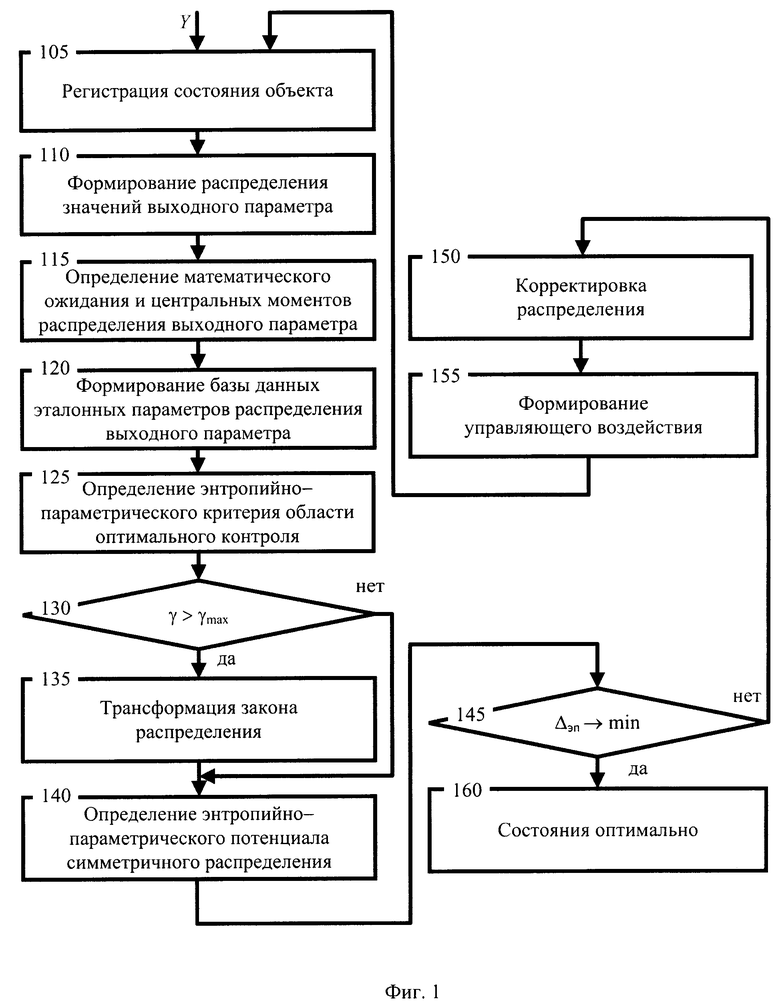
Способ контроля состояния стохастической системы, основанный на анализе состояния неопределенности и целенаправленном изменении распределения выходного параметра к целевому распределению стохастической системы, при котором осуществляют регистрацию выходных параметров; формирование массива значений выходного параметра yi; определение математического ожидания M, второго μ2, четвертого μ4 центральных моментов распределения выходного параметра; трансформацию закона распределения выходного параметра посредством изменения настроек системы; отличающийся тем, что осуществляют:
определение параметрических признаков формы асимметрии Sk, эксцесса Ex для несимметричного распределения выходного параметра системы по формулам
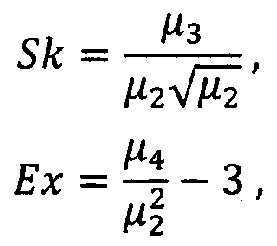
где μ2, μ3, μ4 - второй, третий и четвертый центральные моменты для распределения выходного параметра, которые определены по формуле
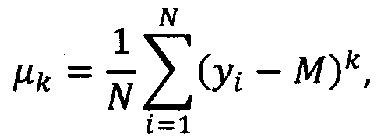
где N - число значений в выборке выходного параметра; k - порядок центрального момента; M - математическое ожидание выходного параметра
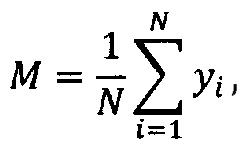
определение коэффициента энтропии KH для несимметричной плотности распределения входного параметра системы по формулам
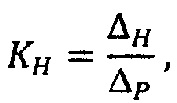
где ΔP и ΔH параметрический и энтропийный интервалы неопределенности системы
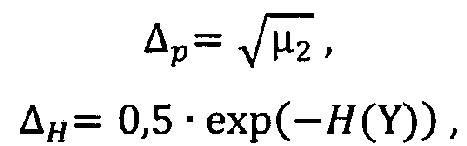
где H(Y) - информационная энтропия массива значений выходного параметра Y, равная математическому ожиданию логарифма вероятности для массива значений Y,
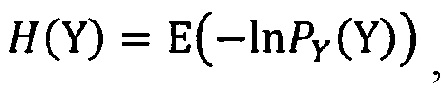
определение критерия формы для области контроля состояния неопределенности стохастической системы при несимметричном распределении выходного параметра
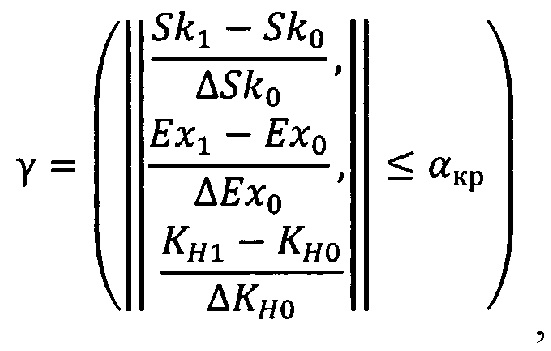
где Sk0, Ex0, KH0 - оптимальные признаки формы асимметрии, эксцесса и коэффициента энтропии для оптимального состояния неопределенности системы; ΔSk0, ΔEx0, ΔKH0 - разбросы признаков формы асимметрии, эксцесса и коэффициента энтропии относительно их оптимальных значений; αкр - критическое значение формы;
проверку принадлежности формы распределения области оптимального состояния системы, и если неравенство (130) верно при γ≠0, то выполняют трансформацию закона распределения выходного параметра посредством изменения настроек системы; и если неравенство (130) ложно при γ=0, то проводят определение рассогласования интервалов неопределенности состояния системы путем
- определения энтропийно-параметрического интервала неопределенности ΔHP состояния системы по формуле
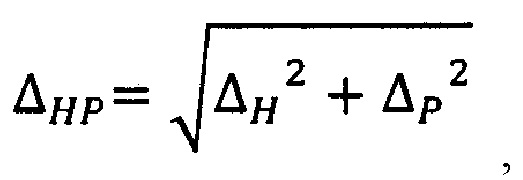
- определения энтропийно-параметрического интервала неопределенности ΔHP0 оптимального состояния стохастической системы по выражению
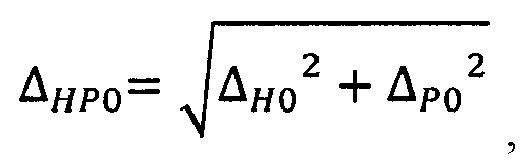
где ΔH0 и ΔP0 - энтропийный и параметрический интервалы неопределенности оптимального состояния;
- определения рассогласования энтропийно-параметрического интервала неопределенности стохастический системы по формуле
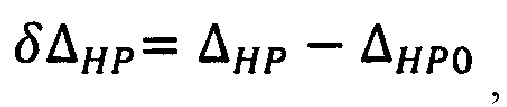
минимизацию рассогласования энтропийно-параметрического интервала неопределенности δΔHP стохастической системы; формирование управляющего воздействия для коррекции параметров масштабирования состояния неопределенности стохастической системы за счет изменения настроек регулятора, визуализацию состояния неопределенности стохастической системы.
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2005 |
|
RU2296356C1 |
| СПОСОБ АВТОМАТИЧЕСКОЙ НАСТРОЙКИ МНОГОПАРАМЕТРИЧЕСКИХ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НА ОПТИМАЛЬНЫЕ УСЛОВИЯ | 2000 |
|
RU2189067C2 |
| СПОСОБ СБОРА ИНФОРМАЦИИ ОБ ЭКОЛОГИЧЕСКОМ СОСТОЯНИИ РЕГИОНА И АВТОМАТИЗИРОВАННАЯ СИСТЕМА АВАРИЙНОГО И ЭКОЛОГИЧЕСКОГО МОНИТОРИНГА ОКРУЖАЮЩЕЙ СРЕДЫ РЕГИОНА | 2010 |
|
RU2443001C1 |
| US 6532454 B1, 11.03.2003. | |||
Авторы
Даты
2021-03-01—Публикация
2020-05-26—Подача