Настоящее изобретение относится к технологии сушки и термовлажностной обработки пористых проницаемых (например, текстильных, теплоизоляционных, пищевых изделий, дисперсных) материалов, в том числе в текстильной, легкой, пищевой отраслях промышленности, в производстве и использовании строительных материалов.
Известен метод исследования термовлажностных процессов, при котором главные показатели процессов тепло- и влагопереноса, а именно - коэффициенты теплопроводности λ и массопроводности λm определяют экспериментально на основе традиционных общепринятых уравнений феноменологической термодинамики, в частности - уравнения Фурье для переноса теплоты и уравнения Фика для переноса массы [1-3].
Недостатком многочисленных разновидностей известных методов является сам факт обязательного эксперимента и связанных с ним трудностей, в частности сложность, а порой и невозможность измерения потенциалов (температуры, парциального давления паров влаги, концентраций и др.), низкая точность этих измерений на мягких пористых, ворсистых и т.п. поверхностях тел.
Техническим результатом предлагаемого способа является упрощение процесса определения коэффициентов тепло- и массопроводности, а также обеспечение получения точных и однозначных результатов измерения указанных параметров.
Этот результат достигается тем, что в способе определения указанных теплофизических величин, входящих в кинетические законы тепло- и массопереноса, а именно: объемной плотности, удельной теплоемкости, массоемкости, движущей силы процесса (разности потенциалов - температур или парциальных давлений паров влаги), геометрических параметров, согласно изобретению одновременно использованы фундаментальные константы переноса - постоянные Планка и Больцмана, а также параметры механизма макроквантования, вытекающие из предложенной физической модели переноса теплоты и массы, а именно: коэффициент релаксации, дискрет времени, квант энергии, параметры макроячейки, при этом физическая модель представляет собой систему элементарных объемов условно шарообразной формы (макроячеек), функционирующую под воздействием движущей силы (разности температур ΔT или парциального давления паров влаги ΔP) в дискретно-пульсирующем режиме генерирования энергетических импульсов и формирующих тем самым поля температур и (или) влагосодержаний.
Иными словами, процесс переноса субстанций, в частности теплоты и влаги, рассматривается на основе механизма макроквантования термодинамических параметров [4] и концепции субстанциональности энергии [5, 6], т.е. соединения физических основ квантовой механики и феноменологической термодинамики. В результате процесс генерации энергии, происходящий на микроуровне, переносится на уровень макроквантовой механики [7]. На основе предлагаемой физической модели переноса стало возможным получить необходимые расчетные квантово-термодинамические уравнения, включающие фундаментальные общепризнанные константы Планка и Больцмана. Благодаря выполнению расчетных процедур на наноуровне обеспечивается высокая точность коэффициентов тепло- и массопереноса, а соответственно, повышается общая точность расчетов проектируемых изделий.
Физические основы способа, вкратце, заключаются в следующем. Основываемся на активно развивающемся в настоящее время переходе от традиционной механики сплошной среды и равновесной термодинамики к расширенному («нелокальному») подходу, при котором традиционные термодинамические функции соединяются со временем передачи импульса энергии («дискрет времени») Δτ, c [4]. Вводится гипотеза о квантовании энергии с квантом, равным постоянной Больцмана k=1,38·10-23 Дж/K. Эта гипотеза позволяет ввести элементарную термодинамическую энергию ΔE=kT. Далее используют два соотношения неопределенностей квантовой механики, записанные со знаком равенства, т.е. для условия термодинамического равновесия:


где ħ=1,055·10-34 Дж·с - постоянная Планка, характеризующая «разрешенный» дискрет энергии (деленная на 2π); Δp, Δx - неопределенности импульса и координаты.
Из соотношения (1) определяют универсальный минимальный макроскопический масштаб времени (дискрет), зависящий только от температуры:

например, при T=300 K Δτ=1,27·10-14 с.
Энергии kT соответствует элементарная масса Δm=kT/c2 - квант коллективного возбуждения (виртуальный фотон); c≈3·108 м/с - фундаментальная скорость (скорость света).
Радиус и объем возбуждения в среде за характерное время Дт составляют:
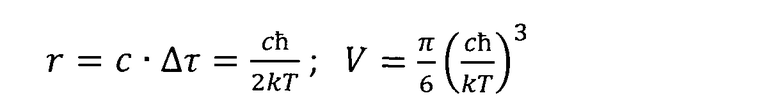
Объем V, полученный с использованием минимальных величин ΔE и Δτ, по физическому смыслу является минимальным макроскопическим (максимальным микроскопическим) объемом. Область пространства, ограниченная этим объемом, получила название макроячейки. Макроячейку можно рассматривать как короткоживущий (мерцающий) физический кластер, своеобразный надмолекулярный уровень иерархии макроскопической системы.
В макроквантовом подходе принимается, что использование объема V и других полученных параметров в соотношениях термодинамики позволяет произвести замену дифференциально малых величин конечными, физически предельно малыми величинами. Последние трактуются как неопределенности или макроквантовые флуктуации макроскопических параметров.
Процессы внутри макроячейки в рамках данного подхода относятся к микроскопическим и детально не описываются.
В результате макроквантовых флуктуаций параметры макроячейки за характерное время Δτ отличаются от параметров окружения и в этом смысле любая равновесная материальная среда неоднородна. Такого рода неоднородность приводит к появлению на границе макроячейки с окружающими частицами флуктуирующих напряжений и вызывает объемную, а также сдвиговую деформацию приповерхностного объема макроячейки. Последние существуют не одновременно, а с характерным пространственным и временным сдвигом. Деформации приводят к появлению локальных потенциалов (температуры, влагосодержания, электрического потенциала и др.), соответствующих полей и потоков энергии.
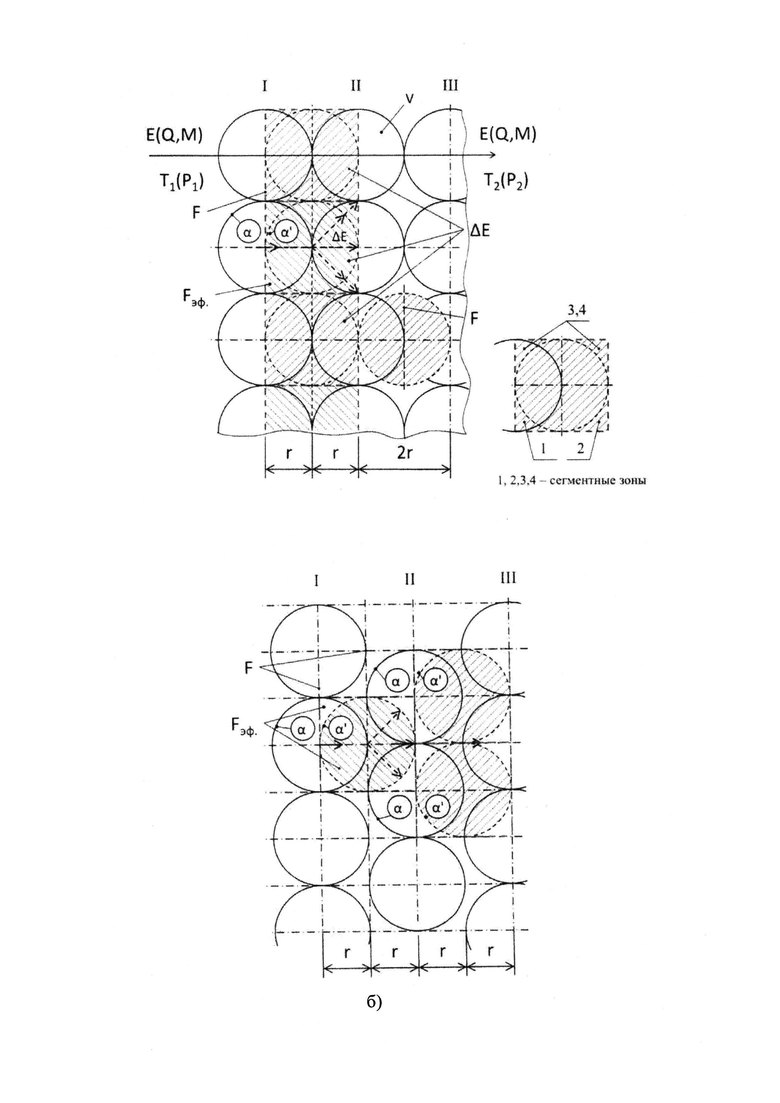
В соответствии с изложенными физическими основами можно представить геометрическую картину системы макроячеек. На рис. 1a, б, в показаны некоторые возможные варианты взаимного расположения и взаимодействия макроячеек, что позволяет получить принципиальное понимание механизма переноса энергетического импульса и, как следствие, соответствующей субстанции - теплоты или массы влаги, в зависимости от движущей силы - разности температур ДТ или разности паров влаги ДР. На рис. 1a, б представлены крайние случаи: а) - когда удар частиц предыдущего слоя I с последующим II приводит к их деформации; б) - удар при касании; рис. 1 в показывает некоторый промежуточный вариант. Во всей случаях принимаем, в качестве допущения, величину перемещения каждой макроячейки - ее радиус r.
В материале конгломерат макроячеек фактически образует систему сплошных единичных стенок, поэтому в практических инженерных расчетах можно оперировать понятием элементарного участка переноса (ЭУП). При этом ряд макроячеек I, работая в дискретно-пульсирующем режиме, передает консолидированный энергетический импульс ΔE смежному слою (участку) II на границе между ними поверхностью F, где F=π·r2 - площадь поперечного сечения условно шарообразной макроячейки (фотонный механизм). То же происходит и на последующих участках. Одновременно, в связи с флуктуациями макроячеек, реализуется фононный механизм переноса и рассеивания энергии, что обусловливает, объясняет и дает возможность количественно оценить соответствующий уровень диссипации [1, 3].
Величина результирующего энергетического импульса на границах участков F будет меняться, что будет выражаться соответствующим изменением температуры и количества массы. Поэтому при выполнении конкретного расчета, определяя количество переносимой энергии (количества теплоты, массы и др.) от одной границы к другой, следует брать усредненные параметры за период полуцикла переноса в пределах каждого элементарного слоя или ЭУП, т.е. по границам F.
Покажем, как получено уравнение для расчета коэффициента теплопроводности материала на основе предложенного способа - «макроквантового термодинамического метода» (МКТМ). Исходили из известного уравнения энергетического баланса с источниковым членом [1, 3], в которое вводили, в соответствии с принятой физической моделью процесса, коэффициент релаксации Kr, выражающий степень динамической активности макроячейки:

где divE - плотность потока тепловой энергии единицы элементарного объема, Дж/(м3·K); ρ - объемная плотность материала кг/м3; cp - удельная теплоемкость, Дж/(кг·K); 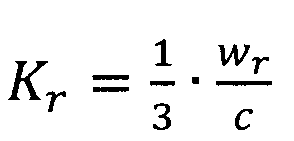 - коэффициент релаксации; wr - ассоциированная скорость частиц макроячейки, м/с; c=3·108 м/с - скорость света.
- коэффициент релаксации; wr - ассоциированная скорость частиц макроячейки, м/с; c=3·108 м/с - скорость света.
Термодинамический цикл макроячейки (ТЦМ) в квантовой физике рассматривается как квантово-термодинамический круговой процесс динамического равновесия. Другими словами - как термодинамический цикл с включением в него электрических и магнитных воздействий. Среди параметров, характеризующих ТЦМ, объем макроячейки V выступает как интенсивный параметр, поскольку определяется только температурой. Макроячейку в состоянии динамического равновесия можно считать объемным резонатором с хорошо проводящей внешней оболочкой, внутри которой существуют свободные электромагнитные колебания. Электрическая емкость и индуктивность резонатора известны. Используя эти соотношения, определяли выделяемое элементарное количество теплоты в контуре ΔQ=2kT, которое в условиях равновесия интерпретируется как теплота Томпсона. В целом же количество тепловой энергии
 генерируемое макроячейкой, представляет собой производство теплоты Томпсона в единице объема.
генерируемое макроячейкой, представляет собой производство теплоты Томпсона в единице объема.
Имея в виду, что тепловой поток имеет электромагнитную природу, это и позволяет рассматривать его как поток электромагнитной энергии равновесного когерентного излучения, генерируемого макроячейкой, т.е. рассматривать его как макроскопический квантовый эффект. Выражение (5) берет свое начало от уравнения Пойнтинга для плотности потока равновесного излучения, записанного в предельно-разностной форме:

где 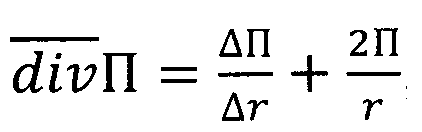 ; П - равновесная плотность потока электромагнитного излучения (вектор Пойнтинга).
; П - равновесная плотность потока электромагнитного излучения (вектор Пойнтинга).
В подобной записи все конечные приращения подразумеваются физически элементарными. Баланс электромагнитной энергии (6) также справедлив и по отношению к объему макроячейки. Поэтому здесь Δr - макроскопически элементарный радиус электромагнитного возбуждения: Δr=r=c·Δτ, т.е. это изменение, аналогичное вектору Пойнтинга П=ΔП. Вместе с тем, для минимального приращения плотности внутренней энергии принимают ΔU=-kT. Знак минус обусловлен тем, что вектор Пойтинга имеет направление фундаментальной скорости c, т.е. так же, как и радиус-вектор r. Следовательно, работа электромагнитной энергии совершается над окружением макроячейки и ее внутренняя энергия убывает. Таким образом, из баланса (6) следует равновесная плотность потока электромагнитного излучения
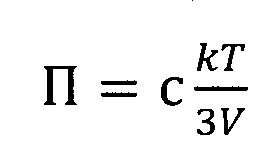 ,
,
а средняя термодинамическая плотность энергии равновесного когерентного излучения макроячейки составляет:
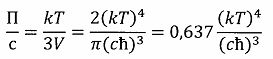
Плотность потока тепловой энергии в (4) можно записать в следующем виде:

Одним из приемов механизма макроквантования является переход от дифференциальной формы записи к предельно-разностной. Тогда, соединяя (4), (5), (7), получим:
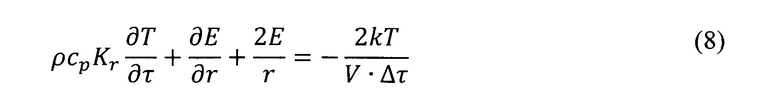
Очевидно, что плотность потока энергии E для макроячейки, как для минимального термодинамического объема в равновесных условиях будет минимально возможной макроскопически, т.е. элементарной, тогда E≈ΔE. Учтем также, что радиус макроячейки r много больше его элементарного приращения: r>>Δr. Получается, что в выражении (8) 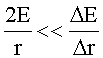
Учитывая изложенные соображения, выражение (8) принимает вид:
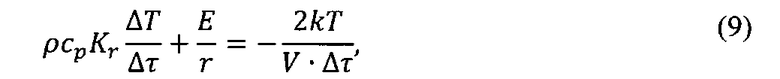
Коэффициент теплопроводности по определению:
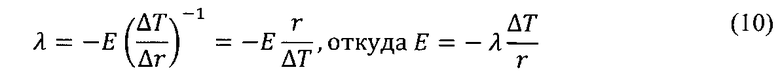
Выполним преобразования уравнения (9) с учетом (10):
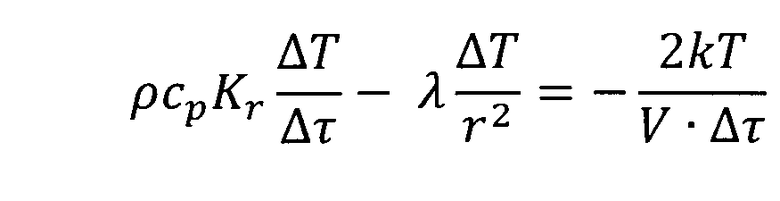 ;
; 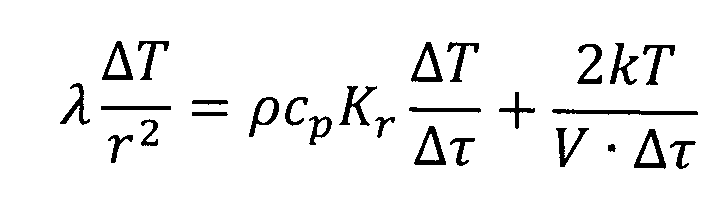 ;
;
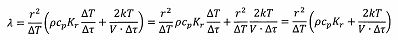
Дискрет времени целесообразно раскрыть через его содержание: 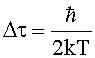
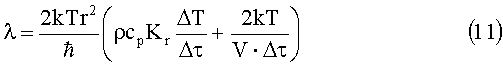
При переходе от макроячейки к ЭУП, когда происходит суммарное воздействие макроячеек и, как следствие, интегральная аккумуляция теплоты как энергетической субстанции, объем V трансформируется в произведение площади поперечного сечения ячейки F на величину ее перемещения r при генерации энергетического импульса (фотона). Таким образом, появляется возможность определить внутреннюю эффективную (смачиваемую) поверхность материала Fэф, найти которую экспериментально с достаточной точностью не представляется возможным. Однако следует отметить, что между величинами V и Fr существует разница порядка 25%, обусловленная: а) различием геометрической формы; б) влиянием плотности и температуры на объем макроячейки. Эти факторы неизбежно отразятся на расчетной величине λ, а соответственно и Fэф. Были введены соответствующие корректирующие коэффициенты: а) объемный форм-фактор, корректирующий объем макроячейки - kV; б) температурный - kT=Tэкс/Т0, где Тэкс - температура материала в условиях эксперимента, K; Т0=273K - эталонная температура. Тогда
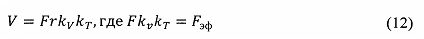
Коэффициент kV найден путем анализа и обобщения всего изученного массива экспериментальных данных.
С учетом изложенных соображений уравнение (11) принимает окончательный вид:
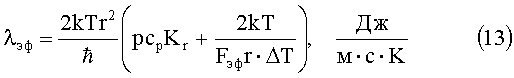
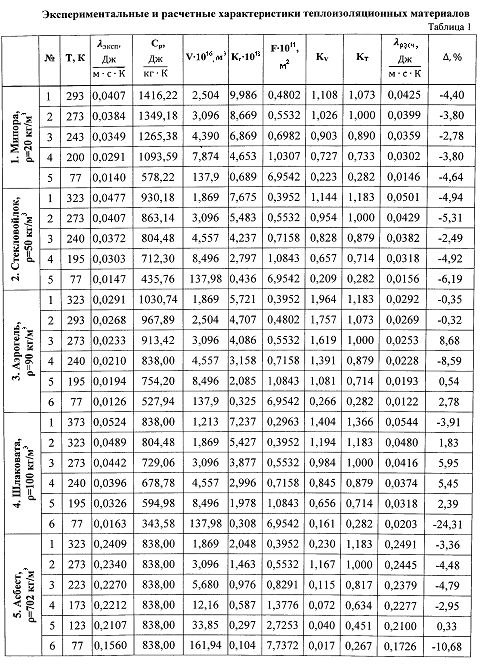
Для проверки полученного макроквантового (квантово-термодинамического) уравнения (13) используем надежные, многократно проверенные известные экспериментальные данные для теплоизоляционных материалов [10], приведенные в таблице 1. Данные подобраны таким образом, чтобы можно было проанализировать влияние параметров в достаточно широком диапазоне: температуры T=323…73 K, плотности ρ=15…800 кг/м3, теплоемкости cp=250…2000 Дж/(кг·K), температуропроводности a=0,024…0,142 м2/с. Остальные величины в табл. 1 - расчетные, на основе соотношений механизма макроквантования. Коэффициент теплопроводности λрасч - по уравнению (13).
Выполним контрольный расчет коэффициента теплопроводности для материала №19: шлаковата, T=273 K; λэкс=0,0442 Дж/(м·с·K); ρ=100 кг/м3, cp=729,06 Дж/(кг·K); ρcp=72,906·103 Дж/(м3·K); kV=0,984; kT=1.
Объем макроячейки:
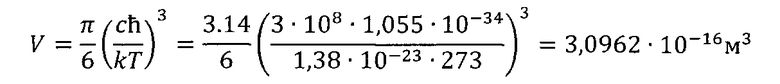
Радиус макроячейки:
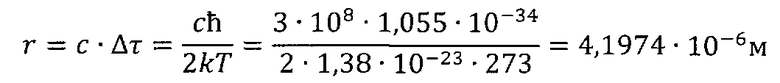
Масса макроячейки:
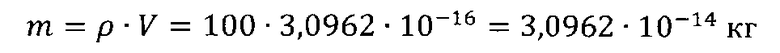
Ассоциированная скорость частиц макроячейки:
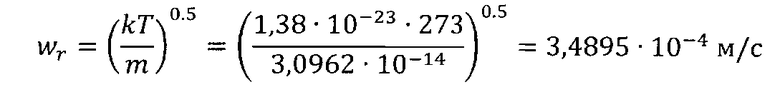
Коэффициент релаксации:
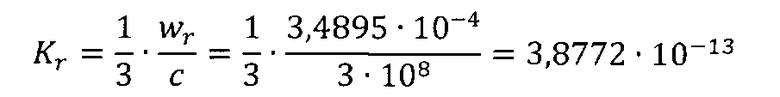
Площадь поперечного сечения макроячейки:
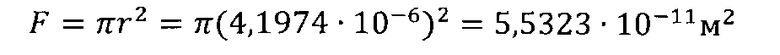
Значение комплексов формулы (13):
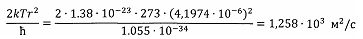 ;
;
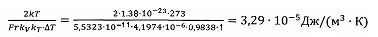 ;
;
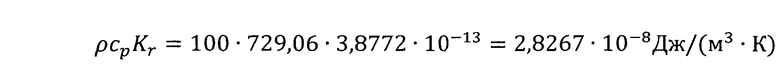 ;
;
Эффективная поверхность Fэф=FkVkT=5,5323·10-11·0,984·1=5,4427·10-11 м2
Расчетное значение коэффициента теплопроводности по уравнению (13):
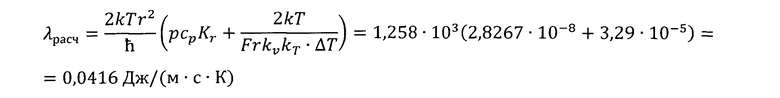
Сравним полученное расчетное значение с экспериментальным:
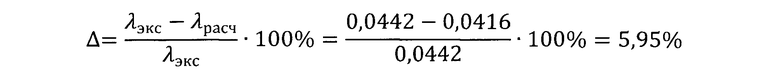
Корреспондирование результата по λэф вполне удовлетворительное.
Квантово-термодинамическое уравнение для определения эффективного коэффициента массопроводности получено также на основе изложенной физической модели и баланса энергии с источниковым членом [3], но записанного для условий генерирования массового однородного потока элементарным объемом (макроячейкой):
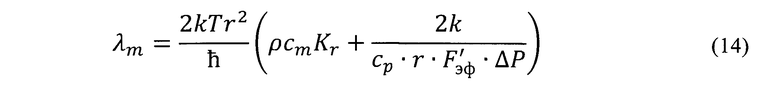
Пример расчета коэффициента массопроводности для кожи хромового дубления для верха обуви. Результаты экспериментального исследования изложены в работах [8, 9].
Радиус макроячейки
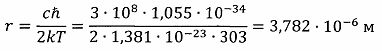
Объем макроячейки
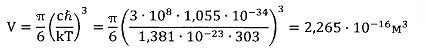
Ассоциированная скорость частиц макроячейки

Коэффициент релаксации
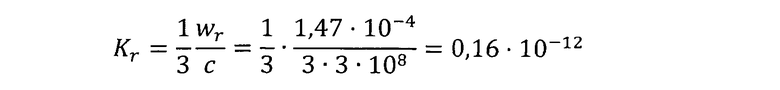
Расчетное значение коэффициента массопроводности по уравнению (14)
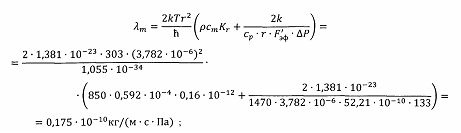
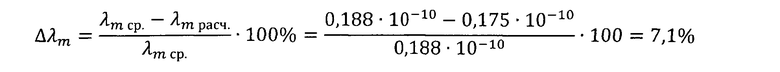
Корреспондирование значений по λm вполне удовлетворительное.
Источники информации
1. Вукалович М.П., Новиков И.И. Термодинамика. - М.: Машиностроение, 1972. - 672 с.
2. Касаткин А.Г. Основные процессы и аппараты химической технологии // Изд. 8е перераб. - М.: Химия, 1971. - 784 с.
3. Лыков А.В. Тепломассообмен // Справочник. - М.: Энергия, 1972. - 560 с.
4. Майков В.П. Расширенная версия классической термодинамики - физика дискретного пространства-времени. - М.: Изд. МГУИЭ, 1997. - 160 с.
5. Планк М. Принцип сохранения энергии // Пер. с нем. - М.: Гостехтеориздат, 1938. - 235 с.
6. Умов Н.А. Уравнения движения энергии в телах // Избр. соч. - М.: Гостехтеориздат, 1950, с. 151-200.
7. Schrödinger Е. Непрерывный переход от микро- к макромеханике. - Naturwiss, 1926, Bd. 14. - S. 664.
8. Чесунов В.М., Захарова А.А. Оптимизация процессов сушки в легкой промышленности. - М.: Легпромиздат, 1985. - 112 с.
9. Старосвитский О.И., Чесунов В.М. и др. Приближенный коэффициент влагопроводности и удельная влагоемкость кож. - Известия вузов. Технология легкой промышленности, №3, 1979, с. 47-50.
10. Малков М.П., Данилов И.Б., Зельдович А.Г., Фрадков А.Б. Справочник по физико-техническим основам глубокого охлаждения // Под ред. М.П. Малкова. - М.: Госэнергоиздат, 1963. - 416 с.
11. Физические величины. Справочник. - М.: Энергоатомиздат, 1991. - 1232 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА МАССОПРОВОДНОСТИ ПОРИСТЫХ ПРОНИЦАЕМЫХ МАТЕРИАЛОВ | 2011 |
|
RU2505796C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА МАССООТДАЧИ ПОРИСТЫХ ПРОНИЦАЕМЫХ МАТЕРИАЛОВ | 2014 |
|
RU2566726C1 |
| ЭЛЕМЕНТАРНЫЙ ЭЛЕМЕНТ | 2014 |
|
RU2696344C2 |
| ФОТОКАТОД | 2013 |
|
RU2542334C2 |
| МУЛЬТИБАРЬЕРНАЯ ГЕТЕРОСТРУКТУРА ДЛЯ ГЕНЕРАЦИИ МОЩНОГО ЭЛЕКТРОМАГНИТНОГО ИЗЛУЧЕНИЯ СУБ- И ТЕРАГЕРЦОВОГО ДИАПАЗОНОВ | 2012 |
|
RU2499339C1 |
| УСТРОЙСТВО ОБРАБОТКИ ЖИДКОГО УГЛЕВОДОРОДНОГО ТОПЛИВА ДЛЯ ИЗМЕНЕНИЯ ЕГО ГРУППОВОГО И ФРАКЦИОННОГО СОСТАВА ПОД ВОЗДЕЙСТВИЕМ ЭЛЕКТРИЧЕСКОГО ПОЛЯ (ВАРИАНТЫ) | 2015 |
|
RU2614562C2 |
| СПОСОБ ПОЛУЧЕНИЯ РЕЛЬЕФА НА ПОВЕРХНОСТИ | 2013 |
|
RU2546719C1 |
| СПОСОБ ПРЕОБРАЗОВАНИЯ ЭНЕРГИИ В ТЕПЛОВОЙ ПОТОЧНОЙ МАШИНЕ | 2002 |
|
RU2239072C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ПОЛИМЕРОВ | 2000 |
|
RU2180440C2 |
| СПОСОБ ИЗМЕРЕНИЯ ЭНЕРГИИ МЕЖАТОМНЫХ И МЕЖМОЛЕКУЛЯРНЫХ ВЗАИМОДЕЙСТВИЙ И КООРДИНАЦИОННОГО ЧИСЛА АТОМНЫХ И МОЛЕКУЛЯРНЫХ ВЕЩЕСТВ | 2005 |
|
RU2287153C2 |

Изобретение относится к технологиям сушки и термовлажностной обработки пористых проницаемых материалов, в частности к способам определения коэффициентов тепло- и массопроводности пористых материалов. Данный способ заключается в определении значений физических констант (объемной плотности, удельной теплоемкости, массоемкости), разности температур или парциальных давлений, определении внутренней эффективной поверхности переноса субстанций (теплоты, влаги) и расчете коэффициентов тепло- и массопроводности по квантово-термодинамическим уравнениям, полученным аналитическим путем. Техническим результатом изобретения является упрощение процесса определения коэффициентов тепло- и массопроводности, а также обеспечение получения точных и однозначных результатов измерения указанных параметров. 4 ил., 1 табл.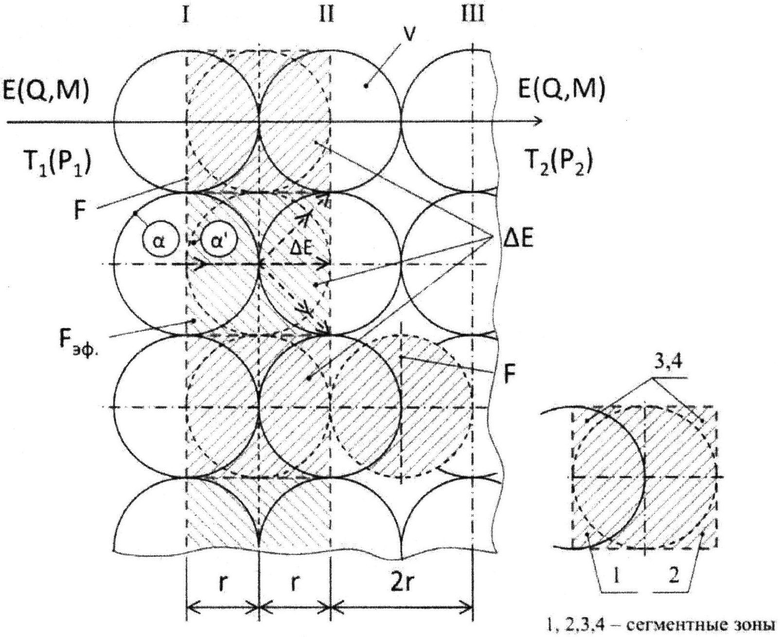
Способ определения эффективных коэффициентов тепло- и массопроводности пористых материалов на основе макроквантового механизма переноса субстанций (теплоты и влаги), заключающийся в: определении физконстант (объемной плотности, удельной теплоемкости, массоемкости), движущей силы процесса (разности потенциалов - температур или парциальных давлений паров влаги); определении внутренней эффективной поверхности переноса субстанций (теплоты, влаги); расчете параметров механизма макроквантования (коэффициента релаксации, дискреты времени, параметров макроячейки) с использованием фундаментальных констант Планка и Больцмана по формулам:
- коэффициент теплопроводности
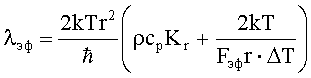
- коэффициент массопроводности
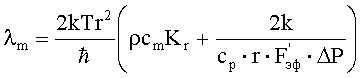
где ħ=1,055·10-34 Дж·с - приведенная константа Планка;
k=1,381·10-23 Дж/К - постоянная Больцмана;
T - температура, K;
r - радиус макроячейки, м;
c≈3·108 м/с - скорость света;
V - объем макроячейки, м3;
ρ - объемная плотность материала, кг/м3;
cp - удельная теплоемкость материала, Дж/(кг·К);
cm - удельная массоемкость материала, кг/(кг·Па);
Kr - коэффициент релаксации макроячейки;
Fэф, 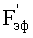
F - площадь поперечного сечения макроячейки, м2;
kV - объемный форм-фактор макроячейки;
kT - температурный коэффициент;
ΔP - разность паров влаги, ΔP = 1 мм рт.ст. ≈133 Па
ΔT - разность температур.
| СПОСОБ ИДЕНТИФИКАЦИИ КОМПЛЕКСА ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ТВЕРДЫХ МАТЕРИАЛОВ | 2004 |
|
RU2263306C1 |
| Способ определения коэффициента теплопроводности тонких труб и стержней | 1990 |
|
SU1782320A3 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ТЕПЛОФИЗИЧЕСКИХ ХАРАКТЕРИСТИК ДИСПЕРСНЫХ ПИЩЕВЫХ ПРОДУКТОВ | 2008 |
|
RU2378957C2 |
| Русская печь | 1944 |
|
SU75748A1 |
| СПОСОБ БЕСКОНТАКТНОГО НЕРАЗРУШАЮЩЕГО КОНТРОЛЯ ТЕПЛОФИЗИЧЕСКИХ СВОЙСТВ МАТЕРИАЛОВ | 2001 |
|
RU2208778C2 |
| Сплав на медной основе для изготовления радиаторных трубок | 1944 |
|
SU66055A1 |
Авторы
Даты
2016-05-27—Публикация
2014-06-27—Подача