Область техники, к которой относится изобретение
Изобретение относится к моделированию импульсных нейронов в качестве элемента нейронных сетей, к нейрокибернетике и может найти применение при разработке нейрокомпьютеров, технических систем на основе нейронных сетей, для распознания образов, анализа и обработки изображений и многих других приложений. Области применения предлагаемого изобретения также: робототехника, нейроморфные нейрочипы, общение на основе нейротехнологий, медицинские протезы органов человека и отдельных систем мозга.
В настоящее время известны нейронные сети «трех поколений». Первое поколение это нейронные сети использующие нейроны МакКаллока-Питтса. Входными сигналами являются бинарные последовательности из 0 и 1. Их основная область применения -распознавание объектов. Обучение распознаванию объектов основывается на соответствующем подборе весовых коэффициентов. Эти ИНС не пригодны для описания динамики процессов в нейронных сетях.
Второе поколение это нейронные сети, описываемые нелинейными дифференциальными уравнениями и другими уравнениями, описывающими нелинейную динамику. Эти уравнения описывают динамику процессов в нейронных сетях, однако, они мало пригодны для решения основной задачи нейронных сетей - распознавание входных объектов.
Третье поколение нейронных сетей это нейронные сети более близкие реальным биологическим, в которых в качестве входных сигналов используются импульсные последовательности (ИП). Эти нейронные сети обладают более широкими возможностями. Перечислим эти возможности:
1) Импульсные последовательности НС могут быстро распространяться по нейронным сетям (нервам) на любое расстояние в теле животного или человека;
2) Способны распознавать входные объекты также как и нейронные сети, основанные на бинарных входных сигналах с нейронами МакКаллока-Питтса;
3) Способны оценивать интенсивность входных объектов;
4) Они достаточно помехоустойчивы и надежны. Установлено, что в импульсных нейронных сетях реализуются специфические методы кодирования информации, обеспечивающие совокупность свойств по пунктам 1-4.
Кодирование импульсных последовательностей используется в следующих областях: 1) в технических системах - радиоэлектронике, телевидении, компьютерной технике; 2) в робототехнике, взаимодействии субъектов, использующих нейротехнологий, медицинских протезах органов - зрения, слуха и других; 3) в нейрофизиологии, нервной системе человека, животных, где кодирование импульсной последовательности является основным механизмом обработки информации. В робототехнике, устройствах, использующих нейротехнологий импульсных последовательностей, могут быть нестабильным вариабельным объектом.
Уровень техники
Дадим общее определение понятия кодирования. Определений импульсного кодирования много, наиболее известное определение кодирования следующее:
Кодирование - процесс изменения или трансформации входящего сообщения из его изначальной формы в некоторую другую форму, или кодирование это трансформация данных из одной формы в другую. Рассмотрим более подробно техническое кодирование импульсной информации в технических системах и кодирование импульсной информации в импульсных (спайковых) нейронных сетях. Методы технического кодирования отличаются от методов кодирования в реальных нейронных сетях. Это отличие обусловлено тем, что не все процессы в технических системах могут быть реализованы в биологических. Известны следующие методы технического кодирования информации 1) фазовый (временной) задается точным положением импульсов во времени (относительно какого-либо общего опорного; 2) временем до появления первого импульса - информация о сигнале задается временем появления первого импульса на каком-либо выходе; 3) порядковый задается порядком получения импульсов на выходах сети; 4) интервальный - информация о сигнале задается расстоянием между импульсами, получаемыми на выходах сети; 5) резонансный - информация о сигнале задается плотной последовательностью импульсов, приводящей к возникновению резонанса, когда одиночные импульсы затухают и не вносят никакого вклада в передачу информации. Иллюстрация известных видов технического кодирования показана на фиг. 1.
Фиг. 1. Иллюстрация известных видов технического кодирования.
Помимо этого, существуют виды кодирования информации, являющиеся смешанной формой нескольких простых видов.
Принципы кодирования информации в нейронных сетях могут быть весьма разнообразными. Отметим, что в нервной системе человека реализуемые импульсные последовательности являются нестабильным вариабельным объектом. Однако амплитуда парциальных импульсных последовательностей является постоянной, что обусловлено электродиффузионными процессами генерации нервного импульса. Это позволяет исключить влияние вариабельности амплитуды на процессы кодирования информации.
Нейронное кодирование - это переработка входящей сенсорной информации нейронами, нейронными сетями и нейронными ансамблями в нервной системе. Нейроны имеют исключительное свойство быстро распространять сигналы на большие расстояния. Они осуществляют это с помощью генерации потенциалов действия - спайков, которые распространяются нервными волокнами [1-12]. Хотя потенциалы действия варьируют во временной протяженности, амплитуде и форме, они обычно рассматриваются как идентичные стереотипные события в изучении нейронного кодирования. Если игнорировать продолжительность потенциалов действия (около 1 мс), последовательность потенциалов действия может быть охарактеризована серией событий типа «все-или ничего» во времени. Продолжительность межспайковых интервалов варьирует скорее случайным образом. Часто сила раздражителя кодируется «средней частотой» возникающих потенциалов действия и распространяющихся по сенсорным волокнам, однако возможны и другие виды импульсного кодирования. Коды, основанные на модуляции временных параметров импульсных ответов, включают в себя многочисленных «кандидатов» в коды, нередко представляют собой составной код, использующий несколько простых кодов для своей реализации. Возможные типы кодирования с помощью импульсных кодов показаны на фиг. 2.
Фиг. 2. Возможные кандидаты в импульсные коды (на примере разрядов электрического органа нильского ската): 1 - отметка стимуляции; 2.амплитудная модуляция импульсов; 3 -частотный код с уменьшением частоты следования импульсов; 4 - код длительностью пачки; 5 - вероятностный код; 6 - микроструктурный код; 7 - частотный код с увеличением частоты следования импульсов.
Возможные и другие виды импульсного кодирования, которые осуществляются частотным, интервальным кодированием, латентным периодом, длительностью реакции, вероятностью появления импульса, которые показаны на фиг. 3.
Фиг. 3. Формы кодирования информации импульсными разрядами нейрона:
а) - изменением латентного периода появления импульса; б) - количеством импульсов;
в) - временем импульсной реакции; г) - временным узором распределения импульсов в ответе; в верхней выборке показан более слабый раздражитель, в нижней выборке - более сильный раздражитель; стрелка - момент нанесения раздражения.
Сравнение известных видов кодирования нейронных импульсных последовательностей
1) Амплитудное кодирование (амплитудная модуляция) сразу исключается, поскольку амплитуда нейронных импульсов неизменна, ввиду фундаментальных свойств их электрохимической генерации.
2) Широтное кодирование - широтная модуляция импульсов сразу исключается, поскольку амплитуда нейронных импульсов неизменна, ввиду фундаментальных свойств их электрохимической генерации.
3) Комбинированное амплитудно широтное кодирование сразу исключается ввиду двух предыдущих свойств.
4) Фазовое кодирование или фазовая модуляция исключается, поскольку понятие фазы для импульсных сигналов не определено, понятие фазы определено для синусоидальных колебаний, для импульсных сигналов определено только понятие задержки импульсов.
5) Кодирование задержкой импульсов теоретически возможно, однако, управление задержкой сложно, связано со значительной нестабильностью, особенно для нейронных сетей. Поэтому практически этот вариант управления нейронными импульсными последовательностями не используется ни в реальных биологических, ни в технических системах
Мы рассмотрели несколько способов кодирования в импульсных нейронных сетях. Общей особенностью всех указанных методов является присущая им нестабильность кодовых ответов. Яркой иллюстрацией такой нестабильности являются результаты, полученные в работе [12]. Реакция регистрирующих нейронов на одни и те же объекты может отличаться, если входная информация подавалась в различные моменты времени На показанной на фиг. 4 картинке приведена реакция четырех разных нейронов, обозначенных как А, В, С, D, на визуальные образы фигурок, различающиеся между собой формой. Очевидно, что эти нейроны определенным образом реагируют на форму изображений. Каждая маленькая вертикальная линия обозначает один потенциал действия. Очевидно, что эти нейроны определенным образом реагируют на форму изображений.
Фиг. 4. Схематическая иллюстрация информационных функций нейронного ответа в виде импульсных последовательностей. На рисунке показаны ответы четырех нейронов (A-D) на набор из пяти разных стимулов, каждый из которых повторяется дважды (геометрические формы в кадрах верхнего ряда). Каждая маленькая вертикальная линия обозначает один потенциал действия.
Раскрытие изобретения
Кодирование информации в импульсных нейронных сетях является сложной задачей, которой посвящены нейрофизиологические исследования, теоретические исследования, патентные разработки [13-23]. Кодирование информации в импульсных нейронных сетях должно выполнять три основные функции: 1) быстро передавать информацию в вышележащие центры от места ее возникновения; 2) осуществлять позиционное кодирование, то есть распознавание информации от различных входных объектов или информации от ее места расположения; 3) осуществлять кодирование интенсивностью входных воздействий.
Наиболее эффективным является способ кодирования информации в импульсных избирательных нейронных сетях при распознавании объектов и интенсивности входного сигнала, когда используют импульсные последовательности постоянной амплитуды и длительности и со «средней» частотой следования импульсов пропорциональной интенсивности входного сигнала, основанный на изменении параметров входных импульсных последовательностей, без использования специальной технологии распознавания объектов. Отметим, что специальные технологии распознавания объектов при использовании кодирования «средней» частотой следования импульсов, пропорциональной интенсивности входного сигнала, основанные на изменении параметров входных импульсных последовательностей, не предложены. Такое кодирование является прототипом заявленного изобретения.
Первое свойство реализуется нейронными сетями очень хорошо. Выполнение одновременно свойств 2), 3) не обеспечивается ни одним из известных методов кодирования. Из рассмотрения методов кодирования импульсных последовательностей вытекает, что кодирование в нервной системе является не стабильным и не надежным. Оно подвержено значительному влиянию шумов, нестабильности генерации импульсов. Ввиду нестабильности самих импульсных последовательностей, которая выражается в нестабильности межимпульсных интервалов, наличии пачек импульсов, также имеющих значительную нестабильность по межимпульсным интервалам в пачке, так и нестабильность по временным интервалам между пачками импульсов. Таким образом, имеет место значительная нестабильность импульсных потоков, как в биологических нейронных сетях, так и в искусственных нейронных сетях. Поэтому все известные методы кодирования импульсных последовательностей по любым параметрам этих последовательностей являются не стабильными и не надежными.
В связи с этим предлагается метод кодирования, не имеющий перечисленных недостатков. Дадим более подробное пояснение. В бинарных нейронных сетях, использующих нейроны МакКаллока-Питтса, единицей информации входной бинарной последовательности является 1, отсутствие 0. В данной работе для импульсных нейронных сетей предполагается в качестве единицы информации использовать всю импульсную последовательность (ИП).
Таким образом, ответом на один пиксель изображения является любая импульсная последовательность, имеющая «среднюю частоту» следования импульсов, пропорциональную интенсивности входного сигнала. Ответная последовательность может иметь любую конфигурацию, это может быть последовательность импульсов с одинаковыми межимпульсными интервалами, последовательность с нестабильными межимпульсными интервалами, последовательность импульсов, сменяющаяся пачками импульсов (беретами) или последовательность с другим законом изменения. Под средней частотой будем принимать величину
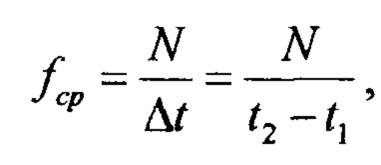
где Δt=t2-t1 - интервал, на котором производится расчет; N - количество импульсов на этом интервале. В реальных физиологических условиях средняя частота пропорциональна интенсивности 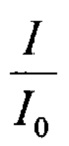 (-нормирующий множитель) сигнала, изменяется по определенному закону, характеризуемому функцией F
(-нормирующий множитель) сигнала, изменяется по определенному закону, характеризуемому функцией F
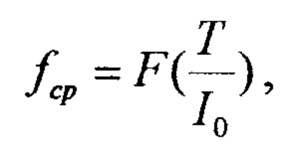
где F - заданная функция. Для многих физических систем 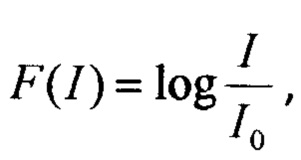 то есть зависимость имеет логарифмический характер, такая зависимость называется законом Фехнера, известны и другие аппроксимации функции F.
то есть зависимость имеет логарифмический характер, такая зависимость называется законом Фехнера, известны и другие аппроксимации функции F.
Таким образом, единицей информации является вся импульсная последовательность полностью, то есть наличие ИП это 1; отсутствие ИП это 0. Иллюстрация единицы информации для биологических нейронных сетей и искусственных бинарных сетей и импульсных нейронных сетей показана на фиг. 5.
Фиг. 5. Иллюстрация единицы-пикселя в изображении, показанной черным цветом, информации для бинарных нейронных сетей и для импульсных искусственных и для биологических нейронных сетей. Слева показана последовательность нулей и единиц, получаемая при развертке контурного изображения с экрана монитора, далее показана бинарная последовательность из 0 и 1, подаваемая на вход бинарной нейронной сети. Справа показано предлагаемое кодирование в виде полных импульсных последовательностей. Значению 1 при бинарном кодировании соответствует полная импульсная последовательность при импульсном кодировании, значению 0 в бинарной последовательности при импульсном кодировании соответствует отсутствие или нулевая импульсная последовательность.
На фиг. 5 одному пикселю на развертке экрана монитора соответствует 1 в бинарной последовательности и полная импульсная последовательность при использовании импульсной нейронной сети. Структура импульсной последовательности практически не влияет на образование импульсов максимальной амплитуды, что следует из фундаментальных свойств почти-периодических функций.
Предлагаемый способ кодирования реализуется средствами аналоговой электроники, технологически пригоден к микро-схемному исполнению, в том числе и средствами нанотехнологий. Материальное выражение изобретения осуществляется структурной схемой системы, осуществляющей предлагаемое кодирование, показано на фиг. 6.
Фиг. 6. Структурная схема системы, осуществляющей предлагаемое кодирование в импульсной нейронной сети.
На фиг. 6 приняты обозначения: Б1 - Избирательное преобразование набора входных импульсных последовательностей кластерами каналов связи импульсного нейрона;
Б2 - Преобразование динамическим сумматором мгновенных значений импульсных сигналов на его входе;
Б3 - Преобразование ждущим автогенератором, реагирующим на мгновенные значения импульсной функции суммы импульсных последовательностей;
x=(х1,…,хm), xk=(xk1,xk2,…,xkn), y=(y1,…,ym); xki=(i=1,…,n; k=1,…,m); xki - импульсные последовательности k-го объекта на входе, уk - импульсные последовательности на выходе, являющиеся продуктом кодирования входных последовательностей.
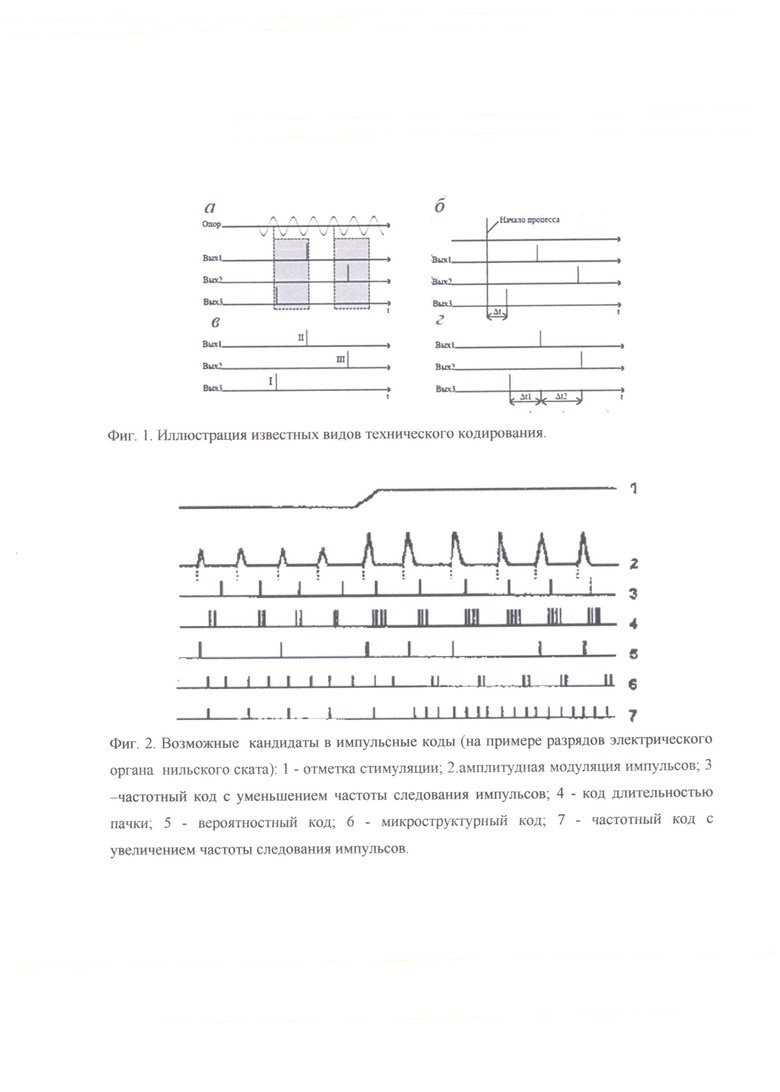
Пример наглядного выполнения операций избирательного преобразования входного сигнала в виде совокупности импульсных последовательностей показано на фиг. 7.
Фиг. 7. Наглядное выполнение операций преобразования входного сигнала в виде совокупности импульсных последовательностей.
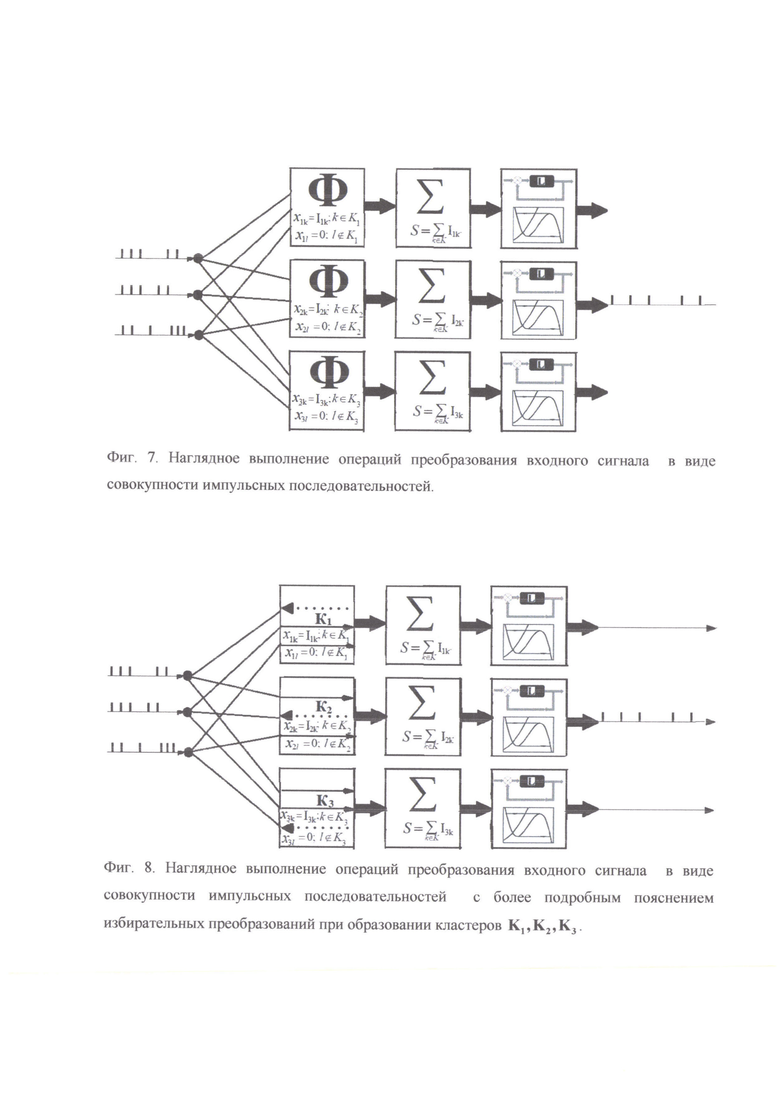
Фиг. 8. Наглядное выполнение операций преобразования входного сигнала в виде совокупности импульсных последовательностей с более подробным пояснением избирательных преобразований при образовании кластеров K1, K2, K3.
Рассмотрим импульсное кодирование 10-ти цифр (10-ти входных объектов) на экране монитора 4×6. Предварительно рассмотрим бинарное кодирование этих цифр в виде бинарных последовательностей из 0 и 1, показанное на фиг. 9.
Фиг. 9. Разложение 10-ти цифр от 0-9 в виде бинарной строки. Учтена значимость каждого разложения в виде нормировки по норме.
Каждой цифре соответствует бинарная строка из 24 ячеек из 0 и 1. Совокупность всех строк показана на рис. 9 справа, в виде матрицы 24×10. Бинарные входные сигналы, характеризующие объекты, показаны строками матрицы 24×10.
При импульсном кодировании 1 в бинарной последовательности соответствует полной импульсной последовательности, 0 соответствует нулевая импульсная последовательность (с амплитудами, равными 0). Кодирование импульсными последовательностями цифры 9 показано на фиг. 10.
Фиг.10. Кодирование цифры 9 импульсными последовательностями, генерируемыми в месторасположении черных пикселей на экране монитора 4×6. Бинарная последовательность цифры 9 показана на втором столбце.
Таким образом, фиг. 10 дает наглядную иллюстрацию выполнения операций преобразования входного сигнала в виде совокупности импульсных последовательностей блоком Б1 на фиг. 6. В реальных физиологических условиях генерация совокупности импульсных последовательностей осуществляется сенсорными клетками.
Рассмотрим закономерности преобразования импульсных потоков в биологических и искусственных нейронных сетях. Как происходит суммирование импульсных последовательностей? Рассмотрим суммирование. Суммирование бинарных последовательностей достаточно просто. Пусть k номер ячейки бинарной последовательности. Тогда суммой S называется сумма всех 1 в ячейках с одинаковым номером.
Как суммируются импульсные последовательности? Этот вопрос намного сложнее. Рассмотрены различные методы суммирования, но все они имеют недостатки, исключающие возможности их практического использования. Основной недостаток, который мы уже отмечали, это значительная нестабильность меж импульсных интервалов, возможность появления пачек импульсов с внутренней нестабильностью меж импульсных интервалов, нестабильность «средней частоты» импульсов и другие виды нестабильностей.
Специфика суммирования состоит в том, что для последовательностей из коротких импульсов с различными периодами временное положение импульсов может не совпадать, и тогда их амплитуды не суммируются. Например, даже для двух импульсных последовательностей с одинаковыми периодами следования, но сдвинутых по фазе, суммирование амплитуд не происходит. В общем случае сумма разно-периодных импульсных последовательностей является равномерной почти-периодической функцией, и их суммирование происходит на основе свойств почти-периодических функций (ППФ) [24].
Согласно теореме Кронекера такая функция имеет сгущения и разряжения импульсов, следующие с интервалами так называемых ε - почти-периодов. Рассмотрим его на примере суммирования периодических импульсных последовательностей с разными несоизмеримыми периодами. Иллюстрация таких ИП показана ниже. Сигналы на входах и на выходах нейронов можно представить в виде суммы почти-периодических функций, как показано на фиг. 11 слева, суммарный импульсный поток показан выше оси времени на фиг. 11 справа.
Фиг. 11. Схематическое изображение последовательности электрических импульсов нейрона в виде прямоугольных импульсов слева. Четыре импульсные последовательности с периодами Т1÷Т4, ε - почти-период приблизительно равен 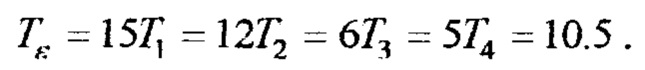 ε - почти-период заключен между двумя максимумами. Сгущения и разрежения для импульсных потоков с несоизмеримыми периодами следования импульсов T1=0.7; Т2=0.875; Т3=1.75; T4=2.1 показаны на фиг. 11 справа.
ε - почти-период заключен между двумя максимумами. Сгущения и разрежения для импульсных потоков с несоизмеримыми периодами следования импульсов T1=0.7; Т2=0.875; Т3=1.75; T4=2.1 показаны на фиг. 11 справа.
Максимальная амплитуда суммы импульсов существует и достигается через ε - почти-период и равна 4А=2, где А-амплитуда импульса равная 0,5. В пределах t ∈ ⎜t-7⎜<ε происходит суммирование амплитуд импульсов, происходящее через каждые ε - почти-периоды. Известно, что для возбуждения нейрона необходимо, чтобы сумма импульсов, пришедших по дендритам, превышала порог возбуждения. Специфическое свойство почти-периодических функций - существование ε - почти-периодов и максимальной суммы импульсов, следующих с интервалом ε - почти-периода, - позволяет осуществить избирательную обработку информации, закодированной в импульсных потоках, и сократить избыточность входной информации.
На фиг. 10 одному пикселю на развертке экрана монитора соответствует 1 в бинарной последовательности и полная импульсная последовательность при использовании спайковой нейронной сети. Структура импульсной последовательности практически не влияет на образование импульсов максимальной амплитуды, что следует из фундаментальных свойств почти-периодических функций.
Рассмотрим преобразование входного сигнала в виде совокупности импульсных последовательностей блоком Б3 на фиг 6.
Рассмотрим нелинейный блок нейрона. Им является аксонный холмик в основании аксона. Нелинейная часть ИМНС является импульсной автоколебательной системой. Эта система может быть потенциально автоколебательной и генерировать в ответ на входной импульс один ответный импульс на выходе. Возможна генерация периодической последовательности импульсов или пачек импульсов (беретов). При этом серии импульсов в пачке обычно имеют убывающий период, но могут иметь примерно одинаковый период следования, или даже хаотическую динамику.
Уравнение автогенератора нелинейной динамической системы с положительной обратной связью с выхода на вход в достаточно общем случае можно написать в виде
y=Ly+x,
где L - характеристика нелинейной динамической системы, х - входной сигнал.
Структурная схема автогенератора показана на фиг. 12.
Фиг.12. Структурная схема ждущего порогового автогенератора
Для использования динамической системы, описываемой системой дифференциальных уравнений второго порядка в качестве запоминающего устройства необходимо, чтобы изоклина имела N-образную или S-образную характеристику. В этом случае система может иметь два устойчивых состояния равновесия, что позволяет запомнить одно из устойчивых состояний и использовать эту систему как устройство памяти. Рассмотрим для примера уравнение Ван дер Поля-ФитцХью, известное в синергетике [25, 26],
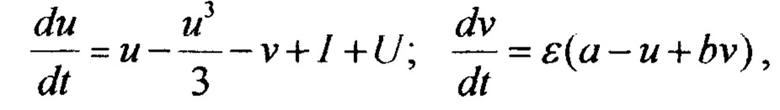
где I - ток смещения, a, b, ε - параметры: а=0.7, b=0.8. Если I=0.142, то решением уравнения является одиночный импульс, который можно вызвать внешним возбуждением. При I=0.4 уравнения описывают релаксационные колебания. Фазовый портрет уравнения Ван дер Поля - Фитцхъю при различных значениях параметров показан на фиг. 13.
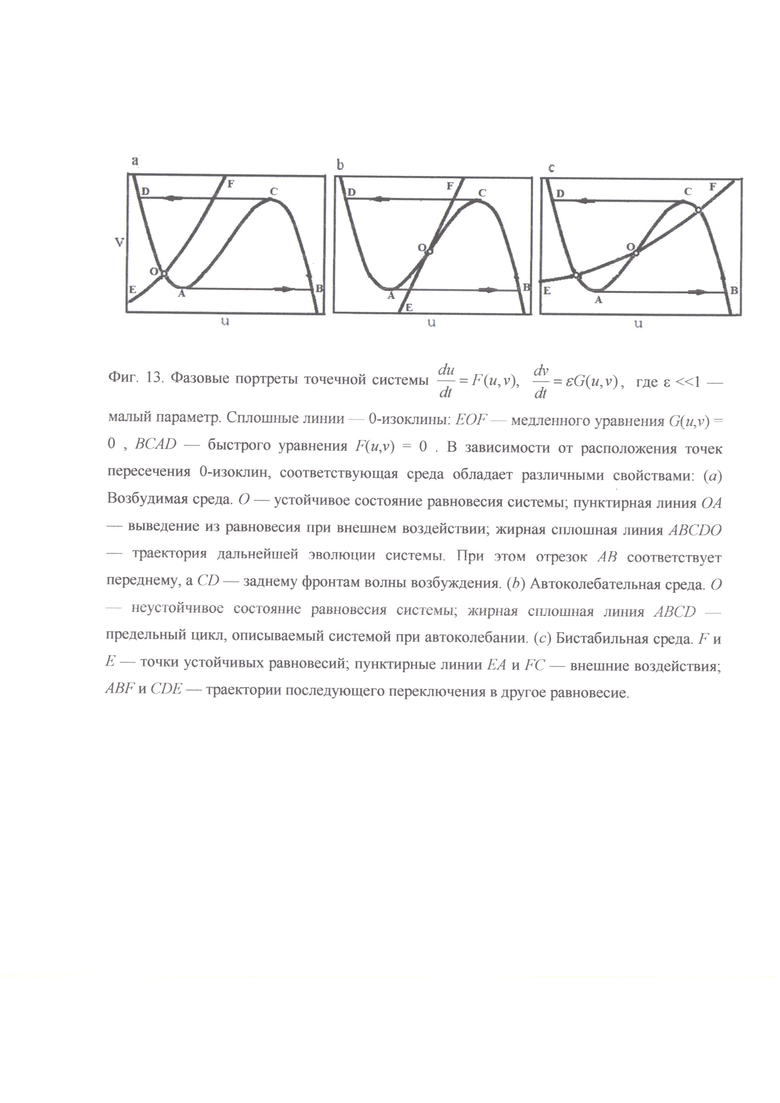
Фиг. 13. Фазовые портреты точечной системы 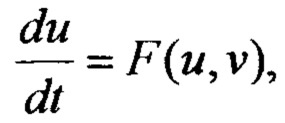
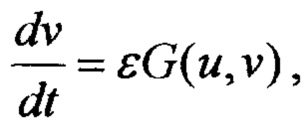 где ε << 1 - малый параметр. Сплошные линии - 0-изоклины: EOF - медленного уравнения G(u,v)=0, BCAD - быстрого уравнения F(u,v)=0. В зависимости от расположения точек пересечения 0-изоклин, соответствующая среда обладает различными свойствами, (а) Возбудимая среда. О - устойчивое состояние равновесия системы; пунктирная линия OA - выведение из равновесия при внешнем воздействии; жирная сплошная линия ABCDO - траектория дальнейшей эволюции системы. При этом отрезок АВ соответствует переднему, a CD - заднему фронтам волны возбуждения. (b) Автоколебательная среда. О - неустойчивое состояние равновесия системы; жирная сплошная линия ABCD - предельный цикл, описываемый системой при автоколебании, (с) Бистабильная среда. F и Е - точки устойчивых равновесий; пунктирные линии ЕА и FC - внешние воздействия; ABF и CDE - траектории последующего переключения в другое равновесие.
где ε << 1 - малый параметр. Сплошные линии - 0-изоклины: EOF - медленного уравнения G(u,v)=0, BCAD - быстрого уравнения F(u,v)=0. В зависимости от расположения точек пересечения 0-изоклин, соответствующая среда обладает различными свойствами, (а) Возбудимая среда. О - устойчивое состояние равновесия системы; пунктирная линия OA - выведение из равновесия при внешнем воздействии; жирная сплошная линия ABCDO - траектория дальнейшей эволюции системы. При этом отрезок АВ соответствует переднему, a CD - заднему фронтам волны возбуждения. (b) Автоколебательная среда. О - неустойчивое состояние равновесия системы; жирная сплошная линия ABCD - предельный цикл, описываемый системой при автоколебании, (с) Бистабильная среда. F и Е - точки устойчивых равновесий; пунктирные линии ЕА и FC - внешние воздействия; ABF и CDE - траектории последующего переключения в другое равновесие.
Таким образом, нелинейный блок нейрона это релаксационная автоколебательная система, которая может генерировать, как это следует из анализа изоклин, показанных на фиг. 13,: одиночный электрический импульс, периодическую последовательность импульсов, пачки импульсов (береты), частота которых последовательно убывает, вплоть до прекращения.
Раскрытие технического эффекта
Способ кодирования информации в импульсных спайковых нейронных сетях позволяет реализовать ряд полезных для практики технических результатов. Более подробно достигаемые технические результаты приведены ниже:
1. Инвариантность (независимость) позиционных распознавательных свойств от интенсивности входных сигналов, то есть не зависимость позиционного распознавания от (интенсивности) частотных свойств входного сигнала.
2. Наличие возможности одновременности распознавательных свойств и оценки интенсивности входных сигналов.
3. Возможность передачи информации на расстояние при увеличении длины каналов связи, соединений (проводов) между входами сигналов и входом сумматора.
4. Значительное повышение устойчивости, надежности кодирования, уменьшение влияния внешних помех, благодаря независимости кодирования от формы импульсных последовательностей и их неизменной амплитуды импульсов.
Осуществление изобретения Осуществление изобретения было реализовано в виде материального макета («в железе»). Электрическая схема избирательных нейронов, используемых в экспериментальном макете, показана на фиг. 14.
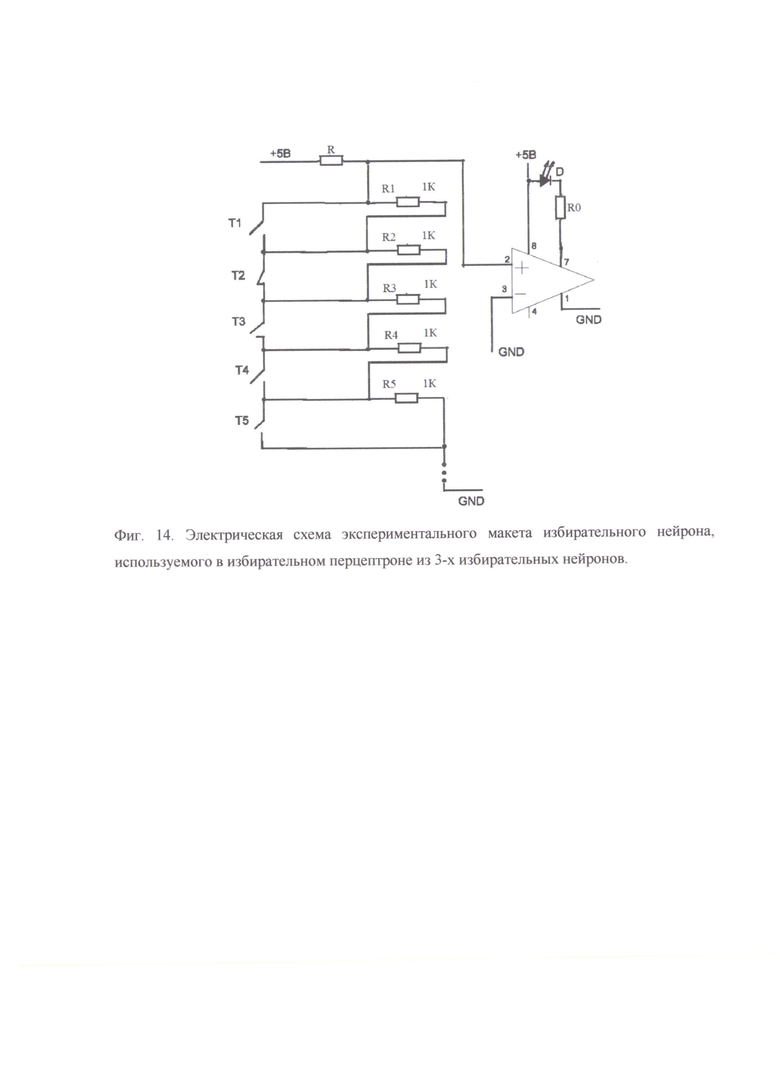
Фиг. 14. Электрическая схема экспериментального макета избирательного нейрона, используемого в избирательном перцептроне из 3-х избирательных нейронов.
Всего нейрон содержит 9 каналов связи, из которых создаются избирательные кластеры. Пороговое значение суммы напряжений на выходе кластеров равно 5 в. Превышение порогового значения U≥5 приводит к зажиганию индикаторного светодиода D.
Переключатели Т1-Т9 служат для реализации кластеров каналов связи нейрона. Если переключатель замкнут, то нейронный канал считается заблокированным, в состав нейронного кластера входят не заблокированные каналы связи нейрона. Управление формированием кластеров из каналов связи осуществляется с пульта управления. Более детальная схема избирательного нейрона, где используются герконовые переключатели для формирования бинарных входных сигналов, показана на фиг. 15.
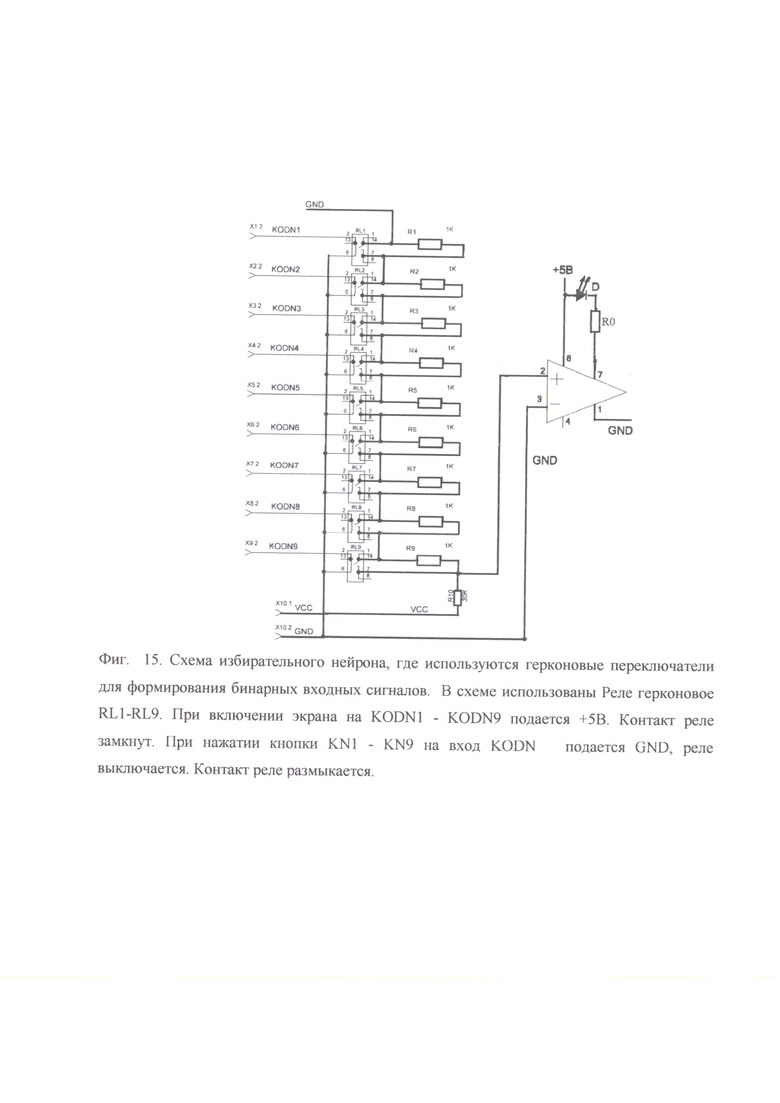
Фиг. 15. Схема избирательного нейрона, где используются герконовые переключатели для формирования бинарных входных сигналов. В схеме использованы Реле герконовое RL1-RL9. При включении экрана на KODN1 - KODN9 подается +5 В. Контакт реле замкнут. При нажатии кнопки KN1 - KN9 на вход KODN подается GND, реле выключается. Контакт реле размыкается.
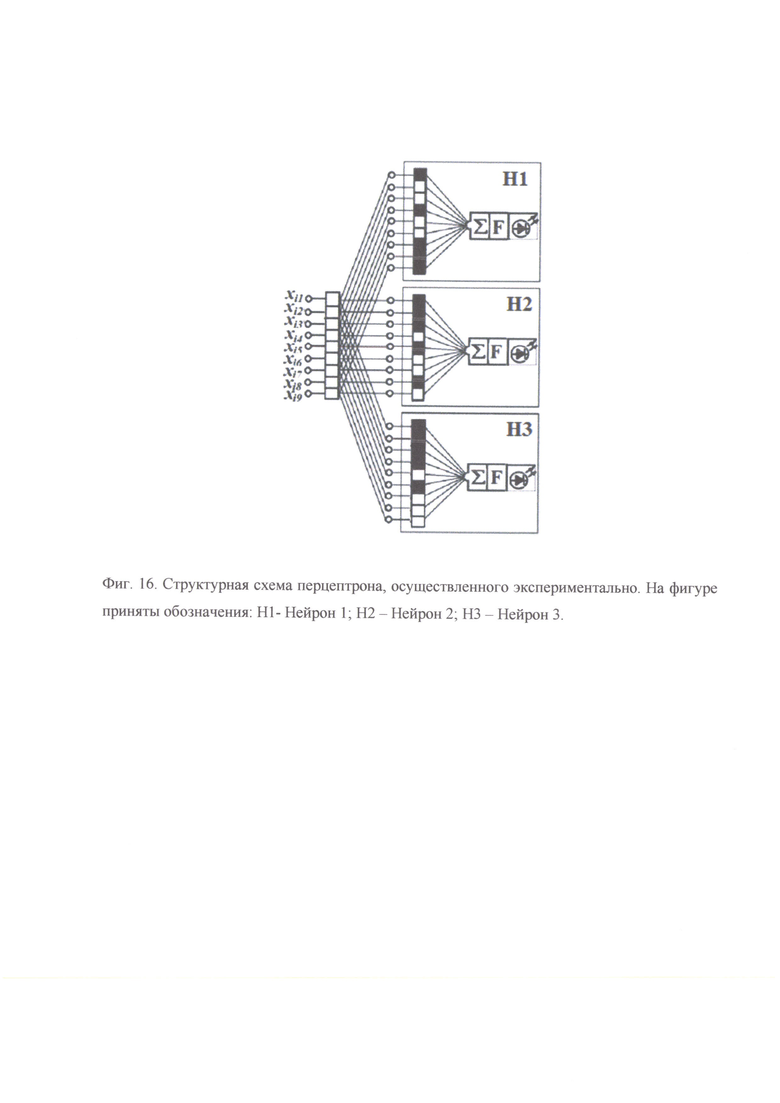
Для проверки изобретения и использования в учебной практике для обучения нейрообразовательным технологиям был разработан однослойный перцептрон с тремя регистрирующими нейронами. Входной сигнал создавался с помощью пульта управления на экране монитора с размерностью 3×3. Входной сигнал представлял бинарную последовательность из 9-ти ячеек, содержащих 0 и 1. Структурная схема разработанного перцептрона показана на фиг. 16.
Фиг. 16. Структурная схема перцептрона, осуществленного экспериментально. На фигуре приняты обозначения: H1 - Нейрон 1; Н2 - Нейрон 2; Н3 - Нейрон 3.
Перцептрон предназначен для распознавания 5-ти пиксельных объектов, в качестве которых были взяты буквы L, Т, X (в качестве входных объектов могли быть взяты любые изображения, содержащие 5 пикселей, равных 1). Входные объекты обозначались хi=(xi1,xi2,xi3) (i=1,2,3). Требуемая конфигурация кластеров каналов связи создавалась с помощью соединительных проводников между пультом управления и макетами нейронов. Типы соединений подбирались в соответствии с кодовыми комбинациями букв. Макет содержал пульт управления с монитором 9×9, на котором можно было набрать буквы L, Т, П. Величина порога распознавания Uпор=4.5. Индикация каналов нейронных кластеров производилась дополнительно с помощью 9-ти светящихся светодиодов (на принципиальной схеме фиг. 16 эти светодиоды не показаны). Эти диоды идентифицируют порядковые номера каналов кластеров. Сумма напряжений на индикаторном диоде равна сумме единиц в кодовой комбинации буквы и равна 5 для нейрона, настроенного на эту букву. На других нейронах сумма напряжений равна 2 и 3, что не вызывает превышения порога и индикатор не горит. Величину напряжения на индикаторных диодах можно оценить по количеству зажженных вспомогательных светодиодов.
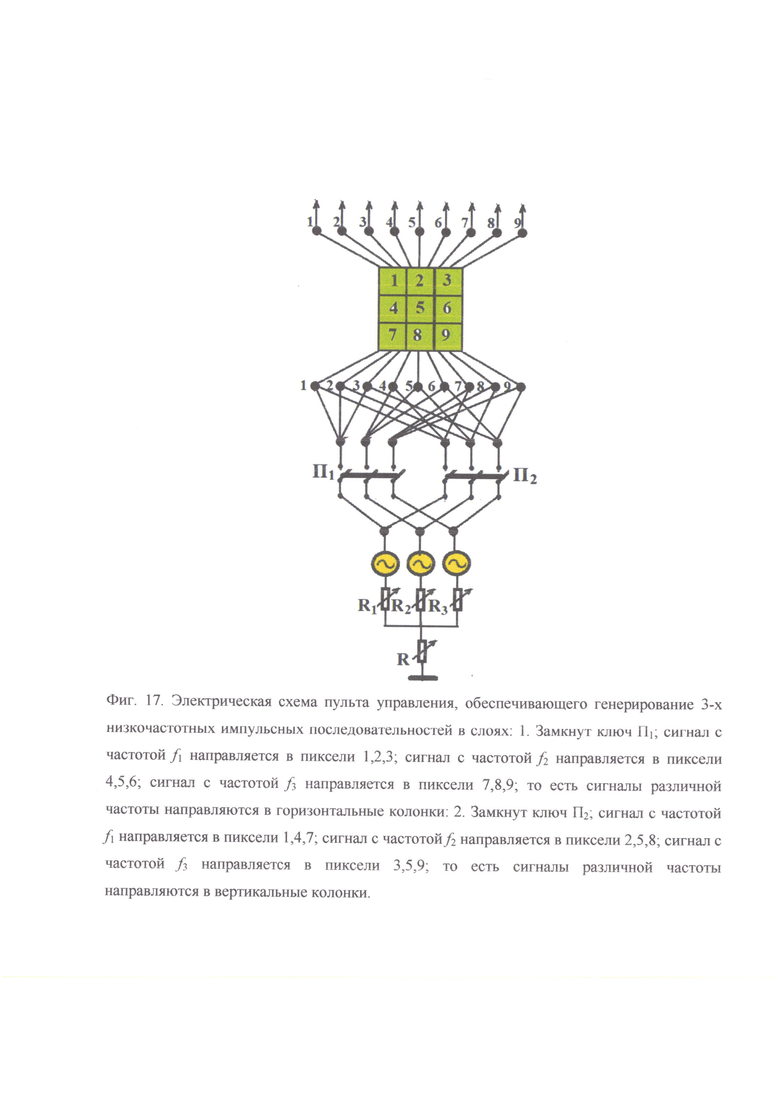
Рассмотрим электрическую схему пульта управления, обеспечивающего генерирование 3-х низкочастотных импульсных последовательностей. Задачей панели управления является подача импульсных последовательностей в различные квадраты -пиксели панели управления. Электрическая схема пульта управления, обеспечивающего генерирование 3-х низкочастотных импульсных последовательностей, показана на фиг. 17.
Фиг. 17. Электрическая схема пульта управления, обеспечивающего генерирование 3-х низкочастотных импульсных последовательностей в слоях: 1. Замкнут ключ П1; сигнал с частотой ƒ1 направляется в пиксели 1,2,3; сигнал с частотой ƒ2 направляется в пиксели 4,5,6; сигнал с частотой ƒ3 направляется в пиксели 7,8,9; то есть сигналы различной частоты направляются в горизонтальные колонки: 2. Замкнут ключ П2; сигнал с частотой ƒ1 направляется в пиксели 1,4,7; сигнал с частотой ƒ2 направляется в пиксели 2,5,8; сигнал с частотой ƒ3 направляется в пиксели 3,5,9; то есть сигналы различной частоты направляются в вертикальные колонки.
Приведенная электрическая схема пульта управления обеспечивает создание на экране монитора импульсных последовательностей с 2-мя вариантами изменения периодов, описанных выше. Сопротивления R1,R2,R3, обеспечивают установку периодов T1,T2,T3 низкочастотных импульсных генераторов. Сопротивление R обеспечивает синхронное изменение периодов всех трех генераторов импульсных сигналов, моделирующее изменение интенсивности входных сигналов. Строенные переключатели ПХ,П2 обеспечивают реализацию одного из двух вариантов распределения периодов импульсных последовательностей на экране монитора.
Вариант нейрообразовательной системы в «железе», созданной для обучения старших школьников, студентов и специалистов смежных профессий. Для проверки эффективности рассматриваемого метода кодирования в избирательных нейронных сетях был реализован на экспериментальном макете. Макет содержал пульт управления с монитором 9×9, на котором можно было набрать буквы L, Т, П. Входные импульсные последовательности создавались с помощью 3-х импульсных генераторов, сигналы которых подавались на тройки пикселей экрана. Величина порога распознавания Uпор=4.5 Сумма светящихся светодиодов равна сумме единиц в кодовой комбинации буквы и равна 5 для нейрона, настроенного на эту букву. На других нейронах сумма горящих светодиодов равна 2 и 3, что не вызывает превышения порога и индикатор зеленого цвета не горит. При распознавании индикатор мигал с частотой ε - почти-периода. Увеличение интенсивности входного сигнала моделировалось синхронным увеличением частоты 3-х импульсных генераторов, обслуживающих тройки пикселей экрана. При этом согласно выбранной теории кодирования распознавание объектов сохранялось, а частота мигания индикаторов распознавания увеличивалась пропорционально эффективности раздражения.
Внешний вид нейрообразовательной системы на основе 3-х избирательных нейронов, в режиме распознавания, предназначенной для распознавания трех входных объектов в виде букв, цифр и других символов, которые можно задавать на экране пульта управления, показан на фотографии фиг. 18.
Фиг. 18. Внешний вид нейрообразовательной системы на основе 3-х избирательных нейронов, настроенных на распознавание букв английского алфавита L, Т, X. Показан эксперимент по распознаванию букв L, Т, X.
На фиг. 18 сверху слева перцептрон распознает букву L, сверху справа перцептрон распознает букву Т, внизу в центре перцептрон распознает букву X.
Нейрообразовательная система реализует способ импульсного кодирования, предложенный в изобретении.
Таким образом, экспериментальным путем доказано, что при использовании предлагаемого механизма кодирования в импульсных нейронных сетях достигается: инвариантность кодирования месторасположения объектов и интенсивности входного сигнала, устойчивость работы нейронных сетей.
Список литературы
1. Александров Ю.И., Анохин К.В., Соколов Е.Н., Греченко Т.Н. и др. Нейрон. Обработка сигналов. Пластичность. Моделирование. Фундаментальное руководство. Изд-во Тюменского государственного университета. 2008. 548 с.
2. Борисюк Г.Н., Борисюк P.M., Казанович Я.Б., Иваницкий Г.Р. Модели динамики нейронной активности при обработке информации мозгом - итоги "десятилетия". Успехи физических наук. 2002. Т. 172 №10. С. 1189-1214.
3. Греченко Т.Н. Психофизиология. М.: Гардарики, 2009. 572 с.
4. Хайкин С. Нейронные сети: полный курс. 2-е изд. М., "Вильяме", 2006.
5. Галушкин А.И. Нейронные сети. Основы теории. М., Горячая линия - Телеком, 2010.
6. Ежов А.А., Шумский С.А. Нейрокомпъютинг и его применения в экономике и бизнесе. М., МИФИ, 1998.
7. Чернявский Д.С. Синергетика и информация: Динамическая теория информации. 2-е изд. М.:УРСС.2004.
8. Анохин К.В. "Нейронные механизмы памяти: синаптическая и геномная гипотезы", Журнал высшей нервной деятельности им. И.П. Павлова, 2011. N 6. С. 660-674.
9. Нейронные сети. Statistica Neural Networks. Методология и технологии современного анализа данных; Горячая Линия - Телеком -, 2008. - 392 с.
10. Редько В.Г. Эволюция, нейронные сети, интеллект.Модели и концепции эволюционной кибернетики; Либроком - Москва, 2013. - 224 с.
11. Melamed О., Gerstner W., Maass W., Tsodyks M., Markram H. Coding and learning of behavioral sequences // Trends in Neurosciences, 2004, V. 27, №. 1, pp. 11-14.
12. Stefano Panzeri, Jakob H. Macke, Joachim Gross & Christoph Kayser. Neural population coding: combining insights from microscopic and mass signals. Trends in Cognitive Sciences 2015. 19 (3): 162-172.
13. Цуриков A.H. Способ обучения искусственной нейронной сети G06N 3/08. 2504006. 2014.
14. Чен Виктор Хоккью, Ханзинджер Джейсон Фрэнк, Бехабади Бардиа Фаллах. Способ и устройство для нейронного временного кодирования, обучения и распознавания G06N 3/08. 2597504.
15. Червяков Николай Иванович. Нейронная сеть для преобразования остаточного кода в двоичный позиционный код. G06N 3/04. 2318238.2008.
17. Нестерук Г.Ф., Молдовян А.А., Нестерук Ф.Г., Нестерук Л.Г. Способ обработки информации в нейронных сетях, пат. №2408053. 2010.
18. Шевченко К.Н., Шевченко Н.В., Шульгин Б.В. Модель нейронной сети. G06N 3/06, G06G 7/60,2309457. 2007.
19. Соловьев СВ.. Цыганков В.Д. Нейрокомпьютер и способ нейронной обработки информации. G06N 3/06. 2351011. 2009.
20. Мазуров М.Е. Нейрон, моделирующий свойства реального нейрона. Патент на изобретение №2597495. 07.11.2014.
21. Мазуров М.Е. Однослойный перцептрон на основе избирательных нейронов. Патент на изобретение №2597497 13.01.2015.
22. Мазуров М.Е. Импульсный нейрон, близкий к реальному. Патент на изобретение №2598298.09.02.2015.
23. Мазуров М.Е. Однослойный перцептрон, моделирующий свойства реального перцептрона. Патент на изобретение №2597496. 24.02.2015.
24. Левитан Б.М. Почти-периодические функции. М.: Гостехиздат, 1953.
25. Fitz Hugh R. Mathematical models of excitation and propagation in nerve // Bioelectronics. New York. McGraw-Hill. 1968.
26. Мазуров M.E. Синхронизация релаксационных автоколебательных систем, синхронизация в нейронных сетях. Изв. РАН. Сер. физ. 2018. Т. 82. №1. С. 83-87.
Краткое описание чертежей
Фиг. 1. Иллюстрация известных видов технического кодирования.
Фиг. 2. Возможные кандидаты в импульсные коды (на примере разрядов электрического органа нильского ската): 1 - отметка стимуляции; 2 - амплитудная модуляция импульсов; 3 - частотный код с уменьшением частоты следования импульсов; 4 - код длительностью пачки; 5 - вероятностный код; 6 - микроструктурный код; 7 - частотный код с увеличением частоты следования импульсов.
Фиг. 3. Формы кодирования информации импульсными разрядами нейрона:
а) - изменением латентного периода появления импульса; б) - количеством импульсов; в) - временем импульсной реакции; г) - временным узором распределения импульсов в ответе; 1 и 2 - различаемые раздражители, 1 - более слабый раздражитель, 2- более сильный раздражитель; стрелка - момент нанесения раздражения.
Фиг. 4. Схематическая иллюстрация информационных функций нейронного ответа в виде импульсных последовательностей. На рисунке показаны ответы четырех нейронов (A-D) на набор из пяти разных стимулов, каждый из которых повторяется дважды (геометрические формы в кадрах верхнего ряда). Каждая маленькая вертикальная линия обозначает один потенциал действия.
Фиг. 5. Иллюстрация единицы-пикселя в изображении, показанной черным цветом, информации для бинарных нейронных сетей и для импульсных искусственных и для биологических нейронных сетей. Слева показана последовательность нулей и единиц, получаемая при развертке контурного изображения с экрана монитора, далее показана бинарная последовательность из 0 и 1, подаваемая на вход бинарной нейронной сети. Справа показано предлагаемое кодирование в виде полных импульсных последовательностей. Значению 1 при бинарном кодировании соответствует полная импульсная последовательность при импульсном кодировании, значению 0 в бинарной последовательности при импульсном кодировании соответствует отсутствие или нулевая импульсная последовательность.
Фиг. 6. Структурная схема системы, осуществляющей предлагаемое кодирование в импульсной нейронной сети
Фиг. 7. Наглядное выполнение операций преобразования входного сигнала в виде совокупности импульсных последовательностей.
Фиг. 8. Наглядное выполнение операций преобразования входного сигнала в виде совокупности импульсных последовательностей с более подробным пояснением избирательных преобразований при образовании кластеров К1,К2,К3.
Фиг. 9. Разложение 10-ти цифр от 0-9 в виде бинарной строки. Учтена значимость каждого разложения в виде нормировки по норме.
Фиг. 10. Кодирование цифры 9 импульсными последовательностями, генерируемыми в месторасположении черных пикселей на экране монитора 4×6. Бинарная последовательность цифры 9 показана на втором столбце.
Фиг. 11. Схематическое изображение последовательности электрических импульсов нейрона в виде прямоугольных импульсов слева. Четыре импульсные последовательности с периодами Т1÷Т4, ε - почти-период приблизительно равен Тε=15Т1=12Т2=6Т3=5Т4=10.5. ε - почти-период заключен между двумя максимумами. Сгущения и разрежения для импульсных потоков с несоизмеримыми периодами следования импульсов Т1=0.7; Т2=0.875; Т3=1.75; Т4=2.1. показаны на фиг. 11 справа.
Фиг. 12. Структурная схема ждущего порогового автогенератора.
Фиг. 13. Фазовые портреты точечной системы 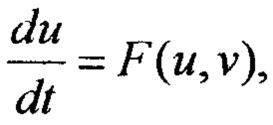
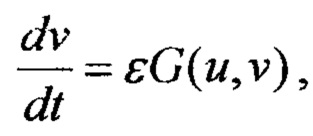 где ε << 1 - малый параметр. Сплошные линии - 0-изоклины: EOF - медленного уравнения G(u,v)=0, BCAD - быстрого уравнения F(u,v)=0. В зависимости от расположения точек пересечения 0-изоклин, соответствующая среда обладает различными свойствами: (а) Возбудимая среда. О - устойчивое состояние равновесия системы; пунктирная линия OA - выведение из равновесия при внешнем воздействии; жирная сплошная линия ABCDO - траектория дальнейшей эволюции системы. При этом отрезок А В соответствует переднему, a CD - заднему фронтам волны возбуждения. (b) Автоколебательная среда. О - неустойчивое состояние равновесия системы; жирная сплошная линия ABCD - предельный цикл, описываемый системой при автоколебании, (с) Бистабильная среда. F и Е - точки устойчивых равновесий; пунктирные линии ЕА и FC - внешние воздействия; ABF и CDE - траектории последующего переключения в другое равновесие.
где ε << 1 - малый параметр. Сплошные линии - 0-изоклины: EOF - медленного уравнения G(u,v)=0, BCAD - быстрого уравнения F(u,v)=0. В зависимости от расположения точек пересечения 0-изоклин, соответствующая среда обладает различными свойствами: (а) Возбудимая среда. О - устойчивое состояние равновесия системы; пунктирная линия OA - выведение из равновесия при внешнем воздействии; жирная сплошная линия ABCDO - траектория дальнейшей эволюции системы. При этом отрезок А В соответствует переднему, a CD - заднему фронтам волны возбуждения. (b) Автоколебательная среда. О - неустойчивое состояние равновесия системы; жирная сплошная линия ABCD - предельный цикл, описываемый системой при автоколебании, (с) Бистабильная среда. F и Е - точки устойчивых равновесий; пунктирные линии ЕА и FC - внешние воздействия; ABF и CDE - траектории последующего переключения в другое равновесие.
Фиг. 14. Электрическая схема экспериментального макета избирательного нейрона, используемого в избирательном перцептроне из 3-х избирательных нейронов. Фиг. 15. Схема избирательного нейрона, где используются герконовые переключатели для формирования бинарных входных сигналов. В схеме использованы Реле герконовое RL1-RL9. При включении экрана на KODN1 - KODN9 подается +5 В. Контакт реле замкнут. При нажатии кнопки KN1 - KN9 на вход KODN подается GND, реле выключается. Контакт реле размыкается.
Фиг. 16. Структурная схема перцептрона, осуществленного экспериментально.
Фиг. 17. Электрическая схема пульта управления, обеспечивающего генерирование 3-х низкочастотных импульсных последовательностей в слоях: 1. Замкнут ключ П1; сигнал с частотой ƒ1 направляется в пиксели 1,2,3; сигнал с частотой ƒ2 направляется в пиксели 4,5,6; сигнал с частотой ƒ3 направляется в пиксели 7,8,9; то есть сигналы различной частоты направляются в горизонтальные колонки: 2. Замкнут ключ П2; сигнал с частотой f1 направляется в пиксели 1,4,7; сигнал с частотой ƒ2 направляется в пиксели 2,5,8; сигнал с частотой f3 направляется в пиксели 3,5,9; то есть сигналы различной частоты направляются в вертикальные колонки.
Фиг. 18. Иллюстрация работоспособности метода кодирования в импульсных нейронных сетях, когда единицей информации считается импульсная последовательность, а интенсивность входного сигнала кодируется частотой раздражения.






Изобретение относится к области моделирования импульсных нейронов и может быть использовано для распознания образов, анализа и обработки изображений. Техническим результатом является обеспечение инвариантности кодирования местоположения объектов и интенсивности входного сигнала, повышение устойчивости работы. Способ содержит этапы, на которых в качестве единичного символа информации для кодирования используют всю целиком парциальную импульсную последовательность из числа всех входных или ее отсутствие; создают кластеры парциальных импульсных последовательностей, избирательно настроенных на позиционную существенную входную информацию; импульсные последовательности, которые соответствуют информативно не существенной входной информации полагают нулевыми; производят безынерционное суммирование мгновенных временных значений всех парциальных импульсных последовательностей каждого из образованных избирательных кластеров и получают в каждом регистрирующем нейроне импульсные последовательности с чередующимися пиками амплитуды, равными сумме пиков парциальных импульсных последовательностей, возбуждают пиками импульсов суммарных последовательностей пороговый ждущий автогенератор, который преобразует пики суммарных импульсных последовательностей на его входе в импульсы или последовательности импульсов на выходе; если интенсивность объекта на входе изменяется, то синхронно изменяется «средняя частота» всех парциальных последовательностей на входе, что приводит к изменению «средней частоты» импульсной последовательности на выходе импульсного автогенератора, равной почти-периоду парциальных импульсных последовательностей на его входе. 18 ил.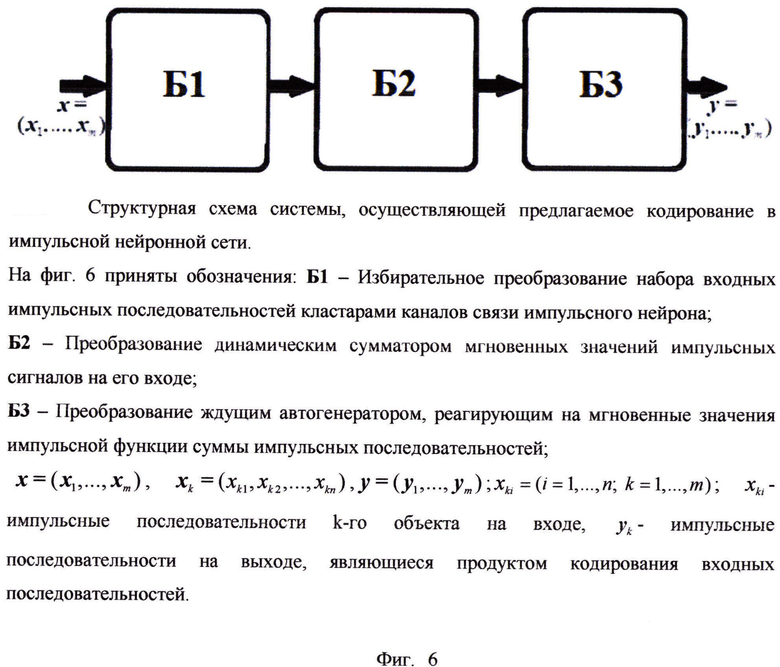
Способ кодирования информации в импульсных избирательных нейронных сетях при распознавании объектов и интенсивности входного сигнала, когда используют импульсные последовательности постоянной амплитуды и длительности со «средней» частотой следования импульсов, пропорциональной интенсивности входного сигнала, основанный на изменении параметров входных импульсных последовательностей, отличающийся тем, что
в качестве единичного символа информации для кодирования используют всю целиком парциальную импульсную последовательность из числа всех входных или ее отсутствие; создают кластеры парциальных импульсных последовательностей, избирательно настроенных на позиционную существенную входную информацию; импульсные последовательности, которые соответствуют информативно не существенной входной информации, полагают нулевыми; далее производят безынерционное суммирование мгновенных временных значений всех парциальных импульсных последовательностей каждого из образованных избирательных кластеров и получают в каждом регистрирующем нейроне после суммирования импульсные последовательности с чередующимися пиками амплитуды, равными сумме пиков парциальных импульсных последовательностей, что автоматически реализуют благодаря фундаментальным свойствам равномерных почти-периодических функций; далее возбуждают пиками импульсов суммарных последовательностей пороговый ждущий автогенератор, который преобразует пики суммарных импульсных последовательностей на его входе в импульсы или последовательности импульсов на выходе; если интенсивность объекта на входе изменяется, то синхронно изменяется «средняя» частота всех парциальных последовательностей на входе, что приводит к синхронному изменению «средней» частоты импульсной последовательности на выходе импульсного автогенератора, равной почти-периоду парциальных импульсных последовательностей на его входе, при этом точность позиционного распознавания остается инвариантной (независимой) относительно интенсивности входного сигнала объекта.
| ИМПУЛЬСНЫЙ НЕЙРОН, БЛИЗКИЙ К РЕАЛЬНОМУ | 2015 |
|
RU2598298C2 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН НА ОСНОВЕ ИЗБИРАТЕЛЬНЫХ НЕЙРОНОВ | 2015 |
|
RU2597497C2 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО ПЕРЦЕПТРОНА | 2015 |
|
RU2597496C1 |
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
| Способ получения цианистых соединений | 1924 |
|
SU2018A1 |
| Колосоуборка | 1923 |
|
SU2009A1 |
Авторы
Даты
2021-05-21—Публикация
2019-02-26—Подача