Введение
Изобретение относится к моделированию нейронных сетей, к нейрокибернетике и может найти применение при разработке нейрокомпьютеров, технических систем на основе нейронных сетей, для распознавания образов, анализа и обработки изображений и многих других приложений. Целью изобретения является расширение области применения нейронных сетей, нейросетевых технологий, создания искусственного интеллекта. Области применения предлагаемого изобретения: робототехника, нейроморфные нейрочипы, общение на основе нейротехнологий, медицинские протезы органов и мозга.
Основным базовым элементом нейронных сетей, на основе которого создаются более сложные нейронные сети, является однослойный перцептрон. В настоящее время известны однослойные перцептроны на основе нейронов МакКаллока-Питтса [1-4], на основе избирательных нейронов [5-9] и другие. Как известно, обучение однослойного перцептрона на основе нейронов МакКаллока-Питтса сводится к нахождению весовых коэффициентов [1-4].
Раскрытие сущности изобретения
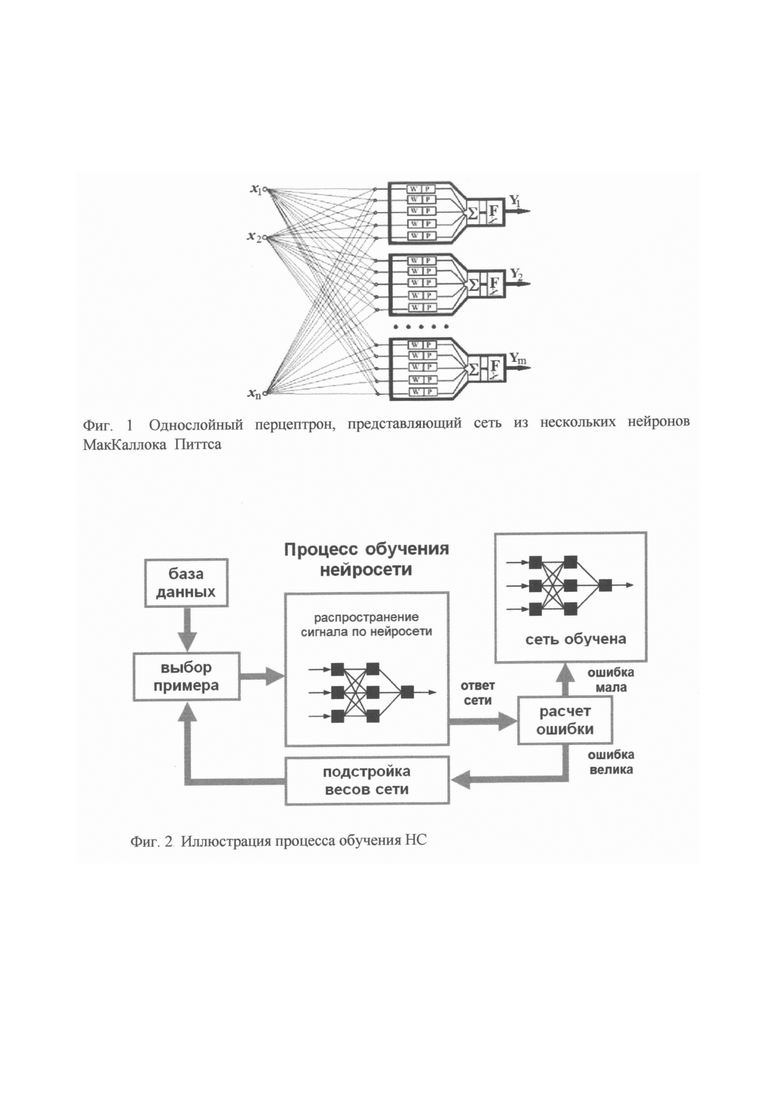
Избирательное выделение входной информации реализуется с помощью однослойного перцептрона, представляющего сеть из нескольких нейронов МакКаллока_Питтса, показанного на фиг. 1.
Фиг. 1. Однослойный перцептрон, представляющий сеть из нескольких нейронов МакКаллока_Питтса.
Как известно, обучение однослойного перцептрона на основе нейронов МакКаллока-Питтса сводится к нахождению весовых коэффициентов.
Рассмотрим более подробно технологию подбора весовых коэффициентов однослойного перцептрона.
Для практического использования перцептрон однослойный или многослойный должен быть обучен. Обучение стандартного перцептрона на основе нейронов МакКаллока-Питтса сводится к вычислению требуемого набора весовых коэффициентов.
Процесс обучения с учителем представляет собой предъявление сети выборки обучающих примеров. Каждый пример подается на входы сети, затем проходит обработку внутри структуры НС, вычисляется выходной сигнал сети, который сравнивается с соответствующим значением целевого вектора, представляющего требуемый выход сети. Затем по определенному правилу вычисляется ошибка, и происходит изменение весовых коэффициентов связей внутри сети в зависимости от выбранного алгоритма. Векторы обучающего множества предъявляются последовательно до тех пор, пока ошибка по всему обучающему массиву не достигнет приемлемо низкого уровня. Структурная схема процесса обучения НС показана на фиг. 2.
Фиг. 2. Иллюстрация процесса обучения НС.
Более детально структурная схема процесса обучения НС иллюстрируется фиг. 3.
Фиг. 3. Структура процесса обучения на примере двухслойного перцептрона.
Основной задачей учителя является выбор вида ошибки обучения, оценка величины этой ошибки, выбор изменяемых переменных, выбор величины изменения изменяемых переменных, замена одного эталонного входного сигнала из базы данных на другой входной сигнал. Наконец, в обязанности учителя входит оценка величины ошибки на основе некоторых критериев, зачастую плохо формализованных. Как видно из этого перечисления роли учителя, эта роль достаточно велика и не достаточно формализована.
При обучении с учителем методом обратного распространения ошибки роль учителя аналогична, описанной выше, с той лишь разницей, что сигнал с выхода нейронной сети попадает на вход автоматически, и все остальные действия учителя реализуются на входе.
Если выбрано множество обучающих примеров - пар и способ вычисления функции ошибки, то обучение нейронной сети превращается в задачу многомерной оптимизации, имеющую очень большую размерность. В общем случае возникает многоэкстремальная невыпуклая задача оптимизации. Для решения этой задачи могут использоваться итерационные алгоритмы.
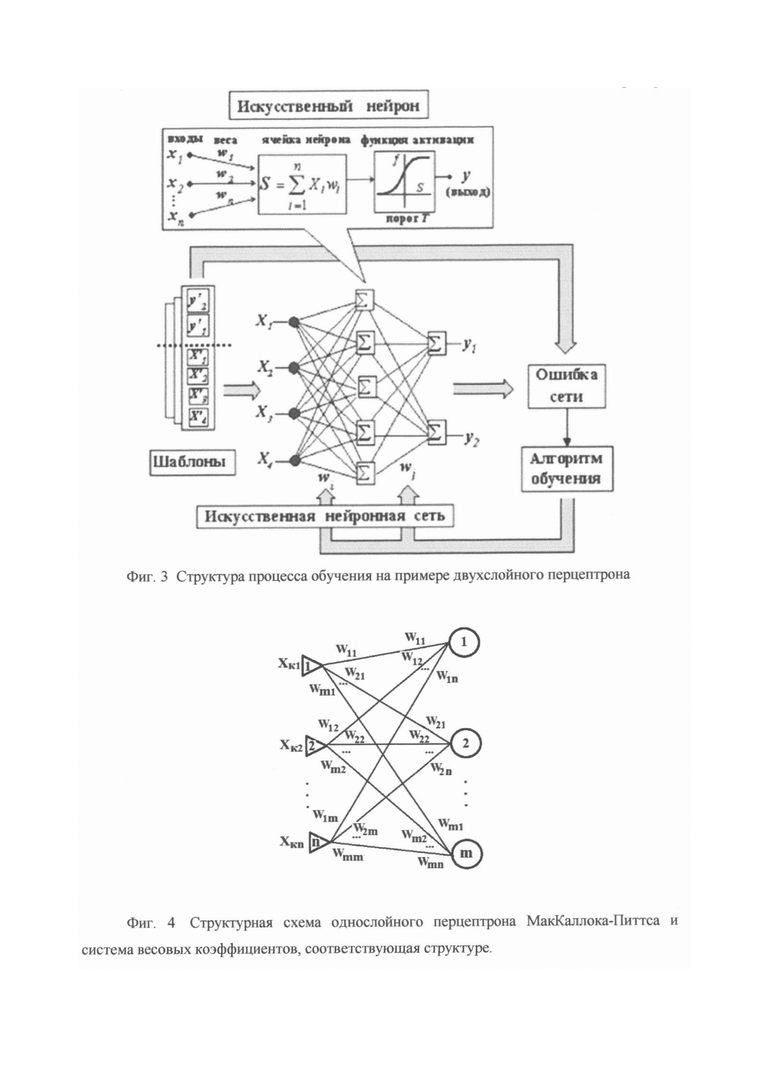
Рассмотрим математическую теорию однослойного перцептрона на основе нейронов МакКаллока-Питтса. Структурная схема однослойного перцептрона МакКаллока-Питтса и система весовых коэффициентов, соответствующая структуре, показана на фиг. 4.
Фиг. 4. Структурная схема однослойного перцептрона МакКаллока-Питтса и система весовых коэффициентов, соответствующая структуре.
Число распознаваемых объектов равно m. Каждому распознаваемому объекту соответствует вектор значений xk=(xk1, xk2, …, xkn).
После преобразований с весовыми коэффициентами получаем суммы
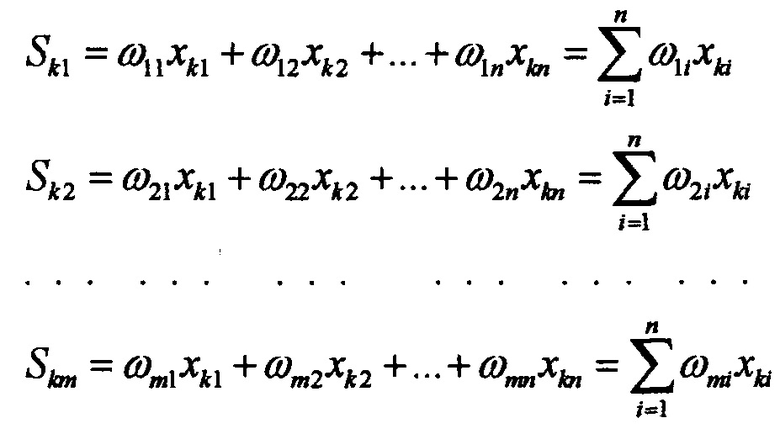
Перцептрон характеризуется матрицей весовых коэффициентов
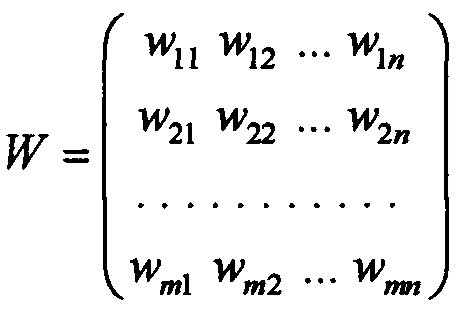
При воздействии сигналом xk на вход перцептрона получаем столбец значений, равный
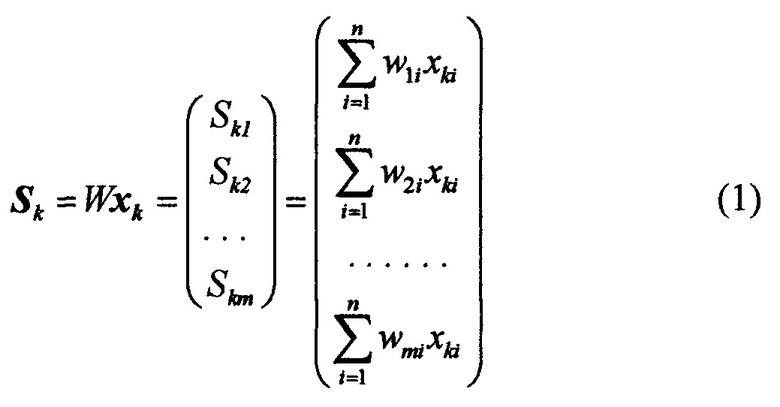
После суммирования получаем суммы входных сигналов с весовыми коэффициентами, которые преобразуются нелинейными пороговыми преобразователями. В результате на выходе однослойного перцептрона получаем сигнал в виде бинарной последовательности, равный
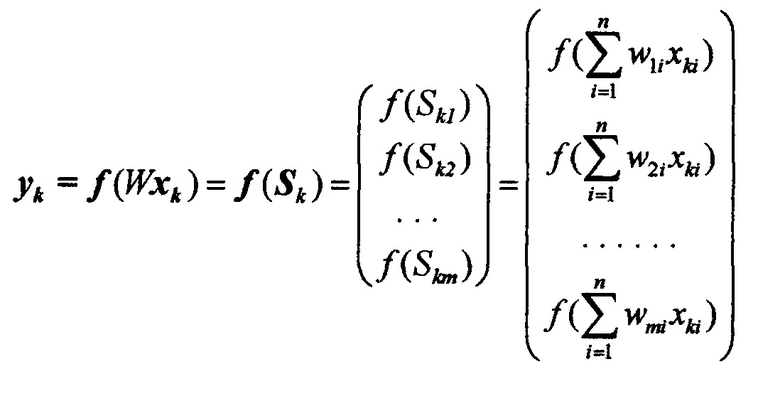
В общем случае yk=ƒ(Wxk-UП), где UП - величина порога.
Для каждого значения k ∈ [1, …, m] имеют место соотношения
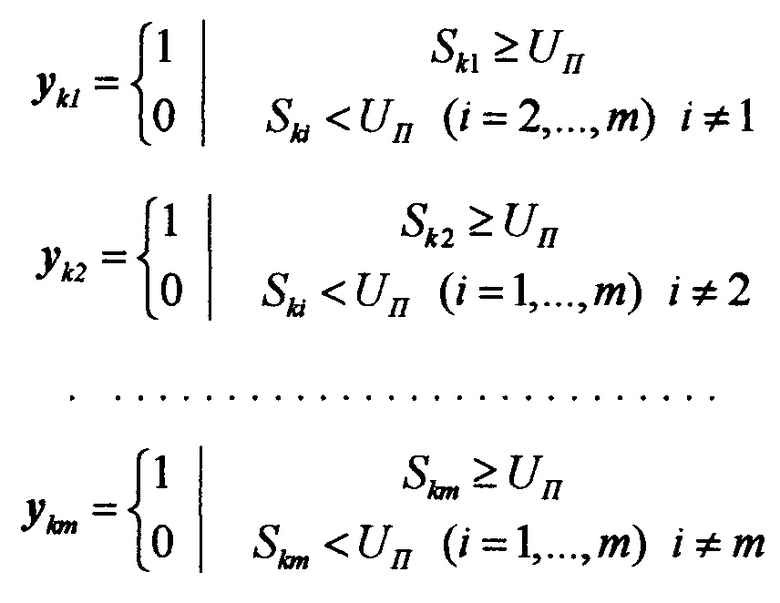
Таким образом, значения yki, Ski должны определяться соотношениями
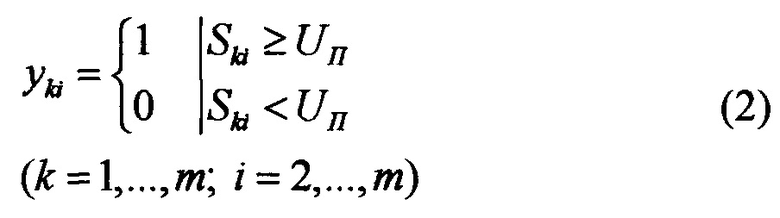
Существенной особенностью решений неравенств (1), (2) является бесконечнозначное число решений задачи определения весовых коэффициентов однослойного перцептрона. Для определения весовых коэффициентов, количество которых равно m×n, мы получаем m×m=m2 соотношений, представляющих неравенства. Следует, однако, иметь в виду, что существует бесконечно большое число множеств допустимых значений W, поскольку любая система линейных неравенств имеет бесконечно большое число решений.
Число неравенств для определения системы весовых коэффициентов при числе входных объектов m меньше, чем число n входных сигналов, что и вызывает еще больший произвол при образовании бесконечно большого множества решений неравенства. Реально реализация того или иного решения из их бесконечного множества определяется типом итерационного процесса, начальными условиями, с которых начинают итерации, величиной выбираемого порога UП и другими факторами.
Неравенства (2) имеют бесчисленное множество решений. Для нахождения этих решений используют различные итерационные процедуры. Однако какое …, что мы найдем после проведения решения неизвестно. Неизвестно и качество полученной системы обучения.
Некоторое прояснение ситуации дает известная теорема американского математика А.Б. Новикова [10]. Суть ее в том, что она утверждает при ряде ограничений (достаточно жестких), что обучение - итерационный процесс закончится за конечное время. А какой набор весовых коэффициентов и какое качество системы мы получаем - неизвестно.
Таким образом, все обучающие системы, использующие перцептроны на основе нейронов МакКаллока-Питтса, имеют органический неустранимый недостаток. Число решений неравенств (2), которые служат основой для нахождения весовых коэффициентов, бесконечно велико. То есть имеется не один, не 10 и не 100 вариантов весовых коэффициентов, а сколько угодно. Поэтому, чтобы нейронная сеть на основе перцептронов МакКаллока-Питтса, работала устойчиво необходимо использование дополнительных структурных дополнений стандартных схем. Этим вопросам посвящена предлагаемая работа. Уменьшение числа нежелательных наборов весовых коэффициентов достигается путем использования компараторов, ограничивающих диапазоны изменения значений весовых коэффициентов путем ограничения диапазонов напряжения в электрической схеме перцептрона.
Недостатки итерационных процедур для расчета весовых коэффициентов следующие:
1) длительность расчетов и ассортимент весовых коэффициентов сильно зависят от выбора начальных условий;
2) длительность расчетов и ассортимент весовых коэффициентов сильно зависят от способа, порядка изменения весовых коэффициентов - переменных, которые должны определять минимум функционала ошибки;
3) длительность расчетов и ассортимент весовых коэффициентов сильно зависят от величины изменения переменных; Обычно регулировку скорости изменения переменных реализуют параметром, называемым коэффициентом скорости обучения, который в общем является липовым критерием, не понятно, что регулирующим.
4) Качество обученной системы определяется несколькими параметрами, кроме условий обученности (2) определяется и рядом других параметров: величиной коэффициентов, поскольку они не должны быть очень маленькими (из-за влияния шумов) и слишком большими (поскольку слишком большие могут повредить систему), средние, умеренные также не всегда пригодны, поскольку может иметь место: 1) неустойчивость к изменениям параметров; 2) возникновение многозначности распознавания и другое.
5) В среде специалистов принято говорить, что набор весовых коэффициентов должен обеспечивать робастность системы, что может оказаться достаточно сложным.
Практическая реализация однослойного перцептрона на основе нейронов МакКаллока-Питтса с избирательным компарированием в виде электрической схемы
Рассмотрим практическую реализацию однослойного перцептрона на основе нейронов МакКаллока-Питтса с избирательным компарированием. Напомним, что компарированием называется ограничение пределов изменения электрической величины напряжения или тока.
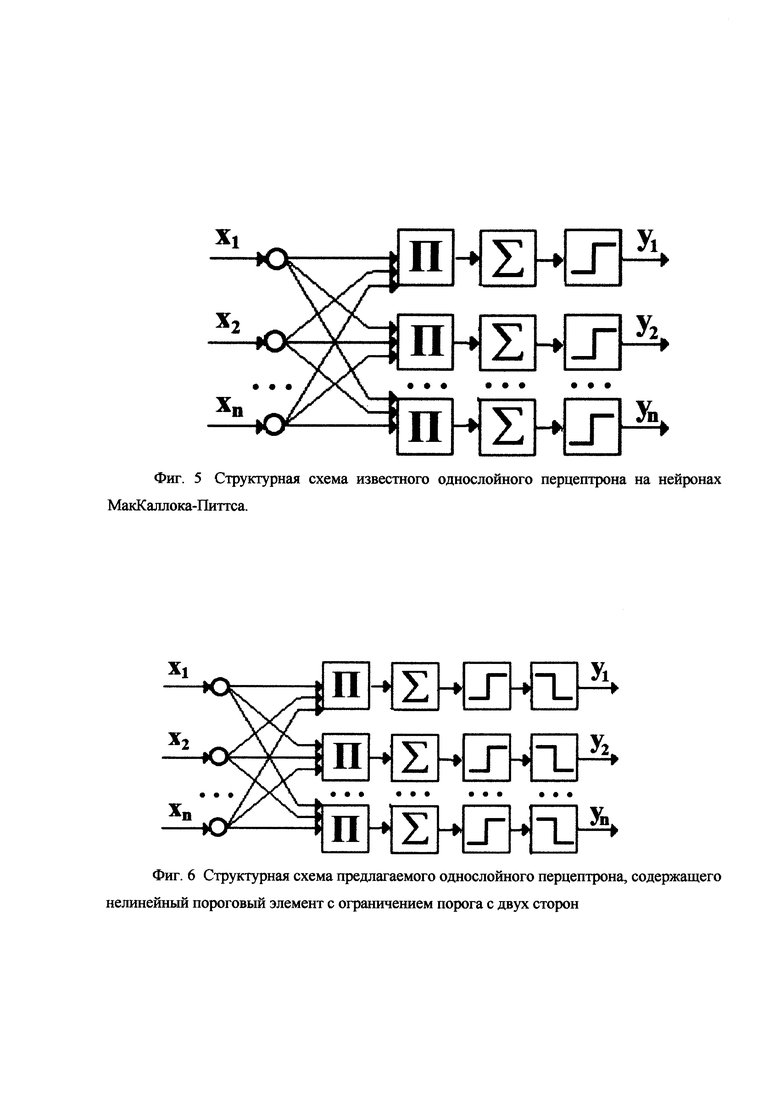
Сравним структурную схему известного однослойного перцептрона на нейронах Маккаллока-Питтса с предлагаемым перцептроном, содержащем компараторы. Изобразим стандартную структурную схему перцептрона с нейронами МакКаллока-Питтса, аналогичную в принципе схеме перцептрона, показанной на фиг. 1, на фиг. 5.
Фиг. 5. Структурная схема известного однослойного перцептрона на нейронах МакКаллока-Питтса.
На фиг. 5 приняты следующие обозначения: x=(х1, х2, …, xn) - входной сигнал; П - перемножители для образования сумм с весовыми коэффициентами; ∑ - суммы с весовыми коэффициентами;  - нелинейные пороговые преобразователи; y=(у1, y2, …, yn) - выходные сигналы, равные 0 или 1.
- нелинейные пороговые преобразователи; y=(у1, y2, …, yn) - выходные сигналы, равные 0 или 1.
Структурная схема предлагаемого однослойного перцептрона, содержащего нелинейный пороговый элемент с ограничением порога с двух сторон, показана на фиг. 6.
Фиг. 6. Структурная схема предлагаемого однослойного перцептрона, содержащего нелинейный пороговый элемент с ограничением порога с двух сторон
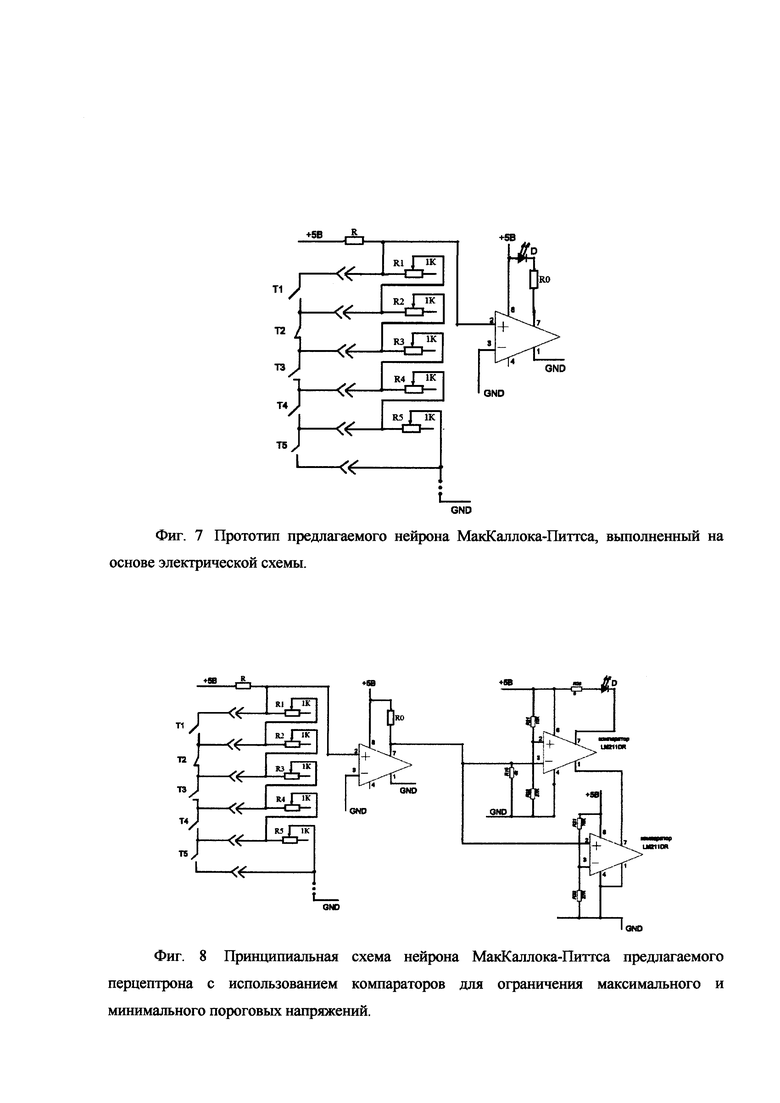
Предлагаемый перцептрон был реализован практически в электронном варианте на основе нейронов МакКаллока-Питтса, реализуемых в виде электрической схемы, показанной на фиг. 7.
Фиг. 7. Прототип предлагаемого нейрона МакКаллока-Питтса, выполненный на основе электрической схемы.
Предлагаемая схема нейрона МакКаллока-Питтса позволяет производить необходимый подбор весовых коэффициентов с помощью системы переменных сопротивлений, и осуществлять реагирование на превышение порогового значения с помощью светодиода.
Приведем теорию работы электрической схемы, показанной на фиг. 7. Напряжение, снимаемое с последовательной цепи сопротивлений, u равняется по закону Кирхгофа
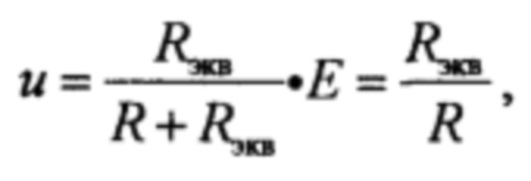
где 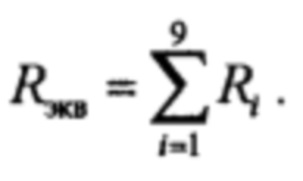
Выбираем величину сопротивления R значительно большей, чем сумма переменных сопротивлений, то есть
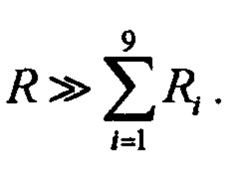
В этом случае, согласно первой формуле
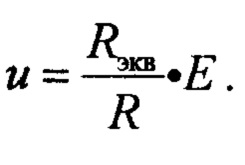
Для блок-схемы с учетом замыкания ключа Т2 получаем
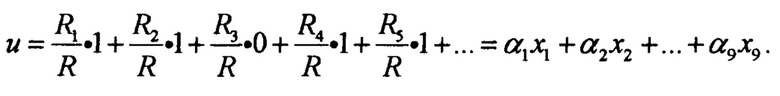
Таким образом, получаем, что сумма линейно зависит от величины переменных сопротивлений и, следовательно, линейно зависит от величины весовых коэффициентов. Подбор величины сопротивления R, переменных сопротивлений и коэффициента усиления добавочного усилителя осуществляется надлежащим образом. Входное сопротивление добавочного усилителя не должно шунтировать общее сопротивление переменных сопротивлений Rэкв, то есть должно выполняться условие Rвх >> Rэкв. Оно должно быть больше чем сопротивление R. Необходимость усилителя связана с тем, что напряжение источника питания ослабляется приблизительно в R/Rэкв раз.
Для повышения устойчивости распознавания входных объектов, уменьшения числа неправильных распознаваний, а также для устранения эффекта всеобщего распознавания при активации всех весовых коэффициентов до максимальных значений используется схема, содержащая компараторы - ограничители напряжений сверху и снизу. Принципиальная схема нейрона МакКаллока-Питтса с двухсторонним компарированием, то есть для ограничения максимального и минимального пороговых напряжений, предназначенного для использования в предлагаемом перцептроне, показана на фиг. 8.
Фиг. 8. Принципиальная схема нейрона МакКаллока-Питтса предлагаемого перцептрона с использованием компараторов для ограничения максимального и минимального пороговых напряжений.
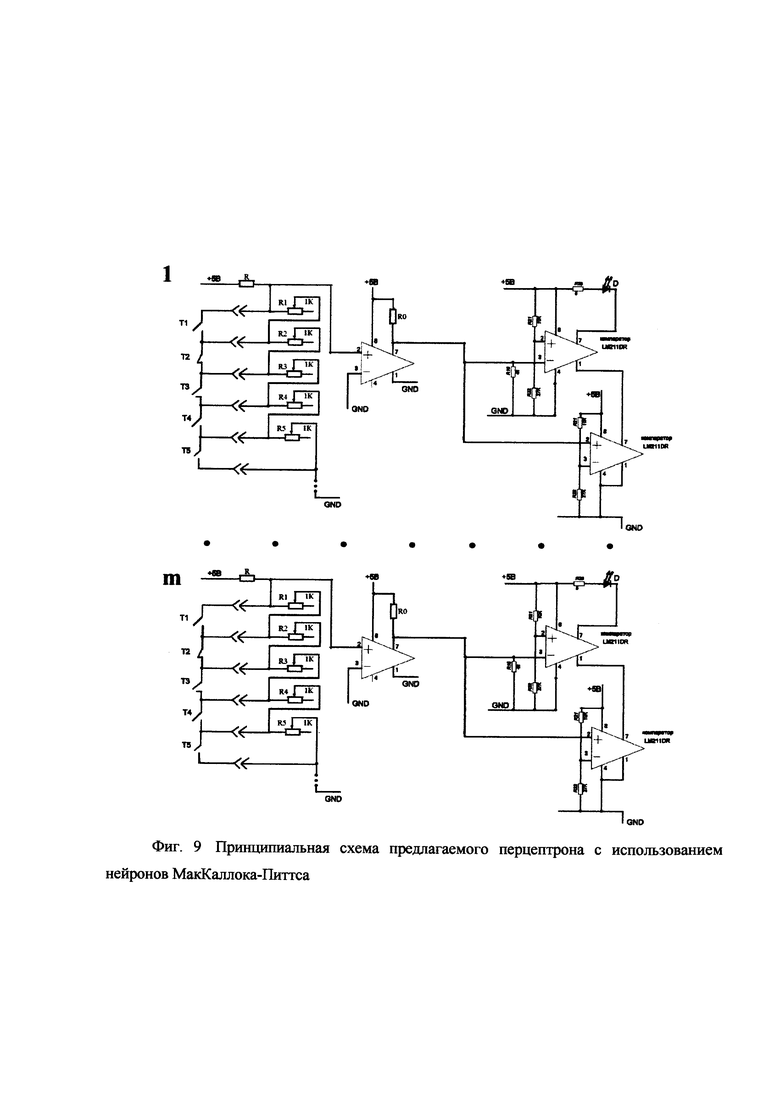
Принципиальная схема предлагаемого перцептрона с использованием нейронов МакКаллока-Питтса, использующих компараторы для ограничения максимального и минимального пороговых напряжений показана на фиг. 9.
Фиг. 9. Принципиальная схема предлагаемого перцептрона с использованием нейронов МакКаллока-Питтса с использованием компараторов для ограничения максимального и минимального пороговых напряжений.
Настройка перцептрона производится следующим образом. Переменные сопротивления устанавливаются в средне положение 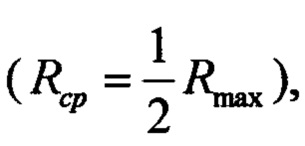 полагаем, что при этом считаем напряжение
полагаем, что при этом считаем напряжение 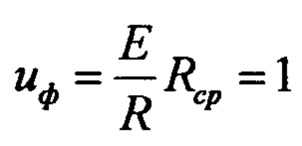 (Е - напряжение ЭДС источника питания). Устанавливаем
(Е - напряжение ЭДС источника питания). Устанавливаем 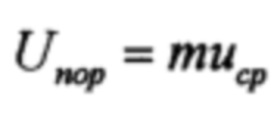 (m - заданное число).
(m - заданное число).
Далее устанавливаем зажигание порогового индикатора - светодиода при сумме
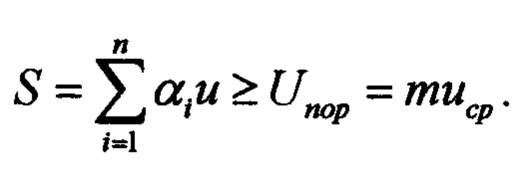
Таким образом, значение бинарной последовательности входных сигналов равные 1 или 0 устанавливаем путем закоротки переменных сопротивлений: если переменное сопротивление закорочено - шунтировано, то значение бинарной последовательности равно 0, если сопротивление не зашунтировано, то значение бинарной последовательности равно 1.
Раскрытие технического эффекта
Предлагаемый перцептрон позволяет реализовать следующие технические преимущества:
1. Повышение устойчивости распознавания, робастность, выражающееся в том, что небольшие изменения весовых коэффициентов не приводит к появлению ошибок распознавания.
2. Уменьшение неоднозначного распознавания при некоторых наборах весовых коэффициентов
3. Устранение эффекта всеобщего одновременного распознавания при максимально возможных значениях всех весовых коэффициентов.
4. Одновременное повышение устойчивости распознавания и уменьшения неоднозначного распознавания при избирательном компарировании значений сумм, не превышающих пороговых значений.
5. Повышение качества обучения нейронной сети за счет уменьшения количества наборов весовых коэффициентов, при которых имеет место неустойчивость и неоднозначность распознавания.
Экспериментальное подтверждение эффективности предлагаемого перцептрона с компараторами для ограничения интервалов изменения взвешенных сумм входных воздействий
Для проверки эффективности работы предлагаемого перцептрона он был реализован на экспериментальном макете. Макет содержал пульт управления с монитором 3×3, на котором можно было набрать буквы L, Т, X
Ниже приведен пример создания кластеров для английских букв L, T, X. Бинарные последовательности создаются на экране монитора с размером 3×3, как показано на фиг. 10.
Фиг. 10. Бинарные последовательности создаются на экране монитора с размером 3×3.
Бинарные последовательности букв L, T, X показаны в виде строк матрицы А

Величина компарированного порога распознавания была выбрана в пределах 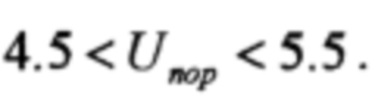 Таким образом,
Таким образом, 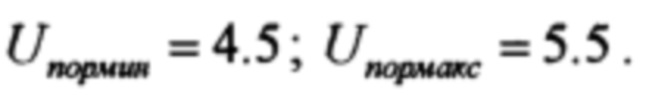
Величина весовых коэффициентов регулируется с помощью движков переменных сопротивлений. Превышение порогового уровня регистрируется индикатором, расположенным за переменными сопротивлениями. Спереди видны гнезда для каналов связи, подводящих входной сигнал х1, или х2, или х3, каждый из этих сигналов является бинарной последовательностью из 9 ячеек из 0 и 1. Внешний вид однослойного перцептрона на основе нейронов МакКаллока-Питтса, показан на фиг. 11.
Фиг. 11. Внешний вид однослойного перцептрона на основе нейронов МакКаллока-Питтса, содержащий три нейрона МакКаллока-Питтса.
Запланирована следующая настройка нейронов, входящих в состав перцептрона. Нейрон, расположенный сверху слева регистрирует букву L, нейрон, расположенный сверху в центре, регистрирует букву Т, нейрон, расположенный сверху справа, регистрирует букву X. Настройка нейронов заключается в установке с помощью движковых сопротивлений, хорошо видных на фиг. 12, необходимых для распознавания значений весовых коэффициентов.
Тестирование перцептрона на основе нейронов МакКаллока-Питтса производится следующим образом. На пульте управления, моделирующем рецепторы входных сигналов, активировать рецепторы - красные квадратики, соответствующие букве L. Индикатор опознавания буквы L «Нейрона L» МакКаллока-Питтса должен загореться, он показан красной стрелкой. Индикаторы опознавания остальных нейронов не должны гореть.
На пульте управления, моделирующем рецепторы входных сигналов, активировать рецепторы - красные квадратики, соответствующие букве Т. Индикатор опознавания буквы Т «Нейрона Т» МакКаллока-Питтса должен загореться, он показан красной стрелкой. Индикаторы опознавания остальных нейронов не должны гореть.
На пульте управления, моделирующем рецепторы входных сигналов, активировать рецепторы - красные квадратики, соответствующие букве X. Индикатор опознавания буквы X «Нейрона X» МакКаллока-Питтса должен загореться, он показан красной стрелкой. Индикаторы опознавания остальных нейронов не должны гореть. Весь процесс обучения иллюстрируется однослойным перцептроном, включающем три нейрона МакКаллока-Питтса. Перцептрон в режиме распознавания букв английского алфавита L, Т, X показан на фиг. 12.
Фиг. 12. Перцептрон в режиме распознавания букв английского алфавита L, Т, X. На фиг. 12 сверху слева перцептрон распознает букву L. На фиг. 12 сверху справа перцептрон распознает букву Т. На фиг. 12 внизу перцептрон распознает букву X.
На фиг. 12 сверху слева перцептрон распознает букву L, сверху справа перцептрон распознает букву Т, внизу в центре перцептрон распознает букву X. Весовые коэффициенты, требуемые для распознавания, были рассчитаны с помощью программного обеспечения «Программа расчета весовых коэффициентов перцептрона с помощью избирательного метода Монте-Карло» [9].
Определяются какие нейроны МакКаллока-Питтса должны реагировать на буквы L, Т, X (соответственно «Нейрон L», «Нейрон Т», «Нейрон X»).
На нейроне МакКаллока-Питтса «Нейрон L» с помощью ползунков установить веса: 1.2, 1.0, 0.0, 1.2, 0.0, 0.2, 0.6, 1.2, 0.8,
На нейроне МакКаллока-Питтса «Нейрон Т» с помощью ползунков установить веса: 1.4, 1.2, 0.6, 0.2, 1.2, 1.0, 0.2, 0.6, 0.2,
На нейроне МакКаллока-Питтса «Нейрон X» с помощью ползунков установить веса: 0.6, 0.6, 0.6, 0.2, 1.4, 0.8, 1.0, 0.0, 1.4.
Значения весовых коэффициентов рассчитываются с помощью инновационного программного обеспечения «Программа расчета весовых коэффициентов перцептрона с помощью избирательного метода Монте-Карло». Несколько вариантов обучающих коэффициентов рассчитаны заранее и используются в процессе обучения. В ходе обучения могут быть рассчитаны и другие наборы обучающих весовых коэффициентов. Эти наборы являются наглядным доказательством неоднозначности процесса обучения нейронных сетей, использующих нейроны МакКаллока-Питтса.
На основании изложенного выше была сформулирована формула изобретения в виде: Однослойный перцептрон на основе нейронов МакКаллока-Питтса, который реализует взвешенное с определенными весовыми коэффициентами суммирование входных сигналов и далее преобразует полученную сумму нелинейным пороговым преобразователем в 1, если порог превышен, и в 0, если превышения нет, отличающийся тем что, в качестве нелинейного преобразователя использует компараторы, которые осуществляют нелинейное пороговое преобразование суммы взвешенных входных значений только в полосе жестко заданного интервала значений от заданного нижнего до заданного верхнего значений, при чем, если сумма находится в полосе, то на выходе сумма преобразуется в 1, если сумма превышает верхнее значение полосы, то она преобразуется в 0.
Список литературы
1. Александров Ю.И., Анохин К.В., Соколов Е.Н., Греченко Т.Н. и др. Нейрон. Обработка сигналов. Пластичность. Моделирование. Фундаментальное руководство. Изд-во Тюменского государственного университета. 2008. 548 с.
2. Хайкин С. Нейронные сети: полный курс.2-е изд. М., "Вильямс", 2006.
3. Галушкин А.И. Нейронные сети. Основы теории. М., Горячая линия - Телеком, 2010.
4. Ежов А.А., Шумский С.А. Нейрокомпьютинг и его применения в экономике и бизнесе. М., МИФИ, 1998.
5. Мазуров М.Е. Синхронизация релаксационных автоколебательных систем, синхронизация в нейронных сетях. Изв. РАН. Сер. физ. 2018. Т. 82. №1. С. 83-87.
6. Мазуров М.Е. "Избирательные нейронные сети для распознавания сложных объектов." В: Математическая биология и биоинформатика: труды VI Международная конф. М.: МАКС Пресс. 2016. С. 82-83.
7. Мазуров М.Е. Импульсный нейрон, близкий к реальному. Патент на изобретение №2598298. 09.02.2015.
8. Мазуров М.Е. Однослойный перцептрон на основе избирательных нейронов. Патент на изобретение №2597497 13.01.2015.
9. Мазуров М.Е. «Программа расчета весовых коэффициентов перцептрона с помощью избирательного метода Монте-Карло». Свидетельство о государственной регистрации программы для ЭВМ №2019612170 12.02.2019.
10. Novikoff, А.В. On convergence proofs on perceptions. Symposium on the Mathematical Theory of Automata, 1962, 12, 615-622. Polytechnic Institute of Brooklyn


Изобретение относится к моделированию нейронных сетей, к нейрокибернетике и может найти применение при разработке нейрокомпьютеров, технических систем на основе нейронных сетей, для распознавания образов, анализа и обработки изображений. Техническим результатом является повышение эффективности работы устройства. Устройство реализует взвешенное с определенными весовыми коэффициентами суммирование входных сигналов и далее преобразует полученную сумму нелинейным пороговым преобразователем в полосе жестко заданного интервала значений от заданного нижнего до заданного верхнего значений, причем если сумма находится в полосе, то на выходе сумма преобразуется в 1, если сумма превышает верхнее значение полосы, то она преобразуется в 0. 12 ил.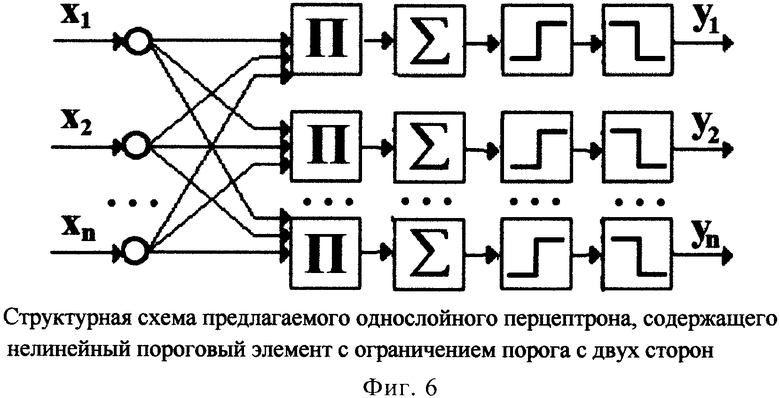
Однослойный перцептрон на основе нейронов МакКаллока-Питтса, который реализует взвешенное с определенными весовыми коэффициентами суммирование входных сигналов и далее преобразует полученную сумму нелинейным пороговым преобразователем в 1, если порог превышен, и в 0, если превышения нет,
отличающийся тем, что в качестве нелинейного преобразователя использует компараторы, которые осуществляют нелинейное пороговое преобразование суммы взвешенных входных значений только в полосе жестко заданного интервала значений от заданного нижнего до заданного верхнего значений, причем если сумма находится в полосе, то на выходе сумма преобразуется в 1, если сумма превышает верхнее значение полосы, то она преобразуется в 0.
| ИМПУЛЬСНЫЙ НЕЙРОН, БЛИЗКИЙ К РЕАЛЬНОМУ | 2015 |
|
RU2598298C2 |
| ОДНОСЛОЙНЫЙ ПЕРЦЕПТРОН НА ОСНОВЕ ИЗБИРАТЕЛЬНЫХ НЕЙРОНОВ | 2015 |
|
RU2597497C2 |
| НЕЙРОН, МОДЕЛИРУЮЩИЙ СВОЙСТВА РЕАЛЬНОГО НЕЙРОНА | 2014 |
|
RU2597495C2 |
| Способ получения алкиловых эфиров транс-хризантемовой кислоты | 1973 |
|
SU535898A3 |
| US 9442726 B1, 13.09.2016. | |||
Авторы
Даты
2020-08-07—Публикация
2019-06-19—Подача