Изобретение относится к цифровой обработке сигналов, в частности к спектральному анализу сигналов в базисе Фурье, и может быть использовано в радиолокации, радиосвязи и измерительной технике.
Известен способ спектрального анализа с использованием весовых окон Ханнинга, Кайзера, Дольфа-Чебышева и др. (Л. Рабинер, Б. Голд. Теория и применение цифровой обработки сигналов. М., 1978)
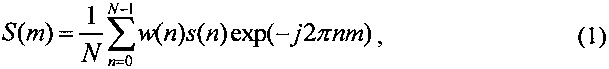
где n=0, … N-1, - номер временного отсчета,
m=0, … M-1, - номер спектральной составляющей, M=N,
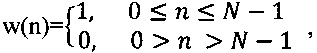
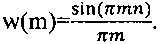
Взвешивание сигнала используется для сокращения уровня боковых лепестков. Боковые лепестки влияют не только на растекание спектра, при котором моногармонический сигнал воспроизводится целой группой спектральных составляющих; их уровень означает коэффициент передачи в полосе подавления и от его величины зависит выигрыш в отношении сигнал/шум, получаемый при спектральном преобразовании сигнала.
Лучшие из «классических» оконных функций, такие как Кайзера, Ханнинга, Дольфа-Чебышева, атомарные функции Кравченко и т.д., обеспечивают подавление «хвостов» частотной характеристики до уровней (-80 ÷ -100) дБ. Однако подавление боковых лепестков достигается ценой двукратного уменьшения разрешающей способности из-за расширения главного лепестка частотной характеристики спектроанализатора. Это общий недостаток для всех оконных функций: какова бы не была форма весового окна, оно сужает и без того короткий временной интервал сигнала, а сужение интервала во временной области неизбежно приводит к расширению спектра.
Двукратное расширение главного лепестка не только ухудшает разрешающую способность, но и двукратно увеличивает уровень шума. Эффективность выделения оконной функцией узкополосного сигнала из шума принято оценивать эквивалентной шумовой полосой (ЭШП), равной ширине полосы пропускания условного прямоугольного частотного фильтра, у которого площадь под кривой амплитудной частотной характеристики равна соответствующей площади оконной функции, а амплитуда равна эффективному значению коэффициента передачи ее главного лепестка:
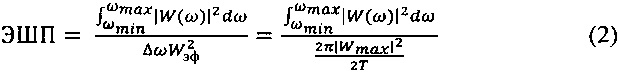
ЭШП измеряется в бинах - количестве шагов по частоте. Для идеальной (прямоугольной) частотной характеристики ЭШП=1. Для прямоугольного временного окна ЭШП=4.1, для окна Ханнинга ЭШП=4.01. Столь незначительная разница показывает неэффективность использования оконных функций для подавления шума. Для сравнения предлагаемый способ дает ЭШП в пределах 1.1÷1.5.
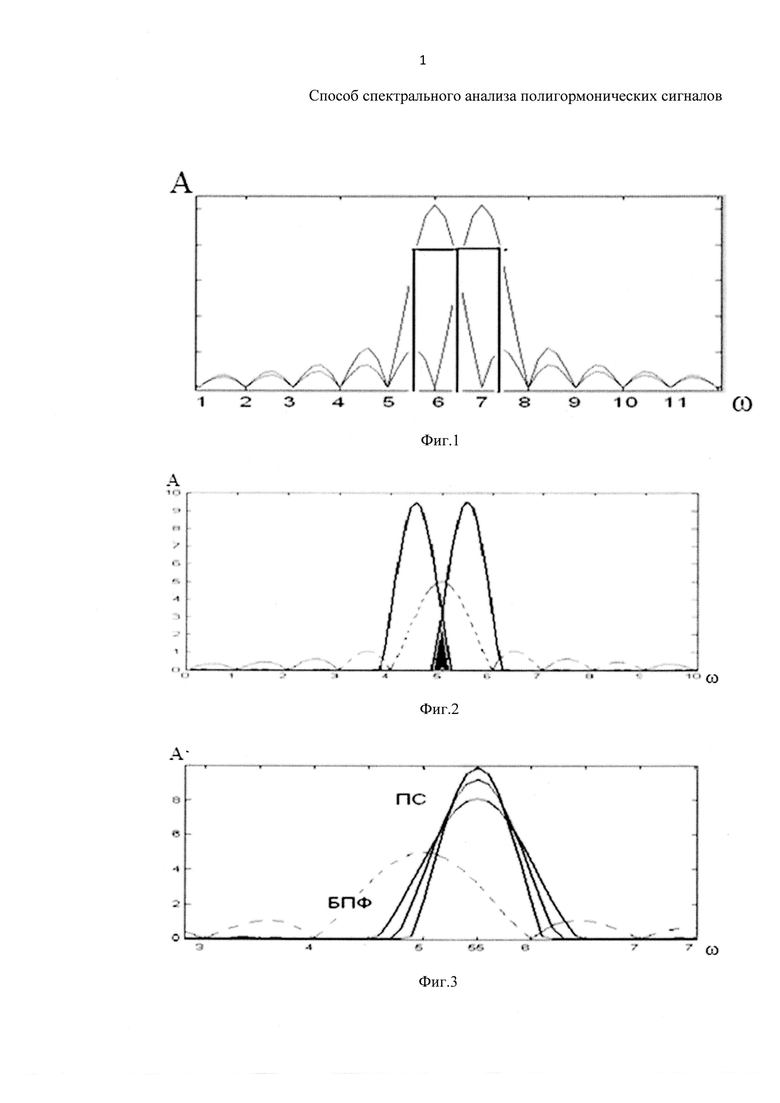
На фиг. 1 представлены частотные характеристики двух соседних каналов быстрого преобразования Фурье (БПФ) - спектроанализатора. Жирной линией показаны желаемые (идеальные) характеристики. В идеальном случае прямоугольность характеристики обеспечивает независимость коэффициента передачи от частоты и гарантирует отсутствие пропуска сигнала на границе между каналами при отсутствии их перекрытия. Чем границы более пологи, тем большее перекрытие необходимо для воспроизведения «пограничных» частот. Для способа БПФ реальная характеристика по первым нулям в два раза шире идеальной. При использовании окна Ханнинга характеристика становится шире еще в два раза. Не намного меньшее расширение главного лепестка дают окна Дольфа-Чебышева и Кравченко-Гаусса.
Известно также, что в случае, когда разрешение является главным параметром, приходится отказываться от способа непосредственного преобразования Фурье исходного сигнала, а использовать такие методы «сверхразрешения», как метод Писаренко, Прони, Кейпона (Современные методы спектрального анализа: Обзор. С.М. Кей, С.Л. Марпл, ТИИЭР, т. 69, №11, ноябрь 1981). Однако для этих методов характерно появление ложных частот и изменение амплитуды от количества анализируемых сигналов.
Известны также способы устранения эффекта растекания спектра подстройкой частоты дискретизации сигнала под частоту основной гармоники при анализе полигармонических сигналов. Так, в способе спектрального анализа полигармонических сигналов и устройстве для его реализации (RU 2363005) такая подстройка осуществляется путем домножения базисных функций Фурье на рассчитываемый коэффициент. Этот способ применим лишь при больших отношениях сигнал/шум, когда измерить основную частоту можно не прибегая к спектральной обработке.
Известен также способ спектрального анализа полигармонических сигналов (Мидлтон В. Введение в статистическую теорию связи. Т. 2. - М.: Сов. радио, 1962), в котором для анализа полигармонических сигналов в частотной области зачастую используется не амплитудный спектр - модуль комплексных отсчетов, полученых процедурой БПФ, - а мгновенная спектральная плотность мощности (СПМ):
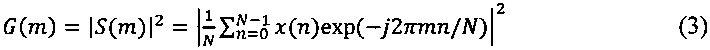
Учитывая комплексный характер S(m), операции вычисления СПМ представим в виде суммы произведений векторов реальной и мнимой части (перемножаем поэлементно комплексные и мнимые части спектров сигналов соответственно):
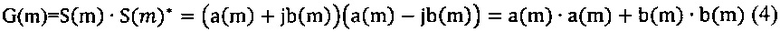
Перемножение вещественной и мнимой части отсчетов на свои копии не устраняет боковые лепестки частотной характеристики, однако по совокупности операций преобразования сигнала является наиболее близким аналогом-прототипом предлагаемого способа.
Техническим результатом предлагаемого способа является уменьшение уровня боковых лепестков без ухудшения разрешающей способности спектрального анализа, что влечет за собой и увеличение отношения сигнал/шум.
Указанный технический результат достигается тем, что над выборкой анализируемого сигнала производят преобразование Фурье, полученные вещественные и мнимые части комплексных отсчетов спектра умножают на свои копии и суммируют произведения, при этом исходную выборку сигнала дополняют спереди и сзади нулевыми интервалами, а вещественные и мнимые части отсчетов спектра умножают на одноименные части соседнего отсчета и после сложения векторов-произведений суммарный вектор умножается на минус один и обнуляются все отсчеты меньше нуля.
Сущность заявляемого технического решения поясняется на фиг. 2-8.
На фиг. 2 сплошной линией приведена частотная характеристика двух соседних каналов, полученная по предлагаемому способу, а пунктирной - частотная характеристика канала БПФ. Черным цветом показана зона перекрытия, в которой спектр моногармонического сигнала будет содержать вместо одного два ненулевых отсчета. Ширина главного лепестка почти в два раза уже лепестка БПФ.
На фиг. 3 показаны частотные характеристики одного канала БПФ (пунктир) и полученного предлагаемым способом. Ширину главного лепестка можно регулировать изменением количества нулевых отсчетов.
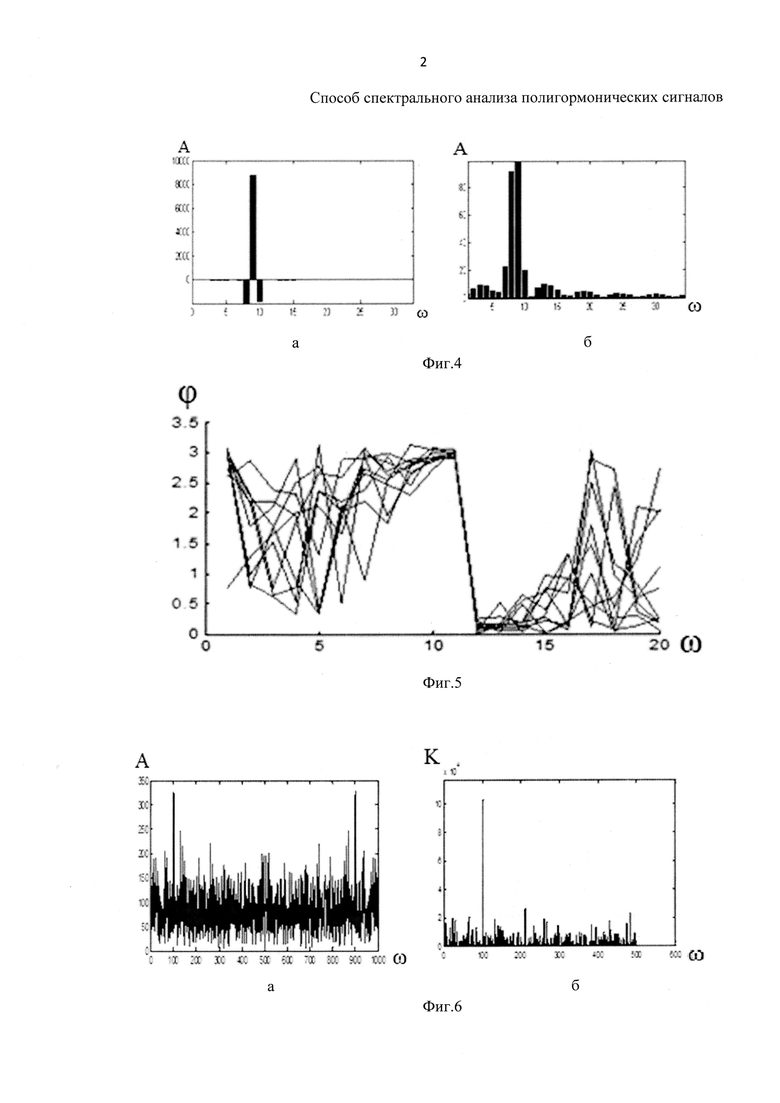
На фиг. 4а показан спектр синусоидального сигнала, полученный по предлагаемому способу (фиг. 4а) до операции обнуления отрицательных отсчетов спектра, а на фиг. 4б показан спектр полученный способом БПФ.
На фиг. 5 показано изменение фазы в спектре моногармонического сигнала частоты 11.5 при наложении шума (БПФ с прямоугольным окном) - даже в шумах разность фаз 11 и 12 отсчетов остается равной π.
На фиг. 6а показан амплитудный спектр зашумленного сигнала, на фиг. 6б - спектр, полученный предлагаемым способом из этих же отсчетов БПФ.
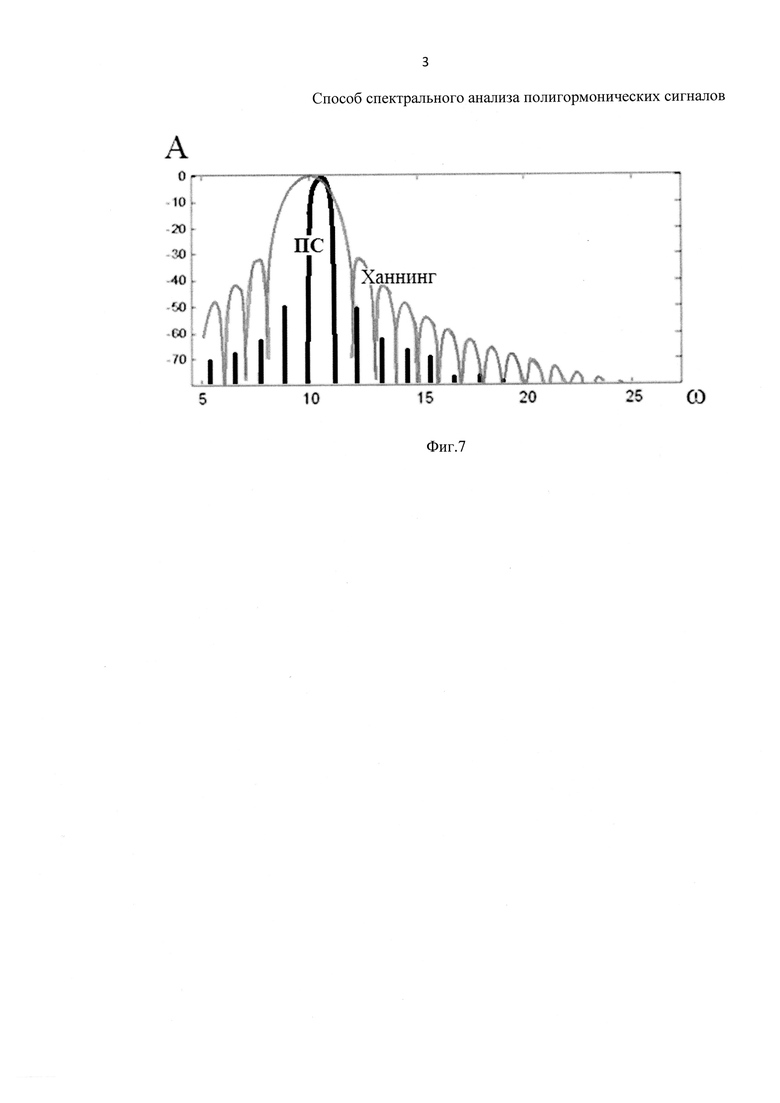
На фиг. 7 представлены частотные характеристики взвешивающего окна Ханнинга и ПС.
Последовательность выполнения операций преобразования сигнала по предлагаемому способу представлена в пунктах 1-4:
1. Выборка сигнала x(n), n=1, 2, … N, дополняется с обеих сторон k нулями:
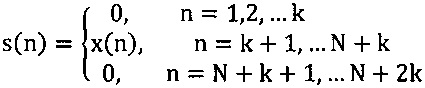
2. Выполняется преобразование Фурье (БПФ):
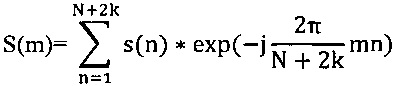
3. Вещественные и мнимые части каждого m-го спектрального отсчета умножаются на одноименные части следующего (m+1)-го отсчета, а произведения суммируются:
S(m)=a(m)+jb(m);
P(m)=a(m)⋅a(m+1)+b(m)⋅b(m+1).
4. Знак вектора P меняется на обратный, после чего отсчетам, имеющим отрицательный знак, присваивается нулевое значение или значение выбранной малой величины в случае пересчета P в децибелы:
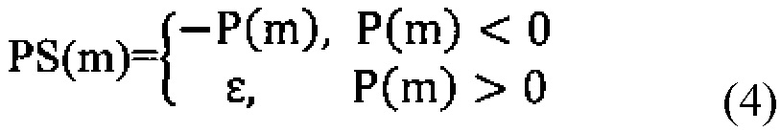
Сопоставляя результат с соотношением (4), можно перечисленные операции записать в форме:
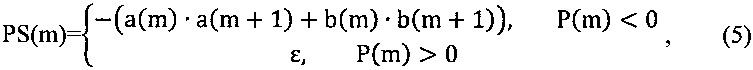
Полученную характеристику назовем «произведением соседних отсчетов спектра (ПС)».
В основе предлагаемого способа лежит следующая закономерность фазочастотной характеристики главного лепестка любого канала спектра Фурье: на всем интервале частот главного лепестка фаза изменяется линейно от -π до +π. Моногармонический сигнал, попавший из-за перекрытия в два соседних канала спектроанализатора, сформирует два спектральных коэффициента, которые можно представить в виде векторов на комплексной плоскости. Линейность фазочастотной характеристики обеспечивает взаимопротивоположное направление этих векторов - постоянный сдвиг фазы в 180 градусов. Наиболее эффективно выделить такие векторы позволяет их скалярное произведение, которое и формируется предлагаемым способом.
Независимо от фазы и частоты моногармонического сигнала и вещественные, и мнимые части комплексных коэффициентов соседних каналов спектра будут иметь противоположные знаки. Поэтому произведение их вещественных частей, также как и произведение их мнимых частей, будет отрицательным. Отрицательной будет и их сумма. Для приведения результата к привычной форме умножим сумму на -1. Теперь все отсчеты со знаком минус могут быть отброшены как не принадлежащие главному лепестку.
Данный способ может быть реализован с помощью вычислительных устройств.
Основными преимуществами предлагаемого способа являются:
1. Ширина главного лепестка наименьшая из всех известных оконных функций и даже в 1.42 раза уже прямоугольного окна. Это сводит к минимуму растекание спектра.
2. Низкий уровень боковых лепестков - большая их часть нули, а суммарный вес всех боковых лепестков составляет 0.16% от главного лепестка.
3. Прямоугольность главного лепестка (отношение ширины лепестка на уровне 0.5 к ширине на уровне нулей) значительно выше, чем у существующих окон (Таблица 1).

4. Расположение максимума главного лепестка соответствует середине интервала между отсчетами спектра, что максимально удобно для комбинированной обработки БПФ-ПС, гарантирующей двукратное увеличение разрешающей способности.
5. Ширину главного лепестка можно регулировать количеством добавляемых нулей, плавно увеличивая ее до ΔF=2 (фиг. 5). Поскольку добавление нулей приводит к увеличению временной базы анализа, одновременно в два раза может быть увеличена разрешающая способность.
6. Это наиболее значимое свойство предлагаемого способа: он дает увеличение отношения сигнал/шум на 10-20 дБ;.
Этот результат объясняется совместным влиянием следующих факторов:
- сужение главного лепестка почти в два раза и резкое уменьшение боковых лепестков дает суммарный выигрыш, который можно оценить отношением ЭШП прямоугольного окна и ПС:
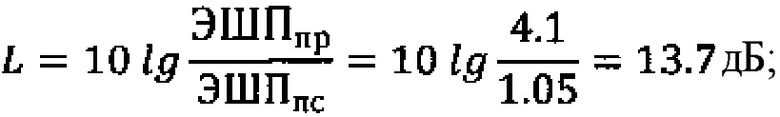
- в основе способа формирования ПС лежит скалярное произведение двух векторов а*b=|а||b|cosϕ, которое позволяет резко увеличить амплитуду синфазных (противофазных) сомножителей и выкинуть (обнулить) около 50% шумов за счет использования различия форм законов распределения разности фаз соседних отсчетов спектра шума и моногармонического сигнала;
- как и любая другая квадратичная характеристика (дисперсия, СПМ, корреляция), ПС контрастирует даже слабозаметную разницу амплитудных значений.
Эффективность очистки сигнала от шума позволяет оценить спектры на фиг. 6а и 6б. На фиг. 6а показан амплитудный спектр зашумленного сигнала 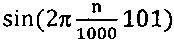 , на фиг. 6б - спектр, полученный предлагаемым способом из этих же отсчетов БПФ.
, на фиг. 6б - спектр, полученный предлагаемым способом из этих же отсчетов БПФ.
Еще более разительно различие спектров проявляется в логарифмическом масштабе. На фиг. 7 представлено наложение амплитудного спектра моногармонического сигнала, взвешенного окном Ханнинга, и спектра ПС.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ЦИФРОВОГО СПЕКТРАЛЬНОГО АНАЛИЗА ПЕРИОДИЧЕСКИХ И ПОЛИГАРМОНИЧЕСКИХ СИГНАЛОВ | 2008 |
|
RU2369879C1 |
| Устройство для измерения относительной задержки импульсных сигналов | 1982 |
|
SU1068886A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭКСТРАПОЛИРОВАННЫХ ЗНАЧЕНИЙ ДАЛЬНОСТИ И СКОРОСТИ СБЛИЖЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА С РАДИОЛОКАЦИОННЫМ ОБЪЕКТОМ | 2019 |
|
RU2709785C1 |
| УСТРОЙСТВО ОБНАРУЖЕНИЯ УЗКОПОЛОСНЫХ ШУМОВЫХ ГИДРОАКУСТИЧЕСКИХ СИГНАЛОВ НА ОСНОВЕ ВЫЧИСЛЕНИЯ ИНТЕГРАЛЬНОГО ВЕЙВЛЕТ-СПЕКТРА | 2007 |
|
RU2367970C2 |
| Цифровой анализатор | 1981 |
|
SU1057872A1 |
| МНОГОКАНАЛЬНАЯ СИСТЕМА ОБНАРУЖЕНИЯ ГИДРОАКУСТИЧЕСКИХ СИГНАЛОВ НА ОСНОВЕ ИНФОРМАЦИОННЫХ ПРИЗНАКОВ | 2024 |
|
RU2832248C1 |
| ОБНАРУЖИТЕЛЬ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ | 2006 |
|
RU2323452C1 |
| СПОСОБ ОБНАРУЖЕНИЯ ГИДРОАКУСТИЧЕСКИХ СИГНАЛОВ НА ОСНОВЕ ИНФОРМАЦИОННЫХ ПРИЗНАКОВ | 2024 |
|
RU2828828C1 |
| Цифровое устройство определения спектра принимаемых сигналов с высоким разрешением по частоте | 2020 |
|
RU2756024C1 |
| СПОСОБ КЛАССИФИКАЦИИ ГИДРОАКУСТИЧЕСКИХ СИГНАЛОВ ШУМОИЗЛУЧЕНИЯ МОРСКОГО ОБЪЕКТА | 2013 |
|
RU2546851C1 |
Способ относится к цифровой обработке сигналов, в частности к спектральному анализу сигналов в базисе Фурье, и может быть использовано в радиолокации, радиосвязи и измерительной технике. Сущность заявленного метода заключается в том, что выборку анализируемого сигнала дополняют нулями, производят преобразование Фурье, вещественные и мнимые части отсчетов спектра взаимно перемножаются на одноименные части соседнего отсчета, суммарный вектор умножается на минус один и обнуляются все отсчеты меньше нуля. Технический результат заключается в уменьшении уровня боковых лепестков без ухудшения разрешающей способности спектрального анализа, а также в увеличении отношения сигнал/шум. 7 ил., 1 табл.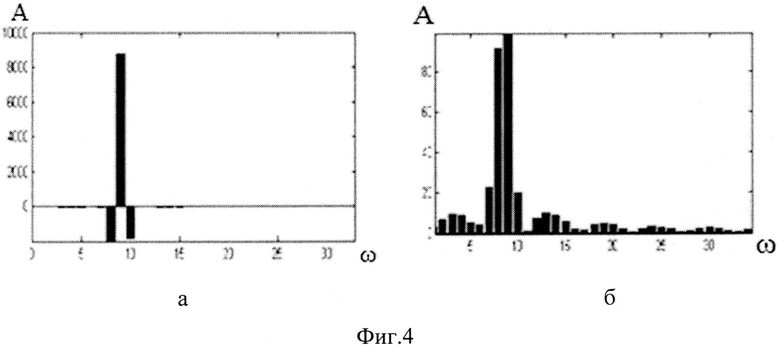
Способ спектрального анализа полигармонических сигналов, заключающийся в том, что над выборкой анализируемого сигнала производят преобразование Фурье, полученные вещественные и мнимые части комплексных отсчетов спектра умножают на свои копии и суммируют произведения, отличающийся тем, что исходную выборку сигнала дополняют спереди и сзади нулевыми интервалами, а вещественные и мнимые части отсчетов спектра умножают на одноименные части соседнего отсчета и после сложения векторов-произведений суммарный вектор умножается на минус один и обнуляются все отсчеты меньше нуля.
| СПОСОБ СПЕКТРАЛЬНОГО АНАЛИЗА ПОЛИГАРМОНИЧЕСКИХ СИГНАЛОВ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2008 |
|
RU2363005C1 |
| US 8321491 B2, 27.11.2012 | |||
| Цифровой анализатор спектра | 1985 |
|
SU1256044A1 |
| Анализатор спектра | 1986 |
|
SU1691852A1 |
| US 6882947 B2, 19.04.2005. | |||
Авторы
Даты
2017-02-21—Публикация
2015-12-14—Подача