Изобретение относится к радиолокации, в частности, может использоваться в радиолокационных системах (РЛС), обеспечивающих определение дальности до радиолокационных объектов (РЛО) и скорости сближения с ними.
В радиолокации наряду с формированием текущих оценок дальности до РЛО и скорости сближения с ними достаточно часто необходимо определять экстраполированные (прогнозируемые) значения дальности и скорости сближения в моменты времени, находящиеся за пределами интервала наблюдения и основанные на данных более ранних моментов времени.
Различают следующие виды экстраполяции: экстраполяция в заданную точку, экстраполяция на заданное число шагов, экстраполяция на фиксированный интервал [1].
Известен ряд способов определения экстраполированных значений дальности и скорости сближения с использованием алгоритмов фильтрации во временной и частотной областях. При применении временной фильтрации этапу прогнозирования предшествует итеративная процедура построения математической модели текущего поведения дальности во времени, основанная на теории идентификации и оценивания [2, с. 116-123]. Затем на этапе прогнозирования полученные оценки параметров математической модели используются в вычислительных алгоритмах для определения экстраполированных значений дальности и скорости. Наиболее известный способ экстраполяции параметров полиномиальной траектории по предварительно полученным оценкам этих параметров на момент последнего измерения применительно к решению задачи экстраполяции дальности и скорости приведен в [3, с. 199-200] и в [4, с. 156-158].
При применении частотной фильтрации на основе априорно заданной математической модели поведения дальности находится передаточная функция фильтра Винера, с помощью которого осуществляется экстраполяция дальности [5, с. 118-131, 151-159].
Таким образом, для реализации известных способов экстраполяции принципиально необходимым является знание математической модели поведения дальности и скорости во времени. Учитывая многообразие условий практического применения РЛС, разработаны различные математические модели, характеризующие временные процессы изменения дальности. Поскольку условия применения одной и той же РЛС при ее работе могут существенно изменяться, то для эффективного функционирования РЛС следует использовать ту математическую модель, которая в максимальной степени соответствует конкретному варианту применения. Для этого необходимо непрерывно отслеживать складывающуюся ситуацию в контролируемом РЛС пространстве с целью формирования ситуационной осведомленности об окружающей обстановке, что достаточно сложно обеспечить на практике.
Технической задачей изобретения является разработка способа определения экстраполированных значений дальности и скорости сближения летательного аппарата (ЛА) с РЛО по измерениям дальности, не требующего использования математических моделей относительного движения ЛА и РЛО, что позволит расширить арсенал известных способов экстраполяции дальности и скорости сближения.
Техническим результатом предлагаемого способа (изобретения) является реализация возможности определения экстраполированных значений дальности до РЛО и скорости сближения с ним на основе использования информации о спектрах последовательностей отсчетов дальности (по измерениям дальности). Использование спектральных характеристик для решения задач экстраполяции основывается на том, что в отличие от традиционных подходов к экстраполяции они характеризуют сигнал в целом и в каждом отсчете спектра присутствует информация о закономерностях динамики сигнала на доступном наблюдению отрезке предыстории. Предлагаемый способ снимает требования по точности соответствия моделей изменения во времени дальности и скорости сближения реальному процессу, предъявляемые в известных способах. Поскольку заявляемый способ не требует знания математической модели поведения во времени дальности, то он не имеет прототипа среди известных способов экстраполяции дальности и скорости сближения. Общим признаком с известными способами является лишь наличие процедуры формирования отсчетов дальности до РЛО.
Сущность предлагаемого способа определения экстраполированных значений дальности и скорости сближения на основе использования информации о спектрах заключается в том, что после излучения последовательности радиоимпульсов, приема отраженных от РЛО сигналов, фильтрации их от шумов, преобразования в цифровую форму дальнейшую обработку осуществляют с применением алгоритма полигармонической экстраполяции [6, с. 120-121] и Чебышевского спектрального дифференцирования [7, с. 78], существо которых сводится к следующему.
Задают: N-количество точек быстрого преобразования Фурье (БПФ), протяженность по времени t отрезка реализации Т; М (число Чебышевских точек М+1); τ-время упреждения.
Способ полигармонической экстраполяции состоит в том, что для экстраполяции дальности выполняют следующие действия:
- формируют N значений дальностей по принятым сигналам на периоде Т. Затем берется другой отрезок с периодом Т, сдвинутый относительно первого на время τ, и также формируют N значений дальностей. Полученные значения дальностей запоминают в виде массива, причем массив формируют так, что первые N значений дальностей (то есть принятых в течение первого периода Т [t-T-τ, t-τ]) запоминают в ячейках первого столбца этого массива, следующие N значений дальностей, полученных в течение второго периода Т [t-T, t], запоминают в ячейках второго столбца массива;
- значения дальностей, находящихся в 1-м и 2-м столбцах массива, подвергают операции БПФ на N точек, и результаты операции БПФ SI(ω) и SII(ω) запоминают. Каждое из полученных чисел этого массива представляет собой комплексную амплитуду спектра дальности;
- знание спектров SI(ω) и SII(ω) позволяет найти комплексный коэффициент передачи Е(ω) некоторого гипотетического четырехполюсника, обеспечивающего преобразование спектра при переходе от первой реализации ко второй, сдвинутой на интервал τ

Учитывая сохранение закономерностей процесса на интервале прогноза и на интервале предыстории, можно утверждать, что коэффициент преобразования спектра отрезка реализации при переходе от второй реализации к третьей, смещенной относительно второй на τ в область прогноза, изменится незначительно относительно коэффициента преобразования спектра при переходе от первого отрезка реализации ко второму;
- вычисляют значения комплексных амплитуд спектра последовательностей отсчетов дальности реализации, смещенной относительно второй на τ в область прогноза, на основании упомянутого утверждения
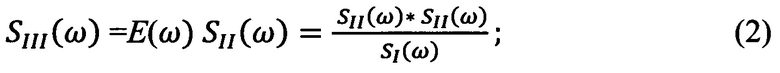
- по вычисленному спектру способом обратного БПФ определяют оценки отсчетов на интервале [t-T+τ, t+τ], который частично перекрывается с областью предыстории, а частично лежит в области прогноза [t, t+τ];
- оцененные значения дальности до РЛО Дэ в области прогноза [t, t+τ] выдают потребителям информации.
Типовые алгоритмы спектрального дифференцирования на равномерно распределенной сетке обеспечивают формирование точных оценок только для гладких периодических функций. В то же время информация о дальностях на интервале Т представляет собой негладкую функцию, когда она периодически продолжена. В такой ситуации целесообразно оценки дальностей формировать в неравномерно расположенных точках по дискретно поступающим равномерно измерениям.
Рассмотрим предлагаемый метод в приложении к определению скорости сближения при условии, что измерения дальности приходят с периодом To.
В общем случае точки должны быть распределены с плотностью (на единицу длины) [7, с. 42]

Здесь М - количество точек; х ∈ [-1, 1] - аргумент сетчатой функции.
Для предлагаемой системы обработки сигналов было выбрано Чебышевское спектральное дифференцирование, при котором х=cos θ и точки, удовлетворяющие (3),
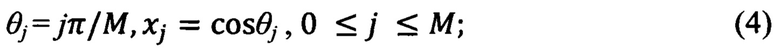
Чебышевские точки xj нумеруются справа налево.
Из полученных N оценок отсчетов дальности на периоде Т, который частично лежит в области прогноза, формируют М+1 значений отсчетов в Чебышевских точках До, …Дм, причем номера n полученных отсчетов, соответствующие j, задают формулой
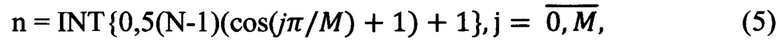
где символ INT означает операцию округления до целого полученного в фигурных скобках числа, cos(jπ/M)=xj.
Расширим эти отсчеты до вектора Д длиной 2М с Д2м-k-=Дk, 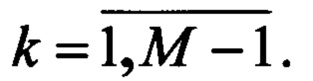
Значения отсчетов Д подвергают операции БПФ на 2М точек, и результаты операции БПФ запоминают в этом массиве. Каждое полученное число этого массива 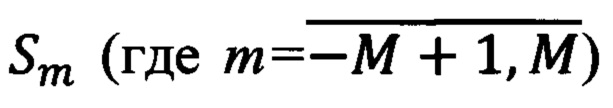 представляет собой комплексную амплитуду спектра сигнала с аргументом
представляет собой комплексную амплитуду спектра сигнала с аргументом 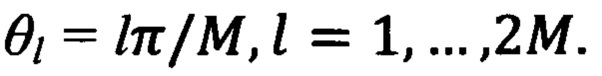
Каждое m-e значение комплексных амплитуд умножают на im, где i - мнимая единица, (за исключением m=М, для которого соответствующее произведение полагают равным нулевому значению), т.е. формируют значения комплексных амплитуд спектра производной сетчатой функции по θ, которые запоминают в соответствующих ячейках упомянутого массива.
2М значений комплексных амплитуд подвергают операции обратного БПФ на 2М точек, и результаты операции обратного БПФ запоминают в упомянутом массиве. Каждое полученное число этого массива 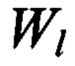 представляет собой производную по θ.
представляет собой производную по θ.
По полученным производным по θ и протяженности отрезка реализации Т определяют значения производной по t во внутренних точках сетки, т.е. вычисляют скорость сближения Vcбл ЛА с РЛО по формуле:
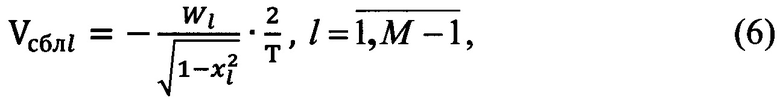
где 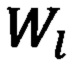 - производные Д по θ,
- производные Д по θ,
а для первой точки существует особая формула, которая не используется из-за больших ошибок дифференцирования [7, с. 78].
В начальной внутренней точке (так как Чебышевские точки нумеруются справа налево, начальные точки оказываются конечными) ошибки дифференцирования также велики и поэтому значение первого внутреннего отсчета при 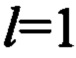 также игнорируется.
также игнорируется.
В проэкстраполированном участке [t, t+τ] вычисляют среднее значение экстраполированной скорости сближения в соответствии с формулой

где 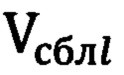 - значения скорости сближения в [t, t+τ] моменты времени,
- значения скорости сближения в [t, t+τ] моменты времени,
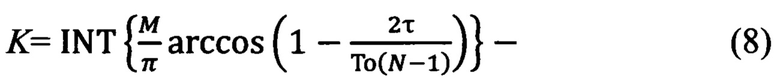
число вычислений (6) в этом интервале.
Оцененные значения скорости сближения 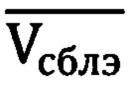 с РЛО выдают в систему управления ЛА для формирования и реализации управляющих сигналов.
с РЛО выдают в систему управления ЛА для формирования и реализации управляющих сигналов.
Далее через интервал времени τ описанные действия по определению экстраполированных на τ значений дальности и скорости сближения повторяют.
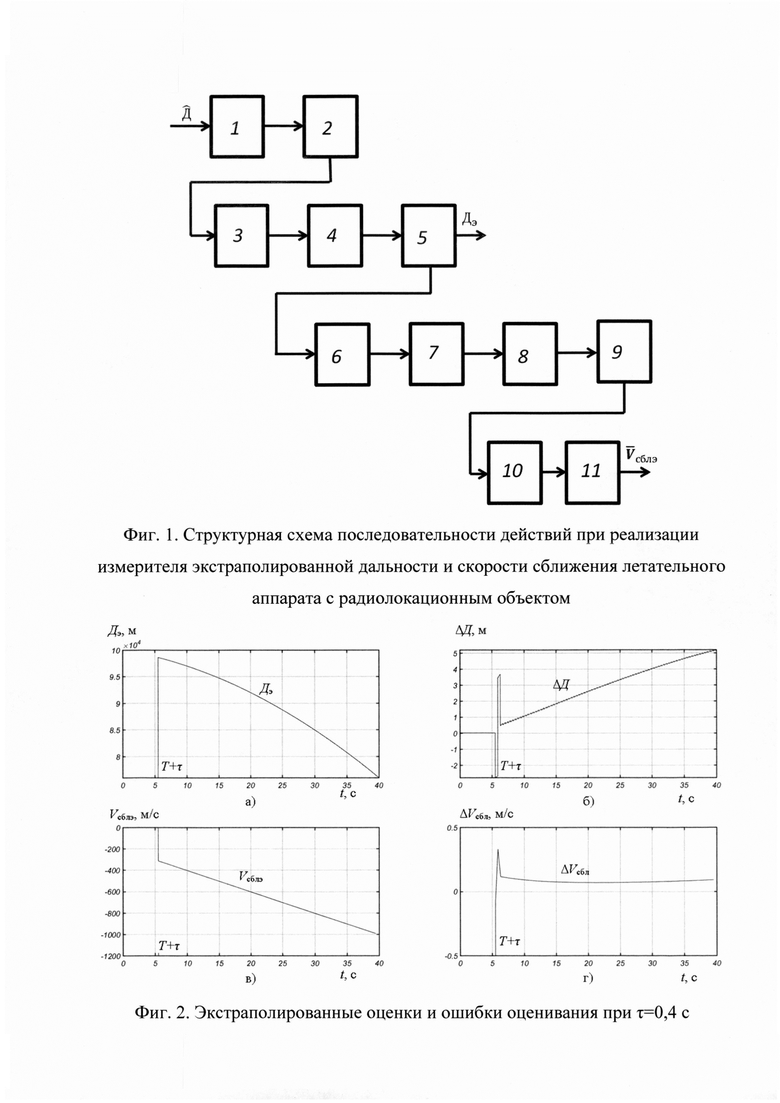
На фиг. 1 представлена блок-схема последовательности действий при реализации измерителя экстраполированной дальности и скорости сближения (ИЭДиС) ЛА с РЛО, где:
1 - измерение дальностей на интервале времени Т через интервал τ;
2 - запоминание отсчетов дальностей;
3 - выполнение БПФ;
4 - определение спектра дальности до РЛО, смещенной в область прогноза;
5 - выполнение обратного БПФ;
6 - определение отсчетов дальностей до РЛО в Чебышевских точках и расширенного вектора;
7 - БПФ в Чебышевских точках;
8 - умножение на im, 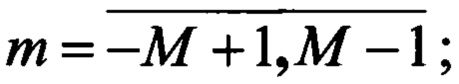
9 - выполнение обратного БПФ;
10 - определение экстраполированной скорости сближения с РЛО;
11 - вычисление средней скорости сближения.
В результате выполнения процедуры 1 формируется периодическая последовательность отсчетов дальностей, поступающих с периодом То. Затем выполняется действие 2 запоминания полученных значений дальности в виде массива в ячейках первого и второго столбцов. В каждом столбце запоминаются N отсчетов дальности, сдвинутых относительно друг друга на время упреждения τ. Число общих отсчетов дальности в столбцах равно (Т-τ)/То.
Принципы измерения и получения отсчетов дальности и выполняемые при этом действия достаточно подробно изложены в литературе, например, в монографии [8, с. 137-152].
Основная новизна изобретения состоит в том, что в предлагаемом способе для определения экстраполированных значений дальности и скорости используются два алгоритма: алгоритм полигармонической экстраполяции 3, 4, 5 и Чебышевское спектральное дифференцирование 6-10, функционирование которых описано выше.
Если значения дальности Д и скорости сближения Vcблэ не известны до начала работы ИЭДиС, то первый после включения интервал Т+τ ИЭДиС работает при условии, что экстраполированная дальность Дэ не сформирована. В этом случае ИЭДиС осуществляет измерение значения дальности Д, которое и используется в момент Т+τ для определения Дэ, а значение Vсблэ0 приравнивают нулю.
Использование заявленного способа не предъявляет дополнительных требований к существующим измерителям дальности, а также к принципам построения вычислителей, поэтому он может быть реализован в большинстве из них.
На фиг. 2 приведены графики, иллюстрирующие поведение экстраполированных значений прогнозов дальности и скорости сближения и ошибок прогнозирования с временем упреждения 0,4 с и повторением прогноза через каждые 0,4 с на участке движения с постоянным ускорением сближения, полученные в результате моделирования. На фиг. 2 а) и б) показаны изменения во времени значений прогнозированной дальности Дэ и ошибок прогнозирования в определении дальности ΔД, а на фиг. 2 в) и г) изменение во времени значений прогнозированной скорости сближения Vсблэ и ошибок прогнозирования в определении скорости ΔVcбл соответственно.
При моделировании были сделаны следующие предположения:
-изменение скорости сближения Vсбл является процессом с постоянным ускорением вида Vсбл=Vсбл0+jсбt, где jсб=-20 м/с2;
- число точек для дискретного преобразования Фурье N=512;
- изменение дальности Д является процессом с неизменным коэффициентом преобразования спектра отрезка реализации измерения дальности при переходе от первой реализации ко второй и при переходе от второй реализации к следующей, смещенной относительно предыдущего отрезка на τ=0,4 с.
Графики, отображающие значения экстраполированных дальности и скорости сближения построены для моделируемого полета ЛА с начальной скоростью Vсбл0=-200 м/с, с дальностью, изменяющейся по закону Д=100000-200t-10t2 м, периодом измерения дальностей То=0,01 с, числом Чебышевских точек интерполяции 21 (М=20), с временем упреждения τ=0,4 с через 5,5 с после начала измерения и осреднением по 3-й и 4-й Чебышевским точкам.
Из приведенных графиков следует, что экстраполированная скорость сближения и экстраполированная дальность определяются с точностью ΔVcбл=0,1 м/с, ΔД=5 м через 5,5 с после начала измерения дальности.
Таким образом, совокупность и последовательность выполнения изложенных выше действий обеспечивает реализацию нового способа экстраполяции дальности и скорости сближения без использования математических моделей поведения дальности и скорости сближения ЛА и РЛО.
Использование изобретения по сравнению с известными способами позволяет упростить оценивание экстраполированной дальности и скорости сближения и обеспечить высокую точность их определения.
Список использованных источников
1. Бар Шалом Я. Траекторная обработка. Принципы, способы и алгоритмы: в 2. ч. Часть 2. Пер. с англ. Д.Д. Дмитриева. - М.: МГТУ им. Н.Э. Баумана. 2011.
2. Грешилов А.А. Анализ и синтез стохастических систем. Параметрические модели и конфлюентный анализ. - М.: Радио и связь, 1990.
3. Кузьмин С.З. Цифровая радиолокация. Введение в теорию. - Киев: Издательство КВIЦ. 2000.
4. Кузьмин С.З. Основы проектирования систем обработки радиолокационной информации. - М.: Радио и связь, 1986.
5. Шахтарин Б.И. Фильтры Винера и Калмана. - М.: Гелиос АРВ, 2008.
6. Евсеев А.П., Сысоев Д.А. Применение алгоритма полигармонической экстраполяции для реставрации аудиозаписей. // Труды Научной конференции по радиофизике. - Нижний Новгород: ННГУ, 2008.
7. Lloyd N. Trefethen. Spectral Methods in Matlab, SIAM, Philadelphia, 2000.
8. Меркулов В.И. и др. Оценивание дальности и скорости в радиолокационных системах. Ч. 1. - М.: Радиотехника. 2004.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЙ И СКОРОСТИ СБЛИЖЕНИЯ С НИМИ В ОДНОПОЗИЦИОННЫХ РАДИОЛОКАЦИОННЫХ СИСТЕМАХ | 2002 |
|
RU2232402C2 |
| Способ распознавания варианта наведения подвижного объекта на один из летательных аппаратов группы | 2019 |
|
RU2713212C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ И ПАРАМЕТРОВ ДВИЖЕНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЙ ПО ИЗМЕРЕНИЯМ ИХ НЕСУЩЕЙ ЧАСТОТЫ | 2021 |
|
RU2776078C1 |
| СПОСОБ ВНЕШНЕГО РАДИОЛОКАЦИОННОГО ВЫЯВЛЕНИЯ ФАКТА НАЛИЧИЯ ТРАЕКТОРНЫХ НЕСТАБИЛЬНОСТЕЙ ПОЛЕТА У ВОЗДУШНОГО ОБЪЕКТА ПО СТРУКТУРЕ ЕГО ИМПУЛЬСНОЙ ХАРАКТЕРИСТИКИ | 2014 |
|
RU2562060C1 |
| СПОСОБ И СИСТЕМА СОВМЕСТНОЙ ОБРАБОТКИ ИЗМЕРЕНИЙ ДАЛЬНОСТИ И СКОРОСТИ ДЛЯ МНОГОДИАПАЗОННОЙ РАДИОЛОКАЦИОННОЙ СИСТЕМЫ КРУГОВОГО ОБЗОРА | 2014 |
|
RU2572079C2 |
| Способ сопровождения крылатой ракеты при огибании рельефа местности в различных тактических ситуациях | 2021 |
|
RU2760951C1 |
| СПОСОБ РАСПОЗНАВАНИЯ СВОБОДНОПЛАВАЮЩИХ МАЛОРАЗМЕРНЫХ ОБЪЕКТОВ | 1987 |
|
SU1841026A1 |
| РАДИОЛОКАЦИОННАЯ СИСТЕМА С ПРОГНОЗОМ ПРОПАДАНИЯ ЦЕЛЕЙ В ЗОНАХ ДОПЛЕРОВСКОЙ РЕЗЕКЦИИ | 2009 |
|
RU2408030C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТ И ПАРАМЕТРОВ ДВИЖЕНИЯ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЙ С ПОМОЩЬЮ ОДНОПОЗИЦИОННОЙ ПАССИВНОЙ РАДИОЛОКАЦИОННОЙ СТАНЦИИ | 2020 |
|
RU2754349C1 |
| СПОСОБ РАДИОЛОКАЦИОННОГО ИЗМЕРЕНИЯ СКОРОСТИ ОБЪЕКТА | 2009 |
|
RU2414721C1 |
Изобретение относится к радиолокационным системам и заключается в том, что по принятым от радиолокационного объекта (РЛО) радиосигналам оценивают значения расстояния от летательного аппарата (ЛА) - носителя РЛС до РЛО. Достигаемый технический результат – возможность определения экстраполированных значений дальности до РЛО и скорости сближения с ним. По оцененным значениям дальностей до РЛО, применяя алгоритм полигармонической экстраполяции и чебышевское спектральное дифференцирование, оценивают экстраполированную дальность до РЛО и скорость сближения с ним. Эти данные передают потребителям, например, в систему управления ЛА для формирования и реализации управляющих сигналов. 2 ил.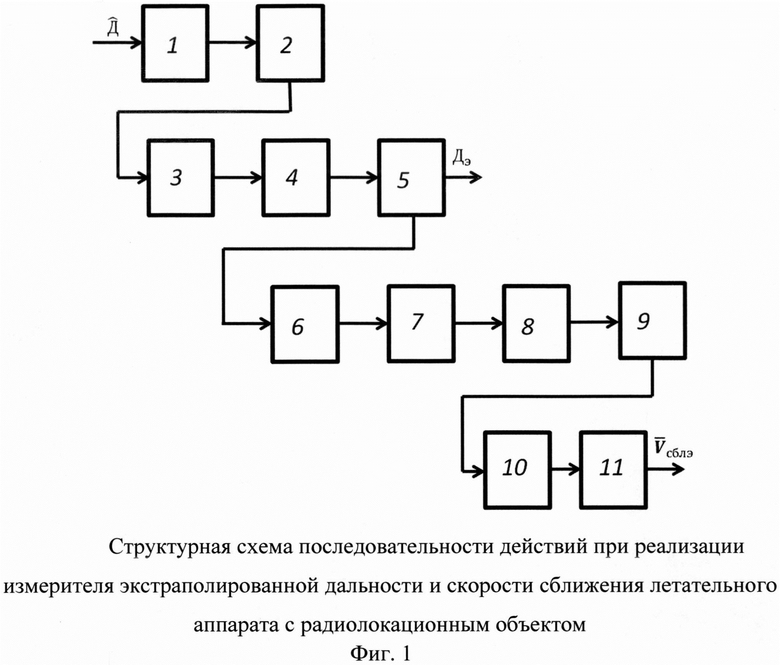
Способ определения экстраполированных значений дальности и скорости сближения летательного аппарата (ЛА) с радиолокационным объектом (РЛО), заключающийся в том, что в РЛС ЛА формируют оценки дальностей до РЛО, задают количество N точек быстрого преобразования Фурье (БПФ), протяженность по времени t отрезка реализации Т, задают число чебышевских точек М+1, τ - время упреждения;
формируют последовательность N значений дальностей по принятым сигналам от РЛО на периоде Т, затем на другом отрезке с периодом Т, сдвинутым относительно первого на время τ, также формируют N значений дальностей, полученные значения дальностей запоминают в виде массива, причем массив формируют так, что первые N значений дальностей запоминают в ячейках первого столбца этого массива, следующие N значений дальностей, полученных в течение второго периода, запоминают в ячейках второго столбца массива;
выполняют БПФ на N точках над значениями дальностей, находящихся в первом и втором столбцах массива, и результаты БПФ SI(ω) и SII(ω) запоминают;
по определенным значениям спектров дальности SI(ω) и SII(ω) вычисляют значение спектра дальности SIII(ω)
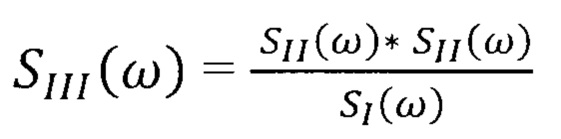
реализации, смещенной на т в область прогноза;
по вычисленному спектру дальности до РЛО SIII(ω) способом обратного БПФ определяют значения отсчетов дальности на интервале, который частично перекрывается с областью предыстории, а частично лежит в области прогноза [t, t+τ];
оцененные значения дальности Дэ в области прогноза выдают потребителям информации;
по N оцененным значениям дальностей до РЛО, частично лежащим в области прогноза, формируют М+1 значений дальностей в чебышевских точках xj=cosθj, где θj=jπ/M, для этого по номеру n отсчета определяют значение отсчета дальности Дj в j-й чебышевской точке, причем номер отсчета, соответствующий j, задают правилом
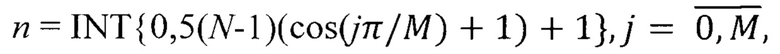
где INT означает операцию округления до целого числа, полученного в фигурных скобках;
полученные значения отсчетов запоминают в виде массива 2М значений, причем массив формируют так, что первые М+1 значений дальностей представляют полученные отсчеты в чебышевских точках, следующие МЛ значений дальностей Д2M-k=Дk, k=1, 2, …, М - 1;
выполняют БПФ на 2М точках над значениями дальностей, находящихся в 2М-массиве, и результаты БПФ запоминают в упомянутом массиве;
путем умножения каждого m-го значения массива, где 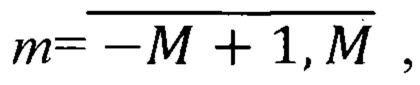 на im, где i - мнимая единица, при этом если значение m=М, то упомянутое произведение обнуляют, вычисляют значения комплексных амплитуд спектра производной по θ, где
на im, где i - мнимая единица, при этом если значение m=М, то упомянутое произведение обнуляют, вычисляют значения комплексных амплитуд спектра производной по θ, где 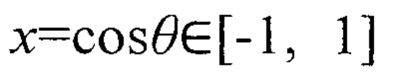 - первоначальный аргумент сетчатой функции, которые запоминают в соответствующих ячейках упомянутого массива;
- первоначальный аргумент сетчатой функции, которые запоминают в соответствующих ячейках упомянутого массива;
выполняют обратное БПФ на 2М точках над комплексными значениями амплитуд спектра производной по θ, находящихся в массиве, и результаты обратного БПФ Wl, 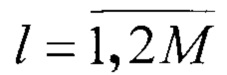 запоминают в упомянутом массиве,
запоминают в упомянутом массиве,
по номеру отсчета, причем чебышевские точки xl нумеруют справа налево, и значению протяженности отрезка реализации Т определяют значение скорости Vсбл сближения ЛА с РЛО во внутренних точках сетки по правилу
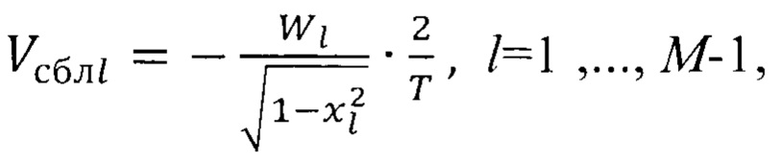
где Wl - производные Д по θ,
Т - значение протяженности отрезка реализации;
для отсчетов, лежащих в области прогноза, путем деления суммы отсчетов на их число вычисляют среднее значение скорости сближения, при этом значение первого внутреннего отсчета при l=1 игнорируют;
оцененное значение средней скорости сближения передают в систему управления ЛА для формирования и реализации управляющих сигналов известным способом.
| КОМПЛЕКСНЫЙ ИЗМЕРИТЕЛЬ ДАЛЬНОСТИ, СКОРОСТИ И УГЛОВЫХ КООРДИНАТ ДЛЯ РАДИОТЕХНИЧЕСКИХ СИСТЕМ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2003 |
|
RU2251711C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ДАЛЬНОСТИ ДО ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЙ И СКОРОСТИ СБЛИЖЕНИЯ С НИМИ В ОДНОПОЗИЦИОННЫХ РАДИОЛОКАЦИОННЫХ СИСТЕМАХ | 2002 |
|
RU2232402C2 |
| СПОСОБ И СИСТЕМА СОВМЕСТНОЙ ОБРАБОТКИ ИЗМЕРЕНИЙ ДАЛЬНОСТИ И СКОРОСТИ ДЛЯ МНОГОДИАПАЗОННОЙ РАДИОЛОКАЦИОННОЙ СИСТЕМЫ КРУГОВОГО ОБЗОРА | 2014 |
|
RU2572079C2 |
| СПОСОБ КОМБИНИРОВАННОГО СГЛАЖИВАНИЯ КООРДИНАТ ПОДВИЖНОЙ ЦЕЛИ | 2013 |
|
RU2556024C2 |
| EP 1902329 B1, 13.02.2013 | |||
| US 7132975 B2, 07.11.2006 | |||
| JP 2007093542 A, 12.04.2007. | |||
Авторы
Даты
2019-12-20—Публикация
2019-03-06—Подача