Изобретение относится к способам организации мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения выходного параметра и может быть использовано в системах контроля и управления различных динамических систем, обладающих хаотическими свойствами.
Известен способ контроля стохастическим процессом, заключающийся в выделении n-мерного вектора выходного параметра Y, определении и минимизации величины среднеквадратического отклонения (СКО) выходного параметра. Типичным примером реализации известного способа является задача определения оптимальной передаточной функции системы, обеспечивающей минимизацию дисперсии или среднеквадратической ошибки выходного параметра. Способы оптимальной фильтрации векторных случайных сигналов реализуются при решении задач построения оптимального фильтра Винера и задач построения систем фильтра Калмана [1, 2].
Известно устройство для измерения характеристик случайного процесса, в котором повышение достоверности определения вида симметричного закона распределения вероятности случайных параметров обеспечивается за счёт определения энтропийного коэффициента и значения контр эксцесса [3]. Несмотря на то, что данное устройство за счёт процедур сравнения коэффициента энтропии и контрэксцесса позволяет установить нормальное, треугольное, арксинусоидальное, трапецеидальное, антимодальное и равномерные распределения, для всех остальных форм устройство выдаёт сообщение «распределение не определено». В устройстве за счёт включения процедуры сравнения характеристики асимметрии реализовано выделение не симметричного распределения без установления его вида.
Известен способ контроль условной плотности распределения выходного сигнала для обобщённых нелинейных и негаусовых стохастических систем [4], при котором оптимальное управление достигается путем встраивания в динамическую систему рекурсивной формулы и минимизации разности между условной выходной и целевой плотности вероятности. В этом случае особенность контроля состоит в использовании частичной аппроксимации траектории в качестве целевой плотности распределения. Основной недостаток контроля состоит в замене реальной плотности вероятности её линейной или параболической аппроксимацией. При этом закон распределения параметра остаётся неизвестен.
Наиболее близким к предлагаемому изобретению является способ контроля и управления динамической системы [5], заключающийся в том, что осуществляется регистрация состояния объекта, формирование выборки yi значений выходного параметра y(t), определение математического ожидания M, среднего квадратического отклонения σ и четвёртого центрального момента μ4 распределения выходного параметра, энтропийного потенциала выходного параметра ΔHs; формирование базы данных эталонных параметров закона распределения выходного параметра, проверку состояния объекта принадлежности области оптимального состояния; трансформация закона распределения управляемого параметра за счёт изменения настроек параметра регулятора, корректировку закона распределения и формирование управляющего воздействия.
Как следует из формулы изобретения, в известном способе контроля и управления динамической системой осуществляется определение коэффициента энтропии симметричного распределения и контрэксцесса; определение энтропийно-параметрического критерия области оптимального управления; определение величины энтропийно-параметрического потенциала симметричных распределений; минимизация величины энтропийно-параметрического потенциала динамической системы и корректировку реального параметра закона распределения выходного параметра [5].
В качестве недостатков данного способа контроля и управления динамической системой следует отметить:
- ограничение моделей поведения системы только набором симметричных форм распределений выходного параметра;
- отсутствие способа выбора формы несимметричного распределения, влияющей на степень неопределённости состояния системы;
- отсутствие оценки границы оптимальной зоны;
- отсутствие алгоритма выбора параметров модели таких, как параметры формы и параметры масштаба распределений выходного параметра.
Краткое описание чертежей
На фигуре 1 приведён пример контроля условной плотности распределения выходного параметра для обобщённой нелинейной и негауссовой стохастической системы.
На фигуре 2 приведена схема процесса, реализующего известный способ контроля и управления динамической системой.
На фигуре 3 приведена топографическая диаграмма, иллюстрирующая состояние динамической системы выходного параметра при реализации известного способ контроля и управления.
На фигуре 4 приведены чертежи моделей задания энтропийных и параметрических неопределённостей при симметричном и несимметричном распределении:
а) модель неопределённостей для симметричного распределения;
б) модель неопределённостей для несимметричного распределения;
На фигуре 5 приведена эпюра координатного пространства признаков, иллюстрирующая состояние системы при несмещённой несимметричной целевой плотности распределений выходного параметра.
На фигуре 6 приведена схема процесса, реализующего предлагаемый способ мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения выходного параметра.
На фигуре 7 приведена схема процесса формирования пространства оптимального состояния стохастической системы.
На фигуре 8 приведена схема процесса определение масштаба модели распределения выходного параметра для стохастической системы
На фигуре 9 приведена проекция зоны контроля на нормированные координаты асимметрии и коэффициента энтропии в нормированном пространстве признаков оптимального состояния системы.
На фигуре 10 приведена проекция зоны контроля на нормированные координаты эксцесса и коэффициента энтропии в нормированном пространстве признаков оптимального состояния системы.
На фигуре 11 приведена проекция зоны контроля на нормированные координаты асимметрии и эксцесса в нормированном пространстве признаков оптимального состояния системы.
На фигуре 12 приведена проекция пространства энтропийной и параметрической неопределённостей несимметричных распределений.
На фигуре 13 приведена функциональная схема устройства мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения.
Подробное описание изобретения
Материал подробного описания содержит пояснения вариантов осуществления изобретения со ссылками на чертежи, где аналогичные ссылочные позиции представляют одинаковые или подобные элементы.
На современном этапе развития техники сравнительно новым направлением контроля для класса нелинейных стохастических систем представляет собой задача отслеживания трека плотности распределения по отношению к целевой функции плотности распределения выходного параметра [6]. Для таких систем цель контроля состоит в минимизации разности между частичной аппроксимацией плотности распределения контролируемого параметра на выходе системы и аппроксимацией, заданной в качестве целевой плотности распределения. Среди особенностей контроля отмечается необходимость выбора текущего значения контролируемого параметра таким образом, чтобы кусочная аппроксимация плотности распределения выходного параметра могла следовать за целевой плотностью распределения [7].
На фигуре 1 дан пример контроля условной плотности распределения выходного параметра для обобщённой нелинейной и негаусовой стохастической системы. При контроле негаусовой условной плотности распределения используется замена реальной функции плотности распределения выходного параметра её нелинейной моделью в виде степенного ряда на ограниченном интервале значений наблюдаемого параметра y. При этом аппроксимация целевой плотности распределения задаётся до четвёртого порядка из условия, что распределение Гаусса принято в качестве желательного распределения выходного параметра.
Среди недостатков известного способа контроля следует отметить чувствительность трека распределения к текущим значениям выходного параметра, обусловленного заменой реальной плотности распределения параметра с длинными хвостами её моделью, которая аппроксимирует распределение на конечном интервале с помощью симметричного степенного ряда четвёртого порядка. При таком подходе появление нестабильности трека плотности распределения выходного параметра обусловлено конечной вероятностью появления значений на хвостах реального распределения, значительно удалённых от центра распределений случайных значений выходного параметра. По этой причине для обеспечения стабильности в подобных системах используются схемы контроля, которые реализуют рекурсивные методы выбора текущего значения выходного параметра, т.е. замену реального значения результатом рекурсивного алгоритма для обеспечения целевой симметричной модели распределения.
В качестве недостатка контроля следует также отметить отсутствие информации об изменении формы принятой модели стохастической системы, так как принятая аппроксимация целевой функции справедлива для большого многообразия моделей негаусовых стохастических систем.
Применение моментов высокого порядка с целью получения формы распределения так же приводит к неустойчивому результату [6]. Основной недостаток применения вероятностные признаков для анализа распределений состоит в тенденции распределений кластеризоваться примерно на одну линию в большей степени, чем допустимо для реального обнаружения изменчивости выборочных наблюдений, принадлежащим различным типам распределений [8]. По этой причине в известных системах анализа распределений после приближённой идентификации распределений проводится выбор распределения путём установления справедливости распределений с помощью специализированных критериев [9, 10].
Известен способ контроля и управления динамической системой, основанный на анализе и целевом изменении величины энтропийного потенциала ΔH выходного параметра, равного произведение величины среднего квадратического отклонения σ на энтропийный коэффициент KH [11]:

отличающийся тем, что минимизация величины энтропийного потенциала выходного параметра системы достигается путём трансформации закона распределения управляемого параметра за счёт изменения параметров регулятора. При этом степень трансформации закона распределения управляемого параметра оценивается по величине энтропийного коэффициента. Величина энтропийного потенциала ΔH определяется как половина диапазона равномерного распределения в интервале от (-ΔH) до ΔH, имеющего такую же энтропию, как и у конкретного параметра.
Недостатком способа контроля и управления на основе анализа и целевого изменения энтропийного потенциала является использование коэффициента энтропии KH для контроля степени трансформации закона распределения. В этом случае система при минимизации энтропийного потенциала может переходить за счёт изменения коэффициента энтропии в низко энтропийное состояние, в котором параметры сигнала остаются неизменными [12].
Развитием способа контроля энтропийного потенциала является способ контроля и управления состоянием неопределённости системы, основанный на анализе и целеноправленом изменении величины комплексного энтропийного потенциала LΔH параметра системы, равного отношению произведения коэффициента энтропии KH и среднего квадратического отклонения к базовому значению XБ, относительно которого рассматриваются состояние неопределённости системы [13]:

В качестве базовой величины используется математическое ожидание параметра, его диапазон, номинальное значение или базовая величина энтропийного потенциала. Управление достигается путём определения комплексного энтропийного потенциала после каждого этапа эволюции системы и управление системой по величине приращения или дифференциала комплексного энтропийного потенциала посредством изменения настроек базового значения, задающих диапазон изменения параметров, предельного или номинального значений, или базовую величину энтропийного потенциала.
Основной недостаток способа контроля и управления состоянием неопределёности системы, основаном на анализе и целеноправленом изменении величины комплексного энтропийного потенциала LΔ параметра, состоит в определении энтропийного потенциала пропорционального энтропийному коэффициенту KH, величина которого определена законом распределения параметра. Дело в том, что при фиксированном значении энтропийного коэффициента возможно множество как симметричных, так и несимметричных распределений с различными формами и свойствами [14, 15]. По этой причине применение базового значения XБ при контроле комплексного энтропийного потенциала LΔH не гарантирует сохранение формы распределения выходной величины.
Известен способ контроля и управления динамической системой, основанный на минимизации энтропийно-параметрического потенциала симметричного распределения выходного параметра в пространстве признаков коэффициента энтропии и контрэксцесса. Схема процесса этапов для известного способа контроля и управления динамической системой дана на фигуре 2, где даны следующие обозначения: этап 205 - этап регистрация состояния объекта; этап 210 - формирование выборки значений выходного параметра; этап 215 - определение математического ожидания, среднего квадратического отклонения и четвёртого центрального момента; этап 220 - формирование базы данных эталонных параметров распределения выходного параметра; этап 225 - определение энтропийно-параметрического критерия области оптимального контроля; этап 230 - проверка состояния системы на принадлежность области оптимального контроля; этап 235 - трансформация закона распределения; этап 240 - определение энтропийно-параметрический потенциал симметричного распределения; этап 245 - минимизация величины энтропийно-параметрического потенциала симметричного распределения; этап 250 - корректировки закона распределения; этап 255 - формирование управляющего воздействия; этап 260 - состояние оптимально.
Согласно схеме процесса на этапе 205 происходит регистрация состояния объекта, включающая предварительное усиление, изменение и оцифровку выходного параметра системы y(t), посредством регистрации через известные дискретные промежутки времени Δt значения yi. На следующем этапе 210 происходи формирование выборки значений выходного параметра y(t) для построения гистограммы и для оценки вероятности наблюдения pj регистрируемых значения уj на интервале [yj, yj+Δy].
При мониторинге и контроле стохастической системы необходим непрерывный процесс формирования выборки значений выходного параметра, сохраняющей энтропийные и параметрические свойства в любой момент времени. Сохранность свойств выборки в любой момент функционирования системы достигается за счёт проведения наблюдений в течение характерного для системы временного цикла Tц, который обладает хаотическими свойствами, к примеру, цикл работы двигателя, цикл сокращения сердца и другие. Количество значений n формируемой выборки равно отношением периода цикла системы к промежутку времени одного измерения Δtи.
Параметры распределения одного цикла, содержат информацию, как о внутреннем состоянии системы, так и внешних воздействиях. Поэтому на следующем этапе 215 для сформированной выборки значений проводится определение математического ожидания M*, среднего квадратического отклонения (СКО) σ* и четвёртого центрального момента  по формулам:
по формулам:

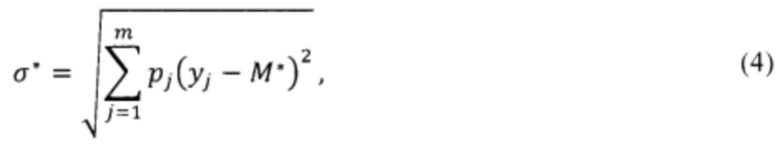

Для проведения процесса статистического измерения и контроля необходима оценка рассогласования выборочных параметров распределения с эталонными параметрами выходного параметра. По этой причине на этапе 220 схемы на фигуре 2 проводится формирование базы данных эталонных параметров распределения выходного параметра. На этом этапе из базы моделей распределения выбирается эталонная модель, параметры которой принимаются в качестве эталонных параметров для оптимального состояния системы.
Так как устойчивое состояние системы возможно в ограниченной области вблизи её оптимального состояния, то для контроля устойчивого состояния системы на этапе 225 проводят определение энтропийно-параметрического критерия области оптимального контроля по формуле:
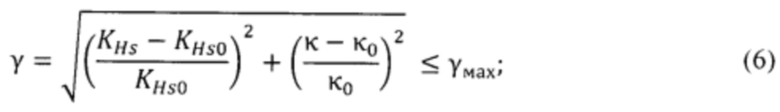
где κ и KHs - контрэксцесс и коэффициент энтропии для симметричного распределения выходного параметры, определяемые по выражениям:


Здесь ΔHs - энтропийный потенциал симметричного распределения:

На этапе 230 схемы процесса на фигуре 2 проводится проверка состояния системы на принадлежность области оптимального контроля. Если критерий γ превышает своё максимальное значение γmax, то динамическая система вышла из области оптимального управления и для дальнейшего управления необходимо принять жёсткие меры, обеспечивающие возврат системы в область оптимального состояния. Для этого необходимо определить возможную трансформацию закона распределения выходного параметра и сформировать управляющее воздействие для органов управления объектом. Трансформацию закона распределения управляемого параметра проводят на этапе 235 фигуры 2 схемы процесса за счет изменения настроечных параметров регулятора. Если динамическая система находится в зоне оптимального контроля и управления, то проводится последующая оптимизация состояния системы путём минимизации энтропийно-параметрического потенциала симметричного распределения ΔНРs. Для этого на этапе 240 схемы на фигуре 2 определяется энтропийно-параметрический потенциал симметричного распределения по формуле

где  - коэффициент нормального стандартного распределения.
- коэффициент нормального стандартного распределения.
Процесс минимизации величины энтропийно-параметрического потенциала симметричного распределения динамической системы иллюстрирует этап 245 схемы процесса на фигуре 2 в соответствии с условием:

Если энтропийно-параметрический потенциал симметричного распределения ΔHPs, не достигает своего минимального значения, то выполняется анализ требуемой корректировки закона распределения на этапе 250, по результатам которого на этапе 255 формируется управляющее воздействие на органы управления объектом. При достижении минимума энтропийно-параметрического потенциала система контроля и управления принимает состояние объекта в качестве оптимального состояния и сохраняет настройки предыдущего цикла управления. Переходу динамической системы в оптимальное состояние на фигуре 2 схемы процесса способа контроля и управления динамической системы соответствует этап 260 “Состояние оптимально”
Особенность реализации известного способа контроля и управления над динамической системой иллюстрирует топографическая диаграмма на фигуре 3, где показаны:
310 - точка положения оптимального состояния системы;
315 - кривая, ограничивающая область пространства, которое соответствует положению системы при её оптимальном функционировании;
320 - кривая (пунктирная кривая), ограничивающая часть пространства наиболее вероятных положений для оптимальных состояний динамической системы;
325 - кривая положения системы при экспоненциальных распределениях выходного параметра с показателями формы от 0 и до ∞;
330 - кривая положения системы при двухмодальном распределений выходного параметра, возникновение которых обусловлено появлением различных форм гистерезиса;
335 - кривая положения системы при распределении выходного параметра типа Шапо с показателем формы, равной 0,5;
340 - кривая положения системы при экспоненциальном распределении с параметром формы равным 0,33;
345, 350 - кривые положения системы с композициями дискретного и экспоненциального распределений выходного параметра;
355, 360 - кривые положения системы с композициями экспоненциального и дискретного двухзначного распределений;
365 - точка положения системы при нормальном распределении выходного параметра (принадлежит кривой 325);
370 - точка положения системы при двухстороннем показательном распределении Лапласа (принадлежит кривой 325).
375 - точка положения системы при равномерном распределении выходного параметра (принадлежит кривой 325);
380, 385 - точка положения системы при двухстороннем экспоненциальном распределении выходного параметра с показателями формы 1/2 и 1/3, соответственно (принадлежат кривой 325);
390, 395 - точки, ограничивающие участок кривой для положений системы с арккосинусоидальными распределениями;
Все кривые и точки положения системы, иллюстрируемые на топографической диаграмме известного способа контроля и управления динамической системой, соответствуют симметричным распределениям. Любое отображение распределений на плоскость контрэксцесса и коэффициента энтропии симметричных распределений можно заменить моделью симметричного распределения. По этой причине способ контроля и управления динамической системой в соответствии со схемой на фигуре 2 формально сводится к контролю и управлению над системой с симметричной плотностью распределения выходного параметра. При управлении и контроле над системой с несимметричным распределением происходит неявная замена с помощью соответствующего симметричного аналога.
Для контроля формы симметричных распределений при реализации известного способа контроля и управления динамической системой определяется энтропийно- параметрического критерий области оптимального управления на этапе 225 схемы фигуре 2 в пространстве признаков симметричных распределений. Такой подход обеспечивает эффективный контроль состояния объекта при симметричной плотности распределения выходного параметра.
При контроле несимметричного распределения происходит отображение состояния выходного параметра на плоскость симметричных распределений выходного параметра, что обуславливает появление многозначности поведения объекта. Дело в том, что коэффициент энтропии симметричного распределения, равный отношению энтропийного потенциала, рассчитанного по формуле симметричного распределения, к среднему квадратическому отклонению несимметричного распределения, при его применении к симметричному распределению выражает отношение неопределённостей различных интервалов и становится сильно зависимым от параметров масштаба распределения. Такой способ реализации управления и контроля создаёт условия, при которых коэффициенту энтропии, рассчитанному по формуле симметричного распределения, соответствует множество форм несимметричного распределения, что делает многозначным выбор формы несимметричной плотности распределения выходного параметра.
Таким образом, известный способ контроля распределения ограничен и сводится к контролю формы аппроксимирующей модели симметричного распределения. При контроле системы с несимметричным распределениям выходного параметра путём замены реального несимметричного распределения его приближённой симметричной моделью происходит переход системы в нерабочие состояния. Дело в том, что при одинаковой модели симметричного распределения сохраняется многозначность выбора несимметричных моделей.
Значение контроля несимметричных несмещённых распределений
Во многих областях техники контроль формы несимметричной несмещённой плотности распределения выходного параметра является эффективным методом анализа и мониторинга стохастической системы. Для примера можно привести следующие области использования предлагаемого изобретения.
медицины [31, 32].
По этой причине из многообразия стохастических систем следует выделить системы, в которых задача контроля состоит в минимизации отклонения параметров для несимметричной несмещённой плотности распределения выходного параметра
Автор предлагаемого изобретения считает, что контроль формы и масштаба моделей распределений в энтропийно-параметрическом пространстве признаков несимметричного распределения выходного параметра обеспечит стабильность мониторинга и контроля стохастической системы и исключит возможность её перехода в нерабочие состояния за счёт целевой корректировки закона распределения и формирования управляющих воздействий для коррекции связей стохастических систем.
Очевидна необходимость отображения моделей состояний стохастической системы в энтропийно-параметрическом пространстве признаков несимметричных распределений выходного параметра для обеспечения однозначного разделение устойчивых работоспособных и неработоспособных состояний системы.
Предлагаемое изобретение направлено на оптимизацию мониторинга и контроля стохастической системой при несмещённой несимметричной целевой плотности распределении путём обеспечения соответствия формы и масштаба модели стохастической системы её реальному состоянию в энтропийно-параметрическом пространстве признаков несимметричного распределения выходного параметра.
Для этого в способе мониторинга и контроля стохастической системой при несмещённой несимметричной целевой плотности распределении выходного параметра заключающийся в том, что осуществляют регистрацию состояния стохастической системы, формирование выборки yi значений выходного параметра y(t) стохастической системы, определение математического ожидания M*, среднего квадратического отклонения σ* и центрального четвёртого момента μ4 распределения выходного параметра; формирование базы данных эталонных параметров закона распределения выходного параметра стохастической системы, проверку состояния стохастической системы принадлежности зоне контроля оптимального состояния; трансформацию закона распределения управляемого параметра за счет изменения настроечных параметров регулятора, корректировку закона распределения и формирование управляющего воздействия, отличающийся тем, что дополнительно осуществляют определение координат пространства признаков формы - асимметрии, эксцесса и коэффициента энтропии несимметричного распределения - для несимметричной несмещённой плотности распределения выходного параметра стохастической системы по формуле матричного вектора:

где  - второй начальный момент, третий центральный момент
- второй начальный момент, третий центральный момент
и энтропийный потенциал несимметричной несмещённой плотности распределения выходного параметра, определяемые по формулам:


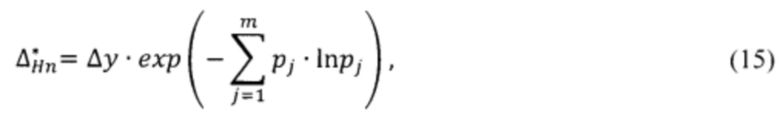
где m - число интервалов группирования; Δy - интервал группирования выходного параметра; pj - статистическая частота попадания отсчётов в j-й интервал группирования;
формирование пространства оптимального состояния стохастической системы включающее в себя следующие действия:
- задание границы зоны контроля в пространстве признаков оптимального состояния при несимметричном распределении выходного параметра стохастической системы:

где γmax - радиус зоны контроля; ξiγ - координаты границы контроля;
- определение нормированных координат положения для состояния распределения выходного параметра в пространстве признаков оптимального состояния стохастической системы по формуле матричного вектора:

где Sk0, Ex0, KHn0 - асимметрия, эксцесс и коэффициент энтропии несимметричной плотности распределения для оптимального состояния системы; a, b, c - коэффициенты интервалов признаков для зоны контроля;
- определение критерия для состояния стохастической системы в пространстве признаков оптимального состояния по формуле:

- определение нормированных координат положений возможных моделей стохастической системы в пространстве признаков оптимального состояния по формуле матричного вектора:

где Sks, Exs, KHns - асимметрия, эксцесс и коэффициент энтропии несимметричного плотности распределения для оптимального состояния системы; s - номер модели стохастической системы:

определение дистанций между положениями возможных моделей и реального состояний в нормированном центрированном пространстве признаков оптимального состояния стохастической системы по формуле

выбор формы модели стохастической системы из условия минимума дистанции между положениями модели и реального состояний

определение масштаба модели распределения выходного параметра стохастической системы включающее в себя следующие действия:
- определение энтропийно-параметрического потенциала 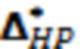 несимметричной плотности распределения выходного параметра стохастической системы
несимметричной плотности распределения выходного параметра стохастической системы

- формирование энтропийно-параметрического потенциала несимметричной модели плотности распределения выходного параметра стохастической системы

где m2λ и KHnλ - второй начальный момент и коэффициент энтропии несимметричной модели распределения выходного параметра;
- определение параметра масштаба из условия минимуму разницы энтропийно-параметрических потенциалов для несимметричной модели и реального состояния плотности распределения выходного параметра стохастической системы

сохранение параметров модели стохастической системы в базе данных;
определение рассогласования энтропийно-параметрических потенциалов модели реального и оптимального состояний стохастической системы

минимизацию рассогласований энтропийно-параметрических потенциалов модели относительно оптимального состояния посредством целевой корректировки закона распределения и формирования управляющего воздействия для коррекции связей стохастической системы и картирование состояния стохастической системы в энтропийно-параметрическом пространстве признаков выходного параметра.
Введённые действия обеспечивают мониторинг и контроль над стохастической системы при несмещённой несимметричной целевой плотности распределения выходного
параметра путём
- определения положения системы в энтропийно - параметрическом пространстве признаков формы несимметричной плотности распределения выходного параметра;
- формирование пространства оптимального состояния системы для обеспечения единства оптимальности управления в различных точках энтропийно-параметрического пространства;
- выбора формы модели распределения выходного параметра из условия минимума дистанции между положением возможных моделей и реального состояний в нормированном центрированном пространстве признаков пространстве оптимального состояния
системы;
- минимизации разницы энтропийно - параметрических потенциалов несмещённой несимметричной модели и реального состояния плотности распределения выходного
параметра для определения параметра масштаба модели;
- минимизации рассогласования параметров модели и параметров оптимального состояния распределения выходного параметра посредством целевой коррекции связей стохастической системы.
В предлагаемой заявке автор использует координатное пространство, построенное одновременно на вероятностных и информационных признаках распределений, для отображения и выбора формы моделей несимметричных распределений выходного параметра. При этом в качестве вероятностных координат принимаются первый и второй признаки формы распределения: асимметрия и эксцесс, которые характеризуют скошенность и островершинность распределения. Для формирования информационных координат автором предлагаемого изобретения предложен коэффициент энтропии несимметричных распределений, характеризующий свойство неупорядоченности при несимметричном распределении выходного параметра. [15]. Особенность построения коэффициента энтропии несимметричного распределения иллюстрирует фигура 4, где даны чертежи моделей задания энтропийных и параметрических неопределённостей при симметричном и несимметричном распределении.
Энтропия информации использована К. Шенноном в качестве меры измерения количества информации в ансамбле дискретных сообщений. Если источник информации выдаёт случайную последовательность независимых сообщений xi с вероятностью P(xi), то энтропия источника сообщений Х определена математическим ожиданием логарифма вероятности сообщений с помощью выражения [37]:

Для непрерывногой плотности распределения параметра y выражение для расчёта энтропии источника сообщений Х имеет вид

Модель неопределённости Шенонна для симметричных распределений предложена в работах Новицкого П.В. [14, 38] как модель независимого описания процесса измерения. Согласно модели Новицкого П.В. условная энтропия измерения при условии получения показания xр с равномерным распределением неопределённости на интервале 2Δ равна логарифмической мере энтропийного интервала неопределённости 2Δ:

Тогда энтропийная погрешность измерения Δ, равная половине интервала неопределённости 2Δ и выраженная через условную энтропию изменения при условии получения показания xр задана выражением вида:

В системах контроля и управления объектом минимизация разница рассогласования выходного параметра и меры обеспечивается за счёт построения отрицательной обратной связи. В качестве меры неопределённости состояния объекта Лазарев В.Л. предложил использовать для построения контроля над объектом половину энтропийного интервала неопределённости и рассматривать его как энтропийный потенциал объекта [9].
Чертёж модели неопределённостей для симметричного распределения рассогласования выходного параметра дана на фигуре 4, a, где использованы следующие обозначения.
410 - симметричная модель равномерного распределения;
415 и 420 - параметрический и энтропийный интервалы неопределённости для симметричной модели распределения
Коэффициент энтропии симметричного распределения вводится как отношение энтропийного интервала 420 неопределённости рассогласования выходного параметра к его параметрическому интервалу 415, равных удвоенным значениям энтропийного потенциала симметричного распределения 2ΔHs и среднего квадратического отклонения 2σ. Формула для определения коэффициента энтропии симметричного распределения имеет вид:

Коэффициент энтропии симметричного распределения KHs, равный отношению энтропийного потенциала симметричного распределения выходного параметра к среднему квадратическому отклонению выходного параметра относительно среднего значения, представляет собой безразмерный нормированный признак симметричной модели распределения, используемого для оценки положения математического ожидания. Коэффициент энтропии симметричного распределения так же, как энтропийный потенциал симметричного распределения базируются на условной энтропии распределения при условии получения оценки среднего значения, равного математическому ожиданию, неопределённость которого моделируется равномерным симметричным распределением.
Отличительная особенность распределений с несимметричной несмещённой плотностью распределения состоит в том, что плотность вероятности распределения равна нулю при отрицательных значениях выходного параметра. Так как предельное выражение под интегралом Шеннона (20) равно нулю,
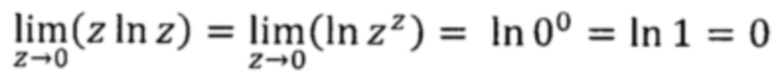
то для определения энтропии несимметрично распределенного несмещенного выходного параметра используется выражение вида

При использовании плотности равномерного распределения в качестве модели несмещённой несимметричной плотности распределения выходного параметра интервал задаётся от 0 до его максимального значения ΔHn, принимаемого в качестве энтропийного потенциала несимметричного несмещённого распределения. Чертёж модели неопределённостей для несимметричного распределения показано на фигуре 4, б, где использованы следующие обозначения:
425 - несимметричная модель равномерного распределения;
430 и 435 - интервалы параметрической и энтропийной неопределённости для несимметричной модели распределения, равные корню квадратному второго начального момента  и энтопийному потенциалу ΔHn несимметричной модели распределения;
и энтопийному потенциалу ΔHn несимметричной модели распределения;
440 - дистанция положения центра распределения относительна начала отсчёта, равная математическому ожиданию M;
Из рассмотрения фигуры 4, а и фигуры 4, б следует, что интервалы параметрической неопределённости 415 и 430 задают разные сущности распределений.
Из рассмотрения фигуры 4, а следует, что интервал 415 равный 2σ определяет среднеквадратический разброс распределения относительно центра распределения, заданного положением математическим ожиданием M. Из рассмотрения фигуре 4, б следует, что интервал 430 задаёт расстояние от начала отсчёта до среднего квадратического значения. Интервал 430 равен корню квадратному из второго начального момента несимметричного распределения. Для несмещённого несимметричного распределения начало отсчёта совпадает с началом координат. Для несимметричного распределения интервал параметрической неопределённости 415, равный удвоенному среднему квадратическому разбросу 2σ выходного параметра, откладывается симметрично относительно центра распределения, который задан дистанцией 440, отложенной от начала отсчёта и равной математическому ожиданию M. Как следует из модели фигуры 4, б, дистанции 415 и 430 имеют различные сущности для распределения выходного параметра.
Аналогично рассматриваются интервалы 420 и 430 для энтиропийной неопределённости. Интервал энтропийной неопределённости 420 на фигуре 4, а откладывается симметрично, относительно положения центра распределения, заданного его математическим ожиданием. Интервал энтропийной неопределённости 435 на фигуре 4, б откладывается от начала отсчёта несимметричного распределения.
Дифференциальная энтропия для определения неопределённости положения центра несимметричного распределения, рассчитывается как условная энтропия измерения при условии получения показания xр, равного математическому ожиданию M:
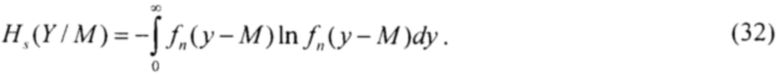
Так как условная энтропия (32) для определения интервала энтропийной неопределённости относительно центра распределений не равна энтропии несиметричного распределения (31), то интервалы энтопийной неопределённости для симметричной модели 420 и для несиметричной модели 435 так же имеют различные значения. Интервал 420 откладывается относительно центра распределения и смещён по отношению к началу координат.
Таким образом, интервалы энтропийно неопределённости 420 и 435 для симметричной и несимметрично модели распределения имеют разные сущности по отношению к распределению выходного параметра.
Коэффициент энтропии KHn для несимметричного распределения параметра x равен отношению интервала энтропийной неопределённости 435 к интервалу параметрической неопределённости 430 выходного параметра, которые равны энтропийному потенциалу несимметричного распределения ΔHn и корню квадратному второго начального момента  , соответственно.
, соответственно.
Формула для определения коэффициента энтропии несимметричного распределения имеет вид:

Коэффициент энтропии нессиметричного распределения (33), равный отношению
энтропийного потенциала несимметричного распределения выходного параметра к корню квадратному, взятому от второго начального момента распределения выходного параметра, представляет собой безразмерный нормированный признак формы несимметричного распределения [15].
Энтропия несимметричного несмещённого распределения обладает свойством пропорциональности по отношению к энтропии симметрированного распределения, полученного посредством отражения несимметричного распределения относительно начала координат. Если fn(X,α,τ,λ) - плотность несимметричного распределения, то плотность соответствующего симметрированного распределения имеет вид:
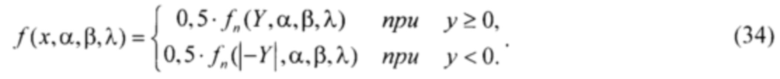
Так как для симметрированного распределения происходит увеличение диапазона выходного параметра в два раза, то справедлива линейная пропорциональность для энтропий симметрированного и несимметричного распределений вида:
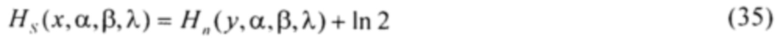
Так как для симметррированного распределения справедливо выражение (28) для условной энтропияи измерения при условии получения показания xp равного нулю, то записав логарифм произведения как сумму логарифмов, получим для энтропии симметрированного распределения выражение вида:

Сопоставляя выражение (35) и выражение (36) получим, что для модели несимметричного распределения выходного параметра следует обеспечить равенство энтропии распределения и логарифма энтропийного потенциала не симметричного распределения:

Формула для расчёта энтропийного потенциала несимметричного распределения ΔHn , при известной энтропии Hn(x,α,β,λ) примет вид:

Таким образом, из выражения (38) следует, что энтропийный потенциал несимметричного несмещённого распределения равен экспоненте с показателем, равным энтропии несимметричного несмещённого распределения выходного параметра.
Так как среднее квадратическое отклонение σS для симметрированного относительно начала отсчёта распределения параметра x, равно корню квадратному от второго начального момента m2, рассчитанному для исходного несимметричного несмещённого распределения выходного параметра y

то коэффициент энтропии несимметричного распределения можно получить как коэффициент энтропии симметрированного распределения, энтропия которого определена свойствами несимметричного распределения.
Поскольку интервалы энтропийной и параметрической неопределённости пропорциональны масштабам распределения, то отношение интервалов для несмещённых несимметричных распределений выходного параметра не зависит от масштаба распределения и полностью определяется параметрами формы.
Таким образом, коэффициент энтропии несимметричных распределений представляет собой независимый признак формы несмещённых несимметричных распределений [15]. Объединение информационного признака формы, в качестве которого использован коэффициент энтропии несимметричных распределений, с вероятностными признаками формы асимметрии и эксцесса позволило получить энтропийно-параметрическое пространство признаков для отображения координат траекторий возможного положения объекта при несимметричном несмещённом распределении выходного параметра.
Возможные положения объекта в координатном энтропийно-параметрическом пространстве признаков несимметричных несмещённых распределений выходного параметра даны на фигуре 5 в виде эпюры проекций траекторий распределений выходного параметра:
- фигура 5, а - проекция траекторий на плоскость, заданную признаками асимметрии и коэффициента энтропии несимметричного распределения;
- фигура 5, б - проекция траекторий на плоскость, заданную признаками эксцесса и коэффициента энтропии несимметричного распределения.
- фигура 5, в - проекция траекторий на плоскость, заданную признаками асимметрии и эксцесса несимметричного распределения.
На проекциях эпюры использованы следующие обозначения:
505 - точка положения оптимального состояния системы при несимметричном распределении выходного параметра;
510 - точка положения реального состояния системы при несимметричном распределении выходного параметра;
515 - граница зоны контроля в пространстве энтропийно - параметрических признаков несимметричного распределения выходного параметра;
520 - кривые положения системы при использовании для выходного параметра целевого распределения из форм семейства Вейбулла-Гнеденко;
525 - кривые положения системы при использовании для выходного параметра целевого распределения из форм семейства гамма распределений;
530 - кривые положения системы при использовании для выходного параметра целевого распределения из форм логарифмического нормального распределения;
535 - точка положения системы при использовании формы несимметричного экспоненциального распределения выходного параметра, совпадающего с распределением Пирсона χ2 с тремя степенями свободы;
540 - точка положения системы при использовании для выходного параметра отражённого относительно центра нормального распределения;
545, 550 - точки положения системы при использовании для выходного параметра симметричных форм логистического и нормального распределений;
555, 560, 565 - кривые положения системы при использовании для выходного параметра целевого распределения из форм распределений Парето при различных смещениях х0 левой границы возможных значений которой соответствуют значения 0,9, 1,1 и 1,3.
В пространстве энтропийно-параметрического потенциала точка положения оптимального состояния системы 505 определяется целевой плотностью несимметричного распределения выходного параметра и совпадает с положением априорно известной несимметричной модели распределения. На фигуре 5 точка оптимального состояния системы 505 при несимметричном распределении находится на кривой 520 возможных положений системы при использовании для выходного параметра целевого распределения из форм семейства гамма распределений. Реальное состояние системы 510 отличается от его оптимального положения 505 вследствие действия внешних влияющих дестабилизирующих факторов и постоянно меняющихся внутренних свойств системы: внутренних связей, параметров элементов и среды, составляющих систему.
Точка положения реального состояния системы 510 находится вблизи оптимального состояния. Так как реальное состояния не совпадает с возможными моделями её состояния, то точка положения реального состояния 510 располагаться вблизи кривых возможных положений системы. Для реального состояния 510 возможно изменение свойств системы, которые отображаются в изменении формы и масштаба модели распределения выходного параметра.
По этой причине при проведении мониторинга и контроля важно определить переход системы в новое состояние из-за изменения свойств модели. Так как возможные состояния модели находятся вблизи оптимального состояния, то в энтропийно-параметрическом пространстве признаков выделяется граница области контроля 515 с известными допустимыми формами моделей несимметричных распределений выходного параметра, которые хранятся в базе данных эталонных параметров распределения выходного параметра. При выходе системы за пределы области контроля происходит трансформация закона распределения управляемого параметра за счёт изменения настроечных параметров регулятора. Для реального состояния системы выбирается наиболее близко расположенная модель, после чего определяются её параметры.
Автор предлагаемого изобретения убеждён в том, что отображение положения объекта в координатном энтропийно-параметрическом пространстве признаков несимметричных несмещённых распределений выходного параметра позволяет реализовать новые возможности при мониторинге и контроле над стохастической системой.
Описание алгоритма мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения выходного параметра
Схема процесса на фигуре 6 иллюстрирует новые возможности и особенности предлагаемого способа мониторинга и контроля над стохастической системой при несимметричной несмещённой целевой плотности распределения выходного параметра. Для реализации новых возможностей в предлагаемом изобретении проводятся следующие действия, иллюстрируемые в виде этапов процесса мониторинга и контроля на фигуре 6:
- этапа 605 определения координат пространства признаков формы для несимметричной плотности распределения;
- этапа 610 формирования пространства оптимального состояния системы;
- этапа 615 определения дистанции между положениями возможных моделей и реального состояний;
- этапа 620 выбора формы модели из условия минимума дистанции между моделью и реальным состоянием;
- этапа 625 определения масштаба модели распределения выходного параметра стохастической системы;
- этапа 630 сохранения параметров модели распределения в базе данных;
- этапа 635 определения рассогласования параметров модели реального и оптимального состояния стохастической системы;
- этапа 640 оптимизации рассогласования параметров модели;
- этапа 645 картирования положения системы в пространстве признаков распределения выходного параметра.
Определение координат пространства признаков формы для несимметричной несмещённой плотности распределения выходного параметра стохастической системы
Первое действие, иллюстрируемое этапом 605 схемы процесса на фигуре 6 заключается в определении координат пространства признаков формы для несимметричной плотности распределения. Координаты пространства заданы безразмерными признаками формы распределения и рассчитываются по формуле матричного вектора (12). В качестве параметрических признаков формы распределения использованы асимметрия и эксцесс, характеризующие скошенность и островершинность распределения. Третья координата задана независимым информационным признаком формы распределения - коэффициентом энтропии несимметричного распределения. Отображение распределения выходного параметра системы в трёхмерном пространстве признаков форм распределения обеспечивает контроль положения системы по отношению к возможным функциональным состояниям. Такие параметры как второй начальный момент, третий центральный момент и энтропийно-параметрический потенциал несимметричной плотности распределения выходного параметра системы определяются по формулам (13), (14) и (15), соответственно
Формировании пространства оптимального состояния стохастической системы
Основная цель действия, иллюстрируемого этапом 610 схемы процесса на фигуре 6, состоит в том, чтобы получить положения моделей и положение состояния несимметричного распределения выходного параметра системы в нормированном пространстве координат оптимального состояния 505 с несимметричным распределением выходного параметра. Схема процесса формирования пространства оптимального состояния стохастической системы дана на фигуре 7 в виде этапов 715, 720, 725 и 730.
Из фигуры 7 следует, что первое отличительное действие предлагаемого способа мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения выходного параметра содержит
- этап 715 задания границ зоны контроля в пространстве признаков оптимального состояния при несимметричном распределении выходного параметра стохастической системы;
- этап 720 определения нормированных координат положения для состояния распределения выходного параметра в пространстве признаков оптимального состояния стохастической системы;
- этап 725 определения критерия для состояния стохастической системы в пространстве признаков оптимального состояния;
- этап 730 определения нормированных координат положений возможных моделей в пространстве признаков оптимального состояния;
Суть схемы процесса формирования пространства оптимального состояния системы состоит в определении координат возможных моделей вблизи оптимального состояния в пределах границы контроля.
Этап 715 схемы процесса на фигуре 7 состоит в задании границ зоны контроля в пространстве признаков оптимального состояния с помощью выражения (16). Для оптимального состояния существует зона работоспособных состояний, которые отслеживаются по форме выходного параметра. Интервалы изменения признаков для зоны контроля заданы с помощью произведения значения признака оптимального состояния (Sk0, Ex0, KHn0) на коэффициенты интервалов признаков a, b, c. Тогда положение возможных значений в энтропийно-параметрическом пространстве состояний выходного параметра ограничено значениями признаков 

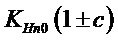
Границы интервалов признаков возможных моделей могут быть определены двумя способами. Первый способ состоит в моделировании объекта и получении границ параметров на основе модели с использованием метода Монте-Карло наложением на модели выходного параметра и моделей дестабилизирующих факторов. В этом случае признаки оптимального состояния Sk0, Ex0, KHn0 определены свойствами модели системы. Другой подход связан с накоплением статистических данных о стохастической системе и оценке интервалов признаков зоны контроля при условии, что система (или подобные системы) находится в работоспособном состоянии для контролируемого режима работы. В этом случае в качестве оптимальных энтропийно-параметрических признаков системы Sk0, Ex0 и KHn0 принимаются оценки среднего значения признаков, полученных из проводимых ранее наблюдений. В качестве интервалов признаков в статистике используют средние квадратические оценки разброса. Так как в способах анализа и статистического накопления используются различные методы оценки интервалов признаков, то для задания границы зоны контроля удобно использовать ограничения интервалов признаков 


Примеры проекций зоны контроля на нормированном пространстве признаков оптимального состояния показаны на фигурах 9, 10 и 11, где использованы следующие обозначения объектов: 505 - точка положения оптимального состояния при несимметричном распределении выходного параметра; 510 - точка положения реальное состояние системы при несимметричном распределении выходного параметра; 515 - граница зоны контроля; 520, 525 и 530 - кривые положения системы при использовании для выходного параметра целевых распределений из форм семейства Вейбулла-Гнеденко, семейства гамма распределения и форм логарифмического нормального распределения, соответственно; 535 - точка положения модели системы при использовании формы несимметричного экспоненциального распределения выходного параметра, совпадающего в параметром Пирсона χ2 с тремя степенями свободы; 910, 920 и 930 - иллюстрируют точки положения возможных моделей состояний системы при использовании форм семейства Вейбулла-Гнеденко, семейства гамма распределения и логарифмического нормального распределения, соответственно; 915, 925 и 935- точки положения моделей состояний системы при использовании кривых положений системы 520, 525 и 530 в качестве распределений выходного параметра форм семейства Вейбулла-Гнеденко, семейства гамма распределения и логарифмического нормального распределения, соответственно. На эпюре 9 дано дополнительно положение модели состояния системы 940 при использовании кривой форм семейства Парето 555. Так как формы распределения Парето находятся вне зоны контроля, то кривая положения 555 отсутствует на фигуре 10 и фигуре 11 других проекциях энтропийно-параметрического пространства, иллюстрируя возможное положение модели при неработоспособном состоянии системы.
Следующий этап 720 схемы процесса на фигуре 7 состоит в определении нормированных координат положения для состояния распределения выходного параметра в пространстве признаков оптимального состояния стохастической системы по формуле матричного вектора (17).
Для отображения состояния системы в пространстве признаков оптимального состояния на этапе 720 процесса на фигуре 7 определяются нормированные координаты положения состояния по формуле матричного вектора (17). Состояние системы выходного параметра на проекции оптимального состояния системы при несимметричном распределении выходного параметра показано на проекциях зоны контроля (фигура 9, фигура 10 и фигура 11) в виде точки положения 510. Для иллюстрации использована точка состояния с признаками асимметрии, эксцесса и коэффициента энтропии несимметричного распределения выходного параметра, равными 2,1, 9 и 1,53, соответственно. При построении проекций положение оптимального состояния системы в энтропийно-параметрическом пространстве задано параметром формы α распределения из многообразия форм гамма семейства, равного 0,692. Проекции пространства оптимального состояния построены для признаков асимметрии, эксцесса и коэффициента энтропии несимметричного распределения оптимального состояния, равных 2,405, 8,674 и 1,65, соответственно. Форма модели оптимального состояния принята в качестве формы целевого распределения выходного параметра стохастической системы. Интервалы признаков асимметрии, эксцесса и коэффициента энтропии, рассчитанные для зоны контроля, равны 0,58, 3,5 и 0,225. Коэффициенты интервалов признаков a, b и c для зоны контроля равны 0,241, 0,404 и 0,136, соответственно. Коэффициенты и признаки точки положения 510 реального состояния системы при несимметричном распределении выходного параметра изменяются при проведении мониторинга и контроля.
На этапе 725 схемы процесса на фигуре 7 определяют критерий γ* для состояния стохастической системы в пространстве признаков оптимального состояния по формуле (18). Критерий позволяет осуществить проверку состояния объекта принадлежности зоне контроля.
Этап 730 состоит в определении нормированных координат положения возможных моделей в пространстве признаков оптимального состояния по формуле (19).
Формирование пространства оптимального состояния необходимо для обеспечения единства оптимальности управления в различных точках энтропийно-параметрического пространства. Дело в том, что в энтропийно-параметрическом пространстве минимальное расстояние зависит от значений признаков распределения и не учитывает интервалы допустимых изменений относительно оптимального состояния, что снижает качество контроля при выборе параметров модели. В целях унификации данных при различных состояниях следует учитывать интервалы контроля вблизи оптимального состояния.
В зоне контроля оптимального состояния количество различимых форм моделей ограничено различием параметра формы возможных моделей. При контроле формы до третьей значащей цифры в зоне контроля возможно 300 моделей из семейства форм гамма распределения c параметрами формы в интервале от 0.55 до 0,85, и 150 моделей из семейства Вейбулла-Гнеденко с параметрами формы от 0,8 до 0,95. Определение координат возможных моделей по формуле (19) в пространстве оптимального состояния относится к формированию пространства.
Определение дистанций между положениями возможных моделей и реального состояний в нормированном центрированном пространстве признаков оптимального состояния стохастической системы
Третье отличительное действие схемы процесса на фигуре 6, иллюстрируемое этапом 615, состоит в определении дистанции между положением возможных моделей и реального состояний для несимметричных распределений выходного параметра стохастической системы в нормированном пространстве координат оптимального состояния. Положениям возможных моделей из отдельных семейств соответствуют модели на пересечении кривых семейства распределений и перпендикуляра из точки положения 510 реального состояния системы при несимметричном распределении выходного параметра к кривой положений системы при использовании семейства возможных моделей.
Выбор формы модели стохастической системы из условия минимума дистанции между положениями модели и реального состояний.
Четвёртое отличительное действие, осуществляемое этапом 620 схемы процесса на фигуре 6, состоит в выборе формы модели из условия минимума дистанции между моделью и реальным состоянием. Модели выбираются из семейства форм распределения и оценки параметра формы модели из базы данных моделей.
При построении мониторинга и контроля стохастической системой при несмещённой целевой плотности распределения выходного параметра в качестве основных параметров контроля принимаются форма распределения и её размах. Обеспечение контроля достигается за счёт использования семейств распределений, содержащих параметры формы и размаха.
Существующие алгоритмы позволяют оценить форму распределения выходного параметра только приближённо. Дело в том, что параметрические признаки формы асимметрии и эксцесса не позволяют получить форму при использовании нескольких подсемейств обобщённых распределений. Близкое расположение траекторий кривых в пространстве только параметрических признаков асимметрии и эксцесса не обеспечивают однозначный выбор формы модели.
В предлагаемом изобретении качество выбора формы осуществляется из условия
минимума (21) между положением модели и состояния системы. Качество выбора формы обеспечено за счёт различимости несимметричных распределений энтропийно-параметрического пространстве признаков и перехода в пространство оптимального состояния системы. При выборе модели распределения параметрам формы присваиваются их специфические значения.
Определение масштаба модели распределения выходного параметра стохастической системы.
Следующее отличительное действие предлагаемого изобретения состоит в определении масштаба распределения выходного параметра стохастической системы на этапе 625 схемы процесса фигуры 6. Схема процесса определения параметра масштаба распределения выходного параметра дана на фигуре 8 в виде этапов 805, 810 и 815. Из фигуры 8 следует, что четвёртое отличительное действие предлагаемого способа мониторинга и контроля стохастической системы при несмещённой несимметричной целевой плотности распределения содержит
- определение на этапе 805 энтропийно-параметрического потенциала несимметричной плотности распределения выходного параметра;
- формирование на этапе 810 энтропийно-параметрического потенциала несимметричной модели плотности распределения выходного параметра;
- определение на этапе 815 параметра масштаба λ из условия минимума (24) разницы энтропийно-параметрических потенциалов для несимметричной модели и реального состояния плотности распределения выходного параметра.
Для пояснения действий, осуществляемых при определении масштаба модели распределения выходного параметра стохастической системы на фигуре 12 дана проекция пространства энтропийной и параметрической неопределённостей несимметричных распределений выходного параметра, где даны следующие обозначения
505 и 510 - точки положения оптимального и реального состояния системы при несимметричном распределением выходного параметра;
- 1205 - начало координат пространства энтропийной и параметрической неопределённостей;
- 1210 - дистанция энтропийно-параметрического потенциала 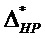
- 1215 - точка положения модели с выбранной формой распределения и энтропийно-параметрическим потенциалом выходного параметра;
- 1220 - линия масштабов модели с выбранной формой распределения;
- 1225 - эквипотенциаль энтропийно-параметрического потенциала 
- 1230 - дистанция энтропийно-параметрического потенциала 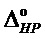
- 1235 - эквипотенциаль энтропийно-параметрического потенциала 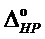
- 1240 - точка положения модели с выбранной формой распределения и энтропийно-параметрическим потенциалом оптимального состояния системы;
- 1245 - линия масштабов модели с формой оптимального состояния.
Пространство энтропийной и параметрической неопределённостей несимметричных распределений выходного параметра на фигуре 12 задано проекцией координаты энтропийного потенциала несимметричного распределения ΔHP и координаты интервала параметрической неопределённости, равной корню квадратному второго начального момента  распределения выходного параметра.
распределения выходного параметра.
В пространстве энтропийной и параметрической неопределённостей несимметричных распределений выбранной модели распределения соответствует линия масштабов модели 1220 с выбранной формой распределения, на которой различным дистанциям от начала координат 1205 до точек прямой 1220 соответствуют различные масштабы λ распределения выходного параметра. Наклон линия 1220 полностью определен отношением коэффициентом энтропии несимметричного распределения, определённого из выражения (33).
Точка положения оптимального состояния системы 505 находится на линии масштабов модели 1245 с формой оптимального состояния распределения, которая определена коэффициентом энтропии несимметричного распределения оптимального состояния. Для формы модели оптимального состояния возможно множество моделей с различными масштабами. Если коэффициент энтропии выбранной модели несимметричного распределения отличается от коэффициента энтропии несимметричного распределения оптимального состояния, то линии масштабов выбранной модели 1220 и модели оптимального состояния 1245 существуют как раздельные объекты.
Если коэффициент энтропии несимметричного распределения выходного параметра 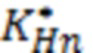 отличается от коэффициента энтропии выбранной модели несимметричного распределения, то точки положения 510 реального состояния системы при несимметричном распределении выходного параметра находится вне линии масштабов 1220 выбранной модели. На фигуре 12 проекции пространства энтропийной и параметрической неопределённостей несимметричных распределений схематично показана схема определения масштаба для модели распределения с выбранной формой, поясняющая действия схемы на фигуре 8 процесса определения масштаба модели распределения выходного параметра.
отличается от коэффициента энтропии выбранной модели несимметричного распределения, то точки положения 510 реального состояния системы при несимметричном распределении выходного параметра находится вне линии масштабов 1220 выбранной модели. На фигуре 12 проекции пространства энтропийной и параметрической неопределённостей несимметричных распределений схематично показана схема определения масштаба для модели распределения с выбранной формой, поясняющая действия схемы на фигуре 8 процесса определения масштаба модели распределения выходного параметра.
На этапе 805 схемы процесса 8 определяется энтропийно-параметрический потенциал несмещённой плотности распределения выходного параметра по формуле (14).
Согласно формуле (33), коэффициент энтропии несимметричного распределения выходного параметра пропорционален отношению энтропийного потенциала несмещённого распределения к корню квадратному второго начального момента распределения. Иллюстрация отношения (33) в пространстве энтропийной параметрической неопределённостей несимметричных распределений выходного параметра дана на фигуре 12, где положения объектов показаны схематично для иллюстрации процессов определения и минимизации параметра масштаба распределения.
Дистанция от точки 1205 начала координат пространства энтропийной и параметрической неопределённостей на фигуре 12 до положения точки 510 реального состояния системы равна энтропийно-параметрическому потенциалу стохастической системы. Для определения энтропийно-параметрического потенциала несимметричного распределения выходного параметра через координаты пространства неопределённостей использована формула (22).
На фигуре 12 энтропийно-параметрическому потенциалу выходного параметра 
Для реального состояния 510 наилучшее соответствие параметра масштаба для модели 1215, расположенной на линии 1220 масштабов моделей с выбранной формой таким образом, что дистанция между точками 510 положения реального состояния и 1215 положения модели с выбранной формы в пространстве энтропийной и параметрической неопределённости минимально. При малых углах рассогласования точка 1215 положения модели с выбранной формой находится как пересечение линии 1220 масштабов модели и эквипотенциали энтропийно-параметрического потенциала выходного параметра. Для определения параметра масштаба λ модели с выбранной формой необходима взаимосвязь параметра масштаба λ модели и энтропийно- параметрического потенциала выходного параметра.
По этой причине на этапе 810 схемы процесса на фигуре 8 проводится формирование энтропийно-параметрического потенциала несимметричной модели плотности распределения выходного параметра.
Энтопийно-параметрический потенциал для модели распределения выходного параметра равен дистанции между началом координат 1205 и положением модели 1215 в пространстве энтропийной и параметрической неопределённости. Формула для определения энтопийно-параметрический потенциал модели 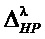

Если форма модели выбрана, то однозначно известен коэффициент энтропии KHnλ для модели несимметричного распределения. Квадрат потенциала энтропии несиметричного распределения равен произведению коэффициент энтропии на второй начальный момент m2λ несимеетричного распределения модели распределения выходного параметра. Для энтропийно-параметрического потенциала несимметричной модели распределения выходгного параматра справедлива формула (23), согласно которой для плотности выходного параметра возможно множество моделей, отличающихся различными параметрами масштаба распределения. Для большинства несимметричных распределений энтропийно-параметрический потенциал пропорционален параметру масштаба модели λ. Тогда определив дистанцию от начала координат 1205 до точки положения модели 1215 при известной форме модели получим значение масштаба λ распределения выходного параметра.
Этапе 815 схемы процесса на фигуре 8 состоит в определении параметра масштаба λ из условия (24) минимума разницы энтропийно-параметрического потенциала для несимметричной модели и реального состояния плотности распределения выходного параметра.
Процесс выбора параметра формы иллюстрирует фигура 12. Очевидно, что наилучшее совпадение между моделью и реальным состоянием распределения системы можно достичь при совпадении точек положения модели 1215 с выбранной формой и реального состояния 510 системы. Так как из-за действия дестабилизирующих внешних факторов положение точки 510 реального состояния системы находится вне линии 1220 моделей выбранной формой, то точки положения модели 1215 соответствует минимальная дистанция между точками положения реального состояния системы 510 и линией 1220 выбранной формы модели. При малом различии коэффициента энтропии модели и реального состояния, угол между линией формы модели и линии формы реального состояния не превышает 1…5°. В этом случае масштаб модели выбирается из условия (24) минимума разницы энтропийно-параметрических потенциалов несимметричной модели и реального состояния распределения выходного параметра
Сохранения параметров модели стохастической системы в базе данных.
Цель мониторинга состоит в сохранении восстанавливаемой информации о состоянии объекта при минимальном объёме переданных данных. По этой причине на этапе 630 схемы процесса на фигуре 6 обеспечивается сохранение параметров модели в базе данных. Сохранение признаков и распределения позволяет обеспечить восстановление информации о состоянии системы.
Определение рассогласования энтропийно-параметрических потенциалов модели реального и оптимального состояний стохастической системы.
Следующее действие, иллюстрируемое этапом 635 схемы процессов на фигуре 6, состоит в определении рассогласования модели реального и оптимального состояния
стохастической системы.
Для оптимального состояния второй начальный момент 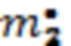 и энтропийный потенциал
и энтропийный потенциал 
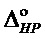
Если энтропйино-параметрические потенциалы оптимального 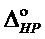

Для оценки дистанции между точками положения модели 1215 с энтропийно-параметрическим потенциалом реального состояния и точкой положения 505 оптимального состояния системы рассчитывается рассогласования квадратов интервалов энтропийной и параметрической неопределённости по формуле:
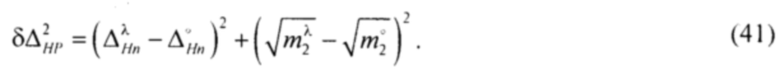
Возведя в квадрат слагаемые выражения (41) и перегруппировав слагаемые, получим, что рассогласование квадратов энтропийной и параметрической неопределённостей определяется разницей между суммой квадратов энтропийно-параметрических потенциалов и удвоенной суммой произведений энтропийных и параметрических неопределённостей:

В выражении (42) первые два слагаемые представляют собой энтропийно-параметрические потенциалы для модели реального и оптимального состояний. Заменив энтропийные неопределённости с помощью выражения (40) через интервалы параметрических неопределённостей, получим формулу для расчёта рассогласования квадратов интервалов энтропийной и параметрической неопределённостей:
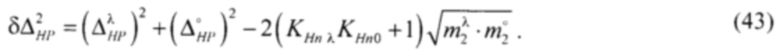
Минимизация выражения (43) позволяет минимизировать рассогласование между моделью реального состояния и оптимальным состоянием.
Коэффициент энтропии несимметричного распределения модели равен сумме коэффициента энтропии оптимального состояния и рассогласования коэффициентов энтропий: 
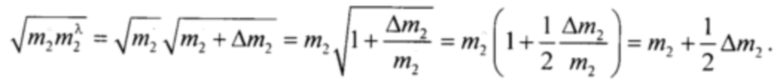
Квадрат энтропийно-параметрического потенциала связан пропорционален второму начальному моменту:

Тогда после преобразования выражения (44) с учётом равенства (44) получим формулу для рассогласования квадратов интервалов энтропийной и параметрической неопределённости вида:
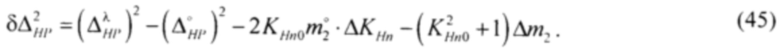
Из полученного выражения следует, что при равенстве энтропийно-параметрических потенциалов модели и оптимального состояния рассогласования квадрата интервалов энтропийной и параметрической неопределённостей определяется рассогласованием вторых начальных моментов и коэффициентов энтропий несимметричных распределений. Таким образом, выражение (45) более жёсткое условие для определения и минимизации рассогласования, чем формула (25).
Минимизация рассогласования энтропийно-параметрических потенциалов модели относительно оптимального состояния
Следующее действие, иллюстрируемое этапом 640 схемы процессов на фигуре 6, состоит в минимизации рассогласования энтропийно-параметрических потенциалов модели и оптимального состояния системы, осуществляемое в соответствии с условиям

Минимизация рассогласования (11) энтропийно-параметрических потенциалов достигается посредством целевой корректировки закона распределения и формирования управляющего воздействия для коррекции связей стохастической системы.
Положения объектов в пространстве энтропийно-параметрической неопределённости на фигуре 12 даны схематично для иллюстрации процессов определения и минимизации параметра масштаба распределения.
Картирование состояния стохастической системы в энтропийно-параметрическом пространстве признаков выходного параметра
Для визуализации состояния системы на этапе 645 схемы процесса на фигуре 6 происходит картирование положения стохастической системы в пространства признаков распределения выходного параметра и в виде проекций зоны контроля на нормированные координаты пространства признаков оптимального состояния. На этапе 260 формируется сообщение относительно оптимальности состояния объекта.
Возможную реализацию материального средства, с помощью которого выполняется действие заявленного способа, иллюстрирует схема технического устройства, приведённая на фигуре 13,
Описание схемы устройства мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения
Для пояснения предлагаемого изобретения на фигуре 13 дана функциональная схема устройства мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения, где использованы следующие обозначения:
1310 - подсистема неконтролируемых процессов стохастической системы;
1315 - связи неконтролируемых процессов стохастической системы с контролируемым процессом выходного параметра стохастической системы.
1317 - связи влияющих факторов с контролируемым процессом выходного параметра стохастической системы.
1320 - контролируемый процесс стохастической системы.
1325 - влияющие факторы искусственного и естественного происхождения.
1330 - регистрирующее устройство;
1335 - устройство формирования распределения выходного параметра;
1340 - блок определения признаков формы распределения выходного параметра;
1345 - блок определения энтропийно-параметрического потенциала выходного параметра;
1350 - устройство формирования пространства оптимального состояния;
1355 - устройство выбора формы модели;
1360 - блок определения параметра масштаба модели;
1365 - устройство картирования состояния стохастической системы;
1370 - база данных;
1375 - устройство проверки принадлежности состояния стохастической системы зоне контроля оптимального состояния;
1380 - блок трансформации распределения;
1385 - устройство воспроизведения мера ЭПП целевого распределения;
1390 - блок целевой корректировки формы распределения;
1395 - блок формирования управляющего воздействия для регулировки связей стохастической систем;
В стохастической системе на фигуре 13 выделены подсистема неконтролируемых процессов 1310 стохастической системы, контролируемый процесс 1320, связи 1315 неконтролируемых процессов стохастической системы с контролируемым процессом стохастической системы и связи 1317 влияющих факторов с контролируемым процессом стохастической системы. Воздействие на контролируемый процесс 1320 возможно за счёт изменения связей 1315 неконтролируемых процессов стохастической системы и за счёт изменения связей 1317 влияющих факторов искусственного и естественного происхождения.
Регистрирующего устройства 1330 проводит регистрацию выходного параметра контролируемого процесса стохастической системы. Устройство формирования распределения выходного параметра 1335 осуществляет процесс формирования выборки [Y] значений выходного параметра стохастической системы, полученных с регистрирующего устройства 1330. Блок определения признаков формы 1340 предназначен для вычисления признаков формы выходного распределения стохастической системы: асимметрии, эксцесса и коэффициента энтропии несимметричных несмещённых распределений. Значения признаков формы передаются в устройство формирования пространства оптимального состояния 1350, на выходе которого формируются матричный вектор [ξ*] нормированных координат положения для состояния распределения выходного параметра и матрица [ξ] нормированных координат положений возможных моделей для состояний распределения выходного параметра в пространстве нормированных признаков формы оптимального состояния стохастической системы. Номер строки матрицы [ξ] нормированных координат соответствует номеру s возможной модели стохастической системы. Номера столбцов матрицы [ξ] определяют нормированные координаты положений возможных моделей состояния стохастической системы. Матричный вектор [ξ*] и матрица [ξ] нормированных координат положений возможных моделей передаются на устройство выбора формы модели 1355, на выходе которого устанавливается номер s формы возможной модели состояния стохастической системы. Так как номера моделей имеют свой специфический номер s, то для моделей известны параметры и признаки формы распределения.
Блок 1345 схемы на фигуре 13 иллюстрирует процесс определения энтропийно-параметрического потенциала выходного параметра стохастической системы по формуле (22). Энтропийно-параметрического потенциала 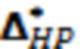 несимметричного несмещённого распределения выходного параметра стохастической системы характеризует положение среднего значения. Устройство 1385 предназначено для воспроизведения меры энтропийно-параметрического потенциала целевого распределения. Рассогласование состояния системы δΔHP оценивается по разнице энтропийно-параметрического потенциала выходного параметра
несимметричного несмещённого распределения выходного параметра стохастической системы характеризует положение среднего значения. Устройство 1385 предназначено для воспроизведения меры энтропийно-параметрического потенциала целевого распределения. Рассогласование состояния системы δΔHP оценивается по разнице энтропийно-параметрического потенциала выходного параметра 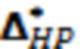 и энтропийно-параметрического потенциала целевого распределения ΔHP. Рассогласование энтропийно-параметрического потенциала реального и оптимального состояний системы, соответствующее разнице оценок средних значений выходного и целевого распределений, и используется блоком 1395 формирования управляющего воздействия χ для регулировки связей 1315 стохастической систем. При формировании управляющего воздействия χ так же учитывается положение модели s реального состояния системы. Согласно номеру модели s блок 1390 обеспечивает целевую корректировку формы распределения, которая учитывается блоком 1395 при формировании управляющего воздействия для регулировки связей стохастической систем. Таким образом, при минимизации рассогласования энтропийно-параметрического потенциала модели относительно оптимального состояния посредством целевой коррекции связей стохастической системы учитывается отклонение формы модели от оптимального состояния.
и энтропийно-параметрического потенциала целевого распределения ΔHP. Рассогласование энтропийно-параметрического потенциала реального и оптимального состояний системы, соответствующее разнице оценок средних значений выходного и целевого распределений, и используется блоком 1395 формирования управляющего воздействия χ для регулировки связей 1315 стохастической систем. При формировании управляющего воздействия χ так же учитывается положение модели s реального состояния системы. Согласно номеру модели s блок 1390 обеспечивает целевую корректировку формы распределения, которая учитывается блоком 1395 при формировании управляющего воздействия для регулировки связей стохастической систем. Таким образом, при минимизации рассогласования энтропийно-параметрического потенциала модели относительно оптимального состояния посредством целевой коррекции связей стохастической системы учитывается отклонение формы модели от оптимального состояния.
По значениям энтропийно-параметрического потенциала  выходного параметра и известному номеру s формы модели реального состояния с помощью устройства 1360 проводится определение параметра масштаба модели λ из условия минимизации разницы энтропийно-параметрических потенциалов модели с номером s и состояния плотности распределения выходного параметра.
выходного параметра и известному номеру s формы модели реального состояния с помощью устройства 1360 проводится определение параметра масштаба модели λ из условия минимизации разницы энтропийно-параметрических потенциалов модели с номером s и состояния плотности распределения выходного параметра.
Устройство 1365 используются для картирования состояния стохастической системы в энтропийно-параметрическом пространстве признаков выходного параметра. Картирование проводится по известным параметрам формы (α, β) модели s и параметру масштаба λ. Для обеспечения процесса мониторинга проводится запись в базу данных 1370 номер s, параметры формы (α, β) и масштаба λ модели распределения выходного параметра для реального состояния стохастической системы.
Устройство 1375 проверки принадлежности состояния стохастической системы зоне контроля оптимального состояния позволяет контролировать выход системы из зоны контроля по изменению признаков формы выходного распределения. Блок 1380 трансформации распределения предназначен для формирования сообщения η о необходимости трансформации распределения для возврата системы в зону контроля. Трансформацию распределения можно достичь изменением свойств системы за счёт изменения настроечных параметров регулятора, расположенного в подсистеме неконтролируемых процессов 1310 стохастической системы, изменением состава влияющих факторов 1325 или изменением выбора оптимального состояния, относительно которого устанавливается мониторинг и контроль над стохастической системой.
Из рассмотрения схемы на фигуре 13 следует, что для обеспечения устойчивости системы блок 1395 формирует управляющее воздействия для регулировки связей 1315 неконтролируемых процессов стохастической системы и связей 1317 влияющих факторов с контролируемым процессов выходного параметра стохастической системы.
Формирование управляющее воздействия блоком 1395 для регулировки связей 1315 и 1317 проводится при условии отличного от нуля номера модели s и/или отличного от нуля рассогласования энтропийно-параметрического потенциала. Блок 1390 целевой корректировки формы закона распределения предназначен для формирования кода S управляющего воздействия, зависящего от положения модели реального состояния системы в энтропийно-параметрическом пространстве и заданного номером s. Заявитель обращает внимание, что определение номера s модели реального состояния позволяет целенаправленно изменять форму распределения к его целевой форме путём дифференцированного регулирования связей 1315 и 1317 согласно коду S. При этом пропорциональное регулирование связей с учётом кода S обеспечивает минимизацию рассогласования энтропийно-параметрического потенциала для обеспечения масштаба модели стохастической системы масштабу её целевого распределения.
Оптимальное состояние стохастической системы - это состояние, отслеживаемое системой и заданное целевой плотностью распределения с известными параметрами формы и масштаба. Энтропийно-параметрический потенциал оптимального состояние стохастической системы так же задан целевым распределением выходного параметра.
Реальное состояние стохастической системы - состояние системы в текущий момент времени, характеристики которого определяются по выборке значений выходного параметра. Параметры распределения значений выходного параметра устанавливаются для модели реального состояния. По этому, выбор формы и масштаба модели, осуществляется по отношению к реальному состоянию стохастической системы.
Контроль направлен на обеспечение минимального рассогласования оценки энтропйино-параметрического потенциала контролируемого распределения выходного параметра для модели реального и оптимального состояний стохастической системы.
Оптимизация системы происходит путём минимизации рассогласования энтропийно-параметрического потенциала между оптимальным и реальным состоянием за счёт изменения параметров модели реального состояния и формирования управляющего воздействия для регулирования связей 1315 и 1317, изображённой на фигуре 13.
Предлагаемое изобретение может быть так же использовано для мониторинга и контроля при эволюции системы или её циклическом изменении. Так как для таких систем происходит переход из одного оптимального состояния в другое оптимальное состояние, то очевидно, что на различных этапах эволюции системы контроль производится относительно различных оптимальных состояний, для которых априорно проводится задание границы зон контроля.
Таким образом, предлагаемый способ мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения устраняет переход системы в нерабочее состояние из-за многозначности выбора форм несимметричных моделей и обеспечивает устойчивость системы посредством контроля соответствия формы и масштаба модели её реальному состоянию в энтропийно-параметрическом пространстве признаков несимметричного распределения выходного параметра.
Источники информации
1. Лукас В.А. Теория управления техническими системами. - Издательство Уральского государственного горного университета. Екатеринбург. - 2005г. - 676 с.
2. Солодовников В.В., Плотников В.Н., Якоалев А.В. Теория автоматического управления техническими системами. М.: Изд-во МГТУ, 1993. - 492 с.
3. Патент RU 2168763 Российская Федерация. Устройство для измерения характеристик случайных процессов / Сытько И.И., Сытько Е.Н., Волков А.В., Аврменко С.Г. - № 99107746/09 заявки, заявлен 19.04.1999; опубл. 10.06.2001.
4. Wang, H., 2003. Control of conditional output probability density functions for general nonlinear and non-Gaussian dynamic stochastic systems. IEE Proceedings: Control Theory and Applications 150 (1), 55-60.
5. Пат. 2 565 367 Российская Федерация. Способ контроля и управления динамической системой / Полосин В.Г., Бодин О.Н. - заявка № 2014111833/08; заявлен 27.03.2014; опубл. 20.10.15 Бюл. №29.
6. Sun Jian-Qiao Stochastic Dynamics and Control. Monograph Series on nonlinear Science and Complexity. Elsevier. AE Amsterdam, The Netherlands, First edition, 2006, 417 p.
7. Guoa L., Wang Н., Wang А.Р. Optimal probability density function control for NARMAX stochastic systems / Autovatica, Vol. 44, 2008, pp. 1904-1911.
8. Rose, C. and Smith, M.D. Mathematical Statistics with Mathematica, Springer-Verlag, New York - 2002 - 481 p.
9. NIST/SEMATECH e-Handbook of Statistical Methods, http://www.itl.nist.gov/ div898/handbook/ date.
10. Вадзинский Р.Н. Справочник по вероятностным распределениям. - СПб.: Наука, 2001. - 298 с.
11. Патент RU №2296356 Российская Федерация. Способ контроля и управления динамической системой / Лазарев В.Л. - № 2005124236/09 заявки; заявл. 29.07.2005; опубл. 27.03.2007, Бюл. №9.
12. Полосин В.Г., Бодин О.Н. Критерии оптимального управления динамической системой. / Труды МФТИ. - 2015. - Том 7, № 3 (27). - С.131-139.
13. Пат. 2334262 Российская Федерация. Способ контроля и управления состоянием неопределённости системы // Лазарев В.Л. - № 2007116079/09 заявки; заявлен 27.04.07; опубл. 20.09.2008 Бюл. №26.
14. Новицкий П.В., Зограф И.А. Оценка погрешности результатов измерений. - Л.: Энергоатомиздат. 1985г. - 248 с.
15. Polosin V.G. Mapping distributions in the entropy-parametric space. International Conference on Metrological Support of Innovative Technologies ICMSIT-2020, St. Petersburg, 4 March, 2020, Journal of Physics: Conference Series (JPCS). Publication number: ICMSIT-2020-4042.
16. Полосин В.Г., Тертычная С.В. Анализ результатов измерения объёмной активности радона с помощью распределения Вейбулла-Гнеденко. / Известия высших учебных заведений. Поволжский регион. Физико-метематические науки. №1 (9), 2009, С. 127-133.
17. Микляев П.С. Закономерности миграции и эсхаляции радона из грунтовов на территории г.Москвы: дис. на соискание степени канд. геолого-минералог. наук. / М., 2002. - 170 с.
18. Пат. 2532365, Российская Федерация. Способ мониторинга загрязнений природных сред техногенными источниками / Девятова А.Ю., Рапута В.Ф. Опубликовано: 10.11.2014, Бюл. № 31.
19. Самуленков Д.А., Мельникова И.Н., Донченко В.К., Сапунов М.В. Исследование загрязнений атмосферы с помощью лидарного мониторинга / Учёные записки Российского Государственного Гидрометеорологического университета., Санкт-Петербург, № 48, 2017, - С. 266-280.
20. Донцова Т.И. Балансный метод оценки загрязнений воздушной среды крупных городов на принципах биосферной совместимости / Волгоград, Дис. канд. техн. наук. 2016.
21. Гнеденко, Б. В. Математические методы в теории надежности / Б. В. Гнеденко, Ю. К. Беляев, А. Д. Соловьёв. - Москва: Наука, 1965. - 524 с.
22. Каштанов В. А., Медведев А. И. Теория надежности сложных систем. Москва: Физматлит, 2010., 607 с.
23. Русев В.Н. Актуальность теоретического исследования распределения Вейбулла−Гнеденко для расчета оценок технологической надежности нефтегазового оборудования // НТЖ «Автоматизация, телемеханизация и связь в нефтяной промышленности». - 2013. - №11. - С. 46−49.
24. ГОСТР 50779.27-2017. (МЭК 61649: 2008) Статистические методы. Распределение Вейбулла. Анализ данных. Москва. Стандартинформ. 2017. 58 с.
25. Ярмоленко И.В., Хуковский М.В., Кирдин И.Я. Исследование свойств логнормального распределения при анализе результатов радоновых обследований / Актуальные проблемы ограничения облучения населения от природных источников ионизирующих излучений. Радон. М., 2000, С. 17 - 20.
26. Elandt-Johnson R., Johnson N. Survival models and data analysis. - New York: John Wiley & Sons, 1999. 457 p.
27. Ярмоненко С. П., Вайнсон А. А. Радиобиология человека и животных. М., Высш. шк., 2004. -54 с.
28. Романовский М.Ю., Романовский Ю.М. Введение в эконофизику. Статистические и динамические модели. М. Ижевск: институт компьютерных исследований, НИЦ «Регулярная и хаотическая динамика», 2007. - 280 с.
29. Яковлева Т.В., Обзор методов обработки магнитно-резонансных изображений и развитие нового двухпараметрического метода моментов, Компьютерные исследования и моделирование, 2014, том 6, выпуск 2, 231-244.
30. Ali H. R., Dariush A. and other, Lymphocyte density determined by computational pathology validated as a predictor of response to neoadjuvant chemotherapy in breast cancer: secondary analysis of the ARTemis trial / Annals of Oncology 28: 1832-1835, 2017.
31. Бекман И.Н. Радиационная и ядерная медицина: физические и химические аспекты. Радиохимия. М., Щёлково: Издатель Мархотин., Том 7. 2012.- 400 с.
32. Котина Е.Д. Некоторые вопросы моделирования динамических процессов в радионуклидных исследованиях. - СПб.: Изд-во ВВМ, 2013. - 150 с
33. Матвеев А.В. Моделирование кинетики радиофармпрепаратов при функциональном исследовании мочевыводительной системы / Международный журнал медицины и психологии (International Journal of Medicine and Psychology) 2019, Том 2, №3, С. 56 - 58.
34. Национальное руководство по радионуклидной диагностике / под ред. Ю.Б. Лишманова, В.И. Чернова. - В 2-х т. - Томск: STT, 2010, Т.2. - 418 с.
35. Варфоломеев С.Д., Гуревич К.Г. Биокинетика: Практический курс. - М.: ФАИР-ПРЕСС, 1999. - 720 с.
36. Белов А.А., Курдяков А.П. Дескрипторные системы и задачи управления. - М.: Физматлит, 2015. - 275 с.
37. Shannon K.E. The mathematical theory of communication. Work on information theory and cybernetics / Ed. R.L. Dobrushina, O.B. Lupanova, M., 1963., 829 p.
38. Новицкий П.В. Понятие энтропийного значения погрешности. - измерительная техника, 1966, № 7, С.11 - 14.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ контроля неопределённости стохастической системы при условной оценке центра плотности распределения | 2020 |
|
RU2746904C1 |
| СПОСОБ КОНТРОЛЯ СОСТОЯНИЯ СТОХАСТИЧЕСКОЙ СИСТЕМЫ | 2020 |
|
RU2743897C1 |
| СПОСОБ И УСТРОЙСТВО ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЯ ПРИ ОКАЗАНИИ ЭКСТРЕННОЙ КАРДИОЛОГИЧЕСКОЙ ПОМОЩИ | 2020 |
|
RU2737860C1 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2014 |
|
RU2565367C1 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2016 |
|
RU2615286C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ АВ-БЛОКАДЫ I, II И III СТЕПЕНИ | 2015 |
|
RU2591839C1 |
| СПОСОБ КОНТРОЛЯ ЭКСТРЕМАЛЬНЫХ СИТУАЦИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ СРЕДЫ | 2015 |
|
RU2589367C1 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2005 |
|
RU2296356C1 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ СОСТОЯНИЕМ НЕОПРЕДЕЛЕННОСТИ СИСТЕМЫ | 2007 |
|
RU2334262C1 |
| УПРАВЛЕНИЕ РАЗРАБОТКОЙ СТВОЛА СКВАЖИНЫ С ИСПОЛЬЗОВАНИЕМ РАСЧЁТОВ НЕОПРЕДЕЛЁННОСТИ | 2013 |
|
RU2643057C2 |

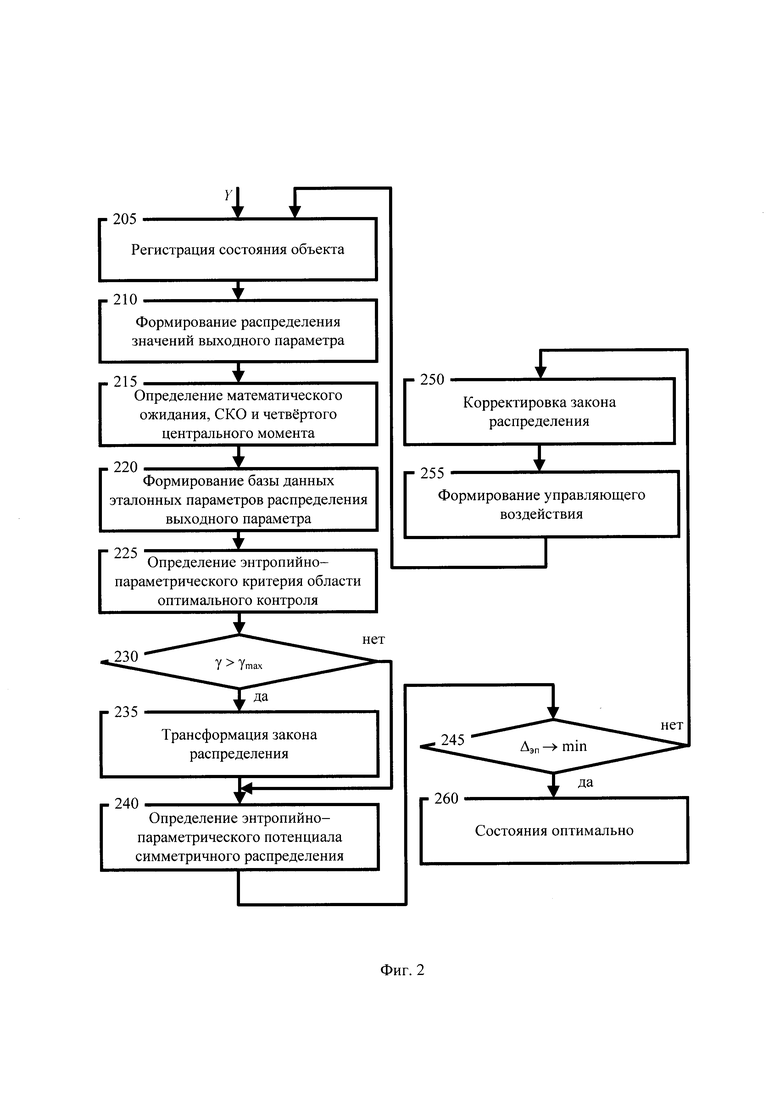
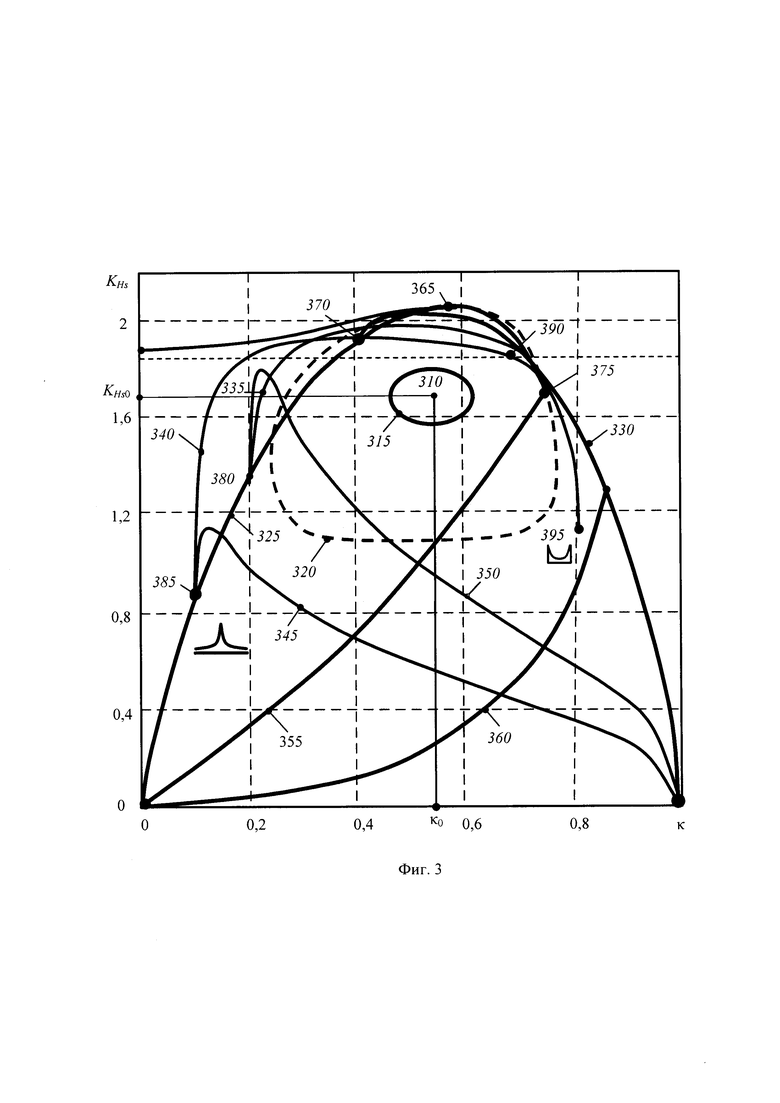



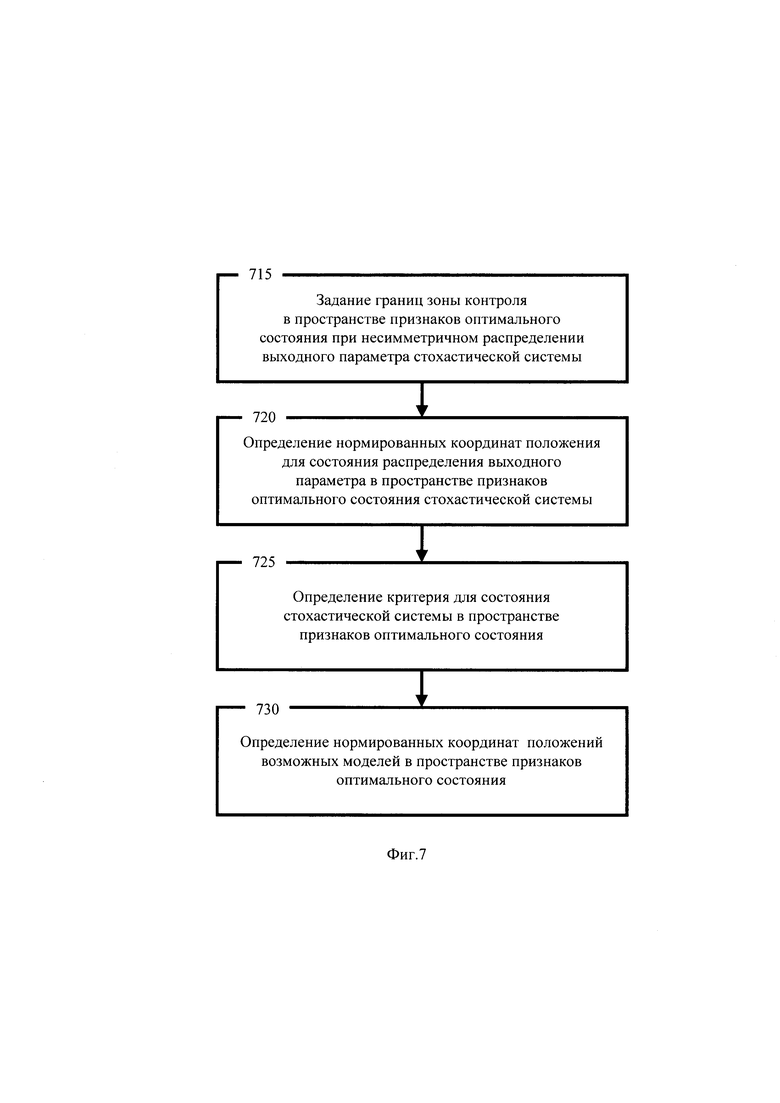
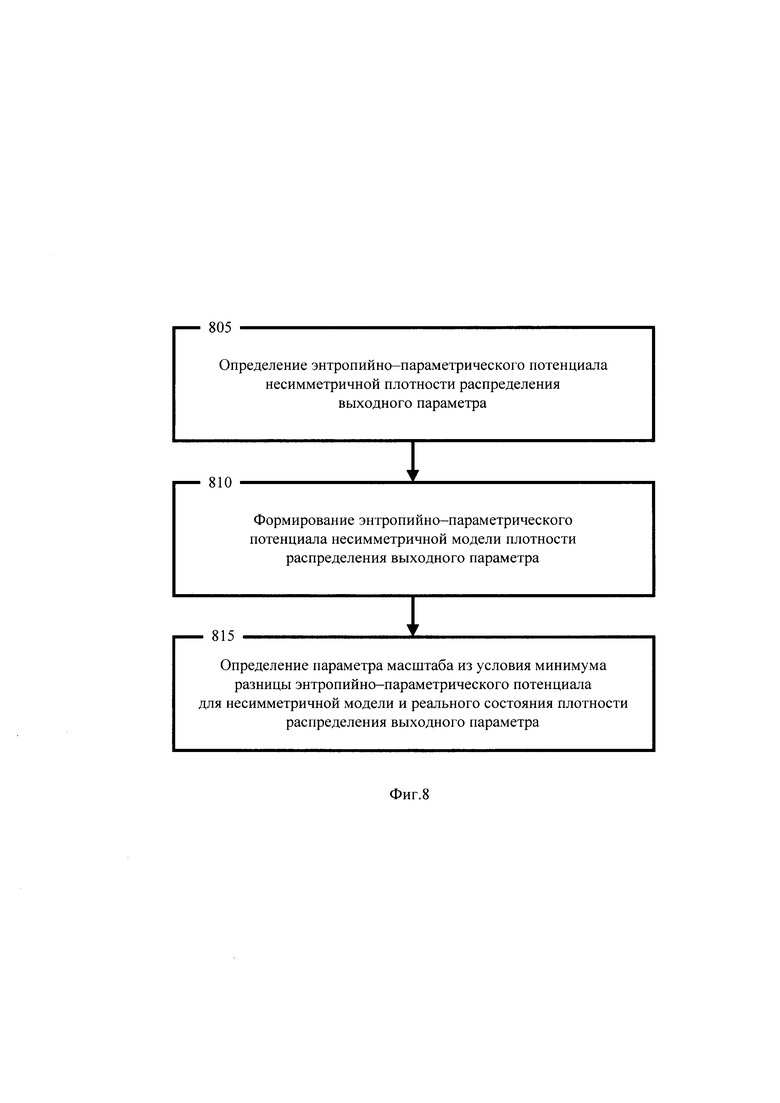


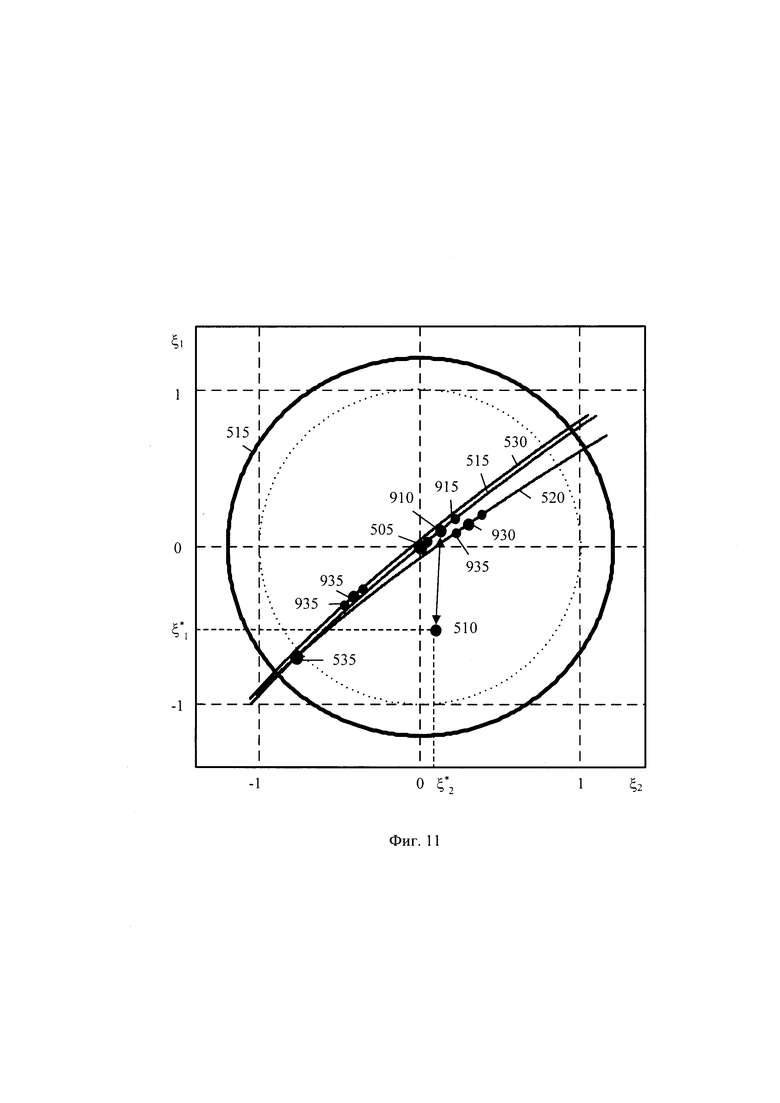

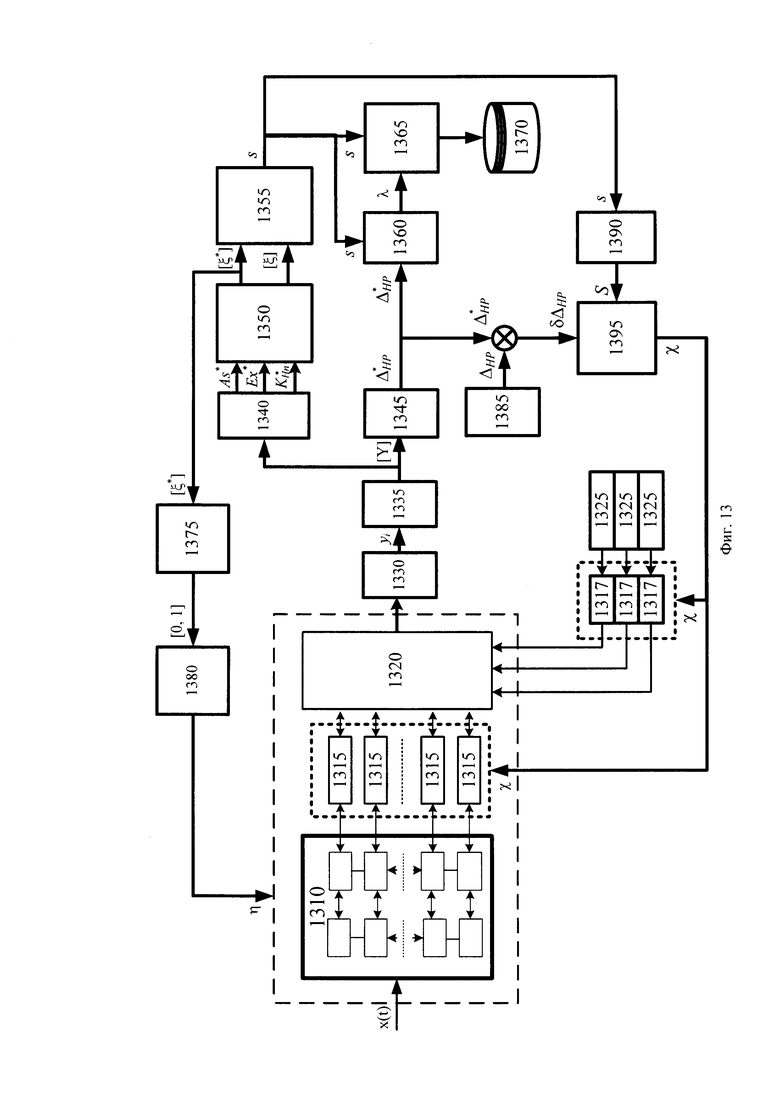
Изобретение относится к способам организации мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения выходного параметра и может быть использовано в системах контроля и управления различных динамических систем, обладающих хаотическими свойствами. На основе регистрации состояния объекта и формирования значений выборочного параметра определяются координаты энтропийно-параметрического пространства признаков формы для несимметричной несмещённой плотности распределения выходного параметра. Для обеспечения единства оптимальности управления в различных точках энтропийно-параметрического пространства проводится формирование пространства оптимального состояния системы. Унификация данных вблизи различных оптимальных состояний системы при выборе формы модели достигается заданием границы зоны контроля, определением нормированных координат положения для распределения выходного параметра в пространстве признаков оптимального состояния системы, определением критерия для состояния системы и определением координат положения возможных моделей в пространство признаков оптимального состояния. Минимизация рассогласования энтропийно-параметрического потенциала несимметричного распределения выходного параметра стохастической системы относительно оптимального состояния обеспечивается посредством целевой корректировки закона распределения и формирования управляющего воздействия для коррекции связей стохастической системы, что обеспечивает контроль масштаба модели распределения системы. Непрерывная запись параметров распределения выходного параметра сохраняет возможность восстановления состояния системы при проведении анализа. Визуализация процессов достигается картированием состояния стохастической системы в энтропийно-параметрическом пространстве признаков выходного параметра. Технический результат - повышение устойчивости функционирования стохастической системы за счёт мониторинга и контроля параметров формы и масштаба несмещённой несимметричной плотности распределения выходного параметра. 13 ил.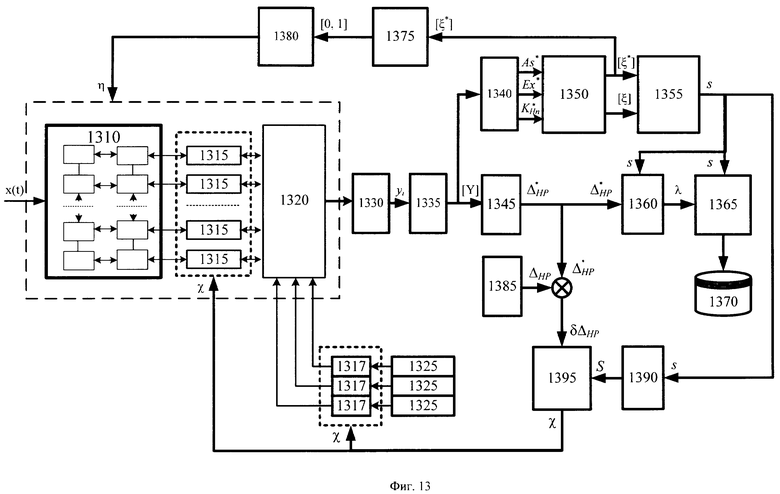
Способ мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения выходного параметра, заключающийся в том, что осуществляют регистрацию состояния стохастической системы, формирование выборки yi значений выходного параметра y(t) стохастической системы, определение математического ожидания M*, среднего квадратического отклонения σ* и центрального четвёртого момента μ4 распределения выходного параметра; формирование базы данных эталонных параметров закона распределения выходного параметра стохастической системы, проверку состояния стохастической системы принадлежности зоне контроля оптимального состояния; трансформацию закона распределения управляемого параметра за счет изменения настроечных параметров регулятора, корректировку закона распределения и формирование управляющего воздействия,
отличающийся тем, что дополнительно осуществляют
определение координат пространства признаков формы - асимметрии, эксцесса и коэффициента энтропии несимметричного распределения - для несимметричной несмещённой плотности распределения выходного параметра стохастической системы по формуле матричного вектора:
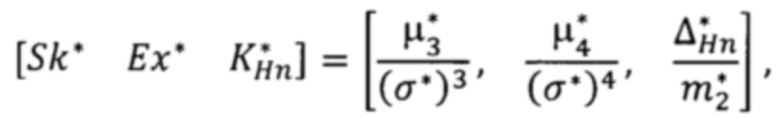
где  - второй начальный момент, третий центральный момент и энтропийный потенциал несимметричной несмещённой плотности распределения выходного параметра, определяемые по формулам:
- второй начальный момент, третий центральный момент и энтропийный потенциал несимметричной несмещённой плотности распределения выходного параметра, определяемые по формулам:


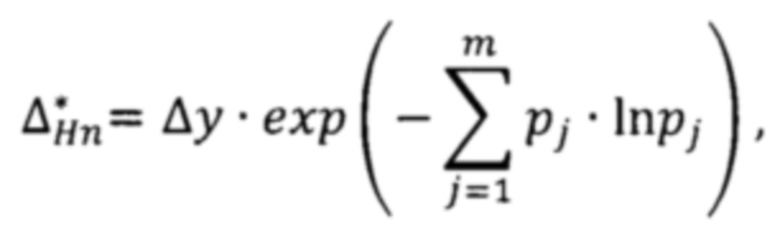
где m - число интервалов группирования; Δy - интервал группирования выходного параметра; pj - статистическая частота попадания отсчётов в j-й интервал группирования;
формирование пространства оптимального состояния стохастической системы включающее в себя следующие действия:
- задание границы зоны контроля в пространстве признаков оптимального состояния при несимметричном распределении выходного параметра стохастической системы:

где γmax - радиус зоны контроля; ξiγ - координаты границы контроля;
- определение нормированных координат положения для состояния распределения выходного параметра в пространстве признаков оптимального состояния стохастической системы по формуле матричного вектора:

где Sk0, Ex0, KHn0 - асимметрия, эксцесс и коэффициент энтропии несимметричной плотности распределения для оптимального состояния системы; a, b, c - коэффициенты интервалов признаков для зоны контроля;
- определение критерия для состояния стохастической системы в пространстве признаков оптимального состояния по формуле:

- определение нормированных координат положений возможных моделей стохастической системы в пространстве признаков оптимального состояния по формуле матричного вектора:
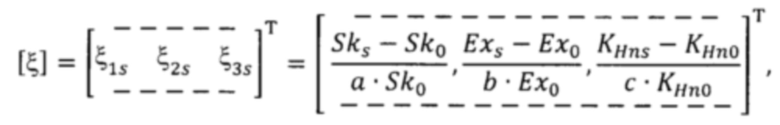
где Sks, Exs, KHns - асимметрия, эксцесс и коэффициент энтропии несимметричной плотности распределения для оптимального состояния системы; s - номер модели стохастической системы:

определение дистанций между положениями возможных моделей и реальным состоянием в нормированном центрированном пространстве признаков оптимального состояния стохастической системы по формуле

выбор формы модели стохастической системы из условия минимума дистанции между положениями модели и реального состояний

определение масштаба модели распределения выходного параметра стохастической системы, включающее в себя следующие действия:
- определение энтропийно-параметрического потенциала 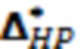 несимметричной плотности распределения выходного параметра стохастической системы
несимметричной плотности распределения выходного параметра стохастической системы
 ,
,
- формирование энтропийно-параметрического потенциала несимметричной модели плотности распределения выходного параметра стохастической системы

где m2λ и KHnλ - второй начальный момент и коэффициент энтропии несимметричной модели распределения выходного параметра;
- определение параметра масштаба из условия минимум разницы энтропийно-параметрических потенциалов для несимметричной модели и реального состояния плотности распределения выходного параметра стохастической системы

сохранение параметров модели стохастической системы в базе данных;
определение рассогласования энтропийно-параметрических потенциалов модели реального и оптимального состояний стохастической системы

минимизацию рассогласований энтропийно-параметрических потенциалов модели относительно оптимального состояния посредством целевой корректировки закона распределения и формирования управляющего воздействия для коррекции связей стохастической системы и картирование состояния стохастической системы в энтропийно-параметрическом пространстве признаков выходного параметра.
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2014 |
|
RU2565367C1 |
| Устройство для измерения корреляционного отношения двух случайных процессов | 1977 |
|
SU696488A2 |
| Энтропиметр | 1974 |
|
SU519718A1 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2005 |
|
RU2296356C1 |
| US 6496761 B1, 17.12.2002. | |||
Авторы
Даты
2021-11-01—Публикация
2021-03-09—Подача