Предлагаемое изобретение относится к области контроля сложными стохастическими системами, и может быть использовано в энергетике, медицине, пищевой, химической, металлургической и других отраслях промышленности. Целью изобретения является установление контроля сложной стохастической системы при условии оценки центра неопределённости путём отслеживания трека целевой плотности распределения выходного параметра.
Неопределённость объекта является неотъемлемая часть любого измерительного процесса и составляет существенную часть анализа изменчивости сложных систем [1, 2]. Существуют различные технические приложения, в которых при наличии случайных возмущений устанавливается контроль над плотностью распределения выходного параметра системы. Примерами процессов контроля плотности вероятностного распределения являются: контроль размера частиц в химической промышленности [3], контроль и анализ случайных процессов [4]; контроль весового распределения хлопкового волокна по длине [5]; контроль толщины и веса бумаги [6, 7], контроль управления распространением микрочастиц [8], контроль распределения биологических параметров в медицине [9, 10]. Изменчивость состояния сложной системы является основной причиной неопределённости значений выходных параметров, для контроля которой в промышленных процессах нашли применение системы контроля плотности распределения стохастических распределения [11, 12, 13, 14].
Известен стохастический контроль [14, 15] нелинейных систем при условной оценке центра неопределённости распределения выходного параметра, при котором осуществляют минимизацию разности между треком уловной выходной плотностью распределения массива значений, формируемого с использованием встроенного в систему слежения рекурсивного процесса, и треком условной целевой плотности распределения, характерным для оптимального состояния системы. Недостаток контроля состоит в использовании для аппроксимации массива значений выходного параметра системы плотности распределений с неизменной формой. При таком подходе обеспечение слежение трека целевой плотности распределения возможно только при использовании рекурсивного процесса для изменения значений выходной плотности в соответствии с заданным алгоритмом.
Наиболее близким к предлагаемому изобретению является способ контроля и управления динамической системы [16], заключающийся в том, что осуществляется регистрация состояния объекта, формирование массива yi значений выходного параметра y(t), определение математического ожидания M, среднего квадратического отклонения σ; формирование базы данных эталонных параметров закона распределения выходного параметра, проверку состояния объекта принадлежности области оптимального состояния; трансформация закона распределения управляемого параметра за счёт изменения настроек параметра регулятора, корректировку закона распределения и формирование управляющего воздействия.
Как следует из формулы изобретения, в известном способе контроля и управления динамической системой осуществляется определение контрэксцесса и коэффициента энтропии симметричного распределения; определение энтропийно-параметрического критерия области оптимального состояния; минимизация величины энтропийно-параметрического потенциала динамической системы и корректировка реального параметра закона распределения выходного параметра [16].
В качестве недостатков данного способа контроля и управления динамической системой следует отметить:
- ограничение моделей поведения системы только набором симметричных форм распределений выходного параметра;
- отсутствие возможности получения параметров для симметричной модели плотности распределения при условии получения оценки среднего значения, что ограничивает возможность её сравнение с треком симметричной плотности целевого распределения с известными параметрами;
- отсутствие возможности построения контроля форм смесей симметричных и несимметричных моделей неопределённости стохастической системы;
- отсутствие возможности получения интегральных и дифференциальных свойств распределения для организации систем пропорционально-интегрально-дифференциального контроля.
Краткое описание чертежей
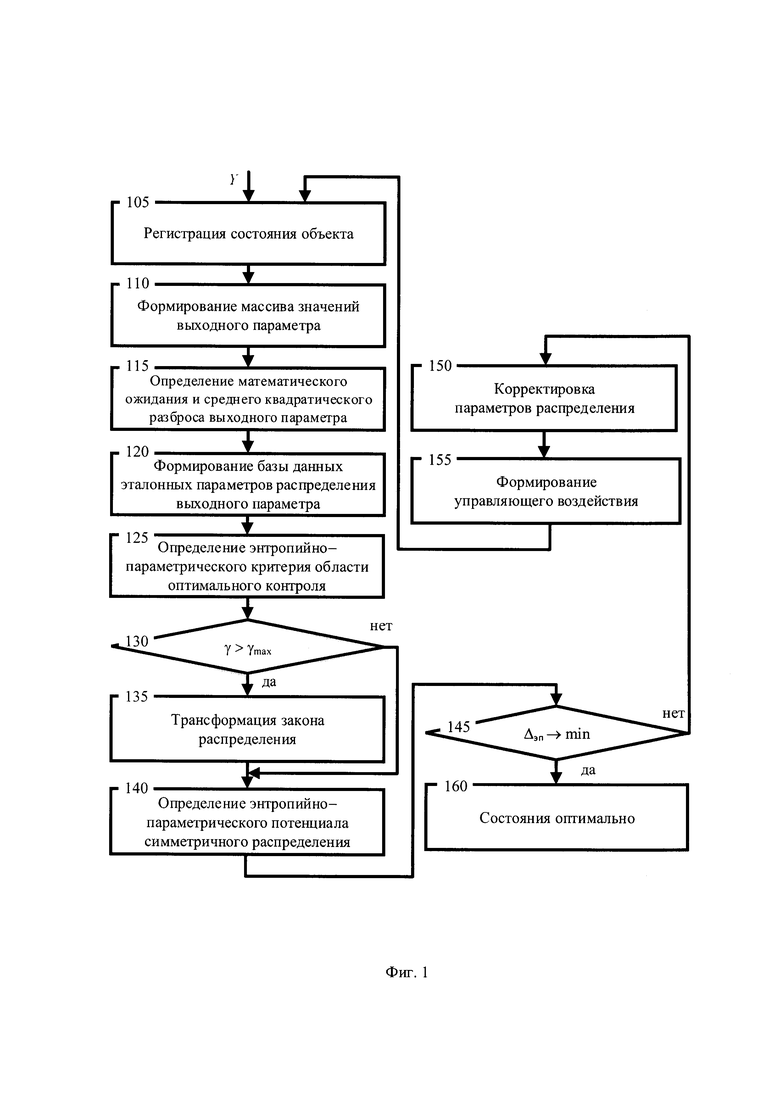
На фигуре 1 приведена схема процесса, реализующего известный способ контроля и управления динамической системой.
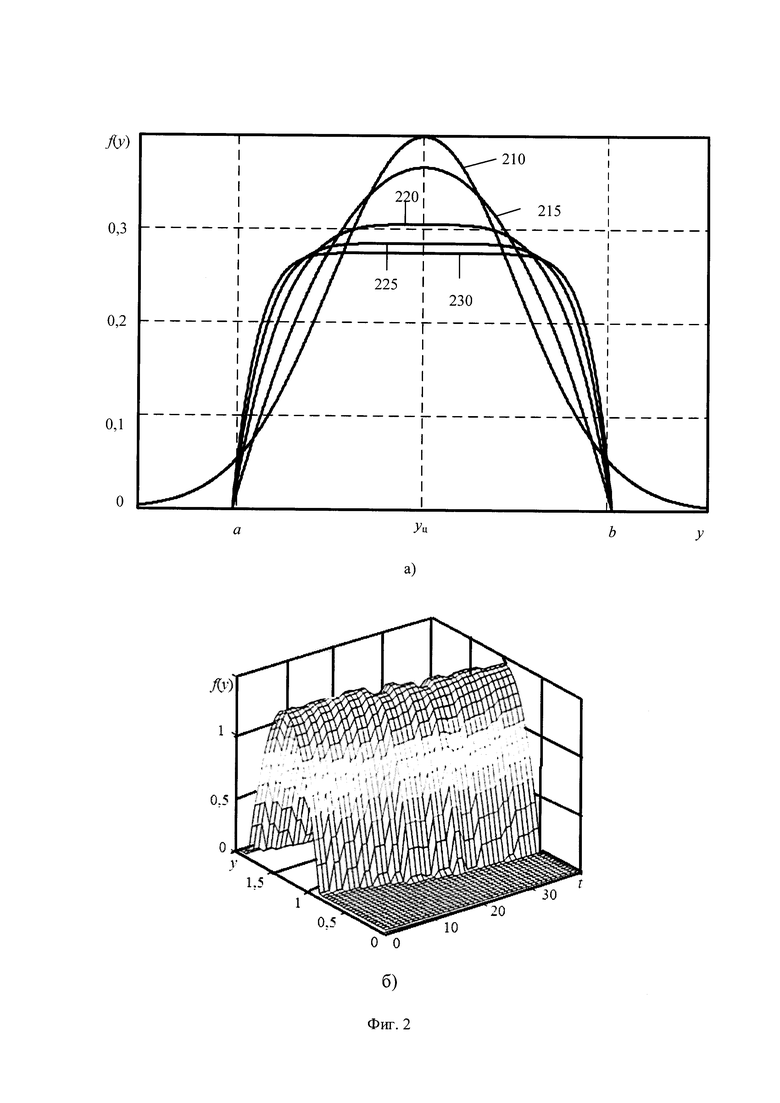
На фигуре 2 приведены модели симметричных плотностей распределения, используемые при контроле целевой плотности распределения:
а) чертежи моделей простых симметричных плотностей распределений;
б) пример трека условной плотности параболического распределения.
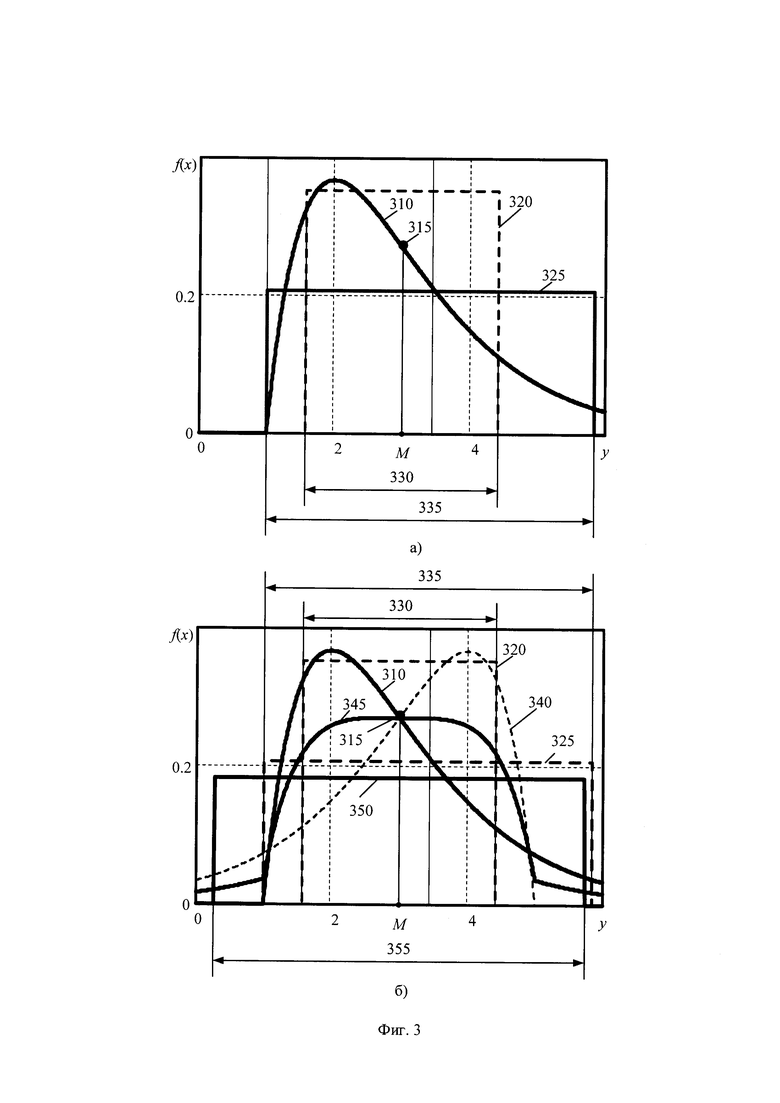
На фигуре 3 приведены чертежи неопределённостей для плотностей распределений массивов значений выходного параметра:
а) чертёж неопределённостей для несимметричной плотности гамма распределения;
б) чертёж неопределённостей для модели плотности симметричной относительно математического ожидания гамма распределения.
На фигуре 4 приведены чертежи неопределённостей для симметричных моделей плотностей распределения при использовании моды в качестве центра распределения;
а) чертёж неопределённостей для модели плотности симметричной относительно моды гамма распределения;
б) чертёж неопределённостей для модели плотности симметричной относительно моды смеси распределений Гаусса.
На фигуре 5 приведено пространство форм распределений, основанное на смеси нормального распределения и нормированной аппроксимации четвёртого порядка.
На фигуре 6 приведена схема процесса, реализующего способ контроля неопределённости стохастической системы при условии получения оценки центра плотности распределения.
На фигуре 7 приведена схема процессов, реализующих определение формы симметричной модели плотности распределения.
На фигуре 8 приведён вариант пространства признаков форм распределений для области контроля стохастической системы.
На фигуре 9 приведён чертёж пространства энтропийной и параметрической неопределённостей симметричной модели.
Подробное описание изобретения
Материал подробного описания содержит пояснения вариантов осуществления изобретения со ссылками на чертежи, где аналогичные ссылочные позиции представляют одинаковые или подобные элементы.
На современном этапе развития техники благодаря интенсивному внедрению информационных технологий возможно построение контроля над нелинейными стохастическими системами по изменению плотности распределения выходного параметра относительно целевой плотности распределения [11, 12, 14]. Сущность контроля состояния системы состоит в обеспечении минимальной разности между симметричной моделью плотности распределения контролируемого параметра на выходе системы и эталонной моделью симметричной целевой плотности распределения. Целью управления является построение управляющего воздействия u для регулировки настроек системы и её параметров, чтобы плотность распределения ρ(yk, u) последовательности стохастического выходного параметра уk следовала за эталонной моделью целевой плотности распределения ρ0(y):

Классические схемы контроля неопределённости системы при известной целевой плотности распределения выходного параметра построены на оценке рассогласований математического ожидания, дисперсии или среднего квадратического разброса стохастического выходного параметра системы при условии, что плотности выходного параметра соответствуют нормальные или параболические распределения.
Недостаток классических схем контроля состоит в том, что для стохастических систем характерны асимметричные не Гауссовы плотности распределения. Задача построение контроля неопределённости стохастической системы может быть решена на основе контроля набора статистической информации, характеризующей рассогласование состояние системы относительно заданной целевой плотности распределения. Контроль направлен на обеспечение соответствия интервалов неопределённостей и параметров модели плотности распределения выходного параметра интервалам неопределённостей и параметрам модели целевой плотности распределения стохастической системы.
В настоящее время при не гауссовой плотности распределения выходного параметра стохастической системы находят распространения схема контроля, при которой проводится замена плотности её аппроксимацией с помощью сплайна, по состоянию которых формируется управляющего воздействия для пропорционально-интегрально-дифференциального контролера. [14, 15]. Так как вид сплайна определяется вектором его параметров и базисный полином не обращается в нуль только на ограниченном локальным промежутке, то изменение положения контрольных точек влияет на кривую в ограниченном диапазоне. Поскольку сплайны являются локальными, изменение координат любой из точек изменяет форму кривой в локальной области сплайна и зависит от количества контрольных точек, включённых в интервал сплайна. Так как выходные параметры стохастической системы имеет вероятностные значения, то вектор параметров сплайна зависит от качества оценки параметров плотностей распределения. По этой причине для выборочных случайных последовательностей выходного параметра необходимо предварительное измерение параметров плотностей распределения для обеспечения заданной точности аппроксимации плотности с помощью сплайнов [14].
Для построения схемы контроля негаусовой плотности распределения при условии, что получена оценка центра распределения, проводят замену реального несимметричного распределения её симметричной относительно оценки центра моделью. В качестве оценки центра распределения принимают математическое ожидание, медиану, моду, среднее квадратическое значение и различные робастные квантильные оценки. При построении симметричных моделей используют нелинейные модели в виде нормального распределения или степенного ряда на ограниченном интервале значений наблюдаемого параметра y. Обычно степенной ряд ограничивается третьим или четвёртым порядка аппроксимации целевой плотности распределения [15].
Основной недостаток применения степенных аппроксимаций состоит в ограниченности интервала положения значений. При таком подходе получение текущего значения выходного параметра за пределами интервала вызывает качественное изменение формы трека распределения вследствие замены реальной неограниченной плотности распределения ограниченным набором симметричных моделей степенного ряд. По этой причине существующие схемы контроля реализуют рекурсивные методы для определения текущего значения выходного параметра, суть которых состоит в обеспечении целевой симметричной модели распределения за счёт искажения реальной выборки отсчётов перенесением значения внутрь интервала.
Таким образом, недостаток контроля неопределённости системы при замене реальных несимметричных неограниченных распределений выходного параметра степенным рядом симметричных распределений состоит в ограниченности выбора формы модели.
В известном способе контроля и управления динамической системой, основанном на минимизации энтропийно-параметрического потенциала симметричного распределения выходного параметра, возможен контроль симметричных распределений в пространстве признаков коэффициента энтропии и контрэксцесса.
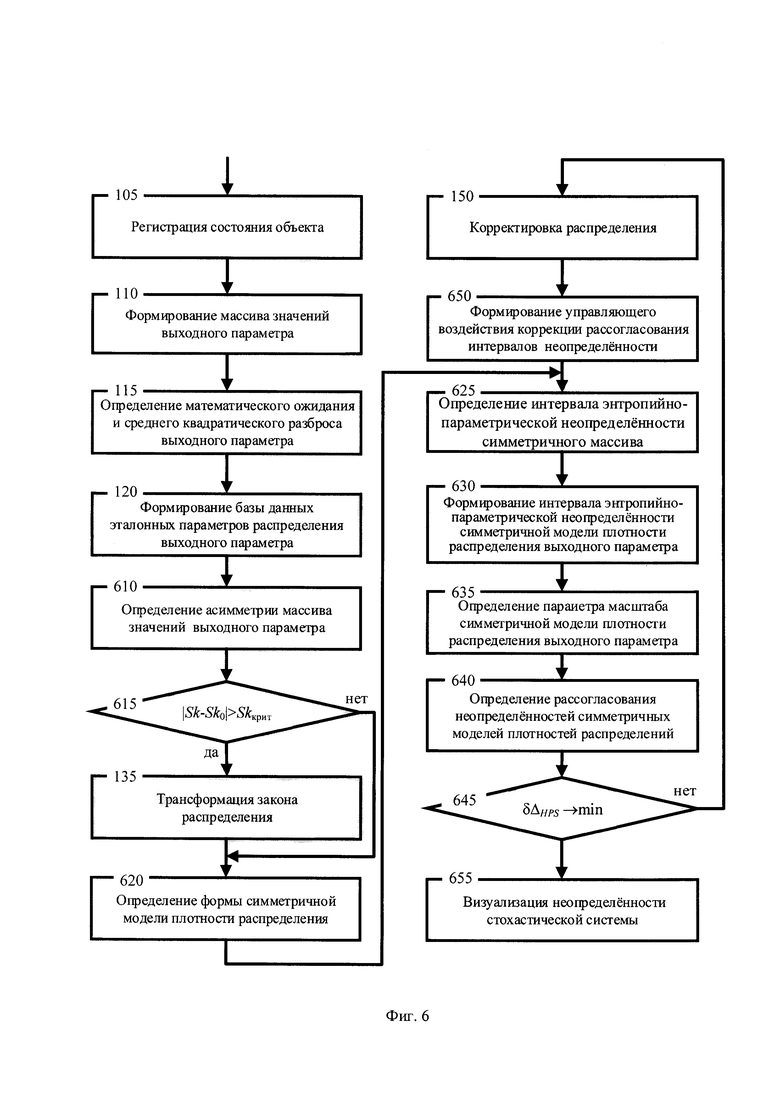
Схема процесса на фигуре 1 иллюстрирует этапы для известного способа контроля динамической системой заключающегося в том, что осуществляется регистрация состояния объекта на этапе 105; формирование массива значений выходного параметра yi на этапе 110; определение математического ожидания и среднего квадратического разброса выходного параметра на этапе 115; формирование базы данных эталонных параметров распределений выходного параметра на этапе 120; определение энтропийно-параметрического критерия области оптимального управления на этапе 125; проверка состояния объекта принадлежности области оптимального управления на этапе 130; транфсформация закона распределения на этапе 135; определение величины энтропийно-параметрического потенциала на этапе 140; минимизация величины энтропийно-параметрического потенциала на этапе 145; корректировка параметров распределения выходного параметра на этапе 150; формирование управляющего воздействия на этапе 155; информирование об оптимальности состояния на этапе 160.
В качестве характерных особенностей известного способа контроля динамической системой выделим следующее.
Первая особенность известного способа контроля динамической системой состоит том, что контроль ограничен признаками формы только симметричных распределений, так как известное топологическое пространство контрэксцесса и коэффициента энтропии, разработанное Новицким П.В. [17], не содержит характерных признаков для анализа и контроля несимметричных распределений.
Другая особенность известного способа контроля динамической системой состоит в том, что минимизация энтропийно-параметрического потенциала направлена на уменьшение неопределённости значений выходного параметра. Минимизация потенциала предполагает, что для наиболее оптимального состояния системы интервал неопределённости выходного параметра стремится к нулевому пределу. Такой подход не позволяет контролировать масштаб интервала неопределённости при оценке центра плотности распределения выходного параметра стохастической системы, для которой неопределённость системы обусловлена непрерывной изменчивостью её внутренней структуры.
Таким образом, известный способ контроля динамической системы имеет следующие недостатки.
Таким образом, известный способ контроля, построенный на основе минимизации интервала неопределённости, не обеспечивает контроль интервала неопределённости для симметричной модели плотности распределения при условии оценки центра выходного параметра путём её целенаправленного изменения к модели целевой плотности распределения.
Предлагаемое изобретение направлено на обеспечение контроля неопределённости стохастической системы при получении условной оценки центра плотности смеси симметричных и несимметричных распределений, достигаемое путём минимизации рассогласования интервалов энтропийной и параметрической неопределённостей модели плотности смеси распределений симметричной относительно оценки центра плотности смеси распределений.
Автор предполагаемого изобретения предлагает для смеси симметричного и несимметричного распределения контролировать признак асимметрии и интервалы энтропийной и параметрической неопределённостей симметричных моделей плотностей распределений, полученных их отображением относительно оценки центра.
Для одновременного анализа смесей симметричных и несимметричных распределений, формируемых вследствие изменчивой структуры стохастической системы, удобно проводить анализ массива значений выходного параметра при условии получения оценки центра распределения. Примером служат алгоритмы [15], в которых несимметричные распределения контролируемого на выходе системы параметра заменяются симметричными относительно оценки центра нормальными или степенными аппроксимациями распределения.
По мнению автора предполагаемого изобретения, обеспечение контроля неопределённости стохастической системы при условии получения оценки центра плотности распределения выходного параметра позволяет проводить целенаправленное изменение свойств стохастической системы таким образом, чтобы сохранялось соответствие симметричной относительно оценки центра модели выходной плотности распределения и симметричной модели её целевой плотности, характерной для оптимального состояния системы.
Способ контроля неопределённости стохастической системы при условии получения оценки центра плотности распределения, основанный на целенаправленном изменении симметричной модели плотности распределения выходного параметра к симметричной целевой плотности распределения стохастической системы, при котором регистрируют состояние объекта; формируют массив значений выходного параметра yi; определяют математического ожидания M и средний квадратический разброс σ выходного параметра; формируют базу данных эталонных параметров распределений выходного параметра; трансформируют закон распределения выходного параметра посредством изменения настроек системы; отличающийся тем, что осуществляют
определение признака асимметрии Sk для несимметричной плотности распределения массива значений выходного параметра системы

где μ3 - третий центральный момент распределения массива значений выходного параметра, определяемый

где N - число значений в выборке выходного параметра;
проверку допустимости рассогласования асимметрии распределения массива значений области оптимального состояния системы

где Sk0 - признак асимметрии оптимального распределения стохастической системы;
ΔSkкрит - критическое значение разности асимметрий области оптимального состояния;
определение формы симметричной модели выходной плотности распределения стохастической системы посредством
- определения центра yц несимметричного массива значений выходного параметра;
- формирования симметричного массива значений Z отображением значений несимметричного массива значений Y выходного параметра относительно оценки центра;
- определения второго μ2S и четвёртого μ4S центральных моментов симметричного массива значений
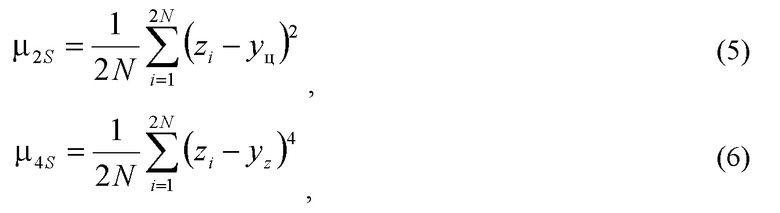
- определения интервалов информационной и параметрической неопределённости симметричного массива значений выходного параметра стохастической системы
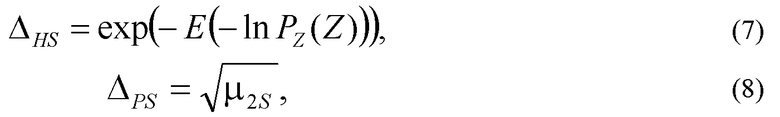
- определения коэффициента энтропии и контрэксцесса симметричного массива значений выходного параметра

- определения критерия области контроля признаков формы симметричной целевой плотности распределения
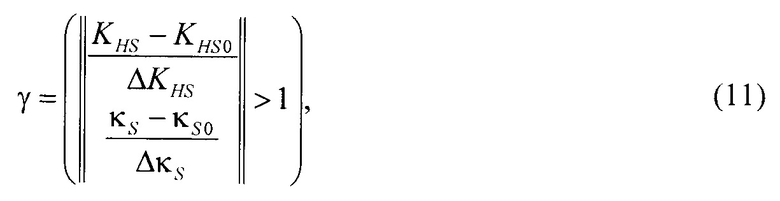
где ΔκS, ΔKHS - разбросы признаков контрэксцесса и коэффициента энтропии симметричного массива относительно контрэксцесса κS0 и коэффициента энтропии KHS0 симметричной целевой плотности распределения стохастической системы;
- проверки принадлежности положения системы области контроля и если критерий γ равен единице (γ=1), то проводят трансформацию закона распределения посредством изменениям настроек системы;
- определения дистанций между положениями возможных моделей и положением симметричного массива значений выходного параметра
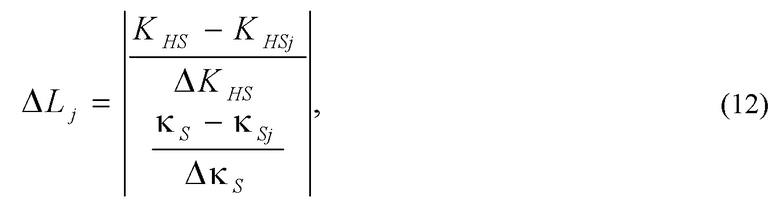
где 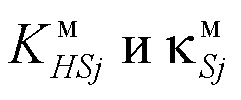 - контрэксцесс и коэффициент энтропии симметричной j-й модели плотности распределения;
- контрэксцесс и коэффициент энтропии симметричной j-й модели плотности распределения;
- выбора формы симметричной модели плотности распределения из условия минимума дистанции между положениями возможных моделей и положением симметричного массива значений выходного параметра

- определения вектора рассогласования признаков формы симметричной моделей плотности распределений выходного параметра и симметричной целевой плотности распределения стохастической системы
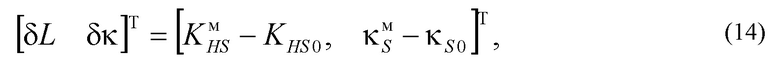
где 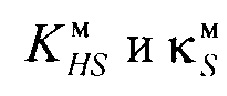 коэффициента энтропии и контрэксцесса выбранной симметричной модели плотности распределения;
коэффициента энтропии и контрэксцесса выбранной симметричной модели плотности распределения;
- формирования управляющего воздействия для коррекции рассогласования признаков формы симметричной модели плотности распределения посредством изменения параметров и настоек системы;
определение интервала энтропийно-параметрической неопределённости симметричного массива значений выходного параметра стохастической системы
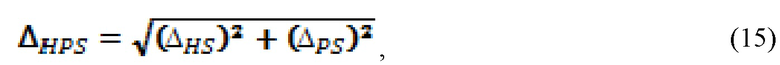
формирование интервала энтропийно-параметрической неопределённости симметричной модели плотности распределения выходного параметра

определение параметра масштаба симметричной модели плотности распределения выходного параметра из условия минимума разницы интервалов энтропийно-параметрических неопределённостей симметричного массива значений выходного параметра и симметричной модели распределения выходного параметра

определение рассогласования интервалов энтропийно-параметрических неопределённостей симметричной модели плотности распределения выходного параметра 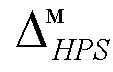 и симметричной целевой плотности распределения
и симметричной целевой плотности распределения 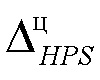

минимизацию рассогласования интервалов энтропийно-параметрических неопределённостей симметричной модели плотности распределения выходного параметра и симметричной модели целевой плотности распределения и формирование управляющего воздействия для коррекции рассогласования интервалов неопределённости стохастической системы, сохранение параметров модели и визуализацию модели неопределённости стохастической системы.
Введённые действия обеспечивают контроль состояния неопределённости стохастической системы и целенаправленного изменения симметричной модели плотности распределения выходного параметра при условии получения оценки центра к симметричной целевой плотности распределения системы путём
- проверки наличия асимметрии массива значений выходного параметра и её соответствие эталонному значению асимметрии плотности смеси;
- контроля формы и масштаба неопределённости симметричной относительно оценки центра массива значений;
- контроля состояния неопределённости стохастической системы за счёт слежения рассогласования интервалов неопределённости симметричной модели трека плотности распределения относительно интервалов неопределённости симметричной целевой плотности распределения.
В современных системах контроля для аппроксимации распределения выходного параметра при условии оценки среднего значения массива используются простые формы симметричных распределений, такие как нормальное и параболическое распределения, степенные симметричные аппроксимации, ограниченные до шестого порядка [15]. Чертежи моделей симметричных плотностей распределений, используемых при контроле целевой плотности распределения в стохастических системах, даны на фигуре 2,а, где обозначено 210 и 215 - нормальное и параболическое распределения, 220, 225 и 230 - нормированные аппроксимации четвёртого, шестого и восьмого порядка. Простые распределения используются в системах контроля слеживания трека плотности распределения для аппроксимации данных при известной оценке центра распределения. Пример трека плотности параболического распределения показан на фигуре 2,б. Из-за ограниченности форм, применяемых в системах, появляются расхождения между реальными выходными плотностями распределений и моделями целевых плотностей распределений. К примеру, применение для аппроксимации параболического распределения ограничивает интервал положение значений выходной величины yi∈[a, b] длиной этого интервала.
Применение степенного ряда симметричных распределений, состоящего из второго, четвёртого и шестого порядка, так же имеет ограниченный интервал возможного положения значений выходного параметра, так как каждое из распределений ограничено и при аппроксимации используются модели с сопоставимыми разбросами значений. Неопределённость сложной системы характеризуется неограниченной смесью распределений, обусловленной непрерывным изменением её внутренних процессов и наложением внешних воздействий. Такие распределения значений представляют сложные не симметричные смеси, значения которых выходят за пределы используемых симметричных аппроксимаций. Замена реального распределения ограниченной аппроксимацией решается за счёт применения рекурсивных алгоритмов, суть которых состоит в отображении реальных значений внутри ограниченного интервала. Применение нормального распределения так же ограничено одной формой распределения, которое значительно отличается от несимметричной плотности распределения выходного параметра.
Несмотря на то, что плотности распределения наблюдаемых параметров сложных стохастических систем заданы смесью симметричных и несимметричных распределений, для задания разброса параметра при условии, что получена оценка среднего значения, возможно использование симметричных распределений.
Автор предполагаемого изобретения полагает, что применение процесса симметрирования позволяет контролировать неопределённость состояние стохастической системы путём отслеживания симметричной модели трека плотности распределения, построенной для массива значений выходного параметра системы, относительно трека симметричной целевой плотности распределения.
Свойства симметричного массива
При получении оценки среднего значения интервалы энтропийной и параметрической неопределённости в окрестности центра содержат информацию о внутреннем устройстве системы. Для исследования интервалов неопределённости в окрестности полученной оценки центра используют симметричные модели распределений. Замена выходного массива данных при условии оценки центра симметричной моделью плотности распределения позволяет рассматривать интервалы энтропийной и параметрической неопределённости центрированными относительно оценки центра массива значений выходного параметра.
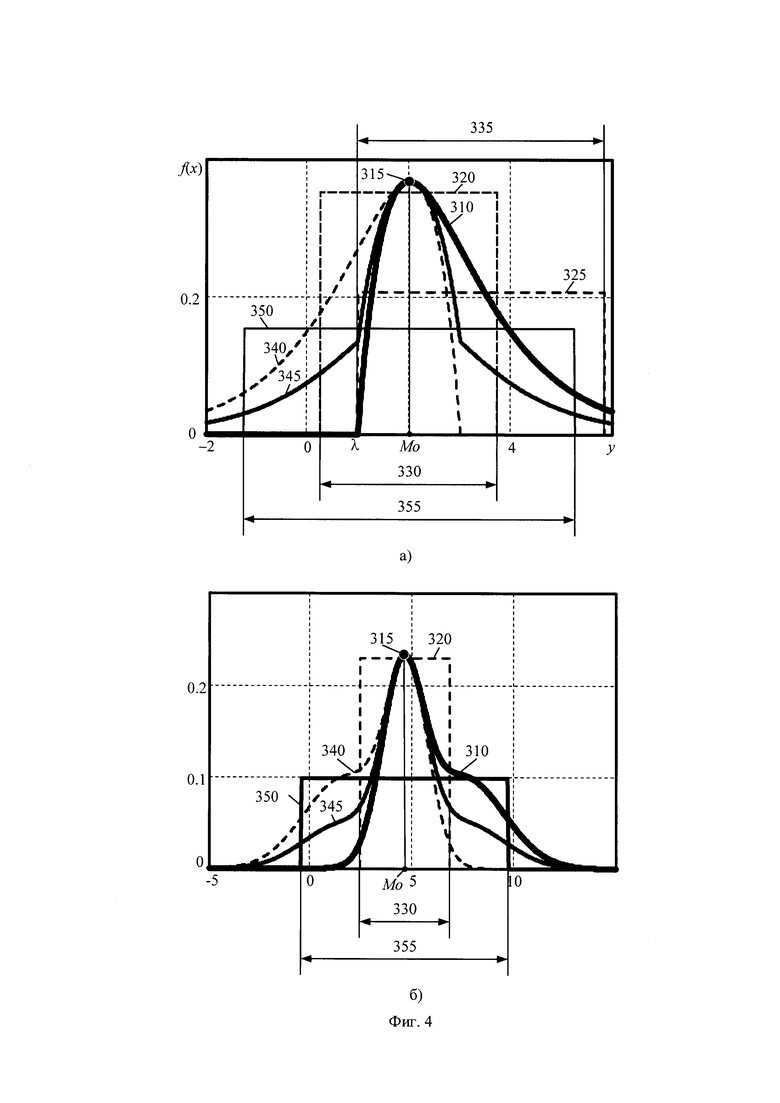
Особенность положения интервалов неопределённости асимметричного массивов значений выходного параметра иллюстрируют фигура 3 а, где приведён чертёж неопределённостей для несимметричной плотности гамма распределения массива значений выходного параметра. На фигуре 3, а даны следующие обозначения
310 - несимметричная смещённая плотность распределение массива значений выходного параметра;
315 - центр несимметричного массива значений выходного параметра;
320 и 325 - равномерные модели интервалов параметрической и энтропийной неопределённостей для несимметричного распределения значений выходного параметра;
330 и 335 - дистанции интервалов параметрической и энтропийной неопределённости, соответственно.
Так как модель интервала параметрической неопределённости 320 определена среднеквадратическим разбросом значений в массиве выходного параметра, то положение интервала 320 симметрично относительно центра 315, определяемого математическим ожиданием массива значений выходного параметра. Дистанции интервала 330 параметрической неопределённости равна среднему квадратическому разбросу значений в массиве выходного параметра.
Модель интервала энтропийной неопределённости 325 смещённого гамма распределения расположена несимметрично относительно полученной оценки центра распределения, так как характеризует распределение значений относительно границы положения значений несимметричного распределения [18]. Дистанция интервала энтропийной неопределённости 335 откладывается относительно точки смещения несимметричного гамма распределения.
Положение интервалов неопределённостей симметричных относительно оценки центра массива значений иллюстрирует чертёж неопределённостей на фигуре 3, б для модели плотности симметричной относительно математического ожидания гамма распределения. На фигуре 3, б дополнительно использованы обозначения
340 - несимметричное распределение массива значений, полученных при симметричном переносе массива значений выходного параметра относительно оценки центра 315 ;
345 - симметричная нормированная модель распределения массива значений выходного параметра;
350 - равномерная модель интервала энтропийной неопределённости симметричной нормированной модели распределения массива значений выходного параметра;
355 - дистанция интервала энтропийной неопределённости симметричной нормированной модели распределения массива значений выходного параметра.
Для анализа несимметричного массива значений выходного параметра, иллюстрируемого распределением 310, формируется симметричная нормированная модель распределения массива значений выходного параметра 345. Формирование симметричной модели получено переносом значений yi массива Y выходного параметра относительно оценки центра yц, показанного на фигуре 3 в виде точки 315. В результате переноса получен несимметричный массив Y* значений y*i. Координаты i-х значений массива Y* определены согласно выражению

В результате объединения двух массивов Y и Y*, для которых i-е значения массивов расположены симметрично относительно оценки центра yц массива Y, получен симметричный массив значений Z

На фигуре 3,б симметричная нормированная модель распределения значений выходного параметра 345 иллюстрирует симметричный массив Z, для которого многие свойства совпадают со свойствами исходного массива Y значений выходного параметра системы. К примеру, если в качестве оценки центра yц массива Y использовано математическое ожидания, то все чётные центральные моменты массивов будут равны:

При использовании математического ожидания в качестве оценки цента симметрии несимметричный массивы значений Y выходного параметра и симметричный массив Z имеют одинаковые эксцессы, т.е. одинаковые признаки островершинности.
Чертежи неопределённостей для симметричных моделей плотностей распределения при использовании моды в качестве центра распределения показаны на фигуре 4, где на фигуре 4,а выполнен чертёж неопределённостей для модели плотности симметричной относительно моды гамма распределения, на фигуре 4,б дан чертёж неопределённостей для модели плотности симметричной относительно моды смеси распределений Гаусса. При использовании моды или медианы в качестве оценки центра 315 чётные робастные моменты несимметричного массива значений выходного параметра будут равны чётным центральным моментам симметричного массива Z. По этой причине для анализа чётных робастных оценок несимметричного массива Y значений выходного параметра можно использовать чётные центральные моменты симметричного массива Z. Сохранение в симметричном массиве Z ряда чётных свойств несимметричного массива значений Y выходного параметра стохастической системы использовано для обеспечения контроля над стохастической системой.
Следует отметить, что при использовании математического ожидания M массива Y в качестве оценки центра симметрии, модель параметрической неопределённости симметричного массива Z совпадает с моделью параметрической неопределённости 320 массива Y. Дистанции интервалов параметрической неопределённости массивов Y и Z равны.
Так как информационные свойства выборки симметричного массива Z также зависят от распределения значений несимметричного массива Y, то свойства равномерной модели интервала энтропийной неопределённости 350 допустимо использовать для контроля интервала энтропийной неопределённости несимметричного массива Y, отображаемого равномерной моделью 325. В частности, энтропийный коэффициент симметричного массива Z представляет собой независимый информационный признак формы несимметричного распределения Y. Формула для определения энтропийного коэффициента симметричного массива Z задано в виде отношения (9) дистанций 355 и 330 интервалов энтропийной ΔHS и параметрической ΔPS неопределённостей симметричного массива значений Z.
Важное свойство модели интервала энтропийной неопределённости 350 симметричного массива Z является его симметричное положение относительно центра 315 несимметричного массива Y значений выходного параметра независимо от выбора в качестве оценки центра математического ожидания, моды, медианы или квантильной оценки. Симметричное положение модели интервала энтропийной неопределённости относительно оценки центра сохраняется при использовании смесей смещённых симметричных и несимметричных распределений для аппроксимации несимметричного массива значений Y выходного параметра.
Таким образом, использование симметричного массива Z позволяет использовать проекцию несимметричного распределения и контролировать его свойства в проекции признаков контрэксцесса κS и коэффициента энтропии KHS симметричных распределений.
Для практического применения имеет значение тот факт, что форму симметричной модели плотности распределения, найденную в пространстве признаков контрэксцесса κS и коэффициента энтропии KHS симметричных распределений, допустимо использовать для построения систем контроля несимметричных массивов выходного параметра сложной стохастической системы, которые могут быть синтезированы на основе смесей простых форм.
Пространство форм смеси симметричных распределений
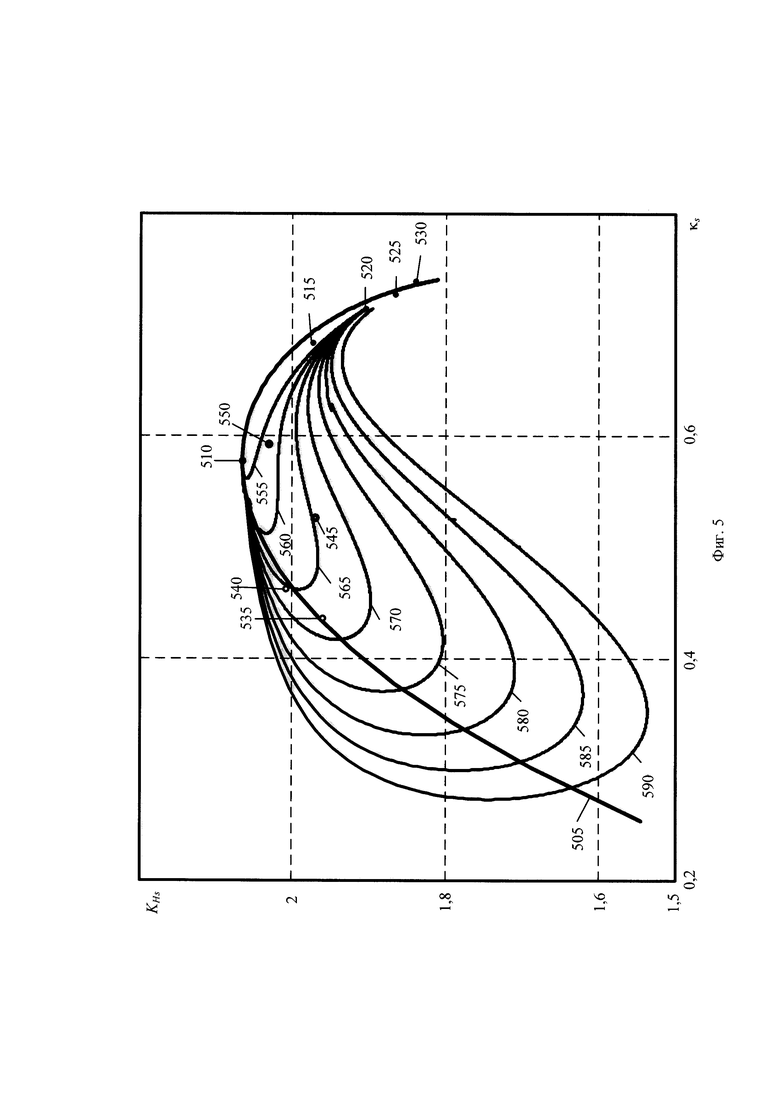
Реализации процесса получения формы распределения возможна за счёт отображения многообразия форм симметричных моделей распределений и их смеси в пространстве признаков формы распределения: контрэксцесса κS и коэффициента энтропии KHS симметричного распределения. Пример пространства форм распределений, основанного на смеси нормального распределения и нормированной аппроксимации четвёртого порядка, показан на фигуре 5, где использованы следующие обозначения:
505 - положение кривой класса экспоненциальных распределений [17, 19];
510 и 515 - точки положения нормального и параболического распределений;
520, 525, и 530 - точки положения нормированных аппроксимаций четвёртого, шестого и восьмого порядка, соответственно;
535 и 540 - симметричные модели несимметричного гамма распределения с параметром формы равным 2, которые получены отображением значений относительно моды и математического ожидания, принятых в качестве центра распределения, соответственно;
545 и 550 - пример симметричных моделей несимметричной смеси нормальных смещённых распределений, полученные относительно моды и математического ожидания, соответственно;
555, 560, 565, 570, 575, 580, 558 и 590 - кривые смесей нормального распределения и нормированной аппроксимации четвёртого порядка при разных соотношениях их среднеквадратических разбросов равных 1,8, 2,2, 2,6, 3, 3,5, 4, 4,5 и 5, соответственно.
Для построений кривых плотности смесей ƒsmes(y,K) распределения на фигуре 5 использовано соотношение вида:
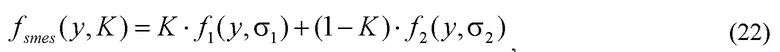
где K - коэффициент веса первой составляющей распределения; ƒ1(y,σ1) и ƒ2(y,σ2) - плотности первой и второй составляющих распределений; σ1 и σ2 - среднеквадратические разбросы значений первой и второй составляющих распределений.
На фигуре 5 использовано нормальное распределение в качестве первой составляющей смеси распределения (22) и нормированная аппроксимация четвёртого порядка в качестве второй составляющей смеси. При построении кривых пространства форм распределений на фигуре 5 варьировался коэффициент веса K составляющих распределений. Кривые построены при различных соотношениях среднеквадратического разброса нормированной аппроксимации четвёртого порядка к среднему квадратическому разбросу нормального распределения.
Из рассмотрения фигуры 5 следует, что формы смесей нормированной аппроксимации четвёртого порядка и нормального распределения покрывают значительную область возможных форм распределения. Полученные смеси могут использоваться в качестве симметричных моделей выходных параметров сложных стохастических систем.
Пространство форм может быть получено на основе смесей распределений, заданных на ограниченном интервале, и распределений, неограниченных на числовой оси: нормального распределения, распределения Лапласа, логистического распределения и других. Целевая плотность распределения формируется на основе модели стохастической системы или на основе априорно известной выборки данных. Выбор рабочей диаграммы осуществляется на основе оценки соответствия форм симметричной модели плотности распределения выходного параметра и симметричной модели целевой плотности распределения.
Описание алгоритма изобретения
Схема процесса на фигуре 6 иллюстрируют новые возможности и особенности предлагаемого способа контроля неопределенности стохастической системы при условии получения оценки центра плотности распределения.
Для реализации новых возможностей в предполагаемом изобретении проводятся следующие действия, иллюстрируемые в виде этапов процесса контроля на фигуре 6:
- этапа 610 определения асимметрии массива значений выходного параметра;
- этапа 615 проверки допустимости рассогласования асимметрии распределения массива значений области оптимального состояния системы;
- этапа 620 определения формы симметричной модели плотности распределения;
- этапа 625 определения интервала энтропийно-параметрической неопределённости симметричного массива;
- этапа 630 формирования интервала энтропийно-параметрической неопределённости симметричной модели плотности распределения выходного параметра;
- этапа 635 определения параметра масштаба симметричной модели плотности распределения выходного параметра;
- этапа 640 определения рассогласования неопределённостей симметричных моделей плотностей распределения;
- этапа 645 минимизации рассогласования неопределённости симметричной модели и симметричной целевой плотности распределения;
- этапа 650 формирования управляющего воздействия коррекции рассогласования интервалов неопределённостей;
- этапа 655 визуализации неопределённости стохастической системы.
Определения признака асимметрии для несимметричной плотности распределения массива значений выходного параметра системы
Первое отличительно действие, иллюстрируемое этапом 610 процесса на фигуре 6, состоит в определении асимметрии массива значений выходного параметра по формуле (2). Огромное количество смещённых симметричных и несимметричных смесей распределений имеют асимметричность, характерную для внутренней организации сложного объекта. Изменение асимметричности распределения массива данных обусловлено изменением настроек и параметров стохастической системы. При оптимальном режиме стохастической системы асимметрия системы сохраняется в ограниченном интервале допустимых значений.
Проверка допустимости рассогласования асимметрии распределения массива значений области оптимального состояния системы
Второе отличительное действие, иллюстрируемое этапом 615 процесса на фигуре 6, необходимо для проверки допустимости рассогласования асимметрии распределения массива значений относительно значения асимметрии, характерного для области оптимального состояния. Если асимметрия находится за пределами интервала допустимых значений, то необходимо проведение трансформации закона распределения за счёт изменения настроек системы за счёт регулирования и изменения настраиваемых параметров стохастической системы. Для проверки используется неравенство (4), согласно которому модуль разности асимметрии распределения массива значений выходного параметра и асимметрии распределения оптимального состояния меньше критического значения разности асимметрий ΔSkкрит, ограничивающего область оптимального состояния системы.
Определение формы симметричной модели выходной плотности распределения стохастической системы
Третье отличительное действие, иллюстрируемое этапом 620 процесса на фигуре 6, состоит в определении формы симметричной модели плотности распределения.
Развёрнутая схема процессов этапа 620, реализующих определение формы симметричной модели плотности распределения дана на фигуре 7, где использованы следующие обозначения:
- этап 710 - определение оценки центра несимметричного массива значений Y выходного параметра;
- этап 715 - формирование симметричного массива Z;
- этап 720 - определение центральных моментов симметричного массива Z;
- этап - 725 определение интервалов неопределённости симметричного массива Z;
- этап - 730 определение коэффициента энтропии и контрэксцесса симметричного массива Z;
этап - 735 определение критерия области контроля признаков формы;
этап - 740 проверка принадлежности положения системы области контроля;
этап - 745 определение дистанций между положениями возможных моделей и положением симметричного массива;
- этап 750 выбор формы симметричной модели плотности распределения выходного параметра;
- этап 755 определение вектора рассогласования признаков формы симметричной модели плотности распределения и симметричной целевой плотности распределения;
- этап 760 формирование управляющего воздействия для коррекции рассогласования признаков формы симметричной модели;
- этап 765 принятие формы симметричной модели плотности распределения выходного параметра.
Содержание этапа 710 схемы процесса на фигуре 7 состоит в определении центра несимметричного массива значений Y выходного параметра, в качестве которого может быть использованы математическое ожидание, мода, медиана или квантильные оценки центра несимметричного массива значений выходного параметра.
При выполнении этапа 715 схемы процесса на фигуре 7 осуществляется формирование симметричного массива Z, для чего путём переноса значений yi массива Y выходного параметра формируется массив Y* значений y*i таким образом, чтобы значения массивов располагались симметрично относительно оценки центра yц. Положение координат i-х значений массива Y* определяются по выражению (19). Симметричный массив значений Z формируется в результате объединения двух массивов Y и Y*, координаты значений которых расположены симметрично относительно оценки центра yц массива Y. Объединение массива выборочных значений выходного параметра Y и массива отображённых относительно центра распределения yц значений задано выражением:

Массив выборочных значений величины Z сохраняет многие свойства исходного массива значений Y. В частности, если в качестве центра распределения yц принято математическое ожидание массива значений Y, то массивы значений Z и Y имеют одинаковые средние квадратические разбросы и контрэксцессы.
На этапе 720 проводится определение центральных моментов симметричного массива Z по формуле (5), которые характеризуют свойства симметричного массива значений. Так как при выборе в качестве центра моды, медианы или другой оценки центра yц несимметричного массива Y центральные моменты симметричного массива Z равны робастным оценкам несимметричного массива Y, то для получения интервалов неопределённости и признаков форм симметричной модели плотности распределения выходного параметра требуется оценка центральных моментов симметричного массива.
При выполнении этапа 725 проводится определение интервалов неопределённости симметричного массива Z. Интервалы информационной и параметрической неопределённости представляют собой своеобразные «индикаторы» распределений. Для определения интервала информационной неопределённости используется формула (7).
Интервала информационной неопределённости симметричного массива Z для значений выходного параметра определяется как потенцирование информационной энтропии содержащейся в симметричном массиве Z;
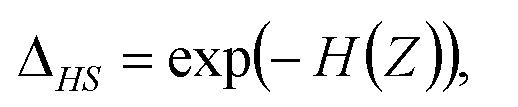
где H(Z) - информационная энтропия массива выборочных значений Z, равная математическому ожиданию логарифма вероятности для выборочных значений массива Z:
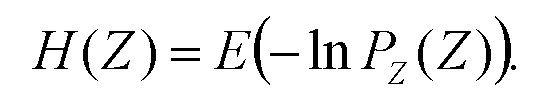
Интервал параметрической неопределённости строится на основе центральных моментов распределения. В простом случае интервал определяется как корень квадратный от второго центрального момента, рассчитываемый по формуле (8).
На этапе 730 проводится определение коэффициента энтропии и контрэксцесса симметричного массива Z значений выходного параметра. Для определения коэффициента энтропии симметричной модели плотности распределения используется отношение интервала информационной неопределённости к интервалу параметрической неопределённости, определяемый по формуле (9). Контрэксцес симметричной модели плотности распределения определяется как отношение второго момента к корню квадратному четвёртого момента симметричного распределения, который рассчитывается по формуле (10).
При выполнении этапа 735 определяется критерий области контроля признаков формы. На этапе 735 для признаков формы симметричной целевой плотности распределения устанавливаются границы признаков, в которых допустим контроль системы. Для целевой плотности распределения оптимального состояния системы возможно выделения области работоспособных состояний. Интервалы изменения признаков формы симметричных моделей плотности распределения ограничены и могут быть определены либо путём моделирование объекта с использованием метода Монте-Карло либо посредством накопления статистических данных о стохастической системе и оценке интервалов признаков зоны контроля при условии, что система находится в работоспособном состоянии. При использовании метода Монте-Карло проводится наложение модели дестабилизирующих факторов на модель неопределённости стохастической системы заданной целевой плотностью выходного параметра. В этом случае признаки формы целевой плотности распределения принимают в качестве координат оптимального состояния пространства признаков формы симметричных моделей: контерэксцесса κS0 и коэффициента энтропии KHS0 симметричных плотностей распределения. При накоплении статистических данных о работоспособных состояниях системы оптимальные признаки формы оцениваются как средние значения признаков из результатов наблюдения. В качестве интервалов в пространстве признаков формы симметричных моделей используются средние квадратические оценки разброса признаков контрэксцесса ΔκS и коэффициента энтропии ΔKHS симметричных моделей относительно признаков контрэксцесса κS0 и коэффициента энтропии KHS0 симметричной целевой плотности распределения стохастической системы. Границы области контроля устанавливаются из условия, что внутри границ области, в которых допустим контроль системы, находится 95 % рабочих состояний при различных дестабилизирующих воздействиях. Границы разброса признаков области контроля ограничены интервалами контрэксцесса [κS0 ± ΔκS] и коэффициента энтропии [KHS0±κKHS] в пространстве признаков формы симметричных моделей плотности распределения. Если положение состояния системы в пространстве признаков форм симметричных моделей задано вектором [κS, KHS]T, положение оптимального состояния стохастической системы задано вектором признаков целевой плотности распределения [κS0, KHS0]T, то для задания критерия границ удобно использовать отношение разностей координат векторов к их разбросам. Критерий границ пространства задан с помощью нормы вектора в виде
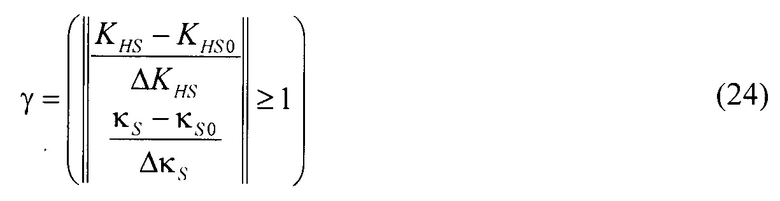
Из соотношения (24) следует, что при норме вектора большей или равной единице неравенство верно и критерий γ равен единице. В этом случае система находится за пределами области контроля и для её возврата в область контроля необходима трансформация симметричной плотности распределения посредством внешней настройки объекта или перенастройки системы для контроля системы в другой области. Процесс трансформации симметричной плотности распределения иллюстрирует этап 135 схемы процессов на фигуре 7. При значении критерия γ равном нулю система находится в области пространства контролируемого оптимального состояния стохастической системы. Проверка принадлежности положения системы области контроля проводится на этапе 740 схемы процессов определения формы симметричной модели распределения выходного параметра, показанной на фигуре 7.
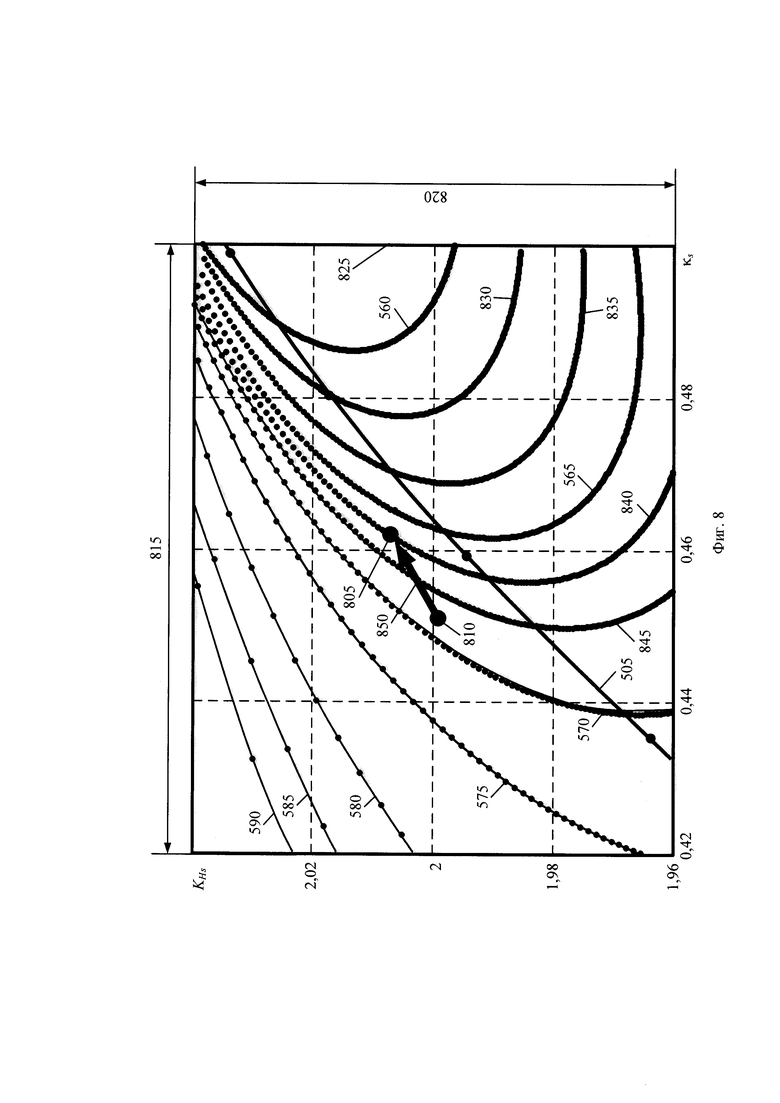
В качестве примера области контролируемого пространства симметричной целевой плотности распределения при использовании m-нормы на фигуре 8 дан вариант пространства признаков форм распределений для области контроля стохастической системы, где использованы обозначения объектов:
805 - положение симметричной целевой плотности распределения;
810 - положение симметричного массива значений выходного параметра;
815 и 820 - интервалы разбросов контрэксцесса [κS0 ± ΔκS] и коэффициента энтропии [KHS0±ΔKHS], соответственно;
825 - область контролируемого пространства;
830, 835, 840, 845 - кривые смесей нормального распределения и нормированной аппроксимации четвёртого порядка при соотношениях их среднеквадратических разбросов, равными 2,46, 2,53, 2,649, 2,7, соответственно;
850 - вектор рассогласования признаков форм.
Пространство на фигуре 8 построено для симметричной целевой плотности распределения, в качестве которой использована симметричная модель несимметричного гамма распределения с параметром формы равным 2. Модель получена относительно математического ожидания, принятого в качестве оценки центра. Для задания критерия границ пространства признаков форм распределений для области контроля стохастической системы использована m-норма, при которой выбирается максимальная координата вектора.
Вследствие воздействия влияющих факторов и изменчивости внутренней структуры стохастической системы её положение отличается от заданного положения симметричной целевой плотности распределения. Позиционирование системы в пространстве признаков форм распределений происходит путём замены положения симметричного массива значений выходного параметра с помощью симметричной модели плотности распределения из условия минимума дистанции между положениями массива и модели распределения.
Для выбора формы симметричной модели плотности распределения выходного параметра на этапе 745 схемы процессов на фигуре 7 проводят определение дистанции ΔLj между положениями возможных моделей и положением симметричного массива значений выходного параметра по формуле (12).
На этапе 750 схемы процессов на фигуре 7 проводят выбор формы симметричной модели плотности распределения выходного параметра с помощью условия (13), согласно которого дистанция между положениям модели плотности распределения и положением симметричного массива имеет минимальное значение. Выбор модели позволяет сопоставить состоянию стохастической системы, характеризуемому массивом значений выходного параметра, форму симметричной модели плотности распределения.
На этапе 755 схемы процессов на фигуре 7 определяют вектор рассогласования признаков формы симметричной модели плотности распределения и симметричной целевой плотности распределения выходного параметра стохастической системы. На фигуре 8 вектор рассогласования признаков форм иллюстрирует объект 850. Вектор рассогласования признаков форм определяет направление коррекции формы симметричной модели плотности распределения в пространстве признаков форм распределений для обеспечения отслеживания трека симметричной целевой плотности распределения.
На следующем этапе 760 проводится формирование управляющего воздействия для коррекции рассогласования признаков формы симметричной модели посредством изменения настроек системы или изменения входных воздействий. Этап 765 схемы процессов на фигуре 7 иллюстрирует процесс принятия формы симметричной модели плотности распределения выходного параметра.
Определение интервала энтропийно-параметрической неопределённости симметричного массива значений выходного параметра стохастической системы
Четвёртое отличительное действие, иллюстрируемое этапом 625 процесса на фигуре 6 состоит в определении интервала энтропийно-параметрической неопределённости симметричного массива значений выходного параметра по формуле (15), равного среднему квадратическому значению суммы интервалов энтропийной и параметрической неопределённости симметричного массива.
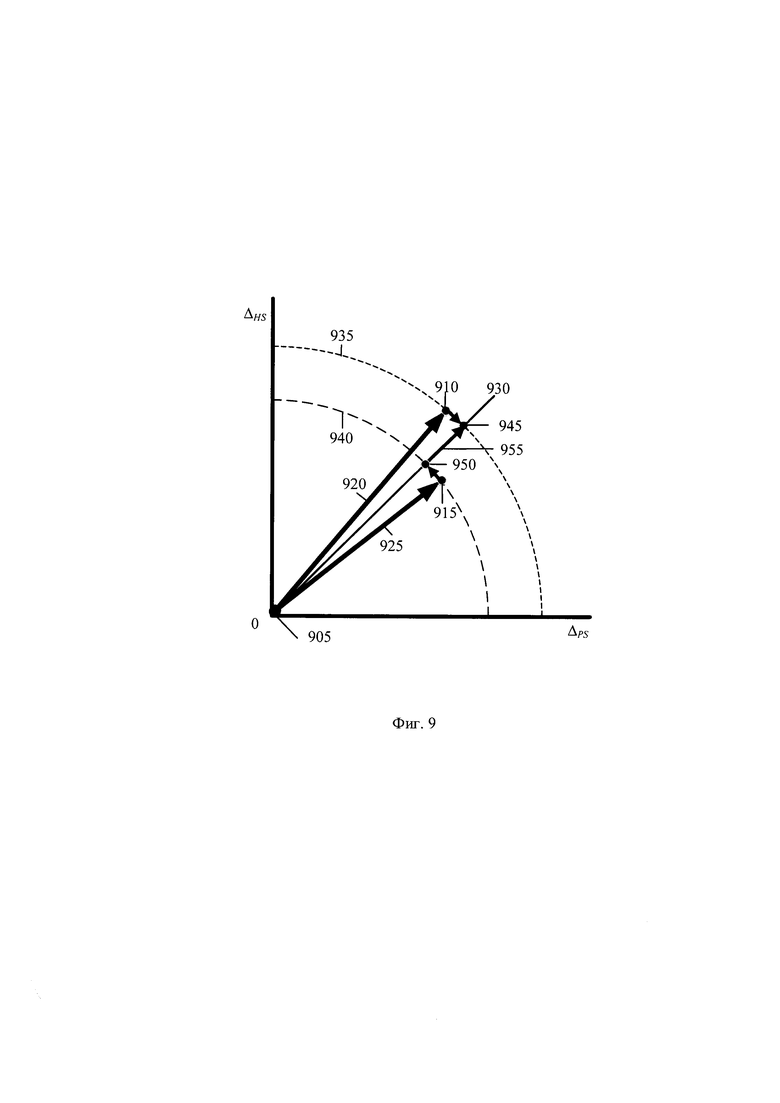
Масштаб симметричной модели плотности распределения выходного параметра можно найти из сопоставления интервалов неопределённости симметричной модели плотности распределения и симметричного массива значений выходного параметра. Для пояснения процесса определения масштаба симметричной модели на фигуре 9 приведён чертёж пространства энтропийной и параметрической неопределённостей, где использованы обозначения:
905 - начало координат пространства энтропийной и параметрической неопределённостей;
910 - точка положения симметричной целевой плотности распределения;
915 - точка положения симметричного массива значений выходного параметра;
920 - дистанция энтропийно-параметрической неопределённости симметричной целевой плотности распределения;
925 - дистанция энтропийно-параметрической неопределённости симметричного массива;
930 - линия положения симметричных моделей плотности распределения с выбранной формой;
935 - эквипотенциаль энтропийно-параметрической неопределённости, равная дистанции интервала симметричной целевой плотности распределения;
940 - эквипотенциаль энтропийно-параметрической неопределённости, равная дистанции интервала симметричного массива значений выходного параметра;
945 - точка положения симметричной модели выбранной формой с интервалом энтропийно-параметрической неопределённости целевой плотности распределения;
950 - точка положения симметричной модели выбранной формой с интервалом энтропийно-параметрической неопределённости симметричного массива значений;
955 - дистанция рассогласование энтропийно параметрической неопределённости для симметричной модели плотности распределения.
Признаки формы симметричной целевой плотности распределения выходного параметра стохастической системы хранятся в базе эталонных параметров. Положение целевой плотности распределения задано точкой 910 с координатами ΔHS0 и ΔPS0, равными интервалам энтропийной и параметрической неопределённостей, соответственно. Направление дистанции 920 в пространстве интервалов энтропийной и параметрической неопределённостей определено коэффициентом энтропии KHS0 симметричной целевой плотности распределения выходного параметра, равным тангенсу угла наклона дистанции 920. Коэффициент энтропии целевой плотности распределения задан отношением

Точка положения 915 симметричного массива значений Z отображает положение стохастической системы в пространстве интервалов энтропийной и параметрической неопределённостей. Координаты точки 915, равные интервалам информационной и параметрической неопределённости симметричного массива значений выходного параметра стохастической системы, определены по формулам (7) и (8), соответственно. Направление дистанции 925 энтропийн-параметрической неопределённости симметричного массива значений Z определено коэффициентом энтропии KHS симметричного массива Z, определённому по формуле (9). Коэффициент энтропии KHS равен тангенсу угла наклона дистанции 925.
Для определения масштаба симметричной модели плотности распределения выполняются следующие отличительные действия, иллюстрируемые этапами 630 и 635 процесса на фигуре 6.
Формирование интервала энтропийно-параметрической неопределённости симметричной модели плотности распределения выходного параметра
Этап 630 на фигуре 6 иллюстрирует процесс формирование интервала энтропийно-параметрической неопределённости симметричной модели плотности распределения выходного параметра с использованием выражения (16), где 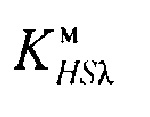 - коэффициент энтропии симметричной модели плотности распределения, μ2λ второй центральный момент плотности смеси распределений.
- коэффициент энтропии симметричной модели плотности распределения, μ2λ второй центральный момент плотности смеси распределений.
Второй центральный момент плотности смесей ƒsmes(y,K) распределения равен
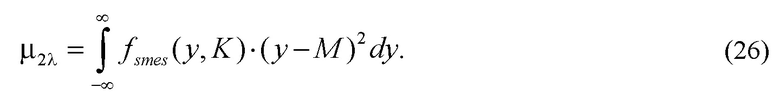
Выполнив подстановку плотности смесей ƒsmes(y,K) распределения (22) в выражение для второго центрального момента (26) смеси распределения, и выполнив преобразования, получим, что выражение для второго центрального момент плотности смеси распределения имеет вид
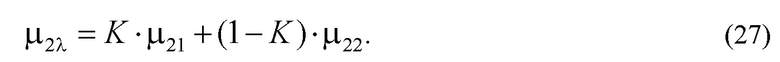
Здесь μ21 и μ22 вторые центральные моменты первой и второй составляющих плотности распределения смеси, соответственно.
Отношение средних квадратических разбросов для каждой кривой плотности распределений смеси на фигуре 5 задано в виде:

где σ1 и σ2 среднее квадратические разбросы первой и второй составляющих распределения смеси.
Тогда второй центральный момент μ2λ плотности смесей ƒsmes(y,K) распределения можно выразить с помощью среднего квадратического разброса первой и второй составляющих смесь
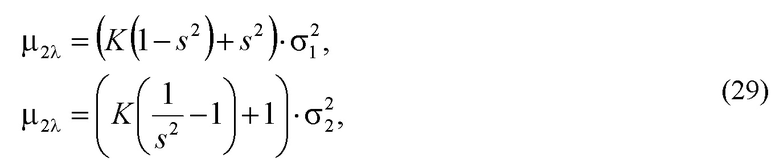
Выполнив подстановку (29) второго центрального момента μ2λ плотности смесей ƒsmes(y,K) распределения в выражение (16) получим выражение, связывающее интервал энтропийно-параметрической неопределённости симметричной модели плотности распределения выходного параметра и средний квадратический разброс σ1 или σ2 одной из составляющих смеси распределений в виде
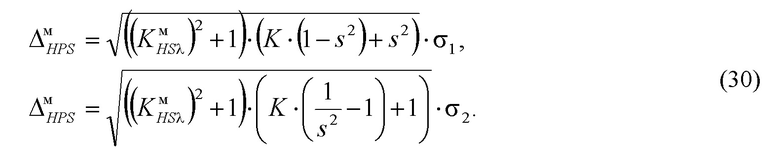
Определение параметра масштаба симметричной модели плотности распределения выходного параметра
Этап 635 фигуры 6 состоит в определении параметров масштаба симметричной модели плотности распределения выходного параметра. Выражения для определения параметров масштаба составляющих смеси получим, преобразовав выражения (30) относительно неизвестных средних квадратических разбросов составляющих смеси распределения. Выражения для средних квадратических разбросов примут вид
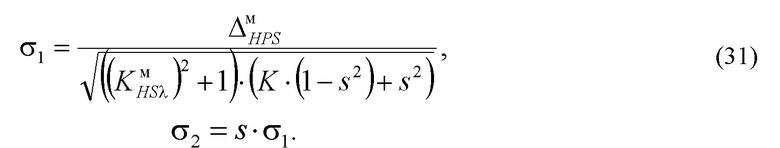
Для распределения Гаусса параметр масштаба λ1 в выражении (31) равен среднему квадратическому разбросу σ1 составляющего смесь распределения. Для других симметричных распределений параметр масштаба λ1 пропорционален среднему квадратическому разбросу σ1. Согласно выражению (31) среднеквадратический разброс σ1 и как следствие, параметр масштаба λ1, пропорциональны интервалу энтропийно-параметрической неопределённости 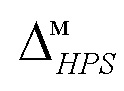 симметричной модели плотности распределения выходного параметра с известными значениями коэффициента энтропии
симметричной модели плотности распределения выходного параметра с известными значениями коэффициента энтропии 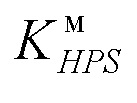 симметричной модели, коэффициента веса K и отношения s средних квадратических разбросов для составляющих смеси распределений (22).
симметричной модели, коэффициента веса K и отношения s средних квадратических разбросов для составляющих смеси распределений (22).
Таким образом, интервал энтропийно-параметрической неопределённости модели полностью определяет её параметр масштаба. При этом интервал энтропийно-параметрической неопределённости качественно отличается от оценки среднего квадратического разброса, так как дополнительно учитывает информационные свойства модели. Так как положение точек симметричного массива значений и симметричной модели распределения выходного параметра отличаются в пространстве интервалов энтропийной и параметрической неопределённостей, для определения параметра масштаба симметричной модели плотности распределения выходного параметра используется условие (5) минимума разницы интервалов энтропийно-параметрических неопределённостей симметричного массива значений и симметричной модели распределения.
Определение рассогласования интервалов энтропийно-параметрических неопределённостей симметричных моделей плотности распределения выходного параметра исимметричной целевой плотности распределения
Следующий этап 640 схемы на фигуре 6 иллюстрирует процесс определения рассогласования неопределённостей симметричных моделей плотностей распределений, найденных для симметричного массива значений выходного параметра и симметричной целевой плотности распределения стохастической системы.
Вследствие воздействия влияющих факторов положение 915 стохастической системы в пространстве интервалов энтропийной и параметрической неопределённостей отлично от точки положения 910 целевой плотности распределения.
Для позиционирования стохастической системы в пространстве интервалов энтропийной и параметрической неопределённостей используется симметричная модель плотности распределения выходного параметра, выбираемой из условия минимума в пространстве признаков формы контрэксцесса и коэффицинта энтропии симметричных моделей, иллюстрируемого фигурой 5. Следовательно, коэффициент энтропии симметричной модели отличен от коэффициента энтропии как симметричного массива значений Z, так и симметричной целевой плотности распределения. Линия 930 на фигуре 9 иллюстрирует возможные положения симметричных моделей плотности распределения с выбранной формой. Положения стохастической системы в пространстве интервалов энтропийной и параметрической неопределённостей задано положением модели 950 пересечения линии 930 симметричных моделей и эквипотенциали 940 энтропийно-параметрической неопределённости симметричного массива значений выходного параметра. Точка положения модели 950 иллюстрирует проекцию дистанции 925 на направление линии 930 моделей с выбранной формой.
Оптимальному состоянию стохастической системы соответствует положения 910 симметричной целевой плотности распределения, которое в пространстве интервалов энтропийно-параметрической неопределённости отлично от линии 925 положения симметричных моделей плотности распределения с выбранной формой. Поэтому положение 910 симметричной целевой плотности распределения заменяется положение модели 945 пересечения линии 930 симметричных моделей и эквипотенциали 935 энтропийно-параметрической неопределённости симметричной целевой плотности распределения. Тогда рассогласованию энтропийно-параметрической неопределённости для симметричной модели плотности распределения соответствует дистанция 955. Рассогласование интервалов энтропийно-параметрических неопределённостей симметричной модели плотности распределения выходного параметра 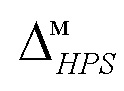 и симметричной целевой плотности распределения
и симметричной целевой плотности распределения 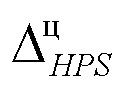 определяется по формуле (17).
определяется по формуле (17).
На фигуре 9 рассогласование интервалов энтропийно-параметрических неопределённости симметричных моделей плотности распределения выходного параметра и целевой плотности распределения стохастической системы иллюстрирует дистанция 955 между точками положения 950 и 945 интервалов неопределённости симметричных моделей.
Минимизация рассогласования интервалов энтропийно-параметрических неопределённостей симметричной модели плотностей распределений выходного параметра и симметричной целевой плотности распределения
На этапе 645 схемы процессов фигуры 6 проводят минимизацию рассогласования неопределённостей симметричной модели и симметричной целевой плотности распределения.
Дистанция 955 соответствует рассогласованию интервалов энтропийно-параметрических неопределённостей симметричных моделей распределения выходного параметра и целевой плотности распределения, заданных точками положения 950 и 945 стохастической системы в пространсчтве интервалов неопределённостей, соответственно. Пунктирные линии 940 и 935 иллюстрируют эквипотенциали, точки которых имеют одинаковые значения равные дистанциям 925 и 920 интервалов энтропийно-параметрических неопределённостей массива значений выходного параметра и целевой плотности распределения стохастической системы. Переход симметричной модели плотности распределения из точки положения 950 в точку положения 945 при проведении корректировки рассогласования на этапе 150 масштаба неопределённости иллюстрирует минимизацию рассогласования неопределённости стохастической системы. Формирование управляющего воздействия коррекции рассогласования масштабов моделей неопределённостей на этапе 650 схемы процессов на фигуре 6 необходимо для физического изменения регулируемых параметров стохастической системы. Сохранившееся рассогласование после коррекции системы иллюстрируют точки положения 910 и 945 симметричной целевой плотности распределения и её модели, уменьшение которого возможно только за счёт коррекции формы симметричной модели плотности распределения выходного параметра стохастической системы. Результат коррекции будет получен при обработке массива значений выходного параметра следующего цикла стохастической системы.
Визуализация модели неопределённости стохастической системы
Заключительный этап 655 схемы процессов на фигуре 6 состоит в визуализации неопределённости стохастической системы для оценки оптимальности её состояния. Из записанного выражения (30) следует, что интервал неопределённости 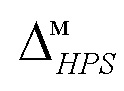 пропорционален среднему квадратическому разбросу составляющей смесь распределения и может быть выражен через параметр масштаба λ этого распределения.
пропорционален среднему квадратическому разбросу составляющей смесь распределения и может быть выражен через параметр масштаба λ этого распределения.
Таким образом, для обеспечения надёжности контроля неопределённости системы при условии, что получена оценка центра смеси распределений выходного параметра, автором изобретения предложено отслеживать модель симметричной относительно центра плотности распределения, которая может быть сравнительно просто восстановлена в пространстве коэффициента энтропии и контрэксцесса с помощью простых функций или их смесей. Благодаря использованию симметричной модели плотности распределения при условии оценки центра массива выходного параметра исключается влияние смещения массива на определение формы и масштаба контролируемой неопределённости стохастической системы. Наличие восстановленной кривой симметричной модели плотности распределения важно для организации систем с использованием пропорционально-интегрально-дифференциального регулирования.
Литература
1. ГОСТ 34100.1 - 2017 / ISO/ IEC Guide 98-1:2009. Неопределённость измерения. Введение в руководство по выражению неопределённости измерения. М.: Стандартинформ, 2018.
2. ГОСТ 3 54500.3 - 2011/ Руководство ИСО/ МЭК 98-3: 2008. Неопределённость измерения. Руководство по выражению неопределённости измерения. М.: Стандартинформ, 2012.
3. Кафаров В.В., Дорохов И.Н., Кольцова Э.М. Системный аналих процессов химический технологии и процессы массовой кристализации из растворов и газовой фазы. М., изд-во «Наука», 1983.
4. Бендат Дж., Пирсол А. Прикладной анализ случайных данных. М.:. Мир, 1989 - 540 с.
5. Айвазян С.А., Бухштабер В.М., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Классификации и снижение размерности. М.: Финансы и статистика, 1989 - 607 с.
6. Острем К.Ю. Введение в стохастическую теорию управления. М., Изд-во «Мир», 1973.
7. Александров А.В., Александрова Т.Н. Реология и гидродинамика процессов отлива и формования бумаги. СПбГТУРП. - СПб., 2015 - 132 с
8. Овсянников Д.А. Математические методы управления пучками. - Л.: Изд-во ЛГУ, 1980.
9. Полосин В.Г. Способ статистического анализа электрокардиографической информации. Известия ЮФУ. Технические науки. 2014. №10.
10. Рубин А.Б. Биофизика. Книга 1. Теоретическая биофизика.М.: Книжный дом «Университет», 1999. - 448 с.
11. Jian-Qiao Sun, 2006. Stochastic Dynamics and Control. Monograph Series on Nonlinear Science and Complexity / Elsevier B.V. 2006. - 410 p.
12. Пухликов А. В. Задачи управления распределениями // Нелинейная динамика и управление. ФИЗМАТЛИТ - №2. - 2010.
13. Пухликов А. В. Задачи управления распределениями в динамических системах //Автоматика и телемеханика. - 1995. - №4. - С. 77 - 87.
14. Wang, H. Bounded Dynamic Stochastic Systems: Modelling and Control. London, Springer-Verlsg, Elsrver, 2000. - 196 p.
15. Guoa L., Wang Н., Wang А.Р. Optimal probability density function control for NARMAX stochastic systems / Autovatica, Vol. 44, 2008 , pp. 1904-1911
16. Пат. 2565367 Российская Федерация. Способ контроля и управления динамической системой / Полосин В.Г., Бодин О.Н. - заявка № 2014111833/08; опубл. 20.10.15, Бюл. №29
17. Новицкий П.В., Зограф И.А., Оценка погрешности результатов измерений. - Л.: Энергоатомиздат. 1985г. - 248 с
18. Polosin V.G., 2020, Mapping distributions in the entropy-parametric space / Journal of Physics: Conf. Ser., 1515 032044, doi:10.1088/1742-6596/1515/3/0320.
19. Назаров И.А., К вопросу о предельных значениях энтропийного коэффициента. - В кн.: Известия ЛЭТИ, вып. 66, ч. 1, 1965, С. 21 - 23.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ мониторинга и контроля над стохастической системой при несмещённой несимметричной целевой плотности распределения выходного параметра | 2021 |
|
RU2758638C1 |
| СПОСОБ КОНТРОЛЯ СОСТОЯНИЯ СТОХАСТИЧЕСКОЙ СИСТЕМЫ | 2020 |
|
RU2743897C1 |
| СПОСОБ И УСТРОЙСТВО ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЯ ПРИ ОКАЗАНИИ ЭКСТРЕННОЙ КАРДИОЛОГИЧЕСКОЙ ПОМОЩИ | 2020 |
|
RU2737860C1 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2014 |
|
RU2565367C1 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2016 |
|
RU2615286C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ АВ-БЛОКАДЫ I, II И III СТЕПЕНИ | 2015 |
|
RU2591839C1 |
| УСТРОЙСТВО ДЛЯ ИЗМЕРЕНИЯ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ПРОЦЕССОВ | 1999 |
|
RU2168763C2 |
| СПОСОБ МНОГОВАРИАНТНОЙ ТОМОГРАФИИ ДАННЫХ СЕЙСМОРАЗВЕДКИ | 2019 |
|
RU2710972C1 |
| СПОСОБ ОРИЕНТАЦИИ И АВТОНОМНОЙ НАВИГАЦИИ КОСМИЧЕСКОГО АППАРАТА СИСТЕМЫ МОНИТОРИНГА ЗЕМЛИ И ОКОЛОЗЕМНОГО ПРОСТРАНСТВА | 2008 |
|
RU2376213C1 |
| СПОСОБ И СИСТЕМА ДЛЯ ОЦЕНКИ ВОЗНИКНОВЕНИЯ ОПАСНОСТИ ВЫСОКОЭНЕРГЕТИЧЕСКИХ ТОЛЧКОВ, ВЫЗЫВАЕМЫХ ПОДЗЕМНОЙ РАЗРАБОТКОЙ | 2014 |
|
RU2587520C1 |

Использование: для контроля неопределённости стохастической системы. Сущность изобретения заключается в том, что при организации контроля неопределённости стохастической системы для зарегистрированного массива значений выходного параметра системы определяют параметры симметричной модели плотности распределения и обеспечивают отслеживание модели плотности распределения путём сравнения интервалов неопределённостей модели плотности распределения с эталонными значениями интервалов неопределённостей симметричной целевой плотности распределения стохастической системы, что позволяет контролировать и целенаправленно изменять форму и масштаб симметричной модели плотности распределения при условии получения оценки центра выходного параметра системы. Применение симметричной модели плотности распределения для контроля неопределённости стохастической системы при условии получения оценки центра массива выходного параметра позволяет обеспечить независимость контроля формы и масштаба неопределённости выходного параметра от положения оценки центра. Технический результат: оптимизация поиска параметров симметричной модели неопределённости стохастической системы при условии получения оценки центра плотности распределения. 9 ил. 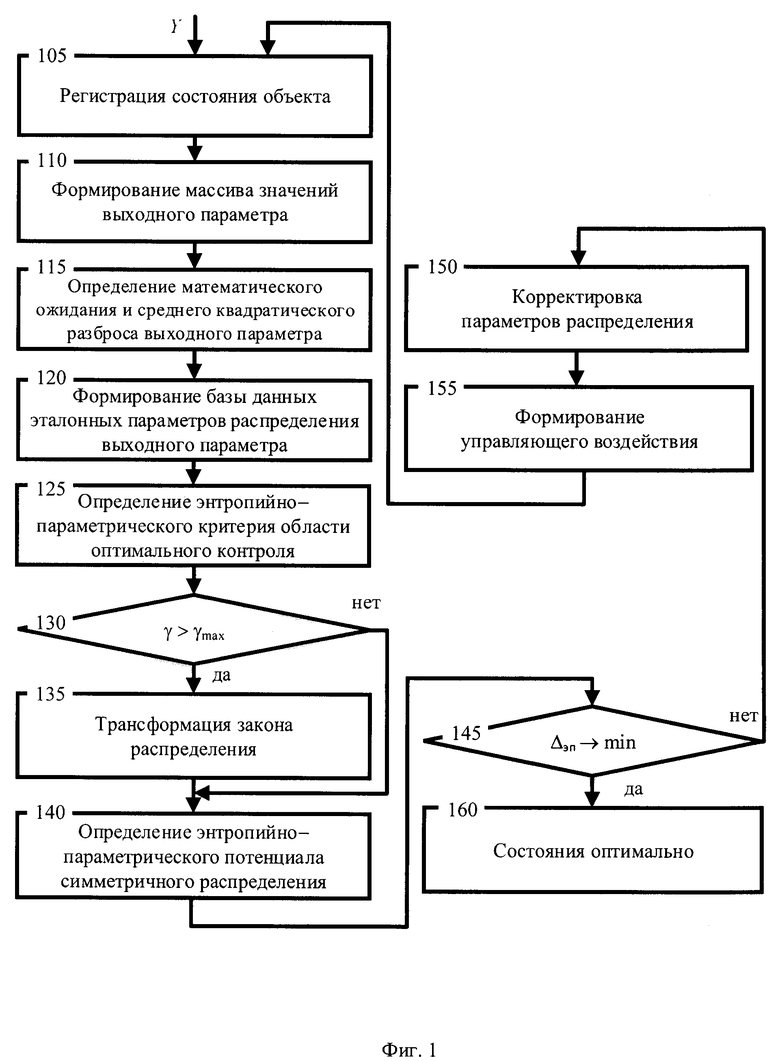
Способ контроля неопределенности стохастической системы при условии получения оценки центра плотности распределения, основанный на целенаправленном изменении плотности симметричной модели распределения выходного параметра к симметричной целевой плотности распределения стохастической системы, при котором регистрируют состояние объекта; формируют массив значений выходного параметра уi; определяют математическое ожидание Μ и средний квадратический разброс σ выходного параметра; формируют базу данных эталонных параметров распределений выходного параметра; трансформируют закон распределения выходного параметра посредством изменения настроек системы; отличающийся тем, что осуществляют определение признака асимметрии Sk для несимметричной плотности распределения массива значений выходного параметра системы
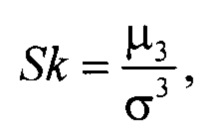
где μ3 - третий центральный момент распределения массива значений выходного параметра, определяемый
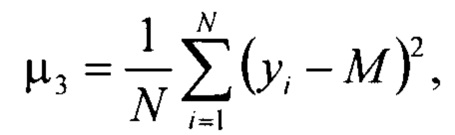
где N - число значений в выборке выходного параметра;
проверку допустимости рассогласования асимметрии распределения массива значений области оптимального состояния системы
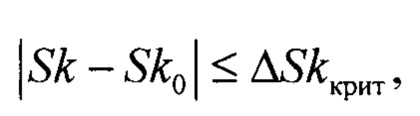
где Sk0 - признак асимметрии оптимального распределения стохастической системы;
ΔSkкрит - критическое значение разности асимметрий области оптимального состояния;
определение формы симметричной модели выходной плотности распределения стохастической системы посредством
- определения центра уц несимметричного массива значений выходного параметра;
- формирования симметричного массива значений Ζ отображением значений несимметричного массива значений Υ выходного параметра относительно оценки центра;
- определения второго μ2S и четвертого μ4S центральных моментов симметричного массива значений
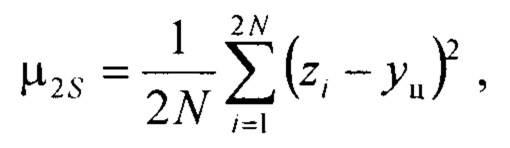
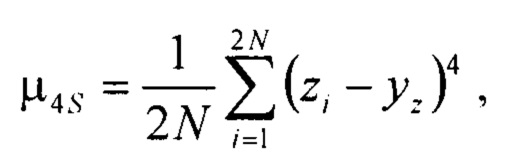
- определения интервалов информационной и параметрической неопределенности симметричного массива значений выходного параметра стохастической системы
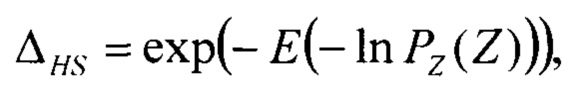
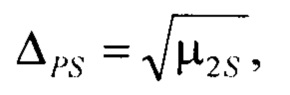
- определения коэффициента энтропии и контрэксцесса симметричного массива значений выходного параметра
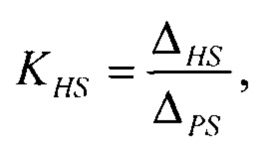
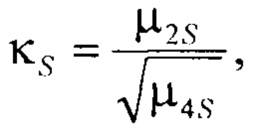
- определения критерия области контроля признаков формы симметричной целевой плотности распределения
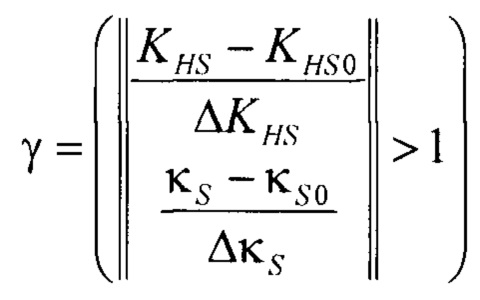
где ΔκS, ΔKHS - разбросы признаков контрэксцесса и коэффициента энтропии симметричного массива относительно контрэксцесса κS0 и коэффициента энтропии KHS0 симметричной целевой плотности распределения стохастической системы;
- проверки принадлежности положения системы области контроля и если критерий γ равен единице (γ=1), то проводят трансформацию закона распределения посредством изменения настроек системы;
- определения дистанций между положениями возможных моделей и положением симметричного массива значений выходного параметра
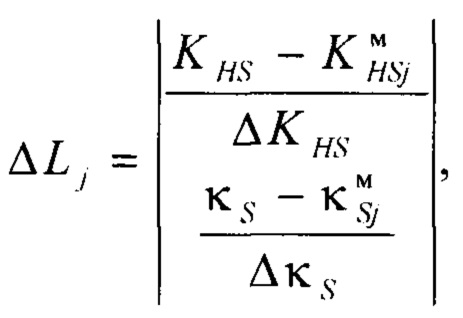
где 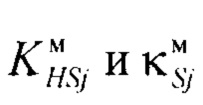 - контрэксцесс и коэффициент энтропии симметричной j'-й модели плотности распределения;
- контрэксцесс и коэффициент энтропии симметричной j'-й модели плотности распределения;
- выбора формы симметричной модели плотности распределения из условия минимума дистанции между положениями возможных моделей и положением симметричного массива значений выходного параметра

- определения вектора рассогласования признаков формы симметричной модели плотности распределения выходного параметра и симметричной целевой плотности распределения стохастической системы
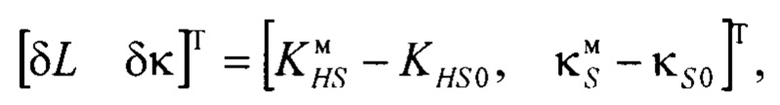
где 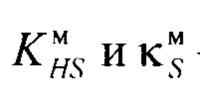 - коэффициент энтропии и контрэксцесс выбранной симметричной модели плотности распределения;
- коэффициент энтропии и контрэксцесс выбранной симметричной модели плотности распределения;
- формирования управляющего воздействия для коррекции рассогласования признаков формы симметричной модели плотности распределения посредством изменения параметров и настроек системы;
определение интервала энтропийно-параметрической неопределенности симметричного массива значений выходного параметра стохастической системы
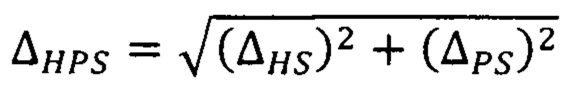 ,
,
формирование интервала энтропийно-параметрической неопределенности симметричной модели плотности распределения выходного параметра
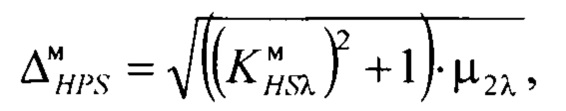
определение параметра масштаба симметричной модели плотности распределения выходного параметра из условия минимума разницы интервалов энтропийно-параметрических неопределенностей симметричного массива значений выходного параметра и симметричной модели распределения выходного параметра
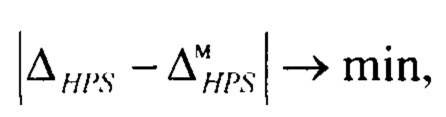
определение рассогласования интервалов энтропийно-параметрических неопределенностей симметричной модели плотности распределения выходного параметра 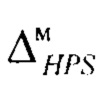 и симметричной целевой плотности распределения
и симметричной целевой плотности распределения 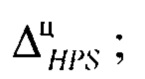

минимизацию рассогласования интервалов энтропийно-параметрических неопределенностей симметричной модели плотности распределения выходного параметра и симметричной модели целевой плотности распределения и формирование управляющего воздействия для коррекции рассогласования интервалов неопределенности стохастической системы, сохранение параметров модели и визуализацию модели неопределенности стохастической системы.
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2014 |
|
RU2565367C1 |
| СПОСОБ НЕИНВАЗИВНОГО ОПРЕДЕЛЕНИЯ ЭЛЕКТРОФИЗИОЛОГИЧЕСКИХ ХАРАКТЕРИСТИК СЕРДЦА | 2016 |
|
RU2615286C1 |
| СПОСОБ НЕЙРОСЕТЕВОГО АНАЛИЗА СОСТОЯНИЯ СЕРДЦА | 2018 |
|
RU2704913C1 |
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2005 |
|
RU2296356C1 |
| US 6496761 B1, 17.12.2002. | |||
Авторы
Даты
2021-04-22—Публикация
2020-08-11—Подача