Изобретение относится к способам контроля и организации оптимального управления и может быть использовано в системах контроля и управления различных динамических систем.
Известен способ контроля и управления динамической системой, заключающийся в выделении выборки значений выходного параметра y(t) и определении о среднеквадратического отклонения (СКО) выходного параметра y(t) [1]. Известный способ контроля и управления основан на анализе и оптимизации величины дисперсии σ2 распределения выходного параметра y(t). Типичным примером реализации известного способа контроля и управления динамической системой является задача определения оптимальной передаточной функции динамической системы, обеспечивающей минимизацию дисперсии выходного параметра y(t) (задача построения оптимального фильтра Винера) [1].
Недостатками известного способа контроля и управления динамической системой, искажающими состояние системы при управлении, являются:
- отсутствие учета влияния, вносимого изменением закона распределения выходного параметра y(t), на степень дестабилизации и неопределенности состояния системы;
- аппроксимация реального закона распределения выходного параметра y(t) только одним законом распределения с неизменной формой.
Наиболее близким к изобретению является способ контроля и управления динамической системой [2], заключающийся в том, что осуществляют регистрацию состояния объекта, формирование выборки yi значений выходного параметра y(t), определение величины среднеквадратического отклонения о выходного параметра, трансформацию закона распределения управляемого параметра за счет изменения настроечных параметров регулятора и формирование управляющего воздействия.
Как следует из формулы изобретения, в известном способе контроля и управления динамической системой осуществляют анализ и определение величины энтропийного потенциала выходного параметра Δэ динамической системы, описываемого зависимостью

где σ - величина среднеквадратического отклонения параметра; Кэ - энтропийный коэффициент, величина которого определяется законом распределения параметра, трансформацию закона распределения управляемого параметра за счет изменения настроечных параметров регулятора, при этом степень трансформации закона распределения управляемого параметра оценивается по величине энтропийного коэффициента [2].
Недостатком данного способа является возможность перехода динамической системы в устойчиво неработоспособное состояние, воспринимаемое динамической системой как оптимальное состояние, с последующим поддержанием контроля и управления.
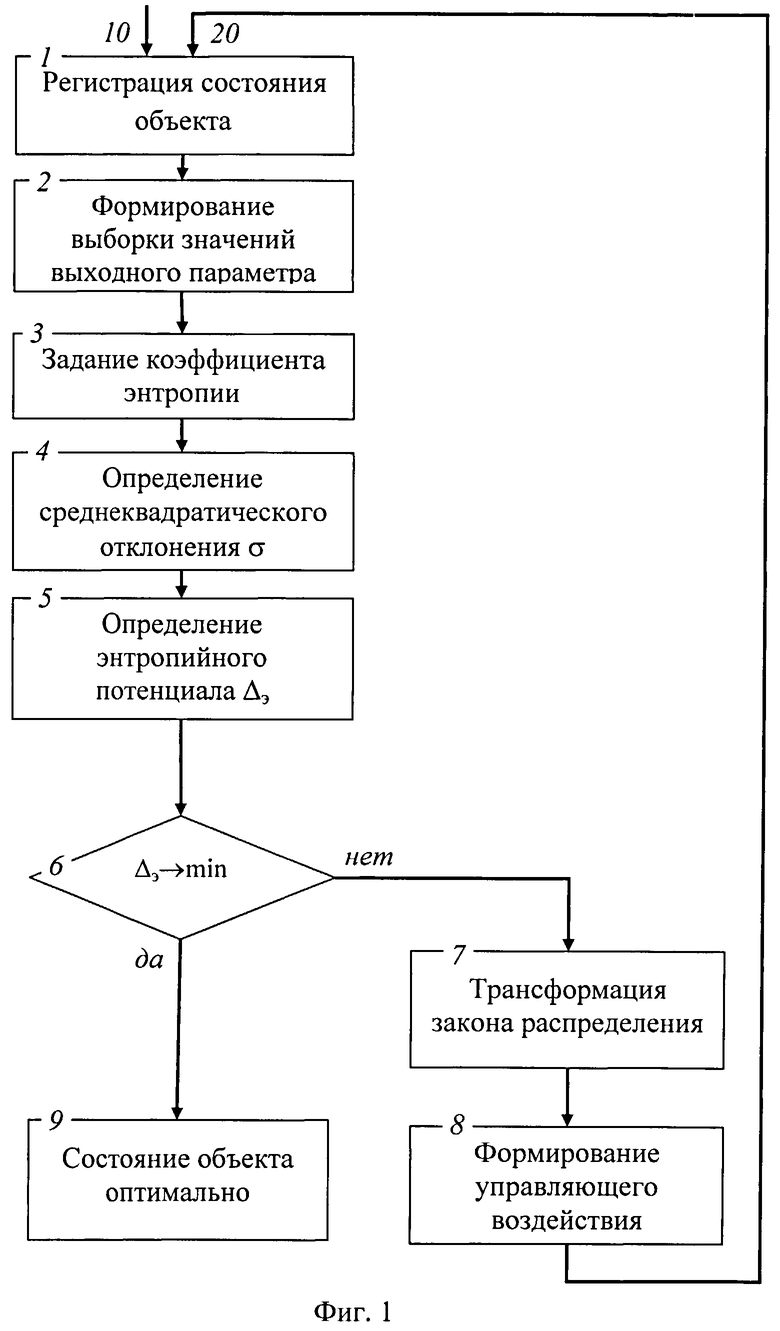
На фигуре 1 приведен алгоритм известного способа контроля и управления динамической системой, основанный на минимизации энтропийного потенциала.
На фигуре 2 приведена структурная схема динамической системы, реализующая известный способ контроля и управления динамической системой.
На фигуре 2 используются следующие обозначения:
11 - объект управления, преобразующий входное случайное воздействие x(t) в выходной параметр y(t);
12 - измерительное устройство (ИУ), регистрирующее дискретные значения yi выходного параметра;
13 - формирователь выборки значений выходного параметра (ФВЗВП), предназначенный для записи и хранения значений параметра yi, с выхода ИУ 12;
14 - вычислительное устройство, предназначенное для расчета энтропийного потенциала Δэ (см. выражение 1) по выборке yi значений выходного параметра y(t);
15 - формирователь вектора управляющего воздействия ξ, предназначенный для организации физического воздействия на органы управления объектом для изменения его состояния.
10 - выходной параметр y(t) объекта управления;
16 - входное случайное воздействие x(f);
17 - дискретные значения yi выходного параметра;
18 - выборка значений выходного параметра;
19 - энтропийный потенциал Δэ;
20 - вектор управляющего воздействия ξ.
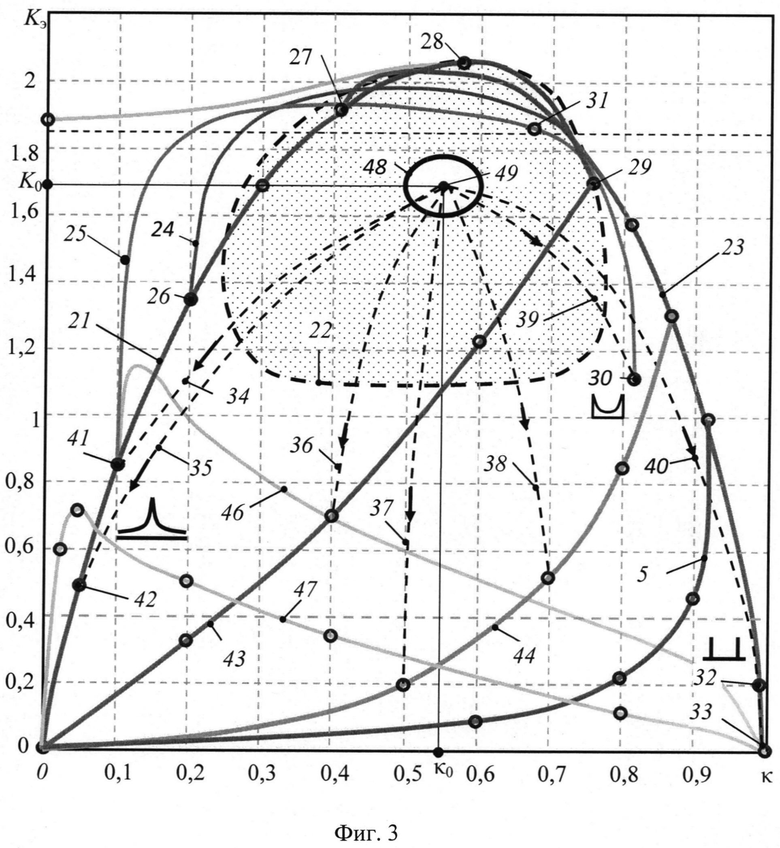
На фигуре 3 приведена топографическая диаграмма, иллюстрирующая состояния динамической системы, реализующей известный способ контроля и управления в осях коэффициента энтропии и контрэксцесса распределения выходного параметра.
Фигура 3 построена по известной топографической диаграмме Новицкого П.В. [3] для моделей распределений.
На фигуре 3 приняты следующие обозначения:
21 - кривая соответствия классу экспоненциальных распределений с показателями степени α от 0 и до ∞.
22 - кривая, ограничивающая часть пространства наиболее вероятного положения состояния системы при ее отимальной работе.
23 - кривая сответствия положению состояний системы с двухмодальным распределением выходного параметра, возникновение которого обусловлено появлением различных форм гистерезиса.
24 - кривая соответствия состояний системы с семейством распределений типа шапо и экспоненциальной составляющей формы, равной 1/2.
25 - кривая соответствия состояний системы семейства распределений с экспоненциальным распределением формы равным 1/3.
26 - точка соответствия состояния системы экспоненциальному распределению с составляющей формы, равной 1/2 (принадлежит кривой 27).
27 - точка соответствия состояния системы распределению Лапласа (принадлежит кривой 21).
28 - точка соответствия состояния системы нормальному распределению (принадлежит кривой 27).
29 - точка соответствия состояния системы равномерному распределению (принадлежит кривой 27).
30, 31 - точки, ограничивающие учаток кривой 25 соответствия состояния системы классу арккосинусоидальных распределений (принадлежит кривой 25).
32, 33 - точки ограничивающие участок кривой 23 состояний системы с дискретными распределениями контролируемой величины.
34, 35, 36, 37, 38, 39, 40 - кривые перехода системы из оптимального состояния в состояния с низким значением энтропии.
41, 42 - точки экспоненциального распределения с показателем формы 1/3 и 1/4, соотвественно (принадлежит кривой 21).
43, 44, 45 - кривые, соответствующие состоянию системы с композициями экспоненциального и дискретного двухзначного распределений.
46, 47 - кривые состояния системы с композициями дискретного и экспоненциального распределений с параметрами формы 1/3 и 1/4, соотвественно.
48 - кривая, ограничивающая область двухмерного пространства в осях коэффициента энтропии и контрэксцесса, которая соответствует оптимальному функционированию данной системы.
49 - точка оптимального состояния системы.
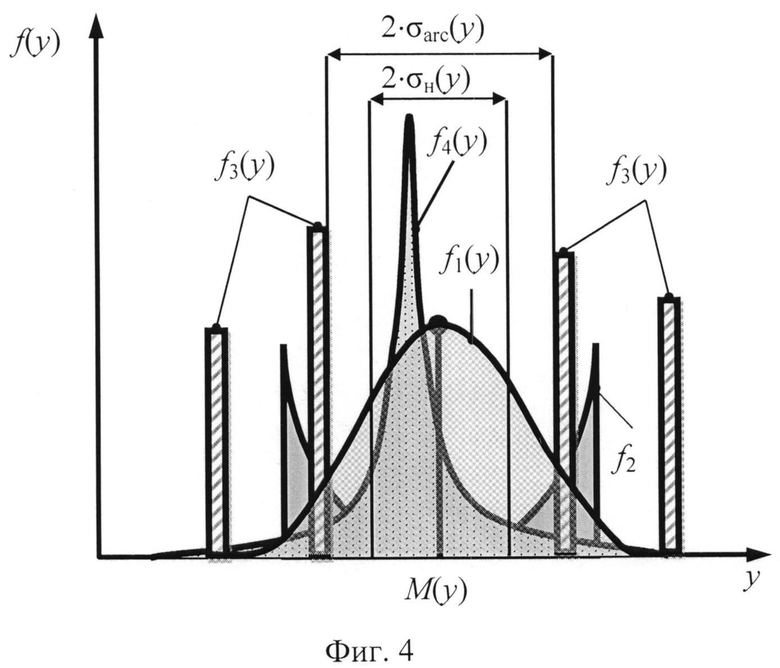
На фигуре 4 даны вероятностные распределения значений выборки выходного параметра yi при различных состояниях системы.
Анализ формулы и описания известного изобретения, а также фигур 1, 2, 3 и 4 показывает, что в известном способе контроля и управления динамической системой принципиально возможны устойчиво неработоспособные состояния системы. Другими словами, критерий оптимальности - признак, по которому функционирование системы признается наилучшим из возможных вариантов, позволяет в известном способе контроля и управления динамической системой существовать априорно неработоспособным состояниям системы.
При воздействии на систему входных случайных возмущений x(t) в ней невозможно наступление установившегося режима, так как случайное воздействие на входе объекта управления непрерывно переводит систему из одного состояния в другое.
Известные способы оценки точности при управлении астатическими системами используют только такие статистические характеристики, как математическое ожидание и дисперсия, применяемые по отношению к случайному входному x(t) или выходному y(t) параметру объекта контроля и управления. [1]
Среди недостатков таких методов управления следует отметить отсутствие контроля системой управления за формой распределения управляемых параметров, в которой заложена информация о внутреннем состоянии объекта.
Покажем это. Структурная схема динамической системы, реализующая известный способ контроля и управления динамической системой, приведена на фигуре 2 и представляет собой «технологический» конвейер обработки информации, состоящий из нескольких этапов. Рассмотрим работу схемы на каждом из этапов.
1 этап: регистрация состояния объекта. На этом этапе происходит регистрация выходного параметра y(t) объекта управления 11 с помощью измерительного устройства 12 посредством регистрации через известные дискретные промежутки времени Δt его значения yi и их передаче на ФВЗВП 13. На алгоритме известного способа контроля и управления динамической системой, приведенном на фигуре 1, этап регистрации состояния объекта показан в виде блока 1, на вход которого поступает непрерывный сигнал выходного параметра y(t) 10.
2 этап: формирование выборки значений выходного параметра. Этот этап состоит в сохранении выборки последних n результатов измерений. Дискретные значения параметра yi с выхода ИУ 12 сохраняются в ФВЗВП 13 в форме выборки выходного параметра. Выборка выходного параметра предназначена для построения гистограммы и оценки вероятности наблюдения pi регистрируемого результата в интервале Δy значения yi.
3 этап: определение параметров распределений. На этом этапе вычислительное устройство:
- определяет вероятности нахождения регистрируемых дискретных значений выходного параметра yi в заданных интервальных границах i-го значения;
- формирует m-мерный вектор выходного параметра, содержащий дискретные значения интервалов группирования данных и вероятности наблюдения выходных параметров в пределах интервалов группирования;
- производит обработку вероятностей m-мерного вектора Ym выходного параметра;
- определяет среднее квадратическое отклонение о для выборки выходного параметра объекта управления.
Для описания информационных свойств объекта задается оценка коэффициента энтропии, полученная на основе выборок значений предыдущих наблюдений или на основе анализа объекта [2]. На алгоритме известного способа контроля и управления динамической системой (см. фигуру 1) этому этапу соответствует блок 3.
Вероятности нахождения регистрируемых дискретных значений выходного параметра в заданных интервальных границах j-го значения yj вычислительным устройством рассчитываются следующим образом. Исходно выделена область наблюдения выходного параметра заданием его минимального ymin и максимального ymax значений. Весь диапазон выходного параметра разбит на интервалы, границы которых определены максимальным и минимальным значением j-го интервала:

Значение yj выходного параметра и j-м интервале определено как половина суммы его граничных значений:
yj=0,5(yjmin+yjmax).
Сначала производится ранжирование ряда в порядке возрастания. Затем подсчитывается число nj элементов ряда, имеющих значения больше нижней границы yjmin и меньше верхней yjmax границы j-го интервала. Разделив число значений nj, попавших в j-й интервал на число значений N всей выборки выходного параметра, получим вероятности pj наблюдения выходного параметра y в интервале j-го дискретного значения:

После этого формируется матрица Ym, в которой каждому j-му дискретному значению yj вариационного ряда сопоставляется вероятность pj его наблюдения в полученной выборке значений.
Таким образом, в результате описанной операции фактически происходит преобразование выборки значений выходного параметра в m-мерный вектор Ym. Рассчитанные вероятности pj наблюдений j-х значений yj вариационного ряда в виде m-мерного вектора Ym используются для определения параметров статистического распределения выходного параметра объекта управления: математического ожидания - М и СКО - σ.
Математическое ожидание М для выборки значений выходного параметра рассчитывается с помощью выражения [3]:

Для оценки СКО σ выборки значений выходного параметра используется выражения вида [3]:

Известный способ контроля и управления динамической системой основан на использовании величины энтропийного потенциала системы Δэ как унифицированной характеристики неопределенности ее состояния. Величина энтропийного потенциала определяется как половина диапазона равномерного распределения в интервале от -Δэ до Δэ, имеющего такую энтропию Н(y) выходного параметра y(t), как и у конкретной системы с конкретным законом распределения этого параметра. При этом величина энтропийного потенциала системы связана с энтропией Н(y) выходного параметра y(t) системы выражением вида [3]:

Возрастание величины Δэ свидетельствует об увеличении степени неопределенности состояния системы и наоборот. Анализ и целенаправленное изменение величин энтропийного потенциала выходного параметра Δэ позволяет эффективно контролировать и управлять объектом. Как следует из анализа формулы (1) и описания известного способа контроля и управления динамической системой, минимизация величины Δэ энтропийного потенциала достигается путем трансформации закона распределения управляемого параметра за счет изменения настроек параметров регулятора.
Энтропийный потенциал определяется из зависимости (1) как произведение среднего квадратического отклонения на коэффициент энтропии [2].
Неточность воспроизведения входного воздействия в известном способе контроля и управления динамической системой оценивается по энтропийному потенциалу Δэ. В качестве критерия оптимальности в этом случае принимают условие минимума энтропийного потенциала:

Для этого вычислительное устройство ВУ определяет статистические параметры распределения и энтропийный потенциал Δэ для выборки значений выходного параметра, после чего оценивает возможность его минимизации. На алгоритме известного способа контроля и управления (см. фигуру 1) заданию коэффициента энтропии, определению СКО и энтропийного потенциала соответствуют блоки 3, 4 и 5 соответственно. Блок 6 иллюстрирует процесс принятия решения, которое заключается в следующем. Если энтропийный потенциал отличен от своего минимального значения Δэ min, то проводится процесс анализа требуемой трансформации закона распределения. Этот процесс на алгоритме контроля и управления иллюстрирует блок 7. При достижении минимума энтропийного потенциала Δэmin система принимает состояние объекта в качестве оптимального состояния и сохраняет настройки предыдущего цикла управления. Переходу системы в оптимальное состояние соответствует на алгоритме обработки блок 9.
4 этап: формирование управляющего воздействия. Если энтропийный потенциал Δэ отличен от своего минимального значения, то по его значению определяют степень и направление трансформации закона распределения. Энтропийный потенциал передается на формирователь управляющего воздействия 15, где устанавливается направление трансформации закона распределения и формируется вектор воздействий ξ, поступающий на органы управления объектом для изменения его состояния. Формирователь управляющего воздействия 15, показанный на алгоритме в форме блока 8, производит такое действие на органы объекта управления, при котором происходит уменьшение энтропийного потенциала Δэ.
Приведенная структурная схема динамической системы реализует известный способ контроля и управления динамической системой, в основе которого лежит минимизация энтропийного потенциала с помощью трансформации закона распределения управляемого параметра и изменения настроек параметров регулятора. При этом возможны два случая минимизации потенциала Δэ.
Первый случай основывается на том, что априорная оценка энтропийного коэффициента Кэ получена без проведения эксперимента методами математического анализа или на основе аналогий при сохранении физических свойств объекта. В этом случае изменение энтропийного потенциала сводится к изменению (масштабированию) СКО, что не позволяет учитывать и использовать изменение формы распределения при его трансформации для контроля и управления объектом.
В результате, неясно, каким образом обеспечивается возможность учета перехода системы в низкоэнтропийное состояние, где минимизация отклонения обеспечивается за счет уменьшения коэффициента энтропии.
Второй случай предполагает целенаправленное изменение величины энтропийного потенциала Δэ с помощью трансформации закона распределения выходного параметра. При этом минимизация величины энтропийного потенциала Δэ достигается за счет изменения, как среднеквадратического отклонения, так и энтропийного коэффициента. Однако такой способ минимизации величины энтропийного потенциала Δэ не учитывает предельный переход системы в состояние с малым значением энтропийного потенциала за счет появления процессов с низким значением энтропии.
Покажем это. Фигура 3 иллюстрирует основные недостатки, возникающие в системе при использовании метода минимизации энтропийного потенциала Δэ путем трансформации энтропийного коэффициента Кэ. В пространстве энтропийного коэффициента Кэ оптимальной работе системы соответствует состояние 49, для которого характерен коэффициент энтропии К0. Пунктирная граница 22 ограничивает часть пространства возможного положения состояния произвольной системы при ее оптимальной работе.
Наличие отклонений состояния ситемы от заданного оптимального состояния приводит к ее переходу в низкоэнтропийное состояние, отражаемому на топографической диаграмме распределений в виде переходов 34, 35, 36, 37, 38, 39, 40.
Приведем примеры перехода системы в низкоэнтропийное состояние. Первый пример. Появление каких-либо форм гистерезиса в системе приводит к образованию двухмодальных распределений, положение которых задано участком кривой 23. В частном случае система способна перейти в состояния с дискретными распределениями при возникновении гистерезиса за счет увеличения внутренних сил трения. Положение таких состояний задано участком кривой между точками 32 и 33, где энтропийный коэффициент меньше 0,2. Кривая 40 иллюстрирует возможное направление подобного перехода.
Фигура 4 демонстрирует различие в поведении системы, находящейся в области оптимального состояния с большим значением коэффициента энтропии (на топографической диаграмме фигуры 1 эта область ограниченна кривой 48), и системы, перешедшей в одно из неблагоприятных состояний с низким значением энтропии. Оптимальному состоянию соответствует кривая распределения f1(y) выходного параметра с большим значением энтропии. В этом случае результаты измерения выходного параметра системы сгруппированы в области его математического ожидания, которое наиболее приближены к оптимальному значению наблюдаемого параметра.
Переходу системы в состояние с дискретными значениями выходного параметра yi, которому на топографической диаграмме фигуры 3 соответствует участок кривой 23 между точками 32 и 33, соответствует дискретное распределение f3(y). Такое состояние образуется в системе при появлении в отдельных ее узлах больших сил трения или других форм гистерезиса. В этом случае все результаты измерения выходного параметра будут находиться на расстоянии СКО относительно математического ожидания и, как следствие, будут наиболее удалены относительно наиболее благоприятного параметра системы. При этом энтропийный потенциал системы Δэ будет также стремиться к нулю.
Следует отметить, что при контроле и управлении системой на основе минимизации энтропийного потенциала Δэ подобное нерабочее состояние система воспринимает как наиболее благоприятное.
Другой пример перехода системы в низкоэнтропийное состояние связан с наличием резонансных свойств системы, что делает возможным появление в системе установившихся гармонических колебаний переменного выходного параметра. В этом случае система переходит по кривой 39 топографической диаграммы на фигуре 3 в состояние 30, которому соответствует арксинусоидальное распределение с более низким значением энтропии. На фигуре 4, где даны плотности распределения вероятности для выборки значений выходного параметра при различных состояниях системы, распределению выходного параметра системы с резонансными свойствами будет соответствовать кривая арккосинусоидального распределения f2(y). Для такого распределения характерно, что значения выходного параметра группируются на расстоянии, превышающем его СКО σ. Следовательно, большая часть значений выходного параметра системы также имеют значения, наиболее удаленные от его благоприятного значения, положение которого приближенно задает математического ожидания М. При этом система контроля и управления будет воспринимать это состояние как наиболее оптимальное состояние, так как энтропийный потенциал этого состояния при равных значениях СКО будет иметь меньшее значение.
Появление в течение длительного времени фиксированных неизменных значений выходного параметра при наличии случайных входных воздействий и случайных внешних влияющих факторов также указывает на неблагоприятное или нерабочее состояние системы. Такое состояние может быть вызвано выходом из строя ее отдельных узлов. Фиксирование значений выходного параметра в течение длительного времени также приводит к трансформации распределения значений выходного параметра в сторону низкоэнтропийных распределений, расположенных на кривой экспоненциальных распределений 21 топографической диаграммы (см. фигуру 3). Примерами таких распределений могут быть точки 26, 41 и 42 с параметрами формы равными 1/2, 1/3 и 1/4 соответственно. Эти распределения характеризуются очень пологими спадами, близкими по своим свойствам к распределению Коши. На фигуре 4 такому состоянию будет соответствовать островершинное распределение f4(y) для значений выборки выходного параметра. В этом случае все измеренные значения выходного параметра группируются непосредственно вблизи математического ожидания, которое может находиться на значительном удалении от его оптимального результата. В связи с низким значением энтропийного коэффициента, это состояние также имеет значение энтропийного потенциала меньшее, чем в оптимальном состоянии, поэтому система воспринимает это состояние также как наиболее благоприятное.
Линии 43, 44 и 45 соответствуют композициям экспоненциального распределения с дискретным двухзначным распределением вида:
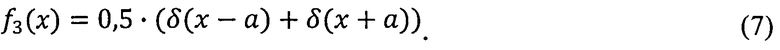
Относительное содержание дискретной составляющей в таких распределениях характеризуют отношением [з]:
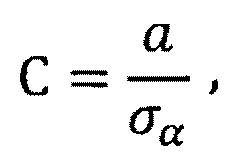
где а - полуразмах дискретного распределения, σα - среднеквадратическое отклонение распределения экспоненциального класса с параметром формы α. Для кривых 43, 44 и 45 отношения С равны: С23=1,8, С24=3,0, С25=5,0 соответственно. Кривые 46 и 47 иллюстрируют положения комбинаций дискретного распределения и распределений экспоненциального класса с параметрами формы 1/3 и 1/4 соответственно. Эти распределения так же относятся к низкоэнтропийным распределениям.
Из сказанного следует, что существует целое множество низкоэнтропийных распределений, которые система, построенная по алгоритму минимизации энтропийного потенциала Δэ путем трансформации энтропийного коэффициента Кэ, будет воспринимать как наиболее благоприятные состояния несмотря на то, что эти состояния системы являются устойчиво неработоспособными состояниями системы. В этих состояниях системы происходит отклонение закона распределения относительно оптимального состояния.
Таким образом, известный способ контроля и управления динамической системой не обеспечивает возможности, необходимые для оптимального управления:
- априорного задания закона распределения выходного параметра y(t);
- контроля формы распределения управляемых параметров, в которой заложена информация о внутреннем состоянии объекта;
- отличия оптимального состояния динамической системы от устойчивых неработоспособных состояний;
- сохранения контроля и управления над динамической системой при ее переходе в низкоэнтропийное состояние;
- получения оценок изменения информационных параметров динамической системы (таких как коэффициент энтропии или энтропийная погрешность) непосредственно по данным выборки значений выходного параметра объекта управления;
- анализа неблагоприятных состояний динамической системы и ее возврата в оптимальное состояние.
Таким образом, в известном способе контроля и управления динамической системой принципиально возможны преднамеренные переходы системы в устойчиво неработоспособные или неблагоприятные состояния с последующим длительным поддержанием ее контроля и управления в этих состояниях, воспринимаемых системой как благоприятные состояния.
По мнению авторов предполагаемого изобретения, критерий оптимальности способа контроля и управления динамической системой должен исключить из функционирования системы устойчиво неработоспособные состояния системы. Очевидно, что устойчиво неработоспособные состояния систем не являются оптимальными состояниями, так как в этих случаях происходит отклонение закона распределения значений выходного параметра относительно оптимального закона, что отражается на уменьшении значения коэффициента энтропии. Дело в том, что нарушение каких-либо процессов в динамической системе отражается в изменении значений выборки результатов выходного параметра и, как следствие, в изменении закона распределения выходного параметра.
Предлагаемое изобретение направлено на оптимизацию контроля и управления динамической системой путем исключения из функционирования системы устойчиво неработоспособных состояний.
Для этого в способе контроля и управления динамической системой заключающемся в том, что осуществляют регистрацию состояния объекта, формирование выборки yi значений выходного параметра y(t), определение величины среднеквадратического отклонения σ выходного параметра, трансформацию закона распределения управляемого параметра за счет изменения настроечных параметров регулятора и формирование управляющего воздействия, дополнительно осуществляют формирование базы данных эталонных параметров закона распределения выходного параметра, определение реальных параметров закона распределения выходного параметра по выражениям:

где Кэ, κ - коэффициенты энтропии и контрэксцесса соответственно, Δэ - энтропийный потенциал, рассчитываемый по формуле:

где Δy - ширина интервалов группирования выходного параметра; nj - число значений выходного параметра в j-м интервале группирования; N - число значений выборки выходного параметра; m - число интервалов группирования;

где µ4 - центральный момент четвертого порядка распределения выходного параметра, yj - среднее значение выходного параметра в j-м интервале группирования; М - математическое ожидание выходного параметра:

определение энтропийно-параметрического критерия области оптимального управления,
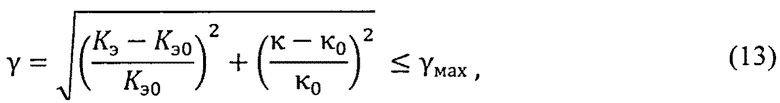
где yмах - максимальное значение энтропийно-параметрического критерия области оптимального управления; проверку состояния объекта принадлежности области оптимального состояния; определение величины энтропийно-параметрического потенциала Δэп по выражению:
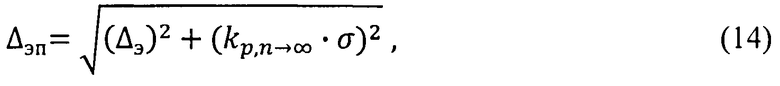
где kp,n→∞ - коэффициент нормального стандартного распределения; минимизацию величины энтропийно-параметрического потенциала Δэп динамической системы и корректировку реальных параметров закона распределения выходного параметра.
На фигуре 5 приведен алгоритм предлагаемого способа контроля и управления динамической системой, основанный на минимизации энтропийно-параметрического потенциала.
На фигуре 6 приведена структурная схема динамической системы, реализующая предлагаемый способ контроля и управления динамической системой, основанной на минимизации энтропийно-параметрического потенциала.
На фигуре 6 даны следующие обозначения:
11 - объект управления (ОУ), преобразующий входное случайное воздействие x(t) в выходной параметр y(t);
12 - измерительное устройство (ИУ), регистрирующее дискретные значения yi выходного параметра;
13 - формирователь выборки значений выходного параметра (ФВЗВП), предназначенный для записи и хранения значений параметра yi с выхода ИУ 12;
14 - вычислительное устройство (ВУ), предназначенное для расчета СКО σ, центрального момента четвертого порядка µ4, энтропийно-параметрического потенциала Δэ, коэффициента энтропии Кэ и контрэксцесса κ, энтропийно-параметрического критерия γ распределения выходного параметра;
57 - формирователь эталонных параметров распределения (ФЭПР), предназначенный для хранения оптимальных параметров статистических распределений выходного параметра;
15 - формирователь управляющего воздействия (ФУВ), предназначенный для организации вектора физического воздействия ξ на органы управления объектом для изменения его состояния по значениям энтропийно-параметрического критерия и энтропийно-параметрического потенциала;
10 - выходной параметр y(t) объекта управления;
16 - входное случайное воздействие x(t);
17 - дискретные значения yi выходного параметра;
18 - выборка значений выходного параметра;
19 - энтропийный потенциал Δэ;
20 - вектор управляющего воздействия ξ.
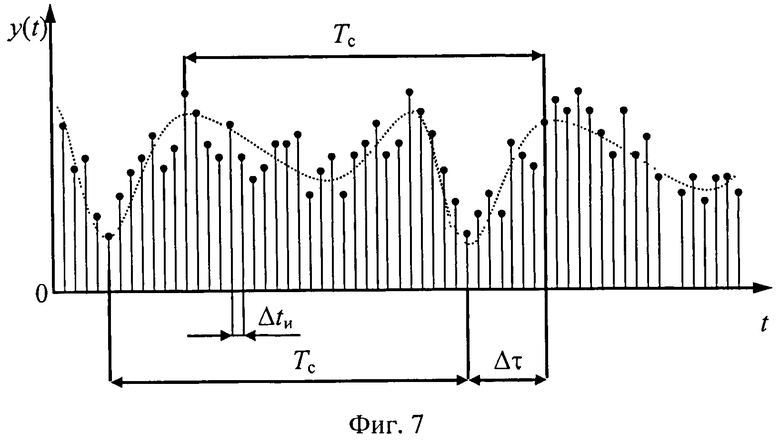
На фигуре 7 приведена временная диаграмма процесса для формирования выборки значений выходного параметра динамической системы.
Предлагаемый способ контроля и управления динамической системой направлен на повышение точности контроля и управления за счет:
- анализа и контроля формы распределения значений выборки выходного параметра динамической системы;
- минимизации энтропийно-параметрического потенциала;
- дифференциации областей устойчивых неработоспособных состояний относительно области оптимального состояния на основе определения и анализа энтропийно-параметрического критерия области оптимального управления;
- сохранения контроля и управления динамической системой при ее нахождении как в низкоэнтропийном состоянии, так и в промежуточных состояниях при возврате системы в оптимальное состояние путем минимизации энтропийно-параметрического потенциала и плавной корректировки закона распределения;
- определения информационных параметров непосредственно по выборке результатов выходного параметра в любой момент процесса контроля и управления динамической системой;
- обеспечения процесса анализа неблагоприятных состояний и возврата динамической системы в оптимальное состояние.
Суть предлагаемого способа контроля и управления динамической системой заключается в обеспечении нахождения системы в области ее оптимальных состояний путем трансформации закона распределения таким образом, чтобы отклонения коэффициента энтропии ΔКэ и контрэксцесса Δκ стремились к нулевым значениям.

На фигуре 3 условия (15) обеспечиваются в области кривой 48. Это достигается посредством постоянного наблюдения за отклонением формы распределения и его целенаправленной трансформации путем изменения свойств системы с помощью органов управления. При этом степень трансформации распределения оценивается на основе анализа энтропийно-параметрического критерия, коррекция распределения проводится на основе минимизации энтропийно-параметрического потенциала.
Рассмотрим подробнее происхождение этих критериев.
В качестве критерия оптимальности системы при случайных внешних воздействиях широкое распространение получило условие минимизации дисперсии или среднего квадратического отклонения:

Критерий (16) получил наибольшее распространение в инженерной практике благодаря сравнительно простым соотношениям связи с характеристиками системы и внешних воздействий. Выбор критерия (16) рекомендуется в случаях, когда потери, возникающие из-за неточного поддержания управляемой величины на заданном уровне, пропорциональны квадрату сигнала ошибки [1].
В известном способе контроля и управления системой [2] для задания в качестве критерия оптимальности системы при случайных воздействиях использовано условие минимизации энтропийного потенциала Δэ. Для дискретной выборки значений m-мерного вектора Ym выходного параметра энтропийный потенциал рассчитывается из выражения (10) [4].
Тогда из зависимости энтропийного потенциала (1) получим выражение для расчета коэффициент энтропии Кэ, как отношение энтропийной погрешности Δэ к СКО σ:

Параметры энтропийного потенциала и СКО для выборки значений выходного параметра при работе системы в оптимальном режиме находятся в области своих минимальных значений, отличных от нуля. Поделив условие (6) на (16), получим в левой части отношение минимальных значений энтропийного потенциала Δэ опт и СКО σопт для m-мерного вектора Ym выходного параметра, характерные при оптимальной работе системы. При сравнении полученного отношения с выражением (8) запишем выражение для коэффициента энтропии Кэ опт при оптимальном состоянии объекта управления:

Стремление энтропийного потенциала Δэ и СКО σ для m-мерного вектора Ym выходного параметра yj к своим оптимальным значениям соответствует условию стремления коэффициента энтропии Кэ так же к оптимальному значению, откуда получим энтропийный критерий оптимальности в виде условия оптимизации:

Полученное условие оптимальности запишем в форме отклонения коэффициента энтропии Кэ от его оптимального значения:

Среди статистических параметров распределения для контроля формы наиболее важен коэффициент эксцесса ε распределения, характеризующий островершинность кривой [3, 4]. Смысл термина «эксцесс» состоит в том, что он показывает, как быстро уменьшается плотность распределения вблизи ее максимального значения. Выражение для расчета эксцесса распределения имеет вид:

здесь µ4 - центральный момент четвертого порядка для распределения выходного параметра, определяемый с помощью выражения (11).
При оптимальном состоянии системы заданному распределению соответствует оптимальное значение эксцесса ε0 распределения. Тогда для нахождения системы вблизи оптимального состояния существует область отклонений эксцесса распределений от его оптимального значения, в которой справедливо условие оптимизации вида:

Подставив в последнее условие выражение (11), записанное через оптимальные параметры системы и параметры распределения для m-мерного вектора Ym выходного параметра, получим, что для обеспечения условия оптимизация (15) необходимо сохранение отношения центрального момента четвертого порядка к четвертой степени СКО вида:

В правой части выражения (22) неизменное значение, характерное для оптимального состояния. Тогда получим условие оптимальности контроля и управления динамической системы для центрального момента четвертого порядка вид:

На практике более удобно применение контрэксцесса κ, или обратного эксцессу распределения:

Значение контрэксцесса κ находится в интервал от 0 до 1, что позволяет отразить все существующие распределения в едином пространстве.
Наличие конечных оптимальных значений для СКО и центрального четвертого момента при нахождении системы в оптимальном состоянии позволяет записать критерий оптимальности в форме отклонения контрэксцесса κ от его оптимального значения:

В пространстве коэффициента энтропии и контрэксцесса отклонения этих параметров откладываются во взаимно перпендикулярных направлениях. Поэтому для нахождения системы в области оптимальных состояний удобно использовать критерий оптимальности (13), полученный путем суммирования отношения квадратов отклонений коэффициента энтропии и контрэксцесса от их оптимальных значений к этим оптимальным значениям.
Для реализации способа контроля и управления динамической системой, основанного на сохранении формы распределения, необходимо выполнить следующие требования:
во-первых, обеспечить нахождение коэффициента энтропии в области своего оптимального значения, что позволит исключить переход системы в низкоэнтропийные неработоспособные состояния;
во-вторых, обеспечить контроль формы статистической кривой за счет нахождения параметров распределения для m-мерного вектора выходного параметра системы в области их оптимальных значений.
Из рассмотренного выше материала следует, что необходимым требованием выполнение критерия оптимальности (15) в динамической системе является одновременное обеспечение целого ряда условий оптимизации системы: условий минимизации энтропийного потенциала, СКО и центрального момента четвертого порядка. Эти условия имеют вид

Очевидно, что построение динамической системы контроля и управления на основе контроля формы кривой распределения m-мерного вектора выходного параметра возможно путем обеспечения условий оптимизации системы (26).
При этом выполнение условий (26.а) и (26.б) позволяют обеспечить нахождение коэффициента энтропии в области допустимых отклонений, ограниченных кривой 48 фигуры 3. Аналогично выполнение условий (26.а) и (26.в) делают возможным обеспечение оценки контрэксцесса так же в области допустимых отклонений, ограниченных кривой 48 фигуры 3.
Следует отметить, что при функционировании системы в оптимальном состоянии такие параметры, как центральный момент четвертого порядка, энтропийный потенциал и СКО, имеют конечные минимальные значения экстремумов в области оптимального функционирования.
Если учесть, что условие оптимальности центрального момента четвертого порядка следует из условия минимизации СКО (см. выражение (23)), то необходимое требование выполнения критерия оптимальности (15) содержит два условия минимизации и имеет следующий вид:

Одновременное обеспечение условий (27.а) и (27.б) возможно при использовании параметра неопределенности, включающего одновременно как информационную, так и статистическую неопределенность выходного параметра. Авторы считают, что в качестве критерия оптимальности системы при случайных внешних воздействиях следует использовать энтропийно-параметрический потенциал (14), учитывающий энтропийный свойства выборки выходного параметра и снижающий влияние энтропийного потенциала при переходе в низкоэнтропийное состояние за счет квадрата среднего квадратического отклонения. Тогда задача контроля и управления динамической системы в области ее оптимальных состояний сводится к условию минимизации энтропийно-параметрического потенциала:

В области оптимального контроля и управления энтропийно-параметрический потенциал наделен следующими свойствами. Энтропийно-параметрический потенциал - это конечная, вещественная, дифференцируемая относительно математического ожидания выходного параметра функция, монотонно возрастающая при отклонении математического ожидания выборки m-мерного вектора от своего оптимального значения.
В области устойчивого состояния системы энтропийно-параметрический потенциал имеет минимальное значение, для которого известны коэффициент энтропии и контрэксцесс распределения выходного параметра. Изменение состояния вызывает изменение этих параметров распределения, отражающееся в увеличении энтропийно-параметрического потенциала.
Вследствие интенсивных внешних воздействий возможен выход динамической системы за границы области оптимального состояния и ее переход в низкоэнтропийное состояние. Возврат системы в оптимальное состояние происходит через ряд устойчивых промежуточных состояний, в которых система может находиться длительное время, большее времени Т одного цикла. В этом случае направленная трансформация распределения и формирование вектора управляющих параметров осуществляется по энтропийно-параметрическому критерию (13).
Таким образом, при контроле и управлении динамической системой на основе сохранения формы распределения можно обеспечить выполнения критерия оптимальности (13).
Структурная схема, реализующая предлагаемый способ контроля и управления динамической системой, приведена на фигуре 6 и включает четыре этапа обработки информации. Рассмотрим работу схемы на каждом из этапов.
1 этап: регистрация состояния объекта. На этом этапе происходит регистрация и измерение выходного параметра y(t) объекта управления с помощью измерительного устройства ИУ 12. ИУ регистрирует через известные дискретные промежутки времени Δt значения yi и передает их на ФВЗВП 13. На алгоритме предлагаемого способа контроля и управления динамической системой, приведенном на фигуре 5, этап регистрации состояния объекта показан в виде блока 1, на вход которого поступает непрерывный сигнал x(t) и вектор управляющего воздействия ξ.
2 этап: формирование выборки значений выходного параметра. Действия на этом этапе заключаются в сохранении выборки последних n результатов измерений. Дискретные значения параметра yi с выхода ИУ 12 сохраняются в ФВЗВП 13. Выборка значений выходного параметра предназначена для построения гистограммы и оценки вероятности наблюдения pi регистрируемого результата в интервале Δy значения yi.
Так как для улучшения работы астатической системы управления необходимо обеспечить идентичность закона распределения контролируемого параметра и оптимального распределения того же параметра, полученного на основе наблюдений за объектом или теоретически, то необходимо обеспечить регистрацию состояния объекта и формирование выборки значений выходного параметра в соответствии с заложенными моделями. Временная диаграмма процесса формирования для выборки значений выходного параметра системы показана на фигуре 7. Для наблюдения за системой необходим непрерывный процесс формирования выборки значений выходного параметра, сохраняющей энтропийные и параметрические свойства в любой момент времени. Сохранность свойств выборки в любой момент функционирования системы достигается за счет проведения наблюдений в течение характерного для системы временного цикла Tc. Тогда для контроля и управления системой появляется возможность проводить определение параметров распределения на основе выборки значений выходного параметра системы за промежуток времени, равный времени цикла системы Tc. Количество значений n формируемой выборки задано отношением периода одного характерного цикла системы к промежутку времени одного измерения Δtи.
n=Tc/Δtи.
Эта и-мерная выборка значений постоянно изменяется на ФВЗВП 13 путем записи результатов, полученных с измерительного устройства с тактовой частотой l/Δtи. Так как ФВЗВП 13 настроен для хранения только n значений, то при получении результата от измерительного устройства происходит исключение из выборки значения, записанного в момент времени (Tc+Δtи), которое отличается более, чем на время одного цикла функционирования системы. В результате в системе всегда хранятся значения только одного цикла, распределение которых при нормальном функционировании системы должно сохранять свои параметры. В силу того, что процесс обработки результатов требует некоторого промежутка времени τ, большего промежутка времени записи ФВЗВП 13, то за это время τ выборка значений выходного параметра изменяется. При этом в выборке отражается переход системы в низкоэнтропийное состояние, что позволяет в системе динамического контроля и управления выработать управляющее воздействие для изменения состояния органов управления объектом в любой текущий момент времени.
На алгоритме предлагаемого способа контроля и управления динамической системой (см. фигуру 5) этому этапу соответствует блок 2.
3 этап: определение параметров распределений. На этом этапе вычислительное устройство:
- рассчитывает вероятности нахождения регистрируемых дискретных значений выходного параметра yi в заданных интервальных границах;
- формирует m-мерный вектор выходного параметра, содержащий дискретные значения интервалов группирования данных и вероятности наблюдения выходных параметров в пределах интервалов группирования;
- проводит обработку рассчитанных вероятностей m-мерного вектора Ym выходного параметра и определяет для выборки выходного параметра объекта управления параметры статистического распределения: математическое ожидание М, СКО σ, центральный момент четвертого порядка µ4 и энтропийный потенциал Δэ;
- определяет оценки коэффициента энтропии Кэ, и контрэксцесса к распределения для m-мерного вектора Ym выходного параметра.
Вероятности нахождения регистрируемых дискретных значений выходного параметра в заданных интервальных границах j-го значения yj вычислительным устройством рассчитываются следующим образом. Весь диапазон выходного параметра разбит на интервалы, заданные границами интервалов и j-м значением yj выходного параметра. Сначала проводится ранжирование ряда в порядке возрастания. Затем подсчитывается число nj элементов ряда, имеющих значения больше нижней границы yj min и меньше верхней yjmax границы j-го интервала. Разделив число значений nj попавших в j-й интервал на число значений n всей выборки выходного параметра, получим вероятности pj наблюдения выходного параметра в интервале j-го дискретного значения:
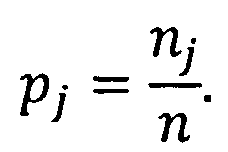
После чего формируется матрица Ym, в которой каждому j-му дискретному значению yj вариационного ряда сопоставляется вероятность pj его наблюдения в полученной выборке значений.
Вычисление основных параметров статистического распределения ВУ проводит в следующем порядке.
1. Определяются математическое ожидание М и СКО σ для выборки значений выходного параметра с помощью выражений (3) и (4) соответственно.
2. Определяется центральный момент четвертого порядка µ4 по выражению (11).
3. Определяется энтропийный потенциал Δэ с помощью выражения (10).
4. Определяется коэффициент энтропии Кэ, как отношение энтропийного потенциала Δэ к СКО σ с помощью выражения (8).
5. Определяется контрэксцесс к распределения по выражению (9).
На алгоритме предлагаемого способа контроля и управления динамической системой (см. фигуру 5) блоки 4 и 50 соответствуют определению параметров распределения.
Параметры статистического распределения позволяют определить оценку энтропийно-параметрического критерия γ нахождения системы в области оптимального контроля и управления. Для получения оценки критерия γ используются эталонные значения коэффициента энтропии Кэ0 и контрэксцесса κ0 оптимального состояния системы, формируемые ФЭПР 57. На алгоритме фигуры 5 определение энтропийно-параметрического критерия у осуществляет блок 51. База данных эталонных параметров распределения представлена на фигуре 5 в виде блока 55.
По мнению авторов, энтропийно-параметрический критерий γ позволяет оценить качество состояния динамической системы. Покажем это. За время τ в выборке значений yi выходного параметра изменяются ΔN=τ/Δtи значений, которые отражают возможный выход системы из зоны оптимального управления или переход в область другого устойчивого состоянии. Очевидно, что такой переход будет отражен в пространстве энтропийного коэффициента Кэ и контрэксцесса κ.
Проверка принадлежности области оптимального состояния системы поводится на основе сравнения критерия оптимальности γ с его максимально допустимым значением γmax. На фигуре 5 алгоритма способа управления динамической системы проверку критерия оптимальности осуществляет блок 52. Если критерий γ превышает свое максимальное значение γmax, то динамическая система вышла из области оптимального управления и для дальнейшего управления необходимо принять жесткие меры, обеспечивающие возврат системы в область оптимального состояния. Для этого необходимо определить возможную трансформацию закона распределения выходного параметра и сформировать управляющее воздействие для органов управления объектом. На алгоритме фигуры 5 эти действия осуществляют блоки 7 и 8.
Если динамическая система находится в зоне оптимального контроля и управления, то проводится последующая оптимизация состояния системы путем минимизации энтропийно-параметрического потенциала Δэп, определяемого с помощью выражения (14) по значениям параметров распределений: Δэп→min. Процессы определения энтропийно-параметрического потенциала и его минимизацию осуществляют блоки 53 и 54 алгоритма предлагаемого способа контроля и управления динамической системы (см. фигуру 5). Если энтропийно-параметрический потенциал Δэп, не достигает своего минимального значения, то выполняется процесс анализа требуемой корректировки закона распределения, по результатам которой так же формируется управляющее воздействие на органы управления объектом. Следует отметить, что изменения в системе при проведении корректировки закона распределения не приводят к изменению качественного состояния самой системы. На фигуре 5 корректировку закона распределения осуществляет блок 56. При достижении минимума энтропийно-параметрического потенциала система контроля и управления принимает состояние объекта в качестве оптимального состояния и сохраняет настройки предыдущего цикла управления. Переходу динамической системы в оптимальное состояние на алгоритме предлагаемого способа контроля и управления динамической системы (см. фигуру 5) соответствует блок 9.
На структурной схеме (см. фигуру 6), реализующей предлагаемый способ контроля и управления динамической системой, этапу обработки информации соответствуют процессы, происходящие в вычислительном устройстве 14.
4 этап: формирование управляющего воздействия.
При выходе динамической системы из области оптимального состояния необходимо провести кардинальные изменения ее свойств с помощью органов управления. Для этого проводится оценка возможных трансформаций распределения выходного параметра и формируется вектор управляющих воздействий ξ для органов управления динамической системы.
При нахождении динамической системы в области оптимального состояния управление происходит за счет минимизации энтропийно-параметрического потенциала Δэ. По его значению определяют степень и направление трансформации закона распределения. Энтропийно-параметрический потенциал передается на формирователь управляющего воздействия 15, где оценивается возможная корректировка закона распределения и формируется вектор воздействий ξ, поступающий на органы управления динамической системы для изменения ее состояния. Формирователь управляющего воздействия 75, действие которого на алгоритме 5 показано в форме блока 72, производит такое действие на органы управления, при котором происходит уменьшение энтропийно-параметрического потенциала Δэп.
Рассмотренный подход управления с помощью энтропийно-параметрического потенциала Δэп имеет важное преимущество по сравнению с управлением посредством энтропийного потенциала Δэ, состоящее в следующем. При функционировании системы в области оптимального состояния энтропийная и среднеквадратическая составляющие энтропийно-параметрического потенциала имеют приблизительно одинаковые значения, что обеспечивает высокое минимальное значение потенциала. Переход системы в низкоэнтропийное состояние, возможный под действием мощных неблагоприятных воздействий, вызывает снижение энтропийной составляющей, значением которой во многих случаях можно пренебречь по сравнению со среднеквадратической составляющей. Выход из этого состояния происходит через ряд промежуточных состояний в течение времени, много большего, чем время τ, равное одному циклу управления. В это время управление динамической системой поддерживается на основе среднеквадратической составляющей, что позволяет сохранить контроль и управление динамической системой при ее временном нахождении в области устойчивых нерабочих или неблагоприятных состояний.
Управление системой в оптимальном высокоэнтропийном состоянии происходит за счет энтропийной составляющей, которая за счет выбора коэффициента kp,n→∞ может быть задано большей по сравнению со среднеквадратической составляющей. В этом случае сохраняются все достоинства управления, основанного на информационных свойствах распределения выходного параметра.
Таким образом, предлагаемый способ «устраняет» целое множество низкоэнтропийных распределений, которые система, построенная по алгоритму минимизации энтропийного потенциала Δэ путем трансформации энтропийного коэффициента Кэ, будет воспринимать как наиболее благоприятные состояния, и сохраняет информационные свойства управления и конроля в области оптимального управления.
ПЕРЕЧЕНЬ ПРИНЯТЫХ СОКРАЩЕНИЙ
ВУ вычислительное устройство
ИУ измерительное устройство
ОУ объект управления
СКО среднеквадратическое отклонение
ФВЗВП формирователь выборки значений выходного параметра
ФУВ формирователь управляющего воздействия
ФЭВП формирователь эталонных параметров распределений
ЛИТЕРАТУРА.
1. Лукас В.А. Теория управления техническими системами. - Издательство Уральского государственного горного университета. Екатеринбург. - 2005 г. - 676 с.
2. Пат. 2296356 Российская Федерация. Способ контроля и управления динамической системой / Лазарев В.Л. - №2005124236/09 заявки; заявл. 29.07.2005; опубл. 27.03.2007; Бюл. №9.
3. Новицкий П.В., Зограф И.А. Оценка погрешности результатов измерений. - Лениград. Энергоатомиздат. - 1985 г. - 248 с.
4. Туричин А.Н., Новицкий П.В., Левшина Е.С., Гутников B.C., Спектор С.А., Зограф И.А., Аршанский Б.Э., Кнорринг В.Г., Пресняков П.Д. Электрические измерения неэлектрических величин. - Ленинград. Энергия. - 1975 г. - 576 с.


Изобретение относится к контролю и организации оптимального управления и может быть использовано в системах контроля и управления различных динамических систем в реальном масштабе времени. Технический результат - оптимизация контроля и управления динамической системой путем исключения из функционирования системы устойчиво неработоспособных состояний. Суть изобретения заключается в использовании критерия оптимальности на основе минимизации энтропийно-параметрического потенциала, позволяющего исключить из функционирования динамической системы устойчиво неработоспособные состояния. Для этого осуществляют формирование базы данных эталонных параметров закона распределения выходного параметра, определение реальных параметров закона распределения выходного параметра, определение энтропийно-параметрического критерия области оптимального управления, проверку состояния объекта принадлежности области оптимального состояния, определение величины энтропийно-параметрического потенциала, минимизацию величины энтропийно-параметрического потенциала и корректировку реальных параметров закона распределения выходного параметра. 7 ил.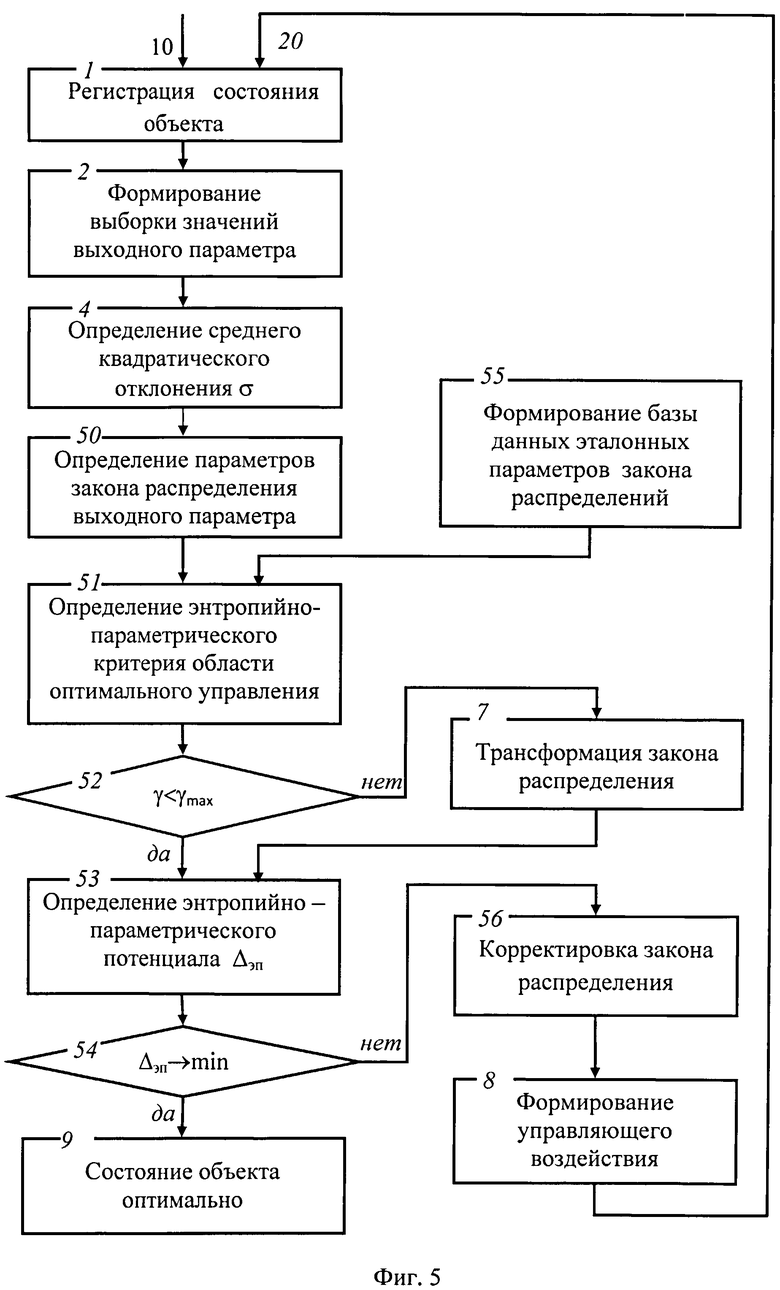
Способ контроля и управления динамической системой, заключающийся в том, что осуществляют регистрацию состояния объекта, формирование выборки yi значений выходного параметра y(t), определение величины среднеквадратического отклонения σ выходного параметра, трансформацию закона распределения управляемого параметра за счет изменения настроечных параметров регулятора и формирование управляющего воздействия, отличающийся тем, что осуществляют формирование базы данных эталонных параметров закона распределения выходного параметра, определение реальных параметров закона распределения выходного параметра по выражениям:
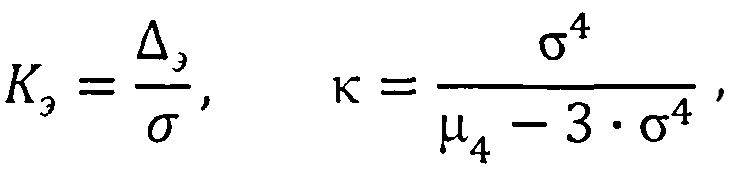
где Кэ, κ - коэффициенты энтропии и контрэксцесса соответственно,
Δэ - энтропийный потенциал, рассчитываемый по формуле:
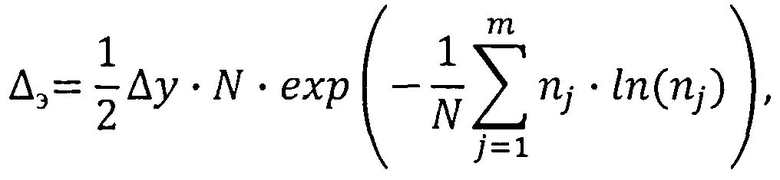
где Δy - ширина интервалов группирования выходного параметра; nj - число значений выходного параметра в j-м интервале группирования; N - число значений выборки выходного параметра; m - число интервалов группирования;
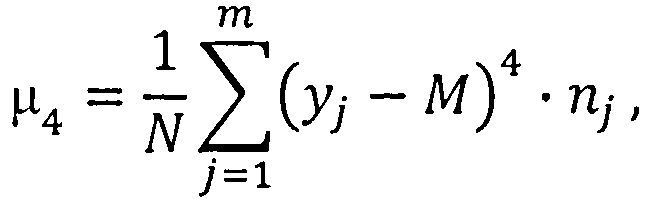
где µ4 - центральный момент четвертого порядка распределения выходного параметра, yj - среднее значение выходного параметра в j-м интервале группирования; М - математическое ожидание выходного параметра:
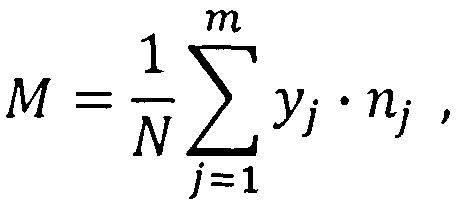
определение энтропийно-параметрического критерия области оптимального управления,
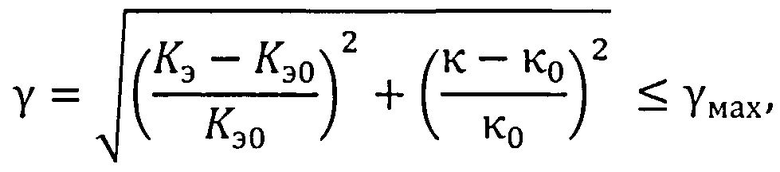
где γмах - максимальное значение энтропийно-параметрического критерия области оптимального управления;
проверку состояния объекта принадлежности области оптимального состояния;
определение величины энтропийно-параметрического потенциала Δэп по выражению:
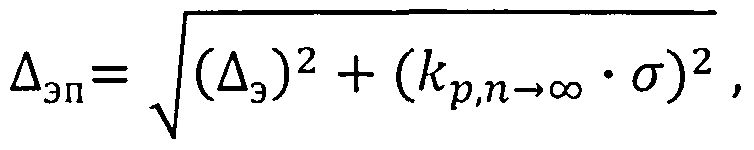
где kp,n→∞ - коэффициент нормального стандартного распределения;
минимизацию величины энтропийно-параметрического потенциала Δэп динамической системы и корректировку реальных параметров закона распределения выходного параметра.
| СПОСОБ КОНТРОЛЯ И УПРАВЛЕНИЯ ДИНАМИЧЕСКОЙ СИСТЕМОЙ | 2005 |
|
RU2296356C1 |
| СПОСОБ ОЦЕНКИ ДОСТОВЕРНОСТИ ДОПУСКОВОГО КОНТРОЛЯ ПАРАМЕТРОВ ПО РЕЗУЛЬТАТАМ ИЗМЕРЕНИЙ | 2003 |
|
RU2246744C2 |
| СПОСОБ ВЫРАБОТКИ УПРАВЛЯЮЩЕГО ВОЗДЕЙСТВИЯ ДЛЯ ПРОМЫШЛЕННОГО ОБЪЕКТА УПРАВЛЕНИЯ | 2011 |
|
RU2450303C1 |
| US 6496761 B1, 17.12.2002 | |||
Авторы
Даты
2015-10-20—Публикация
2014-03-27—Подача