Способ относится к фотограмметрии, в частности к построению геометрической модели местности по цифровым снимкам в автоматическом режиме.
Известен способ оценки точности построения геометрической модели местности по стереопаре снимков, который выполняется с использованием остаточных поперечных параллаксов [1, 2]. При построении модели местности на универсальных фотограмметрических приборах остаточный поперечный параллакс оценивается визуально. Оценка точности построения геометрической модели местности по остаточным поперечным параллаксам производится также и в цифровых технологиях, например в ЦФС PHOTOMOD. Недостатком данного способа в цифровых технологиях является необходимость вычислять трансформированные ординаты точек снимков, по которым, как разность ординат одноименных точек, определяется остаточный поперечный параллакс. Также к недостаткам этого способа следует отнести то, что оценка точности модели выполняется только по одной координате, так как остаточный поперечный параллакс вычисляется только по трансформированным ординатам. Предлагаемый способе свободен от этих недостатков. Сущность предлагаемого способа состоит в том, что в качестве критерия оценки точности геометрической модели местности используется угол между двумя нормалями к базисной плоскости, построенными на одноименных точках.
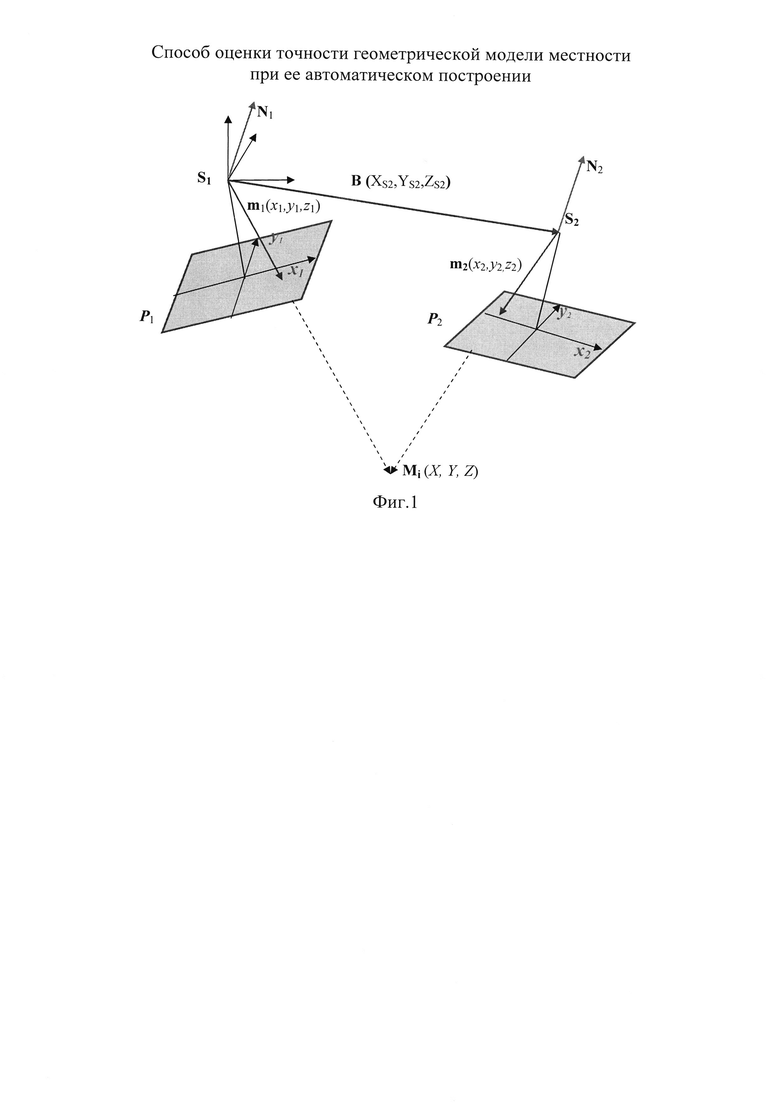
Из определения геометрической модели местности следует, что она является совокупностью точек пересечения одноименных проектирующих лучей, для чего они должны находиться в одной базисной плоскости. Каждая базисная плоскость образуется базисом и двумя одноименными проектирующими лучами (фигура 1). Направления проектирующих лучей на снимках стереопары задаются векторами m1 (x1,y1,z1(-ƒ)) и m2 (x2,y2,z2(-ƒ)), а направление базиса фотографирования В (bx,by,bz). Таким образом, модель будет построена, если все три вектора компланарны. Отступление от компланарности указанных векторов позволит судить о точности построения геометрической модели местности в каждой ее точке.
Степень некомпланарности векторов В, m1, m2 оценивают по значению угла 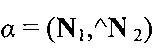 :
:

Здесь вектор нормали N1=bR1m1 к базисной плоскости и вектор нормали N2=bR2m2 к той же базисной плоскости, при этом R1 и R2 матриц поворота первого и второго снимков, a b - кососимметрическая матрица, определяемая как 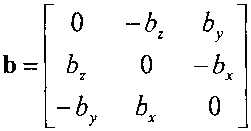 . При этом длина базиса фотографирования значения не имеет, а для первой системы элементов взаимного ориентирования в матрице b остаются только составляющие базиса по оси х.
. При этом длина базиса фотографирования значения не имеет, а для первой системы элементов взаимного ориентирования в матрице b остаются только составляющие базиса по оси х.
Таким образом, для оценки точности построения геометрической модели местности предлагается новый критерий, геометрический смысл которого отличен от остаточного поперечного параллакса, а его определение выполняется проще.
В качестве параметра для определения допустимого отклонения угла α от нулевого значения предлагается вычислять среднее квадратическое значение tgα, а конкретное значение допуска устанавливать в зависимости от масштаба и качества снимков и от точности измерения координат их точек.
Литература
1. Лобанов А.Н. Фотограмметрия. - М.: Недра, 1984. - 550 с.
2. Хрущ P.M. Фотограмметрия, - СПб.: Военно-космическая академия имени А.Ф. Можайского, 2011. - 542 с.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ СОВЕРШЕНСТВОВАНИЯ ФОТОТРИАНГУЛЯЦИИ ПРИ СОЗДАНИИ ЦИФРОВЫХ МОДЕЛЕЙ МЕСТНОСТИ | 2023 |
|
RU2835990C2 |
| Способ определения координат объекта по стереопаре его снимков и по снимку летательных аппаратов | 2024 |
|
RU2840058C1 |
| СПОСОБ ПОСТРОЕНИЯ ЦИФРОВОЙ МОДЕЛИ ПОВЕРХНОСТИ ПО ДАННЫМ КОСМИЧЕСКОЙ СТЕРЕОСЪЕМКИ | 2021 |
|
RU2778076C1 |
| СПОСОБ АНАЛИТИЧЕСКОГО ОРИЕНТИРОВАНИЯ ПАРЫ АЭРОСНИМКОВ | 1997 |
|
RU2125709C1 |
| Способ автоматического создания цифровой модели местности по стереоснимкам | 1991 |
|
SU1793226A1 |
| АНАЛИТИЧЕСКИЙ СТЕРЕОФОТОГРАММЕТРИЧЕСКИЙ ПРИБОР | 1993 |
|
RU2098758C1 |
| СПОСОБ ПОЛУЧЕНИЯ НЕПРЕРЫВНОГО СТЕРЕОИЗОБРАЖЕНИЯ ЗЕМНОЙ ПОВЕРХНОСТИ | 2024 |
|
RU2832645C1 |
| Устройство для графической обработки конвергентных узкоугольных снимков | 1988 |
|
SU1589060A1 |
| Способ определения координат точек местности | 1977 |
|
SU705257A1 |
| Способ измерения снимков на универсальном стереофотограмметрическом приборе | 1977 |
|
SU691688A1 |
Изобретение относится к измерительной технике и может быть использовано в области фотограмметрии при оценке точности геометрической модели местности при ее автоматическом построении. Технический результат – повышение быстродействия за счет сокращения вычислительных операций. Для этого в качестве критерия оценки точности используют значение угла, образуемого двумя нормалями к базисной плоскости, построенными на одноименных точках, а вычисляют его по координатам одноименных точек, матрицам вращения и координатам базиса проектирования. В результате обеспечивается повышение быстродействия выполнения способа оценки точности геометрической модели местности. 1 ил.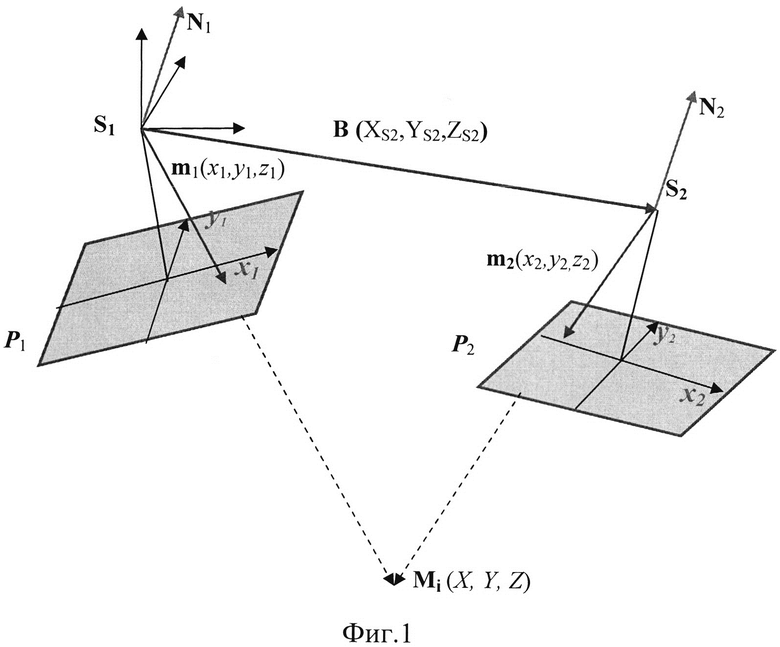
Способ оценки точности построения геометрической модели местности по цифровым снимкам стереопары, заключающийся в измерении координат одноименных точек и отличающийся тем, что в качестве критерия оценки точности используют значение угла, образуемого двумя нормалями к базисной плоскости, построенными на одноименных точках, а вычисляют его по координатам одноименных точек, матрицам вращения и координатам базиса проектирования.
| Карманов А.Г | |||
| Фотограмметрия, - СПб.: ИТМО, 2012, с | |||
| Приспособление для плетения проволочного каркаса для железобетонных пустотелых камней | 1920 |
|
SU44A1 |
| СПОСОБ И СИСТЕМА ДЛЯ ХРАНЕНИЯ И БЫСТРОГО ИЗВЛЕЧЕНИЯ ВЫСОТНЫХ ОТМЕТОК ЦИФРОВЫХ МОДЕЛЕЙ МЕСТНОСТИ ДЛЯ ИСПОЛЬЗОВАНИЯ В СИСТЕМАХ ОПРЕДЕЛЕНИЯ МЕСТОПОЛОЖЕНИЯ | 2003 |
|
RU2326434C2 |
| US 5902347 A1, 11.05.1999 | |||
| Прибор для печатания карт местности с выраженным рельефом по парным аэрофотоснимкам | 1926 |
|
SU10971A1 |
| Прибор для геодезической съёмки местности | 1937 |
|
SU62159A1 |
| Основные группы геометрических преобразований, приведенные в табл | |||
| Способ восстановления хромовой кислоты, в частности для получения хромовых квасцов | 1921 |
|
SU7A1 |
| - М.: Наука | |||
| Физмат-лит, 1999 | |||
| Способ амидирования жидких сульфохлоридов ароматического ряда | 1921 |
|
SU316A1 |
Авторы
Даты
2018-02-15—Публикация
2016-06-01—Подача