Изобретение относится к области измерительной техники и может быть использовано в радиолокации для определения фазы гармонического сигнала при фазовом пеленговании объекта, а также в навигационных системах, в радио- и гидролокации, в космических технологиях, в интерферометрах, в геодезии.
Известен «Цифровой способ и устройство определения мгновенной фазы принятой реализации гармонического или квазигармонического сигнала». [RU патент №2463701]. Принцип определения фазы сигнала основан на обработке зарегистрированного фрагмента сигнала
Uпр=Asin(ωt+ϕ) и сформированной квадратурной составляющей
Uкв=Asin(ωt+ϕ+π/2)=Acos(ωt+ϕ)
Фаза сигнала определяется для момента времени Т0. Для этого измеряют значения сигнала и квадратурной составляющей в моменты времени Т0, T0-t и T0+t, t<T0. Далее определяют параметры Uпр-, Uпр+, вычисляют Sпр=Uпр-+Uпр+, Rпр=Гпр--Uпр+, где Snp и Rnp - сумма и разность равноотстоящих от Т0 мгновенных значений сигнала соответственно, определяют Uкв-, Uкв+, вычисляют Sкв=Uкв-+Uкв+, Rкв=Uкв-Uкв, где Sкв и Rкв - - сумма и разность равноотстоящих от Т0 квадратурных составляющих сигнала соответственно, вычисляют отношения Sпр/Sкв и Rкв/Rпр и получают значение фазы сигнала в точке Т0:
ωT0+ϕ=arctg(Sпр/Sкв);
ωT0+ϕ=-arctg(Rкв/Rпр).
Недостатком данного способа является то, что даже при незначительной зашумленности сигнала определение точного значения фазы невозможно.
При зашумленности сигнала, что характерно для систем фазового пеленгования объектов, максимальная ошибка определения фазы может достигать 100 град., т.е. фактически определение фазы (или разности фаз) этим способом невозможно.
Известен «Способ совместного измерения частоты, амплитуды и начальной фазы гармонического сигнала», выбранный за прототип [RU патент №2486529]. Способ включает в себя дискретизацию аналогового сигнала, представление его фрагмента тремя цифровыми значениями S1, S2, S3, сформированными в моменты времени t1, t2, t3, соответствующие трем последовательным отсчетам, и вычисление частоты, амплитуды, фазы в момент времени t2 и начальной фазы по формулам:
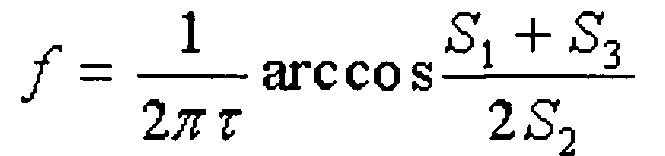
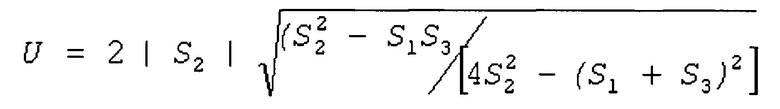
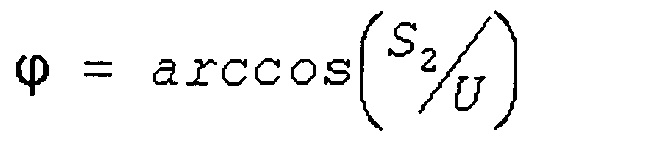
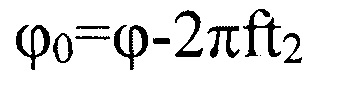
Для реализации данного способа необходимо, чтобы упомянутые три отсчета принадлежали одному периоду сигнала. Системы же фазового пеленгования должны работать с сигналами на частотах до 40 ГГц, поэтому при использовании известного способа требуется использовать аналого-цифровой преобразователь с частотой отсчетов выше 80 ГГц, что технически очень сложно [Кольцов Ю.В. Промышленные сверхскоростные преобразователи сигналов: АЦП и ЦАП // Успехи современной радиоэлектроники. - 2016. - №1. - С. 64-77].
Недостатком способа является то, что частота отсчетов сигнала при измерении должна превышать частоту Найквиста, т.е. более чем вдвое превышать частоту исходного сигнала, что приводит к сложности технической реализации способа. При зашумленности сигнала, что характерно для систем фазового пеленгования объектов, максимальная ошибка определения фазы может достигать 100 град, т.е. фактически определение фазы в системах фазового пеленгования с приемлемой точностью этим способом невозможно.
Технической проблемой является упрощение реализации способа определения фазы гармонического сигнала и повышение точности определения фазы при зашумленности исходного сигнала.
Для решения поставленной задачи предложен цифровой способ измерения фазы гармонического сигнала, который включает прием первичного сигнала x(t) с последующим аналого-цифровым преобразованием с помощью двух аналого-цифровых преобразователей (АЦП) на двух отличающихся частотах, которые могут быть меньше частоты Найквиста. Получение в результате этого двух числовых массивов y1[i], i=1…K и y2[i], i=1…K-d, где K и K-d - количество отсчетов первого и второго АЦП соответственно на интервале измерения Т, d>1. Выбираем для дальнейшей обработки один из этих массивов: y1[i], если max(y1) - min(y1)>max(y2) -min(y2), или y2[i], если max(y1) - min(y1)<max(y2) - min(y2), в результате чего будет сформирован числовой массив y[i], представляющий вторичный сигнал, полученный в результате дискретизации первичного сигнала с частотой ниже частоты Найквиста. Вычисляем с помощью быстрого преобразования Фурье приближенное целое значение количества периодов kp0 вторичного сигнала y[i]. Создаем M*N эталонных сигналов в области количества периодов kp2(р)=kp0-1+p*2/N, N - количество шагов поиска количества периодов вторичного сигнала и фазы ϕ2(j)=-π/2+j*2π/M, М - количество шагов поиска значения фазы вторичного сигнала. Вычисляем суммы квадратов отклонений ssd(j), j=1…M вторичного исходного и эталонных сигналов для каждого значения р.
Находим минимальные значения квадратов отклонений ssd(j); j=1:M, и значения jmin, соответствующего условию ssd(jmin)=min(ssd(j)), j=1:M для каждого значения р и для каждого р вычисляем текущие значения функции фазы ϕ_result(p)=-π/2+jmin*2π/M, p=1…N. Находим значения minϕ_result(p)), p=1:N, и значение pmin, соответствующее условию ϕ_result (pmin)=min(ϕ_result(p)), р=1:М. Вычисляем полное значение фазы ϕ_res=ϕ_result(pmin), и результирующее значение фазы ϕ_out=ϕ_res или ϕ_out=π-ϕ_res, если abs(ϕ_res)>π/2.
Отличительными существенными признаками предлагаемого цифрового способа является дискретизация исходного сигнала с помощью двух аналого-цифровых преобразователей на двух отличающихся частотах и цифровая обработка этих сигналов, в результате чего фаза сигнала может определяться с заданной точностью при частоте отсчетов, сделанных на частоте ниже частоты Найквиста и при зашумленности сигнала.
Идея предлагаемого цифрового способа измерения фазы сигнала заключается в том, что фаза вторичного сигнала, полученного из исходного при дискретизации с частотой меньшей частоты Найквиста, точно равна фазе исходного сигнала или сдвинута на π, несмотря на то что частота вторичного сигнала меньше частоты исходного, что приводит к упрощению реализации способа определения фазы гармонического сигнала. При выборе области поиска значения фазы исходим из того, что в системах фазового пеленгования значение фазы находится в диапазоне [-π/2+π/2]. Благодаря предлагаемому алгоритму определение фазы производится по первому вторичному сигналу, а в случае, если количество отсчетов окажется кратным количеству периодов исходного сигнала и вторичный сигнал теряет колебательный характер и вырождается в прямую линию, что исключает возможность определения фазы, производится автоматический переход к обработке второго вторичного сигнала. Кроме того, поиск фазы вторичного сигнала производится в области [-0.5π 1.5π], чем обеспечивается получение значения фазы как в случае, когда смещения фазы на π нет, так и в случае, когда смещение есть, для учета возможного смещения фазы вторичного сигнала относительно фазы первичного сигнала истинное значение фазы сигнала вычисляется как ϕ_res=π-ϕ_res, если abs(ϕ_res)>π/2, где ϕ_res - полученное значение фазы без учета возможного смещения фазы вторичного сигнала. Погрешность определения фазы зависит от количества отсчетов сигнала kt, уровня зашумленности сигнала и от размерности М*N области поиска количества периодов вторичного сигнала и фазы и может быть сделана сколь угодно малой, что обеспечит повышение точности определения фазы предлагаемым способом при зашумленности сигнала. Таким образом, совокупность отличительных признаков необходима и достаточна для решения поставленной проблемы.
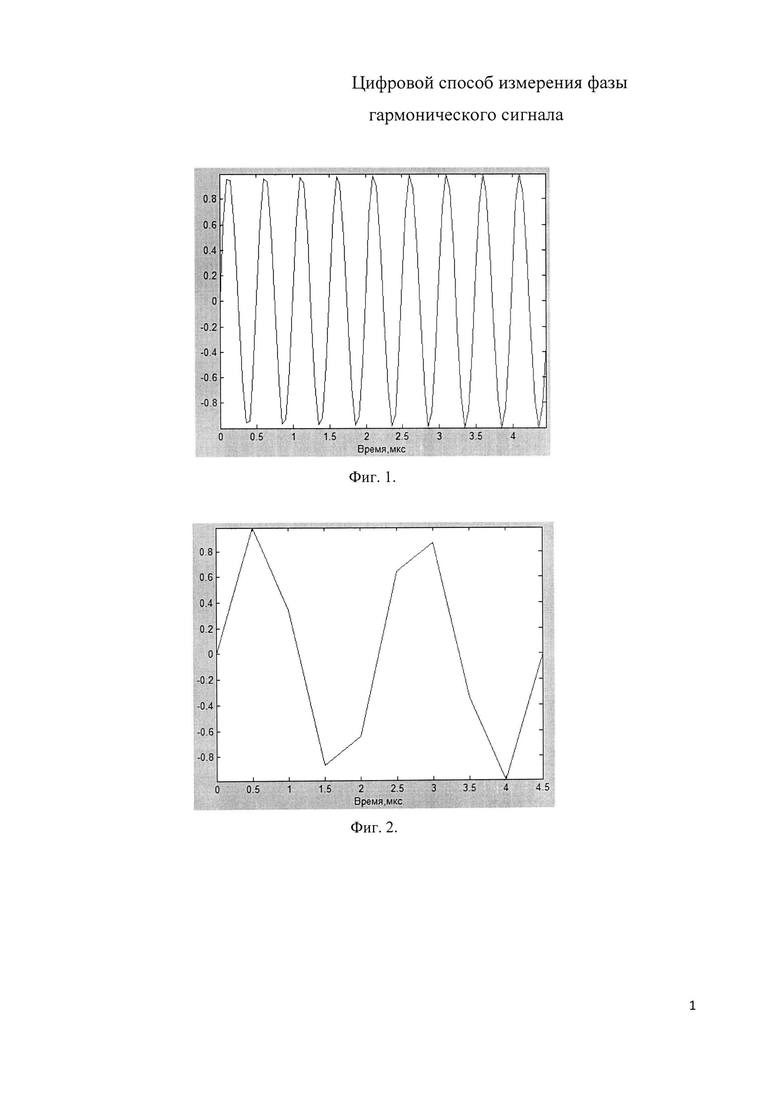
Фиг. 1 и фиг. 2 иллюстрируют эффект, возникающий при дискретизации с частотой, меньшей частоты Найквиста: исходный сигнал представлен на фиг. 1, вторичный сигнал более низкой частоты, получаемый в результате дискретизации с частотой, меньшей частоты Найквиста, приведен на фиг. 2.
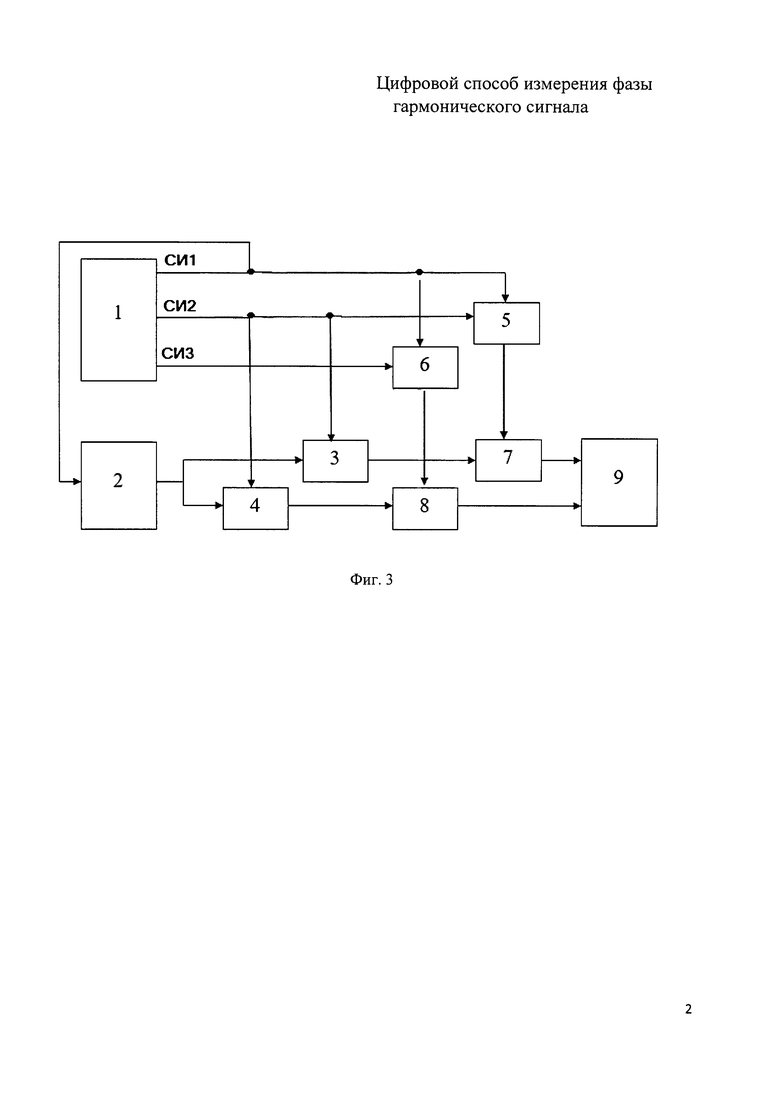
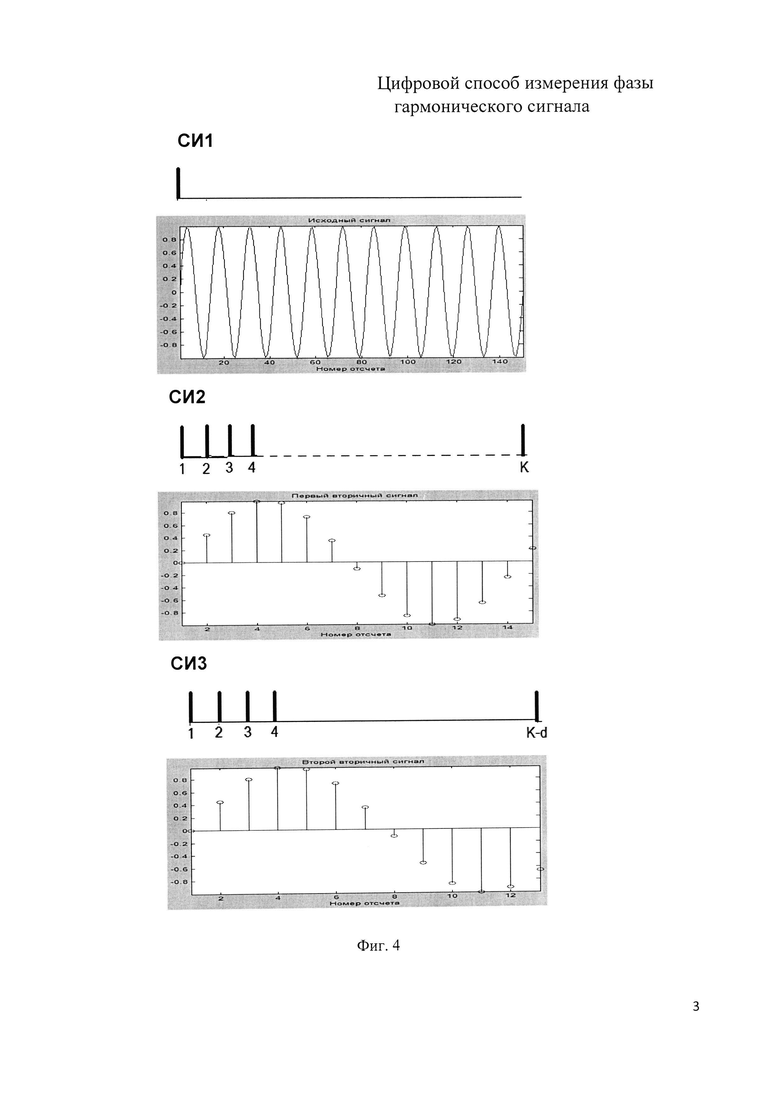
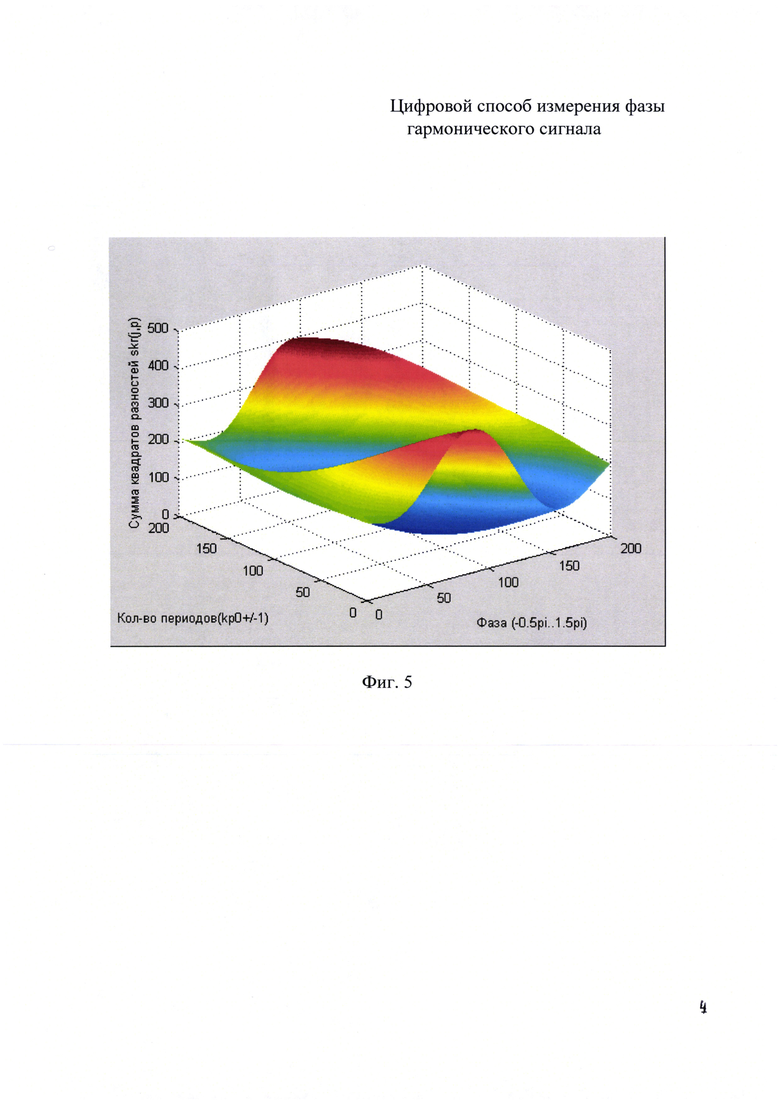
Схема устройства для возможной реализации предлагаемого цифрового способа измерения фазы сигнала [фиг. 3]. Устройство включает: 1 - генератор синхронизирующих импульсов СИ1, СИ2 и СИ3, 2 - источник сигнала, 3 и 4 - аналого-цифровые преобразователи, 5 и 6 - счетчики адреса оперативных запоминающих устройств (ОЗУ), 7 и 8 - ОЗУ, 9 - вычислитель. На фиг. 4 приведена временная диаграмма синхронизирующих импульсов СИ1, СИ2 и СИ3. На фиг.5 приведен типичный график функции суммы квадратов отклонений вторичного исходного и эталонных сигналов ssd(j,p), j=1:M, p=1…N.
Пример реализации предлагаемого цифрового способа в устройстве приведен на фиг. 3.
Генератор синхронизирующих импульсов 1 вырабатывает синхронизирующий импульс СИ1, который производит сброс счетчиков 5 и 6 адреса записи в ОЗУ1 и ОЗУ2. С момента формирования синхронизирующего импульса СИ1 начинается формирование синхроимпульсов СИ2 и СИ3 генератором 1, аналого-цифровое преобразование первичного гармонического входного сигнала x(t), имеющего, например, частоту 5000 МГц, при количестве периодов 1000, амплитуду, равную единице, среднюю квадратическую величину шума 0.05 и начальную фазу 0.8 радиана, с помощью аналого-цифровых преобразователей 3 и 4, при частоте дискретизации сигнала, например, 1000 МГц, количестве дискретизированных значений сигнала 200 у преобразователя 3 и частоте дискретизации сигнала 940 МГц и количестве дискретизированных значений сигнала 188 у преобразователя 4, запись результатов преобразования в оперативные запоминающие устройства 7 и 8 по адресам, задаваемым адресными счетчиками 5 и 6. При этом в ОЗУ 7 будет зафиксировано 200 дискретных отсчетов сигнала, а в ОЗУ 8-200-2=188 дискретных отсчетов сигнала. Далее вычислитель 6 производит чтение и обработку зарегистрированных и хранящихся в оперативных запоминающих устройствах 7 и 8 дискретизированных сигналов в соответствии с алгоритмом, описанным ниже. Действия обработки выполняются в следующем порядке:
1. Производят чтение зарегистрированного в оперативных запоминающих устройствах 7 и 8 входного первичного сигнала, представленного в виде двух числовых массивов: y1[i], i=1…K, K=200 и y2[i], i=1…K-d, K=200, d=2 соответственно.
2. Формируют массив y[i] по правилу: y[i]=y1[i], если max(y1)-min(y1)>max(у2)-min(y2), или y[i]=y2[i], если max(y1)-min(y1)<max(у2)-min(y2). В данном случае величина max(y1) - min(y1) будет близка к нулю, в связи с тем, что количество дискретных отсчетов 200 кратно количеству периодов 1000, а величина max(у2)-min(y2) будет приблизительно равна размаху исходного сигнала x(t). Поэтому в качестве массива вторичного сигнала y[i] будет взят y2[i]. (Если бы количество дискретных отсчетов преобразователей 3 и 4 не было кратно количеству периодов 1000, то в качестве массива вторичного сигнала мог быть взят как y1[i], так и y2[i]).
3. Производят быстрое преобразование Фурье числового массива y [i] вторичного сигнала, в результате чего формируют массив частотного спектра вторичного сигнала в виде набора из K или K-d чисел (в данном случае - набора из K-d, т.е. 188).
4. Определяют номер элемента kp0 массива частотного спектра, которому соответствует максимальное значение. Этот номер kp0 является грубой оценкой количества периодов вторичного сигнала (в данном случае kp0=10).
5. Создают M*N эталонных гармонических сигналов с количеством периодов kp2(p)=kp0-1+p*2/N и фазой ϕ2(j)=-π/2+j*2π/M, например, М=200, N=200.
6. Вычисляют суммы квадратов отклонений ssd(j), j=1…M вторичного исходного и эталонных сигналов для каждого значения р.
7. Находят минимальное значение ssd(j), j=1:M и значения jmin, соответствующего условию ssd(jmin)=min(ssd(j)), j=1:M для каждого значения р.
8. Вычисляют текущие значения функции фазы для каждого значенияр: ϕ_result(p)=-π/2+jmin*2π/M, p=1…N.
9. Находят значения min(ϕ_result(p)), p=1:N и значения pmin, соответствующего условию ϕ_result (pmin)=min(ϕ_result (р)), p=1:N.
10. Вычисляют полное значение фазы ϕ_res=ϕ_result(pmin). В данном случае ϕ_res=0.7992. Полученные таким образом jmin и pmin соответствуют абсолютному минимуму функции ssd(j,p), график которой приведен на фиг. 5.
11. Вычисляют результирующее значения фазы ϕ_out=ϕ_res, если abs(ϕ_res)<π//2 или ϕ_res=π-ϕ_res, если abs(ϕ_res)>π//2. В данном случае abs(ϕ_res)<π//2, поэтому ϕ_out=ϕ_res=0.7992. Типичная погрешность определения фазы в радианах составит 0.8 - 0.7992=0.0018 рад., в градусах - 0.0456 град.
Таким образом, упрощение реализации способа определения фазы гармонического сигнала достигнуто за счет того, что дискретизация сигнала с помощью АЦП произведена с частотой 1 ГГц вместо 10 ГГц которые были бы необходимы в прототипе. Повышение точности определения фазы при зашумленности исходного сигнала подтверждается тем, что по результатам 1000 статистических испытаний максимальная погрешность определения фазы предлагаемым способом составляет 1.76 град, среднеквадратическая - 0.49 град, что значительно меньше, чем в прототипе: 100 град, и 8.5 град, соответственно.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ПОИСКА ШУМОПОДОБНЫХ СИГНАЛОВ С МИНИМАЛЬНОЙ ЧАСТОТНОЙ МАНИПУЛЯЦИЕЙ | 2012 |
|
RU2486683C1 |
| Способ передачи дискретных сообщений между подводными объектами | 2021 |
|
RU2758637C1 |
| СПОСОБ ПРИЕМА ШИРОКОПОЛОСНОГО СИГНАЛА И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ (ВАРИАНТЫ) | 1999 |
|
RU2153770C1 |
| Способ гидроакустического поиска автономного донного подводного объекта | 2019 |
|
RU2727331C1 |
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТЫ СЕРДЕЧНЫХ СОКРАЩЕНИЙ ПЛОДА | 2012 |
|
RU2489968C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ПЕЛЕНГАЦИОННОЙ ПАНОРАМЫ ИСТОЧНИКОВ РАДИОИЗЛУЧЕНИЯ НА ОДНОЙ ЧАСТОТЕ | 2012 |
|
RU2528177C2 |
| СПОСОБ ЧАСТОТНО-ВРЕМЕННОГО КОРРЕЛЯЦИОННОГО АНАЛИЗА ЦИФРОВЫХ СИГНАЛОВ | 2009 |
|
RU2405163C1 |
| УПРАВЛЕНИЕ ОТОБРАЖЕНИЕМ ВИДЕО С РАСШИРЕННЫМ ДИНАМИЧЕСКИМ ДИАПАЗОНОМ | 2014 |
|
RU2647636C2 |
| СПОСОБ ВЫДЕЛЕНИЯ ТРЕНДА ПУТЕМ РАЗМНОЖЕНИЯ ОЦЕНОК ЕГО ЕДИНСТВЕННОЙ ИСХОДНОЙ РЕАЛИЗАЦИИ (РАЗОЦ) И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2000 |
|
RU2207622C2 |
| СПОСОБ И УСТРОЙСТВО ОПРЕДЕЛЕНИЯ УГЛОВОЙ ОРИЕНТАЦИИ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2014 |
|
RU2553270C1 |
Цифровой способ измерения фазы гармонического сигнала позволяет упростить реализацию определения фазы гармонического сигнала и повысить точность определения фазы при зашумленности исходного сигнала. Способ основан на приеме первичного сигнала x(t) с последующим аналого-цифровым преобразованием с помощью двух аналого-цифровых преобразователей (АЦП) на двух отличающихся частотах. Получаем в результате этого два числовых массива y1[i], i=1…K и y2[i], i=1…K-d, где K и K-d - количество отсчетов первого и второго АЦП соответственно на интервале измерения Т, d>1. Выбираем для дальнейшей обработки один из этих массивов, который будет представлять вторичный сигнал, полученный в результате дискретизации первичного сигнала с частотой ниже частоты Найквиста. Вычисляем с помощью быстрого преобразования Фурье приближенное целое значение количества периодов kp0 вторичного сигнала. Создаем M*N эталонных сигналов в области количества периодов kp2(p)=кр0-1+p*2/N, N - количество шагов поиска количества периодов вторичного сигнала и фазы ϕ2(j)=-π/2+j*27π/M, М - количество шагов поиска значения фазы вторичного сигнала. Вычисляем суммы квадратов отклонений ssd(j), j=1…M вторичного исходного и эталонных сигналов для каждого значения р. Находим минимальные значения ssd(j); j=1:M, и значения jmin, соответствующего условию ssd(jmin)=min(ssd(j)), j=1:M для каждого значения р, вычисляем текущие значения функции фазы ϕ_result(p)=-π/2+jmin*2π/M, p=1…N. Находим значения min(ϕ_result(p)), p=1:N, и значения pmin, соответствующее условию ϕ_result (pmin)=min(ϕ_result(p)), р=1:М, вычисляем полное значение фазы ϕ_res=ϕ_result(pmin), вычисляем результирующее значение фазы ϕ_out=ϕ_res или ϕ_out=π-ϕ_res, если abs(ϕ_res)>π/2. Техническим результатом при реализации заявленного способа является упрощение реализации способа и повышение точности определения фазы при зашумленности исходного сигнала. 5 ил.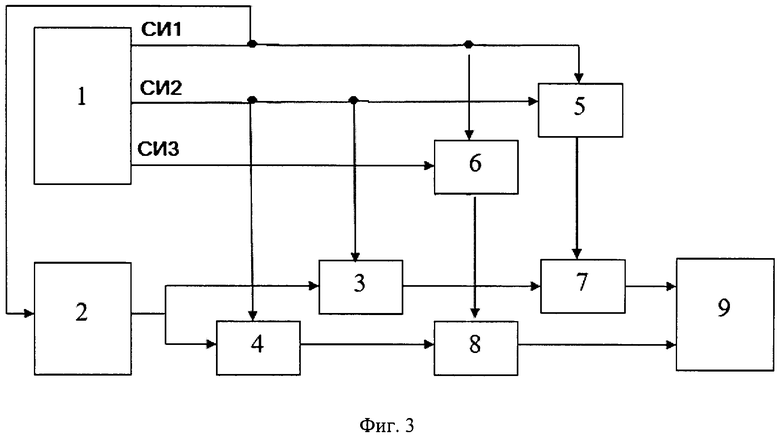
Цифровой способ измерения фазы гармонического сигнала, включающий дискретизацию аналогового сигнала и вычисление фазы сигнала по нескольким отсчетам, отличающийся тем, что производят регистрацию сигнала с помощью двух аналого-цифровых преобразователей, работающих на двух отличающихся частотах, получая при этом числовые массивы вторичных сигналов y1[i], i=1...K и y2[i], i=1...K-d, d>1, из которых формируют массив y[i]: y[i]=y1[i], если max(y1) - min(y1) > max(y2) - min(y2), или y[i]=y2[i], если max(y1) - min(y1) < max(y2) - min(y2), производят преобразование Фурье числового массива y[i] вторичного сигнала, после чего формируют массив частотного спектра вторичного сигнала в виде набора из K или K-d чисел, определяют номер элемента kp0 массива частотного спектра, которому соответствует максимальное значение, являющийся грубой оценкой количества периодов вторичного сигнала, создают M*N эталонных гармонических сигналов с количеством периодов kp2(р)=kp0-1+p*2/N и фазой ϕ2(j)=-π/2+j*2π/М, вычисляют суммы квадратов отклонений ssd(j), j=1...M вторичного исходного и эталонного сигнала для каждого значения p, находят значения jmin, соответствующего условию ssd(jmin)=min(ssd(j)), j=1:M, для каждого значения p, вычисляют текущие значения функции фазы ϕ_result(p)=-π/2+jmin*2π/M, p=1..N, находят значения pmin, соответствующего условию ϕ_result(pmin)=min(ϕ_result(p)), p=1:N, и вычисляют полное значение фазы ϕ_res=ϕ_result(pmin), вычисляют результирующее значения фазы ϕ_out=ϕ_res, если abs(ϕ_res)<π//2 или ϕ_res=π-ϕ_res, если abs(ϕ_res)>π//2.
| ИЗМЕРИТЕЛЬ РАЗНОСТИ ФАЗ РАДИОСИГНАЛОВ | 2009 |
|
RU2388001C1 |
| ЦИФРОВОЙ СПОСОБ ИЗМЕРЕНИЯ ФАЗОВОГО СДВИГА ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ | 2009 |
|
RU2419098C2 |
| RU 98117777 A, 27.06.2000 | |||
| Цифровое устройство для измерения фазы сигнала | 1989 |
|
SU1679405A1 |
| US 6820017 B1, 16.11.2004 | |||
| WO 2017044011 A1, 16.03.2017.. | |||
Авторы
Даты
2018-05-23—Публикация
2017-06-01—Подача