Изобретение относится к области автоматического управления и может быть использовано в самонастраивающихся системах автоматического управления электромеханическими, электротехническими, энергетическими, теплотехническими, механическими объектами и процессами, а также в информационно-измерительной технике для контроля указанных объектов и процессов.
Известен способ идентификации линейной динамической системы (Дейч A.M. Методы идентификации динамических объектов. - М.: Энергия, 1979. - 240 с. С. 50-58), в котором первоначально задают передаточную функцию системы простейшего априорного вида в дробно-рациональной форме, формируют входные гармонические сигналы заданной амплитуды и частоты, по отдельности подают их на вход линейной динамической системы, при воздействии каждого из входных гармонических сигналов измеряют входной сигнал, измеряют выходной сигнал при установившемся колебательном движении системы и определяют его амплитуду и фазу по отношению к входному сигналу, далее для каждого входного гармонического сигнала рассчитывают значения амплитудно-частотной характеристики и фазо-частотной характеристики системы, далее составляют систему уравнений в зависимости от коэффициентов передаточной функции априорного вида, частот входных гармонических сигналов, амплитудно-частотных характеристик, фазо-частотных характеристик, решают ее и идентифицируют коэффициенты передаточной функции, получают модель линейной динамической системы, далее рассчитывают переходную функцию модели, получают переходную функцию линейной динамической системы, затем задают критерий соответствия переходной функции модели и переходной функции линейной динамической системы, затем сравнивают переходные функции по заданному критерию и оценивают соответствие линейной динамической системы и модели, при существенном их отличии итеративно усложняют передаточную функцию априорного вида и повторяют процедуру идентификацию до получения удовлетворительного результата, причем количество входных гармонических сигналов задают в зависимости от числа коэффициентов передаточной функции априорного вида, усложнение передаточной функции априорного вида осуществляют путем увеличения числа ее коэффициентов, а удовлетворительный результат при оценке соответствия переходных функций считают достигнутым, когда дальнейшее усложнение передаточной функции априорного вида не приводит к повышению этого соответствия по заданному критерию.
Недостатком данного технического решения является сложность и громоздкость идентификации линейной динамической системы вследствие необходимости проведения большого объема вычислений при оценке соответствия указанной системы и ее модели, а также вследствие повторов идентификации до получения удовлетворительного результата.
Известен другой способ идентификации линейной динамической системы (Семенов А.Д., Артамонов Д.В., Брюхачев А.В. Идентификация объектов управления: Учебное пособие. - Пенза: Изд-во Пензенского Гос. Университета, 2003. - 211 с. С. 102-108), в котором первоначально задают передаточную функцию системы простейшего априорного вида в дробно-рациональной форме, формируют входные периодические сигналы прямоугольной формы заданной амплитуды и частоты, по отдельности подают их на вход линейной динамической системы, при воздействии каждого из входных гармонических сигналов измеряют входной сигнал и определяют его первую гармоническую составляющую, измеряют выходной сигнал при установившемся колебательном движении системы и определяют его первую гармоническую составляющую, далее определяют амплитуду и фазу первой гармонической составляющей выходного сигнала по отношению к первой гармонической составляющей входного сигнала, далее для первой гармонической составляющей каждого входного периодического сигнала рассчитывают значения амплитудной частотной характеристики и фазовой частотной характеристики системы, далее для каждого входного гармонического сигнала рассчитывают значения амплитудно-частотной характеристики и фазо-частотной характеристики системы, далее составляют систему уравнений в зависимости от коэффициентов передаточной функции априорного вида, частот первых гармонических составляющих входных сигналов, амплитудно-частотных характеристик, фазо-частотных характеристик, решают ее и идентифицируют коэффициенты передаточной функции, получают модель линейной динамической системы, далее рассчитывают переходную функцию модели, получают переходную функцию линейной динамической системы, затем задают критерий соответствия переходных функций модели и линейной динамической системы, затем сравнивают переходные функции по заданному критерию и оценивают соответствие линейной динамической системы и модели, при существенном их отличии итеративно усложняют передаточную функцию априорного вида и повторяют процедуру идентификацию до получения удовлетворительного результата, причем количество входных периодических сигналов прямоугольной формы задают в зависимости от числа коэффициентов передаточной функции априорного вида, усложнение передаточной функции априорного вида осуществляют путем увеличения числа ее коэффициентов, а удовлетворительный результат при оценке соответствия переходных функций считают достигнутым, когда дальнейшее усложнение передаточной функции априорного вида не приводит к повышению этого соответствия по заданному критерию.
Недостатком настоящего технического решения является сложность и громоздкость идентификации линейной динамической системы вследствие необходимости проведения большого объема вычислений при оценке соответствия указанной системы и ее модели, а также вследствие повторов идентификации до получения удовлетворительного результата.
Наиболее близким по технической сущности к заявляемому изобретению является способ идентификации линейной динамической системы (Вещественный интерполяционный метод в задачах автоматического управления: учебное пособие / А.С. Алексеев, А.А. Антропов, В.И. Гончаров, С.В. Замятин, В.А. Рудницкий; Томский политехнический университет. - Томск: Изд-во Томского политехнического университета, 2009. - 219 с. С. 160-163), в котором первоначально задают передаточную функцию системы простейшего априорного вида в дробно-рациональной форме, задают время, в зависимости от заданного времени формируют входной сигнал, подают его на вход линейной динамической системы, в зависимости от времени измеряют входной сигнал, в зависимости от времени измеряют выходной сигнал при неустановившемся движении системы, накапливают массив отсчетов входного сигнала и массив отсчетов выходного сигнала, измеряют длительность неустановившегося движения системы, затем задают узлы интерполяции и в зависимости от них задают весовые функции, далее вычисляют вещественные изображения входного сигнала в узлах интерполяции, затем вычисляют вещественные изображения выходного сигнала в узлах интерполяции, затем вычисляют значения передаточной функции априорного вида в узлах интерполяции, далее составляют систему уравнений в зависимости от коэффициентов передаточной функции априорного вида, узлов интерполяции, значений передаточной функции априорного вида в узлах интерполяции, решают ее и идентифицируют коэффициенты передаточной функции, получают модель линейной динамической системы, далее рассчитывают переходную функцию модели, получают переходную функцию линейной динамической системы, затем задают критерий соответствия переходных функций модели и линейной динамической системы, затем сравнивают переходные функции по заданному критерию и оценивают соответствие линейной динамической системы и модели, при существенном их отличии итеративно усложняют передаточную функцию априорного вида и повторяют процедуру идентификацию до получения удовлетворительного результата, причем входной сигнал задают таким образом, чтобы он в пределе стремился к установившемуся значению, усложнение передаточной функции априорного вида осуществляют путем увеличения числа ее коэффициентов, узлы интерполяции задают в зависимости от длительности неустановившегося движения линейной динамической системы и с равномерным распределением таким образом, чтобы весовые функции в пределах длительности неустановившегося движения стремились к нулю, их число задают в зависимости от числа коэффициентов передаточной функции априорного вида, а удовлетворительный результат при оценке соответствия переходных функций считают достигнутым, когда дальнейшее усложнение передаточной функции априорного вида не приводит к повышению этого соответствия по заданному критерию.
Недостатком данного технического решения является сложность и громоздкость идентификации линейной динамической системы вследствие необходимости проведения большого объема вычислений при оценке соответствия указанной системы и ее модели, а также вследствие повторов идентификации до получения удовлетворительного результата.
Технической задачей предлагаемого изобретения является снижение объема вычислений при получении модели линейной динамической системы.
Технический результат заключается в упрощении процесса идентификации линейной динамической системы.
Это достигается тем, что в известном способе идентификации линейной динамической системы, включающем первоначальное задание передаточной функции системы априорного вида в дробно-рациональной форме, задание времени, в зависимости от заданного времени формирование входного сигнала таким образом, чтобы он в пределе стремился к установившемуся значению, подачу входного сигнала на вход линейной динамической системы, в зависимости от времени измерение входного сигнала, в зависимости от времени измерение выходного сигнала при неустановившемся движении системы, накопление массива отсчетов входного сигнала и массива отсчетов выходного сигнала, измерение длительности неустановившегося движения системы, задание узлов интерполяции, количество которых выбрано в зависимости от числа коэффициентов передаточной функции априорного вида, при этом устанавливают нормированную длительность неустановившегося движения, затем массивы отсчетов входного сигнала и выходного сигнала нормируют по времени в зависимости от измеренной длительности неустановившегося движения и нормированной длительности неустановившегося движения системы, затем задают узлы интерполяции и в зависимости от них задают весовые функции, далее вычисляют нормированные вещественные изображения входного сигнала в узлах интерполяции, затем вычисляют нормированные вещественные изображения выходного сигнала в узлах интерполяции, затем вычисляют значения передаточной функции априорного вида в узлах интерполяции, далее составляют систему уравнений в зависимости от нормированных коэффициентов передаточной функции априорного вида, узлов интерполяции, значений передаточной функции априорного вида в узлах интерполяции, решают ее и идентифицируют коэффициенты нормированной передаточной функции, получают нормированную модель, затем задают критерий значимости коэффициентов нормированной модели, затем проверяют коэффициенты числителя нормированной модели по заданному критерию последовательно от старших к младшим до обнаружения первого значимого коэффициента, остальные коэффициенты числителя считают значимыми, незначимые коэффициенты числителя исключают из нормированной модели, проверяют коэффициенты знаменателя нормированной модели по заданному критерию последовательно от старших к младшим до обнаружения первого значимого коэффициента, остальные коэффициенты знаменателя считают значимыми, незначимые коэффициенты знаменателя исключают из нормированной модели, далее значимые коэффициенты нормированной модели приводят к действительным значениям в зависимости от измеренной длительности неустановившегося движения и нормированной длительности неустановившегося движения системы и получают модель линейной динамической системы, причем передаточную функцию априорного вида задают заведомо более сложной, чем линейная система, нормированную длительность неустановившегося движения устанавливают таким образом, чтобы базовая частота нормированной модели была равна единице, узлы интерполяции задают в зависимости от нормированной длительности неустановившегося движения линейной динамической системы и с равномерным распределением таким образом, чтобы весовые функции в пределах нормированной длительности неустановившегося движения стремились к нулю.
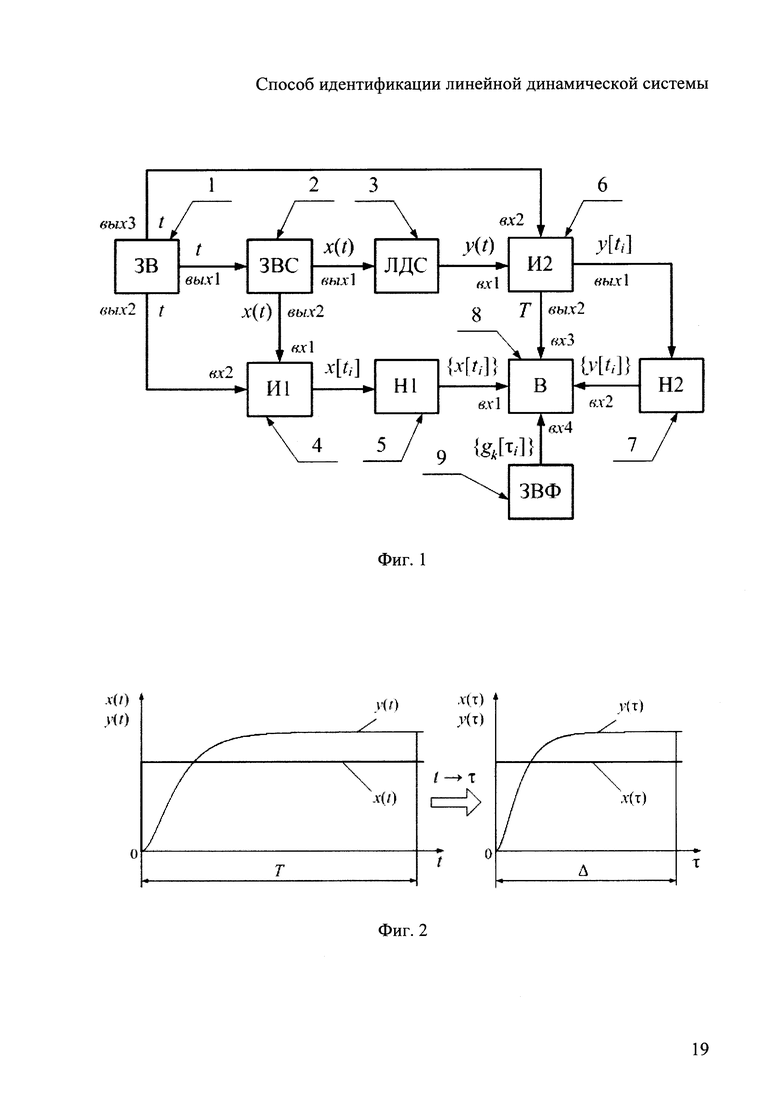
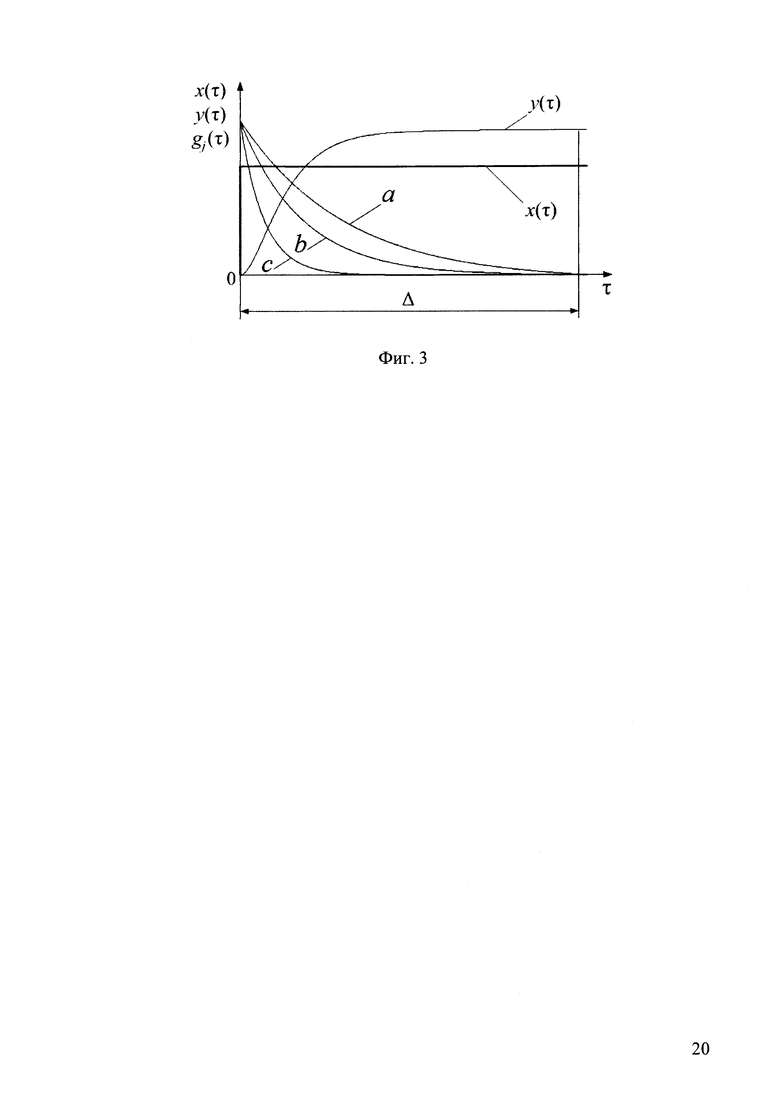
Сущность предлагаемого технического решения поясняется чертежами, где на фиг. 1 изображена функциональная схема устройства, реализующего предлагаемый способ идентификации линейной динамической системы; на фиг. 2 изображены временные диаграммы нормирования по времени массива входного сигнала и массива выходного сигнала в зависимости от измеренной длительности неустановившегося движения и нормированной длительности неустановившегося движения системы; на фиг. 3 изображены графики входного сигнала и выходного сигнала в зависимости от нормированного времени, а также графики весовых функций в зависимости от нормированного времени.
На графических изображениях приняты следующие обозначения: Т - измеренная длительность неустановившегося движения; t - заданное время; τ - нормированное время; ti - i-ый отсчет заданного времени; x(t) - входной сигнал линейной динамической системы в зависимости от заданного времени t; у(t) - выходной сигнал линейной динамической системы в зависимости от заданного времени t; х(τ) - входной сигнал линейной динамической системы в зависимости от нормированного времени τ; у(τ) - выходной сигнал линейной динамической системы в зависимости от нормированного времени τ; x[ti] - i-ый отсчет входного сигнала в зависимости от заданного времени t; у[ti] - i-ый отсчет выходного сигнала в зависимости от заданного времени t; {x[ti]} - массив отсчетов входного сигнала в зависимости от заданного времени t; {у[ti]} - массив отсчетов выходного сигнала в зависимости от заданного времени t; Δ - нормированная длительность неустановившегося движения; τi - i-ый нормированный отсчет нормированного времени; {gk[τi]} - массив отсчетов k-ой весовой функции в зависимости от нормированного времени τ.
Устройство, реализующее предлагаемый способ идентификации линейной динамической системы, содержит задатчик времени (ЗВ) 1, первый выход которого соединен со входом задатчика входного сигнала (ЗВС) 2, первый выход которого соединен со входом линейной динамической системы (ЛДС) 3. Второй выход задатчика входного сигнала 2 соединен с первым входом первого измерителя (И1) 4, второй вход которого соединен со вторым выходом задатчика времени 1. Выход первого измерителя 4 соединен со входом первого накопителя (H1) 5, выход линейной динамической системы 3 соединен с первым входом второго измерителя (И2) 6, второй вход которого соединен с третьим выходом задатчика времени 1. Первый выход второго измерителя 6 соединен со входом второго накопителя (Н2) 7, выход первого накопителя 5 соединен с первым входом вычислителя 8, второй вход которого соединен с выходом второго накопителя 7. Третий вход вычислителя 8 соединен со вторым выходом второго измерителя 6, а четвертый его вход соединен с выходом задатчика весовых функций (ЗВФ) 9.
Линейная динамическая система 3 может иметь любую физическую реализацию, например, электромеханическую, электротехническую, энергетическую, теплотехническую, механическую. Задатчик входного сигнала 2 может быть любого типа, допустимого для соединения с линейной динамической системой 3. Первый 4 и второй 6 измерители реализованы на основе измерительных устройств любого типа, допустимого для соединения с линейной динамической системой 3. Задатчик времени 1, первый накопитель 5, второй накопитель 7, вычислитель 8 и задатчик весовых функций 9 реализованы на основе программно-аппаратных средств вычислительной техники.
Реализация указанным устройством предлагаемого способа идентификации линейной динамической системы осуществляется следующим образом.
Задатчик времени 1 задает время t. В зависимости от времени t задатчик входного сигнала 2 формирует входной сигнал x(t), который в пределе стремится к установившемуся значению. Входной сигнал x(t) подают на вход линейной динамической системы 3. Первый измеритель 4 измеряет входной сигнал x(t) в зависимости от заданного времени t в виде дискретных отсчетов x[ti], которые накапливает первый накопитель 5 в виде массива {x[ti]}. Второй измеритель 6 измеряет выходной сигнал у(t) линейной динамической системы 3 в зависимости от времени t в виде дискретных отсчетов у[ti], которые накапливает второй накопитель 7 в виде массива {у[ti]}.
В вычислительном алгоритме, который выполняет вычислитель 8, задают передаточную функцию W1(p) априорного вида в дробно-рациональной форме:
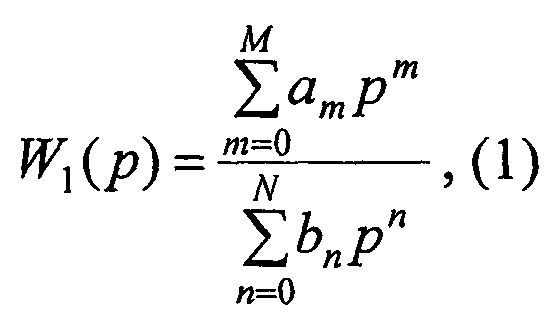
где М - порядок полинома числителя передаточной функции априорного вида; N - порядок полинома знаменателя передаточной функции априорного вида, причем M<N; р - оператор Лапласа; {am} - коэффициенты числителя передаточной функции априорного вида, причем 0≤m≤М; {bn} - коэффициенты знаменателя передаточной функции априорного вида, причем 0≤n≤N.
В вычислительных алгоритмах, которые выполняют вычислитель 8 и задатчик весовых функций 9 задают нормированную длительность неустановившегося движения Δ таким образом, чтобы базовая частота нормированной модели была равна единице Ωнм=1:
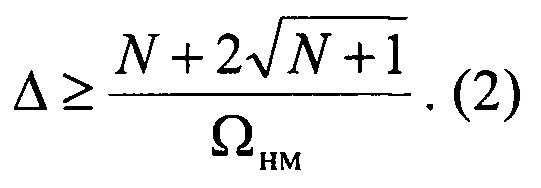
Вычислитель 8 осуществляет нормирование массивов отсчетов входного сигнала {x[ti]} и выходного сигнала {у[ti]} по времени в зависимости от измеренной длительности неустановившегося движения Т и нормированной длительности неустановившегося движения системы Δ путем замены отсчетов времени ti на отсчеты нормированного времени τi следующим образом:
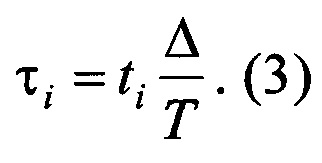
Таким образом получают нормированные массивы отсчетов входного сигнала {х[τi]} и выходного сигнала {у[τi]} в зависимости от нормированного времени τ. Графики, показанные на фиг. 2, иллюстрируют указанное нормирование. На фиг. 2 график выходного сигнала у(t) и график входного сигнала x(t) построены в зависимости от заданного времени t по массивам отсчетов {у[ti]} и {x[ti]} соответственно, а график выходного сигнала у(τ) и график входного сигнала х(τ) построены в зависимости от нормированного времени τ по массивам отсчетов {у[τi]} и {х[τi]} соответственно.
Задатчик входного сигнала 2 формирует входной сигнал x(t) таким образом, чтобы он в пределе стремился к установившемуся значению:
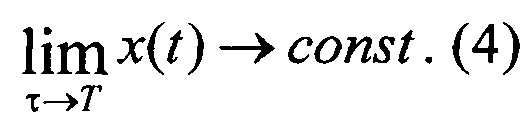
Задатчик весовых функций 9 задает узлы интерполяции {δk} в зависимости от нормированной длительности Δ неустановившегося движения линейной динамической системы и с равномерным распределением:
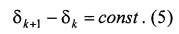
В зависимости от узлов интерполяции задатчик весовых функций 9 задает весовые функции {gk(τ)} по следующему соотношению:
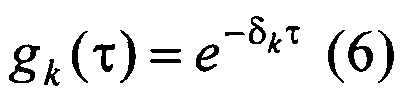
таким образом, чтобы в пределах нормированной длительности Δ неустановившегося движения они стремились к нулю:
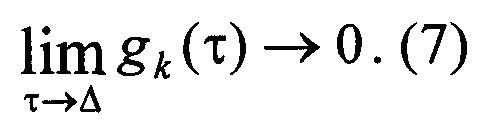
На фиг. 3 показаны графики выходного сигнала у(τ) и входного сигнала х(τ) в зависимости от нормированного времени τ, а также графики весовых функций (gk(τ)} (графики а, b, с) в зависимости от нормированного времени τ, причем график а соответствует весовой функции с минимальным по величине узлом интерполяции.
Число K узлов интерполяции {δk} зависит от числа коэффициентов передаточной функции априорного вида (1), если принять b0=1:
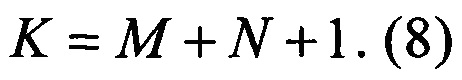
Далее вычислитель 8 вычисляет нормированные вещественные изображения входного сигнала в узлах интерполяции:
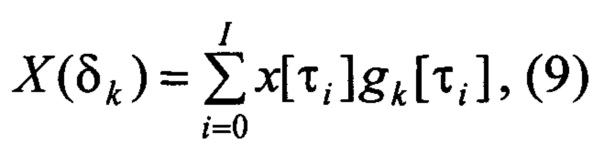
где I - число отсчетов входного сигнала, равное числу отсчетов выходного сигнала, числу элементов массива отсчетов входного сигнала, числу элементов массива отсчетов выходного сигнала, а также числу отсчетов времени, причем 0≤k≤K.
Затем вычислитель 8 вычисляет нормированные вещественные изображения выходного сигнала в узлах интерполяции:
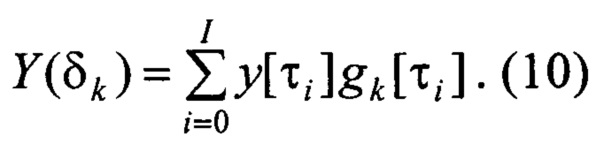
В пределах измеренной длительности неустановившегося движения Т рекомендуется задавать I=200÷250.
Далее вычислитель 8 вычисляет значения передаточной функции априорного вида в узлах интерполяции:
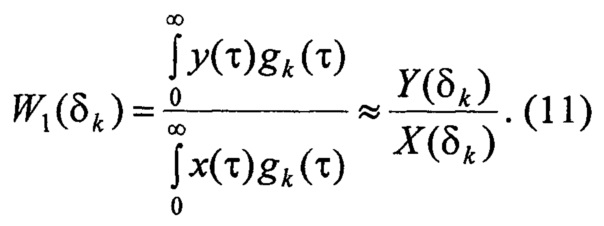
Далее вычислитель 8 осуществляет составление системы из K линейных алгебраических уравнений в зависимости от нормированных коэффициентов передаточной функции априорного вида {aτm} и {bτn}, узлов интерполяции {δk}, значений передаточной функции априорного вида {W1(δk)} в узлах интерполяции и решает ее:
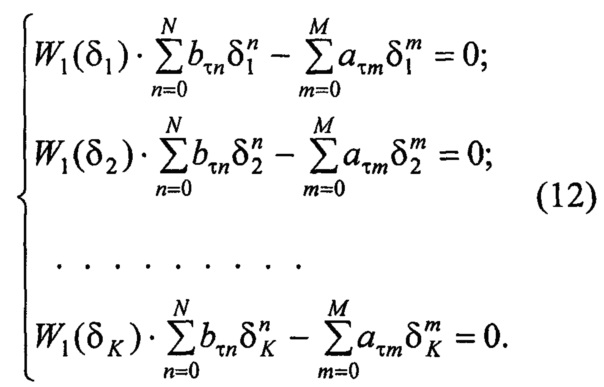
При решении системы уравнений (12) вычислитель 8 идентифицирует коэффициенты нормированной передаточной функции {аτm} и {bτn}.
Далее вычислитель 8 получает нормированную модель, передаточная функция W2(p) которой имеет следующий вид в дробно-рациональной форме:
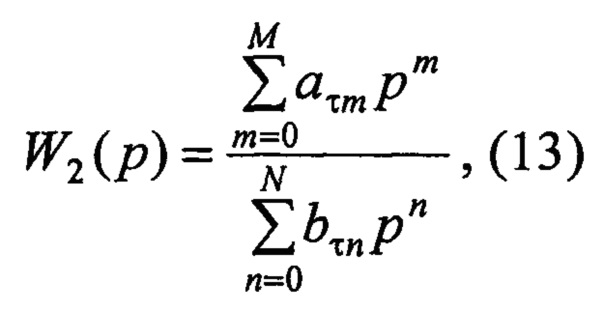
где {аτm} - коэффициенты числителя нормированной модели; {bτn} - коэффициенты знаменателя нормированной модели, причем.
Коэффициенты {аτm} и {bτn} нормированной модели (13), идентифицированные при решении системы уравнений (12), как и коэффициенты модели в способе идентификации линейной динамической системы по прототипу, могут быть значимыми или незначимыми. Значимые коэффициенты отражают свойства линейной динамической системы. Незначимые коэффициенты появляются при решении системы уравнений (12) вследствие неточности измерения сигналов, дискретности их представления в виде массива отсчетов, а также из-за неточности численных методов расчета.
Затем по критерию значимости коэффициентов нормированной модели, заданному в вычислительном алгоритме вычислителя 8, он осуществляет проверку коэффициентов числителя {аτm} нормированной модели последовательно от старших к младшим до обнаружения первого значимого коэффициента:
если 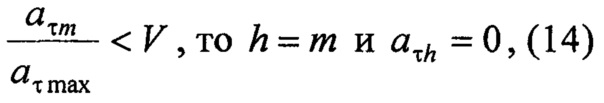
где аτmax - максимальный по величине коэффициент числителя нормированной модели; V - коэффициент критерия значимости коэффициентов.
если 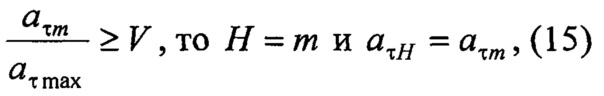
где bτmax - максимальный по величине коэффициент знаменателя нормированной модели.
Остальные коэффициенты числителя считают значимыми:
если 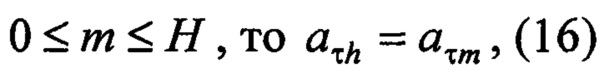
где {aτh} - значимые коэффициенты числителя нормированной модели, причем 0≤h≤H.
Все незначимые коэффициенты числителя исключают из нормированной модели. В результате вычислитель 8 получает значимые коэффициенты {aτh} числителя нормированной модели. При этом 0≤h≤H и Н≤М.
Затем по заданному критерию значимости коэффициентов нормированной модели вычислитель 8 осуществляет проверку коэффициентов знаменателя {bτn} нормированной модели последовательно от старших к младшим до обнаружения первого значимого коэффициента:
если 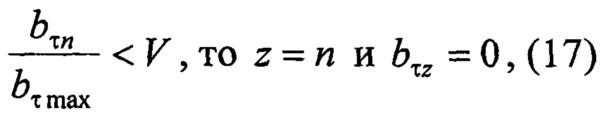
если 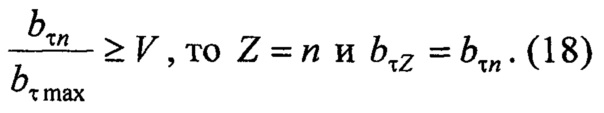
Остальные коэффициенты числителя считают значимыми:
если 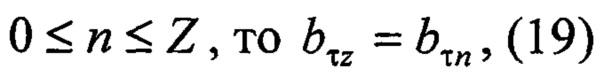
где {bτz} - значимые коэффициенты знаменателя нормированной модели, причем 0≤z≤Z.
Все незначимые коэффициенты знаменателя исключают из нормированной модели. В результате вычислитель 8 получает значимые коэффициенты {bτz} знаменателя нормированной модели. При этом 0≤z≤Z и Z≤N.
Далее значимые коэффициенты нормированной модели {аτh} и {bτz} вычислитель 8 приводит к действительным значениям в зависимости от измеренной длительности Т неустановившегося движения и установленной нормированной длительности Δ неустановившегося движения системы:
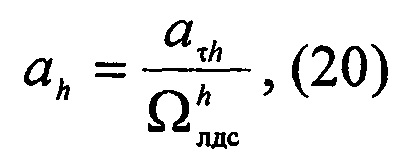
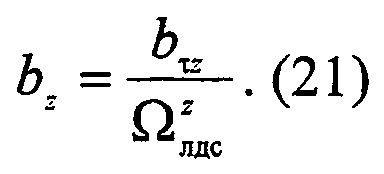
При этом базовую частоту Ωлдс линейной динамической системы определяют по следующему соотношению:
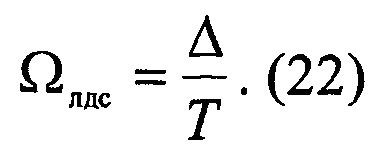
В результате получают модель линейной динамической системы, передаточная функция W3(p) которой в дробно-рациональной форме имеет следующий вид:
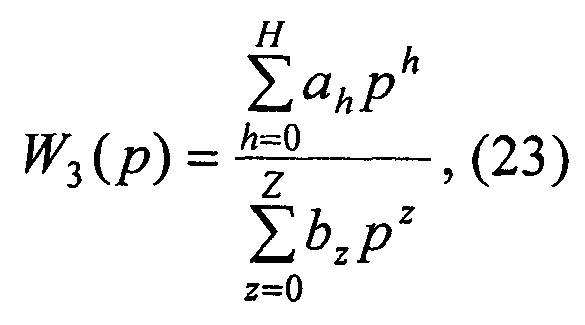
где Н - порядок полинома числителя модели; Z - порядок полинома знаменателя модели, причем H<Z. {ah} - коэффициенты числителя модели, причем 0≤h≤H; {bz} - коэффициенты знаменателя модели, причем 0≤z≤Z.
Достижение заявленного технического результата достигается следующим образом. Нормирование массивов отсчетов входного сигнала и выходного сигнала по времени в зависимости от измеренной длительности Т неустановившегося движения и нормированной длительности А неустановившегося движения системы позволяет получить нормированную модель (13), для коэффициентов которой устанавливают критерий значимости - их величину. Это, в отличие от способа по прототипу, позволяет осуществить оценку значимости ее коэффициентов путем сравнения их величин по соотношениям (14), (15), (16), (17), (18), (19). При этом упрощение процесса идентификации линейной динамической системы по сравнению со способом по прототипу достигается тем, что не требуется рассчитывать переходную функцию модели и сопоставлять ее с переходной функцией системы. Возможность установить в качестве критерия значимости коэффициентов нормированной модели их величину обусловлена тем, что нормированную длительность Δ неустановившегося движения задают таким образом, чтобы базовая частота нормированной модели была равна единице Ωнм=1. В этом случае коэффициенты нормированной модели, имеющие наибольшее влияние на динамику (перерегулирование и колебательность) являются действительными числами примерно одного порядка.
Также, при осуществлении предложенного способа идентификации линейной динамической системы по сравнению со способом идентификации линейной динамической системы по прототипу не требуется итеративно усложнять передаточную функцию системы априорного вида при несоответствии указанных переходных функций и повторять процедуру идентификации до получения удовлетворительного результата. Это также упрощает процесс идентификации линейной динамической системы.
Кроме того, упрощение процесса идентификации при осуществлении предложенного способа по сравнению со способом идентификации линейной динамической системы по прототипу достигается тем, что для каждой длительности Т неустановившегося движения не требуется задавать соответствующие ей наборы узлов интерполяции. Вместо этого используют единый набор узлов интерполяции {δk} и, следовательно, единый набор весовых функций (gk(τ)} независимо от измеренной длительности неустановившегося движения Т линейной динамической системы. При этом узлы интерполяции задают в зависимости от нормированной длительности неустановившегося движения Δ, которую задают независимо от измеренной длительности Т неустановившегося движения линейной динамической системы.
Использование изобретения позволяет упростить процесс идентификации линейной динамической системы за счет снижения объема вычислений при получении модели линейной динамической системы, в том числе в самонастраивающихся системах автоматического управления электромеханическими, электротехническими, энергетическими, теплотехническими, механическими объектами и процессами, а также в информационно-измерительной технике для контроля указанных объектов и процессов.
Изобретение относится к автоматическому управлению. Способ идентификации линейной динамической системы включает первоначальное задание передаточной функции системы априорного вида в дробно-рациональной форме. Устанавливают нормированную длительность неустановившегося движения, затем массивы отсчетов входного и выходного сигналов нормируют по времени в зависимости от измеренной длительности неустановившегося движения системы. Задают критерий значимости коэффициентов нормированной модели, затем проверяют коэффициенты числителя и знаменателя модели по заданному критерию последовательно от старших к младшим до обнаружения первого значимого коэффициента. Незначимые коэффициенты числителя и знаменателя исключают из модели. Значимые коэффициенты модели приводят к действительным значениям в зависимости от измеренной длительности неустановившегося движения и нормированной длительности неустановившегося движения системы и получают модель линейной динамической системы. Упрощается идентификация системы. 3 з.п. ф-лы, 3 ил.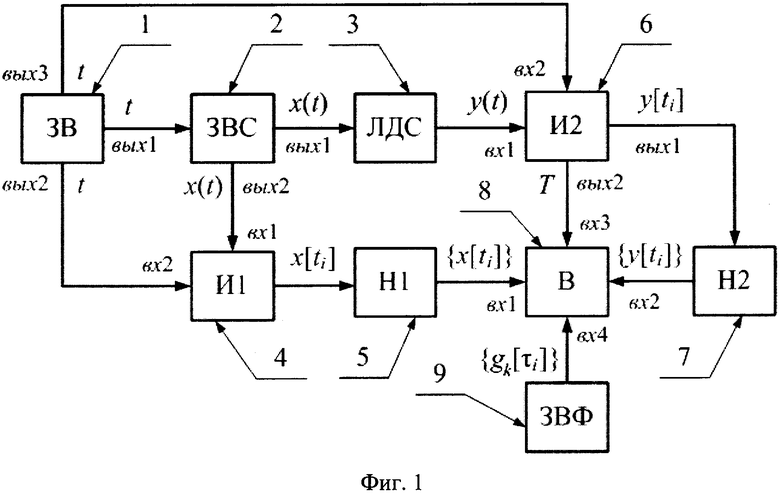
1. Способ идентификации линейной динамической системы, включающий первоначальное задание передаточной функции системы априорного вида в дробно-рациональной форме, задание времени, в зависимости от заданного времени формирование входного сигнала таким образом, чтобы он в пределе стремился к установившемуся значению, подачу входного сигнала на вход линейной динамической системы, в зависимости от времени измерение входного сигнала, в зависимости от времени измерение выходного сигнала при неустановившемся движении системы, накопление массива отсчетов входного сигнала и массива отсчетов выходного сигнала, измерение длительности неустановившегося движения системы, задание узлов интерполяции, количество которых выбрано в зависимости от числа коэффициентов передаточной функции априорного вида, отличающийся тем, что устанавливают нормированную длительность неустановившегося движения, затем массивы отсчетов входного сигнала и выходного сигнала нормируют по времени в зависимости от измеренной длительности неустановившегося движения и нормированной длительности неустановившегося движения системы, затем задают узлы интерполяции и в зависимости от них задают весовые функции, далее вычисляют нормированные вещественные изображения входного сигнала в узлах интерполяции, затем вычисляют нормированные вещественные изображения выходного сигнала в узлах интерполяции, затем вычисляют значения передаточной функции априорного вида в узлах интерполяции, далее составляют систему уравнений в зависимости от нормированных коэффициентов передаточной функции априорного вида, узлов интерполяции, значений передаточной функции априорного вида в узлах интерполяции, решают ее и идентифицируют коэффициенты нормированной передаточной функции, получают нормированную модель, затем задают критерий значимости коэффициентов нормированной модели, затем проверяют коэффициенты числителя нормированной модели по заданному критерию последовательно от старших к младшим до обнаружения первого значимого коэффициента, остальные коэффициенты числителя считают значимыми, незначимые коэффициенты числителя исключают из нормированной модели, проверяют коэффициенты знаменателя нормированной модели по заданному критерию последовательно от старших к младшим до обнаружения первого значимого коэффициента, остальные коэффициенты знаменателя считают значимыми, незначимые коэффициенты знаменателя исключают из нормированной модели, далее значимые коэффициенты нормированной модели приводят к действительным значениям в зависимости от измеренной длительности неустановившегося движения и нормированной длительности неустановившегося движения системы и получают модель линейной динамической системы.
2. Способ по п. 1, отличающийся тем, что передаточную функцию априорного вида задают заведомо более сложной, чем линейная система.
3. Способ по п. 1, отличающийся тем, что нормированную длительность неустановившегося движения устанавливают таким образом, чтобы базовая частота нормированной модели была равна единице.
4. Способ по п. 1, отличающийся тем, что узлы интерполяции задают в зависимости от нормированной длительности неустановившегося движения линейной динамической системы и с равномерным распределением таким образом, чтобы весовые функции в пределах нормированной длительности неустановившегося движения стремились к нулю.
| WO 2014099737 A1, 26.06.2014 | |||
| WO 2014099716 A1, 26.06.2014 | |||
| УСТРОЙСТВО И СПОСОБ ДЛЯ ПРЕОБРАЗОВАНИЯ ДИНАМИЧЕСКОГО ДИАПАЗОНА ИЗОБРАЖЕНИЙ | 2012 |
|
RU2643485C2 |
| АДАПТИВНАЯ СИСТЕМА УПРАВЛЕНИЯ С ИДЕНТИФИКАТОРОМ И НЕЯВНОЙ ЭТАЛОННОЙ МОДЕЛЬЮ ПРИ ВРЕМЕННЫХ ЗАДЕРЖКАХ ИНФОРМАЦИИ В СИСТЕМЕ УПРАВЛЕНИЯ | 2001 |
|
RU2192031C1 |
| СПОСОБ ДИАГНОСТИРОВАНИЯ ДИНАМИЧЕСКИХ ОБЪЕКТОВ | 1999 |
|
RU2153188C1 |
Авторы
Даты
2018-12-18—Публикация
2018-03-28—Подача