Изобретение относится к области автоматики, а именно к измерительной технике и автоматическому регулированию, и может быть использовано для определения коэффициентов передаточных функций динамических объектов сложных структур, например при проектировании и настройке систем регулирования летательных аппаратов, газотурбинным двигателем и т.д.
Известны способы идентификации линейных динамических объектов, основанных на формировании спектральной плотности входного сигнала исследуемого объекта и взаимной спектральной плотности входного и выходного сигналов исследуемого объекта [Пугачев В.С. Теория случайных функций и ее применение к задачам автоматического управления, М. 1957, с. 395-403, 592-597].
Основным недостатком известных спектральных методов идентификации является некорректность их применения для идентификации динамических объектов в тех случаях, когда наблюдаемые сигналы наряду со случайными составляющими содержат неслучайные гармонические составляющие, чем обычно характеризуются сигналы, зафиксированные в режиме нормальной эксплуатации. В этом случае сигналы спектральных плотностей характеризуются наличием узких пиков и нулевых провалов, и получение статистических оценок спектральных плотностей по оценкам сигнала корреляционной функции на конечном интервале наблюдений путем непосредственного применения преобразования Фурье не дает желаемых результатов, так как в этом случае дисперсии оценок сигналов спектральных плотностей имеют тот же порядок, что и сами спектральные плотности, что приводит к большим погрешностям [Пугачев В.С. Теория случайных функций и ее применение к задачам автоматического управления, М. 1957, с. 395-403, 592-597]. Кроме того, указанные способы весьма критичны к помехам, присутствующим одновременно во входном и выходном сигналах.
Известен также способ [Авторское свидетельство СССР N 696416, кл. G 05 B 23/00, 1979 г.] определения коэффициентов передаточных функций динамических объектов путем подачи на вход объекта времястепенных пробных сигналов в виде последовательности одиночных импульсов. По этому способу можно определить коэффициенты передаточных функций более высокого порядка.
Однако реализация этого способа требует значительных временных затрат, что связано с экспериментальным определением всех коэффициентов αk времястепенных пробных сигналов αВХ= αktk и с необходимостью последовательной настройки модели объекта. Кроме того, на точность определения коэффициентов передаточных функций влияет настройки модели.
Наиболее близким к предлагаемому изобретению является способ [Авторское свидетельство СССР N 661511, кл. G 05 B 23/00, 1979 г. (прототип)] определения коэффициентов передаточных функций линейных динамических объектов путем подачи тестового сигнала, стремящегося к установившемуся значению, на вход линейного динамического объекта и интегрирования его выходного сигнала, измерения интервалов времени t1 и t2 от момента подачи тестового сигнала величины A до момента достижения уровней J1 и J2 соответственно и определения постоянной времени
и коэффициента передачи линейного динамического объекта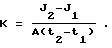
Этот способ не пригоден для определения коэффициентов передаточных функций объектов второго и более высоких порядков.
Задачей, на решение которой направлено заявляемое изобретение, является повышение точности и быстродействия при определении коэффициентов передаточных функций, за счет вычисления интегральных оценок качества и использования их взаимосвязи с коэффициентами передаточных функций линейных, асимптотически устойчивых динамических объектов.
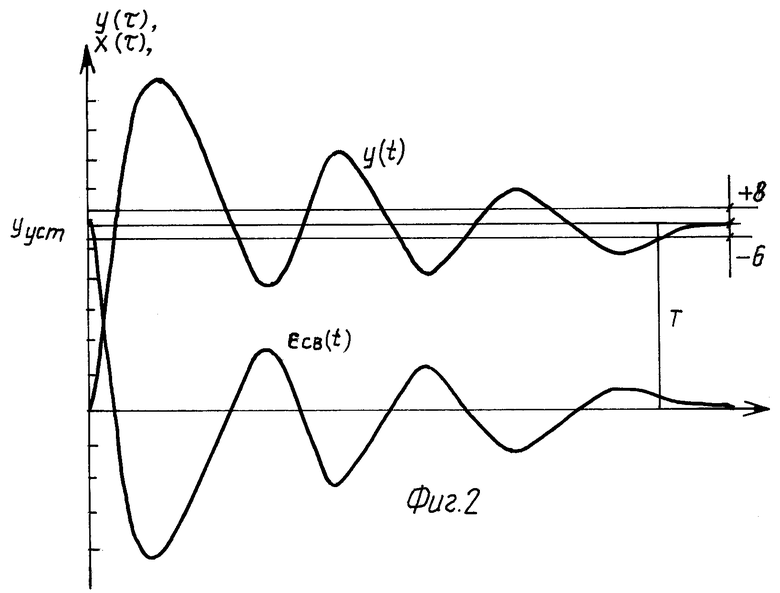
Поставленная задача решается тем, что в способе определения коэффициентов передаточных функций линейных динамических объектов путем подачи на вход объекта исследования ступенчатого тестового сигнала, измеряют длительность T переходного процесса на выходе исследуемого объекта, момент завершения которого определяется по признаку
|yуст-y(t)|≅ Δд ,
где y(t) - значение выходного сигнала исследуемого объекта, yуст - установившееся значение выходного сигнала, Δд - допустимая погрешность завершения свободных колебаний, затем для объектов с передаточной функцией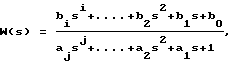
вычисляют линейные интегральные оценки качества, которые можно записать в виде
где k=n+m-l
m - порядок числителя;
n - порядок знаменителя;
εСВ (t)=yуст-y(t),
и по ним, используя взаимосвязь интегральных оценок качества и коэффициентов разложения 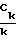 передаточной функции в степенной ряд
передаточной функции в степенной ряд ,
,
вычисляют коэффициенты di полинома числителя и aj полинома знаменателя передаточной функции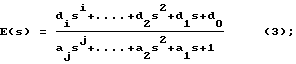
где i=m-l,j=n,
путем решения полученной системы линейных алгебраических уравнений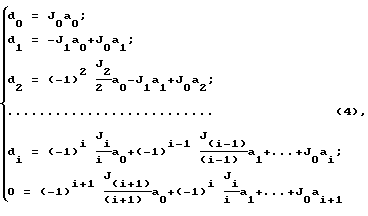
а коэффициенты bi вычисляются по формуле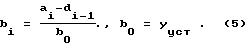
При bi= 0 процесс вычислений завершается. При этом теоретически не существует ограничения на порядок числителя и знаменателя исследуемых объектов. Кроме того, время эксперимента равно T, что позволяет сэкономить время определения коэффициентов для объектов с высоким порядком.
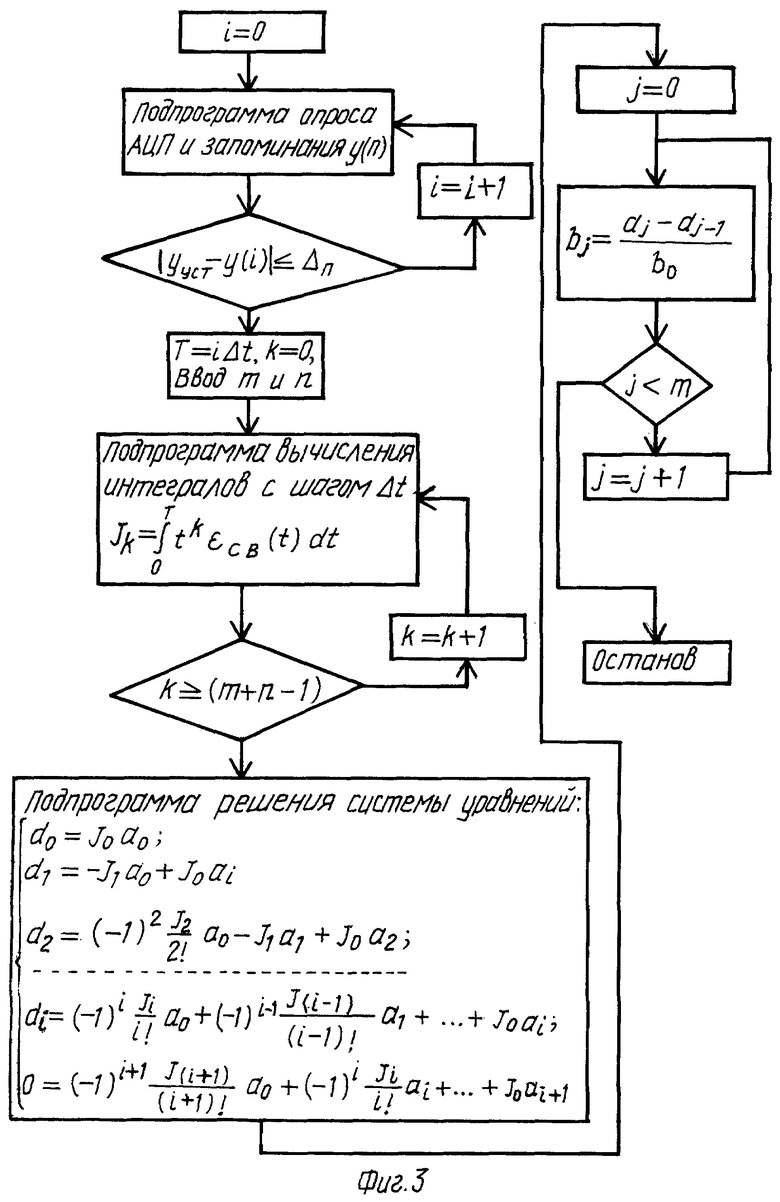
На фиг. 1 приведена структурная схема устройства реализующего предлагаемый способ; на фиг. 2 - иллюстрация процессов определения коэффициентов; на фиг. 3 - блок-схема программы вычислений коэффициентов, реализуемых ЭВМ.
Устройство содержит формирователь входного сигнала 1, исследуемый объект 2, аналого-цифровой преобразователь 3, ЭВМ 4.
Как видно на фиг. 2 и фиг. 3 при определении коэффициентов на временном интервале определяется время завершения переходного процесса T и через равные промежутки времени Δ t, зависящее от частоты квантования, в память ЭВМ заносятся значения отклика объекта y(t) на воздействие единичного ступенчатого сигнала. Далее осуществляется операция интегрирования, вычисляется интеграл и определяется интегральная оценка качества
Затем по формуле (5) и системе уравнений (4) вычисляют коэффициенты bi и aj.
Рассмотрим реализацию данного способа на примере объекта с передаточной функцией вида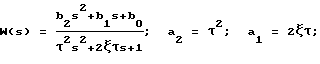
где τ - постоянная времени;
ξ - коэффициент демпфирования.
По переходной функции вычислены линейные интегральные оценки качества Jо= 1,8; J1=2,04; J2=2,976; J3=-74,037; J4=-690,834 при изменении t от 0 до 30 с. Определим изображение свободного движения объекта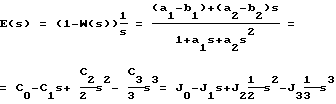
a1-b1=J0a0=1,8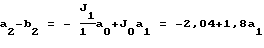
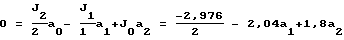
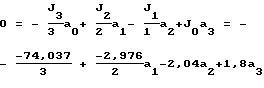
a1-b1=1,8
a2-b2=-2,04+1,8a1
2,04a1-1,8a2=-1,488
1,488a1+2,04a2=12,339
a1=2,803
a2=4,004
b1=1,003
b2=0,9986.
Моделировался объект с передаточной функцией  .
.
Относительная погрешность определения коэффициентов передаточной функции мала.
Таким образом предлагаемый способ позволяет вычислять его коэффициенты с большей точностью и быстродействием.
Изобретение относится к области автоматики, а именно к измерительной технике и автоматическому регулированию. Технический результат заключается в повышении точности и быстродействия. Сущность способа заключается в том, что в момент завершения переходного процесса измеряют длительность переходного процесса Т, вычисляют интегральные оценки качества и по ним, используя взаимосвязь интегральных оценок качества и коэффициентов разложения передаточной функции в степенной ряд, вычисляют коэффициенты аi и bj полиномов числителя и знаменателя передаточной функции. 3 ил.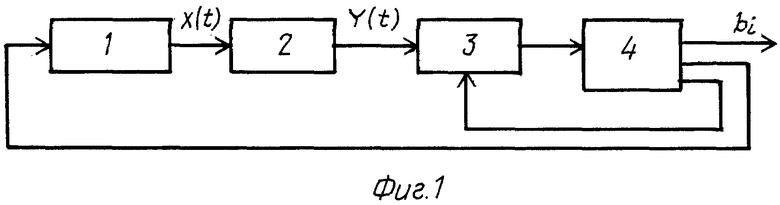
Способ определения коэффициентов передаточных функций линейных динамических объектов путем подачи на вход объекта исследования ступенчатого тестового сигнала, отличающийся тем, что измеряют длительность Т переходного процесса на выходе исследуемого объекта, момент завершения которого определяется по признаку
|yуст - y(t)| ≅ Δд,
где y(t) - значение выходного сигнала исследуемого объекта;
yуст - установившееся значение выходного сигнала;
Δд - допустимая погрешность завершения свободных колебаний,
затем, для объектов с передаточной функцией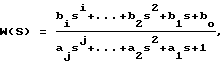
вычисляют линейные интегральные оценки качества, которые можно записать в виде:
где k = n + m - 1;
m - порядок числителя;
n - порядок знаменателя;
εсв(t) = yуст - y(t),
и по ним, используя взаимосвязь интегральных оценок качества и коэффициентов разложения  передаточной функции в степенной ряд
передаточной функции в степенной ряд
вычисляют коэффициенты di полинома числителя и aj полинома знаменателя передаточной функции
где i = m - I, j = n,
путем решения полученной системы линейных алгебраических уравнений: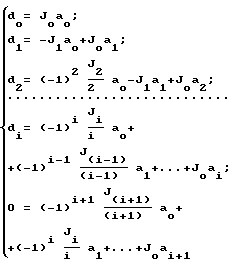
а коэффициенты bi вычисляют по формуле:
| Способ определения параметров передаточных функций линейных динамических объектов | 1977 |
|
SU661511A1 |
| Способ определения коэффициентов передаточных функций систем регулирования | 1975 |
|
SU696416A1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ ОБЪЕКТОВ И ЗАДАТЧИК ПРОБНЫХ СИГНАЛОВ ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1997 |
|
RU2131139C1 |
| ФИЛЬТР ДЛЯ ОЧИСТКИ ВОЗДУХА В ТРАНСПОРТНЫХ СРЕДСТВАХ | 2008 |
|
RU2461469C2 |
| GB 1207187 A, 30.09.1970. | |||
Авторы
Даты
2001-05-10—Публикация
1999-07-06—Подача