Изобретение относится к области космической техники и может быть использовано в бесплатформенных инерциальных системах ориентации (БИСО) для орбитальных космических аппаратов (КА), блок чувствительных элементов (БЧЭ) которых содержит гироинерциальные измерители, например, электростатические гироскопы (ЭСГ).
Известен способ калибровки гироинерциальных измерителей (датчиков угловой скорости) бесплатформенной инерциальной системы ориентации для орбитальных КА [1] в условиях последовательных разворотов КА вокруг его осей рыскания, тангажа и крена с визированием и фиксацией параметров заданных астроориентиров с помощью астровизирующего устройства (АВУ) перед началом и после окончания каждого из калибровочных разворотов; расчета по результатам измерений коэффициентов примененной модели погрешности гироинерциальных измерителей и их корректировки.
Недостатком способа является низкая точность калибровки. Указанный недостаток обусловлен нестабильностью масштабных коэффициентов гироинерциальных измерителей во времени, погрешностями ориентации осей БЧЭ относительно корпусных осей КА, погрешностями ориентации корпусных осей АВУ относительно корпусных осей КА.
Известен также способ калибровки гироинерциальных измерителей (электростатических гироскопов) бесплатформенной инерциальной системы ориентации для орбитальных КА [2], который принят за прототип. При реализации способа калибруют составляющие суммарного вектора погрешностей углов привязки положения осей блока БЧЭ БИСО на ЭСГ, относительно опорных осей АВУ. Для этого осуществляют последовательные калибровочные развороты КА вокруг осей, связанных с корпусом КА, с визированием и фиксацией параметров заданных астроориентиров с помощью АВУ перед началом и после окончания каждого из разворотов. Осуществляют расчет погрешностей. Для расчета используют данные измерений полученные:
1) от АВУ:
- значения эталонного кватерниона 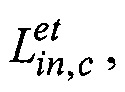 характеризующего угловое положение корпусных осей xcyczc КА относительно инерциальной системы координат, моделируемой в алгоритмах АВУ;
характеризующего угловое положение корпусных осей xcyczc КА относительно инерциальной системы координат, моделируемой в алгоритмах АВУ;
2) от БИСО:
- значения приборного кватерниона 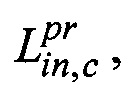 характеризующего угловое положение корпусных осей xcyczc КА относительно инерциальной системы координат in1in2in3, моделируемой в алгоритмах БИСО и периодически корректируемой по данным АВУ.
характеризующего угловое положение корпусных осей xcyczc КА относительно инерциальной системы координат in1in2in3, моделируемой в алгоритмах БИСО и периодически корректируемой по данным АВУ.
Погрешности БИСО на ЭСГ с коррекцией по данным АВУ содержат погрешности привязки, как углового положения корпусных осей БЧЭ БИСО относительно корпусных осей КА, так и положения корпусных осей АВУ относительно корпусных осей КА. Для оценивания погрешностей формируют вектор измерений:
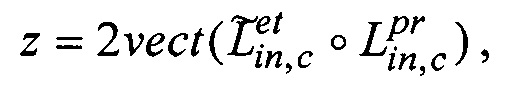
где 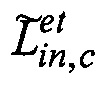 - кватернион, сопряженный по отношению к кватерниону
- кватернион, сопряженный по отношению к кватерниону 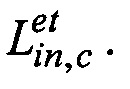
Производят расчет погрешностей с использованием метода наименьших квадратов.
По результатам расчета корректируют коэффициенты примененной модели погрешности.
Недостатком способа является низкая точность калибровки погрешностей БЧЭ БИСО Указанный недостаток обусловлен тем, что:
- в процессе калибровки не учитывается дрейф ЭСГ;
- не учитываются погрешности углов привязки положения измерительных осей каждого ЭСГ относительно корпуса БЧЭ БИСО, что приводит к появлению составляющей погрешности от неортогональности измерительных осей БЧЭ.
В предлагаемом изобретении решается техническая проблема - совершенствование способа калибровки погрешностей ЭСГ БИСО в условиях орбитального КА.
Достигаемый технический результат - повышение точности калибровки погрешностей ЭСГ БИСО.
Поставленная задача изобретения решается тем, что в известном способе калибровки погрешностей ЭСГ БИСО в условиях орбитального КА, заключающегося в последовательном вращении КА вокруг осей, связанных с его корпусом; вычислении углового положения КА относительно инерциальных осей по данным измерений АВУ; вычислении на основе априорных значений коэффициентов модели дрейфа калибруемого гироскопа, расчетных значений направляющих косинусов орта его кинетического момента в инерциальных осях; формировании по данным списывающих устройств гироскопа измеренных значений направляющих косинусов орта его кинетического момента в корпусных осях, вычислении оценок ухода гироскопа в инерциальных осях и их коррекцию,
дополнительно по данным измерений АВУ осуществляют формирование идеального (без дрейфа) гироскопа; вычисляют текущие значения направляющих косинусов орта кинетического момента идеального гироскопа относительно инерциальных и относительно его корпусных осей, совпадающих с корпусными осями КА, при этом в начальный момент времени направление орта кинетического момента идеального гироскопа задают по одной из корпусных осей КА, ортогональной направлению орта кинетического момента калибруемого гироскопа;
по измеренным (с помощью списывающих устройств) значениям направляющих косинусов орта кинетического момента калибруемого гироскопа и значениям направляющих косинусов орта кинетического момента идеального гироскопа формируют правый ортогональный гироскопический трехгранник, вычисляя значения матрицы ориентации осей гироскопического трехгранника относительно корпусных осей блока гироскопов, при этом направление орта кинетического момента идеального гироскопа задают в условиях ортогонализации гироскопического трехгранника в качестве опорного направления;
формируют измеренные значения косинуса угла между ортами кинетических моментов идеального и калибруемого гироскопов, по расчетным (на основе априорных значений коэффициентов модели дрейфов) значениям направляющих косинусов орта кинетического момента калибруемого гироскопа и значениям направляющих косинусов орта кинетического момента идеального гироскопа формируют правый ортогональный инерциальный трехгранник, вычисляют значения матрицы ориентации гироскопического трехгранника относительно инерциального трехгранника, при этом направление орта кинетического момента идеального гироскопа задают в условиях ортогонализации инерциального трехгранника в качестве опорного направления;
формируют расчетные значения косинуса угла между ортами кинетических моментов идеального и калибруемого гироскопов, при этом после коррекции положения орта кинетического момента калибруемого гироскопа в инерциальных осях по данным АВУ формируют правый ортогональный квазиинерциальный трехгранник, вычисляют значения матрицы ориентации квазиинерциального трехгранника относительно инерциального трехгранника, которые в этот момент времени приравнивают значениям матрицы ориентации гироскопического трехгранника относительно инерциального трехгранника;
затем в моменты поступления данных от АВУ пересчитывают расчетные и измеренные значения направляющих косинусов орта кинетического момента калибруемого гироскопа на оси квазиинерциального трехгранника и формируют два скалярных измерения, первое измерение вычисляют как разность расчетного и измеренного значений косинуса угла между ортами кинетических моментов идеального и калибруемого гироскопов, а второе измерение вычисляют как разность первых элементов расчетного и измеренного значений направляющих косинусов орта кинетического момента калибруемого гироскопа в осях квазиинерциального трехгранника;
после чего осуществляют линеаризацию полученных скалярных измерений и с привлечением расчетной модели уходов гироскопа в осях квазиинерциального трехгранника вычисляют оценки погрешностей углов привязки осей калибруемого гироскопа относительно осей АВУ и оценки погрешностей априорных значений коэффициентов его модели дрейфов.
Предлагаемый способ предусматривает калибровку по данным АВУ погрешностей индивидуально каждого из ЭСГ, входящих в состав БЧЭ БИСО.
Сущность предлагаемого технического решения поясняется чертежами фиг. 1 и 2. На фиг. 1 приведена ориентация осей орбитальной системы координат (ОСК) xoyozo относительно осей инерциальной системы координат (ИСК) in1in2in3.
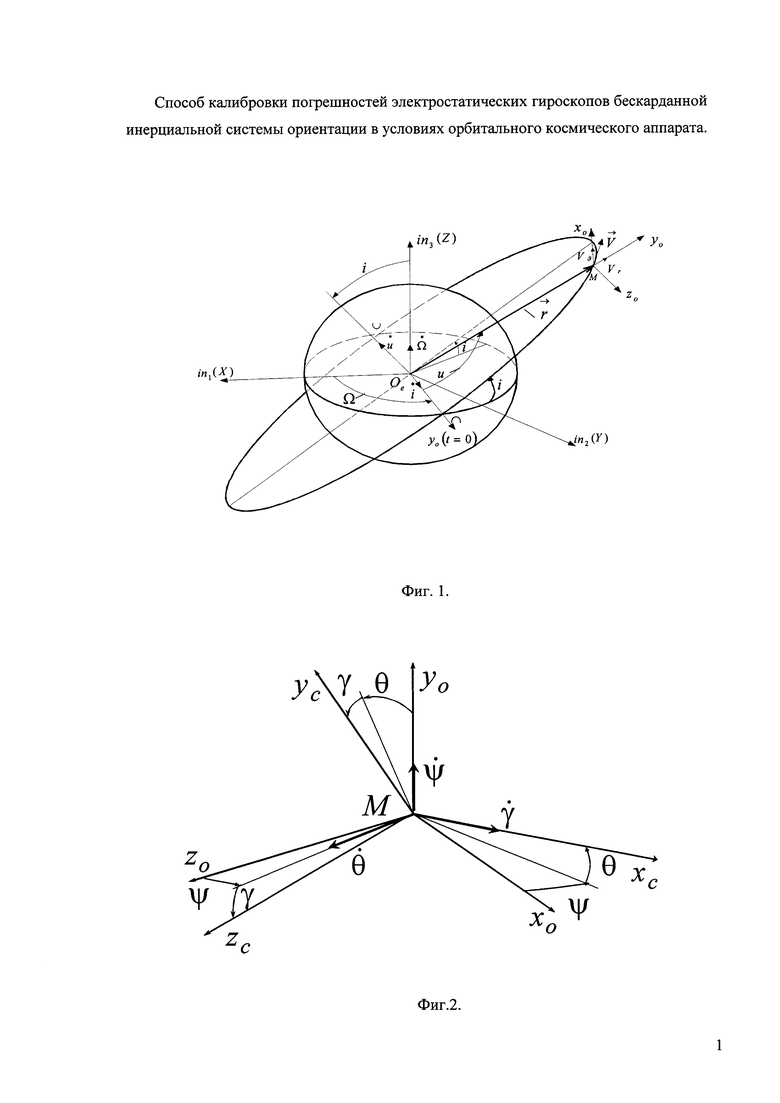
На фиг. 2 приведена ориентация осей связанной с КА системы координат (ССК) xcyczc относительно осей ОСК.
На чертежах приняты следующие обозначения:
ИСК - инерциальная система координат (in1in2in3), правый ортогональный трехгранник с началом в центре масс Земли. Ось in3 направлена по оси суточного вращения Земли, ось in1 - в точку весеннего равноденствия;
Ое - центр масс Земли;
ОСК - орбитальная система координат (xoyozo), правый ортогональный трехгранник с началом в центре масс КА. Ось yo направлена по радиус-вектору r, ось xo - лежит в плоскости орбиты по направлению движения;
ССК - связанная с КА система координат (xcyczc), правый ортогональный трехгранник с началом в центре масс КА. Ось хс - продольная ось КА, ось ус совпадает с осью yo при нулевых значениях углов тангажа и крена КА;
М - центр масс КА;
ψ,θ,γ - углы Эйлера-Крылова (рыскание, тангаж и крен), определяющие угловую ориентацию осей КА xcyczc относительно ОСК xoyozo;
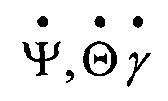 - производные углов Эйлера-Крылова;
- производные углов Эйлера-Крылова;
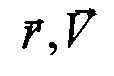 - радиус-вектор и вектор линейной скорости центра масс КА относительно инерциального пространства;
- радиус-вектор и вектор линейной скорости центра масс КА относительно инерциального пространства;
Vr, Vϑ - радиальная и трансверсальная составляющие вектора линейной скорости КА;
Ω - долгота восходящего узла;
i - наклонение орбиты;
u - аргумент широты или фаза КА.
Предлагаемый способ реализуется при выполнении следующих технологических операций:
1. По результатам измерений параметров угловой ориентации КА, проводимых АВУ и БИСО, формируют исходные данные:
- значения эталонного кватерниона 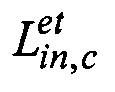 или матрицы
или матрицы 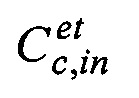 ориентации, характеризующих угловое положение корпусных осей xcyczc КА (далее - оси КА) относительно ИСК, моделируемой в алгоритмах АВУ;
ориентации, характеризующих угловое положение корпусных осей xcyczc КА (далее - оси КА) относительно ИСК, моделируемой в алгоритмах АВУ;
- значения направляющих косинусов 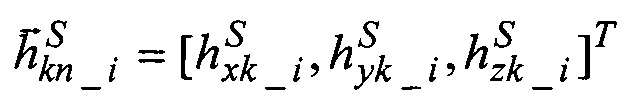 орта кинетического момента калибруемого ЭСГi где: (i=1, 2, 3…), в его корпусных осях;
орта кинетического момента калибруемого ЭСГi где: (i=1, 2, 3…), в его корпусных осях;
- априорные значения матрицы Ckn_i,c ориентации измерительных осей калибруемого ЭСГi относительно осей КА;
- априорные значения коэффициентов модели дрейфа (КМД) калибруемого ЭСГi;
- расчетные значения направляющих косинусов 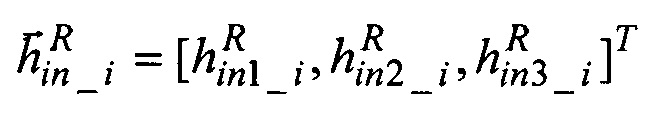 орта кинетического момента калибруемого ЭСГi в инерциальных осях.
орта кинетического момента калибруемого ЭСГi в инерциальных осях.
2. По данным эталонной матрицы 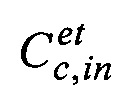 ориентации осуществляют формирование идеального (без дрейфа) гироскопа (далее ЭСГ-И). Для чего:
ориентации осуществляют формирование идеального (без дрейфа) гироскопа (далее ЭСГ-И). Для чего:
- задают направление орта кинетического момента ЭСГ-И по одной из корпусных осей КА, ортогональной направлению орта кинетического момента калибруемого ЭСГi;
- определяют текущие значения направляющих косинусов 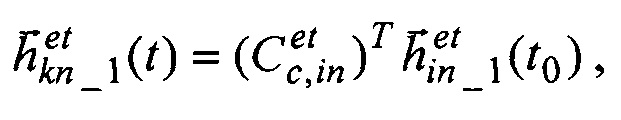 где: t0 - начальный момент времени, орта кинетического момента ЭСГ-И в его корпусных осях, совпадающих с осями КА;
где: t0 - начальный момент времени, орта кинетического момента ЭСГ-И в его корпусных осях, совпадающих с осями КА;
- осуществляют расчет направляющих косинусов 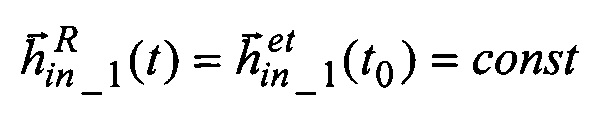 орта кинетического момента ЭСГ-И в инерциальных осях.
орта кинетического момента ЭСГ-И в инерциальных осях.
3. Производят прогнозирование уходов калибруемого ЭСГi в ИСК, вычисляют расчетные значения направляющих косинусов орта кинетического момента ЭСГi в инерциальных осях 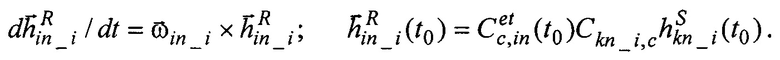 здесь:
здесь: 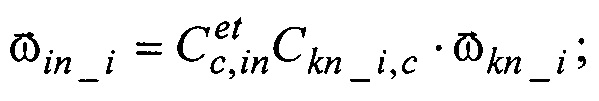
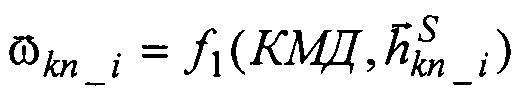 - расчетные значения дрейфов ЭСГi в корпусных осях, как функции от априорных значений КМД [3] и текущих значений
- расчетные значения дрейфов ЭСГi в корпусных осях, как функции от априорных значений КМД [3] и текущих значений 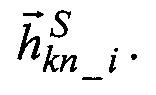
4. По значениям направляющих косинусов 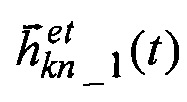 орта кинетического момента идеального ЭСГ-И и измеренным значениям направляющих косинусов
орта кинетического момента идеального ЭСГ-И и измеренным значениям направляющих косинусов 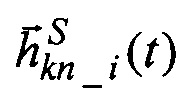 орта кинетического момента калибруемого ЭСГi в корпусных осях, приведенным к корпусным осям БЧЭ, формируют правый ортогональный трехгранник q1q2q3, положение которого относительно корпусных осей БЧЭ характеризуется матрицей Cq,b, орты-столбцы которой согласно принятому условию ортогонализации равны:
орта кинетического момента калибруемого ЭСГi в корпусных осях, приведенным к корпусным осям БЧЭ, формируют правый ортогональный трехгранник q1q2q3, положение которого относительно корпусных осей БЧЭ характеризуется матрицей Cq,b, орты-столбцы которой согласно принятому условию ортогонализации равны:
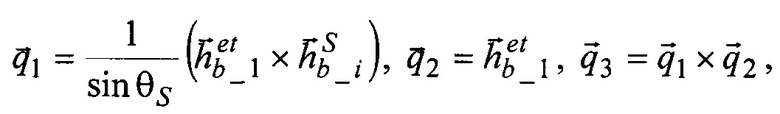
где θS - «измеренное» значение угла между ортами ЭСГ.
5. По значениям направляющих косинусов орта 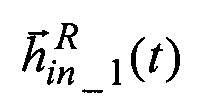 кинетического момента идеального ЭСГ-И и расчетным значениям направляющих косинусов орта
кинетического момента идеального ЭСГ-И и расчетным значениям направляющих косинусов орта 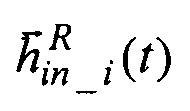 кинетического момента калибруемого ЭСГi в инерциальных осях формируют инерциальный приборный трехгранник in1in2in3, положение которого относительно трехгранника q1q2q3 характеризуется матрицей Cq,in, орты-столбцы которой согласно принятому условию ортогонализации равны
кинетического момента калибруемого ЭСГi в инерциальных осях формируют инерциальный приборный трехгранник in1in2in3, положение которого относительно трехгранника q1q2q3 характеризуется матрицей Cq,in, орты-столбцы которой согласно принятому условию ортогонализации равны
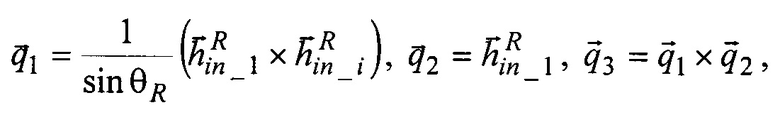
где θR - расчетное значение угла между ортами ЭСГ, причем 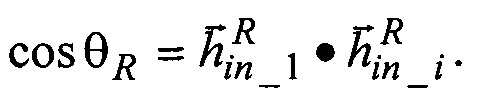
Знак 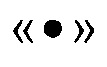 - означает скалярное произведение векторов.
- означает скалярное произведение векторов.
При этом, как известно [3], значения орта 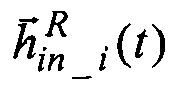 вычисляют как
вычисляют как
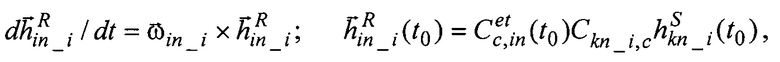
Здесь 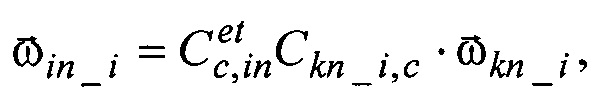
где 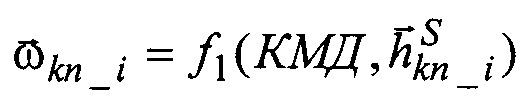 - расчетные значения дрейфа ЭСГi в корпусных осях, как функции от априорных значений КМД и текущих значений
- расчетные значения дрейфа ЭСГi в корпусных осях, как функции от априорных значений КМД и текущих значений 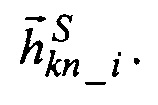
6. Формируют квазиинерциальную int1int2int3 систему координат (квази-ИСК), дискретно учитывающую прецессию гироскопического трехгранника q1q2q3 вследствие дрейфов ЭСГi, положение которой относительно ИСК определяется матрицей Cin,int, равной значениям матрицы (Cq,in)T в моменты после коррекции положения ЭСГi по данным АВУ.
Пересчитывают на оси квази-ИСК расчетные 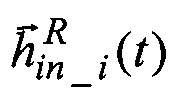 и измеренные
и измеренные 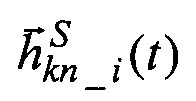 значения орта кинетического момента ЭСГi в моменты прихода данных от АВУ:
значения орта кинетического момента ЭСГi в моменты прихода данных от АВУ:
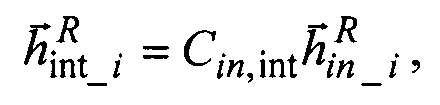
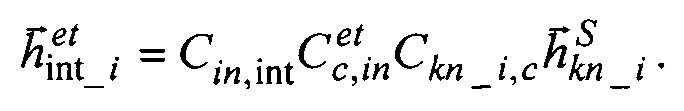
Введение квази-ИСК int1int2int3 позволяет осуществить линеаризацию расчетной модели уходов ЭСГi (погрешностей 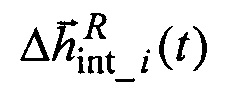 вычисления направляющих косинусов ортов
вычисления направляющих косинусов ортов 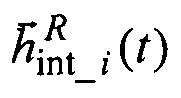 их кинетических моментов) и соответствующих измерений в точках пространства состояния, дискретно движущихся вместе с прецессией векторов кинетических моментов ЭСГi.
их кинетических моментов) и соответствующих измерений в точках пространства состояния, дискретно движущихся вместе с прецессией векторов кинетических моментов ЭСГi.
7. В моменты времени прихода данных от АВУ формируют разностные скалярные измерения:

где: 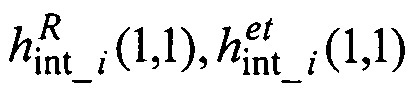 - первые элементы соответствующих векторов
- первые элементы соответствующих векторов 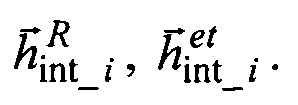
Учитывая, что погрешности 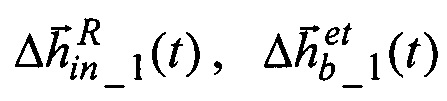 формирования значений орта кинетического момента ЭСГ-И, соответственно в инерциальных осях и осях БЧЭ, определяются уровнем погрешностей АВУ, измерения (1), линеаризованные в точках пространства состояния, дискретно движущихся вместе с прецессией вектора кинетического момента ЭСГi, будут равны:
формирования значений орта кинетического момента ЭСГ-И, соответственно в инерциальных осях и осях БЧЭ, определяются уровнем погрешностей АВУ, измерения (1), линеаризованные в точках пространства состояния, дискретно движущихся вместе с прецессией вектора кинетического момента ЭСГi, будут равны:
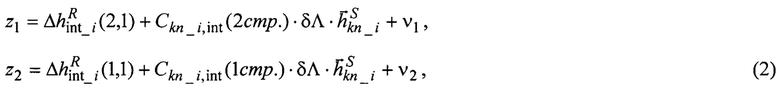
где: 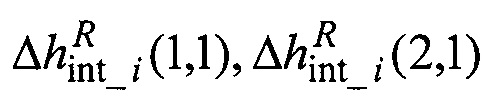 - соответственно первый и второй элементы вектора
- соответственно первый и второй элементы вектора 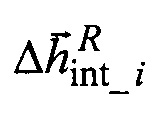 уходов ЭСГi в квази-ИСК, которые описывают линеаризованной расчетной моделью вида:
уходов ЭСГi в квази-ИСК, которые описывают линеаризованной расчетной моделью вида:
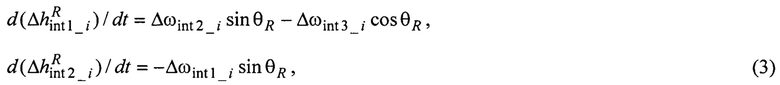
здесь 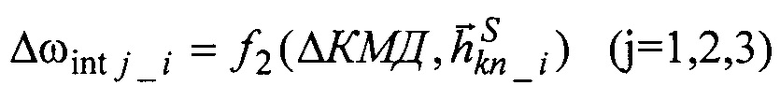 - погрешности прогнозирования дрейфов ЭСГi в осях квази-ИСК, обусловленные погрешностями априорных значений КМД ЭСГi;
- погрешности прогнозирования дрейфов ЭСГi в осях квази-ИСК, обусловленные погрешностями априорных значений КМД ЭСГi;
- Ckn_i,int(1стр.), Ckn_i,int(2стр.) - соответственно первая и вторая строки матрицы ориентации корпусных осей ЭСГi относительно квази-ИСК;
- δΛ - погрешность углов привязки измерительной оси калибруемого ЭСГi относительно его корпусных осей и соответственно корпусных осей АВУ, приведенных к осям КА;
ν1, v2 -шумы измерений, включающие погрешности списывающих устройств АВУ и погрешности списывающих устройств ЭСГi.
Разностные скалярные измерения (1) формируют с дискретностью поступления данных от АВУ в течение всего времени калибровочного вращения КА.
Обработку измерений (1) с учетом расчетной модели уходов ЭСГi (3) осуществляют с помощью алгоритма фильтра Калмана, на выходе которого вычисляют оценки уходов ЭСГi сначала в осях квази-ИСК, затем - в осях ИСК, а также вычисляют оценки погрешностей δΛ углов привязки измерительной оси калибруемого ЭСГi и оценки погрешностей ΔКМД априорных значений коэффициентов его модели дрейфов. Для линеаризации измерений и расчетной модели уходов ЭСГi оценки всех погрешностей поступают в обратную связь для коррекции уходов ЭСГi после обработки каждого поступившего измерения.
По сравнению со способом прототипом точность калибровки погрешностей ЭСГ бескарданной инерциальной системы ориентации в условиях орбитального КА повышается за счет:
- учета и исключения из результатов измерений составляющей погрешности, обусловленной дрейфом ЭСГ;
- учета и исключения составляющей погрешности, обусловленной - погрешностью углов привязки δΛ измерительной оси калибруемого ЭСГi относительно его корпусных осей.
Таким образом, поставленная цель достигнута.
На предприятии АО «Концерн «ЦНИИ «Электроприбор» предлагаемый способ проверен при проведении летных испытаний бескарданной инерциальной системы ориентации с ЭСГ на орбитальном КА «Ресурс». Получены положительные результаты.
Используемая литература:
1. Патент РФ №2092402.
2. Дюмин А.Ф., Корабельщиков В.В., Платонов С.Н., Суринский Д.М. Повышение точности астрокоррекции бесплатформенной инерциальной системы ориентации на электростатических гироскопах // Гироскопия и навигация, 2005, №1(48), С. 76-83.
3. Гуревич С.С., Гусинский В.З., Ландау Б.Е. и др. Система ориентации орбитального КА на базе бескарданных электростатических гироскопов со сплошным ротором. // VIII Санкт-Петербургская международная конференция по интегрированным системам, 2001, с. 52-59.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ИНСТРУМЕНТАЛЬНЫХ ПОГРЕШНОСТЕЙ ИЗМЕРИТЕЛЕЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ НА ЭТАПЕ НАЧАЛЬНОЙ ВЫСТАВКИ | 2005 |
|
RU2300081C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ ОБЪЕКТА И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 2017 |
|
RU2661446C1 |
| Способ калибровки погрешностей бескарданной инерциальной системы на электростатических гироскопах в условиях орбитального полета | 2017 |
|
RU2677099C1 |
| ИНТЕГРИРОВАННЫЙ КОМПЛЕКС ДЛЯ НАВИГАЦИИ И УПРАВЛЕНИЯ МОРСКИХ СУДОВ | 1997 |
|
RU2117253C1 |
| СПОСОБ КАЛИБРОВКИ ПАРАМЕТРОВ БЕСПЛАТФОРМЕННОГО ИНЕРЦИАЛЬНОГО ИЗМЕРИТЕЛЬНОГО МОДУЛЯ | 2004 |
|
RU2269813C2 |
| Способ измерения ошибок начальной выставки инерциальной навигационной системы без привязки к внешним ориентирам | 2021 |
|
RU2779274C1 |
| Способ определения ориентации объекта в бесплатформенной инерциальной навигационной системе | 2022 |
|
RU2794283C1 |
| СПОСОБ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИАЛЬНОЙ НАВИГАЦИИ | 2022 |
|
RU2806707C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ НАВИГАЦИОННЫХ ПАРАМЕТРОВ И БЕСПЛАТФОРМЕННАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2016 |
|
RU2634071C1 |
| СПОСОБ КАЛИБРОВКИ УГЛОВ РАССОГЛАСОВАНИЯ ОСИ ДАТЧИКА УГЛА НЕУПРАВЛЯЕМОГО ГИРОСКОПА ОТНОСИТЕЛЬНО ОСИ ВРАЩЕНИЯ ЕГО КОРПУСА | 2005 |
|
RU2308683C1 |
Изобретение относится к области космической техники и может быть использовано в бесплатформенных инерциальных системах ориентации (БИСО) для орбитальных космических аппаратов (КА), измерительный модуль (блок чувствительных элементов -БЧЭ) которых содержит электростатические гироскопы (ЭСГ). Способ калибровки погрешностей ЭСГ БИСО в условиях орбитального КА заключается в последовательном вращении КА вокруг осей, связанных с его корпусом, вычислении углового положения КА относительно инерциальных осей по данным измерений астровизирующего устройства (АВУ), вычислении на основе априорных значений коэффициентов модели дрейфа калибруемого гироскопа, расчетных значений направляющих косинусов орта его кинетического момента в инерциальных осях, формирование по данным списывающих устройств гироскопа измеренных значений направляющих косинусов орта его кинетического момента в корпусных осях, вычисление оценок ухода гироскопа в инерциальных осях и их коррекцию. При этом по данным измерений АВУ осуществляют формирование идеального (без дрейфа) гироскопа. По измеренным значениям направляющих косинусов орта кинетического момента калибруемого гироскопа и значениям направляющих косинусов орта кинетического момента идеального гироскопа формируют правый ортогональный гироскопический трехгранник, вычисляя значения матрицы ориентации осей гироскопического трехгранника относительно корпусных осей блока гироскопов, формируют измеренные значения косинуса угла между ортами кинетических моментов идеального и калибруемого гироскопов, по расчетным значениям направляющих косинусов орта кинетического момента калибруемого и идеального гироскопов формируют правый ортогональный инерциальный трехгранник. Затем вычисляют значения матрицы ориентации гироскопического трехгранника относительно инерциального трехгранника, формируют расчетные значения косинуса угла между ортами кинетических моментов идеального и калибруемого гироскопов, затем в моменты поступления данных от АВУ пересчитывают расчетные и измеренные значения направляющих косинусов орта кинетического момента калибруемого гироскопа на оси квазиинерциального трехгранника и формируют два скалярных измерения, первое измерение вычисляют как разность расчетного и измеренного значений косинуса угла между ортами кинетических моментов идеального и калибруемого гироскопов, а второе измерение вычисляют как разность первых элементов расчетного и измеренного значений направляющих косинусов орта кинетического момента калибруемого гироскопа в осях квазиинерциального трехгранника, после чего осуществляют линеаризацию полученных скалярных измерений и с привлечением расчетной модели уходов гироскопа в осях квазиинерциального трехгранника вычисляют оценки погрешностей привязки измерительных осей калибруемого гироскопа относительно осей АВУ и оценки погрешностей априорных значений коэффициентов его модели дрейфов. Технический результат – повышение точности калибровки погрешностей ЭСГ БИСО. 2 ил.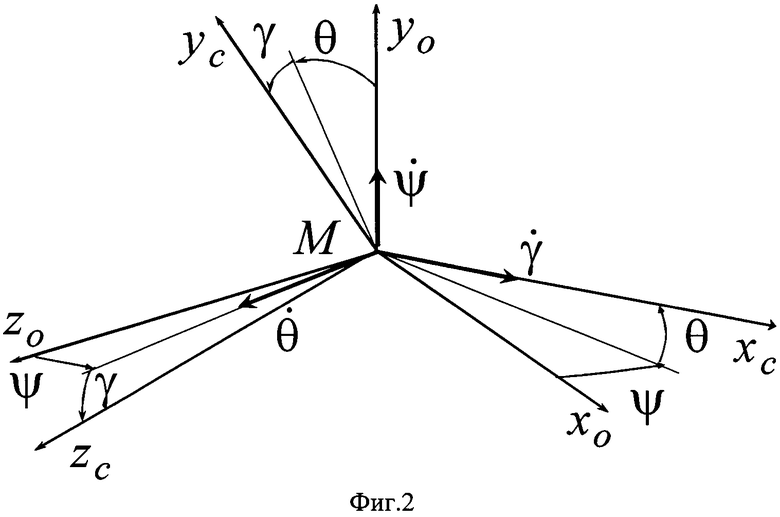
Способ калибровки погрешностей электростатических гироскопов бескарданной инерциальной системы ориентации в условиях орбитального космического аппарата, заключающийся в последовательном вращении космического аппарата вокруг осей, связанных с его корпусом, вычислении углового положения космического аппарата относительно инерциальных осей по данным измерений астровизирующего устройства, вычислении на основе априорных значений коэффициентов модели дрейфа калибруемого гироскопа, расчетных значений направляющих косинусов орта его кинетического момента в инерциальных осях, формирование по данным списывающих устройств гироскопа измеренных значений направляющих косинусов орта его кинетического момента в корпусных осях, вычисление оценок ухода гироскопа в инерциальных осях и их коррекцию, отличающийся тем, что дополнительно по данным измерений астровизирующего устройства осуществляют формирование идеального (без дрейфа) гироскопа; вычисляют текущие значения направляющих косинусов орта кинетического момента идеального гироскопа относительно инерциальных и относительно его корпусных осей, совпадающих с корпусными осями космического аппарата, при этом в начальный момент времени направление орта кинетического момента идеального гироскопа задают по одной из корпусных осей космического аппарата, ортогональной направлению орта кинетического момента калибруемого гироскопа, по измеренным (с помощью списывающих устройств) значениям направляющих косинусов орта кинетического момента калибруемого гироскопа и значениям направляющих косинусов орта кинетического момента идеального гироскопа формируют правый ортогональный гироскопический трехгранник, вычисляя значения матрицы ориентации осей гироскопического трехгранника относительно корпусных осей блока гироскопов, при этом направление орта кинетического момента идеального гироскопа задают в условиях ортогонализации гироскопического трехгранника в качестве опорного направления, формируют измеренные значения косинуса угла между ортами кинетических моментов идеального и калибруемого гироскопов, по расчетным (на основе априорных значений коэффициентов модели дрейфов) значениям направляющих косинусов орта кинетического момента калибруемого гироскопа и значениям направляющих косинусов орта кинетического момента идеального гироскопа формируют правый ортогональный инерциальный трехгранник, вычисляют значения матрицы ориентации гироскопического трехгранника относительно инерциального трехгранника, при этом направление орта кинетического момента идеального гироскопа задают в условиях ортогонализации инерциального трехгранника в качестве опорного направления, формируют расчетные значения косинуса угла между ортами кинетических моментов идеального и калибруемого гироскопов, при этом после коррекции положения орта кинетического момента калибруемого гироскопа в инерциальных осях по данным астровизирующего устройства формируют правый ортогональный квазиинерциальный трехгранник, вычисляют значения матрицы ориентации квазиинерциального трехгранника относительно инерциального трехгранника, которые в этот момент времени приравнивают значениям матрицы ориентации гироскопического трехгранника относительно инерциального трехгранника, затем в моменты поступления данных от астровизирующего устройства пересчитывают расчетные и измеренные значения направляющих косинусов орта кинетического момента калибруемого гироскопа на оси квазиинерциального трехгранника и формируют два скалярных измерения, первое измерение вычисляют как разность расчетного и измеренного значений косинуса угла между ортами кинетических моментов идеального и калибруемого гироскопов, а второе измерение вычисляют как разность первых элементов расчетного и измеренного значений направляющих косинусов орта кинетического момента калибруемого гироскопа в осях квазиинерциального трехгранника, после чего осуществляют линеаризацию полученных скалярных измерений и с привлечением расчетной модели ухода гироскопа в осях квазиинерциального трехгранника вычисляют оценки погрешностей углов привязки измерительной оси калибруемого гироскопа относительно осей астровизирующего устройства и оценки погрешностей априорных значений коэффициентов его модели дрейфов.
| СПОСОБ КАЛИБРОВКИ ГИРОИНЕРЦИАЛЬНЫХ ИЗМЕРИТЕЛЕЙ БЕСПЛАТФОРМЕННОЙ ИНЕРЦИОННОЙ НАВИГАЦИОННОЙ СИСТЕМЫ ОРИЕНТАЦИИ КОСМИЧЕСКОГО АППАРАТА | 1992 |
|
RU2092402C1 |
| ИНТЕГРИРОВАННАЯ ИНЕРЦИАЛЬНО-СПУТНИКОВАЯ СИСТЕМА ОРИЕНТАЦИИ И НАВИГАЦИИ ДЛЯ ОБЪЕКТОВ, ДВИЖУЩИХСЯ ПО БАЛЛИСТИЧЕСКОЙ ТРАЕКТОРИИ С ВРАЩЕНИЕМ ВОКРУГ ПРОДОЛЬНОЙ ОСИ | 2008 |
|
RU2375680C1 |
| СПОСОБ КАЛИБРОВКИ ПАРАМЕТРОВ БЕСПЛАТФОРМЕННОГО ИНЕРЦИАЛЬНОГО ИЗМЕРИТЕЛЬНОГО МОДУЛЯ | 2004 |
|
RU2269813C2 |
| КАЛИБРОВКА ГИРОСКОПИЧЕСКИХ СИСТЕМ С ВИБРАЦИОННЫМИ ГИРОСКОПАМИ | 2009 |
|
RU2509981C2 |
| US 9671248 B2, 06.06.2017. | |||
Авторы
Даты
2019-02-04—Публикация
2018-02-14—Подача