Изобретение относится к системам управления летательными аппаратами (ЛА) и может быть использовано в комплексе функциональных программ управления и наведения ЛА авиационных комплексов для назначения целей перехватчикам при противостоянии групп ЛА.
Анализ особенностей ведения боевых действий в рамках стратегии бесконтактных сетецентрических войн [1] свидетельствует о том, что основным видом воздушно-космического противоборства является групповое применение как средств нападения, так и защиты. В связи с этим оценка возможностей группы ЛА по решению задач группового боестолкновения является весьма актуальной.
В аналогах [2,3] предлагаемого изобретения в основном рассматривается выбор целей, наилучших для перехвата, исходя из решения очень сложной задачи нелинейного целочисленного программирования на основе расчета вероятностей поражения отдельных целей отдельными объектами. Способ назначения различных i-x типов оружия  на j-е цели
на j-е цели 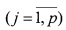 , изложенный в [2], основан на задании вероятностей поражения каждой цели каждым типом оружия. Для всякого возможного назначения типов оружия на цели определяют вероятность их выживания. Выбирают такое назначение xij, которое минимизирует ожидаемую суммарную опасность
, изложенный в [2], основан на задании вероятностей поражения каждой цели каждым типом оружия. Для всякого возможного назначения типов оружия на цели определяют вероятность их выживания. Выбирают такое назначение xij, которое минимизирует ожидаемую суммарную опасность

непораженных целей, где
Vj - коэффициент опасности j - й цели,
qij - вероятность выживания j-й цели при использовании i - го типа оружия,
xij - количество экземпляров i-ro типа оружия, назначенных на j - ю
цель.
С математической точки зрения такая задача представляет собой сложную задачу нелинейного целочисленного программирования. Нахождение ее точного решения практически невозможно уже при рассмотрении двух десятков объектов [2].
При целераспределении по маневрирующим целям необходимо знать время жизни гипотез изменения скорости цели (обычно несколько секунд). По истечении этого интервала необходимо снова решить задачу целераспределения и сформулировать сопутствующий закон управления. Также со временем некоторые цели и истребители могут выбывать из процесса перехвата. При этом назначение целей может измениться.
Целью предлагаемого изобретения является разработка более простого способа целераспределения в групповом противоборстве, эффективность которого определяется не вероятностью поражения цели, а выполнением реальных ограничений на перехват в процессе полета на выбранную для поражения цель.
В качестве прототипа был выбран способ целераспределения, изложенный в работе [4], в котором не учитывается возможное выбывание участников. Кроме того, в отличие от прототипа, в предлагаемом изобретении обеспечивается назначение целей всем перехватчикам, даже если их количество превышает количество целей.
Специфика решаемой задачи предопределяет необходимость учета как временных, так и энергетических затрат на выполнение перехвата.
Предлагаемый в прототипе подход к формированию предполагаемой траектории перехвата, учитывающий эти требования, основан на использовании функционала

временных и энергетических затрат на перехват для каждой пары перехватчика с номером n  и цели с номером m
и цели с номером m  , где
, где
Т - полное время полета перехватчика по траектории,
К - постоянный коэффициент, выбираемый из соображений баланса между временем перехвата и затратами на полет с ускорением,
J - вектор ускорения перехватчика,
t - время действия ускорения перехватчика.
В (2) второе слагаемое учитывает затраты на формирование управляющего сигнала перехватчика.
По минимуму этого функционала, найденному среди определенного класса траекторий, строится матрица эффективности перехвата, процедура построения которой приведена ниже. На основе полученной матрицы при помощи известного алгоритма находится оптимальное распределение, обеспечивающее минимум суммарного функционала качества

среди всех возможных назначений m(n) целей перехватчикам.
Технический результат, который может быть получен от использования предлагаемого изобретения, заключается в возможности автоматического оптимального назначения целей перехватчикам с перераспределением целей при выбывании участников, что снижает информационную нагрузку на операторов (штурманов наведения).
Заявленный технический результат, который может быть получен от реализации предлагаемого технического решения, достигается тем, что решается задача поиска оптимального значения суммарного функционала качества, основанного на временных и энергетических затратах с учетом реальных ограничений на возможности перехватчиков.
Возможность достижения технического результата обусловлена следующими причинами:
- индивидуальный функционал эффективности перехвата (2) для каждой пары перехватчик-цель основывается на рассмотрении временных и энергетических затрат с учетом реальных ограничений на возможности перехватчиков;
- задача поиска минимального значения функционала (2) сводится к задаче поиска корней многочлена, способ решения которой известен [5];
- задача поиска минимума суммарного функционала эффективности перехвата (3) сводится к решению задачи о назначениях [6], которая эффективно решается венгерским алгоритмом [6].
Сущность предлагаемого изобретения заключается в разработке принципиально нового способа автоматического назначения группы целей группе перехватчиков, при котором заранее выбранный функционал качества (2), учитывающий как временные, так и энергетические затраты на выполнение перехвата, периодически и при необходимости коррекции целераспределения вычисляют для каждой пары перехватчик-цель, затем ищут его минимум среди заданного класса траекторий с учетом заданных ограничений на скорости и ускорения перехватчиков, после чего целераспределение определяется решением задачи о назначениях [6].
В решаемой задаче для группы, состоящей из N произвольно расположенных перехватчиков и М целей, необходимо назначить каждому n-му 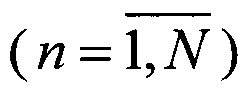 перехватчику m - ю
перехватчику m - ю 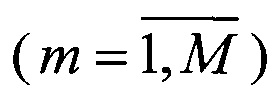 цель, наилучшую по минимуму суммарного функционала эффективности перехвата (3), в котором In,m представляет собой функционал, соответствующий траектории перехвата n-м перехватчиком m - й цели. Минимизация функционала (3) производится по всем возможным назначениям m(n) n-го перехватчика на m - ю цель. В случае если перехватчиков больше чем целей, некоторым целям будут назначены более одного перехватчика, в противоположном случае каждому перехватчику назначается единственная цель.
цель, наилучшую по минимуму суммарного функционала эффективности перехвата (3), в котором In,m представляет собой функционал, соответствующий траектории перехвата n-м перехватчиком m - й цели. Минимизация функционала (3) производится по всем возможным назначениям m(n) n-го перехватчика на m - ю цель. В случае если перехватчиков больше чем целей, некоторым целям будут назначены более одного перехватчика, в противоположном случае каждому перехватчику назначается единственная цель.
Задача будет решаться при условии, что выполняются следующие допущения:
- цели и перехватчики расположены в пространстве произвольно, имеют различные начальные скорости и направления полета;
- цели являются равнозначными;
- цели не маневрируют и летят с постоянными скоростями;
- все перехватчики обладают достаточным запасом топлива;
- траектория каждого перехватчика состоит из двух участков: на первом выполняется доворот на цель до требуемого угла упреждения с постоянным ускорением, а на втором -прямолинейный полет в упрежденную точку встречи;
- заданы максимально допустимые значения скоростей и ускорений перехватчиков;
- в процессе наведения возможно выбывание как целей, так и перехватчиков.
Реализация предлагаемого способа состоит из следующих этапов.
1. На первом этапе проверяют необходимость коррекции целераспределения.
2. На втором этапе выбирают класс траекторий, с помощью которых перехватчики должны перехватывать цели. На основе этого вычисляют индивидуальный функционал качества (2) перехвата для каждой пары «перехватчик-цель» с учетом заданных максимально допустимых значений скоростей и ускорений перехватчиков.
3. На третьем этапе решение задачи поиска минимума индивидуального функционала качества (2) сводят к решению нескольких задач минимизации с ограничениями типа равенств.
4. На четвертом этапе производят назначение целей перехватчикам, обеспечивающее минимум суммарного функционала (3).
Первый этап заключается в анализе необходимости коррекции целераспределения, проводимом периодически, а также при изменении состава перехватчиков или целей.
Второй этап проиллюстрирован фигурой 1. Выберем определенный перехватчик и определенную цель. В начальный момент перехватчик находится в точке А и летит со скоростью V0, а цель находится в точке В и летит со скоростью V. Предполагаемую траекторию перехвата, состоящую из двух участков, строят следующим образом: на первом участке перехватчик летит с постоянным ускорением J, выполняя доворот на цель, до момента t, когда перехватчик находится в точке С, а цель - в точке D, затем на втором участке перехватчик летит с постоянной скоростью до момента Т.
Условие перехвата в случае, когда перехватчик и цель летят с постоянными скоростями, заключается в том, что относительная скорость полета перехватчика направлена по линии визирования цели. Это означает, что в момент t окончания действия ускорения относительная скорость полета должна быть направлена по вектору 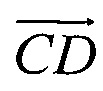 (фиг. 1). Тогда перехватчик и цель встретятся в точке Е. Если обозначить в момент t относительное положение цели
(фиг. 1). Тогда перехватчик и цель встретятся в точке Е. Если обозначить в момент t относительное положение цели 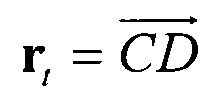 и относительную скорость перехватчика Vt, то из условия перехвата следует, что для некоторого τ≥0 выполнено rt=τVt. Здесь τ является интервалом времени между моментом окончания действия ускорения и моментом перехвата. Обозначив положение цели относительно перехватчика в начальный момент времени
и относительную скорость перехватчика Vt, то из условия перехвата следует, что для некоторого τ≥0 выполнено rt=τVt. Здесь τ является интервалом времени между моментом окончания действия ускорения и моментом перехвата. Обозначив положение цели относительно перехватчика в начальный момент времени  , после выражения rt, Vt через начальные величины получим:
, после выражения rt, Vt через начальные величины получим:
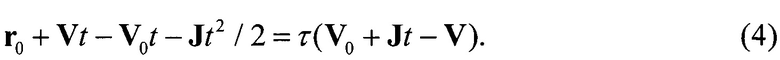
Преобразовав (4), получим
(2τ+t)Jt=2r0+2(τ+t)(V-V0).
Сумма t+τ представляет собой полное время полета Т. Тогда

Согласно принятым допущениям, скорость перехватчика Vt=V0+Jt в момент окончания действия ускорения не может превышать Vmax, а его ускорение - Jmax. Из (5) следует, что ограничение 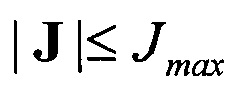 определяет неравенство
определяет неравенство
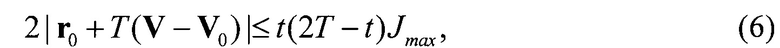
а ограничение |Vt|≤Vmax - неравенство 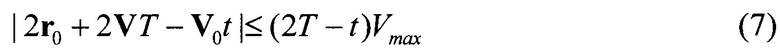
при


Определив Jt из (5) и подставив в (2), получим функцию двух переменных Im,n(T,t), которую требуется минимизировать при ограничениях (6) - (9).
Допустим, что функционал принимает минимальное значение при некоторых значениях T,t, так что все неравенства (6) -(9) являются строгими. Можно утверждать, что при некоторых значениях J* и t* величина  не увеличится, ограничение по скорости будет выполнено и перехват цели произойдет в момент Т*≤Т. В результате значение функционала (2) уменьшится. Поэтому минимальное значение функционала (2)следует искать при условии, что одно или два неравенства из (6) - (9) становятся равенствами.
не увеличится, ограничение по скорости будет выполнено и перехват цели произойдет в момент Т*≤Т. В результате значение функционала (2) уменьшится. Поэтому минимальное значение функционала (2)следует искать при условии, что одно или два неравенства из (6) - (9) становятся равенствами.
На третьем этапе последовательно проверяются следующие условия.
1. Если (7) является равенством, то выполняется условие  . С его помощью функционал (2) можно представить в виде
. С его помощью функционал (2) можно представить в виде
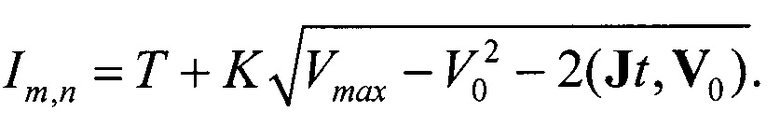
После подстановки Jt из (5) получим

После замены переменной Т на z=2T -t функционал принимает вид 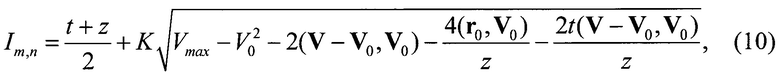
а равенство (7) - 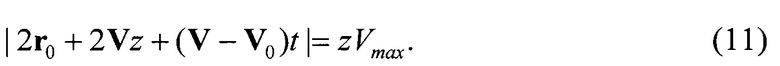
Введем обозначения
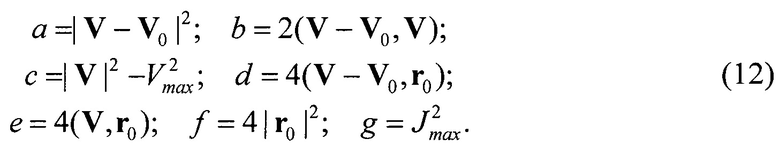
Тогда после возведения (11) в квадрат получим 
а (10) принимает вид
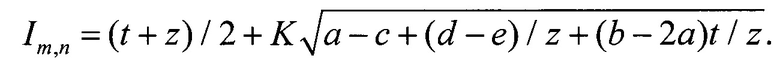
После замены переменных х=1/z; у=t/z поиск минимума (10) сводится к минимизации функционала

при ограничении

Если ввести множитель Лагранжа λ, то необходимым условием минимума будет
 .
.
Обозначим 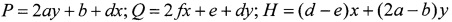 .
.
После исключения λ и вычисления производных получим уравнение

Избавившись от корня с помощью возведения в квадрат, получим равенство
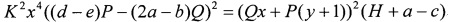 ,
,
которое после упрощения с помощью (15) принимает вид 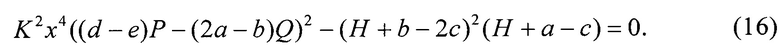
Тем самым, задача минимизации (14) сведена к решению системы уравнений (15), (16). Так как коэффициент  положителен, заменой х=(2ξ-dy-е) / 2ƒ можно привести (15) к виду ξ2=а1у2+b1y+с1. При этом (16) можно записать в виде:
положителен, заменой х=(2ξ-dy-е) / 2ƒ можно привести (15) к виду ξ2=а1у2+b1y+с1. При этом (16) можно записать в виде:
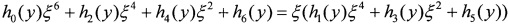 ,
,
где hk(y) - некоторые многочлены степени k. После возведения в квадрат останутся только четные степени ξ, которые выражаются через y. В результате получится уравнение двенадцатой степени относительно у. Численно найдем все его действительные корни при помощи известных алгоритмов нахождения корней многочленов [5]. Подставим найденные корни в (15) и из полученного квадратного уравнения найдем действительные значения х, если таковые существуют. В результате получим несколько пар значений х,у. Перейдем обратно к переменным T, t и выбросим те значения, которые не удовлетворяют (6), (8) и (9). Оставшиеся пары занесем в общий список кандидатов на минимум функционала (2).
2. Если равенством является (6), т.е. | J |=Jmax, то из него можно выразить t:
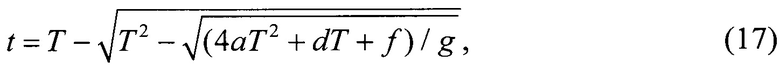
где использованы обозначения (12). Знак перед вторым слагаемым выбран исходя из условия t ≤ Т. В функционале (2) положим  и подставим в него найденное выражение для t. В результате функционал качества становится функцией Т:
и подставим в него найденное выражение для t. В результате функционал качества становится функцией Т:

Вычислим производную dIm,n(T) / dT и приравняем ее нулю. Если обозначить
h=16(1+1 / KJmax)2,ƒ1, (T)=(4аТ2+2dT+ƒ) / g,ƒ2(T)=(8aT+2d) / g, то после ряда преобразований условие равенства нулю производной определяется соотношением
((16-h)T2ƒ1(T)+ƒ2(T)2)2-ƒ1(T)(8Tƒ2(T)-hƒ1(T))2=0,
которое после раскрытия скобок приводит к уравнению восьмой степени по переменной Т. Решим его численно. Для каждого полученного Т найдем t из (17). Из всех полученных пар действительных значений (T, t) оставим только те, которые удовлетворяют (7), (8) и (9). Занесем их в общий список кандидатов на минимум функционала (2).
3. Если равенством является (8) (Т=t), т.е. с начала перехвата цели до его окончания реализуется равноускоренный полет перехватчика, то выразим Jt из (5) и подставим его в (2):
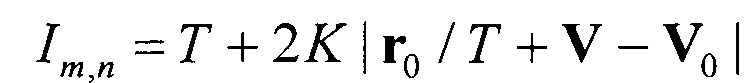
Если перейти к z=1 / T, то в обозначениях (12) получим
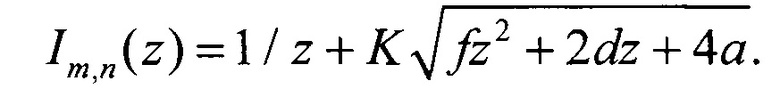
Уравнение dIm,n(z) / dz=0 сводится к уравнению шестой степени
K2z4(ƒz+d)2=ƒz2+2dz+4a.
Решим его численно и те корни, для которых выполнены (6), (7) и (9), добавим в общий список кандидатов на минимум функционала (2).
4. Если равенством является (9) (t=0), т.е. имеет место полет с постоянной скоростью, то расстояние от перехватчика до цели в момент Т* будет 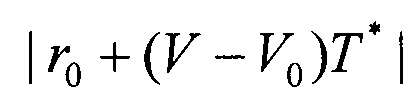 . Оно принимает минимальное значение
. Оно принимает минимальное значение 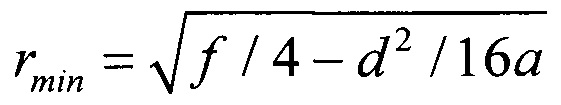 при
при 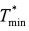 = - d/4a в обозначениях (12). Если
= - d/4a в обозначениях (12). Если 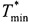 ≥ 0 и величина промаха rmin находится в допустимых пределах, то добавим пару значений
≥ 0 и величина промаха rmin находится в допустимых пределах, то добавим пару значений 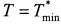 ; t=0 в общий список кандидатов на минимум с соответствующим значением функционала
; t=0 в общий список кандидатов на минимум с соответствующим значением функционала 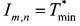 .
.
5. В случае, когда из четырех неравенств (6)-(9) два являются равенствами, возможны следующие ситуации.
5.1. Пусть равенствами являются выражения (6) и (7), т.е. 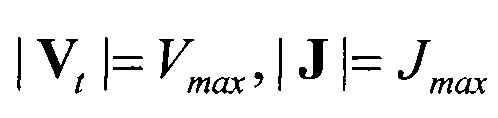 . Сделаем замену z-2T-t. Тогда после возведения в квадрат в обозначениях (12) равенство (7) примет вид (13), а равенство (6) запишется как
. Сделаем замену z-2T-t. Тогда после возведения в квадрат в обозначениях (12) равенство (7) примет вид (13), а равенство (6) запишется как
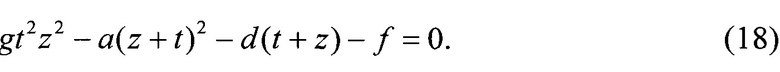
Сложив (18) и (13), получим
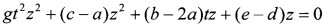 .
.
Можно сократить на z т.к. z -Т+(Т-t)≥T>0:

Выразим отсюда z и подставим в (13). Получится уравнение шестой степени относительно t:
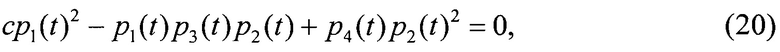
где обозначено
 .
.
Численно найдем все действительные корни t уравнения (20), затем найдем соответствующие значения z из (19) и значения T=(z+t)/2.
Удовлетворяющие неравенствам (8) и (9) значения занесем в общий список кандидатов на минимум функционала (2).
5.2. Пусть равенствами являются (6) и (8). Тогда после подстановки t=T в (6) и возведения в квадрат получится уравнение
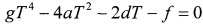 .
.
Его решения, удовлетворяющие неравенствам (7) и (9), добавим в общий список кандидатов на минимум функционала (2).
5.3. Пусть теперь равенствами являются (7) и (8). Подставим t=Т в (7) и возведем в квадрат.В обозначениях (12) получим уравнение
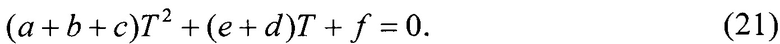
Его решения, удовлетворяющие неравенствам (6) и (9), добавим в общий список кандидатов на минимум функционала (2).
5.4. Вырожденный случай, когда одним из равенств является (9), уже был рассмотрен ранее в п. 4.
Теперь найдем глобальный минимум функционала (2). Для всех пар величин (T, t) из общего списка кандидатов на минимум функционала (2), построенного на предыдущих этапах, вычислим Jt с помощью (5) и подставим полученное значение в (2). Выберем те величины, которые дают минимальное значение. Полученное значение Т вместе с соответствующим значением t, значением функционала Im,n и вектором J определяют наилучшую траекторию перехвата цели и затраты на ее реализацию.
Решив задачу поиска минимума (2) для одиночного перехватчика и цели, перейдем к четвертому этапу. Для каждого перехватчика с номером n и цели с номером m определяют наилучшую траекторию перехвата и соответствующее значение In,m функционала (2).
Затем выполняют итерационную процедуру назначения целей. На шаге с номером k строят матрицу эффективности 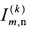 размера N(k) × М и список пар L(k), содержащий набор пар номеров перехватчиков и назначенных им целей. На первом шаге k=1 полагают N(1)=N и ,
размера N(k) × М и список пар L(k), содержащий набор пар номеров перехватчиков и назначенных им целей. На первом шаге k=1 полагают N(1)=N и ,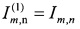 а L(1) полагают пустым. На шаге с номером k решают «задачу о назначениях» [6] с матрицей стоимости
а L(1) полагают пустым. На шаге с номером k решают «задачу о назначениях» [6] с матрицей стоимости 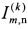 с помощью «венгерского алгоритма» [6], получая тем самым оптимальное с точки зрения минимума суммарных затрат
с помощью «венгерского алгоритма» [6], получая тем самым оптимальное с точки зрения минимума суммарных затрат
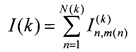
назначение целей перехватчикам в виде набора пар A(k) перехватчик-цель вместе с соответствующими траекториями перехвата. После этого полагают L(k+1) равным объединению L(k) и полученного набора A(k), N(k+1)=N(k)-М, а матрицу 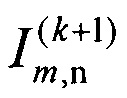 получают из
получают из 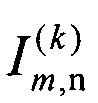 удалением столбцов с номерами перехватчиков из А(k). Если N(k+1)>0, то переходят к k+1 шагу, в противном случае процедуру назначения завершают и формируют итоговый список пар L=L(k+1), содержащий назначение целей для перехватчиков.
удалением столбцов с номерами перехватчиков из А(k). Если N(k+1)>0, то переходят к k+1 шагу, в противном случае процедуру назначения завершают и формируют итоговый список пар L=L(k+1), содержащий назначение целей для перехватчиков.
Сформированный в итерационной процедуре список назначения L по линиям связи передают в систему командного управления, в которой формируют сигналы управления перехватчиками, обеспечивающие их наведение на выбранные цели.
Следует отметить, что для использования алгоритма необходимы оценки: векторов скорости всех перехватчиков и целей; векторов относительного положения для каждой пары перехватчик - цель; максимальных ограничений на величины скорости и ускорения перехватчиков. Эти данные могут быть представлены в любой форме: в декартовых или полярных координатах, в абсолютных или относительных величинах. Нужно лишь указать способ вычисления коэффициентов (12).
Работоспособность разработанного алгоритма (2) - (21) исследовалась в процессе имитационного моделирования. В качестве примера рассмотрим процедуру перехвата целей 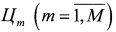 перехватчиками
перехватчиками  .
.
Схема расположения N=3 перехватчиков и М=2 целей при моделировании целераспределения с выбыванием одного перехватчика показана на фиг. 2. По результатам выполнения алгоритма (2)-(21) на вторую цель были назначены первый и третий перехватчик, а на первую цель - второй перехватчик. В соответствии с указанным назначением цели и перехватчики двигались до момента, когда перехватчики и цели переместились в точки, отмеченные звездочками. В этот момент первый перехватчик выбывает из преследования второй цели. Повторное выполнение алгоритма (2)-(21) определяет назначение первой цели для первого перехватчика и второй цели для третьего перехватчика, после чего происходит полет перехватчиков и целей до перехвата.
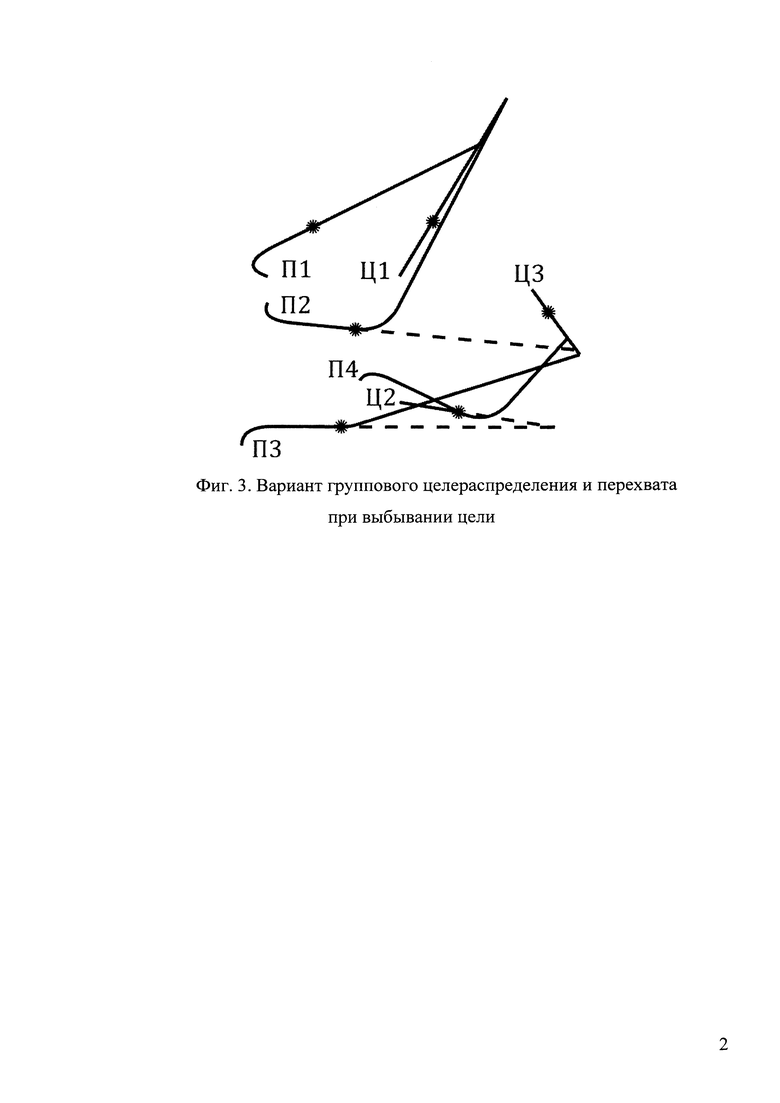
Схема расположения N=4 перехватчиков и М=3 целей при моделировании целераспределения с выбыванием одной цели показана на фиг. 3. По результатам выполнения алгоритма (2) - (21) на первую цель был назначен первый перехватчик, на вторую цель были назначены третий и четвертый перехватчики, а на третью цель был назначен второй перехватчик. В момент времени, когда перехватчики и цели переместились в точки, отмеченные звездочками, вторая цель перехвачена четвертым перехватчиком и считается уничтоженной. Повторное выполнение алгоритма (2) - (21) определяет назначение первой цели для первого перехватчика и второго перехватчика, а третья цель назначена для третьего и четвертого перехватчиков.
Полученный способ группового целераспределения подтвердил свою эффективность в широком поле условий применения. Его достоинством является то, что он позволяет обеспечить не только назначение всех перехватчиков на цели, но и построение предполагаемых траекторий перехвата с учетом реальных ограничений на предельно допустимые скорости и ускорения перехватчиков и возможного выбывания участников перехвата.
Предложенный способ можно использовать для реализации различных методов наведения.
Промышленная применимость предлагаемого технического решения подтверждается также возможностью реализации его назначения с помощью стандартных бортовых вычислительных средств.
Следует отметить, что предлагаемый способ следует общей схеме, используемой в отечественных авиационных комплексах радиолокационного дозора и наведения.
Список использованных источников
1. Е.А. Федосов. Реализация сетецентрической технологии ведения боевых действий потребует создания БРЛС нового поколения. // Фазотрон. 2007. №1, 2.
2. R. Ahuja, A. Kumar, J. Krishna, J. Orlin. Exact and heuristic algorithms for the weapon - target assignment problem. // Operations research, 2007, 55, №6, pp. 1136-1146.
3. J. Zhang, С. Нu, X. Wang, D. Yuan. ACGA algorithm of solving weapon - target assignment problem. // Open journal of applied sciences, 2012.
4. В.И. Меркулов, A.C. Пляшечник. Групповое целераспределение в воздушном противоборстве. // Информационно-измерительные и управляющие системы. 2016. №7. С. 59-63.
5. М.А. Jenkins. Algorithm 493: Zeros of a real polynomial. // ACM transactions on mathematical software, 1975, 1, №2, pp. 178-189.
6. J. Munkres. Algorithms for assignment and transportation problems. // Journal of the society for industrial and applied mathematics, 2000, 5, №1, pp. 32-38.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ автоматического группового целераспределения истребителей с учетом приоритета целей | 2018 |
|
RU2690234C1 |
| Способ автоматического группового целераспределения беспилотных летательных аппаратов и система для его реализации | 2022 |
|
RU2781881C1 |
| СПОСОБ НАВЕДЕНИЯ НА ВЫСОКОСКОРОСТНЫЕ ВЫСОКОМАНЕВРЕННЫЕ ВОЗДУШНЫЕ ОБЪЕКТЫ | 2020 |
|
RU2751378C1 |
| Способ наведения инерционного летательного аппарата с учетом несоответствия динамических свойств цели и перехватчика | 2019 |
|
RU2727777C1 |
| Способ перехвата интенсивно маневрирующих высокоскоростных воздушно-космических объектов | 2017 |
|
RU2666069C1 |
| СПОСОБ ПЕРЕХВАТА ПРИОРИТЕТНОЙ ЦЕЛИ, ОБЕСПЕЧИВАЮЩИЙ СРЫВ НАВЕДЕНИЯ ИСТРЕБИТЕЛЕЙ СОПРОВОЖДЕНИЯ | 2020 |
|
RU2742737C1 |
| Способ управления вооружением многофункциональных самолетов тактического назначения и система для его осуществления | 2020 |
|
RU2757094C1 |
| Способ управления группой беспилотных летательных аппаратов с учетом степени опасности окружающих объектов | 2019 |
|
RU2728197C1 |
| СПОСОБ ПРОГНОЗИРОВАНИЯ КООРДИНАТ ВОЗМОЖНОЙ ТОЧКИ ПЕРЕХВАТА ЛЕТАТЕЛЬНОГО АППАРАТА | 1992 |
|
RU2027198C1 |
| СПОСОБ ИНДИВИДУАЛЬНОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА НА ВОЗДУШНУЮ ЦЕЛЬ В СОСТАВЕ ПЛОТНОЙ ГРУППЫ | 2020 |
|
RU2742626C1 |

Изобретение относится к способу автоматического группового целераспределения истребителей с учетом возможного выбывания участников, который заключается в том, что для каждого перехватчика формируют функционал эффективности перехвата, путем решения множества численных уравнений получают оптимальное назначение целей перехватчикам вместе с траекториями перехвата, формируют сигналы управления перехватчиками, обеспечивающие их наведение на выбранные цели. Обеспечивается автоматическое оптимальное назначение целей перехватчикам с возможностью перераспределения целей при выбывании участников. 3 ил.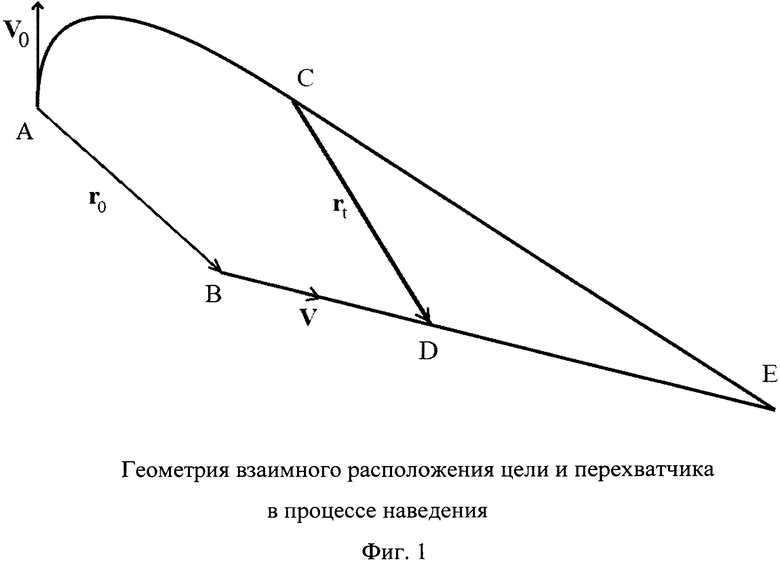
Способ автоматического группового целераспределения истребителей с учетом возможного выбывания участников, заключающийся в том, что для каждого n-го перехватчика  и m-й цели
и m-й цели 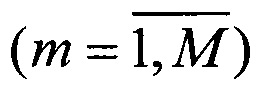 формируют функционал
формируют функционал
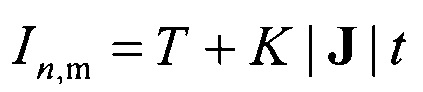 (1)
(1)
эффективности перехвата,
где
Т - время перехвата,
К - коэффициент штрафа,
J - вектор ускорения перехватчика,
t - время действия ускорения перехватчика, далее в фильтрах перехватчика формируют оптимальные оценки параметров
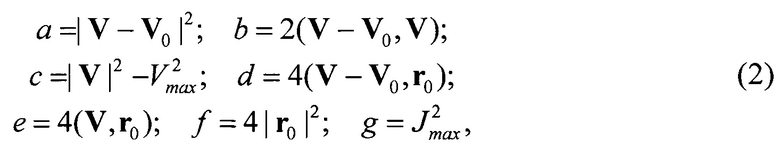
где
V - вектор скорости цели,
V0 - вектор скорости перехватчика,
r0 - вектор положения цели относительно перехватчика,
Vmax - максимально допустимая величина скорости перехватчика,
Jmax - максимально допустимая величина ускорения перехватчика, далее формируют условия реализации ограничений в виде

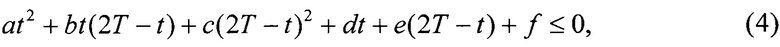


после чего формируют список пар (T, t), последовательно решая с помощью известных алгоритмов численного нахождения корней многочленов следующие семь задач:
а) решают систему уравнений

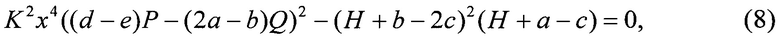
где
х, у - вспомогательные переменные;
Р=2ау+b+dx; Q=2ƒx+е+dy; Н=(d-е)х+(2а-b)у,
затем для всех полученных пар х, у находят пары T, t по формулам
Т=(у+1)/2х;
t=у/x,
и те пары, которые удовлетворяют (3), (5) и (6), заносят в общий список;
б) численно решают уравнение
((16-h)T2ƒ1(T)+ƒ2(T)2)2-ƒ1(T)(8Tƒ2(T)-hƒ1(T))2=0,
где
h=16(1+1/KJmax)2,ƒ1(T)=(4aT2+2dT+ƒ)/g, ƒ2(T)=(8aT+2d)/g,
и, вычислив таким образом T, находят соответствующие значения t по формуле
 ,
,
затем из всех полученных пар (T, t) те, которые удовлетворяют (4), (5) и (6), заносят в общий список;
в) численно решают уравнение
K2z4(ƒz+d)2=ƒz2+2dz+4a,
где
z - вспомогательная переменная,
находят соответствующие значения Т=1/z и те пары значений T; t=T, для которых выполнены (3), (4) и (6), добавляют в общий список;
г) находят  и
и 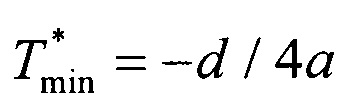 , если
, если  и величина промаха rmin находится в допустимых пределах, то добавляют пару значений
и величина промаха rmin находится в допустимых пределах, то добавляют пару значений 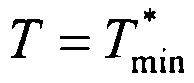 , t=0 в общий список;
, t=0 в общий список;
д) численно решают уравнение
cp1(t)2-p1(t)p3(t)p2(t)+p4(t)p2(t)2=0,
где
p1(t)=(b-2a)t+(e-d); p2(t)=gt2+(с-а); p3(t)=bt+e; p4(t)=at2+dt+ƒ,
находят соответствующие значения
T=(t-((c-a)z+(b-2a)t+(e-d))/gt2)/2
и заносят в общий список пары (T, t), удовлетворяющие неравенствам (5) и (6);
е) численно решают уравнение
gT4 -4aТ2 -2dT-ƒ=0
и пары T; t=T, удовлетворяющие неравенствам (4) и (6), добавляют в общий список;
ж) численно решают уравнение
(a+b+с)Т2+(е+d)T+ƒ=0
и пары (T; t=T), удовлетворяющие неравенствам (3) и (6), добавляют в общий список,
далее для всех пар величин (T, t) из построенного списка вычисляют вектор ускорения перехватчика
J=2(r0+T(V-V0))/t(2T-t)
и величину функционала (1), затем выбирают ту пару (T, t), для которой функционал (1) принимает минимальное значение, получив тем самым минимальное значение Im,n функционала (1) и траекторию перехвата, определяемую величинами (T, t, J), на которой реализуется указанный минимум, затем из величин Im,n составляют матрицу размера N×М, отличающийся тем, что описанную выше процедуру выполняют периодически, а также при изменении состава перехватчиков или целей, при этом процедуру назначения целей выполняют итерационно: на шаге с номером k строят матрицу эффективности  размера N(k)×М и список пар L(k), содержащий набор пар номеров перехватчиков и назначенных им целей, причем на первом шаге k=1 полагают N(l)=N и
размера N(k)×М и список пар L(k), содержащий набор пар номеров перехватчиков и назначенных им целей, причем на первом шаге k=1 полагают N(l)=N и 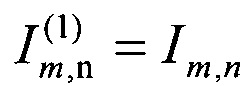 , a L(1) полагают пустым, затем на шаге с номером k решают «задачу о назначениях» с матрицей
, a L(1) полагают пустым, затем на шаге с номером k решают «задачу о назначениях» с матрицей 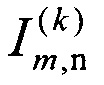 с помощью «венгерского алгоритма», получают тем самым оптимальное с точки зрения минимума суммарных затрат
с помощью «венгерского алгоритма», получают тем самым оптимальное с точки зрения минимума суммарных затрат
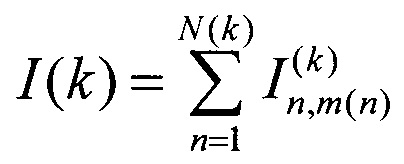
назначение целей перехватчикам в виде набора пар А(k) перехватчик-цель вместе с соответствующими траекториями перехвата, после этого полагают L(k+1) равным объединению L(k) и полученного набора А(k), N(k+1)=N(k) - М, а матрицу  получают из
получают из 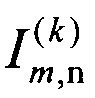 удалением столбцов с номерами перехватчиков из А(k), затем при условии N(k+1)>0 переходят к k+1 шагу, в противном случае процедуру назначения завершают и формируют итоговый список пар L=L(k+1), содержащий назначение целей для перехватчиков, причем для каждого перехватчика назначена своя цель, даже если их число превышает число целей,
удалением столбцов с номерами перехватчиков из А(k), затем при условии N(k+1)>0 переходят к k+1 шагу, в противном случае процедуру назначения завершают и формируют итоговый список пар L=L(k+1), содержащий назначение целей для перехватчиков, причем для каждого перехватчика назначена своя цель, даже если их число превышает число целей,
затем сформированный в итерационной процедуре список назначения L по командным радиолиниям связи передают в систему командного управления, в которой формируют сигналы управления перехватчиками, обеспечивающие их наведение на выбранные цели.
| СПОСОБ РАНЖИРОВАНИЯ ЦЕЛЕЙ | 2000 |
|
RU2190863C2 |
| СПОСОБ ГРУППОВОГО ОПОЗНАВАНИЯ ОБЪЕКТОВ ("СВОЙ-ЧУЖОЙ") И ОБЕСПЕЧЕНИЯ ЦЕЛЕУКАЗАНИЯ НА ОСНОВЕ БЕСПРОВОДНОЙ СИСТЕМЫ ПОЗИЦИОНИРОВАНИЯ В РЕАЛЬНОМ МАСШТАБЕ ВРЕМЕНИ И ИНТЕЛЛЕКТУАЛЬНЫХ РАДАРОВ | 2009 |
|
RU2507538C2 |
| В.И | |||
| МЕРКУЛОВ, А.С | |||
| ПЛЯШЕЧНИК, ГРУППОВОЕ ЦЕЛЕРАСПРЕДЕЛЕНИЕ В ВОЗДУШНОМ ПРОСТРАНСТВЕ, ИНОФРМАЦИОННО-ИЗМЕРИТЕЛЬНЫЕ И УПРАВЛЯЮЩИЕ СИСТЕМЫ, ИЗДАТЕЛЬСТВО "РАДИОТЕХНИКА" 2016 c.59-63 | |||
| Штамп для обтяжки с формовкой | 1991 |
|
SU1794535A1 |
Авторы
Даты
2019-04-16—Публикация
2017-12-22—Подача