Изобретение относится к следящим системам автоматического управления, выходной сигнал которых отслеживает заданный программный сигнал, в частности, к следящим системам автоматического управления нестационарным объектом, описываемым векторно-матричными уравнениями
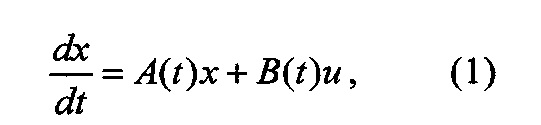
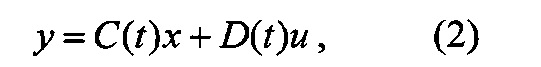

где t - время;
x(t) - n-мерный вектор состояния;
u(t) - r-мерный вектор управления;
y(t) - m-мерный выходной сигнал;
z(t) - m-мерный программный сигнал;
e(t) - m-мерный вектор ошибки отслеживания заданной программы;
A(t), B(t), C(t), D(t) - матрицы размерности n×n, n×r, m×n и m×r соответственно.
В теории и практике автоматического управления известна оптимальная следящая система управления нестационарным динамическим объектом, выбранная в качестве прототипа, содержащая первый векторный сумматор (ВС), к входам которого подключены выходы первого и второго матричных коэффициентов усиления (МКУ), а выход которого через векторный интегратор (ВИ) соединен с входами первого, третьего и четвертого МКУ; вход второго МКУ через пятый МКУ подключен к выходу второго ВС, инвертированный вход которого подключен к выходу четвертого МКУ, а неинвертированный вход - через шестой МКУ к выходу задатчика дополнительного программного сигнала (ДПС), при этом неинвертированный и инвертированный входы третьего ВС соединены с выходами третьего МКУ и задатчика основного программного сигнала (ОПС) (см. [1],стр. 157).
Известная следящая система позволяет реализовать управление линейными нестационарными динамическими объектами, для которых вектор выходного сигнала у зависит только от вектора состояния x (т.е. при D(t) ≡ 0)

Как показано в [1], при соответствующем выборе четвертого и пятого матричных коэффициентов усиления и дополнительного программного сигнала, известная следящая система в случае D(t) ≡ 0 является оптимальной по критерию минимума квадратичного функционала
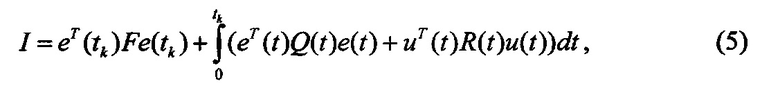
где tk - конечное время.
Однако известная следящая система неприменима в тех случаях, когда выходной сигнал у зависит не только от вектора состояния x, но и от вектора управления u (см. (2)).
Например, в задаче ограничения газодинамических нагрузок на сооружения стартового комплекса, создаваемых струями двигателей ракеты космического назначения (РКН), требуется осуществить управление положением следов струй на стартовой плоскости по заданной программе. При этом компонентами вектора состояния объекта управления являются смещение 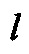 и скорость смещения
и скорость смещения 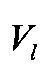 центра масс РКН в заданной плоскости (плоскости увода РКН), а также угол тангажа
центра масс РКН в заданной плоскости (плоскости увода РКН), а также угол тангажа 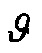 и угловая скорость тангажа ω в указанной плоскости. Выходным сигналом объекта является положение следа струи двигателя на стартовой плоскости
и угловая скорость тангажа ω в указанной плоскости. Выходным сигналом объекта является положение следа струи двигателя на стартовой плоскости 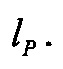 Необходимо, чтобы на начальном участке полета РКН положение струи
Необходимо, чтобы на начальном участке полета РКН положение струи 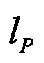 «отслеживало» заданное программное (изменяющееся во времени) значение
«отслеживало» заданное программное (изменяющееся во времени) значение 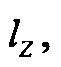 при этом ошибка слежения должна быть минимальной. Управляющим сигналом является угол отклонения камеры сгорания двигателя (вместе с его соплом) δ. Очевидно, что выходной сигнал
при этом ошибка слежения должна быть минимальной. Управляющим сигналом является угол отклонения камеры сгорания двигателя (вместе с его соплом) δ. Очевидно, что выходной сигнал 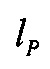 зависит не только от компонент вектора состояния
зависит не только от компонент вектора состояния 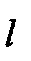 и
и 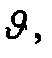 но и от управляющего сигнала δ. Известная следящая система (прототип) в рассматриваемом случае не обеспечивает необходимого качества управления положением следа струи двигателя.
но и от управляющего сигнала δ. Известная следящая система (прототип) в рассматриваемом случае не обеспечивает необходимого качества управления положением следа струи двигателя.
Задачей предлагаемого изобретения является разработка оптимальной по критерию минимума функционала (5) следящей системы автоматического управления нестационарным динамическим объектом, описываемым уравнениями (1) - (3), т.е. для случая, когда выходной сигнал у зависит не только от вектора состояния x, но и от вектора управления u.
Техническим результатом предлагаемого изобретения является расширение области применимости следящей системы.
Указанный технический результат достигается тем, что в систему, содержащую первый ВС, к входам которого подключены выходы первого и второго МКУ, а выход которого через ВИ соединен с входами первого, третьего и четвертого МКУ; вход второго МКУ через пятый МКУ подключен к выходу второго ВС, инвертированный вход которого подключен к выходу четвертого МКУ, а неинвертированный вход - через шестой МКУ к выходу задатчика ДПС, при этом неинвертированный и инвертированный входы третьего ВС соединены с выходами третьего МКУ и задатчика ОПС, в соответствии с изобретением введены седьмой и восьмой МКУ, причем выход пятого МКУ через седьмой МКУ подключен к неинвертированному входу третьего ВС, а выход задатчика ОПС через восьмой МКУ подключен к неинвертированному входу второго ВС.
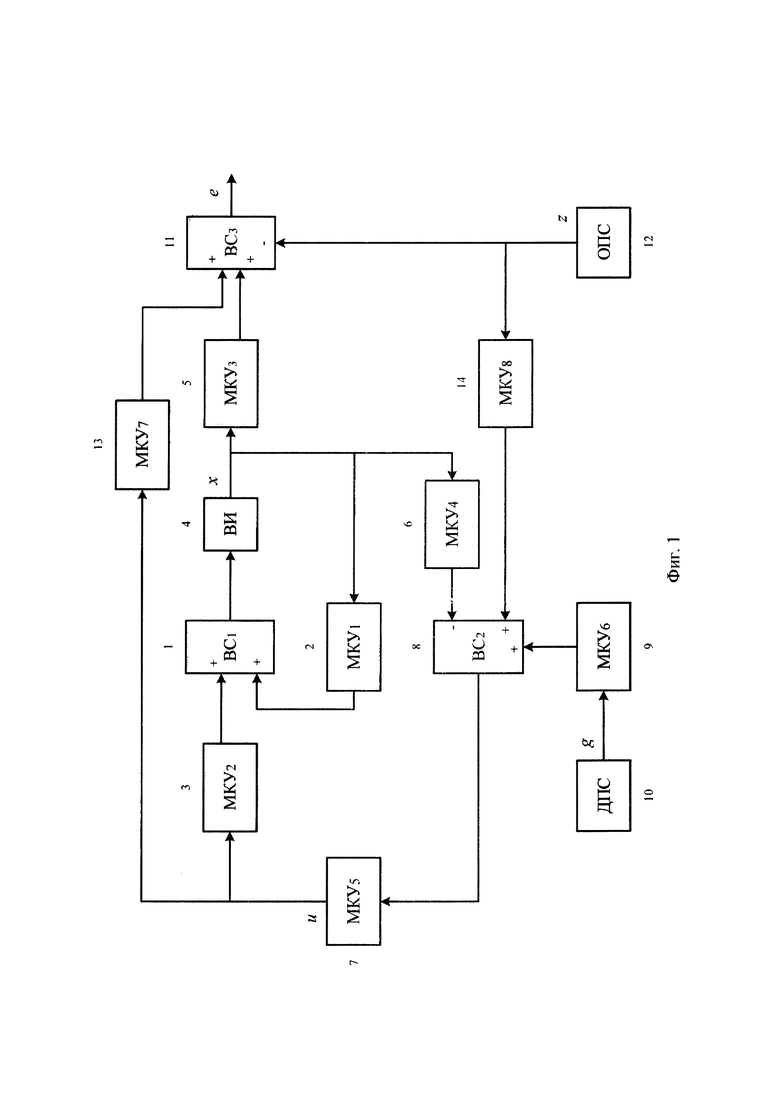
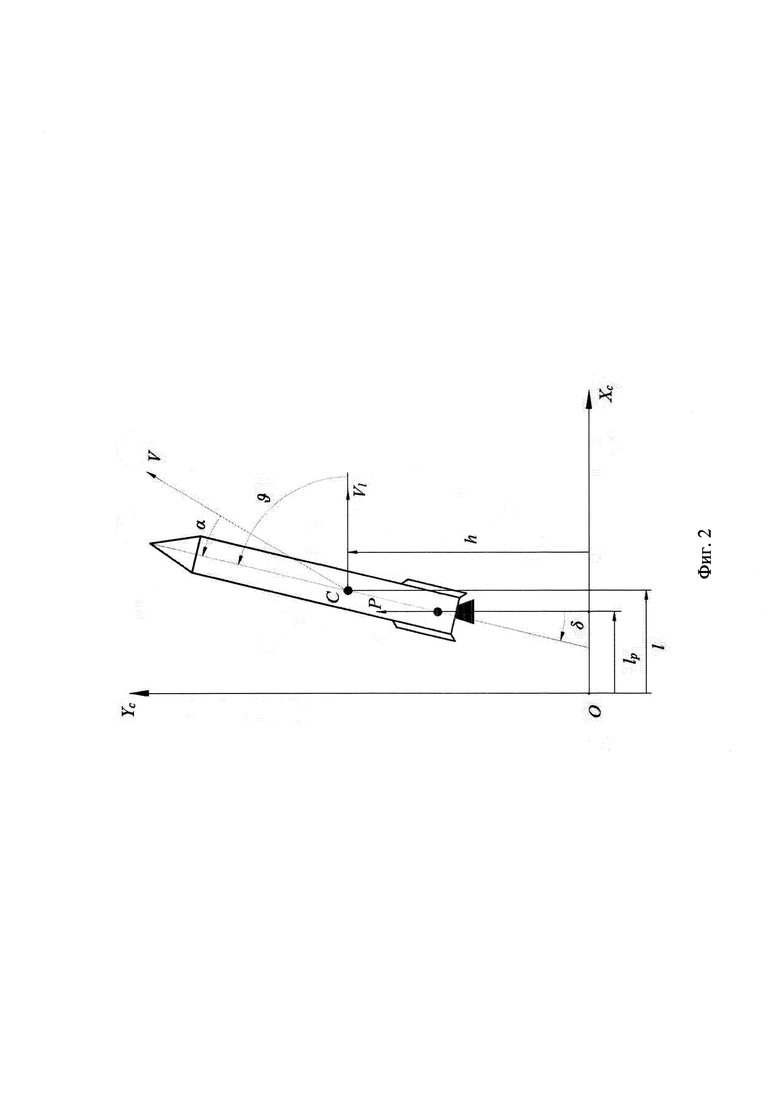
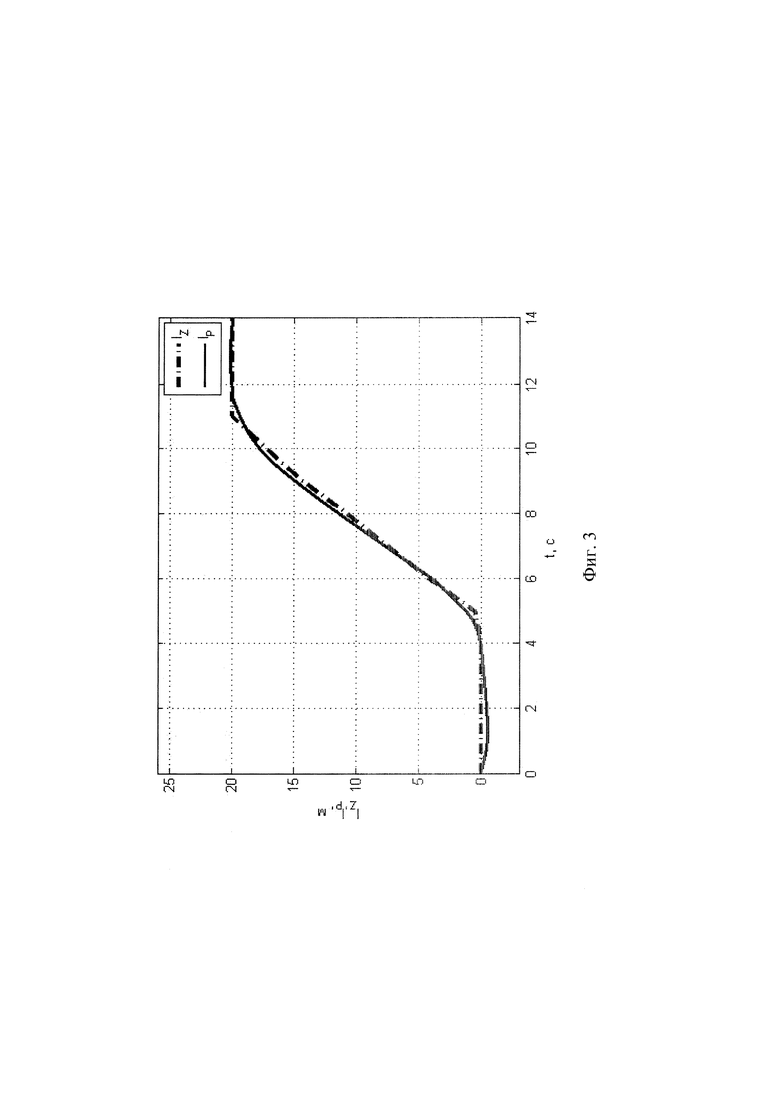
Сущность предлагаемого изобретения иллюстрируется фиг. 1-3. Фиг. 1 - Блок-схема предлагаемой следящей системы. Фиг. 2 - Схема движения РКН на начальном участке полета. Фиг. 3 - Результаты математического моделирования. Зависимости от времени параметров движения РКН на начальном участке полета.
Следящая система содержит первый ВС 1, к входам которого подключены выходы первого и второго МКУ 2 и 3, а выход которого через ВИ 4 соединен с входами первого, третьего и четвертого МКУ 2, 5 и 6 соответственно; вход второго МКУ 3 через пятый МКУ 7 подключен к выходу второго ВС 8, инвертированный вход которого подключен к выходу четвертого МКУ 6, а неинвертированный вход - через шестой МКУ 9 к выходу задатчика ДПС 10, при этом неинвертированные и инвертированный входы третьего ВС 11 соединены с выходами третьего МКУ 5, задатчика ОПС 12 и через седьмой МКУ 13 с выходом пятого МКУ 7, а выход задатчика ОПС 12 через восьмой МКУ 14 подключен к неинвертированному входу второго ВС 8.
Объект управления для предлагаемой следящей системы описывается системой уравнений (1) - (3). Вектор состояния x формируется на выходе ВИ 2, вектор управления u - на выходе пятого МКУ 7, задатчик ОПС 12 выдает программный сигнал z, третий ВС 11 вычисляет вектор е ошибки слежения выходного сигнала y за программным сигналом z. Значения первого, второго, третьего и седьмого матричных коэффициентов усиления 2, 3, 5 и 13 равны соответственно А, В, С и D. Покажем, что остальные МКУ предлагаемой следящей системы, а также дополнительный программный сигнал g, вырабатываемый задатчиком ДПС 10, могут быть выбраны таким образом, чтобы предлагаемая система, как и система-прототип была оптимальной по критерию минимума квадратичного функционала (5).
В соответствии с принципом максимума [1] оптимальное управление должно минимизировать функцию
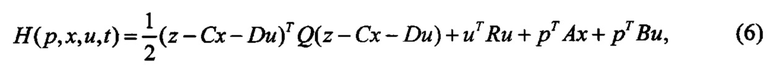
где вектор-функция p(t) удовлетворяет системе уравнений 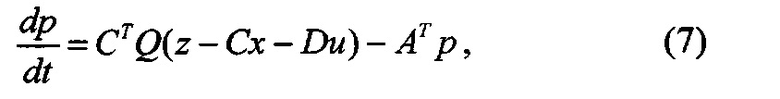
Найдем управление u*, минимизирующее функцию Н:
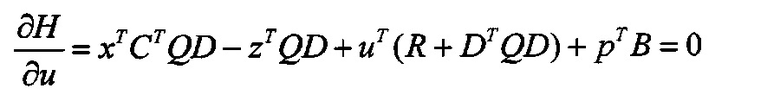
Решая это уравнение, получим
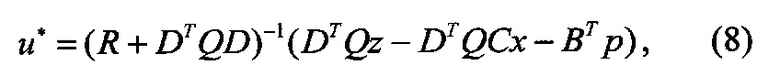
Подставляя управление (8) в уравнения (1) и (7), получим
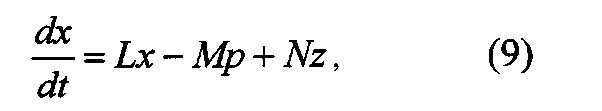
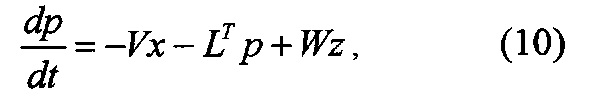
где L=A-B(R+DTQD)-1DTQC
М=B(R+DTQD)-1BT
N=B(R+DTQD)-1DTQ
V=CTQC-CTQD(R+DTQD)-1DTQC
W=CTQ-CTQD(R+DTQD)-1DTQ
Система (9), (10) представляет собой неоднородную линейную систему дифференциальных уравнений относительно переменных x, p. Решение этой системы должно удовлетворять граничным условиям

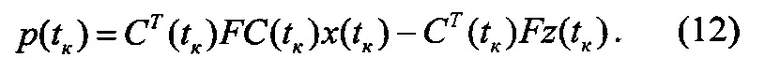
Представим вектор-функцию p в виде
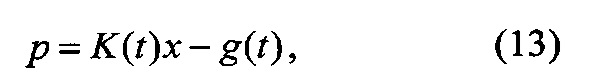
где K(t) - квадратная матрица размера n×n;
g(t) - n-мерный вектор. Найдем уравнения для определения K(t) и g(t). Для этого продифференцируем обе части уравнения (11) по времени
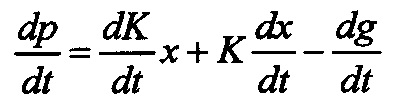
С учетом уравнений (9), (10) и (13)
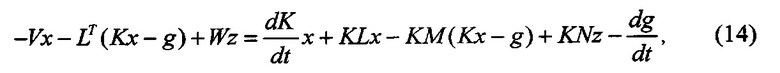
Приравнивая коэффициенты при x и свободные члены в обеих частях равенства (14), получим уравнения
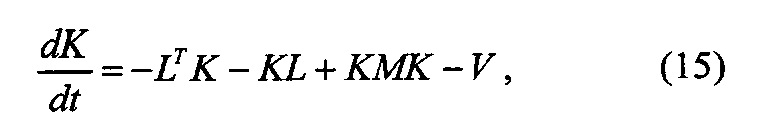
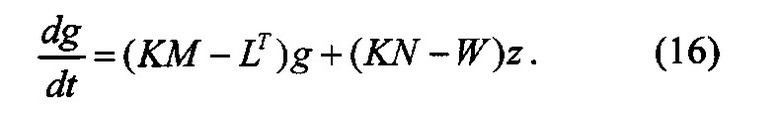
Из граничного условия (12) и формулы (13) следует, что матрица K(t) и вектор g(t) удовлетворяют граничным условиям
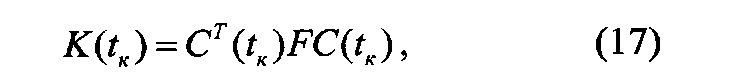
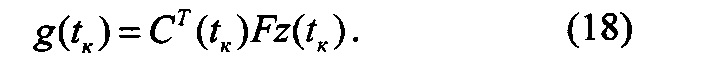
Оптимальное управление u*, как функция вектора состояния, имеет вид
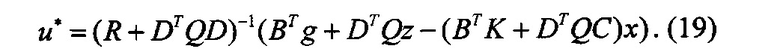
В таблице 1 указаны значения матричных коэффициентов усиления, реализующие полученное оптимальное управление в предлагаемой следящей системе.
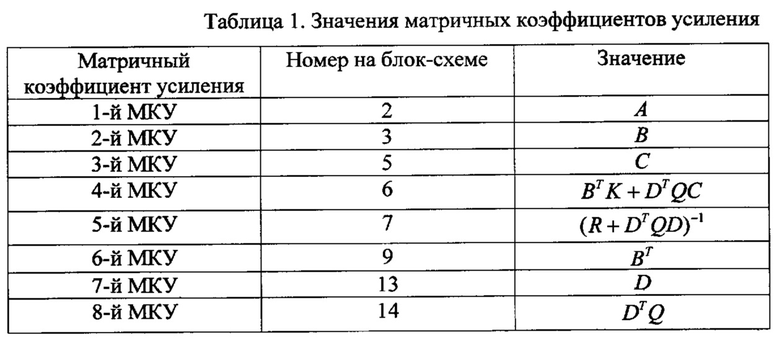
Используемая в вычислении значения четвертого МКУ матрица K(t) рассчитывается заранее как решение уравнения (15) с граничным условием (17). Вектор дополнительного программного сигнала g(t) на выходе задатчика ДПС, также является предварительно вычисленным решением уравнения (16) с граничным условием (18). Матрицы F, Q и R в квадратичном функционале (5) назначаются в каждом конкретном случае исходя из существующих требований к допустимой ошибке отслеживания выходным сигналом его программного значения, а также из располагаемого диапазона изменения управляющего сигнала.
Таким образом, благодаря реализации предложенного в изобретении технического решения, достигается расширение области применимости следящей системы, а именно обеспечивается оптимальное по критерию минимума квадратичного функционала автоматическое управление нестационарным динамическим объектом в случае, когда выходной сигнал у зависит не только от вектора состояния x, но и от вектора управления и.
В качестве примера использования следящей системы предлагается рассмотреть систему управления движением РКН, задача которой состоит в уводе газодинамических струй двигателей РКН от сооружений стартового комплекса по заданной программе увода на начальном участке полета (см. Фиг. 2).
Численные результаты функционирования следящей системы в составе системы управления РКН показывают работоспособность и эффективность разработанного изобретения. На Фиг. 3 проиллюстрирован результат отслеживания программной траектории следа струи РКН. Ошибка рассогласования между текущим и программным положениями следов струи РКН не превышает допустимый предел, в связи с чем можно утверждать, что разработанное изобретение с заданной точностью отслеживает программное положение следа струи на стартовой плоскости.
Литература
1. В.А. Иванов, Н.В. Фалдин. Теория оптимальных систем автоматического управления. М., «Наука», 1981
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ КОМБИНИРОВАННОГО НАВЕДЕНИЯ ЛЕТАТЕЛЬНОГО АППАРАТА | 2014 |
|
RU2586399C2 |
| УСТРОЙСТВО СЛЕДЯЩЕГО УПРАВЛЕНИЯ ПРОДОЛЬНЫМ ДВИЖЕНИЕМ АВТОМОБИЛЯ | 1999 |
|
RU2161814C1 |
| СПОСОБ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ В НЕЛИНЕЙНОЙ СИСТЕМЕ И СЛЕДЯЩАЯ СИСТЕМА ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1999 |
|
RU2149437C1 |
| АДАПТИВНАЯ СИСТЕМА ТЕРМИНАЛЬНОГО УПРАВЛЕНИЯ | 2012 |
|
RU2500009C1 |
| ДВУХКАНАЛЬНАЯ СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ОБЪЕКТОМ | 2000 |
|
RU2171489C1 |
| УСТРОЙСТВО ДЛЯ ФОРМИРОВАНИЯ ПРОГРАММНЫХ СИГНАЛОВ УПРАВЛЕНИЯ ПРОСТРАНСТВЕННЫМ ДВИЖЕНИЕМ ДИНАМИЧЕСКИХ ОБЪЕКТОВ | 2013 |
|
RU2522856C1 |
| Адаптивный идентификатор | 1989 |
|
SU1670674A1 |
| СИСТЕМА АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ОБЪЕКТОМ | 1999 |
|
RU2150728C1 |
| КОМБИНИРОВАННАЯ СИСТЕМА КООРДИНАТНО-ПАРАМЕТРИЧЕСКОГО УПРАВЛЕНИЯ НЕСТАЦИОНАРНЫМ ОБЪЕКТОМ | 2004 |
|
RU2279116C2 |
| СИСТЕМА НЕПРЯМОГО АДАПТИВНОГО УПРАВЛЕНИЯ | 2007 |
|
RU2381539C2 |
Следящая система автоматического управления нестационарным объектом содержит три векторных сумматора, восемь матричных коэффициентов усиления, векторный интегратор, задатчик дополнительного программного сигнала, задатчик основного программного сигнала, соединенные определенным образом. Обеспечивается расширение области применимости следящей системы. 3 ил., 1 табл.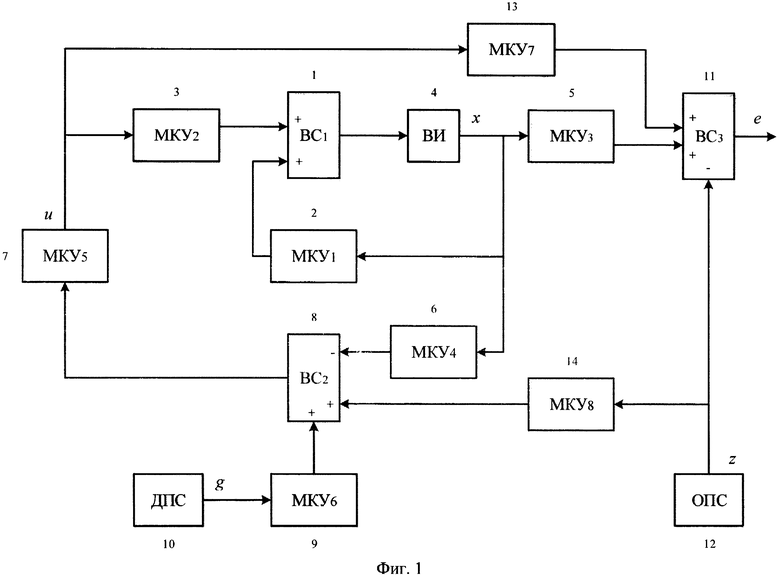
Следящая система автоматического управления нестационарным динамическим объектом, содержащая первый векторный сумматор, к входам которого подключены выходы первого и второго матричных коэффициентов усиления, а выход которого через векторный интегратор соединен с входами первого, третьего и четвертого матричных коэффициентов усиления; вход второго матричного коэффициента усиления через пятый матричный коэффициент усиления подключен к выходу второго векторного сумматора, инвертированный вход которого подключен к выходу четвертого матричного коэффициента усиления, а неинвертированный вход - через шестой матричный коэффициент усиления к выходу задатчика дополнительного программного сигнала, при этом неинвертированный и инвертированный входы третьего векторного сумматора соединены с выходами третьего матричного коэффициента усиления и задатчика основного программного сигнала, отличающаяся тем, что в систему введены седьмой и восьмой матричные коэффициенты усиления, причем выход пятого матричного коэффициента усиления через седьмой матричный коэффициент усиления подключен к неинвертированному входу третьего векторного сумматора, а выход задатчика основного программного сигнала через восьмой матричный коэффициент усиления подключен к неинвертированному входу второго векторного сумматора.
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ДИНАМИЧЕСКОГО ОБЪЕКТА ПО ПРОСТРАНСТВЕННОЙ ТРАЕКТОРИИ | 2011 |
|
RU2451970C1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ДИНАМИЧЕСКОГО ОБЪЕКТА ПО ПРОСТРАНСТВЕННОЙ ТРАЕКТОРИИ | 2010 |
|
RU2445670C1 |
| СПОСОБ УПРАВЛЕНИЯ ДВИЖЕНИЕМ ДИНАМИЧЕСКОГО ОБЪЕКТА ПО ТРАЕКТОРИИ | 2009 |
|
RU2406103C1 |
Авторы
Даты
2019-06-21—Публикация
2018-12-05—Подача