Настоящая заявка относится к назначению оценки релевантности для искусственных нейронных сетей. Такое назначение оценки релевантности может использоваться, например, для идентификации области, представляющей интерес (ROI).
Компьютерные программы способны успешно решать многие сложные задачи, такие как автоматическая классификация изображений и текста или оценка кредитоспособности человека. Алгоритмы машинного обучения особенно успешны, потому что они учатся на основе данных, т.е. программа получает большой маркированный (или слабо маркированный) набор для обучения, и после некоторой фазы обучения она может выполнять обобщение на новые ненаблюдавшиеся примеры. Многие банки имеют систему, которая классифицирует кредитоспособность (например, на основе возраста, адреса, дохода и т.д.) лица, которое подает заявку на получение кредита. Основным недостатком таких систем является интерпретируемость, т.е. система обычно не предоставляет информацию о том, почему и как она приняла решение (например, почему кто-то классифицируется как некредитоспособный); знания и отношения, которые определяют решение классификации, скорее являются ʺнеявнымиʺ.
Понимание и интерпретация решений классификации имеет большое значение во многих приложениях, поскольку позволяет проверять обоснование системы и предоставляет дополнительную информацию эксперту-человеку, например, банкиру, венчурному инвестору или врачу. Методы машинного обучения в большинстве случаев имеют недостаток, заключающийся в их действии по принципу черного ящика, не предоставляя никакой информации о том, что заставило их прийти к определенному решению. В общем случае сложные алгоритмы имеют гораздо лучшую производительность, чем простые (линейные) методы (при наличии достаточного количества данных обучения), однако им особенно не хватает интерпретируемости. В последнее время, классификаторы типа нейронных сетей становятся очень популярными и обеспечивают отличные результаты. Методы этого типа состоят из последовательности нелинейных отображений и особенно трудно интерпретируются.
В типичной задаче классификации изображений, например, может быть задано изображение (например, изображение акулы). См. фиг. 15. Алгоритм 900 машинного обучения (ML) классифицирует изображение 902 как принадлежащее к определенному классу 904 (например, 'изображения акулы'). Отметим, что набор 906 классов (например, акулы, лица, ночная жизнь, на улице) определен априори. Алгоритм 900 является черным ящиком, потому что он не сообщает пользователю, почему он пришел к решению о том, что изображение принадлежит к классу 'изображения акулы'. Было бы интересно объяснить это решение классификации на пиксельном уровне, например, чтобы увидеть, что изображение проклассифицировано как принадлежащее к классу 'изображения акулы', главным образом из-за плавника акулы. Такая ʺкарта релевантностиʺ проиллюстрирована на 908.
Классификация изображений стала ключевым компонентом многих приложений компьютерного зрения, например, поиска изображений [15], робототехники [10], медицинской визуализации [50], обнаружения объекта в радиолокационных изображениях [17] или обнаружения лица [49]. Нейронные сети [6] широко используются для этих задач и входят в число лучших конкурирующих предложений по классификации и ранжированию изображений, таких как ImageNet [11]. Однако, как и многие методы машинного обучения, эти модели часто не имеют прямой интерпретации предсказаний классификатора. Другими словами, классификатор действует как черный ящик и не предоставляет подробной информации о том, почему он достигает определенного решения классификации. То есть возможность интерпретации фиг. 15 недоступна.
Этот недостаток интерпретируемости обусловлен нелинейностью различных отображений, которые обрабатывают пикселы необработанных изображений в их представление признаков и из них в конечную функцию классификатора. Это является значительным недостатком в приложениях классификации, поскольку это мешает эксперту-человеку тщательно проверять решение классификации. Простой ответ ʺдаʺ или ʺнетʺ иногда имеет ограниченное значение в приложениях, где такие вопросы, как, где что-то происходит или как это структурировано, являются более релевантными, чем двоичная или действительнозначная одномерная оценка простого присутствия или отсутствия определенной структуры.
Несколько работ посвящены теме объяснения нейронных сетей. Работа [54] посвящена анализу решений классификаторов в нейронах, применимых также к пиксельному уровню. Здесь выполняется послойная инверсия вниз от выходных уровней к входным пикселам для архитектуры сверточных сетей [23]. Эта работа специфична для архитектуры сверточных нейронных сетей со слоями нейронов с выпрямленными линейными активационными функциями. См. [42], где устанавливается интерпретация работы в [54] как приближение к частным производным относительно пикселов во входном изображении. В высокоуровневом смысле, работа в [54] использует метод из своей собственной предшествующей работы в [55], которая решает задачи оптимизации, чтобы восстановить вход изображения, как проецировать отклики в направлении к входам, [54] использует выпрямленные линейные блоки, чтобы проецировать информацию из развернутых карт по направлению к входам с одной целью - гарантировать, что карты признаков будут неотрицательными.
Другой подход, лежащий между частными производными во входной точке x и полным рядом Тейлора вокруг другой точки x0, представлен в [42]. Эта работа использует точку x0 иную, чем входная точка x, для вычисления производной и остаточного смещения, которые не заданы дополнительно, но избегает по неопределенной причине использования полного линейного весового члена x-x0 ряда Тейлора. Количественное определение входных переменных с использованием модели нейронной сети также изучалось в конкретных областях, таких как экологическое моделирование, где [16, 34] исследовали большой ансамбль возможных анализов, включая вычисления частных производных, анализ возмущений, анализ весов и изучение влияния включения и удаления переменных во время обучения. Другой подход к пониманию решений в нейронной сети заключается в том, чтобы подгонять более интерпретируемую модель (например, дерево решений) к функции, на которой обучается нейронная сеть [41], и извлекать правила, изученные этой новой моделью.
Тем не менее, по-прежнему существует потребность в надежной, простой в реализации и широко применимой концепции для реализации задачи назначения оценки релевантности для искусственных нейронных сетей.
Соответственно, задачей настоящего изобретения является предоставление концепции для назначения оценки релевантности набору элементов, к которым применяется искусственная нейронная сеть, каковая концепция применима к более широкому набору искусственных нейронных сетей и/или снижает вычислительные усилия.
Эта задача решается предметом независимых пунктов формулы изобретения.
Основное новшество настоящей заявки состоит в том, что задача назначения оценки релевантности набору элементов, к которым применяется искусственная нейронная сеть, может быть получена путем перераспределения начального значения релевантности, полученного из выхода сети, на набор элементов посредством обратного распространения начальной оценки релевантности через искусственную нейронную сеть, чтобы получить оценку релевантности для каждого элемента. В частности, это обратное распространение применимо к более широкому набору искусственных нейронных сетей и/или при более низких вычислительных затратах, за счет выполнения его таким образом, что, для каждого нейрона, предварительно перераспределенные оценки релевантности набора соседних вниз по потоку (нисходящих) нейронов соответствующего нейрона распределяются по набору соседних вверх по потоку (восходящих) нейронов соответствующего нейрона в соответствии с функцией распределения.
Предпочтительные реализации и применения настоящего изобретения в соответствии с различными вариантами осуществления являются предметом зависимых пунктов формулы изобретения, и предпочтительные варианты осуществления настоящей заявки описаны ниже более подробно в отношении фигур, среди которых
Фиг. 1а показывает схему примера предсказания с использованием искусственной нейронной сети, к которой может быть применено назначение оценки релевантности с использованием обратного распространения в соответствии с вариантами осуществления настоящего изобретения;
Фиг. 2а показывает схему, иллюстрирующую процесс обратного распространения, используемый в соответствии с вариантами осуществления настоящей заявки, использующими в качестве примера искусственную нейронную сеть, показанную на фиг.1, в качестве основы;
Фиг. 1b и 2b показывают модификацию фиг. 1a и 2a, согласно которой сеть и назначение релевантности действуют на картах признаков, а не на пикселах изображения;
Фиг. 1с и 2с показывают возможность применения фиг. 1а и 2а на цветных изображениях;
Фиг. 1d и 2d показывают модификацию фиг. 1a и 2a, согласно которым сеть и назначение релевантности действуют на текстах, а не на изображениях;
Фиг. 3 схематично иллюстрирует промежуточный нейрон искусственной нейронной сети и его соединение с соседними вверх по потоку (восходящими) и вниз по потоку (нисходящими) нейронами, причем также показаны три восходящих соседних нейрона;
Фиг. 4 показывает блок-схема устройства для назначения значений релевантности множеству элементов в соответствии с вариантом осуществления;
Фиг. 5 показывает классификатор в форме нейронной сети во время предсказания, wij являются весами соединения; ai является активацией нейрона i;
Фиг. 6 показывает классификатор нейронной сети, показанный на фиг.5, в течение времени вычисления послойной релевантности. 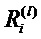 является релевантностью нейрона i, которая должна быть вычислена. Чтобы облегчить вычисление
является релевантностью нейрона i, которая должна быть вычислена. Чтобы облегчить вычисление 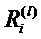 , вводим сообщения
, вводим сообщения 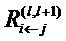 .
. 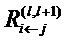 - это сообщения, которые необходимо вычислить таким образом, чтобы сохранялась послойная релевантность в уравнении (2). Сообщения отправляются из нейрона i к его входным нейронам j через соединения, используемые для классификации, например, 2 является входным нейроном для нейронов 4, 5, 6. Нейрон 3 является входным нейроном для 5, 6. Нейроны 4, 5, 6 являются входными для нейрона 7;
- это сообщения, которые необходимо вычислить таким образом, чтобы сохранялась послойная релевантность в уравнении (2). Сообщения отправляются из нейрона i к его входным нейронам j через соединения, используемые для классификации, например, 2 является входным нейроном для нейронов 4, 5, 6. Нейрон 3 является входным нейроном для 5, 6. Нейроны 4, 5, 6 являются входными для нейрона 7;
Фиг. 7 показывает примерную действительнозначную функцию предсказания для классификации с пунктирной черной линией, являющейся границей решения, которая отделяет синие точки в области -0.8 от зеленых точек в области 0.6-0.9. Первые точки обозначены отрицательно, последние точки обозначены положительно. На левой стороне изображен локальный градиент функции классификации в точке предсказания, а на правой стороне показана аппроксимация Тейлора относительно корневой точки на границе решения;
Фиг. 8 иллюстрирует пример для многослойной нейронной сети, аннотированной различными переменными и индексами, описывающими нейроны и взвешенные соединения. Слева: прямой проход. Справа: обратный проход;
Фиг. 9 иллюстрирует попиксельную декомпозицию для нейронной сети, обученной распознавать 1000 классов из набора данных ImageNet.
Фиг. 10 показывает эксперимент, согласно которому концепция вариантов осуществления настоящей заявки была применена к набору данных MNIST (Объединенный национальный институт стандартов и технологий), который содержит изображения чисел от 0 до 9, в качестве примера показывая, с правой стороны, тепловые карты, иллюстрирующие в качестве примера части вокруг чисел ʺ3ʺ и ʺ4ʺ, которые имеют высокую релевантность, чтобы распознавать эти числа как ʺ3ʺ и отличить соответствующее число от ʺ9ʺ соответственно;
Фиг. 11 показывает блок-схему системы обработки данных в соответствии с вариантом осуществления;
Фиг. 12 показывает блок-схему системы обработки данных в соответствии с вариантом осуществления, отличающимся от фиг. 11, в котором обработка выполняется на данных, из которых был получен набор элементов;
Фиг. 13 показывает блок-схему системы выделения (высвечивания) ROI в соответствии с вариантом осуществления;
Фиг. 14 показывает систему оптимизации нейронной сети в соответствии с вариантом осуществления; и
Фиг. 15 показывает схему, иллюстрирующую задачу назначения оценки релевантности относительно искусственной нейронной сети и отношение к обычной задаче предсказания искусственной нейронной сети.
Прежде чем описывать различные варианты осуществления настоящей заявки в отношении блок-схем, концепции, лежащие в основе этих вариантов осуществления, в первую очередь должны быть описаны путем краткого введения в искусственные нейронные сети и затем путем объяснения идей, лежащих в основе концепции вариантов осуществления.
Нейронная сеть представляет собой граф взаимосвязанных нелинейных блоков обработки (процессоров), которые могут обучаться, чтобы аппроксимировать комплексные отображения между входными данными и выходными данными. Отметим, что входными данными является, например, изображение (набор пикселов), а выходом является, например, решение классификации (в простейшем случае +1/-1, что означает ʺдаʺ, в изображении есть акула, или ʺнетʺ, в изображении нет акулы). Каждый нелинейный процессор (или нейрон) состоит из взвешенной линейной комбинации своих входов, к которым применяется нелинейная функция активации. Используя индекс i для обозначения нейронов, входящих в нейрон с индексом j, нелинейная функция активации определяется как:
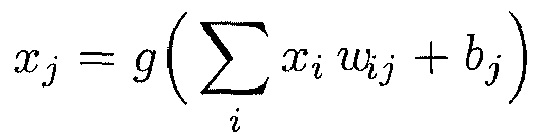
где g(⋅) - нелинейная монотонно возрастающая функция активации, wij - вес, связывающий нейрон i с нейроном j, и bj - член смещения. Нейронная сеть определяется ее структурой связности, ее нелинейной функцией активации и ее весами.
В нижеследующих вариантах осуществления используется концепция, которая может называться и называется в последующем описании распространением релевантности. Она перераспределяет доказательство (основание) для конкретной структуры в данных, как моделируется выходными нейронами, обратно на входные нейроны. Таким образом, она стремится дать объяснение своего собственного предсказания с точки зрения входных переменных (например, пикселов). Отметим, что эта концепция работает для любого типа (не имеющей петель) нейронной сети, независимо от количества слоев, типа функции активации и т.д. Таким образом, ее можно применять ко многим популярным моделям, так как многие алгоритмы могут быть описаны в терминах нейронных сетей.
Ниже приведена иллюстрация процедуры распространения релевантности для сети, состоящей из слоев свертки/субдискретизации, за которыми следует последовательность полностью связанных слоев.
В частности, фиг. 1а показывает пример искусственной нейронной сети упрощенным примерным образом. Искусственная нейронная сеть 10 состоит из нейронов 12, которые изображены на фиг. 1 как круги. Нейроны 12 взаимосвязаны друг с другом или взаимодействуют друг с другом. Как правило, каждый нейрон соединен с расположенными ниже по потоку (нисходящими) соседними (или последующими) нейронами, с одной стороны, и расположенными выше по потоку (восходящими) соседними (или предшествующими) нейронами, с другой стороны. Термины ʺвосходящийʺ, ʺпредшествующийʺ, ʺнисходящийʺ и ʺпоследующийʺ относятся к общему направлению 14 распространения, вдоль которого работает нейронная сеть 10, когда она применяется к набору 16 элементов, чтобы отображать набор 16 элементов на выход 18 сети, то есть выполнять предсказание.
Как показано на фиг. 1а, набор 16 элементов может, например, быть набором пикселов 22, формирующих изображение путем ассоциирования каждого пиксела с пиксельным значением, соответствующим цвету или интенсивности сцены, в пространственном местоположении, соответствующем положению соответствующего пиксела в массиве пикселов изображения 22. В этом случае, набор 16 представляет собой упорядоченный набор элементов, а именно, массив пикселов. В этом случае, элементы будут соответствовать отдельным пиксельным значениям, т.е. каждый элемент будет соответствовать одному пикселу. Дальше будет пояснено, что настоящая заявка не ограничивается полем изображений. Скорее, набор 16 элементов может представлять собой набор элементов без какого-либо порядка, определенного среди элементов. Комбинации между ними также могут иметь место.
Первый или самый нижний слой 24 нейронов 12 образует своего рода вход искусственной нейронной сети 10. То есть, каждый нейрон 12 этого нижнего слоя 24 принимает в качестве своих входных значений по меньшей мере поднабор из набора 16 элементов, то есть, по меньшей мере поднабор пиксельных значений. Объединение поднаборов элементов из набора 16, значения которых вводятся в некоторый нейрон 12 нижнего слоя 24, равно, например, набору 16, т.е., в случае фиг. 1а всему изображению 22. Иными словами, для каждого элемента набора 16, его значение вводится по меньшей мере в один из нейронов 12 нижнего слоя 24.
На противоположной стороне нейронной сети 10, то есть на ее нисходящей/выходной стороне, сеть 10 содержит один или несколько выходных нейронов 12', которые отличаются от нейронов 12 тем, что у первых нет нисходящих соседних/последующих нейронов. После применения к набору 16 и после завершения обработки, значения, хранящиеся в каждом выходном нейроне 12', образуют выход 18 сети. То есть, выход сети может, например, быть скаляром. В этом случае будет присутствовать только один выходной нейрон 12', и его значение после операции сети 10 будет формировать выход сети. Как проиллюстрировано на фиг. 1, такой выход сети может, например, быть мерой вероятности того, что набор 16 элементов, то есть в случае фиг. 1a изображение 22, принадлежит к определенному классу или нет. Выход 18 сети может, однако, альтернативно быть вектором. В этом случае существует более одного выходного нейрона 12', и значение каждого из этих выходных нейронов 12', как получено в конце операции сети 10, формирует соответствующий компонент выходного вектора сети. На фиг. 1 показано, например, что каждый компонент выхода 18 сети является мерой, измеряющей вероятность того, что набор 16 принадлежит к соответствующему классу, ассоциированному с соответствующим компонентом, например, к классу изображений ʺпоказывающих лодкуʺ, ʺпоказывающих грузовикʺ и ʺпоказывающих автомобильʺ. Другие примеры также возможны и будут представлены ниже.
Таким образом, суммируя вышеизложенное, нейронная сеть включает в себя нейроны 12, связанные между собой, чтобы отображать, в операции прямого распространения или нормальной операции, набор 16 элементов на нейронный выход. Подобно выходным нейронам 12', значение которых в конце операции сети формирует выход 18 сети, элементы набора 16, то есть пикселы изображения 22 в примерном случае фиг. 1a, могут рассматриваться как входные нейроны сети 10 с нейронами 12 и слоями, образованными при этом, являющимися промежуточными нейронами или промежуточными слоями, соответственно. В частности, входные нейроны могут соответственно рассматриваться как восходящие соседние или предшествующие нейроны промежуточных нейронов 12, а именно, таковых из слоя 24, так же как выходные нейроны 12' могут образовывать нисходящие соседние/последующие нейроны промежуточных нейронов 12, образующих, например, самый высокий промежуточный слой сети 10 или, если интерпретировать один или несколько выходных нейронов 12' как образующие самый верхний слой сети 10, второй по высоте слой сети 10.
Фиг. 1 показывает упрощенный пример нейронной сети 10, согласно которому нейроны 12 сети 10 строго упорядочены в слоях 26 в том смысле, что слои 26 образуют последовательность слоев с восходящими соседними/последующими нейронами определенного нейрона 12, все из которых являются членами непосредственно более низкого слоя относительно слоя, к которому принадлежит соответствующий нейрон 12, и все нисходящие соседние/последующие нейроны являются членами непосредственно более высокого слоя. Однако фиг. 1 не следует истолковывать как ограничение типа нейронных сетей 10, к которым могут быть применены варианты осуществления настоящего изобретения, описанные далее ниже, в отношении этой проблемы. Скорее, это строго многослойное расположение нейронов 12 может быть модифицировано в соответствии с альтернативными вариантами осуществления, например, когда восходящие соседние/предшествующие нейроны представляют собой поднабор из нейронов более чем одного предшествующего слоя, и/или нисходящие соседние/последующие нейроны представляют собой поднабор из нейронов более чем одного более высокого слоя.
Более того, хотя на фиг. 1 предполагается, что каждый нейрон 12 будет пересекаться только один раз во время операции прямого распространения сети 10, один или несколько нейронов 12 могут пересекаться два или более раз. Другие возможности варьирования будут рассмотрены ниже.
Как описано выше, при применении сети 10 к набору 16, то есть изображению 22 в примерном случае согласно фиг. 1а, сеть 10 выполняет операцию прямого распространения. Во время этой операции, каждый нейрон 12, который принял все свои входные значения от своих восходящих соседних/предшествующих нейронов, вычисляет, посредством соответствующей нейронной функции, выходное значение, которое называется его активацией. Эта активация, обозначенная xj в приведенном выше примерном уравнении, формирует затем входное значение каждого из нисходящих соседних/последующих нейронов. С помощью этой меры, значения элементов набора 16 распространяются через нейроны 12, чтобы завершиться в выходных нейронах 12'. Точнее, значения элементов набора 16 формируют входные значения нейронов 12 нижнего слоя сети 10, и выходные нейроны 12' принимают активации их восходящих соседних/предшествующих нейронов 12 в качестве входных значений и вычисляют их выходные значения, то есть выход 18 сети, посредством соответствующей нейронной функции. Нейронные функции, ассоциированные с нейронами 12 и 12' сети 10, могут быть равны между всеми нейронами 12 и 12' или могут различаться среди них, при этом ʺравенствоʺ означает, что нейронные функции являются параметризируемыми и параметры функции могут различаться среди нейронов, не препятствуя равенству. В случае варьирующихся/различных нейронных функций, эти функции могут быть равны между нейронами одного и того же слоя сети 10 или могут даже отличаться между нейронами в пределах одного слоя.
Таким образом, сеть 10 может быть реализована, например, в форме компьютерной программы, работающей на компьютере, то есть в программном обеспечении, но реализация в аппаратной форме, например, в виде электрической схемы, также будет осуществима. Каждый нейрон 12 вычисляет, как описано выше, активацию на основе своих входных значений, используя нейронную функцию, которая, например, представлена в приведенном выше явном примере как нелинейная скалярная функция g(⋅) линейной комбинации входных значений. Как описано, нейронные функции, ассоциированные с нейронами 12 и 12', могут быть параметризируемыми функциями. Например, в одном из конкретных примеров, описанных ниже, нейронные функции для нейрона j являются параметризируемыми с использованием смещения bj и веса wij для всех входных значений i соответствующего нейрона. Эти параметры проиллюстрированы на фиг. 1а c использованием пунктирного блока 28. Эти параметры 28 могут быть получены путем обучения сети 10. С этой целью сеть 10, например, повторно применяется к тренировочному (обучающему) набору для наборов 16 элементов, для которого известен корректный выход сети, то есть обучающему набору маркированных изображений в иллюстративном случае согласно фиг. 1а. Однако также могут существовать и другие возможности. Даже комбинация может быть осуществимой. Варианты осуществления, описанные ниже, не ограничиваются каким-либо источником или способом определения параметров 28. На фиг. 1а иллюстрируется, например, что восходящая (передняя) часть 21 сети 10, состоящая из слоев 26, продолжающихся от набора 16, т.е. входа сети, до промежуточного скрытого слоя, была искусственно сгенерирована или обучена, чтобы эмулировать извлечение признака изображения 22 посредством сверточных фильтров, например, так, что каждый нейрон (нисходящего) последующего слоя представляет собой значение признака из карт 20 признаков. Каждая карта 20 признаков, например, ассоциирована с определенной характеристикой или признаком или импульсным откликом или тому подобным. Соответственно, каждая карта 20 признаков может, например, рассматриваться как разреженно (суб-) дискретизированная отфильтрованная версия входного изображения 22, причем одна карта 20 признаков различается по ассоциированному признаку/характеристике/импульсному отклику ассоциированного фильтра от другой карты признаков. Если, например, набор 16 имеет Χ⋅Y элементов, а именно, пикселов, то есть X столбцов и Y строк пикселов, каждый нейрон будет соответствовать одному значению признака одной карты 20 признаков, значение которого будет соответствовать локальной оценке признака, ассоциированной с определенной частью изображения 22. В случае N карт признаков с Р⋅Q выборками оценок признаков, например, P столбцами и Q строками значений признаков, число нейронов в нисходящем последующем слое части 21 будут равно, например, N⋅P⋅Q, которое может быть меньше или больше, чем Χ⋅Y. Для установки нейронных функций или параметризации нейронных функций нейронов внутри части 21 можно было бы использовать перевод (преобразование) описаний признаков или фильтров, лежащих в основе карт 20 признаков, соответственно. Однако вновь отметим, что существование такой ʺпереведеннойʺ, а не ʺобученнойʺ части 21 сети не является обязательным для настоящей заявки и ее вариантов осуществления, и что такая часть может альтернативно отсутствовать. В любом случае, устанавливая, что, возможно, нейронные функции нейронов 12 могут быть равны среди всех нейронов или равны среди нейронов одного слоя или т.п., нейронная функция может, однако, быть параметризируемой, и хотя параметризируемая нейронная функция может быть одинаковой среди этих нейронов, параметр(ы) функции этой нейронной функции может (могут) варьироваться среди этих нейронов. Количество промежуточных слоев также является произвольным и может быть равно одному или больше одного.
Подводя итог вышеизложенному, применение сети 10 в нормальном рабочем режиме выглядит следующим образом: входное изображение 22, в своей роли в качестве набора 16, подвергается воздействию или вводится в сеть 10. То есть, пиксельные значения изображения 22 образуют входные значения для нейронов 12 первого слоя 24. Эти значения распространяются, как описано, вдоль прямого направления 14 по сети 10 и дают в результате выход 18 сети. В случае входного изображения 22, показанного на фиг. 1, например, выход 18 сети будет, например, указывать, что это входное изображение 22 относится к третьему классу, то есть к классу изображений, показывающих автомобиль. Более точно, в то время как выходной нейрон, соответствующий классу ʺавтомобильʺ, завершался бы высоким значением, другие выходные нейроны, иллюстративно соответствующие в данном случае классам ʺгрузовикʺ и ʺлодкаʺ, завершались бы в низких (меньших) значениях.
Однако, как описано во вводной части спецификации настоящей заявки, информация о том, показывает ли или нет изображение 22, то есть набор 16, автомобиль или тому подобное, может оказаться недостаточной. Скорее, было бы предпочтительнее иметь информацию на уровне детализации пикселов, указывающую, какие пикселы, т.е. элементы набора 16, были релевантны для решения 10 сети, а какие нет, например, какие пикселы отображают автомобиль, а какие нет. Эта задача решается с помощью вариантов осуществления, описанных ниже.
В частности, на фиг. 2а иллюстративно показано, как варианты осуществления настоящего изобретения, описанные более подробно ниже, действуют для выполнения задачи назначения значения релевантности элементам набора 16, который в иллюстративном случае фиг. 2а представляет собой область пикселов. В частности, фиг. 2а иллюстрирует, что это назначение оценки релевантности выполняется посредством процесса обратного распространения (распространения назад релевантности), в соответствии с которым значение R релевантности, например, обратно распространяется через сеть 10 по направлению к входу сети, то есть набору 16 элементов, тем самым получая оценку Ri релевантности для каждого элемента i набора 16 для каждого пиксела изображения. Например, для изображения, содержащего Χ⋅Y пикселов, i могло бы находиться в пределах {1… Χ⋅Y}, причем каждый элемент/пиксел i соответствует, например, позиции (xi, yi) пиксела. При выполнении этого обратного распространения вдоль направления 32 обратного распространения, которое проходит противоположно направлению 14 прямого распространения согласно фиг. 1, варианты осуществления, описанные ниже, подчиняются определенным ограничениям, которые теперь объясняются более подробно и называются сохранением релевантности и перераспределением релевантности.
Короче говоря, назначение оценки релевантности начинается с завершенного применения искусственной нейронной сети 10 к набору 16. Как объяснялось выше, это применение завершается в выходе 18 сети. Начальное значение R релевантности выводится из этого выхода 18 сети. В примерах, описанных ниже, например, выходное значение одного выходного нейрона 12' используется в качестве этого значения R релевантности. Вывод из выхода сети может, однако, также выполняться по-разному, используя, например, монотонную функцию, примененную к выходу сети. Другие примеры приведены ниже.
В любом случае, это значение релевантности затем распространяется по сети 10 в обратном направлении, то есть 32, указывающем в противоположном направлении по сравнению с направлением 14 прямого распространения, вдоль которого сеть 10 работает, когда применяется к набору 16, чтобы дать в результате выход 18 сети. Обратное распространение выполняется таким образом, что для каждого нейрона 12 сумма предварительно перераспределенных значений релевантности набора нисходящих соседних нейронов соответствующего нейрона распределяется по набору восходящих соседних нейронов соответствующего нейрона, так что релевантность ʺпо существу сохраняетсяʺ. Например, функция распределения может быть выбрана так, что начальное значение R релевантности равно сумме оценок Ri релевантности элементов i набора 16 после завершения обратного распространения либо точно, то есть R=ΣRi, либо через монотонную функцию f(), т.е. R=f(ΣRi). Далее обсуждаются некоторые общие соображения относительно функции распределения и того, как они должны быть предпочтительно выбраны.
При обратном распространении нейронные активации нейронов 12 используются для направления обратного распространения. То есть, активации нейронов искусственной нейронной сети 10 при применении сети 10 к набору 16 для получения выхода 18 сети предварительно сохраняются и повторно используются для того, чтобы направлять процедуру обратного распространения. Как будет описано более подробно ниже, для аппроксимации обратного распространения можно использовать аппроксимацию Тейлора. Таким образом, как показано на фиг. 2а, процесс обратного распространения можно рассматривать как распределение начального значения релевантности R, начиная с выходного нейрона(ов), к входной стороне сети 10 вдоль направления 32 обратного распространения. Посредством этой меры, пути 34 потока релевантности 34 повышенной релевантности, выводимые из выходного нейрона 36 к входной стороне сети 10, а именно, входным нейронам, формируются самим набором 16 элементов. Пути время от времени разветвляются во время прохода через сеть 10, как показано в качестве примера на фиг. 2. Пути, наконец, заканчиваются в горячих точках повышенной релевантности в пределах набора 16 элементов. В конкретном примере использования входного изображения 22, как показано на фиг. 2а, оценки Ri релевантности указывают, на пиксельном уровне, области повышенной релевантности в изображении 22, то есть области в изображении 22, которые играли главную роль в завершении операции сети 10 в соответствующем выходе 18 сети. В дальнейшем описании, вышеупомянутые свойства сохранения релевантности и перераспределения релевантности обсуждаются более подробно с использованием приведенного выше примера для нелинейных функций активации в качестве нейронных функций для нейронов сети 10.
Свойство 1: Сохранение релевантности
Первое основное свойство модели распространения релевантности предполагает, что доказательство (основание) не может быть создано или потеряно. Это применимо как в глобальном масштабе (т.е. от выхода нейронной сети обратно к входу нейронной сети), так и в локальном масштабе (т.е. на уровне отдельных нелинейных процессоров). Такое ограничение сводится к применению законов цепей Кирхгоффа к нейронной сети и замене физического понятия ʺэлектрический токʺ на понятие ʺсемантическое доказательствоʺ. В частности, см. фиг. 3.
Используя индексы i и k для обозначения нейронов, входящих и исходящих в нейрон с индексом j (входящие обозначены на фиг. 3 ссылочной позицией 40 и, таким образом, образуют предшественников или восходящих соседей), должно выполняться тождество
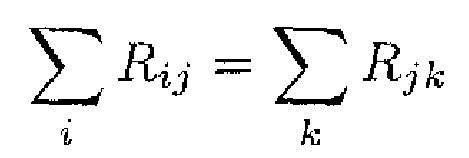
где Rij обозначает релевантность, которая протекает от нейрона j к нейрону i, и Rjk обозначает релевантность, которая протекает от нейрона k к нейрону j. Заметим, что принцип сохранения релевантности утверждает, что сумма релевантностей, которые 'втекают в нейрон', должна быть такой же, как сумма релевантностей, которые 'вытекают из этого нейрона'. Сохранение релевантности гарантирует, что сумма релевантностей входных нейронов (например, релевантностей пикселов) равна выходному значению сети (например, оценке классификации).
Свойство 2: перераспределение релевантности
Вторым основным свойством модели распространения релевантности является то, что локальное перераспределение релевантности должно следовать фиксированному правилу, которое неизменно применяется ко всем нейронам сети. Для перераспределения релевантности может быть определено множество различных правил. Некоторые из правил ʺзначимыʺ (поддаются интерпретации), другие - нет. Одним из таких значимых правил является, например,
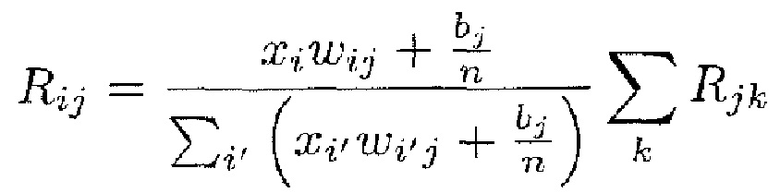
где n - число нейронов, индексированных посредством i. Рационализация этого правила перераспределения заключается в том, что нейроны xi, которые в наибольшей степени способствуют активации нейрона xj, будут относиться к большей части входящей релевантности ΣkRjk. Кроме того, суммируя перераспределенную релевантность Rij по всем входящим нейронам i, должно быть ясно, что свойство 1 удовлетворяется.
Однако приведенное выше детерминистское правило распространения релевантности имеет два недостатка: во-первых, он может быть численно неустойчивым, когда знаменатель близок к нулю. Во-вторых, оно может создавать отрицательные значения для Rij, которые имеют неопределенное значение. Первая проблема разрешается путем переопределения правила как
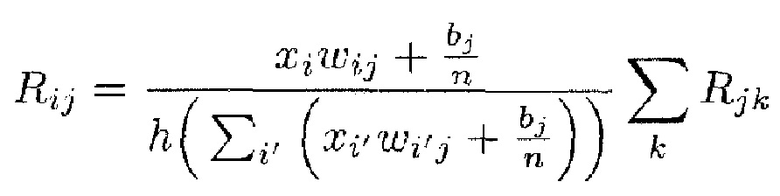
где h(t)=t+ε⋅sign(t) - численный стабилизатор, который не позволяет знаменателю быть близким к нулю, и где ε выбрано очень малым, чтобы соответствовать свойству 1. Вторая проблема разрешается путем учета только положительных вкладов в активации нейронов, в частности,
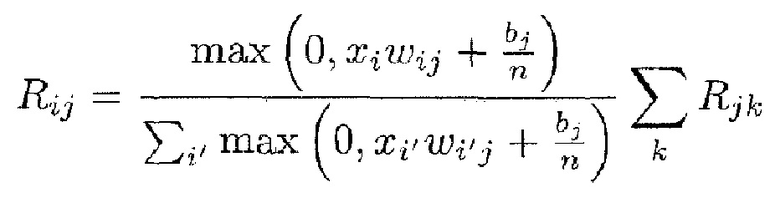
Здесь отметим, что отношение двух положительных величин обязательно положительно и, следовательно, будет иметь релевантность. Эти два усовершенствования могут легко комбинироваться, чтобы удовлетворять как свойства стабильности, так и положительности.
Отметим, что сохранение релевантности указывает, что делает обратное распространение (= распределение выходных релевантностей на входные переменные при сохранении общего значения (суммы) постоянным), тогда как перераспределение релевантности указывает, как это сделать (= ʺзначимоеʺ перераспределение должно обеспечивать, что нейроны, которые в наибольшей степени способствуют активации (имеют большие взвешенные активации xiwij), будут отнесены к большей части входящих релевантностей).
Прежде чем описывать устройство в соответствии с вариантом осуществления настоящей заявки, вышеуказанное введение должно быть расширено, чтобы более четко представить возможные альтернативы.
Например, хотя вариант осуществления, описанный со ссылкой на фиг. 1а и 2а, использовал изображение 22 в качестве набора 16 элементов, с возможным проектированием сети 10 таким образом, что нейронные активации нейронов одного слоя представляют собой ʺлокальные признакиʺ изображения, то есть выборки карт 20 признаков, вариант осуществления, показанный на фиг. 1b и 2b, использует карты 20 признаков в качестве набора 16 элементов. То есть в сеть 10 подаются выборки признаков карт 20 признаков. Карты 20 признаков могут быть получены из входного изображения 22, подвергая его воздействию экстракторов признаков, каждый из которых извлекает соответствующую карту 20 признаков из входного изображения 22. Эта операция экстракции признаков проиллюстрирована на фиг. 1b, используя стрелку 30. Экстрактор признаков может, например, локально применять ядро фильтра к изображению 22, чтобы выводить на каждое применение выборку признаков при перемещении ядра фильтра по изображению, чтобы получать соответствующую карту 20 признаков, состоящую из выборок признаков, расположенных, например, в строках и столбцах. Ядро/шаблон фильтра может быть индивидуальным для соответствующих экстракторов признаков и соответствующих карт 20 признаков соответственно. Здесь сеть 10 согласно фиг. 1b может совпадать с оставшейся частью сети 10 согласно фиг. 1а, остатком сети 10 после удаления части 21. Таким образом, в случае фиг. 1b, значения выборок признаков распространяются как часть так называемого процесса предсказания вдоль направления 14 вперед по сети 10 и дают в результате выход 18 сети. На фиг. 2b показан процесс обратного распространения релевантности для сети, показанной на фиг. 1b: Процесс обратного распространения распространяет обратно значение R релевантности через сеть 10 по направлению к входу сети, то есть набору 16 элементов, тем самым получая оценку Ri релевантности для каждого элемента. В случае, показанном на фиг. 2b, таким образом, оценка Ri релевантности получается для каждой выборки i признака. Однако, поскольку карты 20 признаков связаны с содержанием изображения с помощью функций выделения отдельных фильтров карт признаков, каждая оценка i релевантности может быть переведена в пиксельную область, то есть в пикселы, а именно, путем распределения отдельных оценок релевантности элементов набора 16 фиксированным способом в отдельные положения пикселов изображения 22. ʺФиксированный способʺ однозначно зависит от экстракторов признаков, ассоциированных с картой признаков соответствующей оценки релевантности, и представляет собой своего рода обратную функцию 38 выделения 30 признаков. Эта обратная функция 38, таким образом, образует своего рода расширение процесса обратного распространения, чтобы закрыть промежуток от области набора признаков до пространственной области пикселов.
Кроме того, следует отметить, что в случае фиг. 1а и фиг. 2а было предварительно принято, что каждый пиксел изображения 22, т.е. каждый элемент 16, несет скаляр. Эта интерпретация может применяться, например, в случае изображения 22 шкалы уровней серого, например, при каждом пиксельном значении, соответствующем значению шкалы уровней серого. Однако существуют и другие возможности. Например, изображение 22 может быть цветным изображением. В этом случае каждый элемент набора 16 может соответствовать выборке или пиксельному значению одной из нескольких цветных плоскостей или цветовых компонентов изображения 22. На фиг. 1c и 2c в качестве примера показаны три компонента, которые показывают расширение фиг. 1a и 2а для цветных изображений 22. Таким образом, набор 16 элементов в случае фиг. 1с и 2с будет Χ⋅Y⋅3 в случае наличия для каждого из Χ⋅Y положений пикселов значения цветового компонента для каждого из трех цветовых компонентов. Однако количество цветовых компонентов может отличаться от трех. Кроме того, пространственное разрешение цветовых компонентов не должно быть одинаковым. Обратное распространение на фиг. 2с завершается значением релевантности для каждого элемента, т.е. выборки цветового компонента. В случае наличия значения компонента для всех компонентов для каждого пиксела, окончательная карта релевантности может быть получена путем суммирования значений релевантности, полученных для цветовых компонентов соответствующего пиксела. Это показано как 37.
Хотя фиг. 1-2c относились к изображениям и пикселам, варианты осуществления настоящей заявки не ограничиваются данными такого типа. Например, тексты и их слова могут быть использованы в качестве основы. Приложение анализа социального графа может выглядеть следующим образом: релевантность назначается узлам и соединениям в графе, где граф задается как вход в нейронную сеть 10. В контексте анализа социального графа узлы могут представлять пользователей, а соединения могут представлять связь между этими пользователями. Такие соединения также могут быть направлены на моделирование информационных потоков (например, сеть ссылок) или цепочку ответственности внутри организации. Например, нейронные сети могут обучаться, чтобы предсказывать для графа, заданного в качестве входа, определенное свойство графа (например, производительность, ассоциированную с конкретным социальным графом). В этом случае способ распространения релевантности и тепловой карты будет стремиться идентифицировать на этом графе подструктуры или узлы, которые объясняют предсказанное свойство (то есть высокую или низкую производительность). Нейронные сети также могут обучаться, чтобы предсказывать состояние графа в более поздний момент времени. В этом случае процедура распространения релевантности будет пытаться идентифицировать, какая подструктура в графе объясняет будущее состояние графа (например, какие подструктуры или узлы наиболее влиятельны в социальном графе в их способности распространять информацию в графе или изменять его состояние). Таким образом, нейронная сеть может, например, использоваться для предсказания успеха (например, количества проданных продуктов) рекламной кампании (задача регрессии). Оценки релевантности могут использоваться для идентификации некоторых влиятельных аспектов успеха. Компания может сэкономить деньги, сосредоточившись только на этих релевантных аспектах. Процесс назначения оценки релевантности может выдавать оценку для каждого элемента рекламной кампании. Затем процессор принятия решений может принять этот вход, а также информацию о расходах по каждому элементу рекламной кампании и определить оптимальную стратегию кампании. Однако релевантность может также использоваться для выбора признака, как показано выше.
Назначение оценки релевантности начинается с вывода начального значения R релевантности. Как упоминалось выше, оно может быть установлено на основе одного из выходных нейронов нейронной сети, чтобы получить, путем обратного распространения, значения релевантности для элементов набора 16, ссылаясь на ʺсмысловое значениеʺ этого одного выходного нейрона. Однако выход 18 сети может альтернативно быть вектором, а выходные нейроны могут иметь такие смысловые значения, которые могут быть разделены на перекрывающиеся или неперекрывающиеся поднаборы. Например, выходные нейроны, соответствующие смысловому значению (категории) ʺгрузовикʺ и ʺмашинаʺ, могут объединяться, чтобы приводить к подмножеству выходных нейронов со смысловым значением ʺавтомобильʺ. Соответственно, выходные значения обоих выходных нейронов могут использоваться в качестве начальной точки в обратном распространении, тем самым приводя к оценке релевантности для элементов 16, то есть пикселов, указывая релевантность для смыслового значения поднабора, то есть ʺавтомобиляʺ.
Хотя изложенное выше описание предполагало, что набор элементов представляет собой изображение, и каждый из элементов 42 набора 16 элементов 42 соответствует одному пикселу изображения, это может быть иным. Например, каждый элемент может соответствовать набору пикселов или субпикселов (пиксел имеет обычно значения rgb; субпикселом будет, например, зеленый компонент пиксела), такому как суперпиксел, как показано на фиг. 2c. Кроме того, набор 16 элементов может альтернативно быть видео, и каждый из элементов 42 набора 16 элементов 42 соответствует одному или нескольким пикселам изображений (кадров) видео, кадрам видео или последовательностям кадров видео. Поднабор пикселов, к которым относится элемент, может содержать пикселы кадров с разными временными метками. Кроме того, набор 16 элементов может быть аудиосигналом, и каждый элемент 42 набора 16 элементов 42 соответствует одной или нескольким выборкам аудиосигнала, таким как выборки PCM. Отдельные элементы набора 16 могут быть выборками или любой другой частью аудиозаписи. Или набор элементов может представлять собой пространство произведений частот и времени, и каждый элемент представляет собой набор из одного или нескольких частотно-временных интервалов, таких как спектрограмма, состоящая, например, из MDCT-спектров последовательности перекрывающихся окон. Кроме того, набор 16 может представлять собой карту признаков для локальных признаков, локально извлеченных из изображения, видео или аудиосигнал, с элементами 42 набора 16 элементов 42, соответствующими локальным признакам, или текст с элементами 42 набора 16 элементов 42, соответствующими словам, предложениям или абзацам текста.
Для полноты, на фиг. 1d и 2d показан вариант, согласно которому набор данных 16 элементов представляет собой текст, а не изображение. Для этого случая, фиг. 1d иллюстрирует, что текст, который является фактически последовательностью 41 слов (например, I) слов 43, переносится в ʺабстрактнуюʺ или ʺинтерпретируемуюʺ версию путем отображения каждого слова wi 43 на соответствующий вектор vi 45 общей длины, т.е. общее число J компонентов vij 47, в соответствии с пословным преобразованием 49. Каждый компонент может быть ассоциирован с семантическим значением. Пословное преобразование, которое может быть использовано, представляет собой, например, Word2Vec или векторы указателя слов. Компоненты vij 47 векторов vi 45 представляют элементы набора 16 и подвергаются воздействию сети 10, что приводит к результату 18 предсказания в выходных узлах 12' сети. Обратное распространение, показанное на фиг. 2, приводит к значению релевантности для каждого элемента, т.е. для каждого векторного компонента vij (0<i<I; 0<j<J). Суммирование 53, для каждого слова wi, оценок релевантности для компонентов vij вектора vi, ассоциированного с соответствующим словом wi, при 0<j<J, приводит к суммарному значению релевантности (оценке релевантности) на каждое слово, например, и, таким образом, каждое слово wi в тексте может быть выделено в соответствии с его суммарной оценкой релевантности. Количество опций выделения может быть равно двум или больше. То есть, суммарные значения релевантности слов могут быть квантованы, чтобы получить опцию выделения для каждого слова. Опция выделения может быть ассоциирована с различной интенсивностью выделения, и отображение от суммарных значений релевантности на опции выделения может привести к монотонной ассоциации между суммарными значениями релевантности и интенсивностью выделения. Опять же, подобно примерам, в которых нейронная сеть относилась к характеристикам предсказания на изображениях, часть входной стороны сети 10 согласно фиг. 1d и 2d может иметь некоторое интерпретируемое смысловое значение. В случае изображений это были наборы признаков. В случае фиг. 1d и 2d, входная часть сети 10 могла бы представлять другое векторное отображение векторов, состоящих из компонентов набора 16, на наиболее вероятные векторы меньшей размерности, компоненты которых могут иметь более предпочтительное семантическое значение по сравнению с относящимися к предпочтительному семейству слов компонентами векторов, составленных из компонентов набора 16.
На фиг. 4 показан пример устройства для назначения оценки релевантности набору элементов. Устройство реализовано, например, в программном обеспечении, то есть в программируемом компьютере. Однако можно представить себе другие возможности реализации. В любом случае, устройство 50 сконфигурировано для использования вышеописанного процесса обратного распространения для того, чтобы назначать, поэлементно, оценку релевантности набору 16 элементов, причем оценка релевантности указывает для каждого элемента, какую релевантность имеет этот элемент в получении сетью 10 на его основе выхода 18 сети. Соответственно, на фиг. 4 также показана нейронная сеть. Сеть 10 показана как не являющаяся частью устройства 50: вместо этого сеть 10 определяет источник смыслового значения ʺрелевантностиʺ, для которой должны быть назначены оценки набору 16 элементов устройством 50. Однако, в качестве альтернативы, устройство 50 также может включать в себя сеть 10.
Фиг. 4 показывает сеть 10 в качестве принимающей набор 16 элементов, причем элементы иллюстративно показаны в виде кружков 42. Фиг. 4 также иллюстрирует возможность того, что сеть 10 управляется параметрами 44 нейрона, такими как весовые коэффициенты функции, управляющие вычислением активации нейронов на основе восходящих соседних/предшествующих нейронов данного нейрона, как описано выше, то есть параметрами нейронных функций. Эти параметры 44 могут, например, сохраняться в памяти или хранилище 46. Фиг. 4 также иллюстрирует выход сети 10 после завершения обработки набора 16 элементов 42 с использованием параметров 44, а именно, выход 18 сети и, опционально, нейронные активации нейронов 12, полученные в результате обработки набора 16, причем активации нейронов проиллюстрированы ссылочной позицией 48. Активации 48 нейронов, выход 18 сети и параметры 44 иллюстративно показаны сохраненными в памяти 46, но они также могут храниться в отдельном хранилище или памяти или могут не храниться. Устройство 50 имеет доступ к выходу 18 сети и выполняет задачу 52 перераспределения с использованием выхода 18 сети и вышеописанного принципа обратного распространения, чтобы получить оценку Ri релевантности для каждого элемента i 52 набора 16. В частности, как описано выше, устройство 50 получает начальное значение R релевантности из выхода сети и перераспределяет эту релевантность R, используя процесс обратного распространения, чтобы получить индивидуальные оценки Ri релевантности для элементов i. Отдельные элементы набора 16 показаны на фиг. 4 маленькими кружками, обозначенными ссылочной позицией 42. Как описано выше, перераспределение 52 может управляться параметрами 44 и активациями 48 нейронов, и, соответственно, устройство 50 также может иметь доступ к этим элементам данных. Кроме того, как показано на фиг. 4, фактическую нейронную сеть 10 не требуется реализовывать в устройстве 50. Скорее, устройство 50 может иметь доступ, например, к информации о конструкции сети 10, такой как количество нейронов, функции нейронов, к которым относятся параметры 44, и взаимосвязи нейронов, информация о которых проиллюстрирована на фиг. 4 с использованием описания 54 нейронной сети, которое, как показано на фиг. 4, также может храниться в памяти или хранилище 46 или в другом месте. В альтернативном варианте осуществления, искусственная нейронная сеть 10 также реализуется на устройстве 50, так что устройство 50 может содержать процессор нейронной сети для применения нейронной сети 10 к набору 16 в дополнение к процессору перераспределения, который выполняет задачу 52 перераспределения.
Таким образом, приведенные выше варианты осуществления могут, в том числе, закрывать промежуток между классификацией и интерпретируемостью для многослойных нейронных сетей, которые пользуются популярностью в компьютерном зрении. Для нейронных сетей (например, [6, 31]) мы рассмотрим общие многослойные сетевые структуры с произвольными непрерывными нейронами и функциями опрашивания на основе обобщенных р-средних.
Следующий раздел ʺПопиксельная декомпозиция как обобщенная концепцияʺ объяснит основные подходы, лежащие в основе попиксельной декомпозиции классификаторов. Эта попиксельная декомпозиция была проиллюстрирована со ссылкой на фиг. 1a и 2c. Попиксельная декомпозиция для многослойных сетей применяет тейлоровский подход и подход послойного распространения релевантности, объясняемые в разделе ʺПопиксельная декомпозиция как обобщенная концепцияʺ для архитектур нейронных сетей. Экспериментальная оценка нашей структуры будет дана в разделе ʺЭкспериментыʺ.
Попиксельная декомпозиция как обобщенная концепция
Общая идея попиксельной декомпозиции заключается в том, чтобы понять вклад отдельного пиксела изображения x в предсказание f(x), сделанное классификатором f в задаче классификации изображений. Мы хотели бы узнать, отдельно для каждого изображения x, какие пикселы в какой степени вносят вклад в положительный или отрицательный результат классификации. Более того, мы хотим выразить эту степень количественно мерой. Мы предполагаем, что классификатор имеет действительнозначные выходы, пороговые значения которых равны нулю. В такой установке это соответствует отображению f: RV→R1, так что f(x)>0 означает наличие обученной структуры. Вероятностные выходы для классификаторов двух классов можно рассматривать без потери общности путем вычитания 0,5 или взятия логарифма предсказания и добавления затем логарифма 2.0. Представляет интерес узнать вклад каждого входного пиксела x(d) входного изображения x в конкретное предсказание f(x). Важное ограничение, характерное для классификации, состоит в нахождении дифференциального вклада относительно состояния максимальной неопределенности относительно классификации, который затем представляется набором корневых точек f(x0)=0. Один из возможных способов состоит в декомпозиции предсказания f(x) как суммы членов отдельных входных размерностей xd или пикселов:

Качественная интерпретация заключается в том, что Rd<0 способствует доказательству против наличия структуры, которая должна классифицироваться, тогда как Rd>0 способствует доказательству ее присутствия. С точки зрения последующей визуализации, результирующие релевантности Rd для каждого входного пиксела x(d) могут быть отображены в цветовое пространство и визуализированы таким образом как обычная тепловая карта. Одним из основных ограничений в следующей работе будет то, что знаки Rd должны следовать вышеуказанной качественной интерпретации, то есть положительные значения должны обозначать положительные вклады, отрицательные значения - отрицательные вклады.
В дальнейшем, концепция обозначается как послойное распространение релевантности в качестве концепции с целью достижения попиксельной декомпозиции, как в уравнении (1). Также обсуждается подход, основанный на декомпозиции Тейлора, который дает аппроксимацию послойного распространения релевантности. Будет показано, что для широкого диапазона архитектур нелинейной классификации можно выполнить послойное распространение релевантности без использования аппроксимации посредством разложения Тейлора. Приведенные ниже методы не включают сегментацию. Они не требуют попиксельной тренировки (обучения) в качестве обучающей настройки или попиксельной маркировки для фазы обучения. Используемая здесь настройка - это классификация по изображению, в которой во время обучения одна метка предоставляется для изображения в целом, однако вклад заключается не в обучении классификатора. Методы строятся поверх предварительно обученного классификатора. Они применимы к уже предварительно обученному классификатору изображений.
Послойное распространение релевантности
Послойное распространение релевантности в его обобщенной форме предполагает, что классификатор можно разложить на несколько слоев вычисления. Такие слои могут быть частями выделения признаков из изображения или частями алгоритма классификации, выполняемого на вычисленных признаках. Как показано ниже, это возможно для нейронных сетей.
Первым слоем могут быть входы, пикселы изображения, последним слоем является дествительнозначный выход предсказания классификатора f. l-ый слой моделируется как вектор 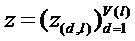 с размерностью V(l). Послойное распространение релевантности предполагает, что для каждой размерности z(d,l+1) вектора z в слое l+1 имеется оценка
с размерностью V(l). Послойное распространение релевантности предполагает, что для каждой размерности z(d,l+1) вектора z в слое l+1 имеется оценка 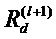 релевантности. Идея состоит в том, чтобы найти оценку
релевантности. Идея состоит в том, чтобы найти оценку 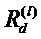 релевантности для каждой размерности z(d,l) вектора z на следующем слое l, который ближе к входному слою, так что выполняется следующее уравнение.
релевантности для каждой размерности z(d,l) вектора z на следующем слое l, который ближе к входному слою, так что выполняется следующее уравнение.
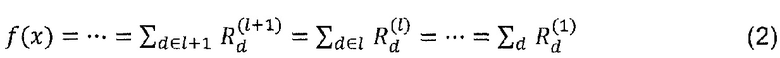
Итерация уравнения (2) из последнего слоя, который является выходом f(x) классификатора, до входного слоя x, состоящего из пикселов изображения, дает тогда требуемое уравнение (1). Релевантность для входного слоя будет служить желательной декомпозицией суммы в уравнении (1). Как будет показано, такая декомпозиция сама по себе не является ни уникальным, ни гарантирующей, что она дает значимую интерпретацию предсказания классификатора.
Приведем здесь простой контрпример. Предположим, что имеется один слой. Входы представляют собой x∈RV. Используем линейный классификатор с некоторым произвольным и специфическим для размерности отображением φd пространства признаков и смещением b

Определим релевантность для второго слоя тривиально как  =f(x). Тогда одной возможной формулой послойного распространения релевантности должно быть определение релевантности R(1) для входов x как
=f(x). Тогда одной возможной формулой послойного распространения релевантности должно быть определение релевантности R(1) для входов x как
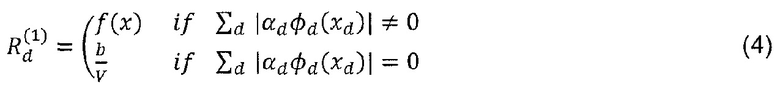
Это явно удовлетворяет уравнениям (1) и (2), однако релевантность R(1)(xd) всех входных размерностей имеет тот же знак, что и предсказание f(x). В терминах интерпретации попиксельной декомпозиции, все входы указывают на наличие структуры, если f(x)>0, и на отсутствие структуры, если f(x)<0. Это для многих задач классификации не является реалистичной интерпретацией.
Обсудим более осмысленный способ определения послойного распространения релевантности. Для этого примера определим

Тогда релевантность размерности xd признака зависит от знака члена в уравнении (5). Это для многих проблем классификации является более правдоподобной интерпретацией. Этот второй пример показывает, что послойное распространение релевантности способно иметь дело с нелинейностями, такими как отображение φd пространства признаков до некоторой степени, и на практике может выглядеть как пример послойного распространения релевантности, удовлетворяющий формуле (2). Заметим, что здесь вообще не требуется предположение о регулярности отображения φd пространства признаков, оно может быть даже не непрерывным или не измеримым по мере Лебега. Основополагающая формула (2) может быть интерпретирована как закон сохранения для релевантности R между слоями обработки признаков.
Приведенный выше пример дает, кроме того, интуитивное представление о том, чем является релевантность R, а именно, локальный вклад в функцию f(x) предсказания. В этом смысле релевантность выходного слоя может быть выбрана в качестве самого предсказания f(x). Этот первый пример показывает, что можно ожидать в качестве декомпозиции для линейного случая. Линейный случай обеспечивает первое интуитивное представление.
Приведем второй, более графический и нелинейный пример. На фиг. 5 показан классификатор нейронной сети с нейронами и весами wij на соединениях между нейронами. Каждый нейрон i имеет выход ai из функции активации.
Верхний слой состоит из одного выходного нейрона, индексированного как 7. Для каждого нейрона i вычислим релевантность Ri. Отбросим верхний индекс R(l) слоя для этого примера, поскольку все нейроны имеют явный индекс нейрона всякий раз, когда индекс слоя очевиден. Инициализируем релевантность 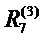 верхнего слоя как значение функции, таким образом, R7=f(x). Послойное распространение релевантности в уравнении (2) требует теперь поддержания
верхнего слоя как значение функции, таким образом, R7=f(x). Послойное распространение релевантности в уравнении (2) требует теперь поддержания
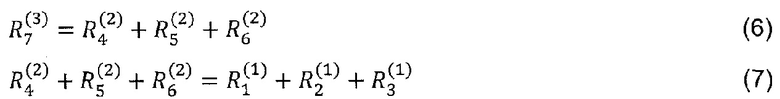
Сделаем два предположения для этого примера. Во-первых, выразим послойную релевантность в терминах сообщений 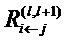 между нейронами i и j, которые могут передаваться по каждому соединению. Однако сообщения направляются от нейрона к его входным нейронам, в отличие от того, что происходит во время предсказания, как показано на фиг. 6. Во-вторых, определим релевантность любого нейрона, кроме нейрона 7, в виде суммы входящих сообщений:
между нейронами i и j, которые могут передаваться по каждому соединению. Однако сообщения направляются от нейрона к его входным нейронам, в отличие от того, что происходит во время предсказания, как показано на фиг. 6. Во-вторых, определим релевантность любого нейрона, кроме нейрона 7, в виде суммы входящих сообщений:
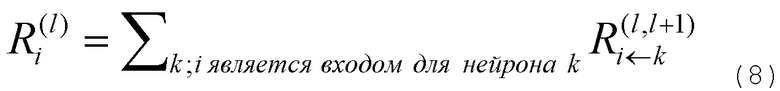
Например, 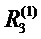 =
=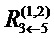 +
+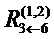 . Отметим, что нейрон 7 не имеет входящих сообщений. Вместо этого его релевантность определяется как
. Отметим, что нейрон 7 не имеет входящих сообщений. Вместо этого его релевантность определяется как 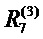 =f(x). В уравнении (8) и следующем тексте термины ʺвходʺ и ʺисточникʺ имеют значение в смысле входа в другой нейрон в направлении, определенном во время классификации, а не во время вычисления послойного распространения релевантности. Например, на фиг. 6 нейроны 1 и 2 являются входами и источниками для нейрона 4, в то время как нейрон 6 является приемником для нейронов 2 и 3. Учитывая два предположения, закодированные в уравнении (8), послойное распространение релевантности по уравнению (2) может быть удовлетворено следующим достаточным условием:
=f(x). В уравнении (8) и следующем тексте термины ʺвходʺ и ʺисточникʺ имеют значение в смысле входа в другой нейрон в направлении, определенном во время классификации, а не во время вычисления послойного распространения релевантности. Например, на фиг. 6 нейроны 1 и 2 являются входами и источниками для нейрона 4, в то время как нейрон 6 является приемником для нейронов 2 и 3. Учитывая два предположения, закодированные в уравнении (8), послойное распространение релевантности по уравнению (2) может быть удовлетворено следующим достаточным условием:
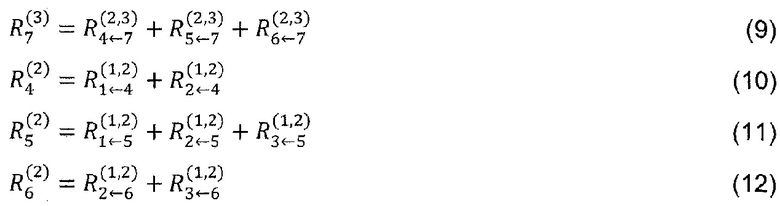
В общем случае это условие может быть выражено как:
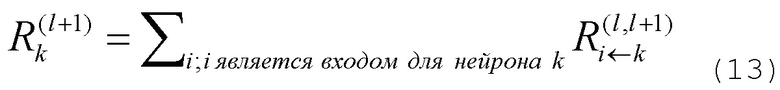
Разница между условием (13) и определением (8) заключается в том, что в условии (13) сумма пробегает по источникам в слое l для фиксированного нейрона k в слое l+1, тогда как в определении (8) сумма пробегает по приемникам в слое l+1 для фиксированного нейрона i в слое l. Это условие является достаточным условием, а не необходимым. Оно является следствием определения (8). Можно интерпретировать достаточное условие (13), говоря, что сообщения 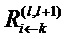 используются для распределения релевантности
используются для распределения релевантности 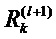 нейрона k на его входные нейроны в слое l. Следующие разделы будут основаны на этом понятии и более строгой форме сохранения релевантности, как задается определением (8) и достаточным условием (13).
нейрона k на его входные нейроны в слое l. Следующие разделы будут основаны на этом понятии и более строгой форме сохранения релевантности, как задается определением (8) и достаточным условием (13).
Теперь можем получить явную формулу для послойного распространения релевантности для нашего примера путем определения сообщений 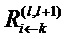 . Послойное распространение релевантности должно отражать сообщения, переданные в течение времени классификации. Мы знаем, что в течение времени классификации нейрон i вводит aiwik в нейрон k, при условии, что i имеет прямое соединение с k. Таким образом, мы можем представить уравнения (9) и (10) посредством
. Послойное распространение релевантности должно отражать сообщения, переданные в течение времени классификации. Мы знаем, что в течение времени классификации нейрон i вводит aiwik в нейрон k, при условии, что i имеет прямое соединение с k. Таким образом, мы можем представить уравнения (9) и (10) посредством
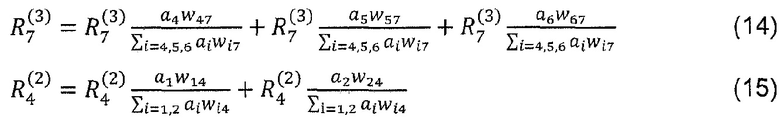
В общем случае это можно выразить как

Хотя это определение еще нужно адаптировать так, что оно может использоваться, когда знаменатель обращается в нуль, пример, приведенный в уравнении (16), дает представление о том, что может представлять сообщение 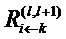 , а именно, релевантность приемного нейрона
, а именно, релевантность приемного нейрона 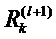 , которая уже была вычислена взвешенно пропорционально входу нейрона i из предыдущего слоя l. Это понятие справедливо аналогичным образом, когда мы используем различные архитектуры классификации и заменяем понятие нейрона на размерность вектора признаков в данном слое.
, которая уже была вычислена взвешенно пропорционально входу нейрона i из предыдущего слоя l. Это понятие справедливо аналогичным образом, когда мы используем различные архитектуры классификации и заменяем понятие нейрона на размерность вектора признаков в данном слое.
Формула (16) имеет второе свойство: знак релевантности, переданной сообщением 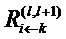 , переключается, если вклад нейрона aiwik имеет другой знак, чем сумма вкладов от всех входных нейронов, т.е. если нейрон срабатывает против общей тенденции для верхнего нейрона, из которого он наследует часть релевантности. Так же, как и для примера с линейным отображением в уравнении (5), входной нейрон может наследовать положительную или отрицательную релевантность в зависимости от знака его входа.
, переключается, если вклад нейрона aiwik имеет другой знак, чем сумма вкладов от всех входных нейронов, т.е. если нейрон срабатывает против общей тенденции для верхнего нейрона, из которого он наследует часть релевантности. Так же, как и для примера с линейным отображением в уравнении (5), входной нейрон может наследовать положительную или отрицательную релевантность в зависимости от знака его входа.
Здесь также показано еще одно свойство. Формула для распределения релевантности применима к нелинейным и даже недифференцируемым или не являющимся непрерывными активациям ak нейрона. Алгоритм будут начинаться с релевантностей R(l+1) уровня l+1, которые уже были вычислен. Тогда сообщения 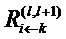 будут вычисляться для всех элементов k из слоя l+1 и элементов i из предыдущего слоя l таким образом, чтобы выполнялось уравнение (13). Тогда определение (8) будет использоваться для определения релевантности R(l) для всех элементов слоя l.
будут вычисляться для всех элементов k из слоя l+1 и элементов i из предыдущего слоя l таким образом, чтобы выполнялось уравнение (13). Тогда определение (8) будет использоваться для определения релевантности R(l) для всех элементов слоя l.
Декомпозиция тейлоровского типа
Одним альтернативным подходом к достижению декомпозиции, как в (1) для общего дифференцируемого предсказателя f, является аппроксимация Тейлора первого порядка.
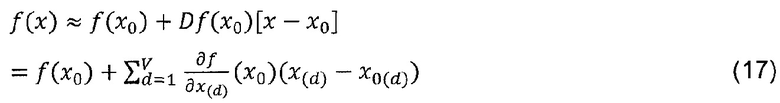
Выбор базовой точки x0 Тейлора является свободным параметром в этой установке. Как было сказано выше, в случае классификации интересно выяснить вклад каждого пиксела относительно состояния максимальной неопределенности предсказания, которая задается набором точек f(x0)=0, так как f(x)>0 обозначает наличие и f(x)<0 обозначает отсутствие изученной структуры. Таким образом, x0 следует выбирать как корень предсказателя f. Для точности аппроксимации Тейлора предсказания, x0 следует выбрать близким к x по евклидовой норме для минимизации остатка Тейлора в соответствии с аппроксимациями Тейлора более высокого порядка. В случае нескольких существующих корней x0 с минимальной нормой, их можно усреднить или интегрировать, чтобы получить среднее значение по всем этим решениям. Вышеприведенное уравнение упрощается до
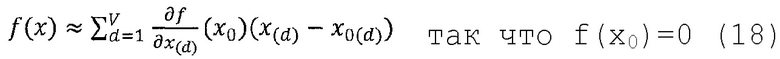
Попиксельная декомпозиция содержит нелинейную зависимость от точки предсказания x за пределами ряда Тейлора, так как нужно найти ближайшую корневую точку x0. Таким образом, полная попиксельная декомпозиция является не линейным, а локально линейным алгоритмом, так как корневая точка x0 зависит от точки x предсказания.
В нескольких работах использовались карты чувствительности [2, 18, 38] для визуализации предсказаний классификаторов, основанных на использовании частных производных в точке x предсказания. Существуют два существенных различия между картами чувствительности, основанными на производных в точке x предсказания, и подходом попиксельной декомпозиции. Во-первых, нет прямой зависимости между значением f(x) функции в точке x предсказания и дифференциалом Df(x) в той же точке x. Во-вторых, интересно объяснить предсказание классификатора относительно некоторого состояния, заданного набором корней функции f(x0) предсказания. Дифференциал Df(x) в точке предсказания не обязательно указывает на корень, который близок к евклидовой норме. Он указывает на ближайший локальный оптимум, который может по-прежнему иметь тот же знак, что и предсказание f(x), и, таким образом, вводить в заблуждение для объяснения разницы с набором корневых точек функции предсказания. Поэтому производные в точке х предсказания не являются полезными для достижения нашей цели. На фиг. 7 показано качественное различие между локальными градиентами (стрелками, направленными вверх) и декомпозицией по размерностям предсказания (стрелкой, направленной вниз). В частности, на этой фигуре изображено интуитивное представление, что градиент в точке х предсказания, показанной здесь квадратом, не обязательно указывает на близкую точку на границе решения. Вместо этого он может указывать на локальный оптимум или на удаленную точку на границе решения. В этом примере вектор объяснения от локального градиента в точке х предсказания имеет слишком большой вклад в нерелевантном направлении. Ближайшие соседи другого класса могут быть найдены под другим углом. Таким образом, локальный градиент в точке х предсказания может не оказаться хорошим объяснением для вкладов отдельных измерений в значение функции f(x). Локальные градиенты в точке предсказания в левом изображении и корневая точка Тейлора в правом изображении обозначены черными стрелками. Ближайшая корневая точка x0 показана как треугольник на границе решения. Стрелка, направленная вниз, в правом изображении визуализирует аппроксимацию f(x) разложением Тейлора вокруг ближайшей корневой точки x0. Аппроксимация задается как вектор, представляющий произведение по размерностям между Df(x0) (серая стрелка на правой панели) и x-x0 (пунктирная линия на правой панели), который эквивалентен диагонали векторного произведения между Df(x0) и x-x0.
Одна из технических трудностей состоит в том, чтобы найти корневую точку x0. Для непрерывных классификаторов мы можем использовать немаркированные тестовые данные или данные, создаваемые генеративной моделью, изученной на данных обучения в подходе дискретизации, и выполнить поиск линии между точкой х предсказания и набором точек-кандидатов {x'}, так что их предсказание имеет противоположный знак: f(x)f(x')<0. Ясно, что линия l(a)=ax+(1-a)x' должна содержать корень f, который может быть найден посредством интервального пересечения. Таким образом, каждая точка-кандидат x' дает один корень, и можно выбрать корневую точку, которая минимизирует остаток Тейлора или использует среднее значение по поднабору корневых точек с низкими остатками Тейлора.
Отметим, что декомпозиция тейлоровского типа, применяемая к одному слою или поднабору слоев, может рассматриваться как примерный способ распространения релевантности, когда функция сильно нелинейна. Это выполняется, в частности, при применении к выходной функции f в качестве функции предыдущего слоя f=f(zi-1), так как уравнение (18) удовлетворяет приблизительно уравнению (2) распространения, когда релевантность выходного слоя инициализируется как значение функции f(x) предсказания. В отличие от аппроксимации Тейлора, послойное распространение релевантности не требует использовать вторую точку, кроме входной точки. Формулы в разделе ʺПопиксельная декомпозиция для многослойных сетейʺ продемонстрируют, что послойное распространение релевантности может быть реализовано для широкого спектра архитектур без необходимости аппроксимировать с помощью разложения Тейлора.
Попиксельная декомпозиция для многослойных сетей
Многослойные сети обычно строятся как набор взаимосвязанных нейронов, организованных послойным способом. При объединении друг с другом они определяют математическую функцию, которая отображает нейроны первого слоя (вход) на нейроны последнего слоя (выход). Каждый нейрон обозначается посредством xi, где i - индекс для нейрона. По соглашению, ассоциируем разные индексы для каждого слоя сети. Обозначим суммирование по всем нейронам данного слоя через ʺΣiʺ и суммирование по всем нейронам другого слоя через ʺΣjʺ. Обозначим через x(d) нейроны, соответствующие активациям пикселов (т.е. с которыми желательно получить декомпозицию решения классификации). Общее отображение от одного слоя на другой состоит из линейной проекции, за которой следует нелинейная функция:

где wij - вес, соединяющий нейрон xi с нейроном xj, bj - член смещения, g - нелинейная функция активации (см. фиг. 8 для пояснения используемых обозначений). Многослойные сети складывают несколько из этих слоев, каждый из которых состоит из большого числа нейронов. Общими нелинейными функциями являются гиперболический тангенс g(t)=tanh(t) или функция выпрямления g(t)=max(0,t). Такая формулировка нейронной сети является достаточно общей, чтобы охватывать широкий спектр архитектур, таких как простой многослойный персептрон [39] или сверточные нейронные сети [25], когда свертка и объединение сумм являются линейными операциями.
Декомпозиция тейлоровского типа
Обозначая через f:RM→RN векторнозначную многомерную функцию, реализующую отображение между входом и выходом сети, первое возможное объяснение решения классификации x→f(x) может быть получено разложением Тейлора вблизи корневой точки x0 решающей функции f:

Производная 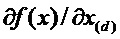 , необходимая для попиксельной декомпозиции, может быть эффективно вычислена путем повторного использования сетевой топологии с использованием алгоритма обратного распространения [39]. В частности, возвратив производные до некоторого слоя j, можно вычислить производную предыдущего слоя i, используя правило цепи:
, необходимая для попиксельной декомпозиции, может быть эффективно вычислена путем повторного использования сетевой топологии с использованием алгоритма обратного распространения [39]. В частности, возвратив производные до некоторого слоя j, можно вычислить производную предыдущего слоя i, используя правило цепи:
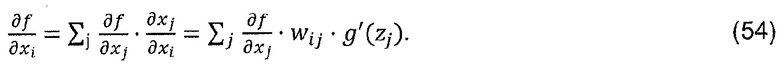
Требование декомпозиции на основе Тейлора состоит в том, чтобы найти корни x0 (т.е. точки на границе классификации), которые поддерживают локальное объяснение решения классификации для x. Эти корни можно найти путем локального поиска в окрестности точки x. Однако, как отмечено в [43], это может привести к точкам входного пространства, которые перцептивно эквивалентны исходной выборке x и выбор которых в качестве корня приведет к неинформативным попиксельным декомпозициям.
В качестве альтернативы, корневые точки могут быть найдены путем поиска линии на сегменте, определяемом посредством x и его ближайшим соседом другого класса. Это решение проблематично, когда множество данных является малонаселенным, как это имеет место для естественных изображений. В этом случае, вполне вероятно, что следование прямой линии между х и его ближайшим соседом будет сильно удаляться от множества данных и создавать корни x0 с одинаково плохими попиксельными декомпозициями.
Послойное обратное распространение релевантности
В качестве альтернативы к декомпозиции тейлоровского типа, можно вычислить релевантности на каждом слое в обратном проходе, то есть выразить релевантности 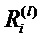 как функцию релевантности выше расположенного слоя,
как функцию релевантности выше расположенного слоя, 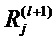 , и обратно распространять релевантности до тех пор, пока не достигнем входа (пикселов).
, и обратно распространять релевантности до тех пор, пока не достигнем входа (пикселов).
Метод работает следующим образом: зная релевантность определенного нейрона 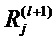 для решения f(x) классификации, желательно получить декомпозицию такой релевантности в терминах сообщений, отправленных к нейронам предыдущих слоев. Назовем их сообщениями
для решения f(x) классификации, желательно получить декомпозицию такой релевантности в терминах сообщений, отправленных к нейронам предыдущих слоев. Назовем их сообщениями 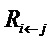 . В частности, как выражается уравнениями (8) и (13), должно поддерживаться свойство сохранения
. В частности, как выражается уравнениями (8) и (13), должно поддерживаться свойство сохранения

В случае линейного нейрона xj=Σizij, где релевантность Rj=f(x), такое разложение сразу задается через 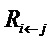 =zij. Однако в общем случае активация xj нейрона является нелинейной функцией от zj. Тем не менее, для гиперболического тангенса и функции выпрямления, двух простых монотонно возрастающих функций, удовлетворяющих условию g(0)=0, предактивации zij все же обеспечивают разумный способ измерения относительного вклада каждого нейрона xi в Rj. Первый возможный вариант декомпозиции релевантности основан на отношении локальных и глобальных предактиваций и определяется следующим образом:
=zij. Однако в общем случае активация xj нейрона является нелинейной функцией от zj. Тем не менее, для гиперболического тангенса и функции выпрямления, двух простых монотонно возрастающих функций, удовлетворяющих условию g(0)=0, предактивации zij все же обеспечивают разумный способ измерения относительного вклада каждого нейрона xi в Rj. Первый возможный вариант декомпозиции релевантности основан на отношении локальных и глобальных предактиваций и определяется следующим образом:

Легко показать, что эти релевантности 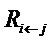 аппроксимируют свойства сохранения уравнения (2), в частности:
аппроксимируют свойства сохранения уравнения (2), в частности:

где множитель учитывает релевантность, которая поглощается (или вводится) членом смещения. При необходимости, релевантность остаточного смещения может быть перераспределена на каждый нейрон xi.
Недостатком правила распространения согласно уравнению (56) является то, что для малых значений zj, релевантности 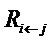 могут принимать неограниченные значения. Неограниченность может быть преодолена путем введения предопределенного стабилизатора ε≥0:
могут принимать неограниченные значения. Неограниченность может быть преодолена путем введения предопределенного стабилизатора ε≥0:
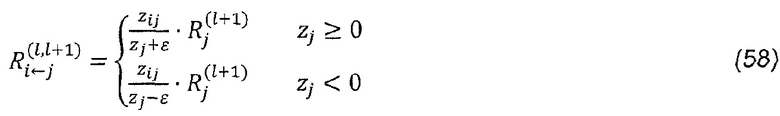
Тогда закон сохранения становится
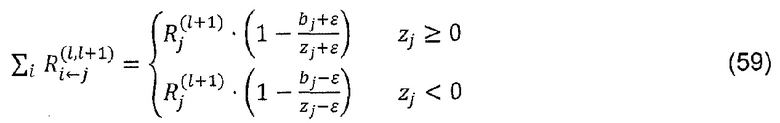
где можно заметить, что некоторая дополнительная релевантность поглощается стабилизатором. В частности, релевантность полностью поглощается, если стабилизатор ε становится очень большим.
Альтернативный метод стабилизации, который не связан с утечкой релевантности, состоит в том, чтобы обрабатывать отрицательные и положительные предактивации отдельно. Допустим
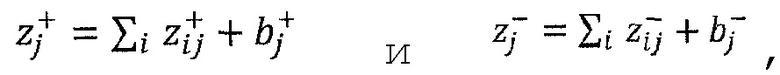 где ʺ-ʺ и ʺ+ʺ означают отрицательную и положительную часть zij и bj. Распространение релевантности определяется теперь как
где ʺ-ʺ и ʺ+ʺ означают отрицательную и положительную часть zij и bj. Распространение релевантности определяется теперь как
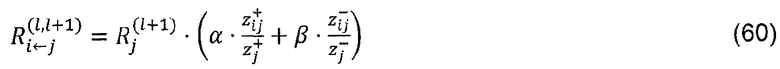
Где α>0, β<0, α+β=1. Например, при α=2, β=-1, закон сохранения принимает вид:
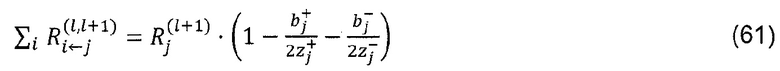
который имеет аналогичную форму с уравнением (57). Этот альтернативный метод распространения также позволяет вручную контролировать важность положительных и отрицательных доказательств, выбирая различные коэффициенты α и β.
Далее, более обобщенно запишем Rij для сообщений релевантности от нейрона j к нейрону i, который является восходящим соседом нейрона j. В частном случае нейронной сети со слоистой структурой, Rij является сокращенным способом записи 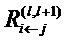 , где i и j являются нейронами слоев l и l+1, соответственно. Аналогично, можно отбросить индекс слоя для оценки релевантности нейрона и записать Rj вместо
, где i и j являются нейронами слоев l и l+1, соответственно. Аналогично, можно отбросить индекс слоя для оценки релевантности нейрона и записать Rj вместо 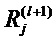 .
.
В дополнение к вышеперечисленным формулам перераспределения, можно определить альтернативные формулы следующим образом:
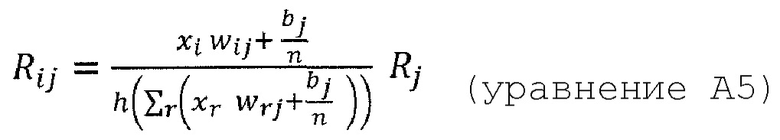
Или
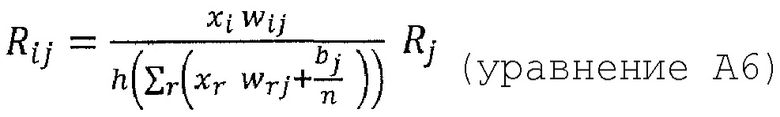
где n - число восходящих соседних нейронов соответствующего нейрона, Rij - значение релевантности, перераспределенное от соответствующего нейрона j к восходящему соседнему нейрону i, и Rj - релевантность нейрона j, который является нисходящим нейроном нейрона i, xi является активацией восходящего соседнего нейрона i при применении нейронной сети, wij - вес, соединяющий восходящий соседний нейрон i с соответствующим нейроном j, wrj - также вес, соединяющий восходящий соседний нейрон r с соответствующим нейроном j, bj - член смещения соответствующего нейрона j, и h() - скалярная функция. Обычно h() представляет собой численный стабилизирующий член, который удерживает значение отличным от нуля путем добавления малого ε, например, h(x)=x+ε⋅sign(х).
Аналогичным образом, другие альтернативы:
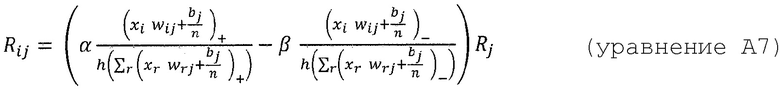
или
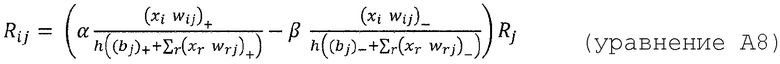
Когда выбрано правило для распространения релевантности, общая релевантность каждого нейрона в более низком слое определяется суммированием релевантности, исходящей от всех нейронов более высокого слоя, в соответствии с уравнениями (8) и (13):

Релевантность распространяется обратно от одного слоя к другому, пока не достигнет входных пикселов x(d), и где релевантности 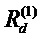 обеспечивают желательную попиксельную декомпозицию решения f(x). В алгоритме 2 суммируется полная процедура попиксельного распространения релевантности для нейронных сетей.
обеспечивают желательную попиксельную декомпозицию решения f(x). В алгоритме 2 суммируется полная процедура попиксельного распространения релевантности для нейронных сетей.
Алгоритм 2. Попиксельная декомпозиция для нейронных сетей
Вход: R(l)=f(x)
для l∈{L-1,…,1} выполнять
Вычислить 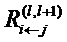 как в уравнениях (58) или (60)
как в уравнениях (58) или (60)
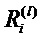 =Σj
=Σj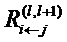
конец для
Выход:∀d:
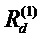
Приведенные выше формулы (58) и (60) непосредственно применимы к слоям, которые удовлетворяют определенной структуре. Предположим, что мы имеем активацию xj нейрона из одного слоя, который моделируется как функция входов из активаций xi из предшествующего слоя. Тогда послойное распространение релевантности непосредственно применимо, если существует функция gj и функции hij такие, что

В таком общем случае, весовые члены zij=xiwij из уравнения (50) необходимо соответственно заменить функцией hij(xi). Вновь заметим, что даже суммирование по максимумам вписывается в эту структуру как предел обобщения, см., например, уравнение (32). Для структур с более высокой степенью нелинейности, таких как локальная перенормировка [26, 36], можно вновь использовать аппроксимацию Тейлора, применимую к активации xj нейрона, для достижения аппроксимации для структуры, как указано в уравнении (63).
Наконец, из формул, установленных в этом разделе, видно, что послойное распространение релевантности отличается от ряда Тейлора или частных производных. В отличие от ряда Тейлора, она не требует второй точки, иной, чем входное изображение. Послойное применение ряда Тейлора может быть интерпретировано как обобщенный способ достижения приближенной версии послойного распространения релевантности. Аналогичным образом, в отличие от любых методов, основанных на производных, свойства дифференцируемости или гладкости активаций нейронов не являются необходимым требованием для определения формул, которые удовлетворяют послойному распространению релевантности. В этом смысле это более общий принцип.
Обобщенное представление
Приведенные выше формулы A5-A8 можно обобщить.
Предположим, что мы уже имеем оценки 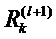 релевантности для всех нейронов k на уровне l+1. Прежде всего, отметим, что основная идея состоит в том, чтобы генерировать сообщения
релевантности для всех нейронов k на уровне l+1. Прежде всего, отметим, что основная идея состоит в том, чтобы генерировать сообщения 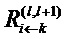 так, что удовлетворяется уравнение (13)
так, что удовлетворяется уравнение (13)
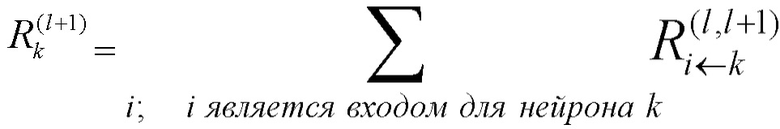
а затем вычислить из этих сообщений релевантности 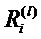 для всех нейронов i в слое l. Как описано выше, уравнения A5-A8 являются примерами того, как вычислять сообщения
для всех нейронов i в слое l. Как описано выше, уравнения A5-A8 являются примерами того, как вычислять сообщения 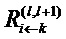 . В описанном выше подходе уравнение (8)
. В описанном выше подходе уравнение (8)
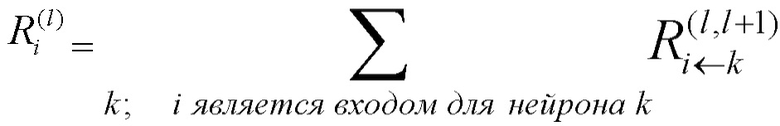
использовалось для вычисления релевантности 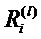 для всех нейронов i в слое l.
для всех нейронов i в слое l.
Первое обобщение можно сделать в отношении уравнения (8):
При задании всех сообщений 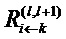 , мы можем вычислить релевантности
, мы можем вычислить релевантности 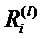 для всех нейронов i на уровне l, используя другую функцию, чем сумма сообщений релевантности
для всех нейронов i на уровне l, используя другую функцию, чем сумма сообщений релевантности 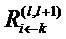 , которую мы обозначим как m(⋅), и которая принимает сообщения
, которую мы обозначим как m(⋅), и которая принимает сообщения 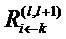 в качестве входа: релевантность нейрона i вычисляется посредством функции m(⋅) как
в качестве входа: релевантность нейрона i вычисляется посредством функции m(⋅) как
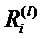 =m({
=m({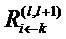 |k: i является входом для нейрона k})
|k: i является входом для нейрона k})
которая должна быть монотонно возрастающей в каждом из своих аргументов и может рассматриваться как обобщение суммы в уравнении (8). При использовании терминологии восходящих и нисходящих нейронов, можно записать:
Ri=m({Ri←k|k является нисходящим нейроном для i})
Несколько менее общим, но, возможно, часто используемым вариантом этого обобщения является:
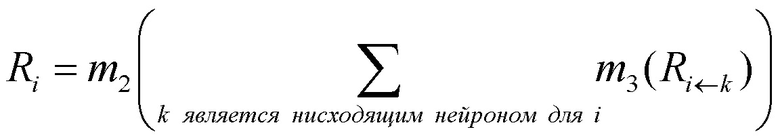
При этом m2 и m3 являются монотонно возрастающей функцией одной переменной.
Например:
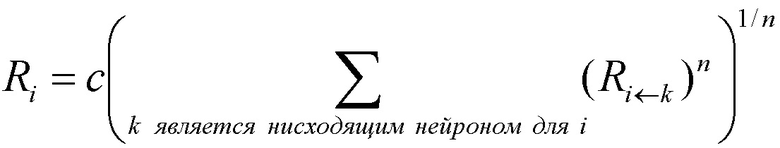
Где c - постоянная, выбранная таким образом, что поддерживается сохранение релевантности. Этот пример при больших значениях n устанавливает больший вес для больших членов.
Второе обобщение может быть сделано в отношении уравнения (13) при рассмотрении формул A5-A8, в которых 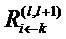 всегда является членом, умноженным на
всегда является членом, умноженным на 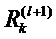 :
:
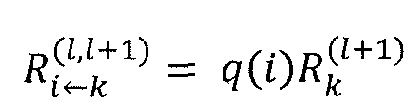
где q (i) - весовая функция такая, что
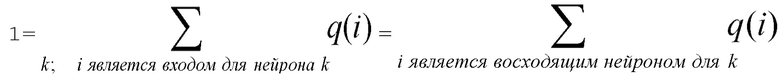
Что гарантирует, что уравнение (13) все еще выполняется.
Поскольку оценки релевантности нейронов для нейронов k в слое l+1 были ранее вычислены из оценок релевантности нейронов для нейронов p в слое l+2, мы также можем переписать приведенное выше уравнение как:
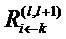 =q(i)m({Rk←p|p является нисходящим нейроном для k})
=q(i)m({Rk←p|p является нисходящим нейроном для k})
Поэтому мы приходим к первому уровню обобщения:
Обобщение 1
При заданном наборе оценок Rk релевантности нейронов для набора нейронов {k}, мы вычисляем сообщения релевантности к набору нейронов {i}, которые являются восходящими нейронами для набора нейронов {k}, так что имеется функция взвешивания сообщения q(⋅) такая, что Ri←k=q(i)Rk.
При заданном наборе сообщений Ri←k релевантности, вычислим оценку релевантности нейрона i посредством функции m(⋅), которая является монотонно возрастающей в своих аргументах, так что:
Ri=m({Ri←k|k является нисходящим нейроном для i})
В частности, когда используются только члены сообщения релевантности, и предполагая, что мы имеем сообщения {Rk←p|p является нисходящим нейроном для k} для всех нейронов k, которые являются нисходящими нейронами нейрона i, тогда мы можем вычислить:
Ri←k=q(i)m{Rk←p|p является нисходящим нейроном для k}
Конец Обобщения 1
Кроме того, мы можем потребовать, чтобы свойство сохранения релевантности выполнялось. Это имеет место, например, если сеть является многослойной, функция m(.) является суммой по элементам, и если выполняется уравнение
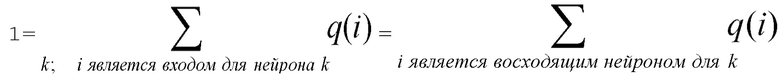
Отметим, что требования к численной стабильности могут потребовать включения численных стабилизирующих членов, так что свойство сохранения релевантности удовлетворяется только приблизительно, например, что послойная сумма релевантностей равна до отклонений 5%. См. функцию h(z)=z+ε⋅sign(z), используемую в формулах A5 и A6 в качестве примера для численного стабилизатора.
Обобщение 2
Требование свойства сохранения релевантности до некоторого допуска выражается такими условиями, как:
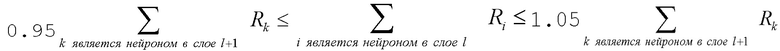
С использованием терминов ʺвосходящийʺ и ʺнисходящийʺ это будет:

Это также можно переформулировать с двумя разными представлениями. В первом представлении мы рассматриваем только начальную релевантность R с выхода и релевантности Ri для каждого элемента в наборе входных элементов, которые служат в качестве входов для нейронной сети. Тогда мы можем сформулировать вышеуказанное требование в этих терминах без указания суммы релевантностей в промежуточных слоях нейронной сети:
0.95R≤Σi в элементах Ri≤1.05R
Во втором представлении, мы рассматриваем вместо оценок релевантностей для нейронов, сообщения релевантности между нейронами, которые входят и выходят из одного фиксированного нейрона.
Мы требуем, чтобы сумма сообщений, которые входят в конкретный нейрон j из всех его нисходящих нейронов, приблизительно равна сумме сообщений, которые отправляются из нейрона j к его восходящим нейронам, вновь, в качестве примера, с 5% допуском:
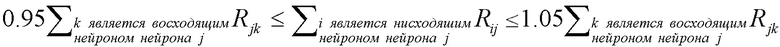
Конец Обобщения 2
Все эти три представления могут быть обобщены далее, если для среднего члена мы рассмотрим монотонную функцию ζ, f или ξ, которая зависит исключительно от ее входа:
Обобщение 2B
Представление 1: оценки Rk релевантности нейронов

Представление 2: оценка R релевантности выходных нейронов и оценки релевантности для элементов в наборе входных элементов
0.95R≤f(Σi в элементах Ri)≤1.05R
Представление 3: сообщения Rjk релевантности для восходящих и нисходящих соседних нейронов для нейрона j.

Конец Обобщения 2B
Теперь рассмотрим третий уровень обобщения.
Проверяя уравнения A5-A8, мы можем выделить некоторые дополнительные требования для вышеуказанных уровней обобщения. Прежде всего, q(i) в уравнениях A5-A8 зависит от взвешенных активаций zij. Разница между формулами A5 по сравнению с A6 и A7 по сравнению с A8 заключается только в определении взвешенных активаций zij.
В A5 и A7 взвешенная активация равна zij=xiwij. В A6 и A8 взвешенная активация равна zij=xiwij+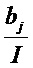 , где bj - смещение нейрона j, и I - число восходящих нейронов для нейрона j. Эта разница в определении взвешенной активации исходит из двух разных представлений члена смещения. В первом уравнении zij=xiwij член смещения моделируется отдельным нейроном, который выдает постоянный выход со значением, равным значению bj. Так как смещение генерируется отдельным нейроном, оно не вводит вычислений взвешенных активаций.
, где bj - смещение нейрона j, и I - число восходящих нейронов для нейрона j. Эта разница в определении взвешенной активации исходит из двух разных представлений члена смещения. В первом уравнении zij=xiwij член смещения моделируется отдельным нейроном, который выдает постоянный выход со значением, равным значению bj. Так как смещение генерируется отдельным нейроном, оно не вводит вычислений взвешенных активаций.
Во втором представлении, смещение является дополнительным термином, который добавляется к каждому входу к нейрону j - это объясняет добавленный член 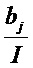 во втором определении взвешенной активации.
во втором определении взвешенной активации.
Таким образом, на самом деле у нас есть только две базовые формулы, полученные из двух уравнений A5 и A7 с двумя разными способами определения взвешенной активации zij.

Где  [[A]]
[[A]] - единица, если определение zij не включает смещение, то есть, если zij определяется как zij=xiwij, и нуль в противном случае. Здесь мы использовали неявно
- единица, если определение zij не включает смещение, то есть, если zij определяется как zij=xiwij, и нуль в противном случае. Здесь мы использовали неявно
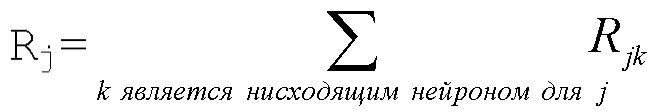
вместо общего определения оценки Rj релевантности нейронов посредством монотонно возрастающей функции m(⋅). В этих особых случаях, заданных уравнениями A5* и A7*, имеем
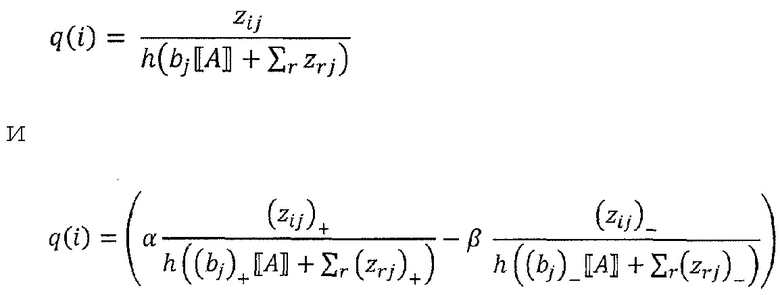
Эта проверка приводит к третьему уровню обобщения:
Обобщение 3
Функция q(i) зависит от взвешенных активаций zij, где взвешенная активация является функцией активаций xi нейронов, весов wij соединений и членов смещения bj.
zij=s(xi, wij, bj).
В качестве специальных случаев
zij=xiwij и zij=xiwij+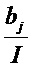
Конец Обобщения 3
Наконец, существует четвертый уровень обобщения. При проверке уравнений A5* и A7* можно видеть одно неявное свойство, а именно, зависимость q(i) от упорядочения взвешенных активаций zij. Интуитивно, если для двух нейронов i1 и i2 одна из взвешенных активаций больше, чем другая: 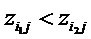 , то нейрон i2 также должен получать большую долю релевантности от нейрона j, чем нейрона i1. Однако следует с осторожностью определять это интуитивное понятие, поскольку оценки Rj релевантности нейронов, взвешенные активации zij и веса q(i) могут иметь разные знаки, что приводит к замене знака в полученном сообщении Ri←j релевантности. Вот почему нельзя просто потребовать
, то нейрон i2 также должен получать большую долю релевантности от нейрона j, чем нейрона i1. Однако следует с осторожностью определять это интуитивное понятие, поскольку оценки Rj релевантности нейронов, взвешенные активации zij и веса q(i) могут иметь разные знаки, что приводит к замене знака в полученном сообщении Ri←j релевантности. Вот почему нельзя просто потребовать 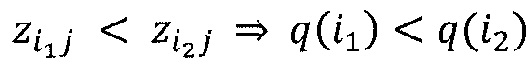 . Приведем контрпример: в формуле A5*, если 0<
. Приведем контрпример: в формуле A5*, если 0<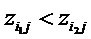 , но
, но 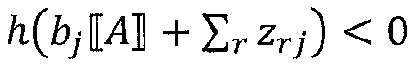 , то следует: q(i1)>q(i2)>0. Однако то, что выполняется в этом случае: |q(i1)|<|q(i2)|, потому что член
, то следует: q(i1)>q(i2)>0. Однако то, что выполняется в этом случае: |q(i1)|<|q(i2)|, потому что член 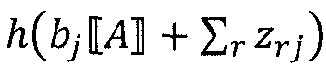 является тем же самым для q(i1) и (i2).
является тем же самым для q(i1) и (i2).
Проверяя формулы A5* и A7*, можно получить набор свойств упорядочения, которым удовлетворяют эти формулы. Одним из способов определения свойств упорядочения является учет обобщения абсолютных значений взвешенных активаций zij и абсолютных значений весовой функции (⋅) сообщения.
Для формулы A5* выполняется следующее свойство упорядочения:
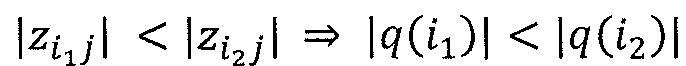
Для формулы A7* выполняется несколько отличающееся свойство упорядочения. Рассмотрим
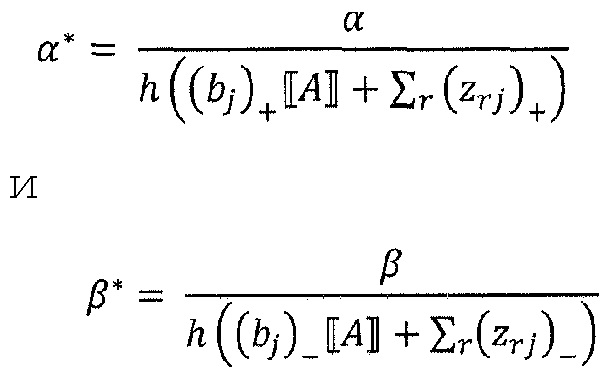
Тогда для функции
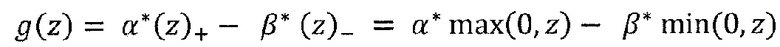
выполняется следующее свойство упорядочения:
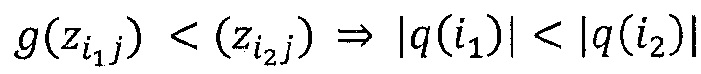
Заметим здесь, что |z|=α(z)+-β(z)- при α=1, β=1, так что функция g(.) также включает свойство упорядочения для формулы A5* с различными значениями для α, β.
Дальнейшее обобщение приведенной выше функции g(⋅) приводит к функции, которая имеет свой минимум в нуле и монотонно убывает на интервале (-∞, 0) и монотонно возрастает на интервале (0, +∞).
Поэтому мы приходим к Обобщению 4
Требуется, чтобы функция q(⋅) сообщения удовлетворяла свойству упорядочения, состоящему в том, что для всех i1 и i2, являющихся восходящими соседними нейронами нейрона j, для которых
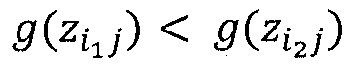
выполняется |q(i1)|≤|q(i2)| для функции g(⋅), которая имеет свой минимум в нуле и монотонно убывает на интервале (-∞, 0) и монотонно возрастает на интервале (0, +∞).
В частности, одним выбором для функции g(⋅) является 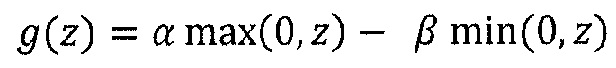 при α≥0, β≥0.
при α≥0, β≥0.
Конец Обобщения 4
Другим способом определения свойств упорядочения является ограничение до случая, когда Rj>0. Это имеет смысл, когда не представляет интереса распространение отрицательных нейронных релевантностей. Чтобы понять это, следует учесть, что обычно представляет интерес предсказание для отдельных элементов в наборе элементов, когда предсказание, полученное нейронной сетью, связано с наличием структуры, что подразумевает, что выход нейрона имеет положительные оценки по набору элементов в качестве входа. Если выход нейронов имеет положительные оценки, то можно ожидать, что большинство релевантных нейронов также положительны, просто потому, что большинство нейронов поддерживают положительное предсказание нейронной сети, и поэтому можно игнорировать незначительную долю нейронов с отрицательной релевантностью на практике.
Чтобы вывести другое свойство упорядочения, отметим, что если Σizij>0, то мы также имеем h(Σizij)>0 для h(t)=t+ε sign(t).
В частности, при рассмотрении формулы A5* выполняется следующее свойство упорядочения: если Σizij>0, то для всех i1 и i2, которые являются восходящими нейронами нейрона j, имеем:
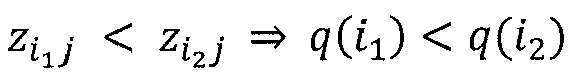
Если Σizij<0, то для всех i1 и i2, которые являются восходящими нейронами нейрона j, имеем:
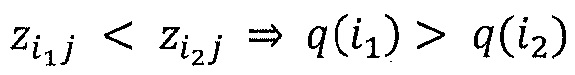
Это свойство не выполняется для формул A7*.
Обобщение 5
Требуется, чтобы функция q(⋅) сообщения удовлетворяла свойство упорядочения, состоящее в том, что если Rj>0 и Σizij>0, то для всех i1 и i2, которые являются восходящими нейронами нейрона j, имеем:
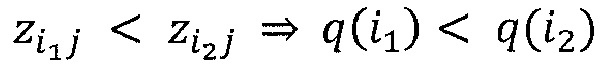
Конец Обобщения 5
Другим свойством упорядочения, которое может быть полезно для случая Rj>0, было бы:
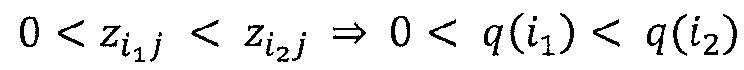
Это справедливо для формулы A7*.
Существует еще одно свойство упорядочения, которое также выполняется для обеих формул A5* и A7*, а именно, если мы сравниваем только взвешенные активации, имеющие один и тот же знак:
Требуется, чтобы функция q(⋅) сообщения удовлетворяла свойство упорядочения, состоящее в том, что если 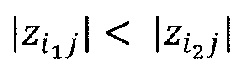 и
и 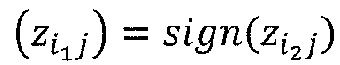 , то справедливо, что
, то справедливо, что 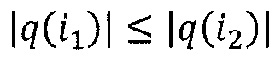 .
.
Это позволяет заменить функцию g(⋅) на абсолютную величину.
Заметим, что формула A5* удовлетворяет более узкому свойству упорядочения, а именно
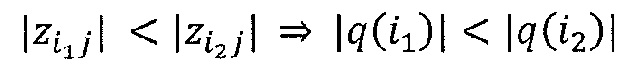
Все эти формулы выполняются, когда мы вставляем zij=xiwij или zij=xiwij+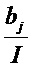 , так что мы могли бы создать из каждый из вышеперечисленных свойств упорядочения две версии в зависимости от того, какое определение взвешенных активаций zij мы используем.
, так что мы могли бы создать из каждый из вышеперечисленных свойств упорядочения две версии в зависимости от того, какое определение взвешенных активаций zij мы используем.
Отметим, что существуют другие возможности определения свойств упорядочения.
Например, следующие восемь условий также дают значимые свойства упорядочения, которые выражаются в терминах сообщений релевантности:
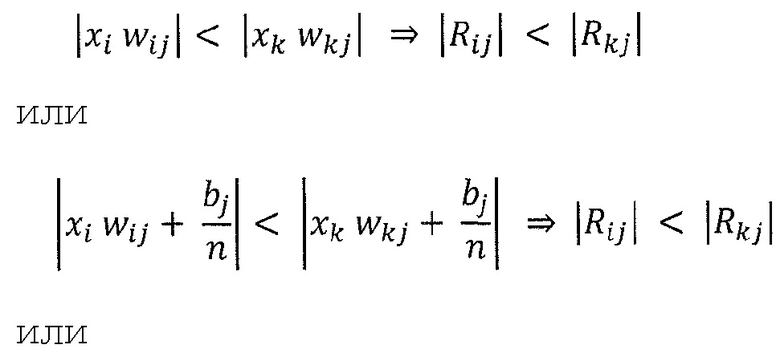
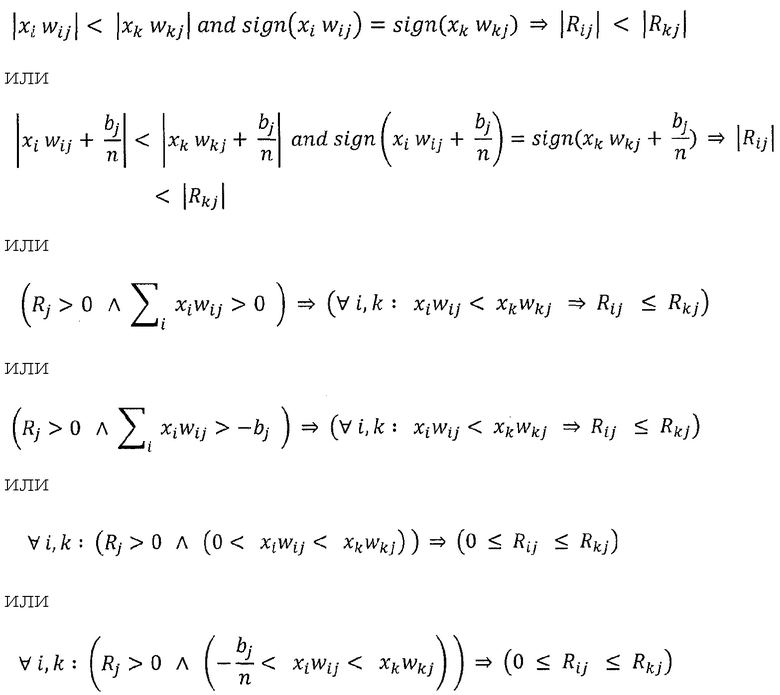
Вместо того чтобы применять разложение Тейлора к функции выхода сети в зависимости от входов сети, разложение Тейлора может также применяться для перераспределения оценки релевантности одного нейрона на его восходящих соседей. Это позволяет объединить представленные выше стратегии для одного набора нейронов с распределением релевантности по распределению Тейлора для другого набора нейронов. Разложение Тейлора можно было бы использовать следующим образом: предположим, что 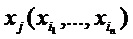 является функцией нейронной активации нейрона j в зависимости от входов
является функцией нейронной активации нейрона j в зависимости от входов 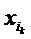 восходящих соседних нейронов i1,…, in. Тогда пусть
восходящих соседних нейронов i1,…, in. Тогда пусть 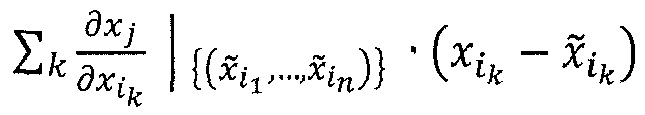 будет разложением Тейлора хj для входов
будет разложением Тейлора хj для входов 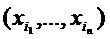 вокруг точки
вокруг точки 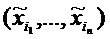 . Затем мы можем использовать разложение Тейлора с приведенными выше формулами, устанавливая:
. Затем мы можем использовать разложение Тейлора с приведенными выше формулами, устанавливая:
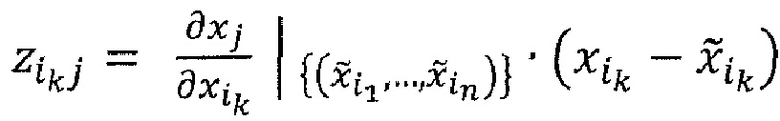
Различные дополнительные пояснения
Таким образом, современные классификаторы, такие как глубокие нейронные сети (DNN), работают следующим образом.
1) Структура сети (например, количество слоев, блоков и т.д.) разрабатывается человеком.
2) Параметры сети (веса) обучаются/оптимизируются с использованием потенциально миллионов маркированных (и немаркированных) выборок данных, например изображений. Отметим, что некоторые предварительно обученные сети доступны в Интернете.
3) Сеть может быть применена к новому изображению и может, например, классифицировать изображение как принадлежащее к определенному классу, например, классу 'изображений, содержащих акулу', 'текстовых документов, которые являются новостями' или 'некредитоспособных лиц'.
4) Поскольку сеть является сильно нелинейной и очень сложной, трудно понять, почему это конкретное изображение классифицируется как 'акула'. Таким образом, сеть действует как черный ящик (см. фиг. 4).
5) Представленные варианты осуществления могут объяснить, почему классификатор приходит к своему решению, то есть мы можем визуализировать, где (например, в терминах пикселов) находится важная информация. В частности, мы можем разбить решение классификации, которое было вычислено в крупном масштабе (например, целое изображение, весь текстовый документ) на меньшие масштабы (например, отдельные пиксели, отдельные слова).
6) Поскольку DNN могут не только обучаться на изображениях, но и применяться практически к каждому типу данных, например, к временным рядам, словам, физическим измерениям и т.д., принципы описанных вариантов осуществления применимы ко многим различным сценариям.
Описание, представленное в отношении фиг. 5-10, в дальнейшем должно быть использовано для предоставления некоторых дополнительных замечаний к описанию устройства назначения оценки релевантности согласно фиг. 4. Уже было описано выше, что устройство 50 может быть просто сконфигурировано для выполнения перераспределения 52. Кроме того, однако, устройство 50 также может быть сконфигурировано для выполнения фактического применения искусственной нейронной сети 10 на наборе 16. Таким образом, устройство 50 может для этой альтернативы считаться состоящим из процессора нейронной сети, для которого может быть повторно использована ссылочная позиция 10, и процессора перераспределения, для которого может быть повторно использована ссылочная позиция 52. В любом случае, устройство 50 может, например, содержать хранилище или память 46. Интересно, однако, отметить, что может быть промежуток между слоем, от которого процесс предсказания, например процесс классификации, использует сеть 10, с одной стороны, и слоем, до которого обратный процесс 52 распространения проходит через сеть 10 обратно. В случае фиг. 1a-c и 2a-c, например, было показано, что прямое распространение 14, участвующее в процессе предсказания, охватывает те же слои сети 10, что и процесс 32 обратного распространения. То есть, процесс 14 прямого распространения или сеть 10 непосредственно применялись к набору 16, и обратное распространение 32 непосредственно завершалось в оценках релевантности для набора 16. В случае фиг. 1b и 2b, например, в рамках процесса предсказания, этот набор 16 был предварительно заполнен посредством процесса 30 извлечения признаков, и для того, чтобы выделить релевантные части оценки повышенной релевантности, например, способом наложения на начальное изображение 22, обращение этого выделения признаков, а именно 38, было использовано, чтобы продолжить процесс обратного распространения и выполнить выделение релевантных частей в пространственной (пиксельной) области. Однако изложенное выше описание также выявило, что процесс 30 извлечения признаков может быть альтернативно преобразован или описан с использованием одного или нескольких дополнительных слоев искусственной нейронной сети, то есть слоев нейронов, предшествующих фактической (обученной) части сети 10 в направлении 14 прямого распространения, то есть слоев или части 21. Эти слои, которые просто отражают задачу извлечения 30 признаков, не требуется фактически пересекать при обратном распространении в процессе назначения релевантности. Однако эти дополнительные (переведенные) слои части 21 на стороне верхнего слоя могут быть пройдены в процессе прямого распространения во время процесса предсказания, а именно на его конце, начинающемся перед обходом фактической (обученной) части сети 10. Таким образом, оценки Ri релевантности будут получены для выборок признаков, а не пикселов. Иными словами, релевантность может быть разложена не только в терминах входных переменных (например, красного, зеленого и синего компонентов каждого пиксела в случае изображений или компонентов вектора, ассоциированного с каждым словом в случае текстов), но и в терминах нелинейного преобразования этих элементов (например, нейронов на определенном слое сети). Таким образом, может быть желательным остановить обратное проецирование релевантности на определенном промежуточном слое. Естественно, пример этого промежутка между начальной точкой прямого распространения, с одной стороны, и конечной точкой в обратном распространении 32, с другой стороны, может быть применен и к другим типам данных, то есть к данным, отличным от изображений, таким как, например, аудиосигналы, тексты или тому подобное.
Дополнительные примечания, по-видимому, заслуживают внимания в отношении вида выхода 18 сети и элементов 42 набора 16. Что касается выхода 18 сети, также было указано выше, что это же может представлять собой скаляр или вектор, причем скаляр или компоненты вектора являются, например, действительными значениями. Значение R релевантности, полученное из них, может быть действительным значением, полученным из скаляра или одного из компонентов вектора, соответственно. Что касается ʺэлементовʺ 42, приведенные выше примеры должны были сделать уже достаточно ясным, что они аналогичным образом могут быть скалярами или векторами. Сопоставление фиг. 1а и 2а, с одной стороны, и фиг.1с и 2с, с другой стороны, делает это ясным. В случае пикселов цветных изображений, например, изображенных на фиг. 1с и 2с, пиксельные значения представляют собой векторы, а именно, здесь иллюстративные векторы из трех или даже более компонентов, соответствующих трем (или более) скалярным цветовым компонентам, таким как RGB, CMYK или т.п. Элементы 42 набора 16 являются скалярными компонентами пиксела. Перераспределение значения релевантности в наборе элементов приводит к значению Ri релевантности для каждого элемента, а именно, каждого компонента для каждого пиксела. Чтобы получить одно скалярное значение релевантности для каждого пиксела, значения релевантности всех компонентов соответствующего пиксела могут быть просуммированы для получения такого общего значения релевантности для этого пиксела. Это было показано в 37 на фиг. 2с. Подобные меры могут применяться и в случае текстов. Таким образом, декомпозиция релевантности по входным переменным может быть перегруппирована так, чтобы обеспечивать простую визуализацию и интерпретацию декомпозиции релевантности. Например, чтобы визуализировать релевантность как тепловую карту в пиксельной области, можно суммировать для каждого пиксела релевантность, ассоциированную с с его красным, зеленым и синим компонентами, как объяснено со ссылкой на фиг. 2с. Аналогично, для текстового анализа, чтобы визуализировать декомпозицию релевантности документа как текст, отображенный на тепловой карте, можно суммировать для каждого слова релевантность, ассоциированную с каждым компонентом соответствующего вектора.
Другие примеры также можно было бы оценить. Однако условия, налагаемые стабилизирующей функцией h(⋅) (см. уравнения A5* и A7*), могут привести к ʺутечкеʺ релевантности, так что свойство релевантности, описанное, например, с помощью вышеупомянутых функций f, ξ и ζ из обобщения 2B, могут, например, не выполняться для каждого набора 16 элементов. Например, это может быть выполнено только для наборов или элементов, приводящих в результате к выходу сети, достигающему не менее 75% от максимального выхода сети. Представим, например, что предсказание, выполненное искусственной нейронной сетью, заключается в том, показывает ли какая-то картинка ʺкошкуʺ, тогда предсказания для изображений, для которых предсказание на выходе сети приводит к значению выше 75%, что они показывают кошку, могут, когда они подвергаются обратному распространению, приводить к оценкам релевантности для пикселов, которые удовлетворяют условию относительно f (для всех из них или по меньшей мере более 99%), в то время как другие картинки могут не удовлетворять или не удовлетворять с уверенностью.
С другой точки зрения, функция распределения должна быть выбрана преимущественно так, что она приводит к ʺзначимымʺ (интерпретируемым) оценкам релевантности обратного распространения. С этой целью, функция распределения может подчиняться некоторому свойству ʺупорядочиванияʺ, дополнительно или альтернативно к свойству сохранения релевантности. Другими словами, даже не соблюдая упомянутое выше свойство сохранения релевантности, функция распределения может приводить к значимым оценкам релевантности обратного распространения. В частности, для каждого нейрона j, функция распределения, обеспечивающая, насколько релевантность Rij перераспределяется от соответствующего нейрона j к восходящему соседнему нейрону i, может быть
Rij=q(i)⋅m({Rik, k является нисходящим нейроном для j})
где m(RK), при K, являющемся числом нисходящих соседей соответствующего нейрона j, является монотонно возрастающей функцией для всех его компонентов и дает предварительно перераспределенное значение релевантности соответствующего нейрона j и
q(i) - функция, удовлетворяющая свойству упорядочения, зависящая от активаций xi восходящих соседних нейронов i соответствующего нейрона j, - при I, являющемся числом восходящих соседних нейронов i, - и весов wij, соединяющих восходящий соседний нейрон i с соответствующим нейроном j, и, если имеется, члена смещения bj соответствующего нейрона j, который считается нулевым, если он отсутствует, где свойство упорядочения является одним из указанных в обобщении 4 и обобщении 5.
Следует также отметить, что на фиг. 4 одновременно показана диаграмма процесса назначения оценки релевантности и что показанные здесь элементы, такие как 10 и 52, представляют этапы процесса, выполняемые во время такого способа/процесса, причем этапы, такие как 30 и 38, представляют собой опциональные этапы или задачи, дополнительно выполняемые во время процесса. Альтернативно, устройство 50 может быть сконфигурировано для дополнительного выполнения задач 30 и 38 или 30. Например, все эти задачи могут представлять разные части кода компьютерной программы, на основе которой реализован процесс или устройство 50.
Кроме того, приведенное выше описание будет излагаться далее с использованием некоторой другой терминологии, чтобы избежать недоразумений в отношении объема настоящей заявки.
В частности, приведенное выше описание показывает анализ предсказания, сделанного на выборке, где ʺвыборкаʺ представляет собой набор из 16 элементов. Предсказание - это процесс вывода выхода сети на основе набора 16 элементов и выполняется путем отображения, которое принимает выборку в качестве входа. Предсказание производится по выборке в целом и приводит к векторнозначному или действительнозначному выходу или к выходу, который может быть преобразован в векторнозначный или действительнозначный выход, то есть выход 18 сети. Отображение предсказания предусматривает прямое распространение 14 через нейронную сеть. Его можно разложить следующим образом: оно состоит из элементов 12, которые принимают входы и вычисляют выход, применяя функцию к входам, а именно, нейронную функцию. По меньшей мере один элемент 12 имеет один элемент выборки, то есть набор 16, в качестве входа. Модель создается без потери общности так, что каждый элемент занимает не более одного элемента выборки в качестве входа. По меньшей мере один элемент 12 принимает выходы других элементов в качестве входа. Они могут быть, как описано выше, взвешенными путем перемножения значения, которое зависит от элемента 12, и его входа. По меньшей мере один из весов отличен от нуля. Выход по меньшей мере одного элемента используется для предсказания выборки. Существует соединение от элемента выборки к предсказаниям в модели.
Говоря иначе, вышеописанное (многослойное) обратное распространение выполняется в предположении, что предсказание по набору элементов уже выполнено. Процесс начинается с инициализации релевантности всех тех элементов, которые были непосредственно вычислены путем предсказания, то есть на основе выхода сети. Если этот выход является действительнозначным, то релевантность R формирует выходной нейрон, который вычислял соответствующее предсказание, выход сети инициализируется с использованием значения предсказания модели. Если выход является векторнозначным, то релевантность R может быть установлена для всех выходных нейронов, может быть инициализирована с использованием инициализации, описанной для случая действительнозначных выходов для случая одного выходного нейрона, и путем установки релевантности в нуль для оставшихся выходных нейронов. После инициализации, необходимо вычислить поочередно следующие две формулы.
В частности, для каждого элемента (нейрона) k, для которого уже вычислена релевантность Rk, сообщения Ri←k вычисляются для всех элементов i, которые обеспечивают входы для элемента k, так, что
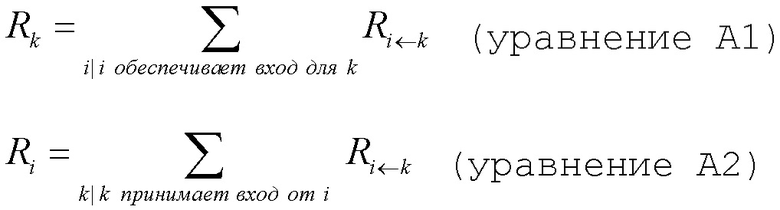
Альтернативно, можно использовать только уравнение A2 и только вычислять сообщения Ri←k неявно таким образом, чтобы они удовлетворяли уравнению A1.
В случае, если нейронная сеть содержит циклы, т.е. нейронная сеть является рекуррентной и имеет зависящее от времени состояние, ее структура может быть развернута во времени, приводя к отображению с прямой связью, к которому мы можем применить ту же процедуру, как описано выше. Под развертыванием во времени имеется в виду наличие одного слоя, который моделирует состояние сети на каждом временном шаге.
По меньшей мере одно из сообщений Ri←k может быть заменено случайным значением перед вычислением релевантности Ri входного элемента i (даже если это сообщение Ri←k может быть вычислено, потому что на каком-то этапе была вычислена релевантность Rk, необходимая для его вычисления).
По меньшей мере одно из сообщений Ri←k может быть заменено на постоянное значение перед вычислением релевантности Ri входного элемента i (даже если это сообщение Ri←k может быть вычислено, потому что на каком-то этапе была вычислена релевантность Rk, необходимая для его вычисления).
Ниже мы предлагаем более техническое представление принципа послойного распространения релевантности. Каждому слою присваивается индекс. Первый слой имеет индекс 1, последний - самый высокий индекс. Оценка для каждого элемента в наборе 16 может быть вычислена следующим образом:
Предполагаем, что уже имеем предсказание по упорядоченному набору элементов.
Во-первых, инициализируем релевантность последнего слоя, который является выходным слоем, как описано ниже:
- Если выход действительнозначный, то инициализируем релевантность для одного элемента в последнем слое как значение предсказания модели.
- Если выход векторнозначный, то инициализируем релевантность для всех элементов в последнем слое либо путем использования инициализации, описанной для случая действительнозначных выходов, по меньшей мере для одного элемента в выходном слое и путем установки релевантности в нуль для остальных элементов.
Во-вторых, выполняем итерацию по слоям от одного индекса слоя к восходящему слою.
Итерация выполняется следующим образом:
- При заданных релевантностях 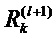 для всех элементов в текущем слое (индексированном как l+1), вычисляем члены сообщения
для всех элементов в текущем слое (индексированном как l+1), вычисляем члены сообщения 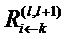 от каждого элемента в текущем слое (индекс l+1) ко всем элементам в восходящем слое (индекс l), так что
от каждого элемента в текущем слое (индекс l+1) ко всем элементам в восходящем слое (индекс l), так что

выполняется с ошибками аппроксимации.
- При заданных сообщениях 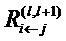 от слоя к его восходящему слою, вычисляем релевантность для восходящего слоя посредством
от слоя к его восходящему слою, вычисляем релевантность для восходящего слоя посредством

Отсюда итерация будет выполняться для следующего восходящего слоя l-1, поскольку все релевантности 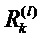 в слое l были вычислены.
в слое l были вычислены.
Результатом итерации по всем слоям до слоя 1 являются оценки 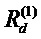 релевантности для всех элементов в первом слое, которые являются оценками для элементов в упорядоченном наборе.
релевантности для всех элементов в первом слое, которые являются оценками для элементов в упорядоченном наборе.
Результатом способа является одна оценка на каждый элемент, что обозначает релевантность элемента для предсказания, сделанного по упорядоченному набору элементов, или результатом является оценка, объединенная с по меньшей мере одним из следующего:
- отображение этих оценок на цвет, так что каждый интервал оценок отображается на один цвет,
- отсортированный список элементов в соответствии с порядком, определяемым оценками для каждого элемента.
Может быть, что
- Если функция находится в слое l, то обозначим выходное значение элемента, индексированного буквой i, как 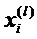 ,
,
- Соединения от одного элемента, индексированного как i, к другому элементу, индексированному как j, могут иметь веса wij,
которые умножаются на выход предыдущего элемента. Поэтому вход в элемент, индексированный как j, из элемента в слое l, индексированного как i, можно записать в виде
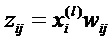
Члены смещений могут быть представлены элементами, которые не принимают никакого входа и обеспечивают постоянные выходы.
В частности, вычисляем члены сообщений 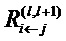 путем применения по меньшей мере к одному элементу в модели и к набору входов этого элемента по меньшей мере один из следующих наборов формул:
путем применения по меньшей мере к одному элементу в модели и к набору входов этого элемента по меньшей мере один из следующих наборов формул:
уравнения A5 или A6 или A7 или A8 (приведенные выше)
Члены сообщений 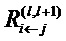 могут быть вычислены путем применения по меньшей мере к одному элементу в модели и к набору входов этого элемента по меньшей мере одного из вышеуказанных уравнений A1-A26.
могут быть вычислены путем применения по меньшей мере к одному элементу в модели и к набору входов этого элемента по меньшей мере одного из вышеуказанных уравнений A1-A26.
Выборка может быть упорядоченной совокупностью элементов. Ниже мы приводим список нескольких возможных примеров упорядоченных совокупностей элементов.
Упорядоченная совокупность элементов может быть изображением, и каждый элемент может представлять собой набор из одного или нескольких его пикселов.
Упорядоченная совокупность элементов может быть текстом, и каждый элемент может быть набором из одного или нескольких его слов.
Упорядоченная совокупность элементов может быть текстом, и каждый элемент может быть набором из одного или нескольких его предложений.
Упорядоченная совокупность элементов может быть текстом, и каждый элемент может быть набором из одного или нескольких его абзацев.
Упорядоченная совокупность элементов может быть списком пар значений ключа, и каждый элемент может быть набором из одной или нескольких пар его значений.
Упорядоченная совокупность элементов может быть списком пар значений ключа финансовых данных или данных, относящихся к компании, и каждый элемент может представлять собой набор из одной или нескольких пар ключа.
Упорядоченная совокупность элементов может быть видео, и каждый элемент может быть набором из одной или нескольких пар пикселов с временными метками.
Упорядоченная совокупность элементов может быть видео, и каждый элемент может быть набором из одного или нескольких кадров.
Упорядоченная совокупность элементов может быть видео, и каждый элемент может быть набором из одного или нескольких пикселов.
Техническая спецификация обучаемой нейронной сети
Следующий раздел описывает нейронную сеть таким образом, что большинство ее слоев изучаются на этапе обучения, что является отличием от других типов алгоритмов неглубокого обучения. Она может иметь следующие свойства:
- Если модель является двухслойной во время тестирования, то весовые коэффициенты первого слоя оптимизируются с использованием набора данных обучения и меры ошибки, которая зависит от поднабора данных обучения.
- Если модель является тех- или четырехслойной во время тестирования, то весовые коэффициенты по меньшей мере первого или второго слоя оптимизируется с использованием набора данных обучения и меры ошибки, которая зависит от поднабора данных обучения.
- Если модель имеет пять или более слоев во время тестирования, то по меньшей мере весовые коэффициенты одного слоя от первого слоя до третьего от конца слоя оптимизируются с использованием набора данных обучения и меры ошибки, которая зависит от поднабора данных обучения (это позволяет также оптимизировать последние слои).
По меньшей мере один из элементов в слое может быть выпрямленными линейными блоками активации.
По меньшей мере один из элементов в слое может быть блоками активации Хевисайда.
По меньшей мере один из элементов в слое может быть блоками активации гиперболического тангенса.
По меньшей мере один из элементов в слое может быть логистическими блоками активации.
По меньшей мере один из элементов в слое может быть сигмоидальными блоками активации.
Эксперименты
Мы показываем результаты по двум наборам данных, двум наборам результатов по MNIST, которые легко интерпретировать, и второй набор экспериментов, которые основываются на 15-слойной уже обученной сети, обеспеченной как часть пакета Caffe с открытым исходным кодом [20], который прогнозирует 1000 категорий из задачи ILSVRC. С одной стороны, посредством экспериментов на цифрах MNIST мы намерены показать, что мы можем обнаружить детали, специфичные для фазы обучения. С другой стороны, результаты для предварительно подготовленной сети из набора инструментов Caffe демонстрируют, что этот метод работает с глубокой нейронной сетью нетривиальным образом и не полагается на возможные спецэффекты во время фазы обучения.
Мы применили назначение опорной оценки к другим реалистичным изображениям с использованием предварительно подготовленной сети. Объяснения решений классификации в виде оценок релевантности выделяют значимые признаки класса, например, плавник акулы для 'акулы', круглую форму для 'чашек', форму горы для 'вулкана' и т.д. Отметим, что назначение оценки релевантности не выделяет все градиенты на изображении, но выделяет отличительные признаки. На фиг. 9, например, показано применение вышеописанного назначения оценки релевантности нейронной сети, обученной распознавать 1000 классов из набора данных ImageNet: верхние изображения показывают вход в сеть, то есть набор 16, и нижние изображения показывают тепловую карту, показывающую оценки релевантности, назначенные пикселам в соответствии с вышеприведенными вариантами осуществления, по одному для каждого входного изображения. Тепловые карты могут, как указано выше, накладываться на входные изображения. Видно, что в случае змей (левое изображение) пикселы, представляющие оболочку, получают большую часть первоначальной оценки релевантности, т.е. идентифицируются как основная причина, приводящая к предсказанию сетью классификации изображения как показывающего змею, в случае акулы (второе слева изображение) пикселы, представляющие плавник, получают большую часть начальной оценки релевантности, в случае холма (второе справа изображение) пикселы, представляющие вершину, получают большую часть начальной оценки релевантности, и в случае спичек (левое изображение) пикселы, представляющие спички и огонь, получают большую часть начальной оценки релевантности.
Мы также обучили нейронную сеть на наборе данных MNIST. Этот набор данных содержит изображения чисел от 0 до 9. После обучения сеть может классифицировать новые, не наблюдавшиеся ранее изображения. С назначением оценки релевантности обратного распространения мы можем спросить, почему сеть классифицирует изображение 3 как класс '3', другими словами, что делает 3 отличным от других чисел. Можно видеть на тепловой карте на фиг. 10, что наиболее важными признаками 3 (по отношению к другим числам) являются средний горизонтальный участок и отсутствие вертикальных соединений слева (которые имелись бы для числа 8). Можно также спросить, например, почему изображение 4 не классифицируется как '9', другими словами, что говорит против 9 при наблюдении изображения 4. Можно видеть, что доказательством против '9' является разрыв наверху 4. Отметим, что красный цвет, указанный с использованием стрелки 62, служит доказательством для определенного класса, а синий цвет, указанный в 60, представляет доказательство против класса. Таким образом, мы показали, что способ обеспечивает осмысленные объяснения решений классификации.
Применения
До сих пор описание концентрировалось на процессе назначения оценки релевантности. Далее будет кратко описано, для чего могут использоваться оценки релевантности, назначенные элементам набора 16.
Общее применение предназначено для использования назначения оценки релевантности (назначения RS), предлагаемого здесь как часть более крупного и более сложного алгоритма (CA). Можно подумать о ситуациях, когда очень дорого применять алгоритм CA, поэтому наше назначение RS может определить некоторые интересующие области, в которых может применяться алгоритм CA. Например:
- Время врача имеет большую ценность. Назначение RS может идентифицировать важные области изображения при скрининге на рак.
- В видеокодировании ширина полосы канала имеет большую ценность. Назначение RS может информировать алгоритм CA о том, какие части видео важнее других, например, для определения лучшей стратегии кодирования (например, использование большего количества битов для важных частей) или лучшего графика передачи (например, сначала передавать важную информацию).
- Тепловая карта может использоваться для вычисления дополнительных признаков для некоторой задачи предсказания. Например, мы могли бы использовать обученную сеть, применять ее к некоторому изображению и извлекать больше признаков из областей, которые являются более важными. Это может привести к сокращению времени вычисления или передачи информации. Альтернативно, области или дополнительная информация, извлеченная из нее, могут использоваться для переподготовки и улучшения обученной сети.
- Назначение RS может использоваться в качестве инструмента исследования в случае, когда пользователь или компания хотели бы знать, какие области или признаки важны для определенной задачи.
Кроме того, в области применения изображения:
- Назначение RS может использоваться в медицинских приложениях, например, в качестве помощи врачам в выявлении опухолей в патологических изображениях или идентификации наблюдений в МРТ-изображениях.
Более конкретные примеры включают в себя:
-- обнаружение признаков воспаления в изображениях биологических тканей,
-- обнаружение признаков рака в изображениях биологических тканей,
-- обнаружение патологических изменений в изображениях биологических тканей,
- Назначение RS может быть применено к общим изображениям. Например, платформы социальных веб-сайтов или поисковые системы имеют много изображений и могут быть заинтересованы в том, что делает изображение 'смешным', 'необычным', 'интересным' или тем, что делает человека или дома или интерьеры домов привлекательными/эстетичными или менее привлекательными/менее эстетичными.
- Назначение RS может использоваться в приложениях наблюдения, чтобы определять, какая часть изображения запускает систему для обнаружения необычного события.
- Обнаружение изменений в землепользовании в изображениях, полученных спутниками, самолетами, или в данных дистанционного зондирования.
В области применения видео:
- Тепловые карты могут использоваться для установки интенсивности сжатия при кодировании, например, с использованием большего количества битов для областей, содержащих важную информацию, и меньшего количества битов для других областей.
- Назначение RS может использоваться для суммирования видео, то есть для идентификации 'релевантных' кадров в видео. Это позволит осуществлять интеллектуальный просмотр видео.
- Анимационные фильмы иногда выглядят не очень реалистично. Не ясно, что 'отсутствует', чтобы сделать фильмы более реалистичными. В этом случае можно использовать тепловые карты, чтобы выделить нереалистичные части видео.
В случае применений текстов:
- Классификация текстовых документов по категориям может выполняться посредством моделей DNN или BoW. Назначение RS может визуализировать, почему документы классифицируются в определенный класс. Релевантность текста для темы может быть выделена или выбрана для дальнейшей обработки. Назначение RS может выделять важные слова и, таким образом, предоставлять резюме длинного текста. Такие системы могут быть полезны, например, для патентных юристов для быстрого просмотра многих текстовых документов.
В случае применений финансовых данных:
Банки используют классификаторы, такие как (глубокие) нейронные сети, чтобы определить, получает ли кто-либо кредит или нет (например, немецкая система Schufa). Не является прозрачным, как работают эти алгоритмы, например, некоторые люди, которые не получают кредит, не знают, почему. Назначение RS может точно показать, почему кто-то не получает кредит.
В области маркетинга/продаж:
- Назначение RS может использоваться для определения того, что делает изображение/текст описания конкретного продукта для продаваемого продукта (например, аренда квартиры, описание продукта ebay).
- Назначение RS может быть использовано для определения того, что делает видеоролик в Интернете или блоге широко просматриваемым или любимым.
- Компании могут быть в целом заинтересованы в том, какие 'признаки' делают, например, их веб-сайт или продукт привлекательными.
- Компании заинтересованы в том, почему некоторые пользователи покупают продукт, а другие не покупают его. Назначение RS может использоваться для определения причины, по которой пользователи не покупают продукт и соответственно не улучшают рекламную стратегию.
В области лингвистики/образования:
- Назначение RS может использоваться для определения того, какая часть текста отличает носителя языка от не-носителя языка для определенного языка, такого как английский, французский, испанский или немецкий.
- Назначение RS может использоваться для поиска элементов доказательства в тексте, что документ был написан конкретным лицом или нет.
В приведенном выше описании были представлены различные варианты осуществления для назначения оценок релевантности множеству элементов. Например, были представлены примеры относительно изображений. В связи с последними примерами были представлены варианты осуществления относительно использования оценок релевантности, а именно, для того, чтобы выделить релевантные части на изображениях с использованием оценок релевантности, а именно с использованием тепловой карты, которая может быть наложена на начальное изображение. Ниже приводятся варианты осуществления, которые используют оценки релевантности, то есть варианты осуществления, которые используют вышеописанное назначение оценки релевантности.
На фиг. 11 показана система для обработки набора элементов. Система в общем обозначена с использованием ссылочной позиции 100. Система включает в себя, кроме устройства 50, устройство 102 обработки. Оба работают на наборе 16. Устройство 102 обработки сконфигурировано для обработки набора элементов, то есть набора 16, чтобы получить результат 104 обработки. При этом устройство 102 обработки сконфигурировано для адаптации его обработки в зависимости от оценок Ri, назначенных элементам набора 16 с помощью модуля назначения 50 оценок релевантности. Устройство 50 и устройство 102 могут быть реализованы с использованием программного обеспечения, выполняемого на одном или нескольких компьютерах. Они могут быть реализованы на отдельных компьютерных программах или на одной общей компьютерной программе. Что касается набора 16, все приведенные выше примеры действительны. Например, представим, что устройство 102 обработки выполняет обработку с потерями, такую как сжатие данных. Например, сжатие данных, выполняемое устройством 102, может включать в себя уменьшение нерелевантности. Набор 16 может, например, представлять данные изображения, такие как картинка или видео, и обработка, выполняемая устройством 102, может быть сжатием с потерями, то есть устройство может быть кодером. В этом случае устройство 102 может, например, быть сконфигурировано таким образом, чтобы уменьшить потерю процесса для элементов, имеющих более высокие оценки релевантности, назначенные им, по сравнению с элементами, имеющими более низкие оценки релевантности, назначенные им. Потери могут, например, варьироваться с помощью размера шага квантования или путем варьирования доступного битрейта управления скоростью кодера. Например, области выборок, для которых оценка релевантности является высокой, могут кодироваться с меньшими потерями, например, с использованием более высокого битрейта, с использованием меньшего размера шага квантования или т.п. Таким образом, назначение оценки релевантности выполняет свое назначение оценки релевантности, например, в отношении обнаружения/предсказания подозреваемых лиц в видеосцене. В этом случае, устройство 102 обработки способно затрачивать большую скорость передачи данных при сжатии с потерями видео, которое в соответствии с этим примером представляет набор 16, в отношении интересующих сцен, т.е. пространственно-временных частей, представляющих интерес, поскольку подозреваемые были ʺобнаруженыʺ внутри них. Или устройство 102 обработки использует ту же самую скорость передачи данных, но из-за взвешивания, достигаемого с помощью оценок релевантности, сжатие является более низким для элементов выборок с высокими оценками релевантности, и сжатие является более высоким для элементов выборок с низкими оценками релевантности. Результатом 104 обработки являются в этом случае сжатые с потерями данные или поток данных, то есть сжатая версия видео 16. Однако, как упоминалось ранее, набор 16 не ограничивается видеоданными. Он может быть изображением или аудиопотоком или тому подобным.
Для полноты, фиг. 12 показывает модификацию системы, показанной на фиг. 11. Здесь назначение 50 оценок релевантности действует на наборе 16, чтобы получить оценки Ri релевантности для элементов набора 16, но устройство 102 обработки действует на обрабатываемых данных 106, которые не эквивалентны набору 16. Скорее, набор 16 был получен из данных 106. На фиг. 12, например, показан примерный случай фиг. 1, согласно которой набор 16 был получен из данных 106 посредством процесса 30 извлечения признаков. Таким образом, набор 16 ʺописываетʺ данные 106. Значения Ri релевантности могут, как описано выше, быть ассоциированы с исходными данными 106 посредством процесса 38 обратного отображения, который представляет собой обратное или реверсивное отображение в отношении процесса 30 извлечения признаков. Таким образом, устройство 102 обработки работает с данными 106 и адаптирует или оптимизирует свою обработку в зависимости от оценок Ri релевантности.
Обработка, выполняемая устройством 102 обработки на фиг. 11 и 12, не ограничивается обработкой с потерями, такой как сжатие с потерями. Например, во многих из приведенных выше примеров для набора 16 или данных 106 элементы набора 16 образуют упорядоченный набор элементов, упорядоченных по 1, 2 или более размерностям. Например, пикселы упорядочены по меньшей мере в 2 размерностях, а именно, x и y являются двумя поперечными размерностями, и в 3 размерностях при включении временной оси. В случае аудиосигналов, выборки, такие как выборки временной области (например, PCM) или коэффициенты MDCT, упорядочиваются вдоль временной оси. Однако элементы набора 16 также могут быть упорядочены в спектральной области. То есть, элементы набора 16 могут представлять коэффициенты спектральной декомпозиции, например, картинки, видео или аудиосигнала. В этом случае, процесс 30 и обратный процесс 38 могут представлять спектральную декомпозицию или прямое преобразование или обратное преобразование, соответственно. Во всех этих случаях, оценки Ri релевантности, как получено модулем назначения 50 оценок релевантности, также упорядочиваются, то есть они образуют упорядоченную совокупность оценок релевантности или, другими словами, образуют ʺкарту релевантностиʺ, которая может быть наложена на набор 16 или, посредством обработки 38, на данные 106. Таким образом, устройство 102 обработки может, например, выполнять визуализацию набора 16 данных 106, используя порядок среди элементов набора 16 или порядок выборок данных 106, и использовать карту релевантности, чтобы выделить релевантную часть визуализации. Например, результатом 104 обработки будет представление картинки на экране и использование устройства 102 отображения релевантности, выделяющего некоторую часть на экране с использованием, например, мигания, инверсии цвета или тому подобного, чтобы указывать часть повышенной релевантности в наборе 16 или данных 106, соответственно. Такая система 100 может, например, использоваться для целей видеонаблюдения, чтобы привлечь, например, внимание охранников к определенной части сцены, представленной данными 106 или набором 16, то есть видео или картинкой.
Альтернативно, обработка, выполняемая устройством 102, может представлять собой пополнение данных. Например, пополнение данных может относиться к считыванию из памяти. В качестве другой альтернативы, пополнение данных может включать в себя дальнейшие измерения. Представим, например, что набор 16 снова представляет собой упорядоченную совокупность, т.е. представляет собой карту признаков, принадлежащую картинке 106, представляет собой собственно картинку или видео. В этом случае, устройство 102 обработки может получать из оценок Ri релевантности информацию ROI, то есть области, представляющей интерес, и может сосредоточить пополнение данных на этой ROI, чтобы избежать выполнения пополнения данных относительно полной сцены, к которой относится набор 16. Например, первое назначение оценки релевантности может быть выполнено устройством 50 на изображении с микроскопа низкого разрешения, и устройство 102 может затем выполнить другое измерение микроскопа относительно локальной части из изображения с микроскопа низкого разрешения, для которого оценки релевантности указывают высокую релевантность. Результатом 104 обработки будет, соответственно, пополнение данных, а именно, дополнительное измерение в форме изображения с микроскопа высокого разрешения.
Таким образом, в случае использования системы 100 согласно фиг. 11 или 12 для цели управления потреблением скорости передачи данных, система 100 приводит к эффективной концепции сжатия. В случае использования системы 100 для процессов визуализации, система 100 способна увеличить вероятность того, что средство просмотра реализует некоторую область, представляющую интерес. В случае использования системы 100 для упорядочения пополнения данных, система 100 может избежать объема пополнения данных, избегая выполнения пополнения данных в отношении областей, которые не представляют интереса.
На фиг. 13 показана система 110 для выделения интересующей области набора элементов. То есть, в случае, показанном на фиг. 13, набор элементов снова считается упорядоченным набором, таким как карта признаков, картинка, видео, аудиосигнал или тому подобное. Модуль назначения 50 оценок релевантности содержится в системе 110 в дополнение к генератору 112 графа, который генерирует граф релевантности в зависимости от оценок Ri релевантности, предоставленных модулем назначения 50 оценок релевантности. Граф 114 релевантности может, как уже было описано выше, тепловой картой, где используется цвет, чтобы ʺизмеритьʺ релевантности Ri. Оценки Ri релевантности, как описано выше, являются скалярными или же могут быть сделаны скалярными путем суммирования оценок релевантности отображения, принадлежащих совместно, таких как оценки релевантности субпикселов различных цветовых компонентов, принадлежащих одному цветному пикселу изображения. Скалярная оценка Ri релевантности может быть затем отображена на шкалу уровней серого или цвет с использованием, например, одномерных скалярных оценок релевантности пиксела, например, как значения CCT. Однако любое отображение из одномерного в трехмерное цветовое пространство, такое как RGB, может использоваться для генерации цветной карты. Например, одно отображает оценки на интервал оттенков, фиксирует размерности насыщенности и значения, а затем преобразует представление HSV в представление RGB.
Однако граф 114 релевантности может альтернативно быть представлен в виде гистограммы или тому подобного. Генератор 112 графа может включать в себя дисплей для отображения графа 114 релевантности. Помимо этого, генератор 112 графа может быть реализован с использованием программного обеспечения, такого как компьютерная программа, которая может быть отдельной или включенной в компьютерную программу, реализующую модуль назначения 50 оценок релевантности.
В качестве конкретного примера, предположим, что набор 16 элементов является изображением. Попиксельные оценки релевантности для каждого пиксела, полученные в соответствии с модулем назначения, могут быть дискретизированы/квантованы в/на набор значений, а индексы дискретизации/квантования могут быть отображены на набор цветов. Отображение может быть выполнено в генераторе 112 графа. Результирующее назначение пикселов цветам, такое как ʺтепловая картаʺ в случае отображения релевантности- цвета, следуя некоторой мере CCT (цветовой температуры) для цветов, может быть сохранено как файл изображения в базе данных или на носителе хранения данных или представлено средству просмотра генератором 112.
Альтернативно, назначение пикселов цветам может быть наложено на начальное изображение. В этом случае процессор 102 согласно фиг. 11 и 12 может выступать в качестве генератора графа. Полученное наложенное изображение может быть сохранено в виде файла изображения на носителе или представлено средству просмотра. ʺНаложениеʺ может быть выполнено, например, путем превращения начального изображения в изображение шкалы уровней серого и использования для отображения попиксельных оценок релевантности на цветовые значения отображения в значения оттенков. Наложенное изображение может быть создано процессором 102 с использованием представления значения насыщенности оттенка, то есть значение (однако с пределом при слишком малых значениях, поскольку почти черный пиксел не имеет четко видимых цветов, и, возможно, также насыщение берется из начального изображения) получается из значения шкалы уровней серого соответствующей выборки версии шкалы уровней серого начального изображения, и значения оттенков берутся из цветовой карты. Процессор 102 может подвергать изображение, сгенерированное, как описано выше, например, цветовую карту или наложение или упорядоченный набор оценок релевантности (который может быть представлен как изображение, но это не является обязательным требованием) сегментации. Те сегменты в таком сегментированном изображении, которые соответствуют областям с очень высокими оценками или областям с оценками, которые имеют большие абсолютные значения, могут быть извлечены, сохранены в базе данных или на носителе хранения и использованы (с последующим ручным контролем или без него) в качестве дополнительных данных обучения для процедуры обучения классификатора. Если набор 16 элементов является текстом, результатом назначения релевантности может быть релевантность оценки на каждое слово или предложение, как описано выше. Затем оценка релевантности может быть дискретизирована в набор значений и отображена на набор цветов. Затем слова могут маркироваться, посредством процессора 102, цветом, полученный выделенный цветом текст может быть сохранен в базе данных или на носителе хранения данных или представлен пользователю. Альтернативно или дополнительно к выделению слов, процессор 102 просто выбирает поднабор слов, частей предложения или предложений текста, а именно, тех, которые имеют наивысшие оценки или самые высокие абсолютные значения оценок (например, путем сравнения с порогом оценки или ее абсолютной величины), и сохраняет этот выбор в базе данных или на носителе хранения данных или представляет его пользователю. Если назначение релевантности применяется к набору 16 данных, так что выборка состоит из набора пар значений ключа, например, финансовых данных о компаниях, хранящихся в таблице в базе данных, то результатом для каждой выборки будет оценка релевантности для пары ключ-значение. Для данной выборки затем можно выбрать поднабор пар ключ-значение с наивысшими оценками или наивысшими абсолютными значениями оценок (например, путем сравнения оценки или ее абсолютного значения с порогом), и этот выбор можно сохранить в базе данных или на носителе хранения данных или представить его пользователю. Это может быть выполнено процессором 102 или генератором 112.
Как уже отмечалось выше в отношении фиг. 12, набор 16 данных может быть изображением или видео. Затем можно использовать попиксельные оценки релевантности, чтобы найти области с высокими оценками. С этой целью в качестве примера можно использовать вышеупомянутую сегментацию или сегментацию видео. В случае видео, область с высокой оценкой будет пространственно-временным поднабором или частью видео. Для каждой области может вычисляться оценка по области, например, путем вычисления p-среднего 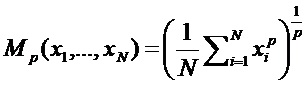 или квантиля попиксельных оценок для пикселов области. Затем набор данных, например видео, подвергается алгоритму сжатия процессором 102, для которого степень сжатия может быть скорректирована для областей в соответствии с вычисленной оценкой. Могут использоваться монотонные (спадающие или нарастающие) отображения оценок областей на скорости сжатия. Затем каждая из областей будет кодироваться в соответствии с отображением оценок области на скорости сжатия.
или квантиля попиксельных оценок для пикселов области. Затем набор данных, например видео, подвергается алгоритму сжатия процессором 102, для которого степень сжатия может быть скорректирована для областей в соответствии с вычисленной оценкой. Могут использоваться монотонные (спадающие или нарастающие) отображения оценок областей на скорости сжатия. Затем каждая из областей будет кодироваться в соответствии с отображением оценок области на скорости сжатия.
Кроме того, процессор 102 мог бы действовать следующим образом в случае изображения в виде набора 16: описанная выше сегментация может быть применена к набору оценок для всех пикселов или к наложенному изображению или к карте цветов, и сегменты, соответствующие областям с очень высокими оценками или областям с оценками, которые имеют большие абсолютные значения, могут быть извлечены. Затем процессор может представить эти совместно расположенные сегменты начального изображения 16 пользователю или в другой алгоритм для проверки содержимого на возможность заметного или аномального содержимого. Это может быть использовано, например, в приложениях охранной безопасности. Аналогично, набор 16 может представлять собой видео. В свою очередь, полное видео состоит из набора кадров. Элементом в наборе 16 элементов может быть кадр или подмножество кадров или набор областей из поднабора кадров, как уже указано выше. Сегментация пространственно-временного видео может быть применена к назначению оценки релевантности для элементов, чтобы найти пространственно-временные области с высокими средними оценками для элементов или высокими средними абсолютными значениями оценками для элементов. Как упоминалось выше, средние значения, присвоенные элементам внутри области, можно измерить, например, с использованием оценки p-среднего или оценщика квантилей. Пространственно-временные области с самыми высокими такими оценками, например, оценками выше некоторого порога, могут быть извлечены процессором 102 (например, посредством сегментации изображения или видео) и представлены пользователю или в другой алгоритм для проверки содержимого на возможность заметного или аномального содержания. Алгоритм проверки может быть включен в процессор 102 или может быть внешним относительно него, причем это справедливо также для вышеупомянутых случаев упоминания проверки областей с (самой) высокой оценкой.
В соответствии с вариантом осуществления, вышеупомянутые пространственно-временные области с самыми высокими такими оценками используются для улучшения обучения для предсказаний, сделанных на видео. Как указано, набор 16 элементов представляет собой полное видео, которое может быть представлено набором кадров. Элементом в наборе элементов является кадр или поднабор кадров или набор областей из поднабора кадров. Затем сегментация видео применяется для поиска пространственно-временных областей с высокими средними оценками для элементов или высокими средними абсолютными значениями оценок для элементов. Процессор 102 может выбирать нейроны нейронной сети, которые соединены с другими нейронами, так что через непрямые соединения вышеупомянутые области являются частью входа выбранных нейронов. Процессор 102 может оптимизировать нейронную сеть следующим образом: при условии, что входное изображение и нейрон выбраны, как указано выше (например, путем прямых или косвенных входов из областей с высокими оценками релевантности или их высокими абсолютными значениями), процессор 102 пытается увеличить выход сети или квадрат выхода сети или уменьшить выход сети путем изменения весов входов выбранного нейрона и весов тех нейронов, которые являются прямыми или косвенными восходящими соседями выбранного нейрона. Такое изменение может быть выполнено, например, путем вычисления градиента выхода нейрона для данного изображения относительно изменяемых весов. Затем веса обновляются с помощью градиента, умноженного на постоянную с размером шага. Излишне говорить, что пространственно-временная область также может быть получена путем сегментации попиксельных оценок, то есть с использованием пикселов в качестве элементов набора 16, с последующим выполнением оптимизации, которая была изложена выше.
В альтернативном варианте, назначение релевантности может применяться к данным графа, состоящего из узлов, а также ориентированных или неориентированных ребер с весами или без них; элемент набора 16 тогда был бы, например, подграфом. Для каждого подграфа вычислялась бы поэлементная оценка релевантности. Подграф может быть входом в нейронную сеть, например, если он закодирован как целое число путем кодирования узлов и их ребер с весами целыми числами при разделении семантических единиц целыми числами, которые зарезервированы как знаки остановки. Альтернативно, элемент набора 16 для вычисления оценки релевантности для каждого элемента может быть узлом. Затем мы вычисляем поэлементные оценки релевантности. После этого можно найти набор подграфов с высокой средней оценкой (средняя оценка может быть вычислена с помощью p-среднего 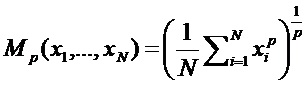 или квантиля оценок по узлам) посредством сегментации графа. Оценки для каждого узла дискретизируются в набор значений, и индексы дискретизации отображаются на набор цветов. Результирующее назначение узлов и подграфов цветам и/или извлеченных подграфов может быть сохранено как файл в базе данных или на носителе хранения данных или представлено средству просмотра.
или квантиля оценок по узлам) посредством сегментации графа. Оценки для каждого узла дискретизируются в набор значений, и индексы дискретизации отображаются на набор цветов. Результирующее назначение узлов и подграфов цветам и/или извлеченных подграфов может быть сохранено как файл в базе данных или на носителе хранения данных или представлено средству просмотра.
На фиг. 14 показана система для оптимизации нейронной сети. Система в общем обозначена ссылочной позицией 120 и включает в себя модуль назначения 50 оценок релевантности, устройство 122 приложений и устройство 124 обнаружения и оптимизации. Устройство 122 приложений сконфигурировано, чтобы применять устройство 50 к множеству различных наборов 16 элементов. Таким образом, для каждого приложения, устройство 50 определяет оценки релевантности для элементов набора 16. На этот раз, однако, устройство 50 также выводит значения релевантности, назначенные отдельным промежуточным нейронам 12 нейронной сети 10 во время обратного распространения, тем самым получая вышеупомянутые пути 34 релевантности для каждого приложения. Другими словами, для каждого применения устройства 50 на соответствующем наборе 16, устройство 124 обнаружения и оптимизации получает карту 126 распространения релевантности нейронной сети 10. Устройство 124 обнаруживает часть 128 повышенной релевантности в нейронной сети 10 путем накопления 130 или наложения релевантностей, назначенных промежуточным нейронам 12 сети 10 во время применения устройства 50 к разным наборам 16. Другими словами, устройство 124 накладывает или накапливает посредством наложения различные карты 126 распространения релевантности, чтобы получить часть 128 нейронной сети 10, включающую в себя те нейроны, которые распространяют высокий процент релевантности в процессе обратного распространения устройства 50 по совокупности наборов 16. Эта информация затем может использоваться устройством 124 для оптимизации 132 искусственной нейронной сети 10. В частности, например, некоторые из взаимосвязей нейронов 12 искусственной нейронной сети 10 могут прекращаться, чтобы сделать искусственную нейронную сеть 10 меньшей, без компрометации ее способности предсказания. Однако существуют и другие возможности.
Кроме того, может быть, что процесс назначения оценки релевантности приводит к созданию тепловой карты, которая анализируется, например, в отношении гладкости и других свойств. На основе анализа могут быть инициированы некоторые действия. Например, обучение нейронной сети может быть остановлено, поскольку оно фиксирует понятия ʺдостаточно хорошоʺ в соответствии с анализом тепловой карты. Далее следует отметить, что результат анализа тепловой карты может использоваться вместе с результатами предсказания нейронной сети, то есть предсказанием, чтобы что-то сделать. В частности, полагаться на результаты тепловой карты и предсказания может быть более предпочтительным по сравнению с тем, чтобы полагаться только на результаты предсказания, потому что, например, тепловая карта может сообщить сведения о достоверности предсказания. Качество нейронной сети может быть потенциально оценено путем анализа тепловой карты.
Наконец, подчеркивается, что предлагаемое распространение релевантности в основном проиллюстрировано выше в отношении сетей, обученных на задачах классификации, но, без потери общности, описанные выше варианты осуществления могут применяться к любой сети, которая назначает оценку, относящуюся к выходным классам. Этим оценкам можно обучаться с использованием других методов, таких как регрессия или ранжирование.
Таким образом, в приведенном выше описании были представлены варианты осуществления, которые воплощают методологию, которая может быть названа послойным распространением релевантности, которая позволяет понять предсказатели нейронной сети. Были продемонстрированы различные применения этого нового принципа. Для изображений было показано, что вклады пикселов могут визуализироваться как тепловые карты и могут предоставляться эксперту-человеку, который может интуитивно не только проверить достоверность решения классификации, но и сосредоточить дальнейший анализ на областях, представляющих потенциальный интерес. Этот принцип может быть применен к множеству задач, классификаторов и типов данных, то есть не ограничивается изображениями, как отмечено выше.
Хотя некоторые аспекты были описаны в контексте устройства, очевидно, что эти аспекты также представляют собой описание соответствующего способа, где блок или устройство соответствует этапу способа или признаку этапа способа. Аналогично, аспекты, описанные в контексте этапа способа, также представляют собой описание соответствующего блока или элемента или признака соответствующего устройства. Некоторые или все из этапов способа могут быть выполнены с помощью (или с использованием) аппаратного устройства, такого как, например, микропроцессор, программируемый компьютер или электронная схема. В некоторых вариантах осуществления такое устройство может выполнять один или несколько наиболее важных этапов способа.
В зависимости от определенных требований реализации, варианты осуществления изобретения могут быть реализованы на аппаратных средствах или в программном обеспечении. Реализация может быть выполнена с использованием цифрового носителя хранения данных, например дискеты, DVD, Blu-Ray, CD, ROM, PROM, EPROM, EEPROM или флэш-памяти, с сохраненными на них электронно-считываемыми управляющими сигналами, которые взаимодействуют (или могут взаимодействовать) с программируемой компьютерной системой, так что выполняется соответствующий способ. Следовательно, цифровой носитель хранения данных может считываться компьютером.
Некоторые варианты осуществления в соответствии с изобретением содержат носитель данных, имеющий электронно-считываемые управляющие сигналы, которые способны взаимодействовать с программируемой компьютерной системой, так что выполняется один из способов, описанных здесь.
Как правило, варианты осуществления настоящего изобретения могут быть реализованы как компьютерный программный продукт с программным кодом, причем программный код работает для выполнения одного из способов, когда компьютерный программный продукт выполняется на компьютере. Например, программный код может храниться на машиночитаемом носителе.
Другие варианты осуществления содержат компьютерную программу для выполнения одного из описанных здесь способов, сохраненную на машиночитаемом носителе.
Другими словами, вариантом осуществления способа согласно изобретению является, следовательно, компьютерная программа, имеющая программный код для выполнения одного из описанных здесь способов, когда компьютерная программа выполняется на компьютере.
Таким образом, другим вариантом осуществления способов согласно изобретению является носитель данных (или цифровой носитель хранения данных или считываемый компьютером носитель), содержащий записанную на нем компьютерную программу для выполнения одного из способов, описанных здесь. Носитель данных, цифровой носитель хранения данных или записываемый носитель типично являются материальными и/или не-временными (не-транзиторными).
Другим вариантом осуществления способа согласно изобретению является, следовательно, поток данных или последовательность сигналов, представляющих компьютерную программу для выполнения одного из способов, описанных здесь. Например, поток данных или последовательность сигналов могут быть сконфигурированы для передачи через соединение передачи данных, например, через Интернет.
Еще один вариант осуществления содержит средство обработки, например компьютер, или программируемое логическое устройство, сконфигурированное или адаптированное для выполнения одного из способов, описанных здесь.
Другой вариант осуществления содержит компьютер, на котором установлена компьютерная программа для выполнения одного из способов, описанных здесь.
Еще один вариант осуществления в соответствии с изобретением содержит устройство или систему, сконфигурированную для передачи (например, электронным или оптическим способом) компьютерной программы для осуществления одного из способов, описанных здесь, к приемнику. Приемник может, например, быть компьютером, мобильным устройством, устройством памяти и т.п. Устройство или система могут, например, содержать файловый сервер для передачи компьютерной программы в приемник.
В некоторых вариантах осуществления, программируемое логическое устройство (например, программируемая вентильная матрица) может использоваться для выполнения некоторых или всех функциональных возможностей способов, описанных здесь. В некоторых вариантах осуществления, программируемая вентильная матрица может взаимодействовать с микропроцессором для выполнения одного из способов, описанных здесь. Как правило, способы предпочтительно выполняются любым аппаратным устройством.
Устройство, описанное здесь, может быть реализовано с использованием аппаратного устройства или с использованием компьютера или с использованием комбинации аппаратного устройства и компьютера.
Способы, описанные здесь, могут быть выполнены с использованием аппаратного устройства или с использованием компьютера или с использованием комбинации аппаратного устройства и компьютера.
Вышеописанные варианты осуществления являются просто иллюстративными для принципов настоящего изобретения. Понятно, что модификации и варианты компоновок и деталей, описанные здесь, будут очевидны для специалистов в данной области техники. Таким образом, намерение заключается в ограничении только объемом представленных пунктов формулы изобретения, а не конкретными деталями, представленных путем описания и объяснения вариантов осуществления настоящего изобретения.
Список источников
[6] Christopher M Bishop et al. Pattern recognition and machine learning, volume 1. springer New York, 2006.
[10] Hendrik Dahlkamp, Adrian Kaehler, David Stavens, Sebastian Thrun, and Gary R. Bradski. Self-supervised monocular road detection in desert terrain. In Robotics: Science and Systems, 2006.
[11] Jia Deng, Alex Berg, Sanjeev Satheesh, Hao Su, Aditya Khosla, and Fei-Fei Li. The ImageNet Large Scale Visual Recognition Challenge 2012 (ILSVRC2012). http://www.image-net.org/challenges/LSVRC/2012/.
[12] Dumitru Erhan, Yoshua Bengio, Aaron Courville, and Pascal Vincent. Visualizing higher-layer features of a deep network. Technical Report 1341, University of Montreal, June 2009.
[15] L. Fei-Fei and P. Perona. A bayesian hierarchical model for learning natural scene categories. In Computer Vision and Pattern Recognition, 2005. CVPR 2005. IEEE Computer Society Conference on, volume 2, pages 524-531 vol. 2, 2005.
[16] Muriel Gevrey, Ioannis Dimopoulos, and Sovan Lek. Review and comparison of methods to study the contribution of variables in artificial neural network models. Ecological Modelling, 160(3):249-264, 2003.
[17] Ronny Hänsch and Olaf Hellwich. Object recognition from polarimetric SAR images. In Uwe Soergel, editor, Radar Remote Sensing of Urban Areas, volume 15 of Remote Sensing and Digital Image Processing, pages 109-131. Springer Netherlands, 2010.
[20] Yangqing Jia. Caffe: An open source convolutional architecture for fast feature embedding. http://caffe.berkeleyvision.org/, 2013.
[23] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton. Imagenet classification with deep convolutional neural networks. In Peter L. Bartlett, Fernando C. N. Pereira, Christopher J. C. Burges, Léon Bottou, and Kilian Q. Weinberger, editors, NIPS, pages 1106-1114, 2012.
[25] Yann LeCun and Corinna Cortes. The MNIST database of handwritten digits. http://yann.lecun.com/exdb/mnist/, 1998.
[26] Yann LeCun, Koray Kavukcuoglu, and Clément Farabet. Convolutional networks and applications in vision. In ISCAS, pages 253-256. IEEE, 2010.
[27] Quoc V. Le. Building high-level features using large scale unsupervised learning. In ICASSP, pages 8595-8598, 2013.
[31] Grégoire Montavon, Geneviève B. Orr, and Klaus-Robert Müller, editors. Neural Networks: Tricks of the Trade, Reloaded, volume 7700 of Lecture Notes in Computer Science (LNCS). Springer, 2nd edn edition, 2012.
[34] Julian D Olden, Michael K Joy, and Russell G Death. An accurate comparison of methods for quantifying variable importance in artificial neural networks using simulated data. Ecological Modelling, 178(3-4):389-397, 2004.
[36] Nicolas Pinto, David D Cox, and James J DiCarlo. Why is real-world visual object recognition hard? PLoS Comput Biol, 4(1):27, 1 2008.
[39] David E. Rumelhart, Geoffrey E. Hinton, and Ronald J. Williams. Learning representations by back-propagating errors. Nature, 323:533-536, Oct 1986.
[41] Rudy Setiono and Huan Liu. Understanding neural networks via rule extraction. In IJCAI, pages 480-487. Morgan Kaufmann, 1995.
[42] Karen Simonyan, Andrea Vedaldi, and Andrew Zisserman. Deep inside convolutional networks: Visualising image classification models and saliency maps. CoRR, abs/1312.6034, 2013.
[43] Christian Szegedy, Wojciech Zaremba, Ilya Sutskever, Joan Bruna, Dumitru Erhan, Ian J. Goodfellow, and Rob Fergus. Intriguing properties of neural networks. CoRR, abs/1312.6199, 2013.
[49] Paul A. Viola and Michael J. Jones. Rapid object detection using a boosted cascade of simple features. In CVPR (1), pages 511-518, 2001.
[50] Ross Walker, Paul Jackway, Brian Lovell, and Dennis Longstaff. Classification of cervical cell nuclei using morphological segmentation and textural feature extraction. In Australian New Zealand Conference on Intelligent Information Systems, 1994.
[54] Matthew D. Zeiler and Rob Fergus. Visualizing and understanding convolutional networks. CoRR, abs/1311.2901, 2013.
[55] Matthew D. Zeiler, Graham W. Taylor, and Rob Fergus. Adaptive deconvolutional networks for mid and high level feature learning. In ICCV, pages 2018-2025, 2011.
| название | год | авторы | номер документа |
|---|---|---|---|
| СИСТЕМА ОБНАРУЖЕНИЯ ПРИСУТСТВИЯ ОБЪЕКТОВ С САМОКОНТРОЛЕМ | 2020 |
|
RU2742803C1 |
| СПОСОБЫ ОБУЧЕНИЯ ГЛУБОКИХ СВЕРТОЧНЫХ НЕЙРОННЫХ СЕТЕЙ НА ОСНОВЕ ГЛУБОКОГО ОБУЧЕНИЯ | 2018 |
|
RU2767337C2 |
| Быстрый двухслойный нейросетевой синтез реалистичных изображений нейронного аватара по одному снимку | 2020 |
|
RU2764144C1 |
| СПОСОБ ОЦЕНКИ КАЧЕСТВА АНАЛИЗА МЕДИЦИНСКОГО ИЗОБРАЖЕНИЯ | 2023 |
|
RU2838577C1 |
| ТЕКСТУРИРОВАННЫЕ НЕЙРОННЫЕ АВАТАРЫ | 2019 |
|
RU2713695C1 |
| РАСПОЗНАВАНИЕ РУКОПИСНОГО ТЕКСТА ПОСРЕДСТВОМ НЕЙРОННЫХ СЕТЕЙ | 2020 |
|
RU2757713C1 |
| КЛАССИФИКАЦИЯ САЙТОВ СПЛАЙСИНГА НА ОСНОВЕ ГЛУБОКОГО ОБУЧЕНИЯ | 2018 |
|
RU2780442C2 |
| ГЕНЕРАТОРЫ ИЗОБРАЖЕНИЙ С УСЛОВНО НЕЗАВИСИМЫМ СИНТЕЗОМ ПИКСЕЛЕЙ | 2021 |
|
RU2770132C1 |
| Повторный синтез изображения, использующий прямое деформирование изображения, дискриминаторы пропусков и основанное на координатах реконструирование | 2019 |
|
RU2726160C1 |
| ОБНАРУЖЕНИЕ ТЕКСТОВЫХ ПОЛЕЙ С ИСПОЛЬЗОВАНИЕМ НЕЙРОННЫХ СЕТЕЙ | 2018 |
|
RU2699687C1 |
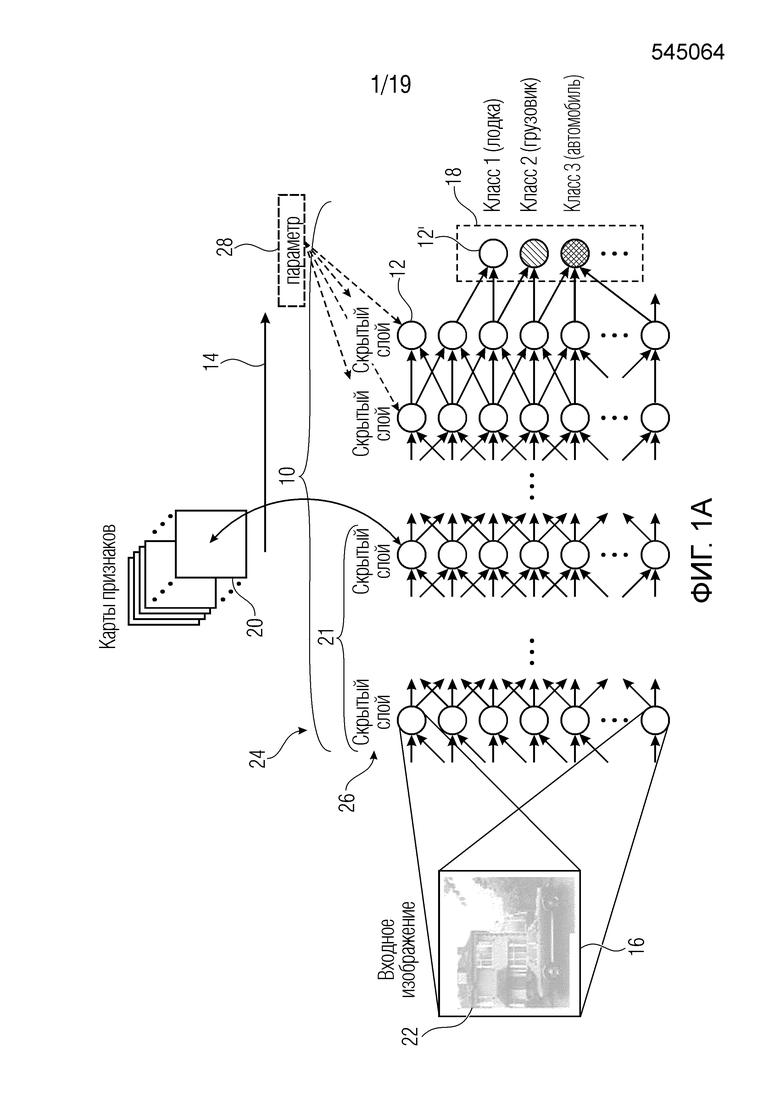
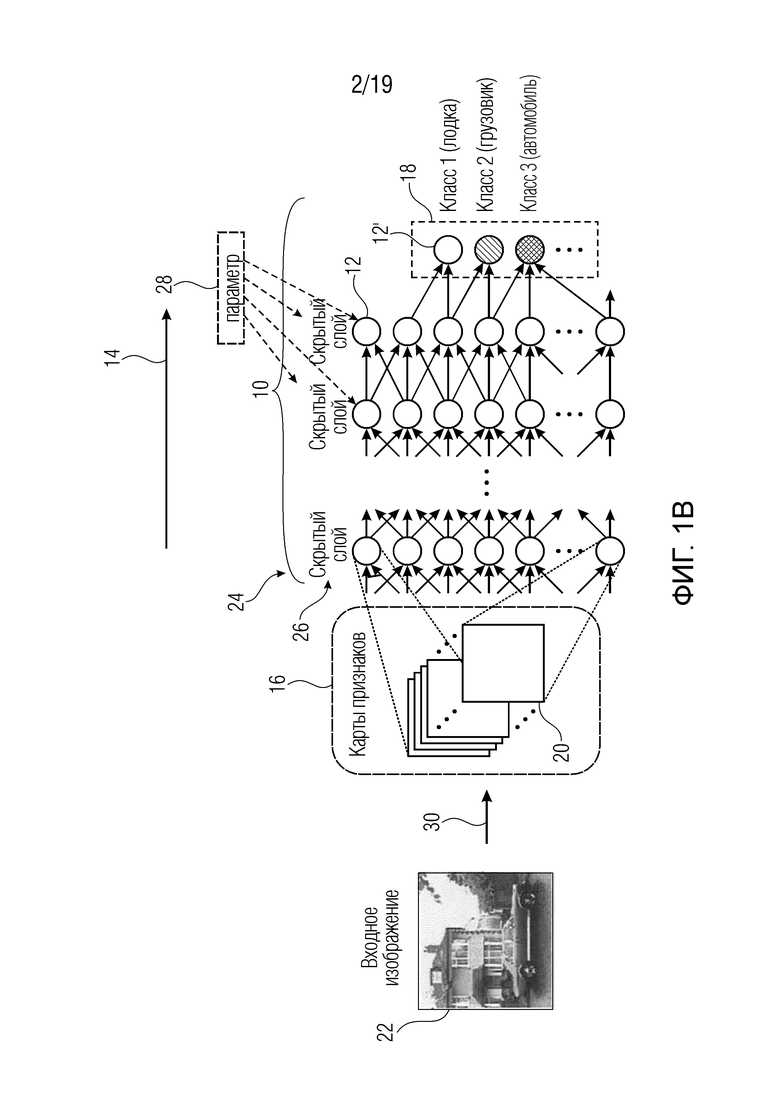
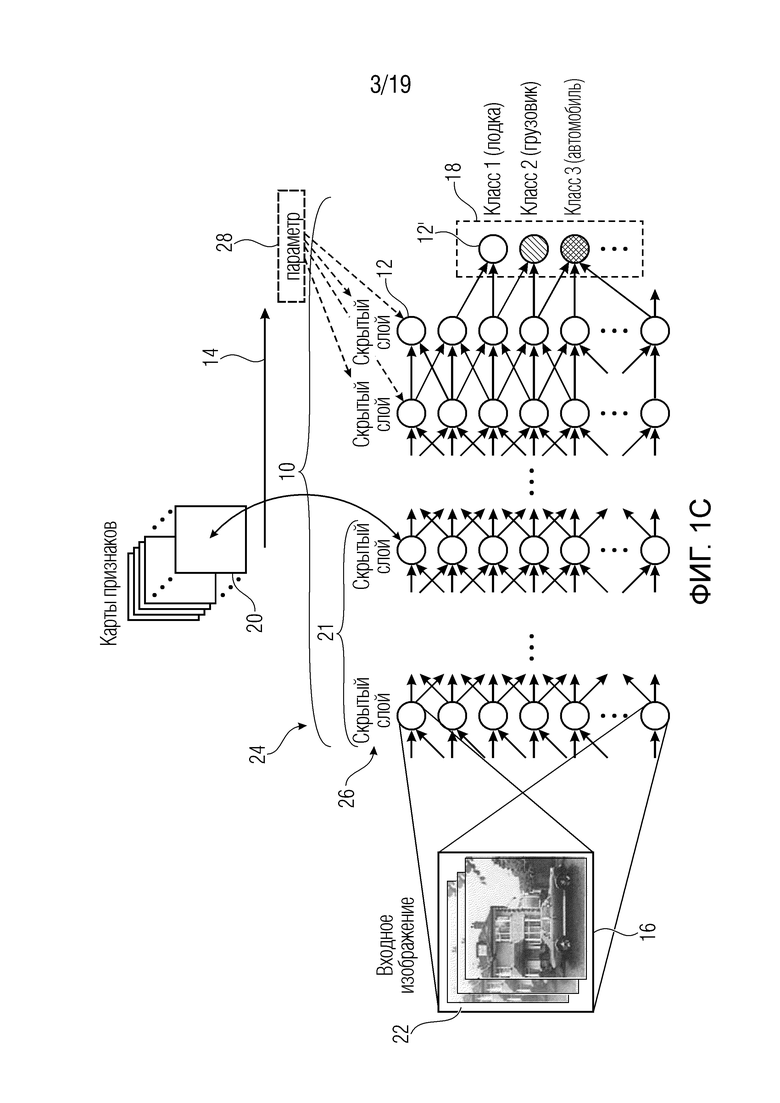
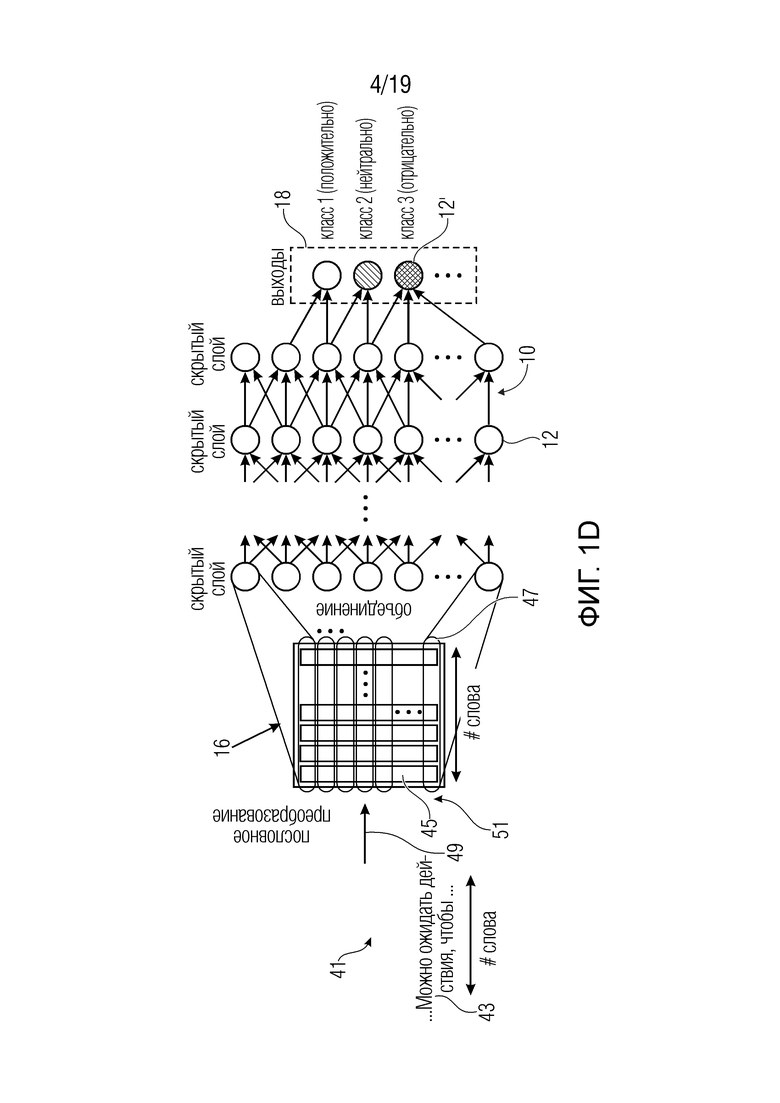
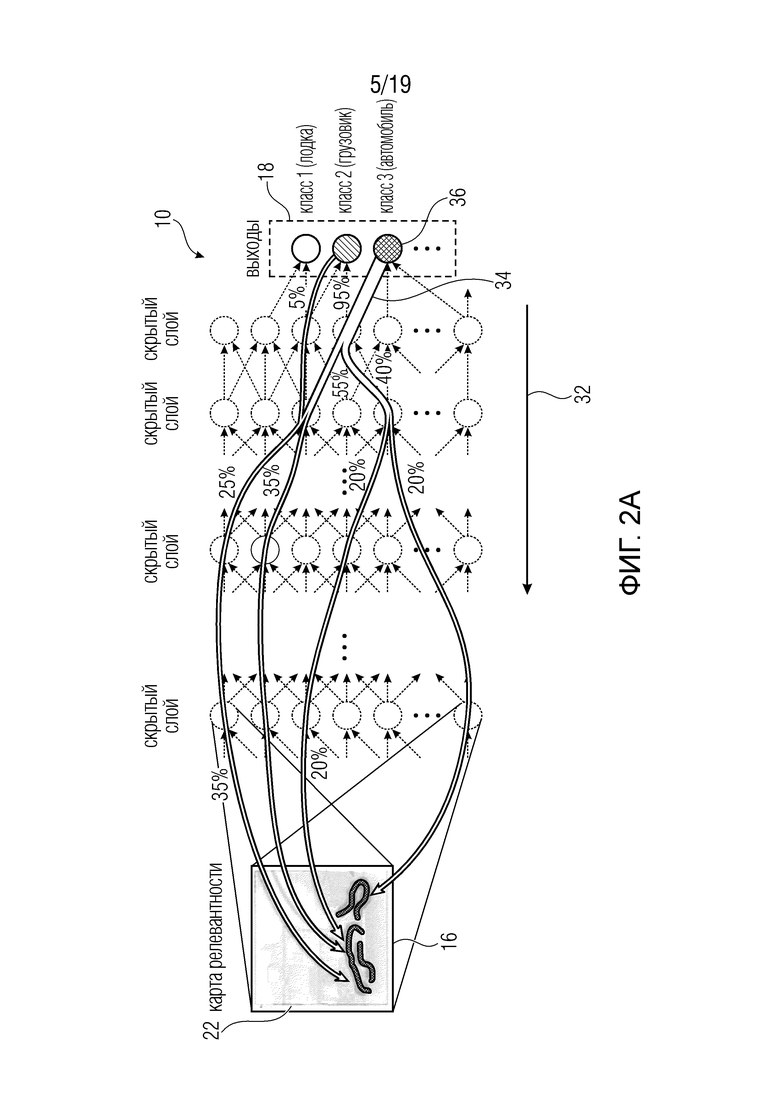
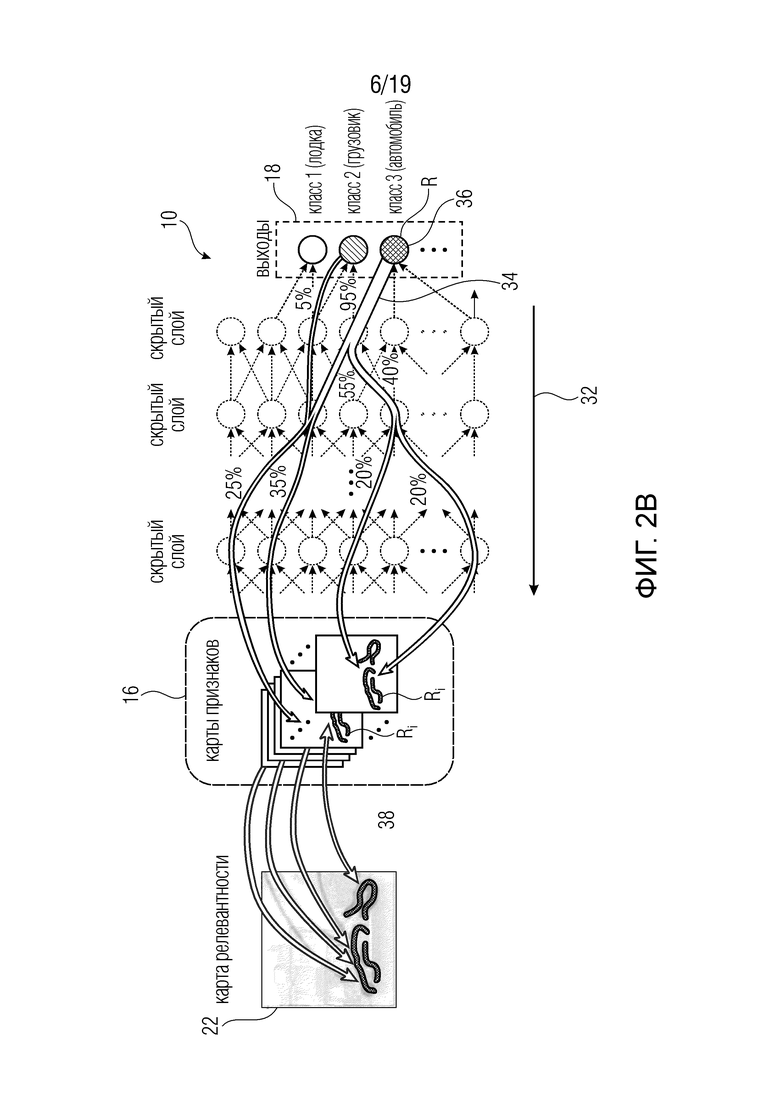
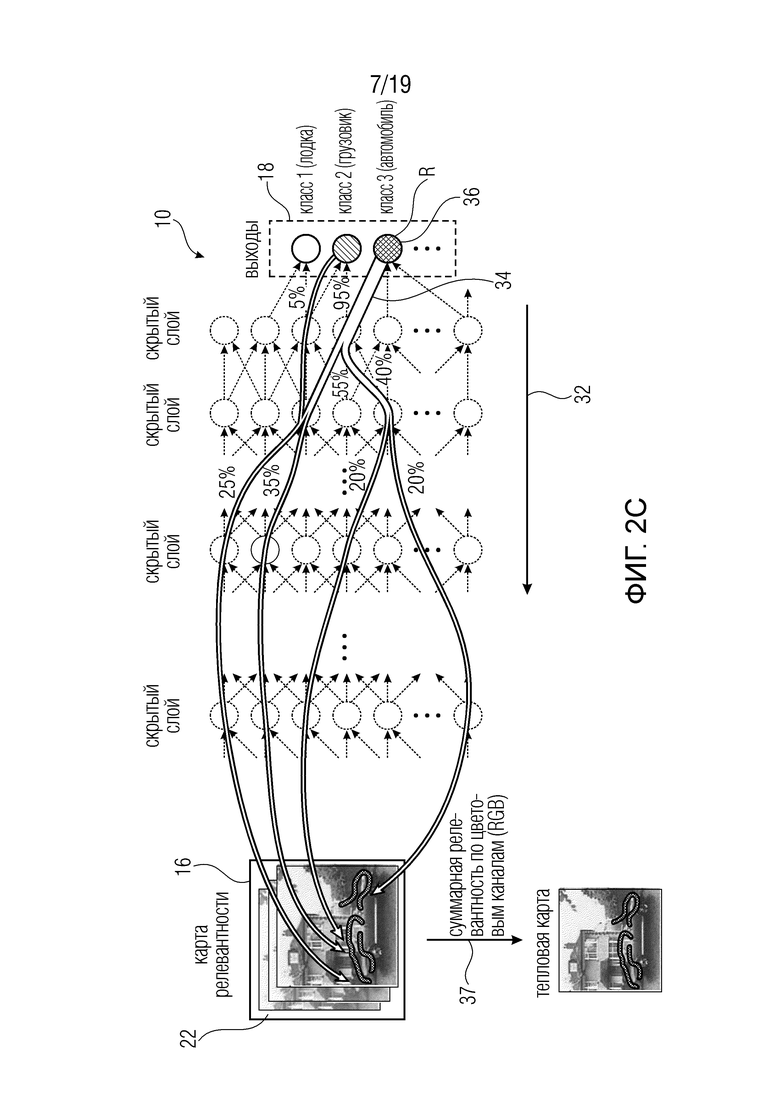
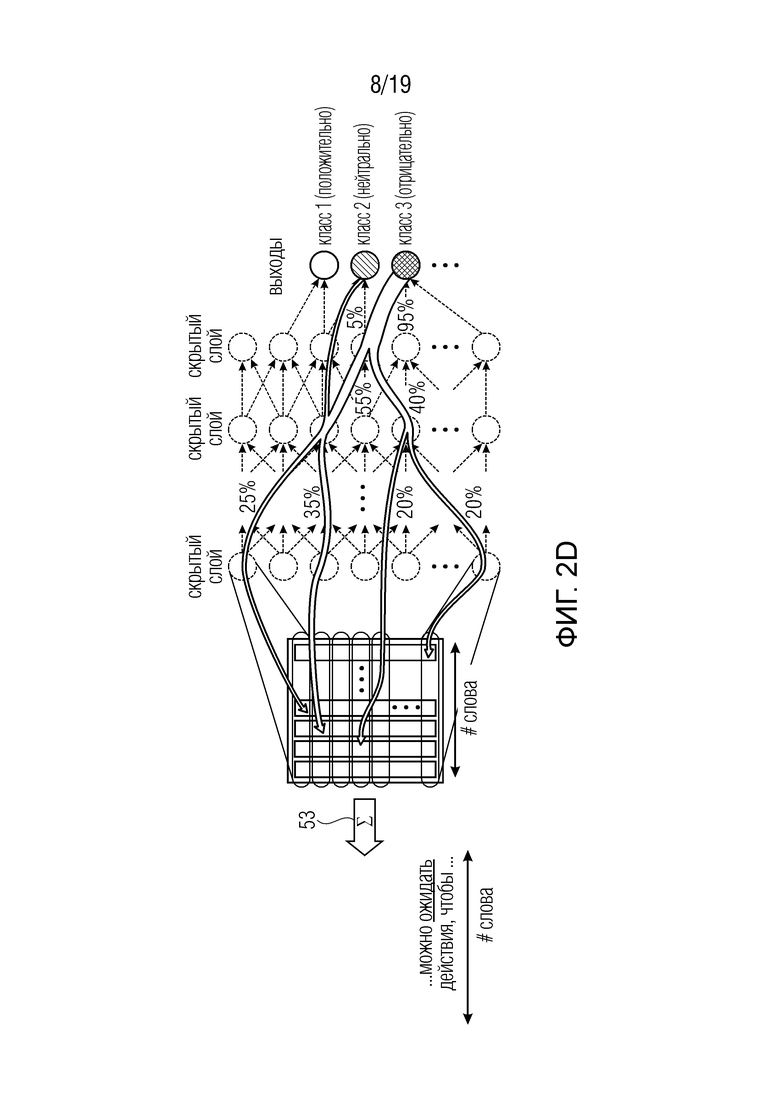
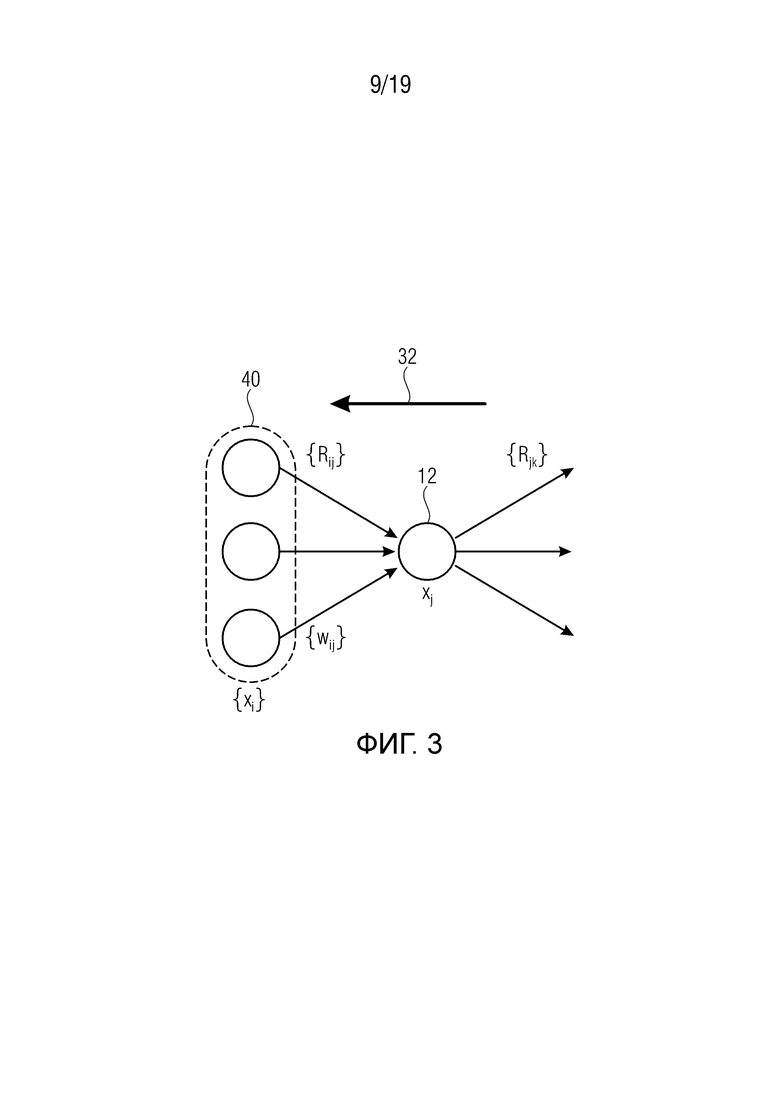
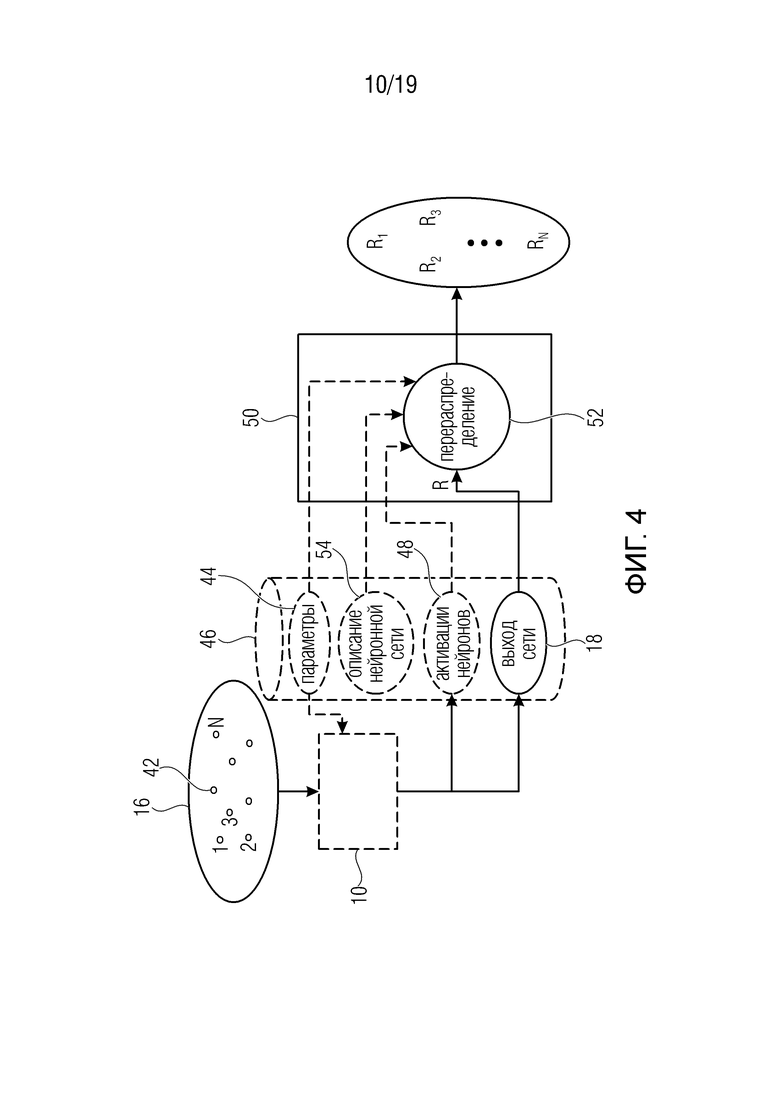
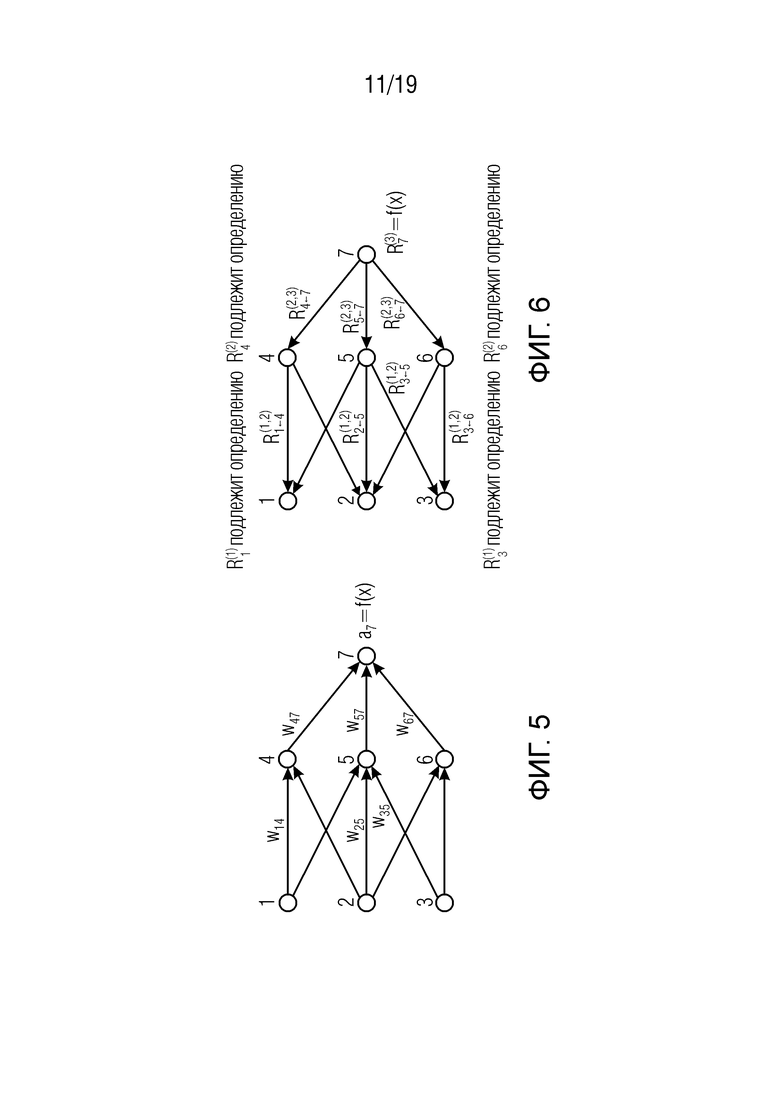
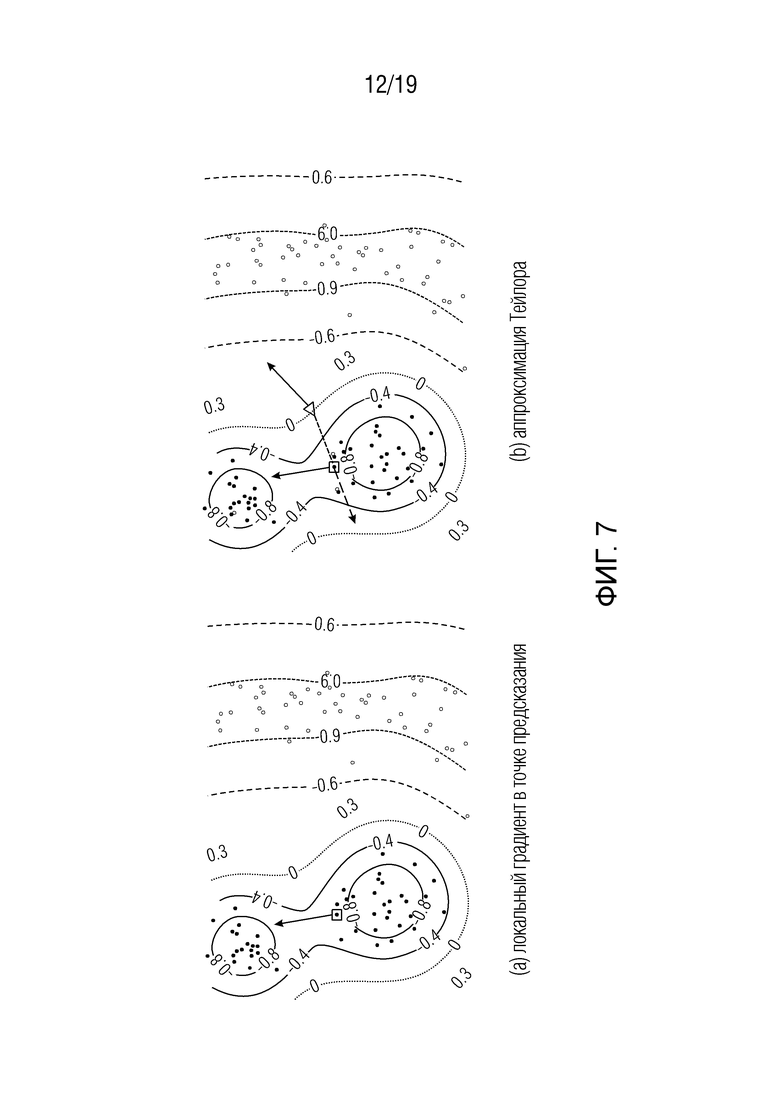
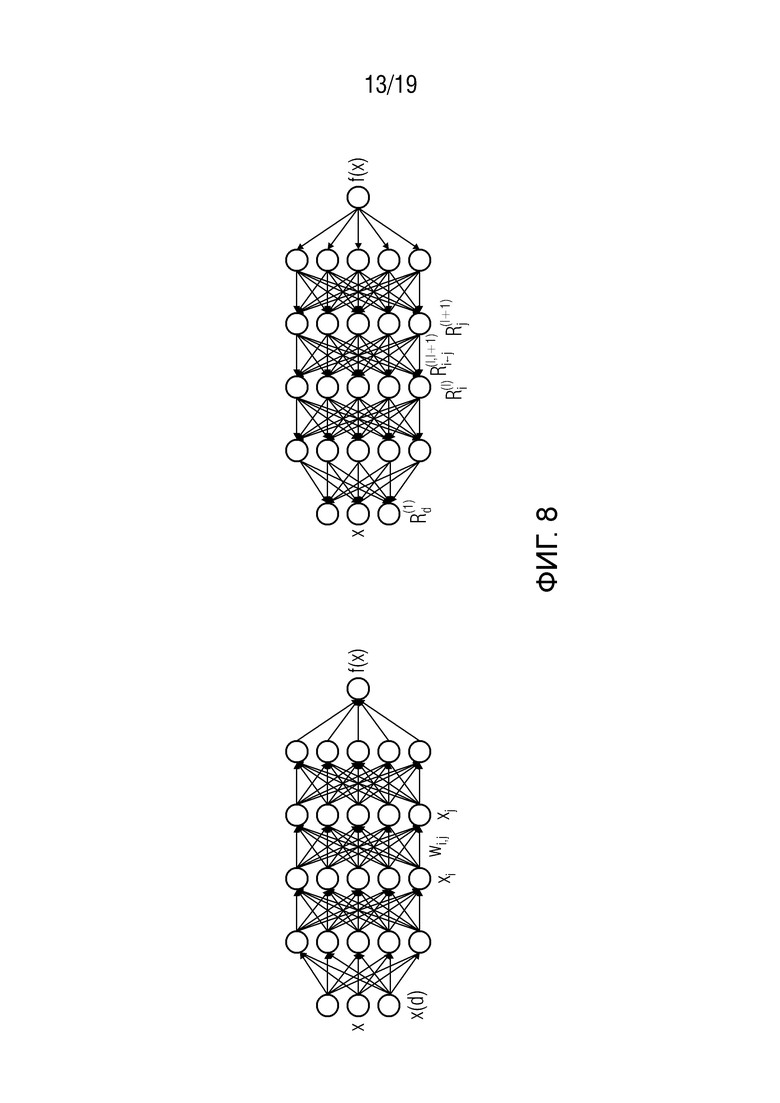

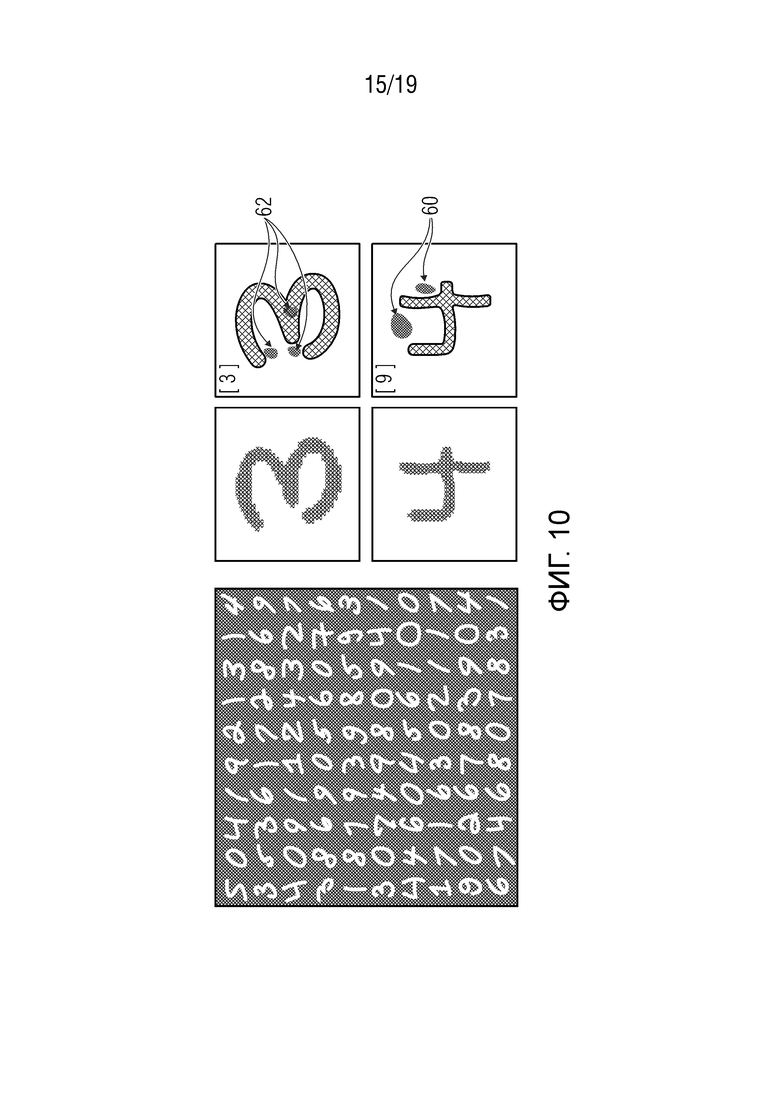
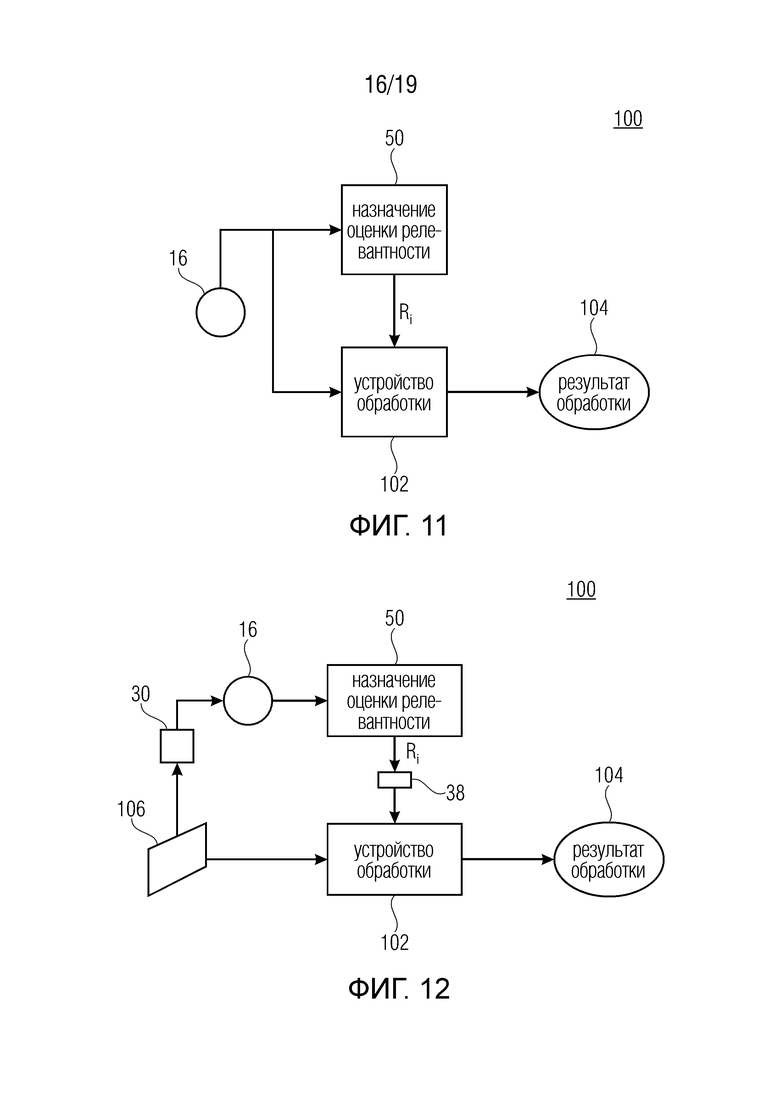

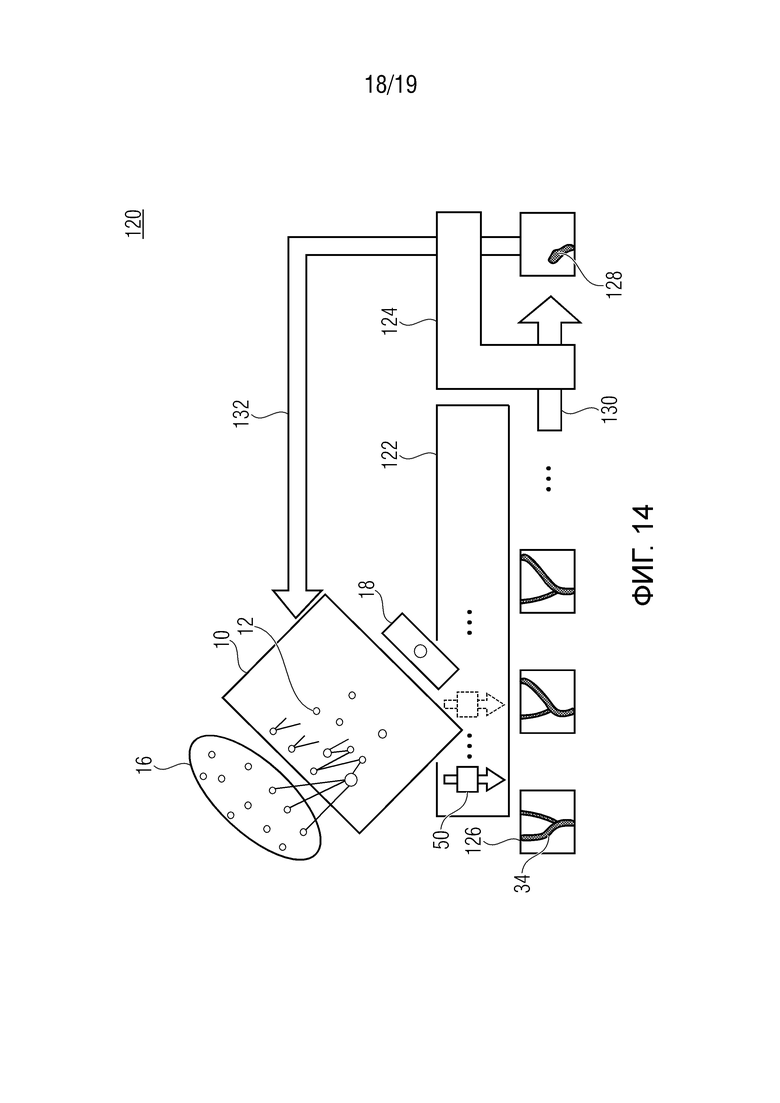
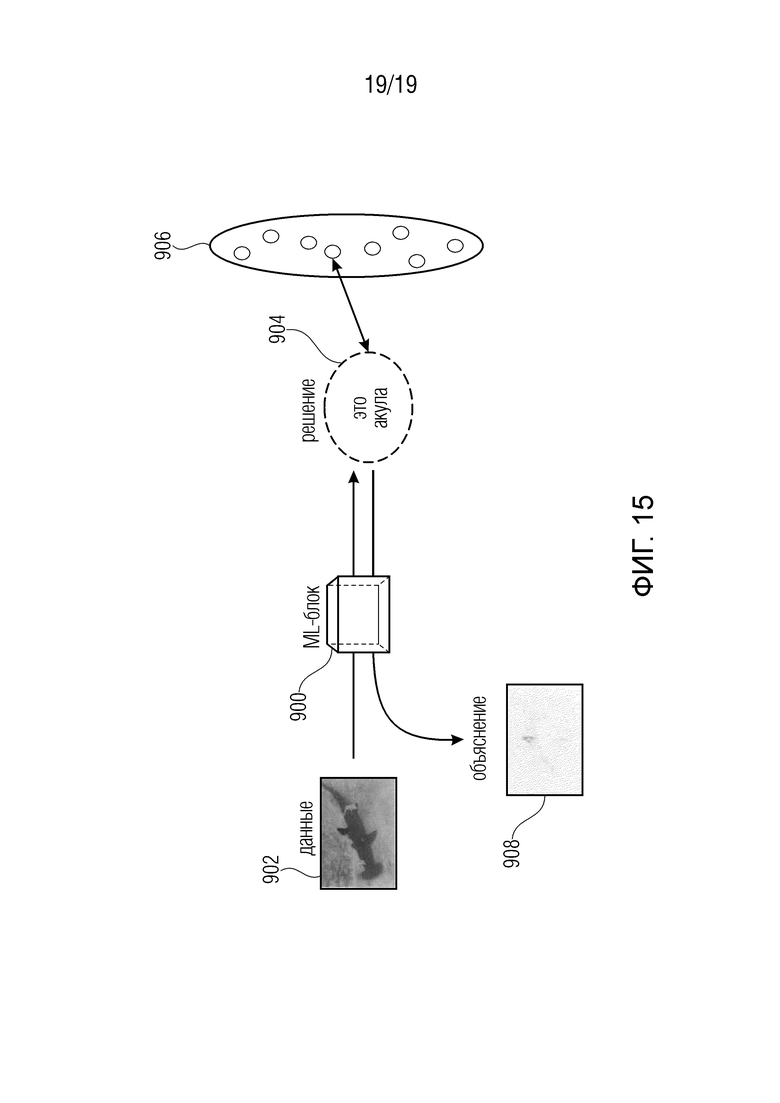
Группа изобретений относится к области вычислительной техники и может быть использована в искусственных нейронных сетях. Техническим результатом является обеспечение назначения оценки релевантности для искусственных нейронных сетей. Устройство сконфигурировано таким образом, чтобы перераспределять начальную оценку релевантности, полученную из выхода сети, на набор элементов путем обратного распространения начальной оценки релевантности через искусственную нейронную сеть, чтобы получить оценку релевантности для каждого элемента, причем устройство сконфигурировано, чтобы выполнять обратное распространение таким образом, что для каждого нейрона предварительно перераспределенные оценки релевантности набора нисходящих соседних нейронов соответствующего нейрона распределяются по набору восходящих соседних нейронов соответствующего нейрона с использованием функции распределения. 6 н. и 29 з.п. ф-лы, 21 ил.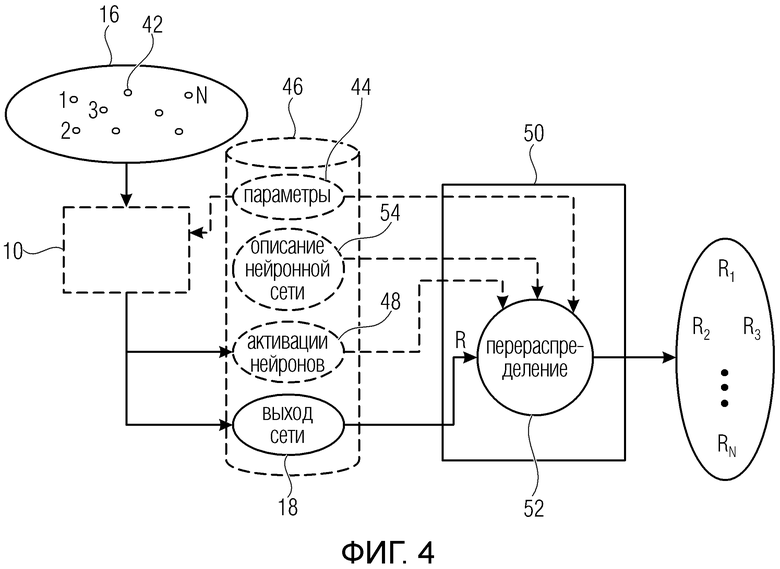
1. Устройство для назначения оценки релевантности набору элементов, причем оценка релевантности указывает релевантность в отношении применения искусственной нейронной сети (10), состоящей из нейронов (12), к набору (16) элементов (42), чтобы отображать набор (16) элементов (42) на выход (18) сети, причем устройство сконфигурировано, чтобы
перераспределять начальную оценку (R) релевантности, полученную из выхода (18) сети, на набор (16) элементов (42) путем обратного распространения начальной оценки релевантности через искусственную нейронную сеть (10), чтобы получить оценку релевантности для каждого элемента,
причем устройство сконфигурировано, чтобы выполнять обратное распространение таким образом, что для каждого нейрона предварительно перераспределенные оценки релевантности набора нисходящих соседних нейронов соответствующего нейрона распределяются по набору восходящих соседних нейронов соответствующего нейрона с использованием функции распределения.
2. Устройство по п. 1, причем устройство сконфигурировано таким образом, что функция распределения имеет свойство сохранения релевантности.
3. Устройство по п. 1, причем устройство сконфигурировано, чтобы выполнять обратное распространение с одинаковым использованием одной функции распределения для всех нейронов искусственной нейронной сети.
4. Устройство по п. 1, причем устройство сконфигурировано таким образом, что функция распределения является функцией
весов искусственной нейронной сети, определяющих степень влияния соответствующего нейрона набором восходящих соседних нейронов соответствующего нейрона,
нейронных активаций набора восходящих соседних нейронов, проявляющихся при применении искусственной нейронной сети (10) к набору (16) элементов (42), и
суммы предварительно перераспределенных оценок релевантности набора нисходящих соседних нейронов соответствующего нейрона.
5. Устройство по п. 1, причем устройство сконфигурировано таким образом, что для каждого нейрона j функция распределения, обеспечивающая то, насколько релевантность перераспределяется как сообщение Rij релевантности от соответствующего нейрона j к восходящему соседнему нейрону i, представляет собой
Rij=q(i)⋅m({Rjk, k является нисходящим соседним нейроном для j}),
где m(RK) при K, являющемся числом нисходящих соседей соответствующего нейрона j, является монотонно возрастающей функцией для всех ее компонентов и дает предварительно перераспределенную оценку релевантности Rj=m({Rjk, k является нисходящим нейроном для j}) соответствующего нейрона j и q(i) является функцией, зависящей от весов wij, соединяющих восходящий соседний нейрон i с соответствующим нейроном j, активации xi восходящего соседнего нейрона i соответствующего нейрона j в результате применения искусственной нейронной сети (10) к набору (16) элементов (42) и, возможно, имеющего нулевое значение члена смещения bj нейрона j.
6. Устройство по п. 5, в котором m({Rjk, k является нисходящим нейроном для j})=ΣkRjk.
7. Устройство по п. 5, в котором устройство сконфигурировано таким образом, что функция q(i) является функцией p взвешенных активаций zij=s(xi, wij, bj), которые вычисляются посредством функции s, так что q(i)=p({zij|i является восходящим соседним нейроном для j}).
8. Устройство по п. 7, в котором функция s выбрана так, что взвешенная активация zij задается как
zij= xiwij,
или 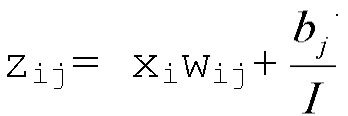
где I - число восходящих соседних нейронов i нейрона j.
9. Устройство по п. 5, причем устройство сконфигурировано таким образом, что функция q(i) удовлетворяет для каждого нейрона j, для которого Rj>0, свойству упорядочения,
причем свойство упорядочения удовлетворяется, если
а) если Σizij>0, то для всех i1 и i2, являющихся восходящими соседними нейронами нейрона j, для которых
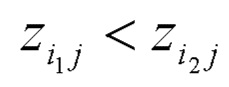 ,
,
справедливо, что q(i1)<q(i2);
b) или для всех i1 и i2, являющихся восходящими соседними нейронами нейрона j, для которых
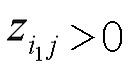 и
и 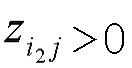 и
и  ,
,
то справедливо, что 0≤q(i1)≤q(i2).
10. Устройство по п. 5, причем устройство сконфигурировано таким образом, что функция q(i) удовлетворяет свойству упорядочения,
причем свойство упорядочения удовлетворяется, если для всех i1 и i2, являющихся восходящими соседними нейронами нейрона j, для которых
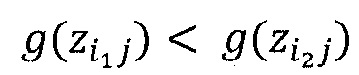 ,
,
справедливо, что |q(i1)|≤|q(i2)| для функции g(⋅), которая имеет свой минимум в нуле и которая монотонно убывает на интервале (-∞, 0) и монотонно возрастает на интервале (0, +∞).
11. Устройство по п. 10, причем устройство сконфигурировано таким образом, что функция g(.) задается следующим образом:
g(z)=α max(0,z)-β min(0,z) при α>0, β≥0.
12. Устройство по п. 5, причем устройство сконфигурировано таким образом, что функция q(i) наследует или пропорциональна декомпозиции Тейлора функции искусственной нейронной сети нейронов.
13. Устройство по п. 5, причем устройство сконфигурировано таким образом, что сообщение Rij релевантности пропорционально декомпозиции Тейлора функции, которая обучается на данных и которая отображает активации xi восходящих соседей I нейрона j на значение m({Rjk, k является нисходящим нейроном для j}) до погрешности аппроксимации.
14. Устройство по п. 1, причем устройство сконфигурировано таким образом, что функция распределения представляет собой
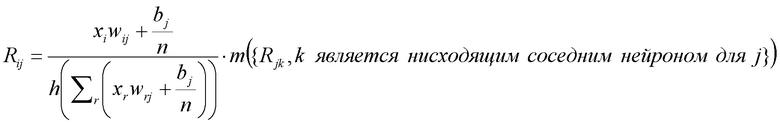
или

где n - число восходящих соседних нейронов соответствующего нейрона j, Rij - сообщение релевантности, перераспределенное от соответствующего нейрона j к восходящему соседнему нейрону i, и Rjk - сообщение релевантности, перераспределенное от нисходящего соседнего нейрона k к соответствующему нейрону j, xi - активация восходящего соседнего нейрона i во время применения искусственной нейронной сети к набору (16) элементов (42), wij - вес, соединяющий восходящий соседний нейрон i с соответствующим нейроном j, wrj - также вес, соединяющий восходящий соседний нейрон r с соответствующим нейроном j, и bj - член смещения соответствующего нейрона j, и h() является скалярной функцией, при этом m(RK), где K является числом нисходящих соседей соответствующего нейрона j, является монотонно возрастающей функцией для всех ее компонентов и дает предварительно перераспределенную оценку релевантности Rj=m({Rjk, k является нисходящим нейроном для j}) соответствующего нейрона j.
15. Устройство по п. 1, причем устройство сконфигурировано таким образом, что распределение на набор восходящих соседних нейронов i соответствующего нейрона j выполняется с использованием функции распределения, причем функция распределения представляет собой

⋅m({Rjk, k является нисходящим соседним нейроном для j})
или
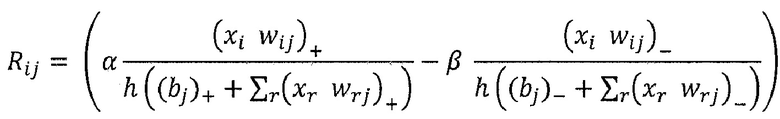
⋅m({Rjk, k является нисходящим соседним нейроном для j}),
где (z)+=max(0,z), (z)-=min(0,z), n - число восходящих соседних нейронов соответствующего нейрона, Rij - сообщение релевантности, перераспределенное от соответствующего нейрона j к восходящему соседнему нейрону i, и Rjk - сообщение релевантности, перераспределенное от нисходящего соседнего нейрона k к соответствующему нейрону j, xi - активация восходящего соседнего нейрона i во время применения нейронной сети к набору (16) элементов (42), wij - вес, соединяющий восходящий соседний нейрон i с соответствующим нейроном j, wrj - также вес, соединяющий восходящий соседний нейрон r с соответствующим нейроном j, и bj - член смещения соответствующего нейрона j, и h() является скалярной функцией, и α>0, β≥0, α-β=1 и m(RK), где K является числом нисходящих соседей соответствующего нейрона j, является монотонно возрастающей функцией для всех ее компонентов и дает предварительно перераспределенную оценку релевантности Rj=m({Rjk, k является нисходящим нейроном для j}) соответствующего нейрона j.
16. Устройство по п. 14, в котором m({Rjk, k является нисходящим нейроном для j})=ΣkRjk.
17. Устройство по п. 14, в котором h() является стабилизирующей функцией h(t)=t+ε⋅sign(t).
18. Устройство по п. 1, причем устройство сконфигурировано, чтобы вычислять для каждого элемента i оценки Ri релевантности соответствующего элемента i путем суммирования сообщений релевантности нейронов, имеющих соответствующий элемент в качестве восходящего соседнего нейрона, перераспределенных на соответствующий элемент.
19. Устройство по п. 1, причем искусственная нейронная сеть непосредственно применяется к набору элементов, так что элементы набора (16) элементов (42) образуют восходящих соседей для поднабора искусственных нейронов искусственной нейронной сети, и выход сети соответствует нейронной активации нейрона на нисходящем конце искусственной нейронной сети.
20. Устройство по п. 1, причем выход (18) сети представляет собой скаляр с начальной оценкой релевантности, полученной из него, равной значению скаляра или полученной путем применения монотонно возрастающей функции к значению скаляра, или выход сети представляет собой вектор с начальным значением релевантности, равным значению одного или нескольких компонентов вектора, или полученным путем применения монотонно возрастающей функции к значению одного или нескольких компонентов вектора.
21. Устройство по п. 1, причем устройство сконфигурировано для осуществления обратного распространения, так что 0.95⋅R≤f(ΣRi)≤1.05⋅R, где ΣRi обозначает сумму по оценкам релевантности всех элементов i набора (16) элементов (42) и f является монотонной функцией, зависящей только от ΣRi.
22. Устройство по п. 21, причем устройство сконфигурировано таким образом, что f является функцией тождественности.
23. Устройство по п. 1, причем устройство сконфигурировано таким образом, что для каждого нейрона сумма значений сообщений релевантности, распределенных по набору восходящих соседних нейронов соответствующего нейрона с помощью функции распределения, равна ξ(SN) или отклоняется от этого не более чем на 5%, причем SN обозначает сумму сообщений релевантности из набора нисходящих соседних нейронов соответствующего нейрона к соответствующему нейрону и ξ обозначает монотонную функцию, зависящую только от SN.
24. Устройство по п. 23, причем устройство сконфигурировано таким образом, что ξ является функцией тождественности.
25. Устройство по п. 1, причем искусственная нейронная сеть выполнена многослойной, так что каждый нейрон (12) принадлежит к одному из последовательности слоев, и устройство сконфигурировано, чтобы выполнять обратное распространение с одинаковым использованием одной функции распределения для всех нейронов искусственной нейронной сети.
26. Устройство по п. 1, причем искусственная нейронная сеть выполнена многослойной, так что каждый нейрон (12) принадлежит одному из последовательности слоев, и устройство сконфигурировано, чтобы выполнять обратное распространение так, что для каждого уровня сумма значений сообщений релевантности, распределенных для нейронов соответствующего уровня, равна ζ(SL) или отклоняются от этого не более чем на 5%, причем SL обозначает сумму предварительно перераспределенных оценок релевантности нейронов слоя, нисходящего относительно соответствующего слоя, и ζ обозначает монотонную функцию, зависящую только от SL.
27. Устройство по п. 1, в котором набор (16) элементов представляет собой комбинацию
изображения с каждым из элементов (42) набора (16) элементов (42), соответствующих одному или нескольким пикселам или субпикселам изображения, и/или
видео с каждым из элементов (42) набора (16) элементов (42), соответствующих одному или нескольким пикселам или субпикселам изображений видео, изображениям видео или последовательностям изображений видео, и/или
аудиосигнала с каждым элементом (42) набора (16) элементов (42), соответствующих одной или нескольким аудиовыборкам аудиосигнала, и/или
карты признаков локальных признаков или преобразования, локально или глобально извлеченных из изображения, видео или аудиосигнала с элементами (42) набора (16) элементов (42), соответствующих локальным признакам, и/или
текста с элементами (42) набора (16) элементов (42), соответствующих словам, предложениям или абзацам текста, и/или
графа, такого как граф отношений социальных сетей, с элементами (42) набора (16) элементов (42), соответствующих узлам, или ребрам, или наборам узлов, или набору ребер, или подграфам.
28. Система (100) для обработки данных, содержащая
устройство (50) для назначения оценки релевантности набору элементов в соответствии с любым из предыдущих пунктов, и
устройство (102) для обработки набора (16) элементов или данных, подлежащих обработке (106) и полученных из набора элементов с адаптацией обработки в зависимости от оценок релевантности.
29. Система по п. 28, в которой обработка представляет собой обработку с потерями и устройство для обработки сконфигурировано для уменьшения потери обработки с потерями для элементов, имеющих более высокие оценки релевантности, назначенные им, по сравнению с элементами, имеющими более низкие оценки релевантности, назначенные им.
30. Система по п. 28, в которой обработка представляет собой визуализацию, причем устройство для адаптации сконфигурировано, чтобы выполнять выделение в визуализации в зависимости от оценок релевантности.
31. Система по п. 28, в которой обработка представляет собой пополнение данных путем считывания из памяти или выполнение дополнительного измерения, причем устройство (102) для обработки сконфигурировано, чтобы фокусировать пополнение данных в зависимости от оценок релевантности.
32. Система (110) для выделения области, представляющей интерес, содержащая
устройство (50) для назначения оценки релевантности набору элементов по п. 1 и
устройство (112) для генерирования графа (114) релевантности в зависимости от оценок релевантности.
33. Система (120) для оптимизации искусственной нейронной сети, содержащая
устройство (50) для назначения оценки релевантности набору элементов по п. 1;
устройство (122) для применения устройства для назначения к множеству различных наборов элементов; и
устройство (124) для обнаружения части повышенной релевантности (128) в искусственной нейронной сети путем накопления релевантностей, назначенных нейронам сети во время применения устройства для назначения к множеству различных наборов элементов, и оптимизации искусственной нейронной сети в зависимости от части повышенной релевантности.
34. Способ назначения оценки релевантности набору элементов, причем оценка релевантности указывает релевантность в отношении применения искусственной нейронной сети (10), состоящей из нейронов (12), к набору (16) элементов (42), чтобы отображать набор (16) элементов (42) на выход (18) сети, причем способ содержит:
перераспределение начальной оценки (R) релевантности, полученной из выхода (18) сети, на набор (16) элементов (42) путем обратного распространения начальной оценки релевантности через искусственную нейронную сеть (10), чтобы получить оценку релевантности для каждого элемента,
причем обратное распространение выполняется таким образом, что для каждого нейрона предварительно перераспределенные оценки релевантности набора нисходящих соседних нейронов соответствующего нейрона распределяются по набору восходящих соседних нейронов соответствующего нейрона с использованием функции распределения.
35. Машиночитаемый носитель данных, на котором сохранена компьютерная программа, имеющая программный код для выполнения, при исполнении на компьютере, способа по п. 34.
| Приспособление для суммирования отрезков прямых линий | 1923 |
|
SU2010A1 |
| Станок для изготовления деревянных ниточных катушек из цилиндрических, снабженных осевым отверстием, заготовок | 1923 |
|
SU2008A1 |
| Полимерная композиция | 1981 |
|
SU1006458A1 |
| РАНЖИРОВАНИЕ РЕЗУЛЬТАТОВ ПОИСКА С ИСПОЛЬЗОВАНИЕМ РАССТОЯНИЯ РЕДАКТИРОВАНИЯ И ИНФОРМАЦИИ О ДОКУМЕНТЕ | 2009 |
|
RU2501078C2 |
Авторы
Даты
2019-10-16—Публикация
2015-03-20—Подача