Изобретение относится к области управления и может быть использовано в системах управления электромеханическими, электротехническими, энергетическими, теплотехническими, механическими объектами и процессами.
Известен способ настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы (Ziegler J.G., Nichols N.B. Optimum settings for automatic controllers // Trans. ASME. 1942. Vol. 64. P. 759-768), в котором объекту управления задают гармонический испытательный сигнал, регулируют частоту гармонического испытательного сигнала, контролируют реакцию объекта управления на него, достигают сдвига в сто восемьдесят градусов между гармоническим испытательным сигналом и реакцией объекта управления на него, фиксируют граничную величину периода гармонического испытательного сигнала и граничную величину динамического коэффициента усиления объекта управления, затем определяют величину пропорционального коэффициента в зависимости от граничной величины периода гармонического испытательного сигнала и весового множителя при пропорциональном коэффициенте, определяют величину интегрального коэффициента в зависимости от величины пропорционального коэффициента, граничной величины периода гармонического испытательного сигнала и весового коэффициента при интегральном коэффициенте, определяют величину дифференциального коэффициента в зависимости от величины пропорционального коэффициента, граничной величины периода гармонического испытательного сигнала и весового коэффициента при дифференциальном коэффициенте, далее пропорционально-интегрально-дифференциальный регулятор включают последовательно с объектом управления, далее замыкают динамическую систему по целевой координате, затем задают коэффициентам их определенные значения, причем весовые множители при пропорциональном, интегральном и дифференциальном коэффициентах задают в соответствии с настройкой регулятора на максимальное быстродействие при минимальной колебательности замкнутой динамической системы.
Недостатком данного технического решения является возникновение неустойчивости при его осуществлении, если объект управления замкнутой динамической системы является двукратно интегрирующим.
Известен другой способ настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы (Сhien K.L., Hrones J.A., Reswick J.B. On automatic control of generalized passive systems // Trans. ASME. 1952. Vol. 74. P. 175-185), в котором объекту управления задают скачкообразный испытательный сигнал, контролируют переходную функцию объекта управления, далее определяют величину транспортного запаздывания и темп нарастания переходной функции до установившегося значения, затем определяют величину пропорционального коэффициента в зависимости от транспортного запаздывания и весового множителя при пропорциональном коэффициенте, определяют величину интегрального коэффициента в зависимости от величины пропорционального коэффициента, темпа нарастания переходной функции до установившегося значения и весового коэффициента при интегральном коэффициенте, определяют величину дифференциального коэффициента в зависимости от величины пропорционального коэффициента, темпа нарастания переходной функции до установившегося значения и весового коэффициента при дифференциальном коэффициенте, далее пропорционально-интегрально-дифференциальный регулятор включают последовательно с объектом управления, далее замыкают динамическую систему по целевой координате, затем задают коэффициентам их определенные значения, причем переходную функцию контролируют в виде изменения во времени целевой координаты движения при действии на объект управления скачкообразного испытательного сигнала, а весовые множители при пропорциональном, интегральном и дифференциальном коэффициентах задают в соответствии с настройкой регулятора на максимальное быстродействие при минимальной колебательности замкнутой динамической системы.
Недостатком данного технического решения является возникновение неустойчивости при его осуществлении, если объект управления замкнутой динамической системы является двукратно интегрирующим.
Наиболее близким по технической сущности к заявляемому изобретению является способ настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы (Ziegler J.G., Nichols N.B. Optimum settings for automatic controllers // Trans. ASME. 1942. Vol. 64. P. 759-768), в котором пропорционально-интегрально-дифференциальный регулятор включают последовательно с объектом управления, далее замыкают динамическую систему по целевой координате, затем первоначально задают пропорциональный, интегральный и дифференциальный коэффициенты регулятора равными нулю, регулируют величину пропорционального коэффициента и при каждой его величине задают замкнутой динамической системе скачкообразные испытательные сигналы, контролируют переходную функцию замкнутой динамической системы, достигают возникновения в замкнутой динамической системе установившихся незатухающих колебаний, фиксируют величину пропорционального коэффициента, равного граничному значению, измеряют величину периода установившихся незатухающих колебаний, далее определяют величину пропорционального коэффициента в зависимости от граничного значения пропорционального коэффициента и весового множителя при пропорциональном коэффициенте, определяют величину интегрального коэффициента в зависимости от величины пропорционального коэффициента, весового множителя при интегральном коэффициенте и периода установившихся незатухающих колебаний, определяют величину дифференциального коэффициента в зависимости от величины пропорционального коэффициента, весового множителя при дифференциальном коэффициенте и периода установившихся незатухающих колебаний, затем задают коэффициентам их определенные значения, причем переходную функцию контролируют в виде изменения во времени целевой координаты движения при действии на замкнутую динамическую систему скачкообразного испытательного сигнала, а весовые множители при пропорциональном, интегральном и дифференциальном коэффициентах задают в соответствии с настройкой регулятора на максимальное быстродействие при минимальной колебательности замкнутой динамической системы.
Недостатком данного технического решения является возникновение неустойчивости при его осуществлении, если объект управления замкнутой динамической системы является двукратно интегрирующим.
Технической задачей предлагаемого изобретения является расширение функциональности настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы.
Технической результат заключается в обеспечении устойчивости замкнутой динамической системы при настройке ее пропорционально-интегрально-дифференциального регулятора, если объект управления замкнутой динамической системы является двукратно интегрирующим.
Это достигается тем, что в известном способе настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы, включающем включение пропорционально-интегрально-дифференциальный регулятора последовательно с объектом управления, замыкание динамической системы по целевой координате, первоначальное задание пропорционального, интегрального и дифференциального коэффициентов регулятора равными нулю, при этом регулируют величину дифференциального коэффициента и при каждой его величине задают замкнутой динамической системе скачкообразные испытательные сигналы, контролируют переходную функцию замкнутой динамической системы, достигают переходной функции граничного вида между апериодическим видом и колебательным видом, дифференциальный коэффициент считают настроенным, затем регулируют величину пропорционального коэффициента и при каждой его величине задают замкнутой динамической системе скачкообразные испытательные сигналы, контролируют переходную функцию замкнутой динамической системы, достигают возникновения в замкнутой динамической системе установившихся незатухающих колебаний, фиксируют величину пропорционального коэффициента, равного граничному значению, измеряют величину периода установившихся незатухающих колебаний, далее определяют величину пропорционального коэффициента в зависимости от граничного значения пропорционального коэффициента и весового множителя при пропорциональном коэффициенте, определяют величину интегрального коэффициента в зависимости от величины пропорционального коэффициента, весового множителя при интегральном коэффициенте и периода установившихся незатухающих колебаний, затем задают коэффициентам их определенные значения, причем переходную функцию контролируют в виде изменения во времени целевой координаты движения при действии на замкнутую динамическую систему скачкообразного испытательного сигнала, а весовые множители при пропорциональном и интегральном коэффициентах задают в соответствии с настройкой регулятора на максимальное быстродействие при минимальной колебательности замкнутой динамической системы.
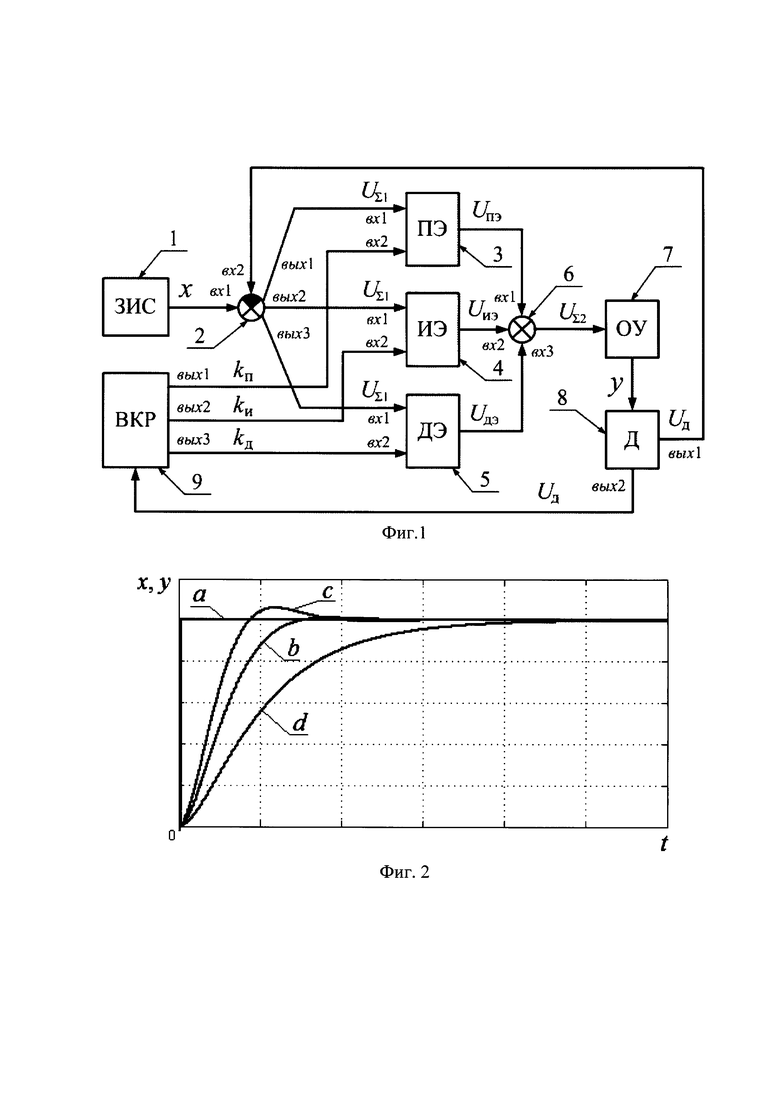
Сущность предлагаемого технического решения поясняется чертежами, где на фиг. 1 изображена функциональная схема устройства, реализующего предлагаемый способ настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы; на фиг. 2 изображены графики испытательного сигнала и переходной функции замкнутой динамической системы при регулировании дифференциального коэффициента регулятора при разных его величинах; на фиг. 3 изображены графики испытательного сигнала и переходной функции замкнутой динамической системы при регулировании пропорционального коэффициента регулятора при разных его величинах; на фиг. 4 изображен график переходной функции замкнутой динамической системы с двукратно интегрирующим объектом управления, полученный в результате настройки регулятора согласно заявленному способу.
На графических изображениях приняты следующие обозначения: Ту - период установившихся незатухающих колебаний; t - время; х - испытательный сигнал; у - переходная функция (реакция замкнутой динамической системы на испытательный сигнал), целевая координата замкнутой динамической системы; Uд - сигнал обратной связи по целевой координате замкнутой динамической системы; U∑1 - выходной сигнал первого сумматора (рассогласование испытательного сигнала и сигнала обратной связи); U∑2 - выходной сигнал второго сумматора (выходной сигнал пропорционально-интегрально-дифференциального регулятора); kп - пропорциональный коэффициент регулятора; kи - интегральный коэффициент регулятора; kд - дифференциальный коэффициент регулятора; Uпэ - выходной сигнал пропорционального элемента регулирования; Uиэ - выходной сигнал интегрального элемента регулирования; Uдэ - выходной сигнал дифференциального элемента регулирования.
Устройство для осуществления способа настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы содержит задатчик испытательного сигнала (ЗИС) 1, выход которого соединен с первым входом первого сумматора 2, первый выход первого сумматора 2 соединен с первым входом пропорционального элемента регулирования (ПЭ) 3, второй выход первого сумматора 2 соединен с первым входом интегрального элемента регулирования (ИЭ) 4, третий выход первого сумматора 2 соединен с первым входом дифференциального элемента регулирования (ДЭ) 5, выход пропорционального элемента регулирования 3 соединен с первым входом второго сумматора 6, выход интегрального элемента регулирования 4 соединен со вторым входом второго сумматора 6, выход дифференциального элемента регулирования 5 соединен с третьим входом второго сумматора 6, выход которого соединен со входом объекта управления 7, выход объекта управления 7 соединен с датчиком (Д) 8, первый выход которого соединен со вторым входом первого сумматора 2, а второй его выход соединен со входом вычислителя коэффициентов регулятора (ВКР) 9, первый выход вычислителя коэффициентов регулятора 9 соединен со вторым входом пропорционального элемента регулирования 3, второй выход вычислителя коэффициентов регулятора 9 соединен со вторым входом интегрального элемента регулирования 4, третий выход вычислителя коэффициентов регулятора 9 соединен со вторым входом дифференциального элемента регулирования 5.
Объект управления 7 может иметь любую физическую реализацию, например, электромеханическую, электротехническую, энергетическую, теплотехническую, механическую. Задатчик испытательного сигнала 1 и первый сумматор 2 могут быть любого типа, допустимого для использования в замкнутой динамической системе. Пропорциональный элемент регулирования 3, интегральный элемент регулирования 4, дифференциальный элемент регулирования 5 и второй сумматор 6 образуют пропорционально-интегрально-дифференциальный регулятор и могут быть любого типа, допустимого для использования в замкнутой динамической системе. Датчик 8 реализован на основе измерительных устройств любого типа, допустимого для соединения с объектом управления 7, первым сумматором 2 и вычислителем коэффициентов регулятора 9. Вычислитель коэффициентов регулятора 9 реализован на основе программно-аппаратных средств вычислительной техники.
Реализация указанным устройством предлагаемого способа настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы осуществляется следующим образом. С помощью задатчика испытательного сигнала 1 задают замкнутой динамической системе скачкообразные испытательные сигналы х. С помощью датчика 8 контролируют переходную функцию замкнутой динамической системы:
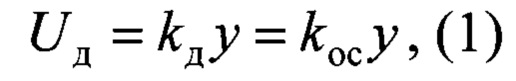
где kос - коэффициент датчика (коэффициент обратной связи).
С помощью датчика 8 и первого сумматора 2 замыкают динамическую систему по целевой координате у:
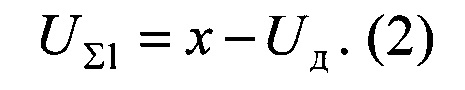
Пропорционально-интегрально-дифференциальный регулятор, образованный пропорциональным 3, интегральным 4, дифференциальным 5 элементами регулирования и вторым сумматором 6, включен последовательно с объектом управления 7. Второй сумматор 6 вычисляет выходной сигнал регулятора как сумму выходных сигналом пропорционального 3, интегрального 4 и дифференциального 5 элементов регулирования:
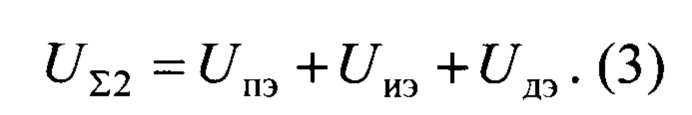
Следовательно, передаточная функция пропорционально-инетгрально-дифференциального регулятора имеет следующий вид:
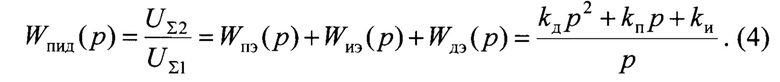
где р - оператор Лапласа.
Передаточная функция Wпэ пропорционального элемента регулирования, передаточная функция Wиэ интегрального элемента регулирования и передаточная функция Wдэ дифференциального элемента регулирования следующие:
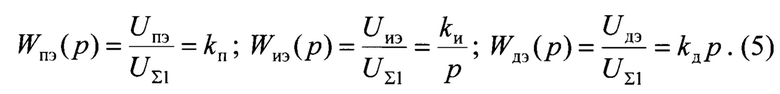
Выходной сигнал пропорционально-интегрально-дифференциального регулятора является входным сигналом объекта управления 7. Передаточная функция двукратно интегрирующего объекта управления имеет следующий вид:
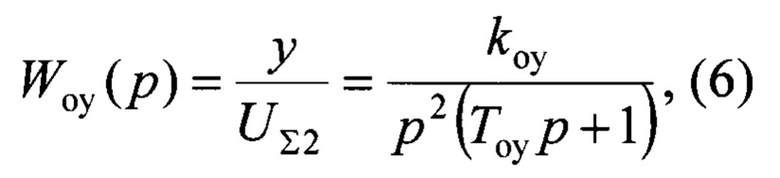
где kоу - коэффициент передачи объекта управления; Тоу - постоянная времени объекта управления.
С помощью вычислителя коэффициентов регулятора 9 первоначально задают пропорциональный kп, интегральный kи и дифференциальный kд коэффициенты регулятора равными нулю. С его же помощью регулируют величину дифференциального коэффициента kд. Для этого вычислитель коэффициентов 9 передает величину дифференциального коэффициента kд дифференциальному элементу регулирования 5. При каждом из значений kд задатчиком испытательного сигнала 1 задают замкнутой динамической системе скачкообразные испытательные сигналы х, датчиком 8 контролируют переходную функцию у замкнутой динамической системы, чтобы достигнуть переходной функции граничного вида между апериодическим видом и колебательным видом.
Используя вычислитель коэффициентов регулятора 9, обнаруживают достижение переходной функции у граничного вида между апериодическим видом и колебательным видом. На фиг. 2 изображены графики испытательного сигнала (а) и переходной функции замкнутой динамической системы при регулировании дифференциального коэффициента регулятора при разных его величинах: b - граничный вид переходной функции между апериодическим видом и колебательным видом; с - переходная функция колебательного вида; d - переходная функция апериодического вида.
При регулировании дифференциального коэффициента kд при kп=kи=0 передаточная функция замкнутой динамической системы имеет следующий вид, свидетельствующий об устойчивости этой системы на данном этапе:
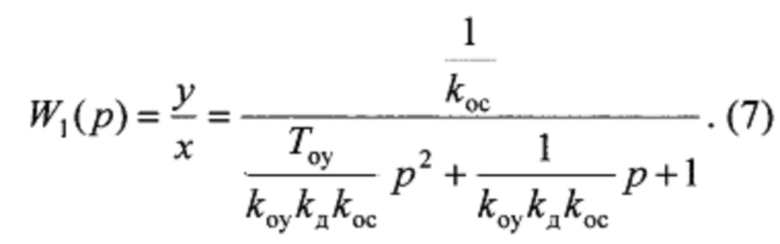
При достижении переходной функции граничного вида b (фиг. 2) между апериодическим видом d и колебательным видом с дифференциальный коэффициент kд является настроенным.
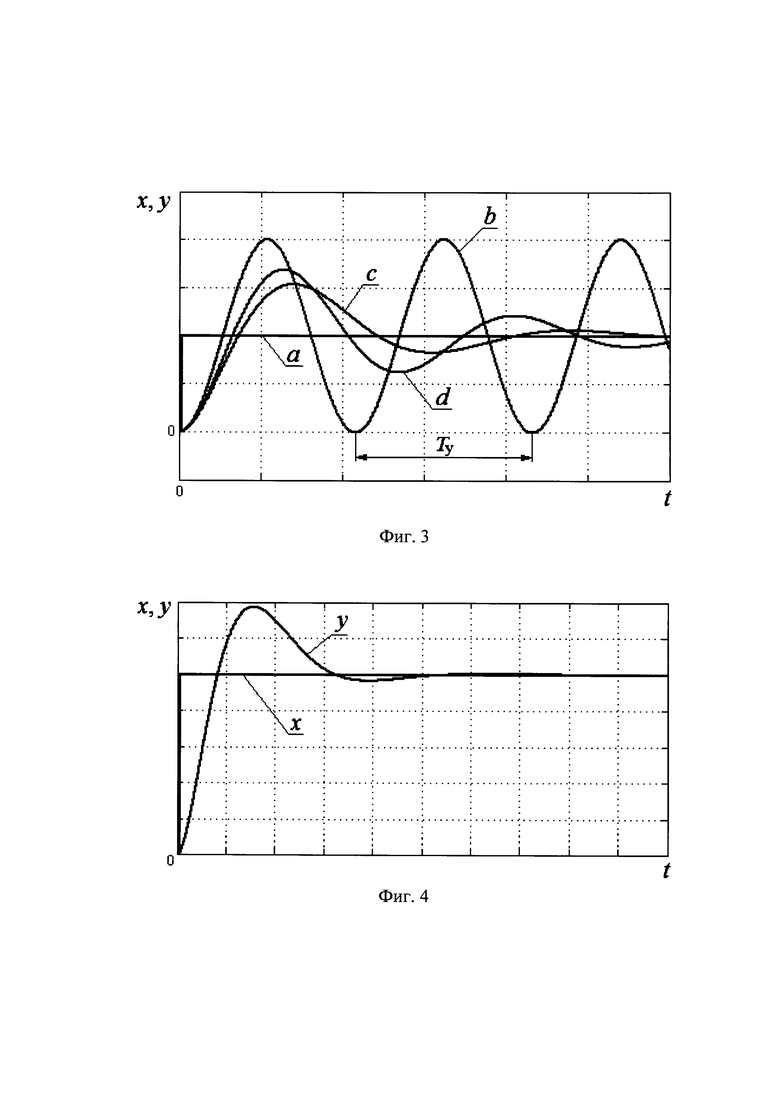
Далее с помощью вычислителя коэффициентов регулятора 9 регулируют величину пропорционального коэффициента kп. Для этого вычислитель коэффициентов 9 передает величину пропорционального коэффициента kп пропорциональному элементу регулирования 3. При каждом из значений kп с помощью задатчика испытательного сигнала 1 задают замкнутой динамической системе скачкообразные испытательные сигналы х, показанные на фиг. 3 (график а), с помощью датчика 8 контролируют переходную функцию замкнутой динамической системы у, достигают возникновения в замкнутой динамической системе установившихся незатухающих колебаний, пример которых показан на фиг. 3 (график b).
В процессе регулирования пропорционального коэффициента kп меняется колебательность переходной функции у - графики с и d, которые являются реакциями на испытательный сигнал x (график а).
При регулировании пропорционального коэффициента kп при kи=0 и ранее настроенном дифференциальном коэффициенте kд передаточная функция замкнутой динамической системы имеет следующий вид, свидетельствующий об устойчивости этой системы на данном этапе:
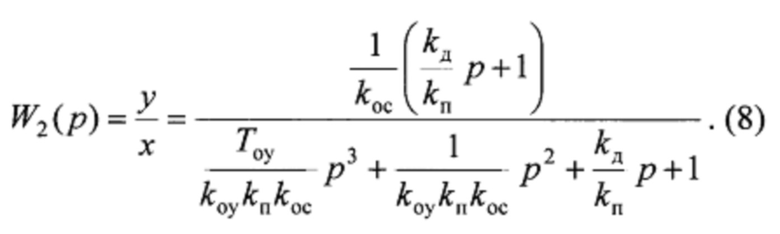
Далее с помощью вычислителя коэффициентов регулятора 9 фиксируют величину пропорционального коэффициента, равного граничному значению kгр и измеряют величину периода установившихся незатухающих колебаний Ту.
Далее с помощью вычислителя коэффициентов регулятора 9 определяют величину пропорционального коэффициента kп в зависимости от граничного значения kгр пропорционального коэффициента и весового множителя kп при пропорциональном коэффициенте, определяют величину интегрального коэффициента kи в зависимости от величины пропорционального коэффициента kп, весового множителя hи при интегральном коэффициенте и периода установившихся незатухающих колебаний Ту по следующим соотношениям:
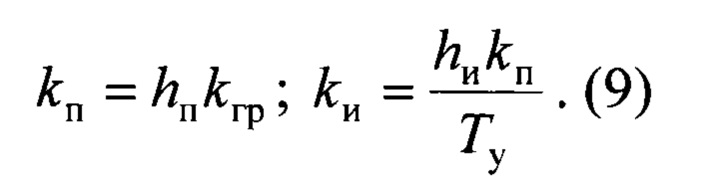
Затем задают коэффициентам их определенные по (9) значения. Для этого вычислитель коэффициентов 9 передает величины коэффициентов регулятора пропорциональному 3, интегральному 4 и дифференциальному 5 элементам регулирования. В результате настройки передаточная функция замкнутой динамической системы имеет вид, свидетельствующий об устойчивости этой системы на данном этапе:
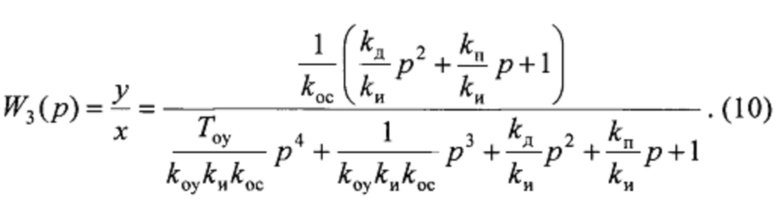
Весовые множители при пропорциональном и интегральном коэффициентах задают в соответствии с настройкой регулятора на максимальное быстродействие при минимальной колебательности замкнутой динамической системы следующим образом:
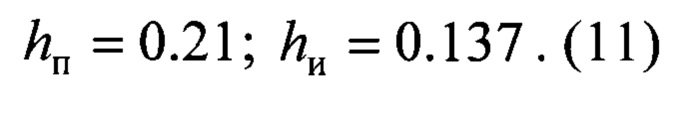
При выполнении этого условия (11) переходная функция у замкнутой динамической системы имеет вид, показанный на фиг. 4.
На всех этапах осуществления предложенного способа настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы она является устойчивой, если объект ее управления является двукратно интегрирующим. Это свидетельствует о достижении заявленного технического результата.
Использование изобретения позволяет расширить функциональность настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы, в том числе в системах управления электромеханическими, электротехническими, энергетическими, теплотехническими, механическими объектами и процессами.
| название | год | авторы | номер документа |
|---|---|---|---|
| ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫЙ РЕГУЛЯТОР | 2002 |
|
RU2234116C1 |
| СПОСОБ АДАПТИВНОГО АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ ГАЗОВЫМИ И ГАЗОКОНДЕНСАТНЫМИ СКВАЖИНАМИ | 2015 |
|
RU2591870C1 |
| Способ автоматического регулирования частоты вращения ротора синхронного генератора и регулятор для его реализации | 2023 |
|
RU2823536C1 |
| АВТОМАТИЧЕСКИЙ РЕГУЛЯТОР НАПРЯЖЕНИЯ СИНХРОННОГО ГЕНЕРАТОРА | 2011 |
|
RU2465717C1 |
| СИСТЕМА АДАПТИВНОГО УПРАВЛЕНИЯ ЭЛЕКТРОДВИГАТЕЛЕМ | 2015 |
|
RU2605946C1 |
| Система автоматического регулирования загрузки мельницы | 1982 |
|
SU1255207A1 |
| СПОСОБ НАСТРОЙКИ ПАРАМЕТРОВ РЕГУЛЯТОРА ВОЗБУЖДЕНИЯ СИНХРОННОГО ЭЛЕКТРИЧЕСКОГО ГЕНЕРАТОРА | 2012 |
|
RU2498495C1 |
| Адаптивный регулятор | 1982 |
|
SU1076873A1 |
| СИСТЕМА УПРАВЛЕНИЯ ЭЛЕКТРОМАГНИТНЫМ ПОДВЕСОМ РОТОРА | 2008 |
|
RU2395150C2 |
| СИСТЕМА С ОБРАТНОЙ СВЯЗЬЮ | 2013 |
|
RU2541684C1 |
В способе настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы включают регулятор последовательно с объектом управления, замыкают систему по целевой координате, задают коэффициенты регулятора равными нулю. Регулируют дифференциальный и пропорциональный коэффициенты и задают системе скачкообразные испытательные сигналы. Контролируют переходную функцию системы, достигают возникновения в ней установившихся незатухающих колебаний. Фиксируют величину пропорционального коэффициента, равного граничному значению. Измеряют величину периода незатухающих колебаний. Определяют величину пропорционального и интегрального коэффициента. Задают коэффициентам их определенные значения. Переходную функцию контролируют в виде изменения во времени целевой координаты движения при действии на систему скачкообразного испытательного сигнала. Весовые множители при пропорциональном и интегральном коэффициентах задают в соответствии с настройкой регулятора на максимальное быстродействие. Повышается устойчивость системы, если объект управления двукратно интегрирующий. 4 ил.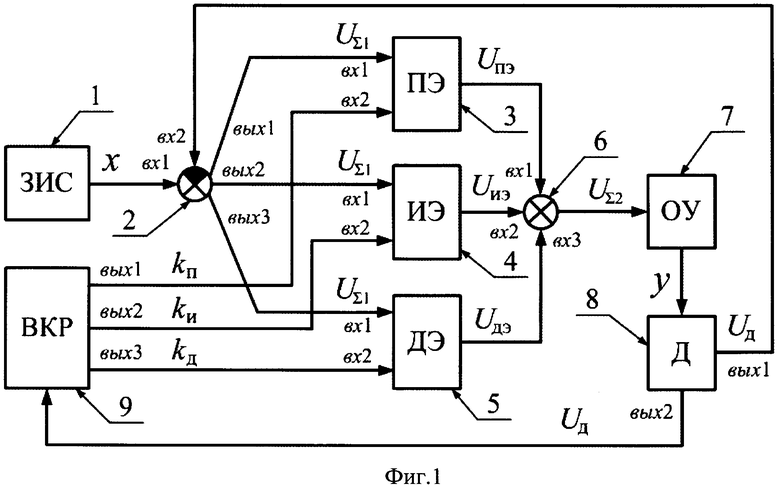
Способ настройки пропорционально-интегрально-дифференциального регулятора замкнутой динамической системы, включающий включение пропорционально-интегрально-дифференциального регулятора последовательно с объектом управления, замыкание динамической системы по целевой координате, первоначальное задание пропорционального, интегрального и дифференциального коэффициентов регулятора равными нулю, отличающийся тем, что регулируют величину дифференциального коэффициента и при каждой его величине задают замкнутой динамической системе скачкообразные испытательные сигналы, контролируют переходную функцию замкнутой динамической системы, достигают переходной функции граничного вида между апериодическим видом и колебательным видом, дифференциальный коэффициент считают настроенным, затем регулируют величину пропорционального коэффициента и при каждой его величине задают замкнутой динамической системе скачкообразные испытательные сигналы, контролируют переходную функцию замкнутой динамической системы, достигают возникновения в замкнутой динамической системе установившихся незатухающих колебаний, фиксируют величину пропорционального коэффициента, равного граничному значению, измеряют величину периода установившихся незатухающих колебаний, далее определяют величину пропорционального коэффициента в зависимости от граничного значения пропорционального коэффициента и весового множителя при пропорциональном коэффициенте, определяют величину интегрального коэффициента в зависимости от величины пропорционального коэффициента, весового множителя при интегральном коэффициенте и периода установившихся незатухающих колебаний, затем задают коэффициентам их определенные значения, причем переходную функцию контролируют в виде изменения во времени целевой координаты движения при действии на замкнутую динамическую систему скачкообразного испытательного сигнала, а весовые множители при пропорциональном и интегральном коэффициентах задают в соответствии с настройкой регулятора на максимальное быстродействие при минимальной колебательности замкнутой динамической системы.
| СПОСОБ НАСТРОЙКИ ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО- ДИФФЕРЕНЦИАЛЬНОГО РЕГУЛЯТОРА | 0 |
|
SU259228A1 |
| SU 1835215 A3, 20.02.1996 | |||
| ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНЫЙ РЕГУЛЯТОР | 1990 |
|
RU2047887C1 |
| ВЫЧИСЛИТЕЛЬНОЕ УСТРОЙСТВО ЦИФРОВОГО ПРОПОРЦИОНАЛЬНО-ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНОГО РЕГУЛЯТОРА | 1989 |
|
RU2012033C1 |
| RU 2002289 С1, 30.10.1993 | |||
| СПОСОБ АДАПТИВНОГО УПРАВЛЕНИЯ ПО ПИД-ЗАКОНУ И СИСТЕМА ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2012 |
|
RU2510956C2 |
| СИСТЕМА УПРАВЛЕНИЯ С ОБРАТНОЙ СВЯЗЬЮ | 2013 |
|
RU2566339C2 |
Авторы
Даты
2020-02-14—Публикация
2019-06-18—Подача