Изобретение относится к вычислительной технике и может быть использовано в системах связи и обработки информации, функционирующих в системе остаточных классов (СОК).
Известно устройство для преобразования числа из системы остаточных классов в позиционный код (патент РФ №2293437, опубл. 10.02.2007), содержащее группу сдвиговых регистров, группу постоянных запоминающих устройств, причем информационные входы группы сдвиговых регистров являются соответствующими информационными входами устройства, при этом выходы группы сдвиговых регистров соединены с адресными входами группы постоянных запоминающих устройств, каждое из которых содержит пару констант 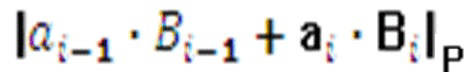 разрядностью
разрядностью 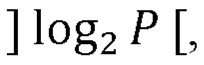 причем количество постоянных запоминающих устройств в группе составляет
причем количество постоянных запоминающих устройств в группе составляет 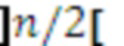 , и если
, и если 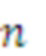 - нечетное число, то количество констант в последнем постоянном запоминающем устройстве группы составляет
- нечетное число, то количество констант в последнем постоянном запоминающем устройстве группы составляет 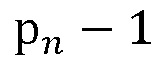 , выходы группы постоянных запоминающих устройств соединены с соответствующими входами разрядно-параллельно сумматора по модулю, выходы которого являются выходами устройства, где
, выходы группы постоянных запоминающих устройств соединены с соответствующими входами разрядно-параллельно сумматора по модулю, выходы которого являются выходами устройства, где 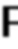 - произведение всех модулей системы остаточных классов;
- произведение всех модулей системы остаточных классов; 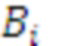 - ортогональные базисы системы остаточных классов;
- ортогональные базисы системы остаточных классов; 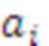 - остаток по
- остаток по 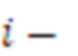 му модулю системы остаточных классов;
му модулю системы остаточных классов; 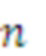 - количество модулей системы остаточных классов, при этом
- количество модулей системы остаточных классов, при этом 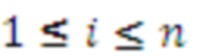 ;
; 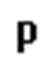 - n-ый модуль системы остаточных классов.
- n-ый модуль системы остаточных классов.
Недостатком данного устройства является аппаратная избыточность и сложность нахождения остатков от деления по большому модулю 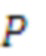 . Также недостатком является ограниченная функциональность, а именно невозможность расширения оснований.
. Также недостатком является ограниченная функциональность, а именно невозможность расширения оснований.
Известно устройство для преобразования чисел из кода системы остаточных классов в позиционный код с контролем ошибок (авторское свидетельство №1797119, опубл. 23.02.1993), основанное на использовании Китайской теоремы об остатках и методе проекций.
Недостатком данного устройства является сложность алгоритма перевода в позиционную систему счисления и нахождение остатков от деления по большому модулю. Также недостатком является ограниченная функциональность, а именно невозможность расширения оснований.
Наиболее близким к заявленному изобретению является нейронная сеть для расширения кортежа числовой системы вычетов (патент РФ №2256226), содержащая входной слой нейронов для фиксирования числа нейронов и вычисления значений вычетов по модулям 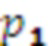 ,
, 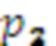 , …,
, …, 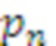 , усеченную треугольную матрицу нейронных сетей конечного кольца по модулям системы остаточных классов, нейронной сети конечного кольца по модулям системы остаточных классов, при этом упомянутые нейронные сети конечного кольца предназначены для вычисления значения
, усеченную треугольную матрицу нейронных сетей конечного кольца по модулям системы остаточных классов, нейронной сети конечного кольца по модулям системы остаточных классов, при этом упомянутые нейронные сети конечного кольца предназначены для вычисления значения 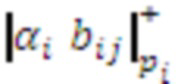 с учетом переноса, где
с учетом переноса, где 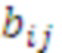 - коэффициенты обобщенной позиционной системы счисления,
- коэффициенты обобщенной позиционной системы счисления, 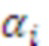 - вычеты из числа А по
- вычеты из числа А по 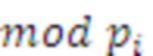 , в нее введены нейронные сети конечного кольца для выполнения модульного суммирования по всем основаниям и дополнительному расширяемому модулям и нейронная сеть для выполнения финального шага вычисления вычета по дополнительно расширяемому модулю, при этом в ней выходы нейронов входного слоя разветвлены на входы нейронных сетей конечного кольца усеченной треугольной матрицы, выполненной в виде распределенной памяти, выходы которых соединены с входами нейронных сетей конечного кольца с единичными синаптическими весами для выполнения модульного суммирования по всем основным и дополнительно расширяемому модулям, выходы переносов которых
, в нее введены нейронные сети конечного кольца для выполнения модульного суммирования по всем основаниям и дополнительному расширяемому модулям и нейронная сеть для выполнения финального шага вычисления вычета по дополнительно расширяемому модулю, при этом в ней выходы нейронов входного слоя разветвлены на входы нейронных сетей конечного кольца усеченной треугольной матрицы, выполненной в виде распределенной памяти, выходы которых соединены с входами нейронных сетей конечного кольца с единичными синаптическими весами для выполнения модульного суммирования по всем основным и дополнительно расширяемому модулям, выходы переносов которых 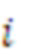 модулей, где
модулей, где 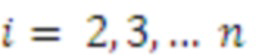 , соединены с входами
, соединены с входами 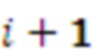 модулей, а выход суммы
модулей, а выход суммы 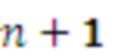 модуля соединен с входом нейронной сети для выполнения финального шага вычисления вычета по дополнительно расширяемому основанию.
модуля соединен с входом нейронной сети для выполнения финального шага вычисления вычета по дополнительно расширяемому основанию.
Общим с прототипом является использование обобщенной позиционной системы счисления (ОПСС), треугольной матрицы коэффициентов базисов ОПСС.
Недостатком прототипа является необходимость нахождения большого числа остатков от деления, а также невозможность перевода в позиционную систему счисления.
Техническим результатом заявляемого изобретения является расширение функциональных возможностей, а именно возможность получить остаток от деления по произвольному дополнительному модулю, а также восстановленное число в позиционной системе счисления.
Данный технический результат достигается тем, что в устройство для перевода чисел из системы остаточных классов и расширения оснований с модулями 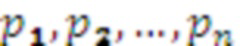 , содержащее n входов остатков, выход остатка по расширенному основанию, n регистров хранения остатков, (n-1) модулярный сумматор по модулю, треугольную матрицу из
, содержащее n входов остатков, выход остатка по расширенному основанию, n регистров хранения остатков, (n-1) модулярный сумматор по модулю, треугольную матрицу из 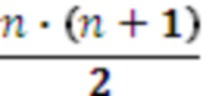 умножителей, где умножители производят умножение на коэффициенты
умножителей, где умножители производят умножение на коэффициенты 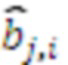 ортогональных базисов
ортогональных базисов 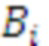 системы остаточных классов (СОК), где
системы остаточных классов (СОК), где 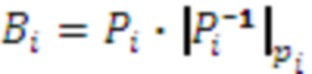 ,
, 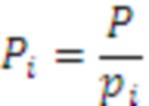 ,
, 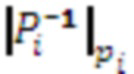 - мультипликативная инверсия,
- мультипликативная инверсия, 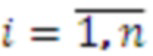 ,
, 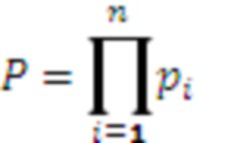 - рабочий диапазон СОК, представленных в обобщенной позиционной системе счисления (ОПСС) с основаниями
- рабочий диапазон СОК, представленных в обобщенной позиционной системе счисления (ОПСС) с основаниями 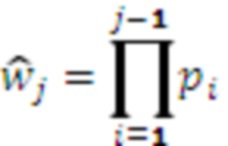 ,
, 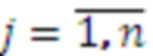 , причем входы остатков соединены с соответствующими регистрами хранения остатков, выход первого регистра хранения остатка одновременно подключен к n умножителям, в которых происходит умножение на коэффициенты
, причем входы остатков соединены с соответствующими регистрами хранения остатков, выход первого регистра хранения остатка одновременно подключен к n умножителям, в которых происходит умножение на коэффициенты 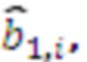
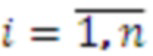 , выход второго регистра хранения остатка одновременно подключен к (n-1) умножителю, в которых происходит умножение на коэффициенты
, выход второго регистра хранения остатка одновременно подключен к (n-1) умножителю, в которых происходит умножение на коэффициенты 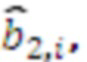
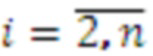 , и так далее, наконец выход n-го регистра хранения остатка подключен к умножителю, в котором происходит умножение на коэффициенты
, и так далее, наконец выход n-го регистра хранения остатка подключен к умножителю, в котором происходит умножение на коэффициенты 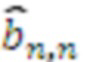 , выходы умножителей, в которых происходит умножение на
, выходы умножителей, в которых происходит умножение на 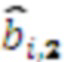 ,
, 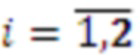 , подключены ко входам модулярного сумматора по модулю
, подключены ко входам модулярного сумматора по модулю 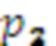 , выход переноса которого подключен к ко входу переноса модулярного сумматора по модулю
, выход переноса которого подключен к ко входу переноса модулярного сумматора по модулю 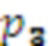 , на входы которого поступают значения с выходов умножителей, в которых происходит умножение на
, на входы которого поступают значения с выходов умножителей, в которых происходит умножение на 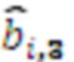 ,
, 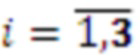 , а выход переноса соединен с входом переноса следующего модулярного сумматора, и так далее, наконец, выходы умножителей, в которых происходит умножение на
, а выход переноса соединен с входом переноса следующего модулярного сумматора, и так далее, наконец, выходы умножителей, в которых происходит умножение на 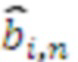 ,
, 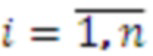 , подключены ко входам модулярного сумматора по модулю
, подключены ко входам модулярного сумматора по модулю 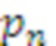 , дополнительно введены модулярный сумматор по модулю
, дополнительно введены модулярный сумматор по модулю 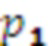 , n умножителей на основания ОПСС
, n умножителей на основания ОПСС 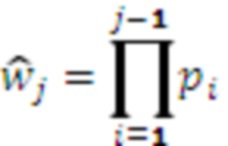 ,
, 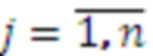 , сумматор с выходом восстановленного числа и модулярный сумматор с входом расширенного основания, причем выход умножителя, в котором происходит умножение на
, сумматор с выходом восстановленного числа и модулярный сумматор с входом расширенного основания, причем выход умножителя, в котором происходит умножение на 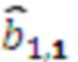 , подключен к входу модулярного сумматора по модулю
, подключен к входу модулярного сумматора по модулю 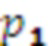 , выход переноса которого подключен ко входу переноса модулярного сумматора по модулю
, выход переноса которого подключен ко входу переноса модулярного сумматора по модулю 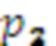 , выходы n модулярных сумматоров по модулю подключены к n соответствующим умножителям на основания ОПСС, выходы которых подключены одновременно ко входам сумматора и модулярного сумматора, выход которого является выходом остатка по расширенному основанию.
, выходы n модулярных сумматоров по модулю подключены к n соответствующим умножителям на основания ОПСС, выходы которых подключены одновременно ко входам сумматора и модулярного сумматора, выход которого является выходом остатка по расширенному основанию.
Сущность изобретения основана на следующем математическом аппарате. В системе остаточных классов любое число 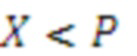 однозначно представляется набором остатков
однозначно представляется набором остатков 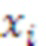 от деления числа
от деления числа 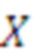 на взаимно простые модули СОК
на взаимно простые модули СОК 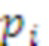 , называемые также основаниями, где
, называемые также основаниями, где 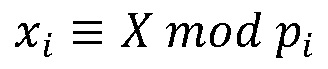 ,
, 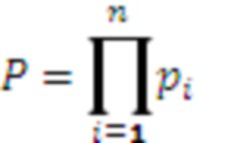 - рабочий диапазон СОК,
- рабочий диапазон СОК, 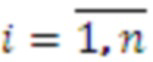 . СОК позволяет выполнять операции сложения и умножения по каждому остатку независимо, без переносов между разрядами, как в позиционной системе счисления. Однако в ряде случаев, например, для обнаружения переполнения диапазона или при обнаружении и исправлении ошибок необходимо добавление одного или нескольких дополнительных модулей. Пусть добавлен модуль
. СОК позволяет выполнять операции сложения и умножения по каждому остатку независимо, без переносов между разрядами, как в позиционной системе счисления. Однако в ряде случаев, например, для обнаружения переполнения диапазона или при обнаружении и исправлении ошибок необходимо добавление одного или нескольких дополнительных модулей. Пусть добавлен модуль 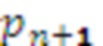 , тогда новый диапазон позволит отображать любое число
, тогда новый диапазон позволит отображать любое число 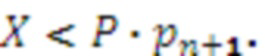 Также в ряде случаев необходимо восстановить позиционное представление числа из системы остаточных классов. Основным методом восстановления числа
Также в ряде случаев необходимо восстановить позиционное представление числа из системы остаточных классов. Основным методом восстановления числа 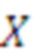 из СОК в позиционную систему счисления является Китайская теорема об остатках
из СОК в позиционную систему счисления является Китайская теорема об остатках
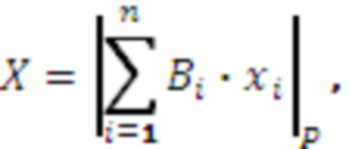
где 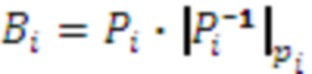 , - ортогональные базисы СОК,
, - ортогональные базисы СОК, 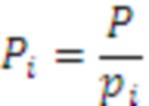 ,
, 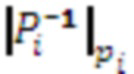 - мультипликативная инверсия. Однако данный метод подразумевает нахождение остатка от деления по большому модулю
- мультипликативная инверсия. Однако данный метод подразумевает нахождение остатка от деления по большому модулю 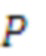 , что является вычислительно сложной задачей.
, что является вычислительно сложной задачей.
Работа устройства основана на следующем алгоритме. Задается система остаточных классов с модулями 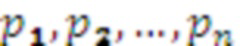 , для которых вычисляют ортогональные базисы СОК
, для которых вычисляют ортогональные базисы СОК 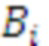 ,
, 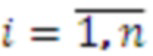 . Вычисляются основания ОПСС
. Вычисляются основания ОПСС 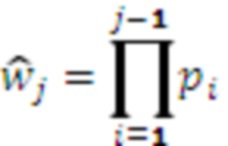 ,
, 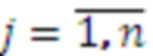 , при этом
, при этом 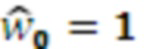 . Ортогональные базисы СОК представляются в ОПСС как вектор значений
. Ортогональные базисы СОК представляются в ОПСС как вектор значений 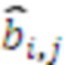 , для которых
, для которых 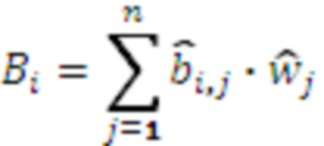 . При этом значения
. При этом значения 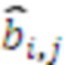 образуют треугольную матрицу.
образуют треугольную матрицу.
Пусть задано число 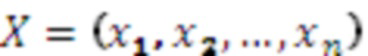 и надо по представлению в СОК
и надо по представлению в СОК 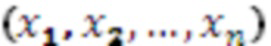 восстановить число
восстановить число 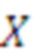 в позиционной системе счисления, а также найти остаток от деления X по дополнительному модулю
в позиционной системе счисления, а также найти остаток от деления X по дополнительному модулю 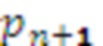 , который будем обозначать
, который будем обозначать 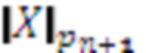 . Для этого
. Для этого 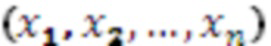 умножается на треугольную матрицу, т.е. находятся
умножается на треугольную матрицу, т.е. находятся 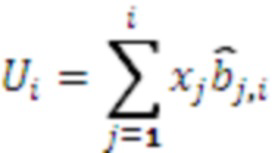 ,
, 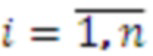 . Затем вычисляются
. Затем вычисляются 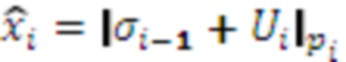 и
и 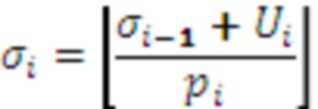 , при этом полагает, что
, при этом полагает, что 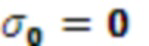 . Можно заменить, что
. Можно заменить, что 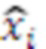 и
и 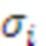 соотносятся как остаток от деления суммы
соотносятся как остаток от деления суммы 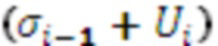 на модуль
на модуль 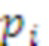 и ранг суммы, т.е. перенос, во сколько раз значение суммы превосходит модуль.
и ранг суммы, т.е. перенос, во сколько раз значение суммы превосходит модуль.
Затем для перевода числа из СОК в позиционную систему счисления находят значение выражения 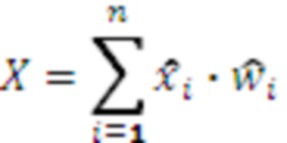 , а для расширения оснований находят
, а для расширения оснований находят 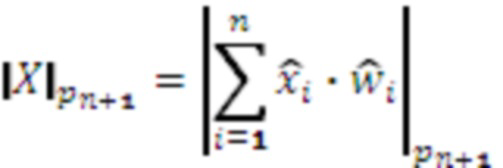 .
.
Рассмотрим пример, иллюстрирующий работу алгоритма. Пусть задана система остаточных классов с 4 основаниями 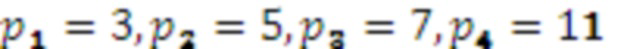 . Тогда
. Тогда 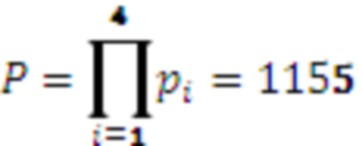 .
.
Вычислим 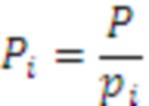 ,
, 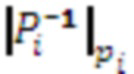 и
и 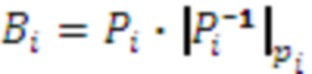 :
:
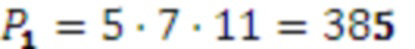 ,
, 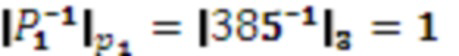 , следовательно
, следовательно 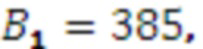
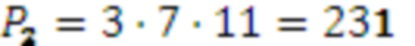 ,
, 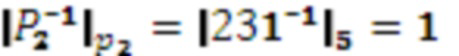 , следовательно
, следовательно 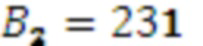 ,
,
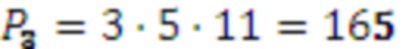 ,
, 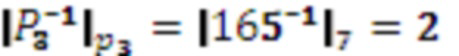 , следовательно
, следовательно 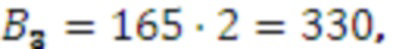
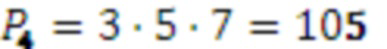 ,
, 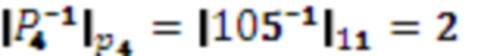 , следовательно
, следовательно 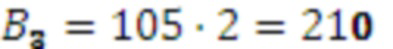 .
.
Вычислим 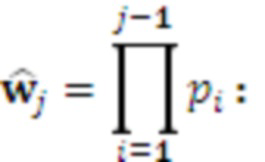
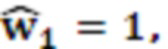
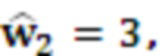
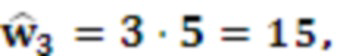
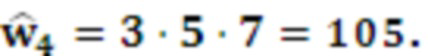
Вычислим представление 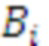 в ОПСС:
в ОПСС:
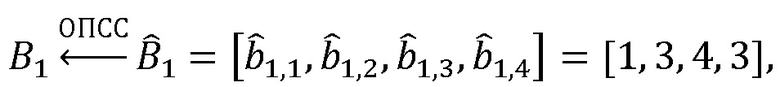 проверка
проверка 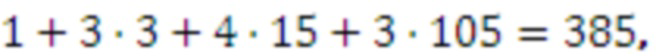
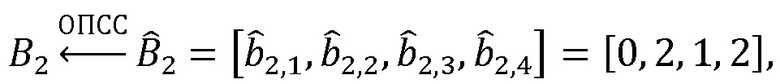 проверка
проверка 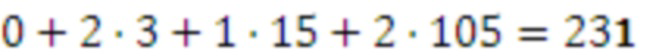 ,
,
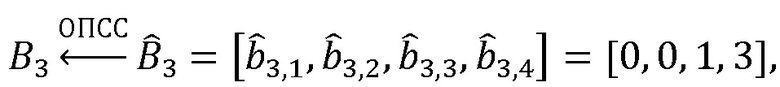 проверка
проверка 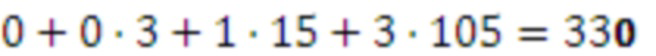 ,
,
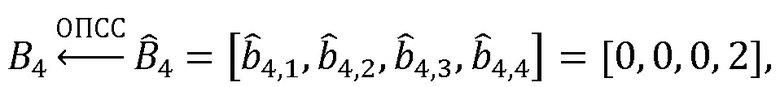 проверка
проверка 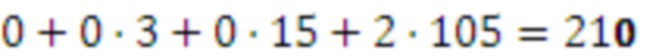 .
.
Пусть задано число числа 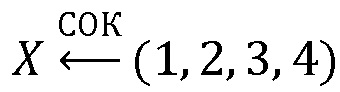 , тогда вычислим
, тогда вычислим 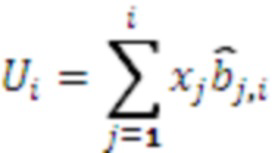 :
:
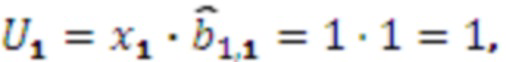
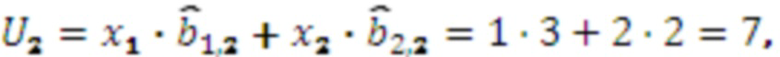
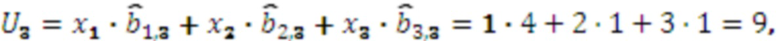
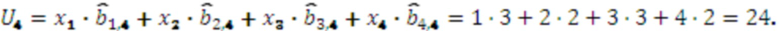
Вычислим 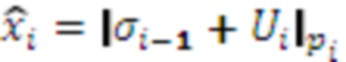 и
и 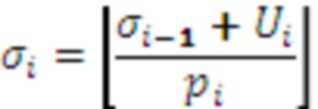 :
:
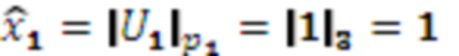 ,
, 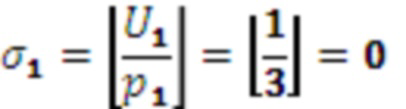 ,
,
 ,
, 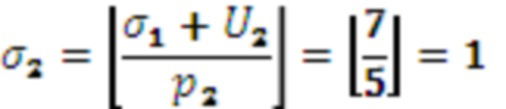 ,
,
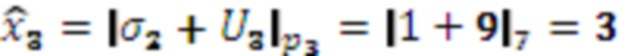 ,
, 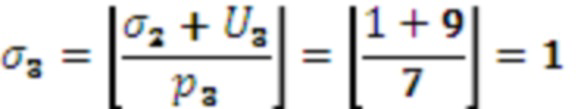 ,
,
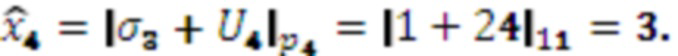
Отсюда получим:
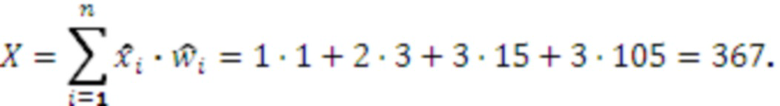
Проверим полученное значение, 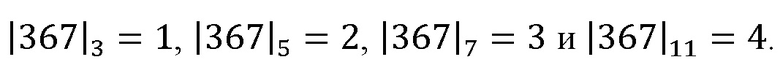
Пусть необходимо расширить основания на 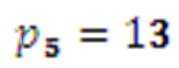 . Тогда
. Тогда
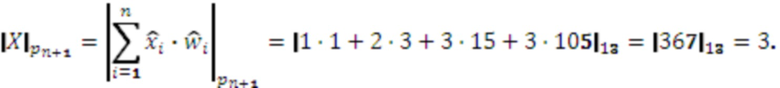
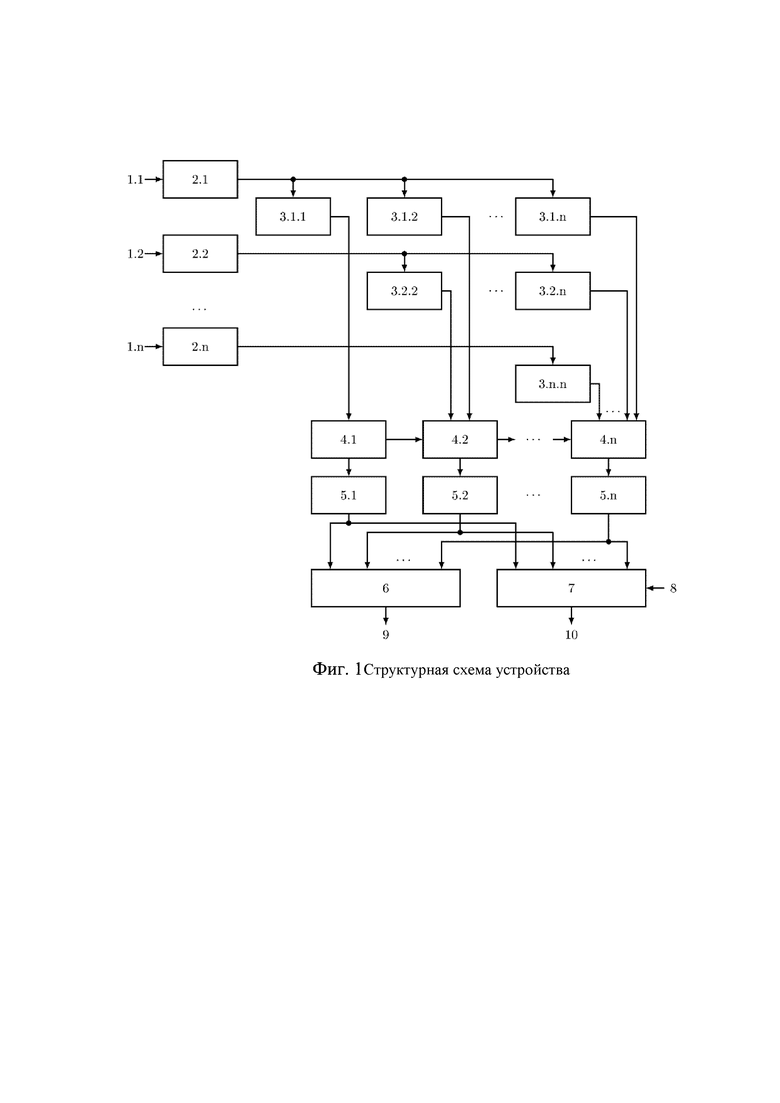
Изобретение поясняется фигурой 1, на которой изображена структурная схема устройства для перевода чисел из системы остаточных классов и расширения оснований. На входы остатков 1.1-1.n, где 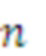 - количество оснований системы остаточных классов подается число
- количество оснований системы остаточных классов подается число 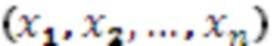 , представленное в СОК. Остатки с соответствующих входов остатков 1.1-1.n записываются в регистры хранения остатков 2.1-2.n, которые в прототипе обозначены как нейроны входного слоя. С выходов регистров хранения остатков 2.1-2.n остатки по соответствующим модулям подаются на умножители 3, которые образуют треугольную матрицу и вычисляют значения произведений остатка на коэффициенты базиса в ОПСС
, представленное в СОК. Остатки с соответствующих входов остатков 1.1-1.n записываются в регистры хранения остатков 2.1-2.n, которые в прототипе обозначены как нейроны входного слоя. С выходов регистров хранения остатков 2.1-2.n остатки по соответствующим модулям подаются на умножители 3, которые образуют треугольную матрицу и вычисляют значения произведений остатка на коэффициенты базиса в ОПСС 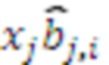 . В прототипе функцию умножителей выполняют нейронные сети конечного кольца, однако помимо умножения остатка на коэффициент ОПСС, в прототипе дополнительно вычисляется остаток от деления по модулю и перенос, обозначающий во сколько раз произведение
. В прототипе функцию умножителей выполняют нейронные сети конечного кольца, однако помимо умножения остатка на коэффициент ОПСС, в прототипе дополнительно вычисляется остаток от деления по модулю и перенос, обозначающий во сколько раз произведение 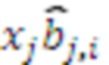 превосходит модуль
превосходит модуль 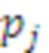 . Выход первого регистра хранения остатка 2.1 по модулю
. Выход первого регистра хранения остатка 2.1 по модулю 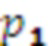 подключен ко входам n умножителей 3.1.1-3.1.n, которые вычисляют значения
подключен ко входам n умножителей 3.1.1-3.1.n, которые вычисляют значения 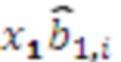 ,
, 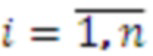 , выход второго регистра хранения остатка 2.2 по модулю
, выход второго регистра хранения остатка 2.2 по модулю 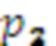 подключен ко входам
подключен ко входам 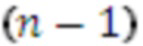 умножителя 3.2.2-3.2.n, которые вычисляют значения
умножителя 3.2.2-3.2.n, которые вычисляют значения 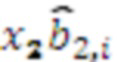 ,
, 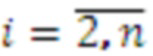 , и так далее, выход n-го регистра хранения остатка 2.n по модулю
, и так далее, выход n-го регистра хранения остатка 2.n по модулю 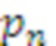 подключен ко входу умножителя 3.n.n, который вычисляет значение
подключен ко входу умножителя 3.n.n, который вычисляет значение 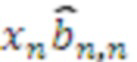 . Выходы умножителей 3 подключены ко входам n модулярных сумматоров 4 по модулям
. Выходы умножителей 3 подключены ко входам n модулярных сумматоров 4 по модулям 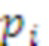 ,
, 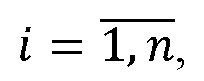 при этом выход умножителя 3.1.1 подключен ко входу первого модулярного сумматора 4.1 по модулю
при этом выход умножителя 3.1.1 подключен ко входу первого модулярного сумматора 4.1 по модулю 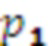 и выполняет вычисления
и выполняет вычисления 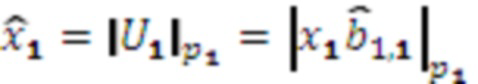 ,
, 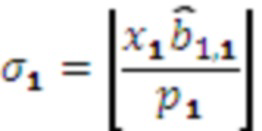 , значение
, значение 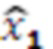 поступает на выход первого модулярного сумматора 4.1 по модулю
поступает на выход первого модулярного сумматора 4.1 по модулю 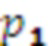 , значение
, значение 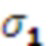 поступает на выход переноса первого модулярного сумматора 4.1 по модулю
поступает на выход переноса первого модулярного сумматора 4.1 по модулю 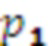 , выходы умножителей 3.1.2 и 3.2.2 подключены ко входам второго модулярного сумматора 4.2 по модулю
, выходы умножителей 3.1.2 и 3.2.2 подключены ко входам второго модулярного сумматора 4.2 по модулю 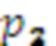 , вход переноса которого подключен к выходу переноса первого модулярного сумматора 4.1 по модулю
, вход переноса которого подключен к выходу переноса первого модулярного сумматора 4.1 по модулю 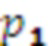 , и выполняет вычисления
, и выполняет вычисления 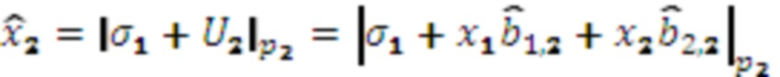 ,
, 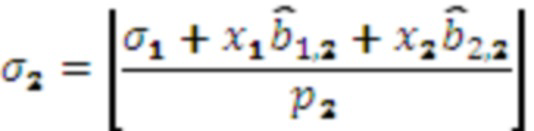 , значение
, значение 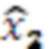 поступает на выход второго модулярного сумматора 4.2 по модулю
поступает на выход второго модулярного сумматора 4.2 по модулю 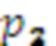 , значение
, значение 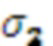 поступает на выход переноса второго модулярного сумматора 4.2 по модулю
поступает на выход переноса второго модулярного сумматора 4.2 по модулю 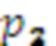 , и так далее, выходы умножителей 3.i.n,
, и так далее, выходы умножителей 3.i.n, 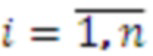 , подключены ко входам n-го модулярного сумматора 4.n по модулю
, подключены ко входам n-го модулярного сумматора 4.n по модулю 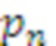 , вход переноса которого подключен к выходу переноса (n-1)-го модулярного сумматора 4.n-1 по модулю
, вход переноса которого подключен к выходу переноса (n-1)-го модулярного сумматора 4.n-1 по модулю 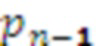 , и выполняет вычисления
, и выполняет вычисления 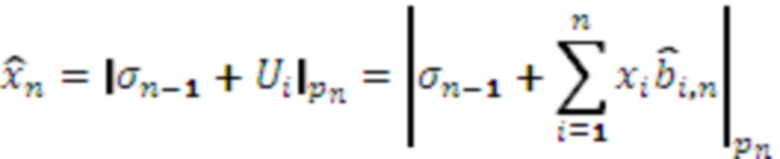 ,
, 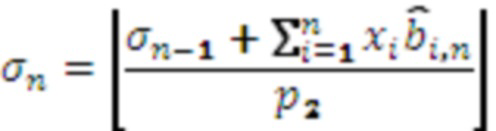 , значение
, значение 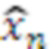 поступает на выход n-го модулярного сумматора 4.n по модулю
поступает на выход n-го модулярного сумматора 4.n по модулю 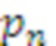 , значение
, значение 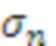 поступает на выход переноса n-го модулярного сумматора 4.n по модулю
поступает на выход переноса n-го модулярного сумматора 4.n по модулю 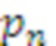 , который не подключен к другим элементам. Значения
, который не подключен к другим элементам. Значения 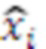 c выходов i-х модулярных сумматоров 4.i по модулю
c выходов i-х модулярных сумматоров 4.i по модулю 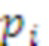 подаются на входы i-x умножителей 5.i на основания ОПСС,
подаются на входы i-x умножителей 5.i на основания ОПСС, 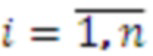 , в которых происходит умножение
, в которых происходит умножение 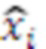 на
на 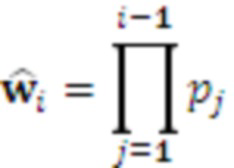 . Выход i-го умножителя 5.i на основания ОПСС подключен к i-м входам сумматора 6 и модулярного сумматора 7,
. Выход i-го умножителя 5.i на основания ОПСС подключен к i-м входам сумматора 6 и модулярного сумматора 7, 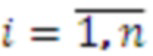 , на вход расширенного основания 8 модулярного сумматора 7 подается значение модуля
, на вход расширенного основания 8 модулярного сумматора 7 подается значение модуля 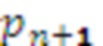 , на выход восстановленного числа 9 сумматора 6 подается восстановленное число X в позиционной системе счисления, а на выход остатка по расширенному основанию 10 модулярного сумматора 7 значение числа по расширенному основанию, т.е.
, на выход восстановленного числа 9 сумматора 6 подается восстановленное число X в позиционной системе счисления, а на выход остатка по расширенному основанию 10 модулярного сумматора 7 значение числа по расширенному основанию, т.е. 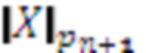 .
.
На основе предыдущего примера рассмотрим работу устройства. n=4, 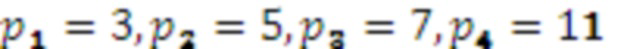 . На входы остатков 1.1-1.4 подаются значения (1,2,3,4), которые затем записываются в регистры хранения остатка 2.1-2.4 по соответствующим модулям. Значение 1 с выхода регистра хранения остатка 2.1 по модулю
. На входы остатков 1.1-1.4 подаются значения (1,2,3,4), которые затем записываются в регистры хранения остатка 2.1-2.4 по соответствующим модулям. Значение 1 с выхода регистра хранения остатка 2.1 по модулю 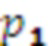 одновременно поступает на входы умножителя 3.1.1, где происходит умножение остатка
одновременно поступает на входы умножителя 3.1.1, где происходит умножение остатка 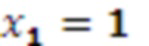 , на первый коэффициент базиса
, на первый коэффициент базиса 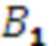 в ОПСС
в ОПСС 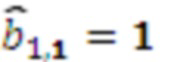 , результат умножения
, результат умножения 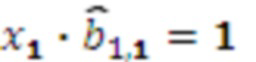 , умножителя 3.1.2, где происходит умножение на
, умножителя 3.1.2, где происходит умножение на 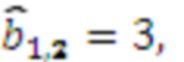 результат умножения
результат умножения 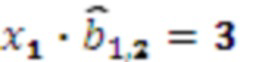 , умножителя 3.1.3, где происходит умножение на
, умножителя 3.1.3, где происходит умножение на 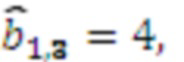 результат умножения
результат умножения 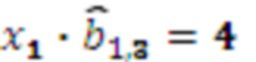 , умножителя 3.1.4, где происходит умножение на
, умножителя 3.1.4, где происходит умножение на 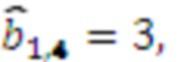 результат умножения
результат умножения 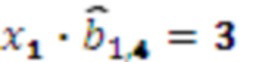 . Значение 2 с выхода регистра хранения остатка 2.2 по модулю
. Значение 2 с выхода регистра хранения остатка 2.2 по модулю 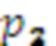 одновременно поступает на входы умножителя 3.2.2, где происходит умножение остатка
одновременно поступает на входы умножителя 3.2.2, где происходит умножение остатка 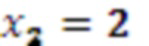 , на второй коэффициент базиса
, на второй коэффициент базиса 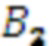 в ОПСС
в ОПСС 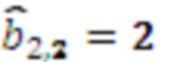 , результат умножения
, результат умножения 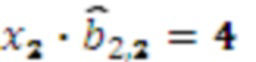 , умножителя 3.2.3, где происходит умножение на
, умножителя 3.2.3, где происходит умножение на 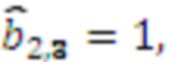 результат умножения
результат умножения 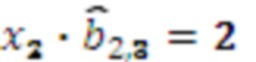 , умножителя 3.2.4, где происходит умножение на
, умножителя 3.2.4, где происходит умножение на 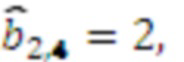 результат умножения
результат умножения 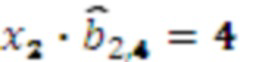 . Значение 3 с выхода регистра хранения остатка 2.3 по модулю
. Значение 3 с выхода регистра хранения остатка 2.3 по модулю 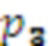 одновременно поступает на входы умножителя 3.3.3, где происходит умножение остатка
одновременно поступает на входы умножителя 3.3.3, где происходит умножение остатка 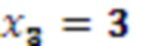 , на третий коэффициент базиса
, на третий коэффициент базиса 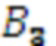 в ОПСС
в ОПСС 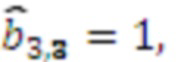 результат умножения
результат умножения 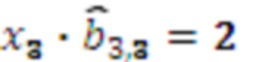 , умножителя 3.3.4, где происходит умножение на
, умножителя 3.3.4, где происходит умножение на 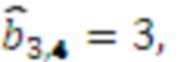 результат умножения
результат умножения 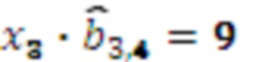 . Значение 4 с выхода регистра хранения остатка 2.4 по модулю
. Значение 4 с выхода регистра хранения остатка 2.4 по модулю 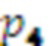 поступает на вход умножителя 3.4.4, где происходит умножение остатка
поступает на вход умножителя 3.4.4, где происходит умножение остатка 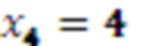 , на четвертый коэффициент базиса
, на четвертый коэффициент базиса 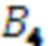 в ОПСС
в ОПСС 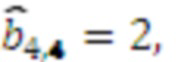 результат умножения
результат умножения 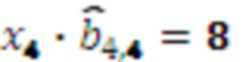 . Значения коэффициентов ОПСС
. Значения коэффициентов ОПСС 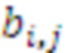 зависят только от заданной СОК и могут быть записаны в память.
зависят только от заданной СОК и могут быть записаны в память.
Далее значение 1 с умножителя 3.1.1 поступает на первый модулярный сумматор 4.1 по модулю 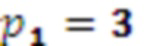 . Поскольку
. Поскольку 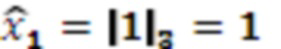 и
и 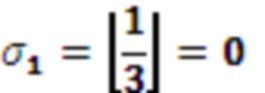 , на выход модулярного сумматора 4.1 подается 1, а на выход переноса 0.
, на выход модулярного сумматора 4.1 подается 1, а на выход переноса 0.
Значение 3 с умножителя 3.1.2, значение 4 с умножителя 3.2.2 и значение 0 с выхода переноса модулярного сумматора 4.1 поступают на второй модулярный сумматор 4.2 по модулю 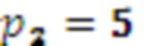 . Поскольку
. Поскольку 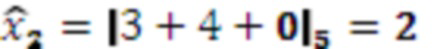 и
и 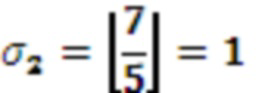 , на выход модулярного сумматора 4.2 подается 2, а на выход переноса 1.
, на выход модулярного сумматора 4.2 подается 2, а на выход переноса 1.
Значение 4 с умножителя 3.1.3, значение 2 с умножителя 3.2.3, значение 3 с умножителя 3.3.3 и значение 1 с выхода переноса модулярного сумматора 4.2 поступают на третий модулярный сумматор 4.3 по модулю 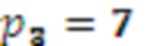 . Поскольку
. Поскольку 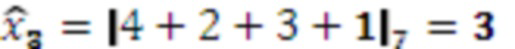 и
и 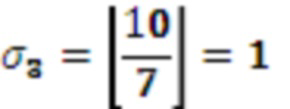 , на выход модулярного сумматора 4.3 подается 3, а на выход переноса 1.
, на выход модулярного сумматора 4.3 подается 3, а на выход переноса 1.
Значение 3 с умножителя 3.1.4, значение 4 с умножителя 3.2.4, значение 9 с умножителя 3.3.4, значение 8 с умножителя 3.4.4 и значение 1 с выхода переноса модулярного сумматора 4.3 поступают на четвертый модулярный сумматор 4.4 по модулю 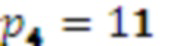 . Поскольку
. Поскольку 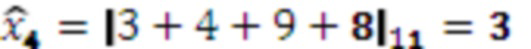 , на выход модулярного сумматора 4.4 подается 3.
, на выход модулярного сумматора 4.4 подается 3.
Значение 1 с выхода модулярного сумматора 4.1 поступает на вход умножителя 5.1 на основания ОПСС, где умножается на 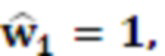 на выход умножителя 5.1 подается 1. Значение 2 с выхода модулярного сумматора 4.2 поступает на вход умножителя 5.2 на основания ОПСС, где умножается на
на выход умножителя 5.1 подается 1. Значение 2 с выхода модулярного сумматора 4.2 поступает на вход умножителя 5.2 на основания ОПСС, где умножается на 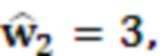 на выход умножителя 5.2 подается 6. Значение 3 с выхода модулярного сумматора 4.3 поступает на вход умножителя 5.3 на основания ОПСС, где умножается на
на выход умножителя 5.2 подается 6. Значение 3 с выхода модулярного сумматора 4.3 поступает на вход умножителя 5.3 на основания ОПСС, где умножается на 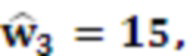 на выход умножителя 5.3 подается 45. Значение 3 с выхода модулярного сумматора 4.4 поступает на вход умножителя 5.4 на основания ОПСС, где умножается на
на выход умножителя 5.3 подается 45. Значение 3 с выхода модулярного сумматора 4.4 поступает на вход умножителя 5.4 на основания ОПСС, где умножается на 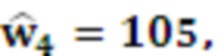 на выход умножителя 5.4 подается 315. При этом основания ОПСС
на выход умножителя 5.4 подается 315. При этом основания ОПСС  зависят только от модулей СОК и могут быть записаны в память.
зависят только от модулей СОК и могут быть записаны в память.
Значения с выходов умножителей 5.1-5.4 на основания ОПСС поступают на входы сумматора 6, где происходит сложение 1+6+45+315=367, результат которого подается на выход 9 восстановленного числа. Одновременно значения с выходов умножителей 5.1-5.4 на основания ОПСС поступают на входы модулярного сумматора 7, на вход 8 расширенного модуля которого поступает значение 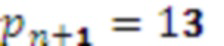 . В модулярном сумматоре вычисляется сложение по модулю
. В модулярном сумматоре вычисляется сложение по модулю 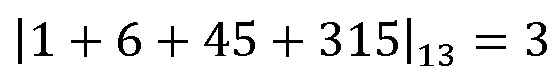 , результат которого подается на выход 10 остатка по расширенному основанию.
, результат которого подается на выход 10 остатка по расширенному основанию.
Можно заметить, что при реализации устройства отсутствует ресурсоемкая операция нахождения остатка по большому модулю 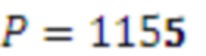 . Также в отличие от прототипа сокращено количество умножителей 3 и упрощены реализуемые ими функции. За счет введения входа 8 расширенного основания устройство позволяет вычислить остаток по произвольному расширенному основанию, а введение сумматора 6 позволяет получить позиционное представление числа.
. Также в отличие от прототипа сокращено количество умножителей 3 и упрощены реализуемые ими функции. За счет введения входа 8 расширенного основания устройство позволяет вычислить остаток по произвольному расширенному основанию, а введение сумматора 6 позволяет получить позиционное представление числа.
Реализация всего устройства возможна с использованием программируемых логических интегральных схем (ПЛИС) и может использоваться как отдельное устройство, так и как сопроцессор для выполнения немодульных операций.
| название | год | авторы | номер документа |
|---|---|---|---|
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| Система распределенного хранения данных | 2021 |
|
RU2780148C1 |
| Система надежного облачного хранения с регулируемой избыточностью данных | 2021 |
|
RU2782681C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ВЫЧИСЛЕНИЯ ПОЗИЦИОННЫХ ХАРАКТЕРИСТИК НЕПОЗИЦИОННОГО КОДА | 2003 |
|
RU2257615C2 |
| НЕЙРОННАЯ СЕТЬ С ПОРОГОВОЙ (k, t) СТРУКТУРОЙ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2008 |
|
RU2380751C1 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ОБНАРУЖЕНИЯ, ЛОКАЛИЗАЦИИ И ИСПРАВЛЕНИЯ ОШИБОК В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2301442C2 |
| НЕЙРОННАЯ СЕТЬ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2008 |
|
RU2400813C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ДЕЛЕНИЯ ЧИСЕЛ, ПРЕДСТАВЛЕННЫХ В СИСТЕМЕ ОСТАТОЧНЫХ КЛАССОВ | 2005 |
|
RU2305312C2 |
| УСТРОЙСТВО ДЛЯ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2013 |
|
RU2559771C2 |
Изобретение относится к вычислительной технике и может быть использовано в системах связи и обработки информации, функционирующих в системе остаточных классов (СОК). Техническим результатом заявляемого изобретения является расширение функциональных возможностей, а именно возможность получить остаток от деления по произвольному дополнительному модулю, а также восстановленное число в позиционной системе счисления. Данный технический результат достигается тем, что в устройство для перевода чисел из системы остаточных классов и расширения оснований с модулями 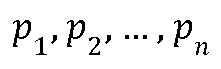 , содержащее n входов остатков, выход остатка по расширенному основанию, n регистров хранения остатков, (n-1) модулярный сумматор по модулю, треугольную матрицу из
, содержащее n входов остатков, выход остатка по расширенному основанию, n регистров хранения остатков, (n-1) модулярный сумматор по модулю, треугольную матрицу из 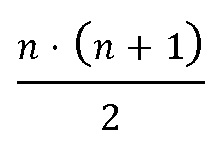 умножителей, где умножители производят умножение на коэффициенты
умножителей, где умножители производят умножение на коэффициенты 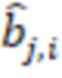 ортогональных базисов
ортогональных базисов 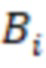 системы остаточных классов (СОК), где
системы остаточных классов (СОК), где 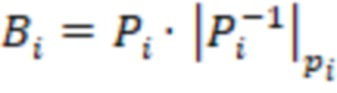 ,
, 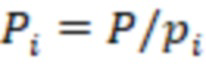 ,
, 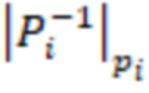 – мультипликативная инверсия,
– мультипликативная инверсия, 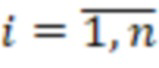 ,
, 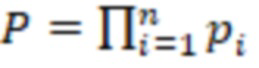 - рабочий диапазон СОК, представленных в обобщенной позиционной системе счисления (ОПСС) с основаниями
- рабочий диапазон СОК, представленных в обобщенной позиционной системе счисления (ОПСС) с основаниями 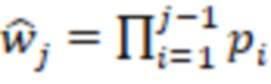 ,
, 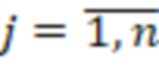 , дополнительно ввели модулярный сумматор по модулю
, дополнительно ввели модулярный сумматор по модулю 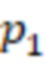 , n умножителей на основания ОПСС
, n умножителей на основания ОПСС 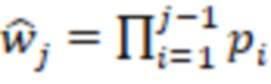 ,
, 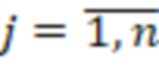 , сумматор с выходом восстановленного числа и модулярный сумматор с входом расширенного основания. 1 ил.
, сумматор с выходом восстановленного числа и модулярный сумматор с входом расширенного основания. 1 ил.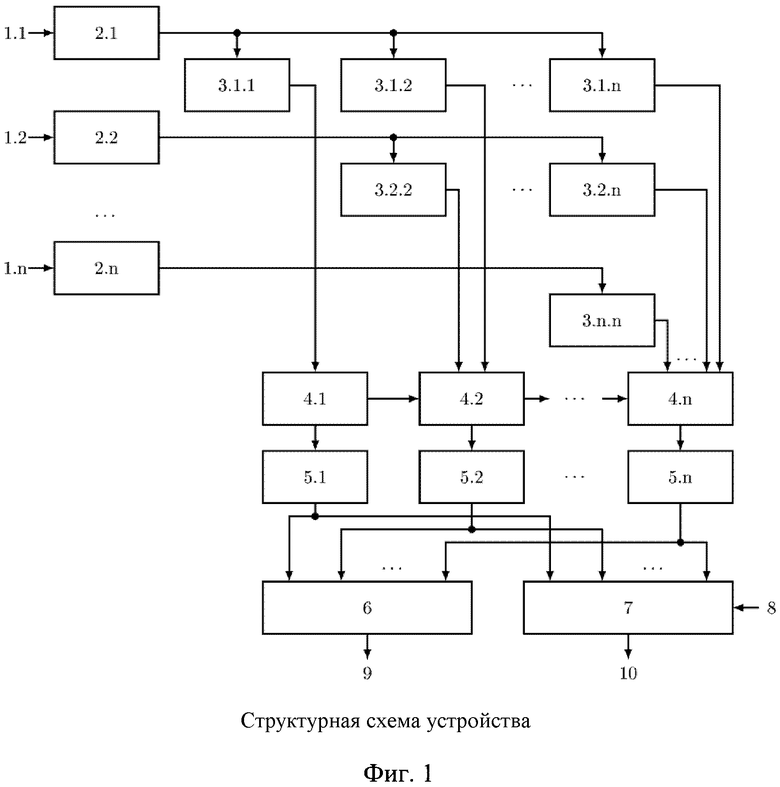
Устройство для перевода чисел из системы остаточных классов и расширения оснований с модулями 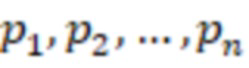 , содержащее n входов остатков, выход остатка по расширенному основанию, n регистров хранения остатков, (n-1) модулярный сумматор по модулю, треугольную матрицу из
, содержащее n входов остатков, выход остатка по расширенному основанию, n регистров хранения остатков, (n-1) модулярный сумматор по модулю, треугольную матрицу из 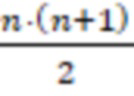 умножителей, где умножители производят умножение на коэффициенты
умножителей, где умножители производят умножение на коэффициенты 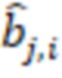 ортогональных базисов
ортогональных базисов 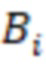 системы остаточных классов (СОК), где
системы остаточных классов (СОК), где 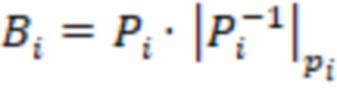 ,
, 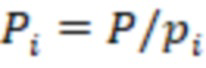 ,
, 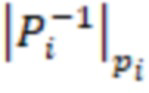 – мультипликативная инверсия,
– мультипликативная инверсия, 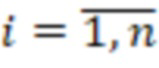 ,
, 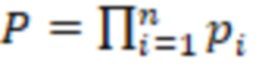 - рабочий диапазон СОК, представленных в обобщенной позиционной системе счисления (ОПСС) с основаниями
- рабочий диапазон СОК, представленных в обобщенной позиционной системе счисления (ОПСС) с основаниями 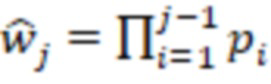 ,
, 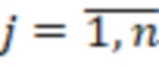 , причем входы остатков соединены с соответствующими регистрами хранения остатков, выход первого регистра хранения остатка одновременно подключен к n умножителям, в которых происходит умножение на коэффициенты
, причем входы остатков соединены с соответствующими регистрами хранения остатков, выход первого регистра хранения остатка одновременно подключен к n умножителям, в которых происходит умножение на коэффициенты 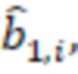
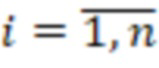 , выход второго регистра хранения остатка одновременно подключен к (n-1) умножителю, в которых происходит умножение на коэффициенты
, выход второго регистра хранения остатка одновременно подключен к (n-1) умножителю, в которых происходит умножение на коэффициенты 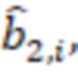
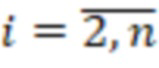 и так далее, наконец, выход n-го регистра хранения остатка подключен к умножителю, в котором происходит умножение на коэффициенты
и так далее, наконец, выход n-го регистра хранения остатка подключен к умножителю, в котором происходит умножение на коэффициенты 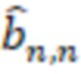 , выходы умножителей, в которых происходит умножение на
, выходы умножителей, в которых происходит умножение на 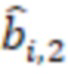 ,
, 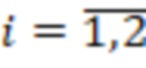 , подключены к входам модулярного сумматора по модулю
, подключены к входам модулярного сумматора по модулю 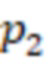 , выход переноса которого подключен к входу переноса модулярного сумматора по модулю
, выход переноса которого подключен к входу переноса модулярного сумматора по модулю 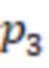 , на входы которого поступают значения с выходов умножителей, в которых происходит умножение на
, на входы которого поступают значения с выходов умножителей, в которых происходит умножение на 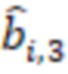 ,
, 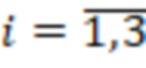 , а выход переноса соединен с входом переноса следующего модулярного сумматора и так далее, наконец, выходы умножителей, в которых происходит умножение на
, а выход переноса соединен с входом переноса следующего модулярного сумматора и так далее, наконец, выходы умножителей, в которых происходит умножение на 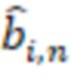 ,
, 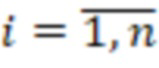 , подключены к входам модулярного сумматора по модулю
, подключены к входам модулярного сумматора по модулю 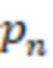 , отличающееся тем, что в него введены модулярный сумматор по модулю
, отличающееся тем, что в него введены модулярный сумматор по модулю 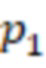 , n умножителей на основания ОПСС
, n умножителей на основания ОПСС 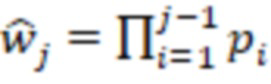 ,
, 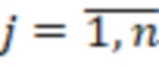 , сумматор с выходом восстановленного числа и модулярный сумматор с входом расширенного основания, причем выход умножителя, в котором происходит умножение на
, сумматор с выходом восстановленного числа и модулярный сумматор с входом расширенного основания, причем выход умножителя, в котором происходит умножение на 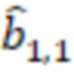 , подключен к входу модулярного сумматора по модулю
, подключен к входу модулярного сумматора по модулю 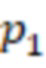 , выход переноса которого подключен к входу переноса модулярного сумматора по модулю
, выход переноса которого подключен к входу переноса модулярного сумматора по модулю 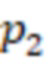 , выходы n модулярных сумматоров по модулю подключены к n соответствующим умножителям на основания ОПСС, выходы которых подключены одновременно к входам сумматора и модулярного сумматора, выход которого является выходом остатка по расширенному основанию.
, выходы n модулярных сумматоров по модулю подключены к n соответствующим умножителям на основания ОПСС, выходы которых подключены одновременно к входам сумматора и модулярного сумматора, выход которого является выходом остатка по расширенному основанию.
| НЕЙРОННАЯ СЕТЬ ДЛЯ РАСШИРЕНИЯ КОРТЕЖА ЧИСЛОВОЙ СИСТЕМЫ ВЫЧЕТОВ | 2003 |
|
RU2256226C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЕЛ ИЗ СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В ПОЗИЦИОННУЮ СИСТЕМУ СЧИСЛЕНИЯ | 2004 |
|
RU2275741C2 |
| УСТРОЙСТВО ДЛЯ ПРЕОБРАЗОВАНИЯ ЧИСЕЛ ИЗ КОДА СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ В ПОЛИАДИЧЕСКИЙ КОД | 2001 |
|
RU2187886C1 |
| US 6049858 A, 11.04.2000 | |||
| Накидная гайка | 1981 |
|
SU992885A1 |
Авторы
Даты
2021-03-16—Публикация
2020-06-22—Подача