Настоящее изобретение относится к области радиоэлектроники, а именно к способам обработки и обнаружения сигнала на фоне помех. Задача, на решение которой направлено заявленное изобретение, заключается в реализации разработки оптимального метода обнаружения гидроакустического сигнала в условиях помех, описываемых нелинейными стохастическими уравнениями, минимизирующего ошибку оценивания процесса. Поставленная задача решается за счет того, что в заявленном способе нелинейная функция представляется через сплайны, что дает возможность проводить линейную обработку на каждом интервале и представлять нелинейный алгоритм как композицию линейного фильтра Калмана-Бьюси, оцениваемого по критерию минимума среднего квадрата ошибки.
Достигаемый технический результат заключается в повышения точности оценки помехи и эффективности обнаружения сигнала на ее фоне и в универсальности обработки при различных помехах. Возможность работы в реальном масштабе времени, получение более эффективного алгоритма фильтрации, требующего меньше вычислительных затрат, обуславливают высокую экономическую выгоду, которая может быть использована при внедрении в систему обработки гидроакустических сигналов.
На сегодняшний день приближенные решения уравнений фильтрации основаны на аппроксимации решения - апостериорной плотности вероятности некоторой функцией из параметризованного класса, при этом используют нормальную плотность вероятности [1]. Однако в ряде случаев апостериорная плотность вероятности существенно отличается от нормальной (к примеру, процесс ближней реверберации) и при возникновении больших ошибок фильтрации (малое отношение сигнал-шум, помеха-шум) требуются более точные приближения. С этой точки зрения особенно привлекательными являются аппроксимации, основанные на сплайновых представлениях, так как при их применении никаких допущений по поводу законов распределений не делается.
Известен метод кусочного разложения оценок (патент №2257610), который основан на разбиении исходной дискретной реализации на прикрывающиеся интервалы одинаковой длины, с последующей оценкой на каждом из них полезного сигнала (аналог) [2, с. 4-10]. Исходя из данного метода, предполагается, что полезный сигнал описывается некоторой кусочно-непрерывной гладкой функцией, которая удовлетворяет условиям теоремы Вейерштрассе об аппроксимации на локальных отрезках. Такой подход позволяет получить множество оценок полезной составляющей в каждом сечении процесса с последующим их усреднением. Использование системы ортогональных многочленов при решении задачи аппроксимации позволяет получить общее решение задачи оценки сигнала и обрабатывать одномерные дискретные реализации сигналов в условиях непараметрической априорной неопределенности, что делает метод сплайн-фильтрации по сравнению с методом кусочного разложения оценок более универсальным.
Существует способ сплайн-фильтрации сигналов (патент №2651640), основывается на методе условной марковской фильтрации, который включает в себя: решение уравнений фильтрации для гипотезы наличия/отсутствия сигнала; уравнения правдоподобия; уравнения для вычисления коэффициентов усиления (прототип) [3]. Отличительной особенностью способа сплайн-фильтрации является то, что для получения оценок помехи, которая не является гауссовской и описывается стохастическим дифференциальным уравнением состояния, дополнительно используется сплайн-интерполяция нелинейной функции, а область динамического диапазона изменений нелинейной функции разбивается на интервалы, в каждом из которых реализуется линейное представление уравнения состояния, что позволяет на каждом из поддиапазонов реализовать фильтр Калмана-Бьюси, включающего в себя: два уравнения оценки состояния при гипотезах наличия/отсутствия сигнала; уравнения оценки дисперсии на различных интервалах и уравнения правдоподобия, включающего эти оценки, и по результатам вычисления которого выносится решение об обнаружении или не обнаружении сигнала [4, 5]. Аппроксимация проводится по узловым точкам, т.е. в точках, где значение нелинейной функции и ее аппроксиманта кусочно-линейной функции совпадают. Способ сплайн фильтрации представлен на фиг. 1, где:
блок 1 - блок определения узловых точек на интервале;
блок 2 - блок формирования системы интервалов;
блок 3 - блок сравнения оценки помехи с системой интервалов;
блок 4 - блок определения значения оценки помехи [х*(1)];
блок 5 - блок определения величины коэффициента [ai];
блок 6 - блок определения величины коэффициента [bi];
блок 7 - блок усиления на коэффициент 
блоки 8, 12, 26 - интеграторы;
блоки 9, 13, 21 - квадраторы;
блок 10 - блок усиления на коэффициент 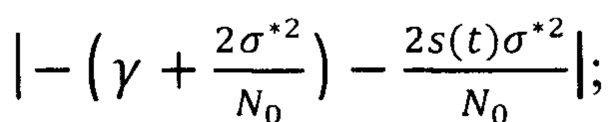
блоки 11, 15, 22 - блоки усиления на коэффициент [-1];
блок 14 - блок усиления на коэффициент 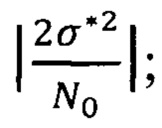
блоки 16, 19 - блоки усиления на коэффициент [2];
блоки 17, 20 - перемножители;
блок 18 - блок формирования опорного сигнала;
блок 25 - блок усиления на коэффициент 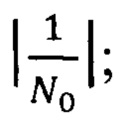
блок 27 - двухпороговое устройство;
блок 28 - однопороговое устройство;
блоки 29, 32 - блоки принятия решения при гипотезе наличия сигнала;
блок 30 - блок принятия решения при гипотезе отсутствия сигнала;
блок 31 - блок, реализующий продолжение наблюдения.
блок 23 - блок вычисления значения следующей оценки помехи [х*(2)];
блок 24 - блок вычисления значения следующей оценки помехи [x*(3)];
Повышение точности аппроксимации сплайн-функциями достигается за счет снижения ошибки оценивания наблюдаемого процесса на этапе его представления линейным сплайном на каждом интервале линеаризации. Когда оцениваемый процесс описывается стохастической динамической системой вида:
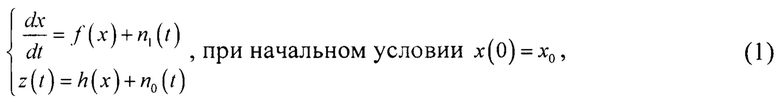
и ограничениях вида:
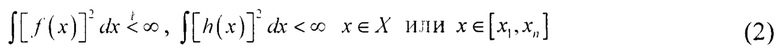
где: ƒ(.), h(.) - нелинейные функции ∈ L2.
Тогда представление НДС (1) может быть аппроксимировано системой дифференциальных уравнений вида:

Соответствующее уравнение фильтрации обнаружения будет иметь вид:
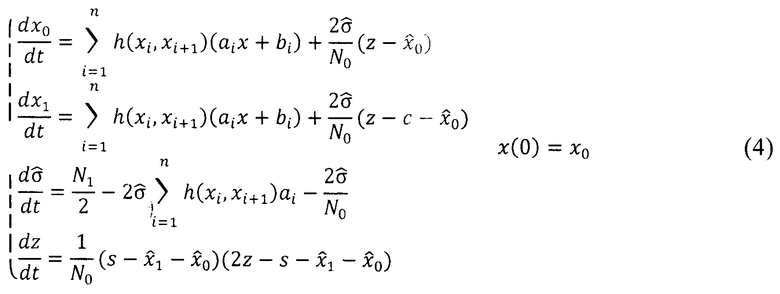
Тогда исходя из того, что в каждом интервале фильтр является линейным фильтром Калмана-Бьюси и удовлетворяет условиям устойчивости [11], а ошибки в целом и локально меньше пороговых, то из этого следует, что сплайн-аппроксимация является устойчивой.
Отличительной особенностью предлагаемого способа по сравнению с прототипом, является выбор коэффициентов ai, bi. В прототипе коэффициенты ai, bi, определяются через узловые точки, которые определяются с помощью интерполяционных многочленов Ньютона или Лагранжа. Недостатком такого подхода является то, что ошибка аппроксимации нелинейной функции определяется не через оптимальную процедуру, а только фактом совпадения нелинейной функции и линейного сплайна в узловых точках, что вполне приемлемо, если бы на перестройку коэффициентов фильтра Калмана-Бьюси влияли разрывы 1-го рода, аппроксимирующей функции. Но так как разрывы не влияют, так как коэффициенты всегда меняются скачкообразно. Поэтому нет необходимости накладывать столь жесткое условие на аппроксимирующую функцию, как ее непрерывность. Последнее позволяет находить коэффициенты ai, bi независимо в каждом интервале (секции) используя критерий минимизации ошибки.
Определим оптимальные значения коэффициентов ai, bi, которые выбираются в каждой секции (интервал [xi, xi+1]), исходя из критерия минимума среднего квадрата ошибки. При расчете коэффициентов для решения выражения (3) произведем следующие вычисления:
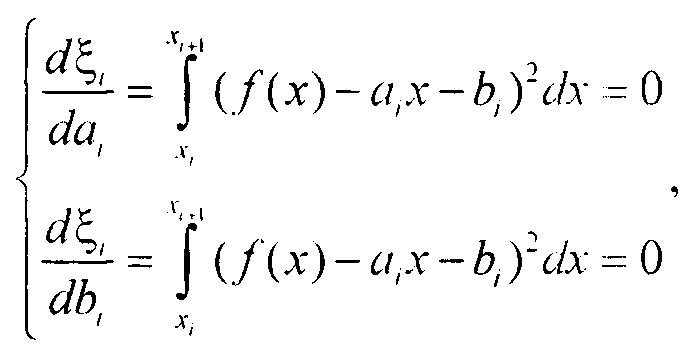
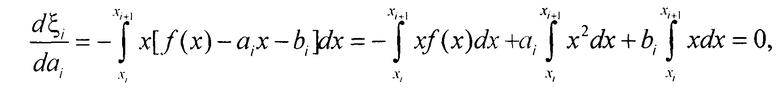
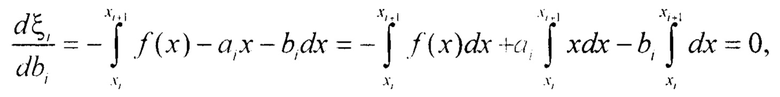
Таким образом, для [xi, xi+i] имеем
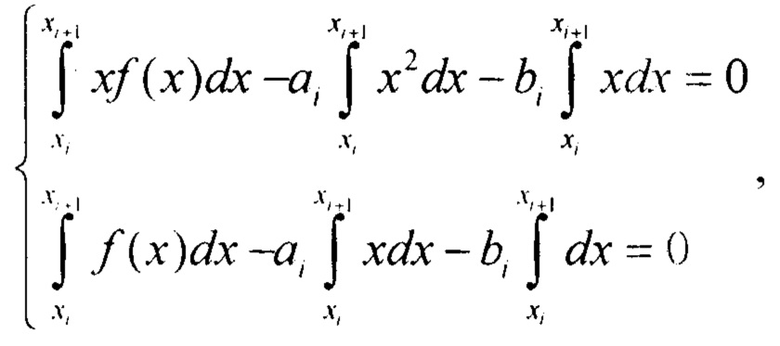
Обозначим:
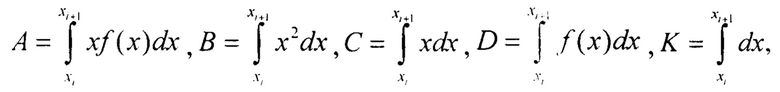
Тогда:
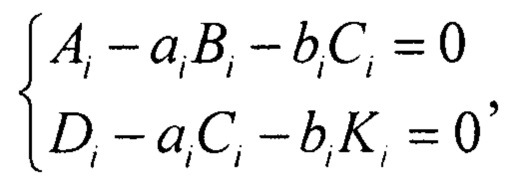
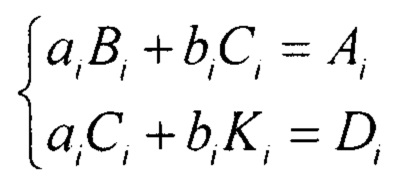
Воспользуемся методом Крамера и тогда:

Значение ошибки в каждой секции будет иметь следующий вид:
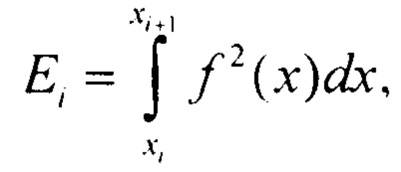
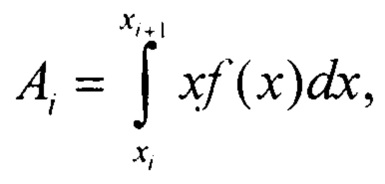

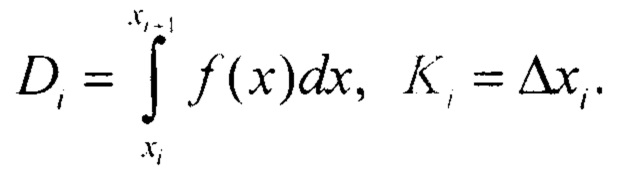
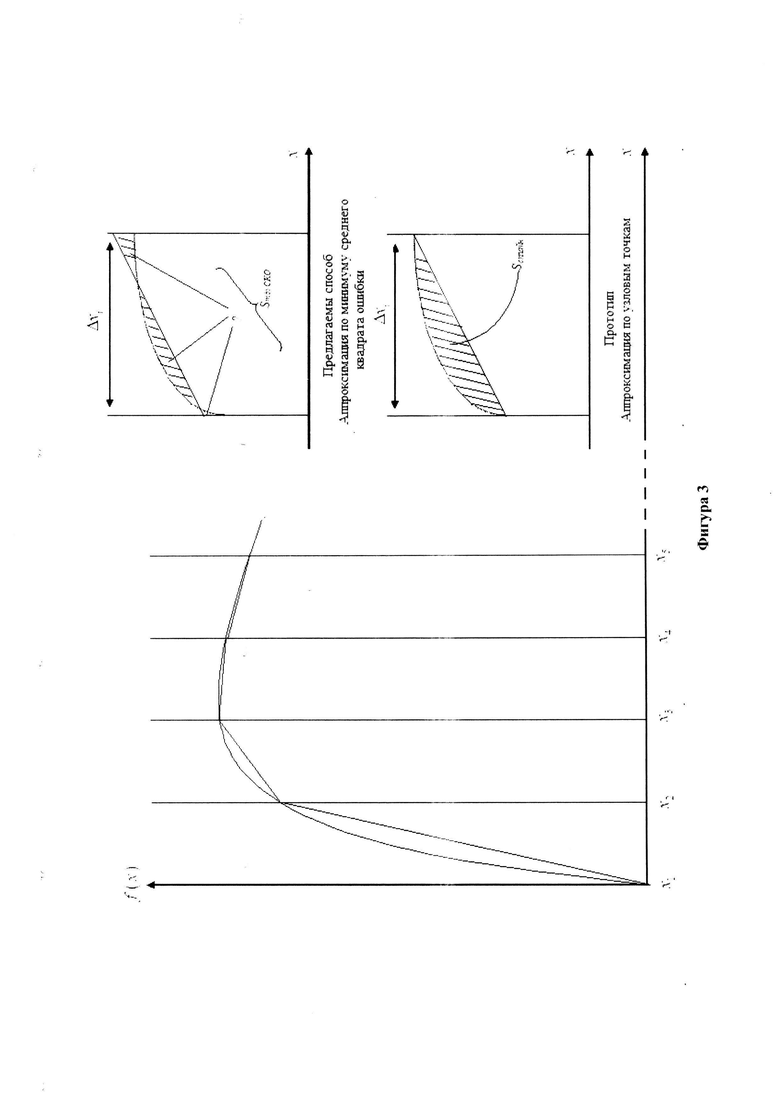
В прототипе нелинейная функция аппроксимировалась линейной функцией по точкам, а значение ошибки рассчитывалось по формуле (фигура 3) [10]:
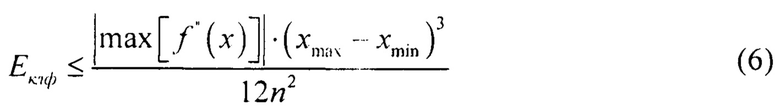
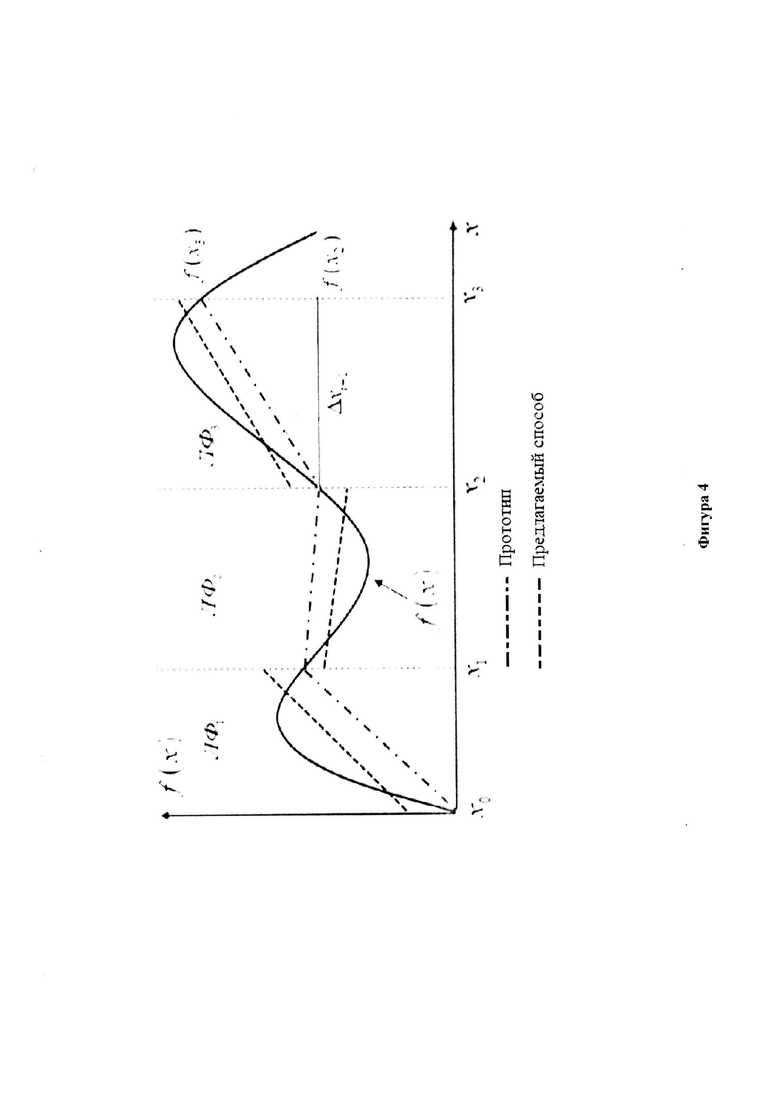
В предлагаемом способе даже если вычислять по формуле средних прямоугольников ошибка рассчитывается по формуле (фигура 4) [10]:
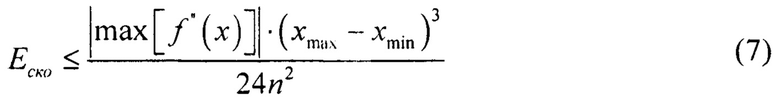
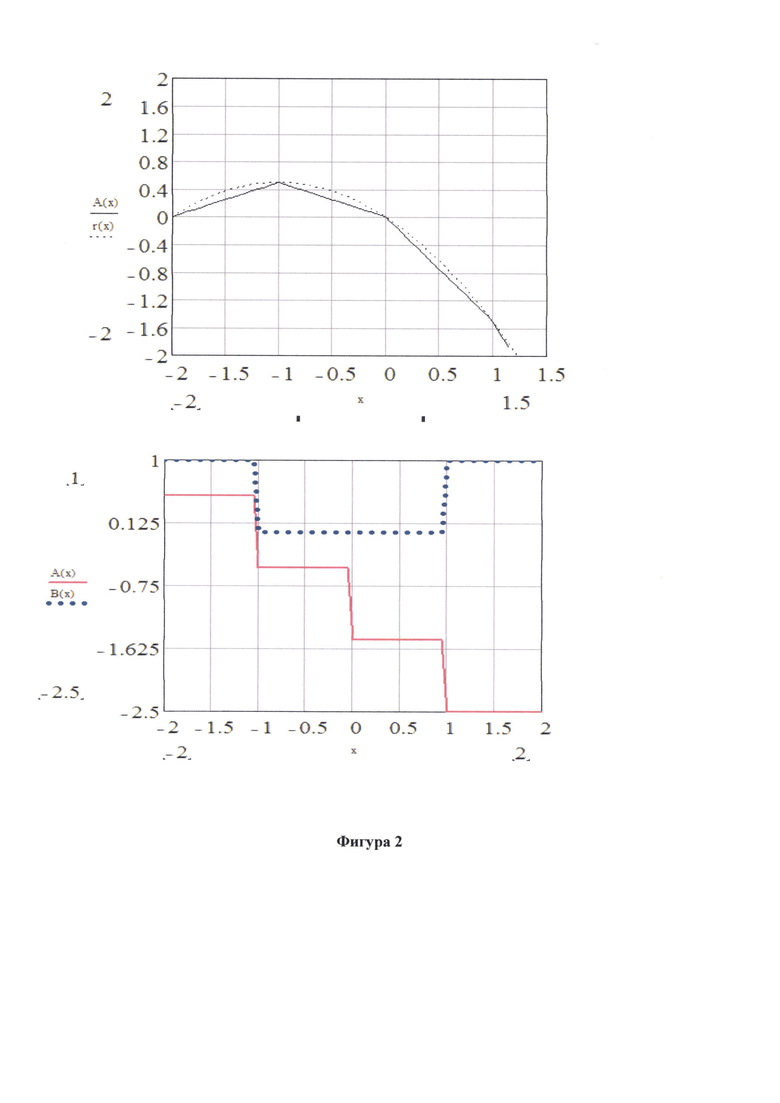
Из анализа 6 и 7 видно, в предлагаемом способе ошибка как минимум меньше в 2 раза. Однако на фигуре 4 наглядно видно, что при аппроксимации с применением критерия минимума среднего квадрата ошибки возникают разрывы первого рода на границах интервалов, однако данным фактом при реализации можно пренебречь по причине того, что работа реализуемого фильтра осуществляется перестройкой фильтра с одних коэффициентов на другие (фигура 2).
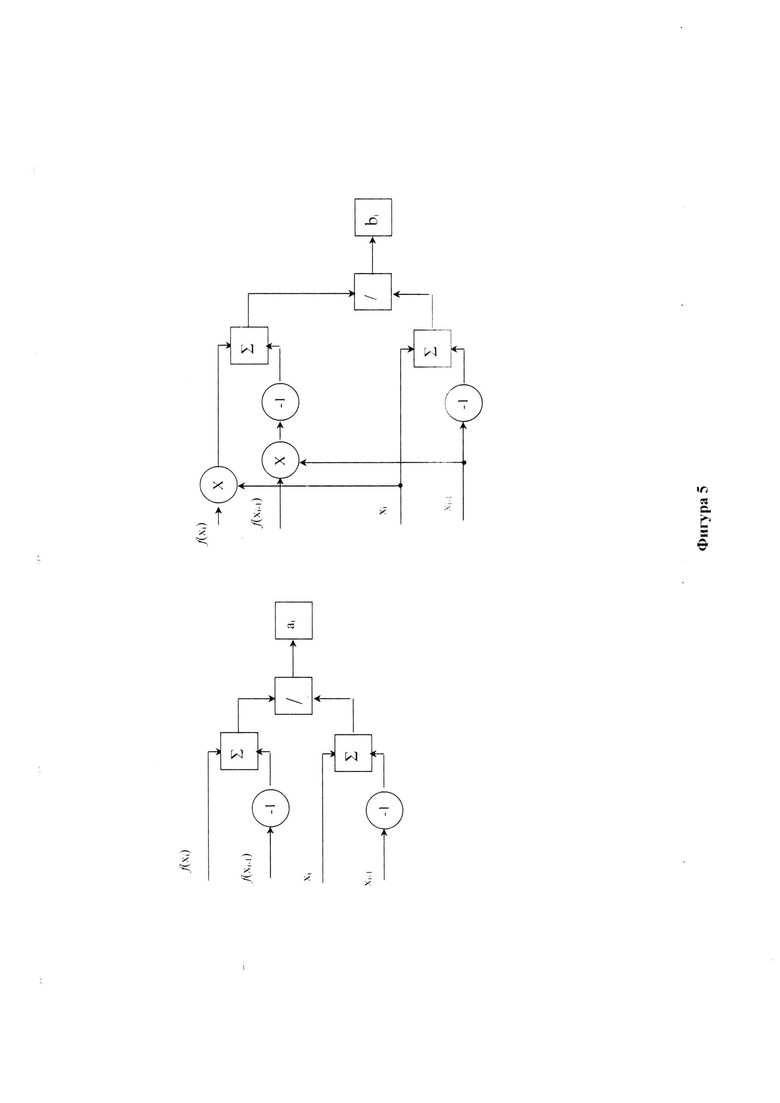
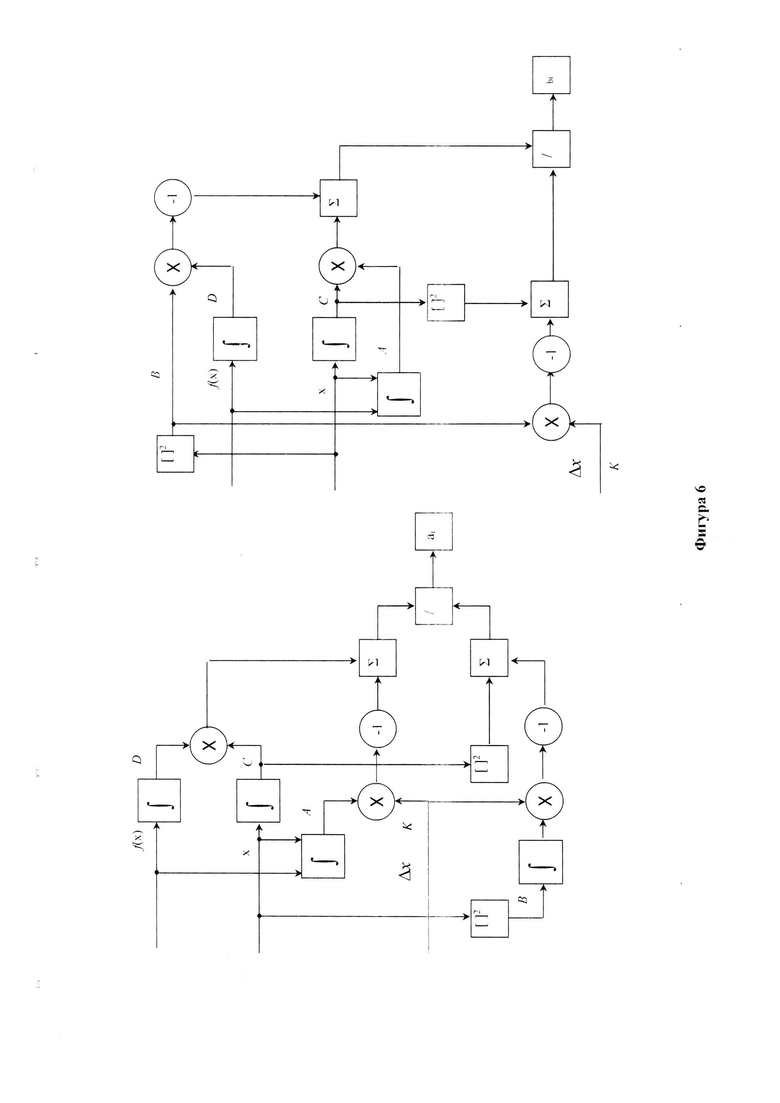
Предлагаемый способ сплайн фильтрации на основе прототипа и системы уравнений (23) представлен на фиг.5, где:
блок 1 - блок определения узловых точек на интервале;
блок 2 - блок формирования системы интервалов;
блок 3 - блок сравнения оценки помехи с системой интервалов;
блок 4 - блок определения значения оценки помехи [х*(1)];
блок 5 - блок определения величины коэффициента [ai];
блок 6 - блок определения величины коэффициента [bi];
блок 7 - блок усиления на коэффициент 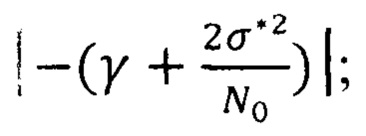
блоки 8, 12, 26 - интеграторы;
блоки 9, 13, 21 - квадраторы;
блок 10 - блок усиления на коэффициент 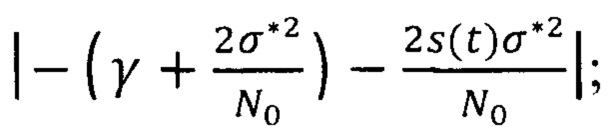
блоки 11, 15, 22 - блоки усиления на коэффициент [-1];
блок 14 - блок усиления на коэффициент 
блоки 16, 19 - блоки усиления на коэффициент [2];
блоки 17, 20 - перемножители;
блок 18 - блок формирования опорного сигнала;
блок 25 - блок усиления на коэффициент 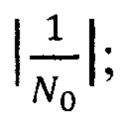
блок 27 - двухпороговое устройство;
блок 28 - однопороговое устройство;
блоки 29, 32 - блоки принятия решения при гипотезе наличия сигнала;
блок 30 - блок принятия решения при гипотезе отсутствия сигнала;
блок 31 - блок, реализующий продолжение наблюдения.
блок 23 - блок вычисления значения следующей оценки помехи [х*(2)];
блок 24 - блок вычисления значения следующей оценки помехи [х*(3)];
В прототипе вычисление значения ai, bi могут быть получены априори, исходя из вида зависимости ƒ(x) и необходимой точности аппроксимации, так как уравнение Риккати для коэффициента усиления фильтра Калмана не содержит измеряемых данных (фигура 5):
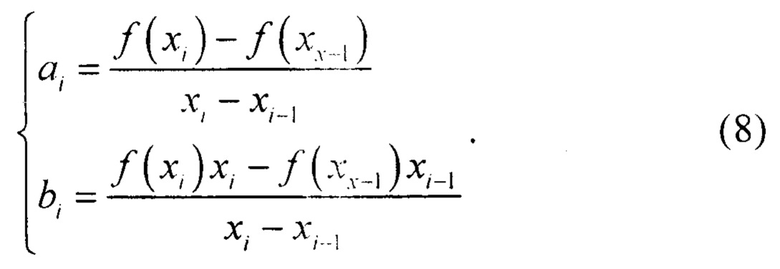
Совокупная помеха n∑(t) представляет собой сумму истинного значения n1(t) помехи плюс погрешность аппроксимации:
nΣ(t)=n1(t)+ncko(t), ncko(t) - предлагаемый способ,
nΣ(t)=n1(t)+nклф(t), nклф(t) - прототип.
В предлагаемом способе с учетом ошибки в соответствии с выражением (3) (фигура 6) вычисление значений ai, bi также могут быть получены априори, но ошибки при этом будут меньше, чем в прототипе, и, как следствие, отношение сигнал/помеха на выходе обнаружителя будет выше (так как ncko (t) у предлагаемого способа меньше, чем у прототипа, а следовательно, и nΣ(t)).
Геометрическая интерпретация сравнения предлагаемого способа и прототипа (фигуры 7-10).
На фигуре 7 представлен способ аппроксимации нелинейной функции на интервале кусочно-линейной функцией. На фигуре 8 этот же способ аппроксимации показан на одном интервале Δxi. Ошибка на этом интервале определяется площадью Ei → (Sклф(i). Соответственно, общая ошибка равна 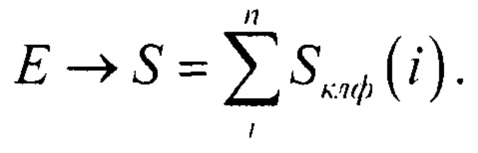
На фигуре 9 представлен способ аппроксимации нелинейной функции на интервале линейной функцией на основе среднего квадрата ошибки. На фигуре 10 этот же способ аппроксимации показан на одном интервале Δхi. Ошибка на этом интервале определяется площадью Ескоi → (Sско(i). Общая ошибка равна 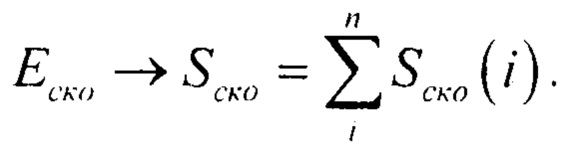 так как для каждого интервала имеет место неравенство Sско(i)<Sклф(i) ⇒ (Sско(i)<Sклф(i). Как следствие получаем, что дисперсия процесса ncko(t) меньше, чем дисперсия процесса nклф(t), а ОСПско>ОСПклф и соответственно задача обнаружения решается более эффективно.
так как для каждого интервала имеет место неравенство Sско(i)<Sклф(i) ⇒ (Sско(i)<Sклф(i). Как следствие получаем, что дисперсия процесса ncko(t) меньше, чем дисперсия процесса nклф(t), а ОСПско>ОСПклф и соответственно задача обнаружения решается более эффективно.
Предлагаемый способ обработки сигналов позволяет оценивать случайные процессы, заданные не только скалярными, но и матрично-векторными уравнениями. Экстраполяция полученных результатов на этот случай не представляет трудностей, а преимущества предлагаемого способа в решении задачи обнаружения по сравнению с известными методами нелинейной фильтрации и прототипом, становятся еще более существенными.
Список использованных источников
1. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем. М, Радио и связь, 1991, 608 с.
2. Казаков В.А. Введение в теорию марковских процессов и некоторые радиотехнические задачи. М.: Советское радио, 1973. 232 с. (Аналог, с. 213-222).
3. Бутырский Е.Ю., Васильев В.В., Шклярук О.Н., Обухов Е.В. Способ сплайн-фильтрации сигналов, патент на изобретение 2651640, 2018 (Прототип).
4. Бурова И.Г., Демьянович Ю.К. Теория минимальных сплайнов. - СПб.: Издательство СПбГУ, 2001. - 315 с.
5. Завьялов Ю.С., Квасов Б.Н., Мирошниченко В.Л. Метод сплайн-функций. М.: Наука, 1980.
6. Розов А.К. Нелинейная фильтрация сигналов. - СПб.: Политехника, 1994. - 381 с.
7. Бутырский Е.Ю. Обнаружение сигналов на фоне марковской реверберационной помехи // Научное приборостроение. - 2012. - Т. 22. - №1. - С. 87-95.
8. Бутырский Е.Ю. Основы сплайн-фильтрации сигналов // Информация и космос-2010. №1. - С. 34-39.
9. Бутырский Е.Ю. Сплайн модели сигналов и сплайн фильтрация // Национальная безопасность и стратегическое планирование. - 2014. - №2 (6). - С. 43-56.
10. Самарский А.А., Гулин А.В. Численные методы. М.: Наука, 1989. - 430 с.
11. Ашинянц Р.А., Морозова Т.Ю. Регуляризация алгоритма фильтрации Калмана-Бьюси при плохой обусловленности кореляционной матрицы шума // Цифровая обработка сигналов, №4, 2007. С. 29-32.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ | 2022 |
|
RU2801897C1 |
| Способ сплайн-фильтрации сигналов | 2017 |
|
RU2651640C1 |
| СПОСОБ ОБРАБОТКИ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ АЛГОРИТМА СИГМА-ТОЧЕЧНОГО ФИЛЬТРА КАЛМАНА | 2024 |
|
RU2840100C1 |
| СПОСОБ ДИФФЕРЕНЦИАЛЬНОЙ ИМПУЛЬСНО-КОДОВОЙ МОДУЛЯЦИИ - ДЕМОДУЛЯЦИИ СИГНАЛОВ | 2011 |
|
RU2446558C1 |
| УСТРОЙСТВО АДАПТИВНОГО ОЦЕНИВАНИЯ СОСРЕДОТОЧЕННОЙ ПОМЕХИ | 2008 |
|
RU2381620C1 |
| СПОСОБ ИЗМЕРЕНИЯ ПАРАМЕТРОВ РАДИОЛОКАЦИОННЫХ СИГНАЛОВ НА ФОНЕ ШУМОВЫХ ГАУССОВСКИХ ПОМЕХ | 2000 |
|
RU2204148C2 |
| АДАПТИВНЫЙ ДВУМЕРНЫЙ СПОСОБ РАЗМНОЖЕНИЯ ОЦЕНОК И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2010 |
|
RU2461874C2 |
| Способ определения координат радиоизлучающего объекта в рабочей зоне многопозиционного пассивного радиотехнического комплекса и устройство для его осуществления | 2020 |
|
RU2757197C1 |
| СПОСОБ ОБНАРУЖЕНИЯ НЕСКОЛЬКИХ ЦЕЛЕЙ, ИСПОЛЬЗУЕМЫЙ ПРЕЖДЕ ВСЕГО В ОБЗОРНЫХ РАДИОЛОКАТОРАХ С БОЛЬШИМ КОЛИЧЕСТВОМ ЛУЧЕЙ, ФОРМИРУЕМЫХ ПО УГЛУ МЕСТА | 2003 |
|
RU2317565C2 |
| СПОСОБ ОБНАРУЖЕНИЯ И УСТРАНЕНИЯ ИМПУЛЬСНОГО ШУМА ПРИ ОБРАБОТКЕ ИЗОБРАЖЕНИЙ И УСТРОЙСТВО, ЕГО РЕАЛИЗУЮЩЕЕ | 2010 |
|
RU2449355C2 |

Использование: изобретение относится к области радиоэлектроники и гидроакустики, а именно к способам обработки сигнала при наличии помех. Изобретение заключается в реализации разработки оптимального метода обнаружения гидроакустического сигнала в условиях помех, описываемых нелинейными стохастическими уравнениями. Сущность: способ обработки сигналов основывается на методе условной марковской фильтрации, который включает в себя: решение уравнений фильтрации для гипотезы наличия/отсутствия сигнала; уравнения правдоподобия; уравнения для вычисления коэффициентов усиления. Отличительной особенностью способа является то, что область динамического диапазона изменений нелинейной функции разбивается на интервалы, в каждом из которых реализуется независимая аппроксимация нелинейной функции, входящей в уравнение состояния, описывающего динамику изменения помехи, линейной функцией, а в целом нелинейная функция аппроксимируется кусочно-ломаной функцией с разрывами первого рода на границах интервалов, что позволяет на каждом из интервалов реализовать фильтр Калмана-Бьюси, включающего в себя: два уравнения оценки состояния при гипотезах наличия/отсутствия сигнала; уравнения оценки дисперсии на различных интервалах и уравнения правдоподобия, включающего эти оценки, и по результатам вычисления которого выносится решение об обнаружении или не обнаружении сигнала, а для получения значения коэффициентов сплайна применяется критерий минимума среднего квадрата ошибки. Технический результат: уменьшение вычислительных затрат по отношению к существующим и перспективным способам обработки сигналов, обеспечение высокой эффективности обнаружения сигнала при различных помехах, получение более эффективного алгоритма фильтрации, и возможность работы в реальном масштабе времени. 6 ил.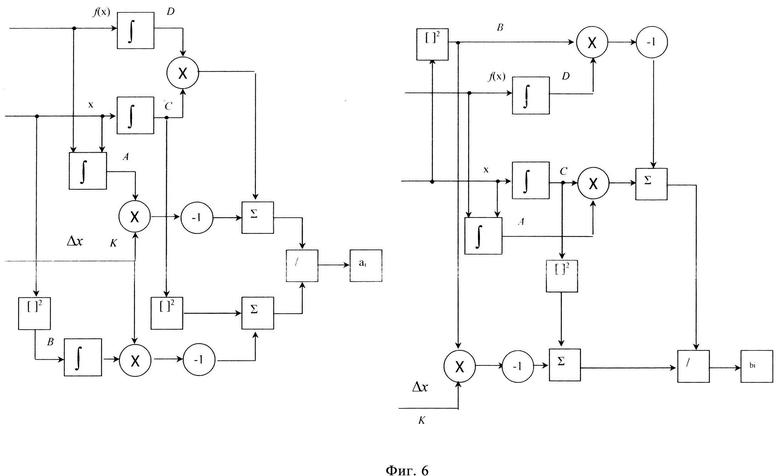
Способ обработки сигналов, основанный на операции сплайн-фильтрации сигналов, содержащий: операцию решения уравнений фильтрации для гипотезы наличия/отсутствия сигнала; операцию решения уравнения правдоподобия; операции решения уравнения для вычисления коэффициентов усиления, для получения оценок помехи при нелинейном уравнении состояния и уменьшения вычислительных затрат при нелинейной фильтрации, использующей сплайн-интерполяцию нелинейной функции, область динамического диапазона изменений нелинейной функции разбивается на интервалы, в каждом из которых реализуется операция линейной аппроксимации нелинейной функции, входящей в уравнение состояния, описывающего динамику помехи, что позволяет на каждом из поддиапазонов реализовать фильтр Калмана-Бьюси, включающего в себя: операции решения двух уравнений оценивания помехи при гипотезах наличия/отсутствия сигнала; операции решения уравнения оценки дисперсии на различных интервалах и операции решения уравнения правдоподобия, включающего эти оценки, и по результатам вычисления которого выносится решение об обнаружении или не обнаружении сигнала, отличающийся тем, что на концах интервалов операция аппроксимации нелинейной функции кусочно-линейной функцией осуществляется с разрывами первого рода, которая аппроксимирует нелинейную функцию линейной независимо в каждом из интервалов в соответствии с критерием минимума среднего квадрата ошибки, дополнительно осуществляются операции определения значений коэффициентов кусочно-ломаной кривой аппроксимации нелинейной функции в соответствии с выбранной величиной ошибки.
| Способ сплайн-фильтрации сигналов | 2017 |
|
RU2651640C1 |
| УСТРОЙСТВО АДАПТИВНОГО ОЦЕНИВАНИЯ СОСРЕДОТОЧЕННОЙ ПОМЕХИ | 2008 |
|
RU2381620C1 |
| Устройство для многоточечного дистанционного контроля, регулирования и сигнализации физических параметров | 1956 |
|
SU118443A1 |
| Устройство для обнаружения сигналов и определения направления на их источник | 2016 |
|
RU2617884C1 |
| US 3462590 A1, 19.08.1969. | |||
Авторы
Даты
2022-10-21—Публикация
2021-06-16—Подача