ОБЛАСТЬ ТЕХНИКИ
Изобретение относится к конструкции беспилотных летательных аппаратов, а именно тенсегрити дрона, и может быть использовано для планирования движения и последовательности деформации тенсегрити дрона.
ПРЕДШЕСТВУЮЩИЙ УРОВЕНЬ ТЕХНИКИ
Современные воздушные роботы и, в частности, дроны развиваются быстрыми темпами. Актуальным является вопрос обеспечения безопасности дронов с точки зрения их механических повреждений при взаимодействии с окружающей средой, а также безопасности людей в случае контакта с дронами. Для решения указанных задач целесообразным представляется использование тенсегрити дронов, обладающих деформируемой конструкцией и способностью адаптироваться к изменяющимся параметрам окружающего пространства с учетом встречающихся на пути движения препятствий. Такие дроны могут производить управляемую деформацию своего корпуса в процессе перемещения, что делает их более мобильными в сложный средах.
Из уровня техники известны, например, структуры тенсегрити с силовым движением и их применение (см. US2021129657A1, опубл. 06.05.2021)(1). В одном аспекте в настоящем документе описаны конструкции или устройства для тенсегрити, содержащие кольца или обручи. Вкратце, тенсегрити-конструкция содержит множество колец, разнесенных вдоль центральной оси и соединенных распорками, при этом распорки соединены с узлом силового привода с помощью тросов, при этом узел силового привода находится в объеме, определяемом стойками. В некоторых вариантах в конструкции тенсегрити используются три распорки для соединения колец, хотя возможно любое желаемое количество распорок. Кроме того, тросы могут проходить от противоположных концов узла силового привода для соединения со стойками. Рабочее пространство центра масс оси должно в оптимальном случае обеспечивать наведение статического момента на ободе, но можно также использовать момент оси.
Этот метод импульса более применим к позиционным изменениям, которые могут потребовать преодоления устойчивости, когда потребуются большие отклонения за пределы рабочего пространства оси для создания статических поперечных моментов.
Известна также модульная архитектура с распределенным приводом и управлением для сферических роботов тенсегрити (см. US2018326577A1, опубл. 15.11.2018). В соответствии с некоторыми вариантами осуществления изобретения тенсегрити-робот включает в себя множество сжимающих элементов и множество растягивающихся элементов, соединенных со сжимающими элементами для формирования пространственно определенной конструкции без образования сжимающими элементами прямых соединений друг с другом для передачи нагрузки. Каждый сжимаемый элемент имеет осевое продолжение с первым осевым концом и вторым осевым концом, а также центральную осевую область. Тенсегрити-робот также включает в себя множество исполнительных механизмов, каждый из которых прикреплен к одному из сжимающих элементов в пределах соответствующей его центральной осевой области. Тенсегрити-робот также включает в себя множество контроллеров, каждый из которых прикреплен к одному из сжимающих элементов. Каждый исполнительный механизм функционально соединен с соответствующим натяжным элементом, чтобы избирательно изменять натяжение на натяжном элементе в ответ на команды от контроллеров, тем самым изменяя центр масс тенсегрити-робота для осуществления его движения.
Известен также четырехроторный беспилотный летательный аппарат с защитой от столкновений на основе тенсегритной конструкции из двенадцати стержней (см. CN114802692A, опубл. 29.07.2022). Изобретение раскрывает противостолкновительный четырехроторный беспилотный летательный аппарат на основе тенсегритной конструкции из двенадцати стержней. Беспилотный летательный аппарат состоит из двенадцатистержневой тенсегритной рамы и несущих винтов. Рама имеет хорошую пространственную симметрию, структурную стабильность и ударопрочность, а также малый вес, так что влияние на крейсерскую способность беспилотного летательного аппарата может быть уменьшено, в то время как квадрокоптерный беспилотный летательный аппарат защищен. Беспилотный летательный аппарат снабжен тремя группами пружин растяжения разной жесткости; при столкновении беспилотного летательного аппарата с препятствием жесткость самого верхнего слоя, жесткость среднего слоя и жесткость самого нижнего слоя беспилотного летательного аппарата последовательно увеличиваются, так что величина деформации упругих втягивающих тросов последовательно уменьшаются сверху вниз под действием силы столкновения, а сталкивающаяся с препятствием рама равностороннего треугольника приводит к наклону узлов несущего винта в противоположном направлении столкновения; движущая составляющая сила создается в направлении, так что беспилотный летательный аппарат находится далеко от препятствия, и реализуется функция предотвращения столкновения беспилотного летательного аппарата.
Предложенный аналог имеет аналогичную конструкцию с конструкцией заявленного тенсегрити дрона, однако способы планирования траектории и последовательности деформаций для тенсегрити дрона в аналоге не раскрыты.
Наиболее близким аналогом заявленного способа, по мнению заявителя может быть выбран БПЛА вертикального взлета и посадки (см. RU2747006, 23.04.2021), который содержит защитную оболочку, внутри которой установлены полетный контроллер, датчики, элементы питания, и, по меньшей мере, один двигатель с воздушным винтом. Защитная оболочка содержит стержни, между которыми натянуты тросы так, что стержни не соприкасаются между собой. Полетный контроллер, датчики, элементы питания и двигатель с воздушным винтом установлены внутри объема, образованного концами стержней и тросами, натянутыми между концами стержней.
Для целей управления используется математическая модель БПЛА как твердого тела. Данная математическая модель вырабатывает управляющие команды на органы управления БПЛА. Управляющая программа отслеживает точность исполнения команд сравнивая ожидаемую траекторию движения БПЛА с реальной траекторией движения БПЛА, получаемую обработкой бортовым компьютером сигналов с гироскопа и акселерометра. Расхождение между ожидаемой и реальной траекторией движения рассматривается как результат воздействия внешней возмущающей силы, которая вызвана такими факторами, как воздействие среды, неточность модели и вибрация элементов защитной оболочки и т.п. На основании этих расчетов вносится корректировка в программу управления полетом.
Заявляемый метод является более эффективным по сравнению с методом, предложенном в ближайшем аналоге, поскольку относится к динамическим методам планирования движения.
КРАТКОЕ ИЗЛОЖЕНИЕ ИЗОБРЕТЕНИЯ
Техническим результатом заявленного изобретения является повышение эффективности и точности планирования траектории и последовательности деформаций для тенсегрити дрона.
Заявленный технический результат достигается посредством создания способа одновременного планирования траектории и последовательности деформаций для тенсегрити дрона, включающего установление соответствия между накрывающими эллипсоидами и конфигурациями тенсегрити структуры, затем планирование последовательности деформаций эллипсоидов на заданной карте, затем переход от последовательности деформированных эллипсоидов к последовательности конфигураций тенсегрити структуры используя установленное ранее соотвествие; причем, для определения соответствия между заданной конфигурацией тенсегрити структуры и эллипсоидом находят соответствующий ей внешний накрывающий эллипсоид наименьшего объема, а для нахождения ближайшей к заданному эллипсоиду конфигурации используют табличный метод: формируют базу данных конфигураций тенсегрити структуры, причем при ее формировании не учитывают конфигурации с провисаниями тросов или с касающимися друг друга стержнями, и для каждой конфигурации определяют соответствующий ей внешний эллипсоид, также при формировании базы данных в нее записывают разложение матрицы эллипсоида по собственному базису и норму вектора содержащего отклонения длин упругих элементов структуры в данной конфигурации от начального значения; для определения степени соответствия конфигурации тенсегрити заданному эллипсоиду вычисляют произведение обратной матрицы этого эллипсоида, собственного базиса и диагональной матрицы собственных чисел обратной матрицы накрывающего эллипсоида данной конфигурации, после чего нормы столбцов полученной матрицы подставляются в барьерную функцию − таким образом осуществляют проверку на вхождение эллипсоида конфигурации в заданный эллипсоид, далее, добавив к полученному результату норму вектора изменений управляемых длин упругих элементов, формируют оценку близости конфигурации к заданному эллипсоиду.
КРАТКОЕ ОПИСАНИЕ РИСУНКОВ
Сущность изобретения поясняют схемы, на которых:
Рис. 1 – Пространственное (а) и плоское (б) отображение двухкомнатного R1, R2 лабиринта с тремя шахтами 3-5;
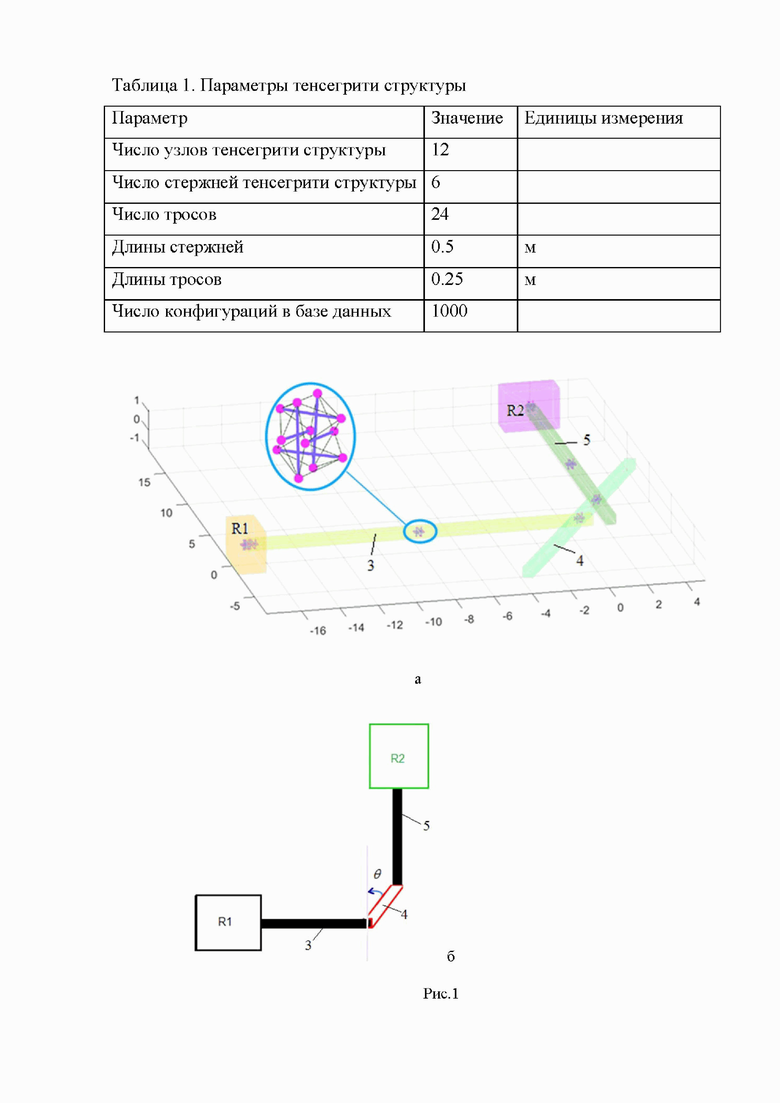
Рис.2 – Решение задачи планирование пути: найденные вписанные эллипсоиды (а) и поставленные им в соответствие накрывающие эллипсоиды из базы данных (б);
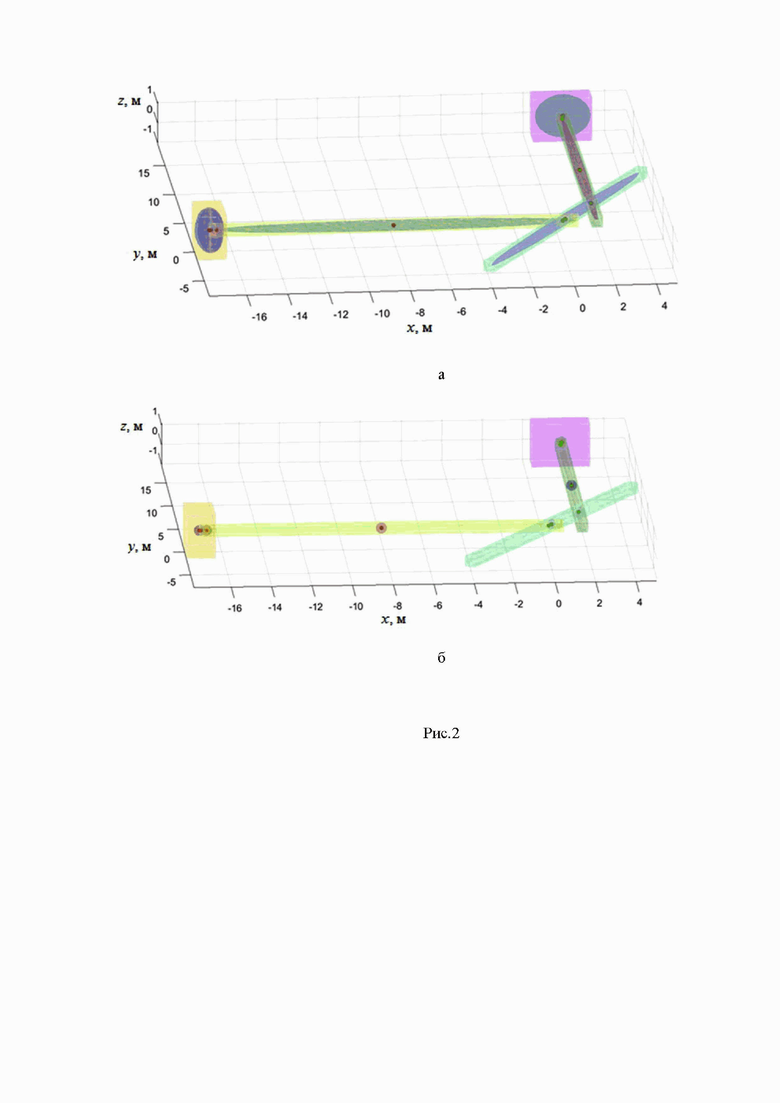
Рис.3 – Зависимости: (а), (б), (в).
ВАРИАНТ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ
Заявленный способ одновременного планирования траектории и последовательности деформаций для тенсегрити дрона предназначен для одного из перспективных направлений эволюции БПЛА, предназначенных для использования при возможных незапланированных столкновениях и падениях, может быть разработка устройств со складными и податливыми защитными конструкциями, имеющими минимальную массу и при этом отвечающими стандартам безопасности, а именно новый конструктивный принцип проектирования дронов, базирующийся на использовании тенсегрити структур.
Тенсегрити структуры состоят из элементов, испытывающих чистое сжатие (стержни), и элементов, испытывающих чистое растяжение (тросы). В тенсегрити системах звенья не соприкасаются друг с другом, а вся конфигурация обретает статическое равновесие под действием набора тросов, находящихся в деформированном состоянии (далее будем называть это преднатяжением).
Преимущества структур тенсегрити многочисленны. Например, они имеют хорошее соотношение массы к жесткости и могут эффективно распределять нагрузки между элементами, делая общую конструкцию устойчивой к механическим повреждениям. Эти свойства могут использоваться для разработки коллаборативных роботов, поскольку тенсегрити более легкие и более устойчивые к столкновениям по сравнению с другими механическими конструкциями. К другим преимуществам тенсегрити можно отнести гибкость и высокую способность складываться.
На основании вышесказанного можно сделать вывод о том, что тенсегрити структуры с учетом их преимуществ являются перспективным направлением в области создания дронов, безопасных с точки зрения столкновений с препятствиями окружающей среды, а также безопасных для человека.
Заявленный способ основан на описании геометрии тенсегрити структуры через накрывающие эллипсоиды. Заявленный способ одновременного планирования траектории и последовательности деформаций для тенсегрити дрона заключается в следующем.
Установив соответствие между накрывающими эллипсоидами и конфигурациями тенсегрити структуры, планируется последовательность деформаций эллипсоидов на заданной карте, а затем осуществляется переход к плану в конфигурационном пространстве тенсегрити структуры. Для определения соответствия между заданной конфигурацией тенсегрити структуры и эллипсоидом необходимо найти соответствующий ей внешний эллипсоид Джона-Лоунера (в англ. литературе − outer Lцwner-John ellipsoid), что может быть сделано решением одной SDP программы (от англ. semidefinite programming). Для нахождения ближайшей к заданному эллипсоиду конфигурации используется табличный метод: формируется база данных конфигураций тенсегрити структуры, причем при ее формиро-вании не учитываются конфигурации с провисаниями тросов или с касаю-щимися друг друга стойками, и для каждой конфигурации определяется соответствующий ей внешний эллипсоид. Также при формировании базы данных в нее записывается разложение матрицы эллипсоида по собственному базису и норма вектора изменений управляемых длин упругих элементов структуры, приведших её к заданной конфигурации. Изменения отсчитываются от некоторых заданных предпочтительных значений, которые могут соответствовать центру интервалов возможных значений управляемых длин. Тогда для определения степени соответствия конфигурации тенсегрити заданному эллипсоиду вычисляется произведение обратной матрицы этого эллипсоида, собственного базиса и диагональной матрицы собственных чисел обратной матрицы накрывающего эллипсоида данной конфигурации, после чего нормы столбцов полученной матрицы подставляют-ся в барьерную функцию − таким образом осуществляется проверка на схождение эллипсоида конфигурации в заданный эллипсоид. Далее, доба-ив к полученному результату норму вектора изменений управляемых длин упругих элементов, формируется оценка близости конфигурации к заданному эллипсоиду. Столь сложная процедура предложена для экономии вычислительных ресурсов, что позволяет не только минимизировать объем вычислений на этапе сопоставления эллипсоидов и конфигураций, но и распараллелить процесс вычислений; единственной последовательной операцией в процессе является поиск минимума в массиве полученных оценок.
Для планирования последовательности деформаций предложен способ, основанный на поиске вписанных эллипсоидов Джона-Лоунера, что требует решения единственной SDP задачи и представления свободного от препятствий пространства как объединения выпуклых многогранников. Планирование пути тенсегрити на объединении конечного числа выпуклых многогранников сводится к целочисленной выпуклой задаче (в англ. литературе mixed-integer convex programming) путем использования big-M метода. Такая задача может быть решена с использованием целочисленных решателей (солверов, от англ. solver − специализированные программные библиотеки для решения задач выпуклого про-граммирования).
Результаты исследований
В этом разделе представлены результаты численных исследований, выполненных для проверки предложенного алгоритма и анализа его численных свойств. В качестве объекта исследования рассматривается тенсегрити структура с шестью стержнями, известная как six-bar тенсегрити. Будем использовать параметры модели тенсегрити структуры, представленные в таблице 1.
Эксперименты разделены на 2 части: 1) рассматривается, имеет ли поставленная задача решение, 2) исследуется влияние геометрии пространства на числовые свойства метода, решая набор задач с немного отличающимися формами.
Рассмотрим первый эксперимент: даны две комнаты R1 и R2, соединённые тремя узкими наклонными шахтами 3, 4 и 5 (рис. 1, а), образующий-ми угол и=300 (рис. 1, б).
Задача состоит в том, чтобы пройти от начальной точки в комнате R1 до конечной точки в комнате R2 с использованием функции деформации и SDP планировщика пути. Для формулировки задачи используется CVX, а для ее решения − SDPT3 4.0. В этом эксперименте получено 373 ограничения в виде равенств и 1148 переменных.
Решение было найдено, на рис. 2. показаны соответствующие эллипсоиды и поставленные им в соответствие конфигурации. Найденное решение потребовало 1,27 с с разрывом (relativegap) 9,06∙10-9. Это указывает, что метод можно использовать для планирования пути в реальном времени.
Влияние геометрии пространства, свободного от препятствий, на объем вычислений, необходимых для поиска решения
Во втором эксперименте рассмотрен такой же двухкомантный лабиринт с тремя шахтами (рис. 1), для которого проведен эксперимент для 15 интервалов угла θ, сформированных как 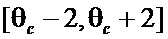 , где центры интервалов задаются в виде
, где центры интервалов задаются в виде 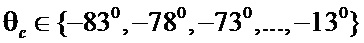 . Угол изгиба берем случайно с равномерным распределением как
. Угол изгиба берем случайно с равномерным распределением как 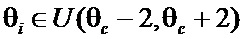 со стандартной ошибкой значения угла, равной 20. Для каждого интервала проведено по 100 экспериментов. Кроме того, для каждого интервала рассчитываются средние значения количества переменных
со стандартной ошибкой значения угла, равной 20. Для каждого интервала проведено по 100 экспериментов. Кроме того, для каждого интервала рассчитываются средние значения количества переменных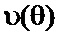 , числа итераций
, числа итераций 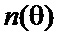 и процессорного времени (CPU)
и процессорного времени (CPU) 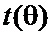 , а стандартная ошибка вычисляется как
, а стандартная ошибка вычисляется как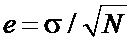 , где
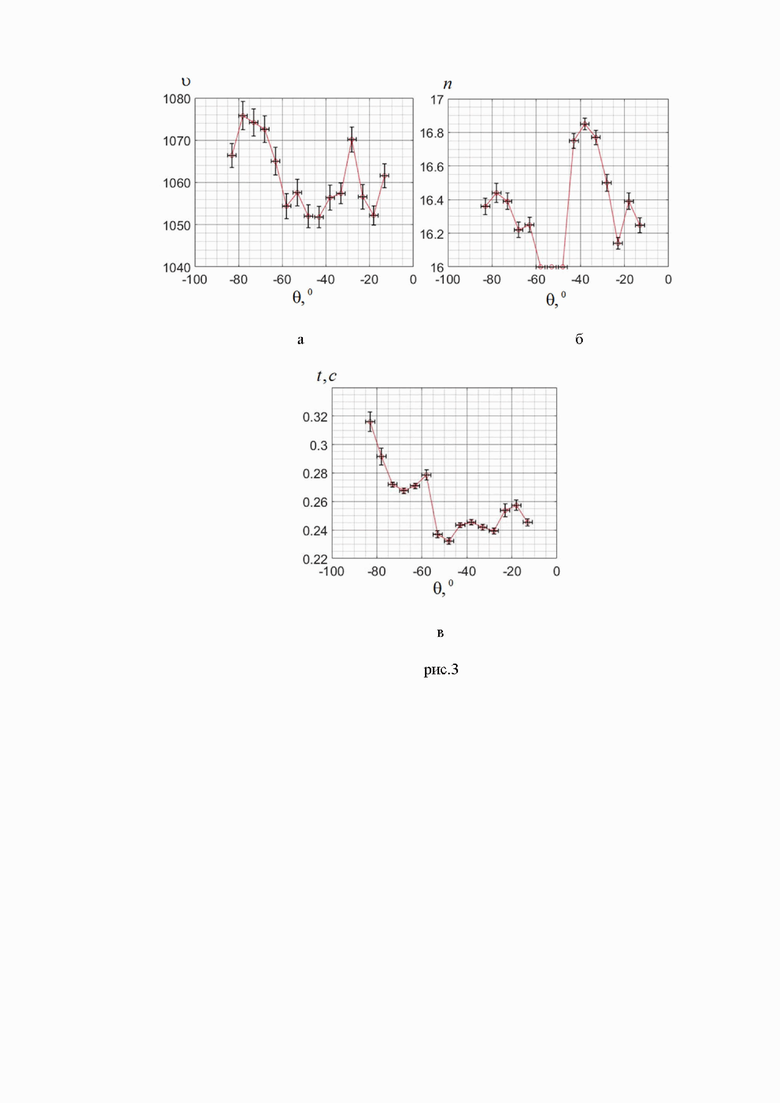
, где 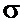 − стандартное отклонение,
− стандартное отклонение, 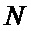 − количество выборок. После проведения экспериментов были исключены результаты, которые отличались от среднего значения более чем на три стандартных отклонения. Это сделано с целью определения необходимого количества переменных υ (рис. 3, а), числа итераций n (рис. 3, б) и процессорного времени t (рис. 3, в) как функций угла θ с учетом возникающих погрешностей.
− количество выборок. После проведения экспериментов были исключены результаты, которые отличались от среднего значения более чем на три стандартных отклонения. Это сделано с целью определения необходимого количества переменных υ (рис. 3, а), числа итераций n (рис. 3, б) и процессорного времени t (рис. 3, в) как функций угла θ с учетом возникающих погрешностей.
На основании анализа графиков можно сделать следующие выводы:
− во всех экспериментах решатель достиг решения задачи, т.е. все эксперименты допустимы,
− на количество переменных влияет изменение угла и,
− на сложность, определяемую числом итераций, влияет изменение угла и,
− процессорное время практически не зависит от угла и,
− при проектировании маршрута прохождения лабиринта необходимо искать оптимальный интервал углов, в котором будет наблюдаться меньшее количество переменных и меньшее число итераций, что приведет к вычислительной эффективности алгоритма,
− в целом изменение параметра угла и лабиринта не влияет на реализуемость задачи построения маршрута движения, но при этом существенно влияет как на количество переменных, так и на сложность алгоритма.
В результате проведения экспериментов по влиянию нетопологических воздействий на производительность предложенного алгоритма путем изменения параметра угла и было установлено, что они не влияют на выполнимость задачи планирования движения, но при этом оказывают существенное влияние на процессорное время, количество переменных и число итераций.
ПРОМЫШЛЕННОЕ ПРИМЕНЕНИЕ
Наиболее перспективными областями применения дронов являются доставка «последней мили» и «последнего метра», автоматизированное наблюдение за стихийными бедствиями и реагирование на них. К проблемам, требующим решения при эксплуатации дронов, можно отнести безопасное взаимодействие человека и дрона, безопасность столкновений, надежность летательных аппаратов и другие.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ автономного приземления беспилотного летательного аппарата на мобильную платформу | 2023 |
|
RU2821253C1 |
| СПОСОБ МОНИТОРИНГА ТЕРРИТОРИИ С ПОМОЩЬЮ БПЛА | 2023 |
|
RU2828511C1 |
| Многоцелевой БПЛА-перехватчик | 2020 |
|
RU2723203C1 |
| АВТОМАТИЗИРОВАННАЯ СИСТЕМА ДЛЯ ВНЕСЕНИЯ РАСХОДНЫХ МАТЕРИАЛОВ В ПРОЦЕССЕ ВЫПОЛНЕНИЯ ПОЛЕВЫХ СЕЛЬСКОХОЗЯЙСТВЕННЫХ РАБОТ | 2022 |
|
RU2800212C1 |
| СПОСОБ УПРАВЛЕНИЯ ГРУППОЙ МАНЕВРЕННЫХ БЕСПИЛОТНЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ | 2022 |
|
RU2818981C1 |
| Мобильный робототехнический комплекс | 2023 |
|
RU2836437C2 |
| Беспилотный авиационный робототехнический комплекс для внесения пестицидов | 2022 |
|
RU2779780C1 |
| Способ точной посадки беспилотного летательного аппарата и устройство для реализации способа | 2021 |
|
RU2773978C1 |
| ВОЗДУХОПЛАВАТЕЛЬНЫЙ ЭЛЕКТРОПОЕЗД | 2017 |
|
RU2734559C2 |
| Способ выявления беспилотных летательных аппаратов, осуществляющих незаконный полет над режимным объектом, с помощью нескольких датчиков | 2024 |
|
RU2830710C1 |
Изобретение относится к способу одновременного планирования траектории и последовательности деформаций для тенсегрити дрона. Для осуществления способа устанавливают соответствие между накрывающими эллипсоидами и конфигурациями тенсегрити структуры определенным образом, планируют последовательность деформаций эллипсоидов на заданной карте, осуществляют переход от последовательности деформированных эллипсоидов к последовательности конфигураций тенсегрити структуры, используя установленное ранее соответствие. Обеспечивается повышение эффективности и точности планирования траектории и последовательности деформаций для тенсегрити дрона. 3 ил., 1 табл.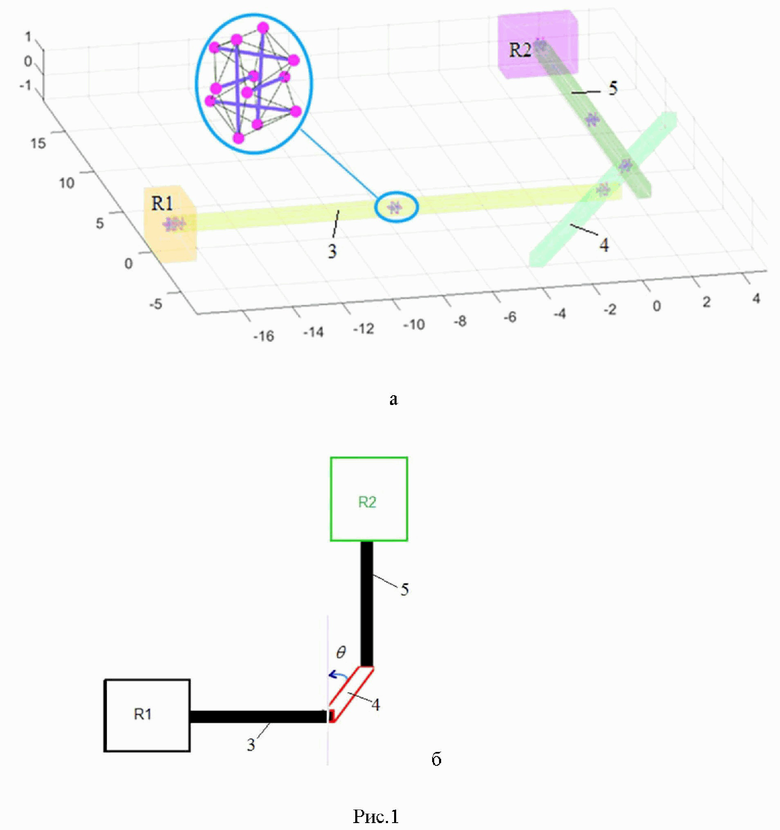
Способ одновременного планирования траектории и последовательности деформаций для тенсегрити дрона, включающий установление соответствия между накрывающими эллипсоидами и конфигурациями тенсегрити структуры, затем планирование последовательности деформаций эллипсоидов на заданной карте, затем переход от последовательности деформированных эллипсоидов к последовательности конфигураций тенсегрити структуры, используя установленное ранее соотвествие, причем для определения соответствия между заданной конфигурацией тенсегрити структуры и эллипсоидом находят соответствующий ей внешний накрывающий эллипсоид наименьшего объема, а для нахождения ближайшей к заданному эллипсоиду конфигурации используют табличный метод, при котором формируют базу данных конфигураций тенсегрити структуры, причем при ее формировании не учитывают конфигурации с провисаниями тросов или с касающимися друг друга стержнями, и для каждой конфигурации определяют соответствующий ей внешний эллипсоид, также при формировании базы данных в нее записывают разложение матрицы эллипсоида по собственному базису и норму вектора, содержащего отклонения длин упругих элементов структуры в данной конфигурации от начального значения, для определения степени соответствия конфигурации тенсегрити заданному эллипсоиду вычисляют произведение обратной матрицы этого эллипсоида, собственного базиса и диагональной матрицы собственных чисел обратной матрицы накрывающего эллипсоида данной конфигурации, после чего нормы столбцов полученной матрицы подставляются в барьерную функцию − таким образом осуществляют проверку на вхождение эллипсоида конфигурации в заданный эллипсоид, далее, добавив к полученному результату норму вектора изменений управляемых длин упругих элементов, формируют оценку близости конфигурации к заданному эллипсоиду.
| Савин С.И., Ворочаева Л.Ю., Куренков В.В | |||
| Математическое моделирование тенсегрити-роботов с жесткими стержнями, Компьютерные исследования и моделирование, 2020, т | |||
| Способ гальванического снятия позолоты с серебряных изделий без заметного изменения их формы | 1923 |
|
SU12A1 |
| БПЛА вертикального взлета и посадки | 2020 |
|
RU2747006C1 |
| Способ создания трека пути движения для автономного движения подвижного объекта и способ осуществления автономного движения подвижного объекта по треку пути движения | 2018 |
|
RU2691679C1 |
| US 20160221671 A1, 04.08.2016 | |||
| CN 109515714 A, 26.03.2019 | |||
| CN 109572987 A, 05.04.2019. | |||
Авторы
Даты
2023-05-05—Публикация
2022-12-27—Подача