Предлагаемое изобретение относится к электротехнике, а именно к области полупроводниковой преобразовательной техники (силовой электроники), и может быть использовано для управления многоуровневым трехфазным автономным инвертором напряжения с произвольным числом одинаковых по величине формируемых уровней выходного линейного напряжения с целью получения регулируемого трехфазного переменного напряжения, например, в системах управляемого электропривода трехфазного переменного тока, в системах с возобновляемыми источниками энергии и т.д.
Известен способ пространственно-векторной широтно-импульсной модуляции (ПВШИМ) выходного напряжения многоуровневого трехфазного автономного инвертора напряжения (МУИН) [Bin Wu, High-Power Converters and AC Drives. Wiley-IEEE Press, 2006, см. стр. 148-154], состоящий в том, что период выходного напряжения разбивается на равные тактовые интервалы ШИМ, и для каждого такого интервала формируется меняющийся во времени выполняемый обобщенный пространственный вектор выходного напряжения, за счет действия трех векторов, ближайших к отсчитанному для данного такта комплексному значению (положению на плоскости) обобщенного пространственного вектора задания, средние значения модуля и компонентов выполняемого пространственного вектора на тактовом интервале равны соответствующим значениям пространственного вектора задания (ЗПВ), получаемым по его отсчитанному для данного такта комплексному значению (положению на плоскости), при этом длительности действия трех ближайших к заданному векторов вычисляются через тригонометрические функции модуля отсчета пространственного вектора задания (или пропорционального ему коэффициента амплитудной модуляции) и аргумента отсчета пространственного вектора задания.
Однако указанный способ приводит к большому объему вычислений при нахождении длительностей действия трех векторов, ближайших к заданному (из-за многократных вычислений значений тригонометрических функций и операций с ними), что предъявляет повышенные требования к используемым в системе управления аппаратным средствам и ограничивает применение метода.
Известен также способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения [D.G. Holms, T.A. Lipo, Pulse Width Modulation for Power Converters. Piscataway, NJ: IEEE Press, 2003, см. стр. 531-543], принятый за прототип, состоящий в том, что период выходного напряжения разбивается на равные тактовые интервалы ШИМ, и для каждого такого интервала формируется меняющийся во времени выполняемый обобщенный пространственный вектор выходного напряжения, за счет действия трех векторов, ближайших к отсчитанному для данного такта комплексному значению (положению на плоскости) обобщенного пространственного вектора задания ЗПВ, средние значения модуля и компонентов выполняемого пространственного вектора на тактовом интервале равны соответствующим значениям пространственного вектора задания ЗПВ, получаемым по отсчитанному для данного такта его комплексному значению, а координаты и длительности действия трех ближайших к заданному векторов вычисляются через целые и дробные части относительных величин двух линейных напряжений как косоугольных координат пространственного вектора задания ЗПВ, при этом длительности действия трех векторов на такте разбиваются таким образом, чтобы сформировать симметричную относительно середины такта последовательность из принятого нечетного числа сегментов (подинтервалов действия различных векторов).
Использование 60-градусных координат и функции округления позволяет избежать избыточного применения тригонометрических функций на каждом тактовом интервале ШИМ, которое имеет место в большинстве традиционных схем ПВШИМ. Однако формирование симметричной относительно середины такта последовательности подинтервалов действия отдельных векторов в указанном способе приводит к большому числу переключений (коммутаций) в фазном плече МУИН за период выходного напряжения и, как следствие, к существенному значению мощности потерь на переключение в силовых полупроводниковых ключах МУИН, что не позволяет получать потенциально достижимые высокие значения коэффициента полезного действия (КПД) МУИН без снижения частоты ШИМ и соответствующего увеличения амплитуд высших гармоник выходного напряжения.
Задачей предлагаемого изобретения является формирование регулируемого трехфазного переменного напряжения с пониженным содержанием высших гармоник как самого напряжения, так и потребляемого от МУИН тока, при том же или меньшем значении числа переключений в фазном плече МУИН за период выходного напряжения, что позволяет либо улучшить качество выходной энергии при том же значении КПД, либо увеличить КПД МУИН при том же качестве энергии за счет снижения значения мощности динамических потерь (потерь на переключение) в силовых полупроводниковых ключах МУИН.
Кроме того, предлагаемый способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения позволяет ограничивать мгновенные значения синфазного напряжения трехфазного МУИН, сохраняя их внутри диапазона 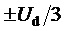
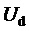
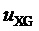
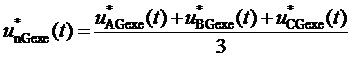
здесь и далее звездочки в надстрочных индексах обозначают относительные, т.е. нормированные по постоянному напряжению единичного (базового) уровня 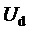
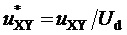
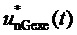
Указанный технический результат достигается тем, что в известном способе пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения, состоящем в том, что период выходного напряжения разбивается на равные тактовые интервалы ШИМ, и для каждого такого интервала формируется меняющийся во времени выполняемый обобщенный пространственный вектор (ВПВ) выходного напряжения, за счет действия трех векторов, ближайших к отсчитанному для данного такта комплексному значению (положению на плоскости) обобщенного пространственного вектора задания ЗПВ, средние значения модуля и компонентов выполняемого пространственного вектора на тактовом интервале равны соответствующим значениям пространственного вектора задания ЗПВ, получаемым по отсчитанному для данного такта его комплексному значению, а координаты и длительности действия трех ближайших к заданному векторов вычисляются через целые и дробные части относительных величин двух линейных напряжений как косоугольных координат пространственного вектора задания, выполняемый обобщенный пространственный вектор выходного напряжения формируется по координатам относительных значений двух выполняемых линейных напряжений, каждое из которых на каждом такте складывается из двух компонент, одна из которых равна значению целой части отсчета относительного значения соответствующего линейного напряжения пространственного вектора задания, а вторая представляет собой на такте функцию времени, принимающую значения только 0 или 1 и имеющую среднее значение на такте, равное дробной части отсчета относительного значения соответствующего линейного напряжения пространственного вектора задания, положение импульса (или импульсов) единичной величины на такте указанных функций каждого из двух выполняемых напряжений определяется характером изменения значений соответствующих задающих напряжений, учитывает номер сектора и тип модуляционного треугольника (направленного вверх или направленного вниз) и образует несимметричную на такте ШИМ последовательность переключения трех модуляционных векторов, разбивающую такт в общем случае на три сегмента (подинтервала действия различных векторов), при этом для каждого пространственного вектора, являющегося значением меняющегося во времени выполняемого обобщенного пространственного вектора выходного напряжения, вычисляются достижимое для него нормированное по постоянному напряжению единичного (базового) уровня значение синфазного напряжения многоуровневого трехфазного автономного инвертора напряжения из набора -1/3, 0, 1/3 и необходимые для его достижения нормированные значения фазных напряжений относительно заземляемого узла инвертора.
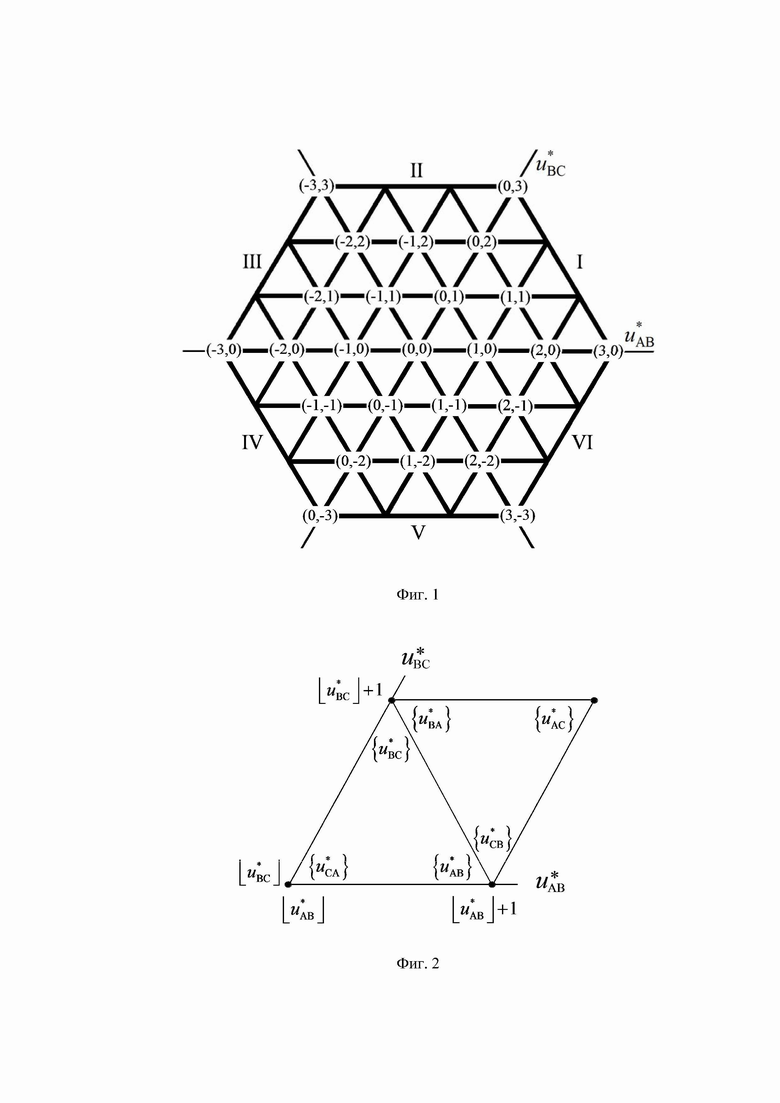
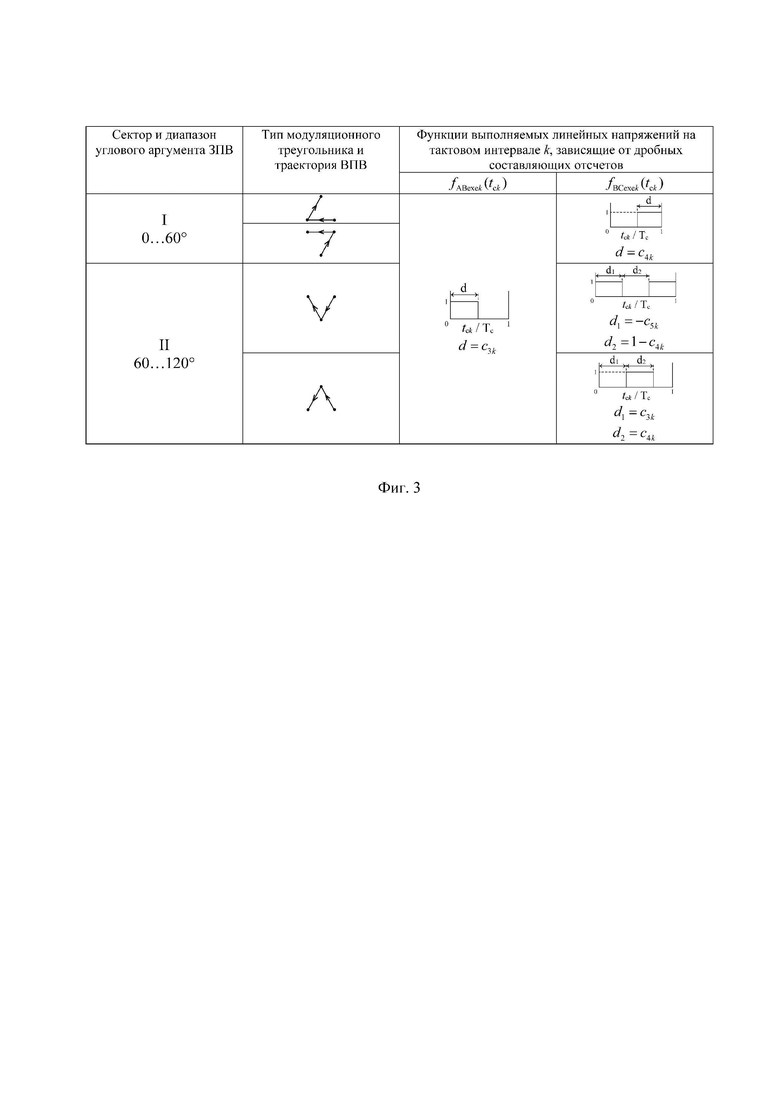
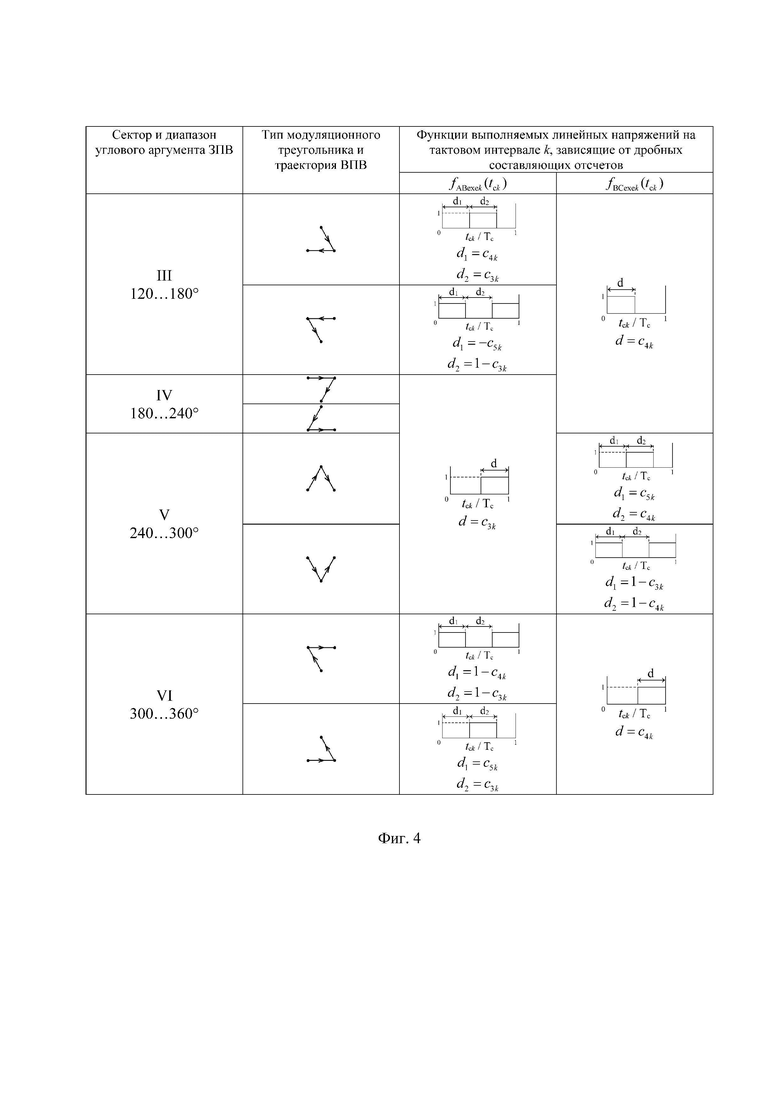
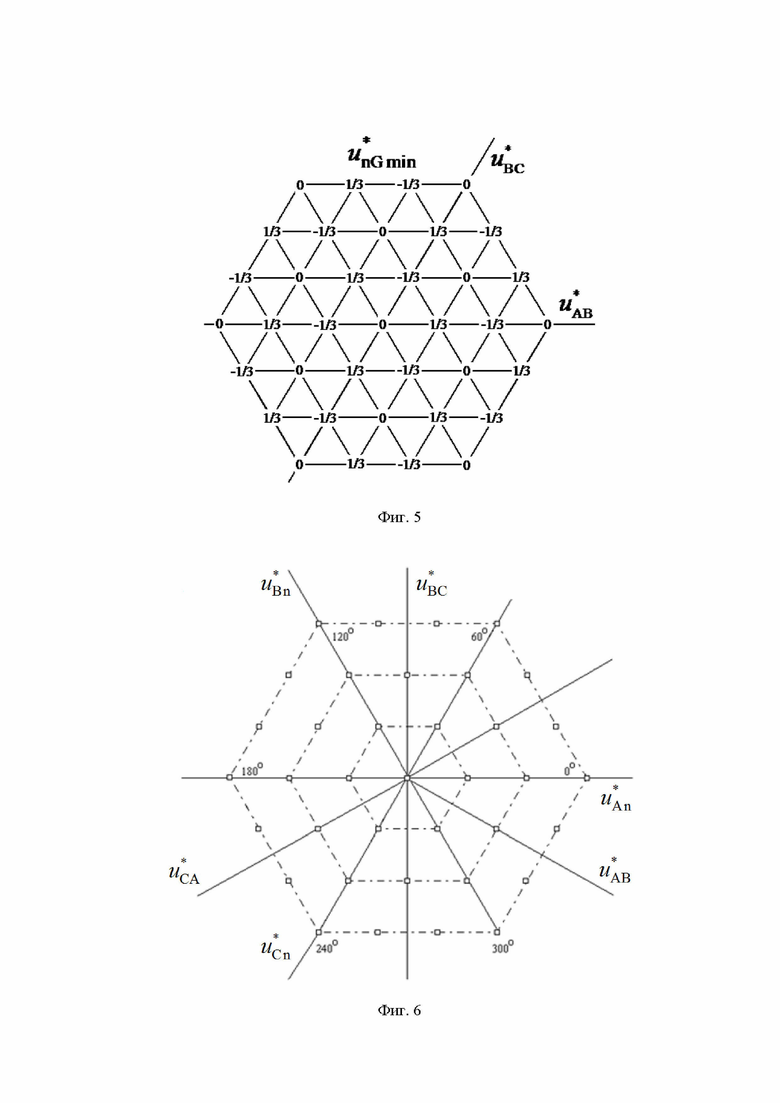
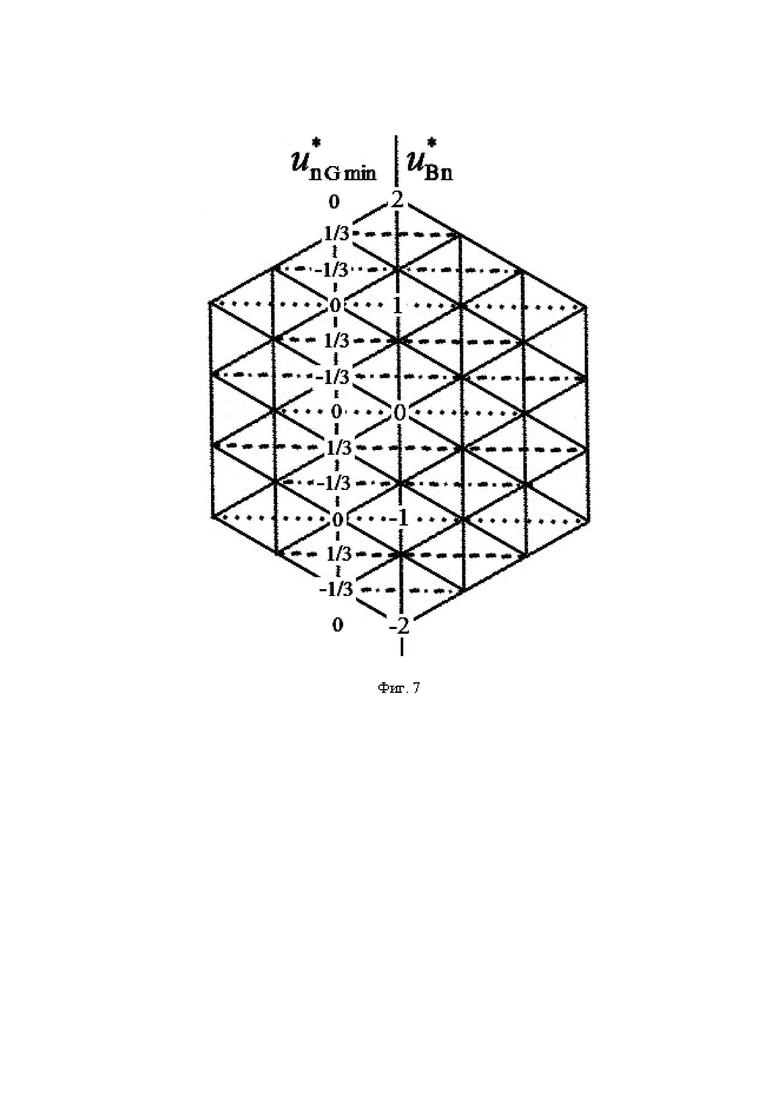
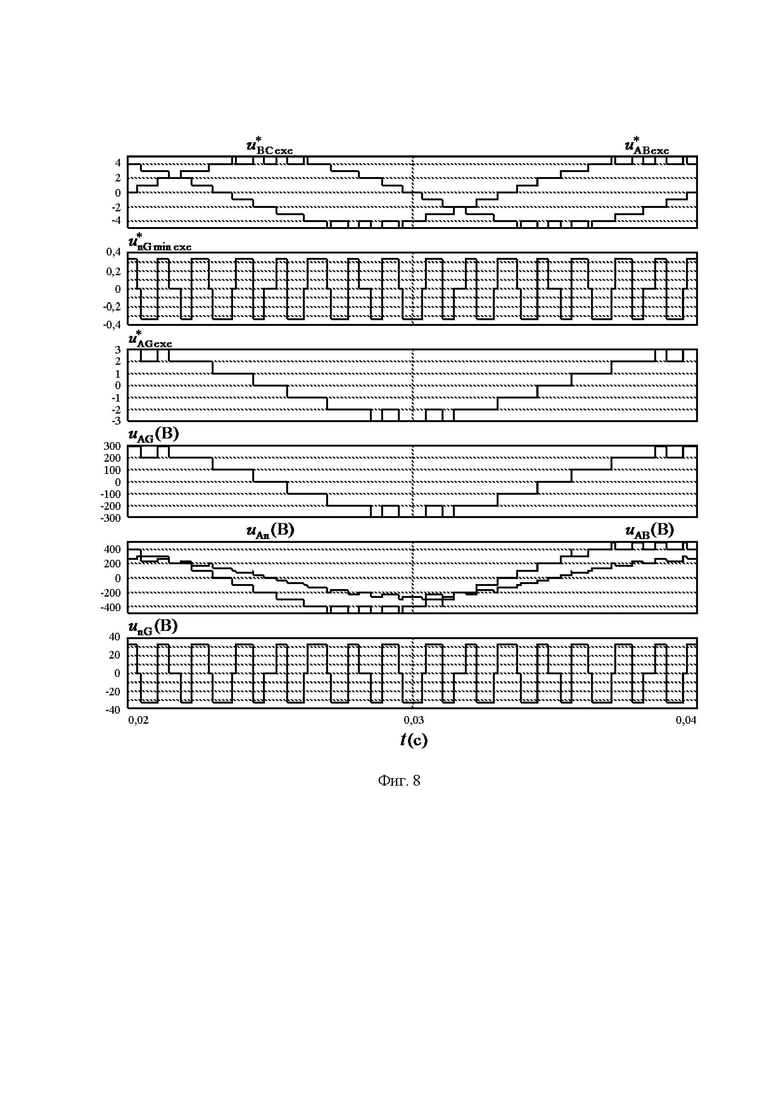
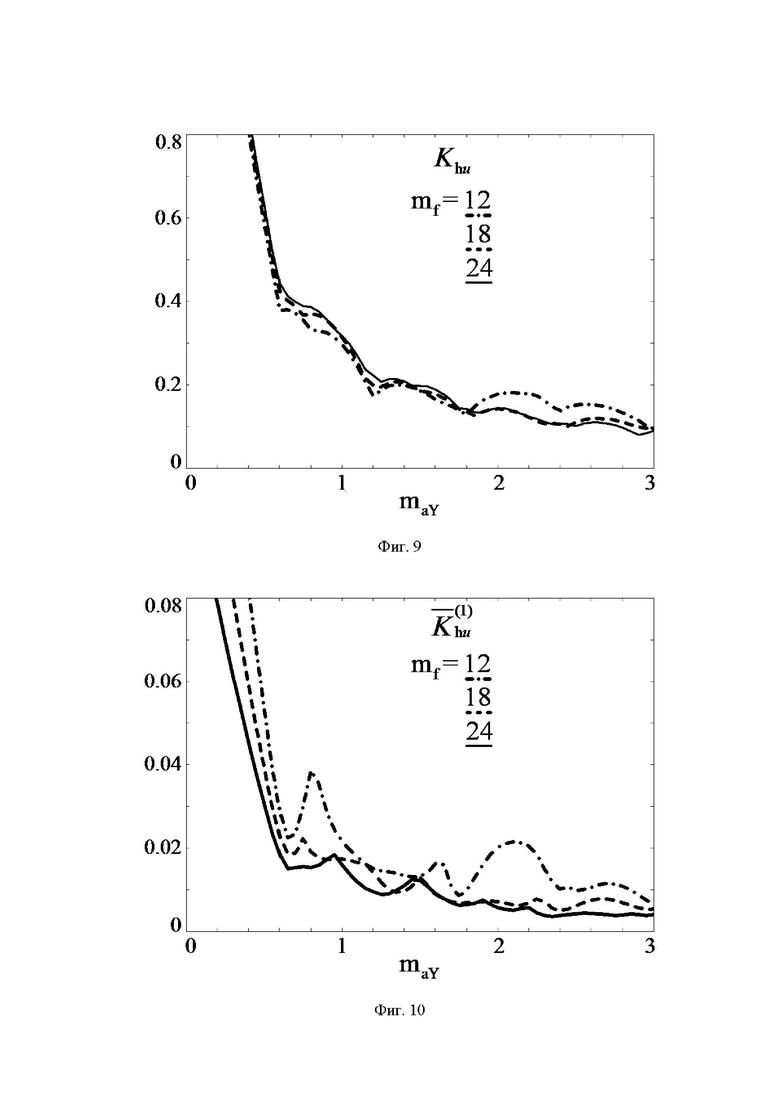
На фиг. 1 показана векторная диаграмма (все возможные векторы, местоположение которых может принимать выполняемый пространственный вектор выходного напряжения ВПВ в координатной системе косоугольных 60-градусных координат для случая четырехуровневого инвертора напряжения; на фиг. 2 представлены координаты и суммарные на такте ШИМ относительные длительности действия каждого из трех векторов, ближайших к местоположению пространственного вектора задания ЗПВ для каждого из двух типов модуляционных треугольников; на фиг. 3 и фиг. 4 - в табличной форме описаны функции тех компонент выполняемых двух линейных напряжений, которые зависят от значений дробных частей отсчетов относительных значений линейных напряжений ЗПВ, для секторов I-II и III-VI, соответственно; на фиг. 5 представлены минимальные (по абсолютной величине) доступные нормированные значения синфазного напряжения МУИН для случая четырехуровневого инвертора; на фиг. 6 - векторная диаграмма четырехуровневого инвертора в естественных осях фазных и линейных напряжений; на фиг. 7 показано соответствие между минимальными доступными нормированными значениями синфазного напряжения пространственных векторов и нормированными значениями фазного напряжения нагрузки фазы “В” МУИН; на фиг. 8 представлены осциллограммы выполняемых сигналов напряжений и напряжений силовой схемы МУИН, полученные моделированием в программном пакете PSIM; на фиг. 9 и фиг. 10 - зависимости от коэффициента амплитудной модуляции фазного напряжения значений, соответственно, коэффициента гармоник и интегрального коэффициента гармоник первого порядка выходного напряжения МУИН.
Способ реализуется следующим образом. Выполняемый обобщенный пространственный вектор выходного напряжения 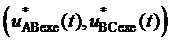
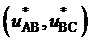
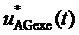


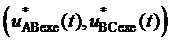
Способ включает описанные ниже 10 основных операций.
1. Определение значения коэффициента амплитудной модуляции линейного напряжения 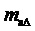
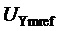
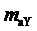
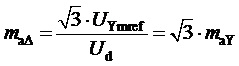
2. Генерирование функции номера тактового интервала ШИМ k:
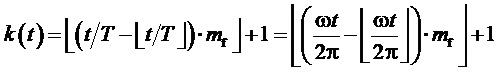
где 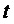
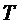
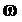
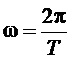
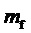
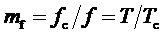
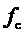
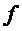
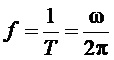
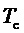
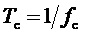
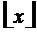
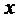
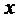
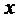
За период выходного напряжения k пробегает значения 1…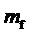
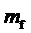
3. Генерирование отсчетов 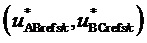
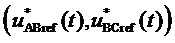
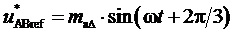
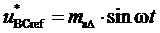
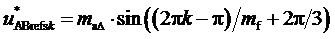
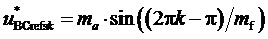
Таким образом, в соответствии с (4) значения отсчетов 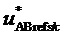
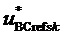
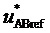
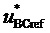
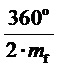
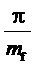
4. Вычисление для очередного тактового интервала ШИМ с номером k пяти основных величин, имеющих отношение к координатам и относительным временам действия на такте четырех ближайших к отсчету ЗПВ векторов и к определению вида модуляционного треугольника, в котором он находится:
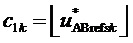
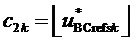
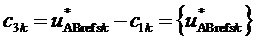
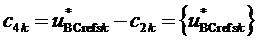
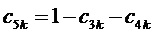
где 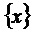
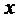
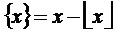
Таким образом, согласно фиг. 2, определяются, соответственно, следующие координаты и суммарные относительные длительности действия трех векторов на тактовом интервале ШИМ с номером k (порядок векторов условный): для треугольника, направленного вверх, 1) 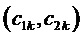
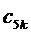
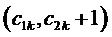
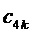
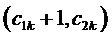
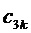
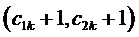
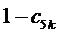
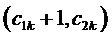
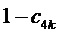
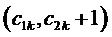
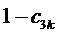
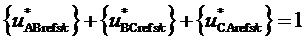
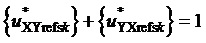
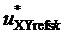
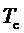
5. Вычисление для очередного тактового интервала ШИМ с номером k номера сектора 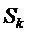
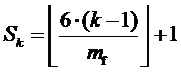
На фиг. 1 последовательно проходимые ЗПВ секторы пронумерованы римскими цифрами.
6. Вычисление для очередного тактового интервала ШИМ с номером k идентификаторов вида модуляционного треугольника 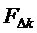
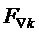
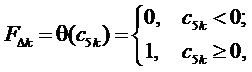
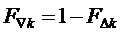
(здесь 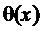
Если отсчет ЗПВ придется точно на сторону треугольника, принадлежащую двум смежным треугольникам ромба, образованного четырьмя ближайшими к отсчету ЗПВ векторами (на диагональ ромба), то в результате по (5) и (7) получим 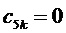
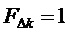
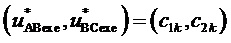
7. Согласно предлагаемой несимметричной на такте последовательности переключения трех модуляционных векторов, разбивающей такт ШИМ на три сегмента (подинтервала действия трех ближайших векторов) и соответствующей характеру изменения задаваемых линейных напряжений в каждом из двух типов модуляционных треугольников в рассматриваемом секторе, формируются принимающие значения 0 и 1 функции 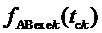

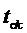
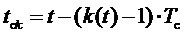
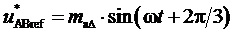
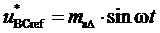
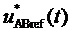
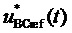
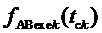

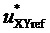
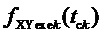
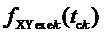
Для каждой из двух функций 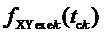
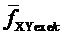
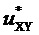
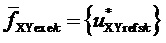
8. Вычисление для очередного тактового интервала ШИМ с номером k мгновенных относительных значений двух выполняемых линейных напряжений по двум компонентам:
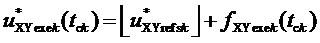
т.е. 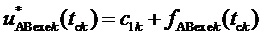
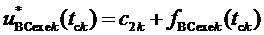
9. Вычисление мгновенных относительных значений трех выполняемых фазных напряжений относительно узла G для очередного тактового интервала ШИМ с номером k 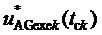
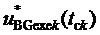
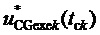
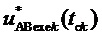
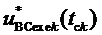
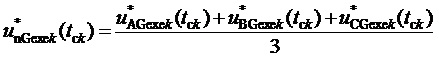
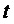
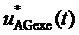


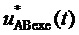

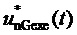
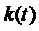
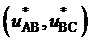
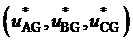
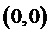
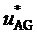
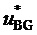
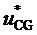
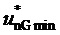
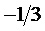
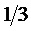
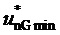
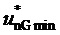
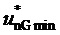
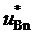
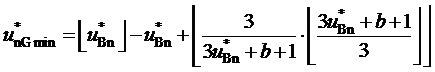
где 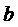
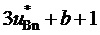
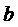
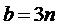
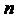
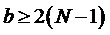
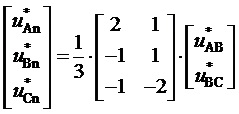
Подстановка 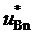
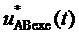

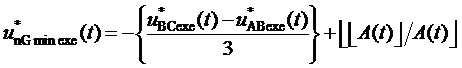
где 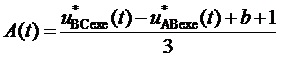
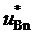
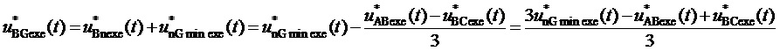

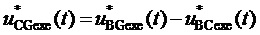
10. Выработка системой управления МУИН в соответствии с топологией МУИН сигналов непосредственно для полупроводниковых ключей для получения рассчитываемых значений фазных напряжений 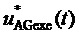


Верификация предложенного способа ПВШИМ выходного напряжения МУИН проведена на модели программного пакета моделирования устройств и систем силовой электроники PSIM (Франция). Осциллограммы сигналов как результат применения способа показаны на фиг. 8, где выполняемые сигналы системы управления на первых трех диаграммах являются безразмерными, а напряжения силовой схемы на оставшихся трех диаграммах выражены в вольтах. Осциллограммы соответствуют 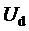
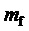
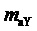
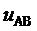
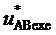
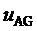
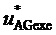
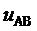
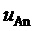
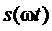
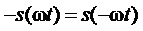
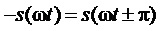
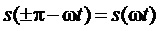
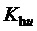
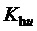
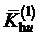
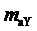
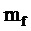
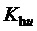
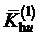
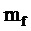
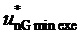
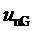
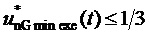
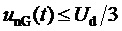
Таким образом, предлагаемый способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения по сравнению с прототипом позволяет формировать регулируемое трехфазное переменное напряжение с пониженным содержанием высших гармоник как самого напряжения, так и потребляемого от инвертора тока, при том же или меньшем значении числа переключений в фазном плече инвертора за период выходного напряжения, что позволяет либо улучшить качество выходной энергии при том же значении КПД, либо увеличить КПД инвертора при том же качестве энергии за счет снижения значения мощности динамических потерь в силовых полупроводниковых ключах МУИН, при гарантированном ограничении нормированных значений синфазного напряжения до одной трети единичного уровня питания постоянного тока, что смягчает проблему синфазного напряжения и упрощает меры по защите от сопровождающих его нежелательных явлений.
| название | год | авторы | номер документа |
|---|---|---|---|
| Пространственно-векторный способ управления выходным напряжением многоуровневого трехфазного автономного инвертора напряжения | 2024 |
|
RU2837271C1 |
| ПРЕОБРАЗОВАТЕЛЬ ПОСТОЯННОГО НАПРЯЖЕНИЯ В ТРЕХФАЗНОЕ КВАЗИСИНУСОИДАЛЬНОЕ С ШИРОТНО-ИМПУЛЬСНОЙ МОДУЛЯЦИЕЙ | 2013 |
|
RU2563247C1 |
| Преобразователь постоянного напряжения в квазисинусоидальное трёхфазное напряжение повышенной мощности | 2021 |
|
RU2762829C1 |
| МНОГОУРОВНЕВЫЙ АВТОНОМНЫЙ ИНВЕРТОР НАПРЯЖЕНИЯ | 2008 |
|
RU2393619C1 |
| СПОСОБ УПРАВЛЕНИЯ ТРЕХФАЗНЫМ ИНВЕРТОРОМ НАПРЯЖЕНИЯ СО СТАБИЛИЗАЦИЕЙ ТОКА ПРИ ПЕРЕХОДЕ В РЕЖИМ ПЕРЕГРУЗКИ | 2012 |
|
RU2522036C2 |
| СПОСОБ ЧАСТОТНОГО УПРАВЛЕНИЯ ЭЛЕКТРОПРИВОДОМ С СИНХРОННЫМ ДВИГАТЕЛЕМ БЕЗ ДАТЧИКА ПОЛОЖЕНИЯ РОТОРА | 2020 |
|
RU2746795C1 |
| Способ управления трехфазным инвертором напряжения по мостовой схеме | 2017 |
|
RU2661938C1 |
| Способ управления трехфазным инвертором с квазисинусоидальным выходным напряжением | 1989 |
|
SU1767667A1 |
| Способ управления матричным преобразователем частоты | 2016 |
|
RU2641653C1 |
| Вентильный электропривод с цифровым управлением | 1988 |
|
SU1582291A1 |
Изобретение относится к электротехнике, а именно к области силовой электроники, и может быть использовано для управления многоуровневым трехфазным автономным инвертором напряжения (в дальнейшем называемым «инвертор») с произвольным числом одинаковых по величине уровней выходного линейного напряжения с целью получения регулируемого трехфазного переменного напряжения, например, в системах управляемого электропривода трехфазного переменного тока, в системах с возобновляемыми источниками энергии и т.д. Способ пространственно-векторной широтно-импульсной модуляции выходного напряжения инвертора формирует выполняемый пространственный вектор выходного напряжения по координатам относительных значений двух линейных напряжений, каждая из которых на каждом такте складывается из двух компонент, одна из которых равна значению целой части отсчета относительного значения соответствующего линейного напряжения задания, а вторая зависит от дробных частей отсчетов двух указанных напряжений, номера сектора и вида модуляционного треугольника и принимает на такте значения только 0 или 1, в соответствии с используемым 3-сегментным вариантом последовательности переключения трех модуляционных векторов. Выбор ключевых состояний фаз трехфазного инвертора способствует минимизации значений его синфазного напряжения в каждый момент времени, т.е. при использовании любого вектора из полного набора пространственных векторов инвертора. Техническим результатом является формирование регулируемого трехфазного переменного напряжения с пониженным содержанием высших гармоник как самого напряжения, так и потребляемого от инвертора тока (благодаря четвертьволновой симметрии кривых выходных фазных и линейных напряжений) при том же или меньшем значении числа переключений в фазном плече инвертора за период выходного напряжения, что позволяет либо улучшить качество выходной энергии при том же значении КПД, либо увеличить КПД инвертора при том же качестве энергии за счет снижения значения мощности динамических потерь в силовых полупроводниковых ключах инвертора. При этом мгновенное значение синфазного напряжения трехфазного инвертора всегда остается в пределах ±1/3 от величины питающего постоянного напряжения единичного (базового) уровня. 10 ил.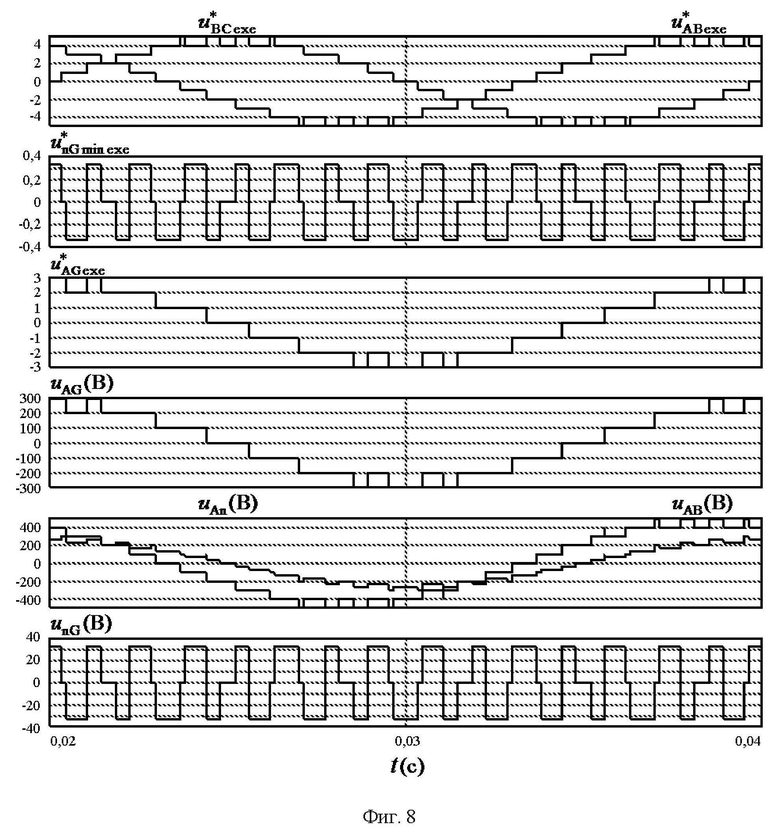
Способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения, состоящий в том, что период выходного напряжения разбивается на равные тактовые интервалы ШИМ, и для каждого такого интервала формируется меняющийся во времени выполняемый обобщенный пространственный вектор выходного напряжения, за счет действия трех векторов, ближайших к отсчитанному для данного такта комплексному значению (положению на плоскости) обобщенного пространственного вектора задания, средние значения модуля и компонентов выполняемого пространственного вектора на тактовом интервале равны соответствующим значениям пространственного вектора задания, получаемым по отсчитанному для данного такта его комплексному значению, а координаты и длительности действия трех ближайших к заданному векторов вычисляются через целые и дробные части относительных величин двух линейных напряжений как косоугольных координат пространственного вектора задания, отличающийся тем, что выполняемый обобщенный пространственный вектор выходного напряжения формируется по координатам относительных значений двух выполняемых линейных напряжений, каждое из которых на каждом такте складывается из двух компонент, одна из которых равна значению целой части отсчета относительного значения соответствующего линейного напряжения пространственного вектора задания, а вторая представляет собой на такте функцию времени, принимающую значения только 0 или 1 и имеющую среднее значение на такте, равное дробной части отсчета относительного значения соответствующего линейного напряжения пространственного вектора задания, положение импульса (или импульсов) единичной величины на такте указанных функций каждого из двух выполняемых напряжений определяется характером изменения значений соответствующих задающих напряжений, учитывает номер сектора и тип модуляционного треугольника (направленного вверх или направленного вниз) и образует несимметричную на такте ШИМ последовательность переключения трех модуляционных векторов, разбивающую такт в общем случае на три сегмента (подинтервала действия различных векторов), при этом для каждого пространственного вектора, являющегося значением меняющегося во времени выполняемого обобщенного пространственного вектора выходного напряжения, вычисляются достижимое для него нормированное по постоянному напряжению единичного (базового) уровня значение синфазного напряжения многоуровневого трехфазного автономного инвертора напряжения из набора -1/3, 0, 1/3 и необходимые для его достижения нормированные значения фазных напряжений относительно заземляемого узла инвертора.
| СПОСОБ УПРАВЛЕНИЯ ТРЕХФАЗНЫМ МОСТОВЫМ ПРЕОБРАЗОВАТЕЛЕМ | 2007 |
|
RU2379819C2 |
| Способ управления матричным преобразователем частоты | 2016 |
|
RU2641653C1 |
| Способ управления инвертором напряжения в системах бесперебойного питания и системах накопления электрической энергии при резкопеременной нагрузке | 2018 |
|
RU2697262C1 |
| Устройство для пневматического дистанционного управления люками полувагона типа Хоппер | 1957 |
|
SU117747A1 |
| US 4772996 A1, 20.09.1988 | |||
| US 9496717 B2, 15.11.2016. | |||
Авторы
Даты
2024-05-08—Публикация
2023-08-24—Подача