Предлагаемое изобретение относится к электротехнике, а именно к области полупроводниковой преобразовательной техники (силовой электроники), и может быть использовано для управления многоуровневым трехфазным автономным инвертором напряжения с произвольным числом одинаковых по величине формируемых уровней выходного линейного напряжения с целью получения регулируемого трехфазного переменного напряжения, например, в системах управляемого электропривода трехфазного переменного тока, в системах с возобновляемыми источниками энергии и т.д.
Известен пространственно-векторный способ управления выходным напряжением многоуровневого трехфазного автономного инвертора напряжения (МУИН), использующий широтно-импульсную модуляцию (ШИМ) [Bin Wu, High-Power Converters and AC Drives. Wiley-IEEE Press, 2006, см. стр. 148-154], состоящий в том, что период выходного напряжения разбивается на равные тактовые интервалы ШИМ, и для каждого такого интервала формируется меняющийся во времени выполняемый обобщенный пространственный вектор выходного напряжения (ВПВ), за счет действия трех векторов, ближайших к отсчитанному для данного такта положению на плоскости обобщенного пространственного вектора задания, средние значения модуля и компонентов выполняемого пространственного вектора на тактовом интервале равны соответствующим значениям пространственного вектора задания (ЗПВ), получаемым по его отсчитанному для данного такта положению на плоскости, при этом длительности действия трех ближайших к заданному векторов вычисляются через тригонометрические функции модуля отсчета пространственного вектора задания (или пропорционального ему коэффициента амплитудной модуляции) и аргумента отсчета пространственного вектора задания.
Однако указанный способ с использованием ШИМ, во-первых, характеризуется наличием переключений уровней выходного напряжения на такте, что приводит к множеству переключений (коммутаций) силовых полупроводниковых ключей МУИН на периоде выходного напряжения и, как следствие, к существенному значению мощности потерь на переключение в них, и не позволяет получать потенциально достижимые высокие значения коэффициента полезного действия (КПД) МУИН, во-вторых, приводит к большому объему вычислений при нахождении длительностей действия трех векторов, ближайших к заданному (из-за многократных вычислений значений тригонометрических функций и операций с ними), что предъявляет повышенные требования к используемым в системе управления аппаратным средствам и ограничивает применение метода.
Известен также пространственно-векторный способ управления выходным напряжением МУИН, реализующий выбор ближайшего вектора [J. Rodriguez, L. Moran, P. Correa, C. Silva, “A vector control technique for medium-voltage multilevel inverters,” IEEE Transactions on Industrial Electronics, Vol. 49, Iss. 4, August 2002, pp. 882-888, см. стр. 883-885; J. Rodriguez, L. Moran, J. Pontt, P. Correa, C. Silva, “A high-performance vector control of an 11-level inverter,” IEEE Transactions on Industrial Electronics, Vol. 50, Iss. 1, February 2003, pp. 80-85, см. стр. 81-83], принятый за прототип, состоящий в том, что период выходного напряжения разбивается на равные тактовые интервалы, и на каждом таком интервале формируемый меняющийся во времени выполняемый обобщенный пространственный вектор выходного напряжения принимает значение доступного для реализации инвертором пространственного вектора, ближайшего к отсчитанному для данного такта положению на плоскости обобщенного пространственного вектора задания, при этом выбор ближайшего вектора производится по значениям нормированных ортогональных координат пространственного вектора задания в момент отсчета, которые могут быть определены через относительные значения его фазных напряжений относительно нейтральной точки инвертора или линейных напряжений, номер прямоугольника, в котором на момент отсчета находится пространственный вектор задания, идентифицируется по координатам наиболее удаленной от начала координат вершины прямоугольника, каждая из указанных координат находится как произведение значений функции сигнум («знаковая» функция со значениями -1, 0 и 1) и функции округления модуля до ближайшего целого числа в большую сторону (функции “потолок”) от значения соответствующей нормированной ортогональной координаты пространственного вектора задания, для каждого такого прямоугольника заранее рассчитываются и помещаются в таблицы поиска коэффициенты линейного уравнения границы зон близости двух ближайших векторов, а для выбора одного из них производится сравнение нормированной вертикальной координаты пространственного вектора задания с результатом подстановки нормированной горизонтальной координаты в линейное уравнение границы зон близости векторов.
Переход на такте формирования выходного напряжения МУИН от ШИМ к выбору ближайшего к заданному вектора существенно сокращает число коммутаций силовых полупроводниковых ключей МУИН и соответствующие потери мощности в них, сохраняя, в зависимости от числа уровней МУИН, приемлемое или даже высокое качество выходных напряжения и тока с точки зрения их гармонического состава. Также данный способ позволяет избежать избыточного применения тригонометрических функций на каждом тактовом интервале, которое имеет место в традиционных схемах пространственно-векторных ШИМ. Однако реализация выбора ближайшего вектора содержит излишне много операций и не является оптимальной из-за использования прямоугольной системы координат. В частности, кроме текущего расчета номера прямоугольника, требуется заранее выполненный расчет коэффициентов линейных уравнений границ зон близости двух ближайших векторов для каждого прямоугольника векторной диаграммы при заданном количестве уровней МУИН и помещение их в таблицы поиска, что предъявляет повышенные требования к используемым в системе управления аппаратным средствам и ограничивает применение метода.
Задачей предлагаемого изобретения является формирование регулируемого трехфазного переменного напряжения МУИН произвольной схемной конфигурации с произвольным числом одинаковых по величине формируемых уровней выходного линейного напряжения путем выбора на каждом такте доступного вектора, ближайшего к отсчету пространственного вектора напряжения задания, при упрощенной процедуре идентификации трех ближайших векторов и выбора одного из них, которая позволяет понизить требования к используемым в системе управления аппаратным средствам, что расширяет применение метода выбора ближайшего вектора при пространственно-векторном управлении выходным напряжением МУИН.
Кроме того, предлагаемый пространственно-векторный способ управления выходным напряжением МУИН позволяет применить подход, ограничивающий мгновенные значения синфазного напряжения трехфазного МУИН (с сохранением их внутри диапазона 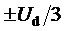 , где
, где 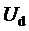 - постоянное напряжение единичного, т.е. базового уровня), предложенный автором (см. описание изобретения к патенту № 2818965 «Способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения»).
- постоянное напряжение единичного, т.е. базового уровня), предложенный автором (см. описание изобретения к патенту № 2818965 «Способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения»).
Указанный технический результат достигается тем, что в известном пространственно-векторном способе управления выходным напряжением многоуровневого трехфазного автономного инвертора напряжения, состоящем в том, что период выходного напряжения разбивается на равные тактовые интервалы, и на каждом таком интервале формируемый меняющийся во времени выполняемый обобщенный пространственный вектор выходного напряжения принимает значение доступного для реализации инвертором пространственного вектора, ближайшего к отсчитанному для данного такта положению на плоскости обобщенного пространственного вектора задания, данный ближайший вектор выбирается как соответствующий той из барицентрических координат отсчета пространственного вектора задания на треугольнике трех ближайших векторов, которая имеет максимальное значение, при этом для обоих видов треугольников ближайших векторов координаты трех ближайших к отсчитанному вектору задания векторов и барицентрические координаты отсчета на идентифицированном треугольнике вычисляются, соответственно, через целые и дробные части отсчетов сигналов относительных величин двух линейных напряжений как косоугольных координат отсчета пространственного вектора задания, для каждого пространственного вектора, являющегося значением меняющегося во времени выполняемого обобщенного пространственного вектора выходного напряжения, вычисляются достижимое для него минимальное по модулю нормированное по постоянному напряжению единичного (базового) уровня значение синфазного напряжения многоуровневого трехфазного автономного инвертора напряжения из набора -1/3, 0, 1/3 и необходимые для его достижения нормированные значения фазных напряжений относительно заземляемого узла инвертора.
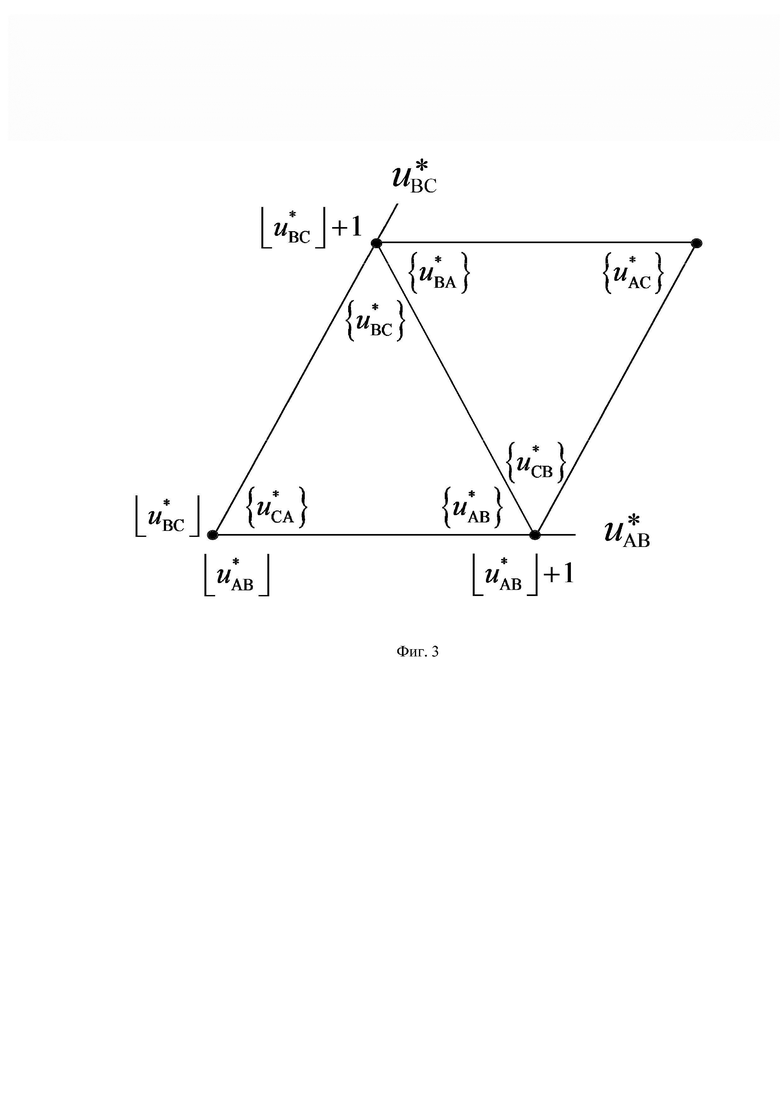
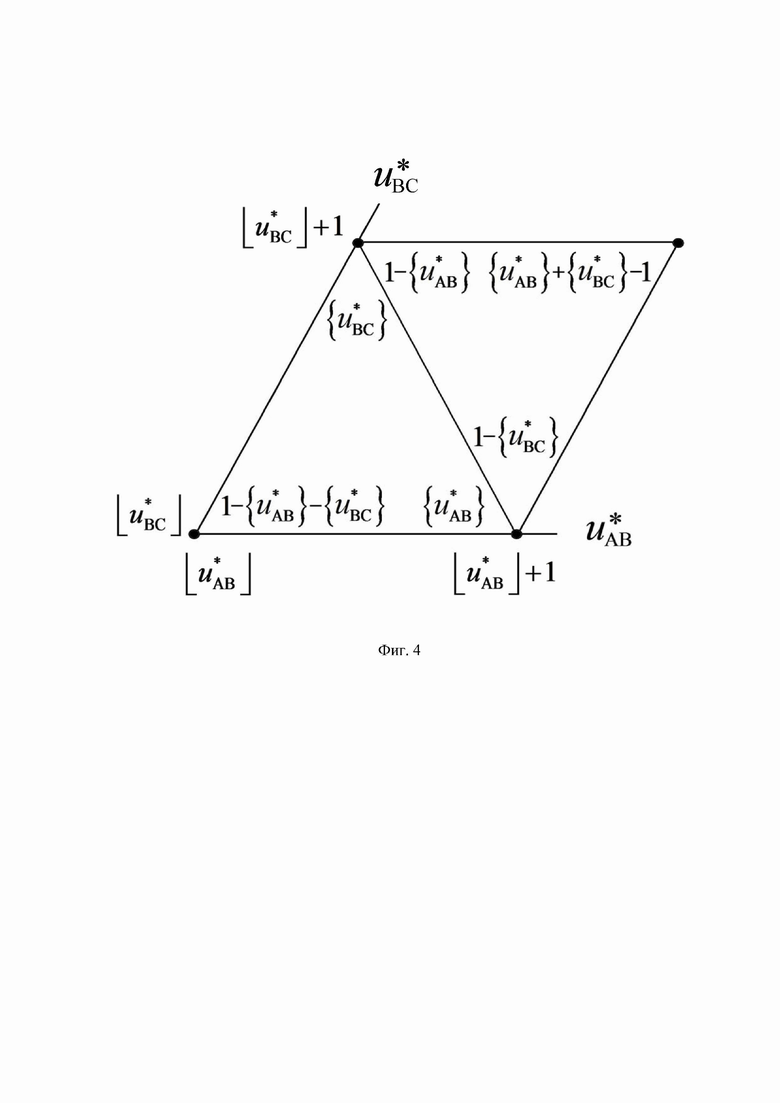
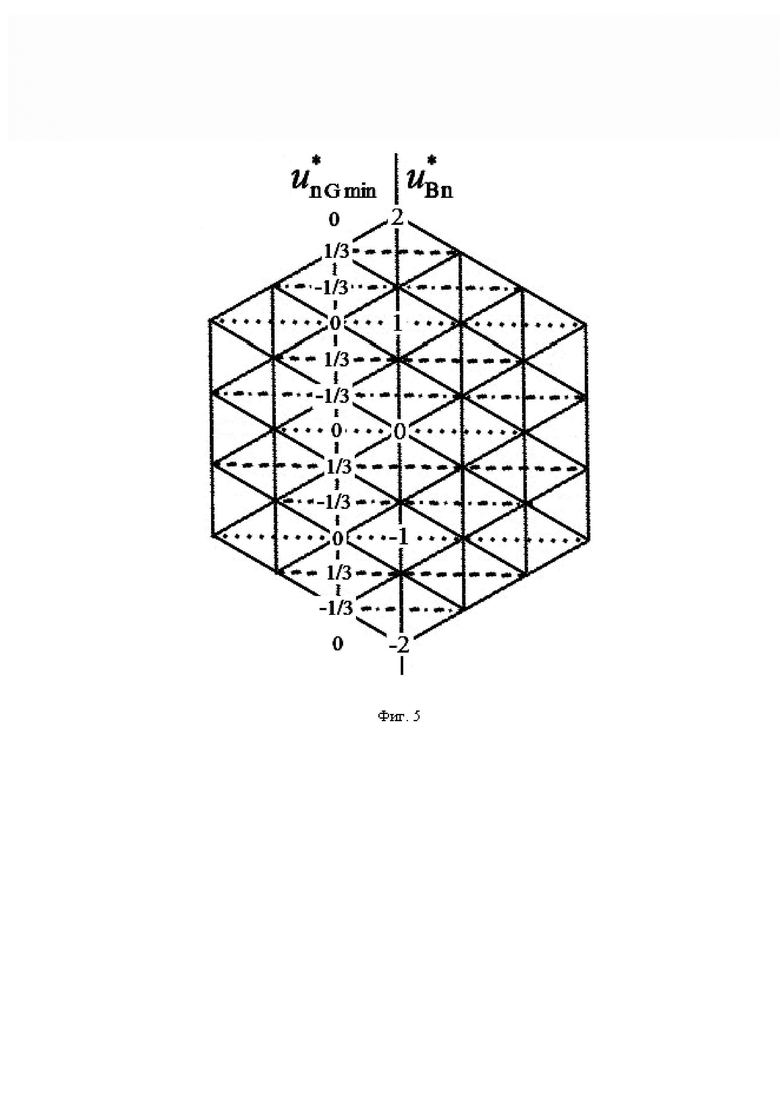
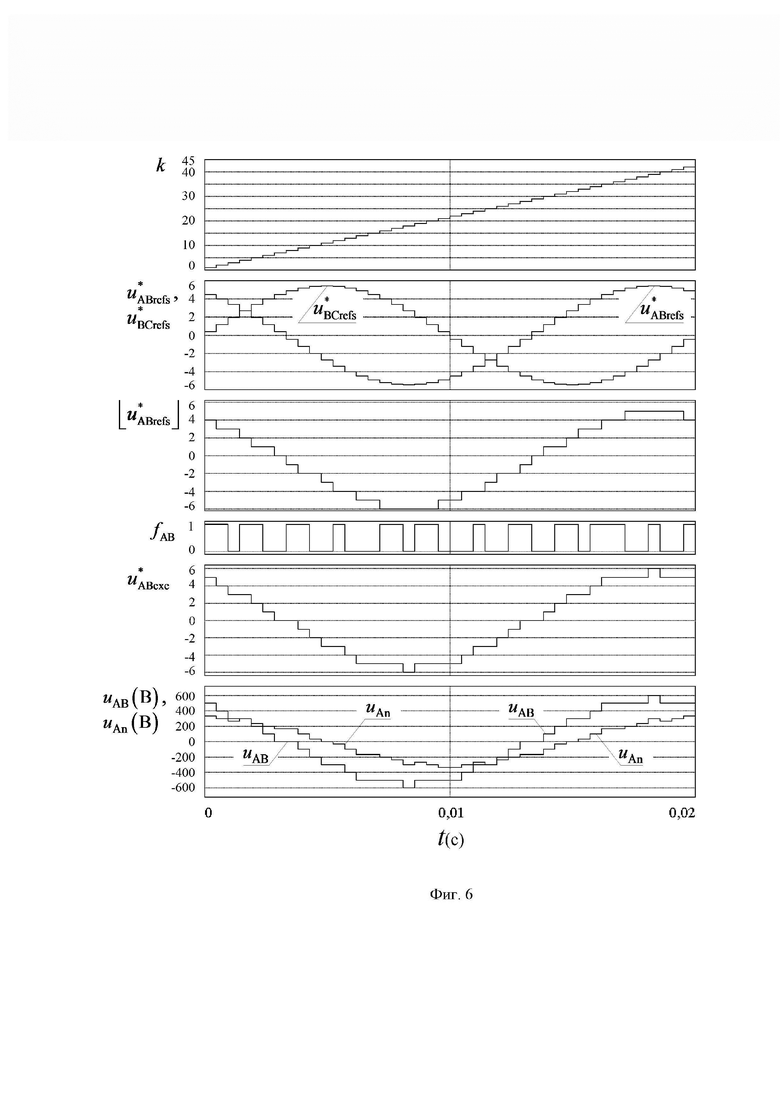
На фиг. 1 показана векторная диаграмма (все возможные векторы, местоположение которых может принимать выполняемый пространственный вектор выходного напряжения ВПВ) в координатной системе косоугольных 60-градусных координат для случая четырехуровневого инвертора напряжения (римскими цифрами пронумерованы проходимые ВПВ секторы); на фиг. 2 представлены координаты вершин ромба четырех векторов, ближайших к концу обобщенного пространственного вектора (точка R), в координатных системах косоугольных 60-градусных координат нормированных значений прямых и обратных линейных напряжений, а также показано положение точки R относительно сторон ромба; на фиг. 3 представлены координаты трех векторов, ближайших к местоположению пространственного вектора для каждого из двух видов треугольников ближайших векторов, и его барицентрические координаты относительно вершин этих треугольников; на фиг. 4 показаны значения барицентрических координат пространственного вектора относительно вершин треугольников, выраженные через дробные части нормированных значений только двух прямых линейных напряжений, на фиг. 5 показано соответствие между минимальными доступными нормированными значениями трехфазного синфазного напряжения пространственных векторов и нормированными значениями фазного напряжения нагрузки фазы “В” МУИН; на фиг. 6 и фиг. 7 представлены осциллограммы основных выполняемых сигналов напряжений (сигналов системы управления) и напряжений силовой схемы МУИН, полученные моделированием в программном пакете PSIM.
Здесь и далее звездочки в надстрочных индексах обозначают относительные, т.е. нормированные по постоянному напряжению единичного (базового) уровня 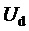 значения напряжений,
значения напряжений, 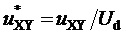 ; «exe» в нижних индексах обозначает исполняемые (выполняемые) сигналы напряжений, форма которых (зависимость от времени) является результатом применения рассматриваемой методики и далее воспроизводится в напряжениях силовых цепей. Трехфазное синфазное напряжение (разность потенциалов нейтральной точки соединенной звездой нагрузки МУИН n и заземляемого узла МУИН G) для всех типов трехфазных МУИН, независимо от положения заземляемого узла G, определяется через значения фазных напряжений
; «exe» в нижних индексах обозначает исполняемые (выполняемые) сигналы напряжений, форма которых (зависимость от времени) является результатом применения рассматриваемой методики и далее воспроизводится в напряжениях силовых цепей. Трехфазное синфазное напряжение (разность потенциалов нейтральной точки соединенной звездой нагрузки МУИН n и заземляемого узла МУИН G) для всех типов трехфазных МУИН, независимо от положения заземляемого узла G, определяется через значения фазных напряжений 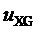 относительно узла G:
относительно узла G:
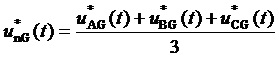 . (1)
. (1)
Способ реализуется следующим образом. Выполняемый обобщенный пространственный вектор выходного напряжения 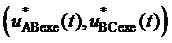 формируется по мгновенным относительным значениям двух выполняемых линейных напряжений в 60-градусных координатах
формируется по мгновенным относительным значениям двух выполняемых линейных напряжений в 60-градусных координатах 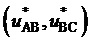 , см. фиг. 1.
, см. фиг. 1.
Необходимые для выбора ближайшего вектора барицентрические координаты (БК) пространственного вектора на двух треугольниках (при нахождении его в одном или в другом, соответственно) численно равны дробным частям относительных значений трех прямых линейных напряжений 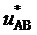 ,
, 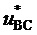 и
и 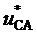 или трех обратных им линейных напряжений
или трех обратных им линейных напряжений 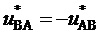 ,
, 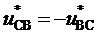 и
и 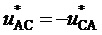 . Значения БК на двух треугольниках показаны на фиг. 3 у соответствующих вершин внутри треугольников.
. Значения БК на двух треугольниках показаны на фиг. 3 у соответствующих вершин внутри треугольников.
При этом благодаря выполнению соотношения для случая нецелых значений линейных напряжений 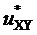 (см. фиг. 2)
(см. фиг. 2)
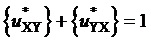 (2)
(2)
и соотношений
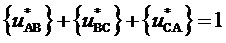 ,
, 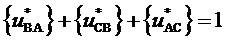 , (3)
, (3)
верных при нахождении пространственного вектора в треугольниках, направленных, соответственно, одной вершиной вверх и одной вершиной вниз (см. фиг. 3), БК пространственного вектора на двух треугольниках (при нахождении его в одном или другом, соответственно) могут быть выражены через дробные части относительных значений двух рассматриваемых линейных напряжений, как это показано на фиг. 4. Таким образом, все основные операции для обоих видов треугольников ближайших векторов производятся только над отсчетами сигналов ЗПВ, соответствующих двум базовым прямым линейным напряжениям 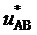 и
и 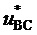 (исключается рассмотрение отсчетов сигналов, соответствующих прямому линейному напряжению
(исключается рассмотрение отсчетов сигналов, соответствующих прямому линейному напряжению 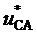 и обратным линейным напряжениям
и обратным линейным напряжениям 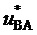 ,
, 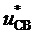 и
и 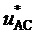 ). Самым близким из трех ближайших векторов является тот, которому соответствует барицентрическая координата с наибольшим значением. После определения координат ВПВ
). Самым близким из трех ближайших векторов является тот, которому соответствует барицентрическая координата с наибольшим значением. После определения координат ВПВ 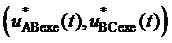 , соответствующих ближайшим векторам векторной диаграммы в текущий момент времени, определяются сигналы мгновенных относительных значений трех выполняемых фазных напряжений относительно заземляемого узла G
, соответствующих ближайшим векторам векторной диаграммы в текущий момент времени, определяются сигналы мгновенных относительных значений трех выполняемых фазных напряжений относительно заземляемого узла G 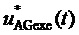 ,
,  и
и  , необходимые для получения
, необходимые для получения 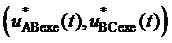 при минимальных по модулю возможных значениях трехфазного синфазного напряжения МУИН, и система управления МУИН вырабатывает сигналы непосредственно для драйверов полупроводниковых ключей для получения данных значений фазных напряжений.
при минимальных по модулю возможных значениях трехфазного синфазного напряжения МУИН, и система управления МУИН вырабатывает сигналы непосредственно для драйверов полупроводниковых ключей для получения данных значений фазных напряжений.
Способ включает 9 описанных ниже основных операций.
1. Определение значения коэффициента амплитудной модуляции линейного напряжения 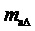 по задаваемому значению амплитуды выходного фазного напряжения
по задаваемому значению амплитуды выходного фазного напряжения 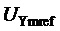 (значение модуля ЗПВ) или по задаваемому значению коэффициента амплитудной модуляции фазного напряжения
(значение модуля ЗПВ) или по задаваемому значению коэффициента амплитудной модуляции фазного напряжения 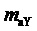 :
:
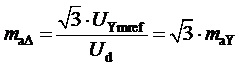 . (4)
. (4)
2. Генерирование непрерывной функции номера интервала действующего отсчета k:
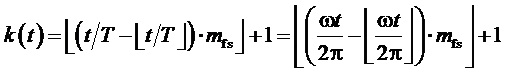 , (5)
, (5)
где 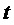 - время,
- время,
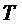 - период сигналов модулирующих (задаваемых) линейных напряжений,
- период сигналов модулирующих (задаваемых) линейных напряжений,
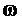 - круговая частота сигналов модулирующих (задаваемых) линейных напряжений,
- круговая частота сигналов модулирующих (задаваемых) линейных напряжений, 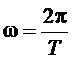 ,
,
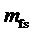 - кратность частоты отсчетов, т.е. общее число отсчетов за период выходного напряжения,
- кратность частоты отсчетов, т.е. общее число отсчетов за период выходного напряжения, 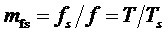 ,
, 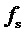 и
и 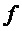 - соответственно, частота отсчетов и частота модулирующих (задаваемых) линейных напряжений,
- соответственно, частота отсчетов и частота модулирующих (задаваемых) линейных напряжений, 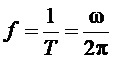 ,
, 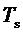 - длительность интервала отсчета,
- длительность интервала отсчета, 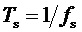 ,
,
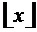 - функция взятия целой части величины
- функция взятия целой части величины 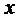 (антье
(антье 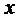 ), то есть функция округления величины
), то есть функция округления величины 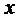 в меньшую сторону до ближайшего целого числа (с учетом знака).
в меньшую сторону до ближайшего целого числа (с учетом знака).
За период выходного напряжения 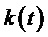 принимает целочисленные значения 1…
принимает целочисленные значения 1…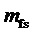 . Для улучшения гармонического состава напряжений МУИН значение кратности частоты отсчетов
. Для улучшения гармонического состава напряжений МУИН значение кратности частоты отсчетов 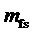 выбирается кратным 2 (число полуволн) и 3 (число фаз МУИН), таким образом, оно должно быть кратно 6.
выбирается кратным 2 (число полуволн) и 3 (число фаз МУИН), таким образом, оно должно быть кратно 6.
3. Генерирование отсчетов 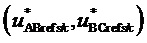 пространственного вектора задания с координатами в форме сигналов мгновенных относительных значений двух задаваемых линейных напряжений
пространственного вектора задания с координатами в форме сигналов мгновенных относительных значений двух задаваемых линейных напряжений 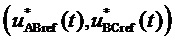 , где
, где 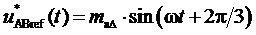 и
и 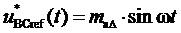 . При этом отсчеты сигналов базисных линейных напряжений
. При этом отсчеты сигналов базисных линейных напряжений 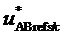 и
и 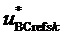 соответствуют середине тактового интервала с номером k, так что их значения опережают значения сигналов соответствующих задаваемых линейных напряжений
соответствуют середине тактового интервала с номером k, так что их значения опережают значения сигналов соответствующих задаваемых линейных напряжений 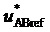 и
и 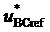 по фазе на половину такта,
по фазе на половину такта, 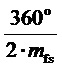 или
или 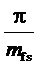 :
:
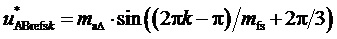 ,
, 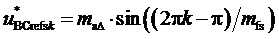 . (6)
. (6)
В качестве альтернативы могут быть использованы функция номера интервала действующего отсчета k, сдвинутая по времени относительно заданной в (5) функции 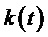 на половину интервала отсчета влево,
на половину интервала отсчета влево, 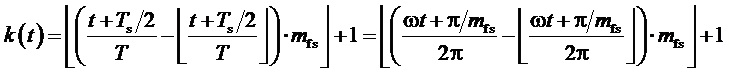 , и отсчеты, задаваемые следующими выражениями:
, и отсчеты, задаваемые следующими выражениями: 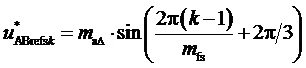 ,
, 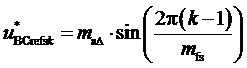 . Однако изменение поведения функции
. Однако изменение поведения функции  (принимающей значения
(принимающей значения 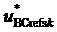 , меняющиеся с течением времени) вблизи
, меняющиеся с течением времени) вблизи 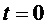 не влияет на поведение в этой точке сигнала выполняемого линейного напряжения
не влияет на поведение в этой точке сигнала выполняемого линейного напряжения  , и результирующие зависимости гармонических коэффициентов генерируемого напряжения (коэффициента гармоник напряжения THD, и интегральных коэффициентов гармоник, т.е. взвешенных THD напряжения различных порядков) не меняются принципиальным образом, см. Lopatkin N.N., “Assessment of output voltage quality of three-phase multilevel inverter with nearest vector selecting space vector control”, 14th International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Proceedings, volume 1, part 6, pp. 158-163, IEEE, Russia, Novosibirsk, 2018.
, и результирующие зависимости гармонических коэффициентов генерируемого напряжения (коэффициента гармоник напряжения THD, и интегральных коэффициентов гармоник, т.е. взвешенных THD напряжения различных порядков) не меняются принципиальным образом, см. Lopatkin N.N., “Assessment of output voltage quality of three-phase multilevel inverter with nearest vector selecting space vector control”, 14th International Scientific-Technical Conference on Actual Problems of Electronics Instrument Engineering (APEIE), Proceedings, volume 1, part 6, pp. 158-163, IEEE, Russia, Novosibirsk, 2018.
Отсчеты производятся в моменты изменения значения функции 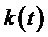 , они хранятся и используются до начала обслуживания следующего тактового интервала с номером k+1, т.е. обновление отсчетов происходит в момент окончания старого и начала нового интервала.
, они хранятся и используются до начала обслуживания следующего тактового интервала с номером k+1, т.е. обновление отсчетов происходит в момент окончания старого и начала нового интервала.
4. Вычисление для очередного интервала отсчета с номером k четырех основных величин, необходимых для определения координат вершин ромба четырех ближайших к отсчету ЗПВ векторов, барицентрических координат отсчета на каждом из треугольников трех ближайших векторов и вида треугольника:
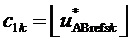 ,
, 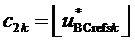 ,
, 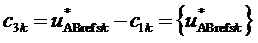 ,
, 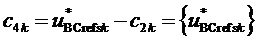 , (7)
, (7)
где 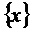 - функция взятия дробной части величины
- функция взятия дробной части величины 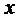 ,
, 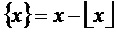 .
.
Согласно фиг. 2 сразу могут быть определены координаты четырех векторов вершин ромба на интервале отсчета с номером k: 1) 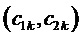 - корневой вектор ромба, 2)
- корневой вектор ромба, 2) 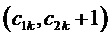 , 3)
, 3) 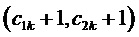 , 4)
, 4) 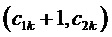 .
.
При этом значения величин 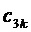 и
и 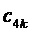 являются барицентрическими координатами отсчета ЗПВ на треугольнике векторов, направленном одной вершиной вверх, относительно вершин
являются барицентрическими координатами отсчета ЗПВ на треугольнике векторов, направленном одной вершиной вверх, относительно вершин 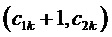 и
и 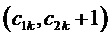 , соответственно, см. фиг. 3. Все остальные БК (БК относительно вершины корневого вектора ромба
, соответственно, см. фиг. 3. Все остальные БК (БК относительно вершины корневого вектора ромба 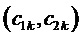 в этом же треугольнике и БК на треугольнике векторов, направленном одной вершиной вниз) выражаются через
в этом же треугольнике и БК на треугольнике векторов, направленном одной вершиной вниз) выражаются через 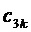 и
и 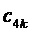 по свойству дробных величин для ромба (2) и по свойству БК для случая нахождения ЗПВ в каждом из двух треугольников ромба (3), см. фиг.4.
по свойству дробных величин для ромба (2) и по свойству БК для случая нахождения ЗПВ в каждом из двух треугольников ромба (3), см. фиг.4.
5. Вычисление для очередного интервала отсчета с номером k значения (рассматриваемого как логический уровень) идентификатора вида модуляционного треугольника 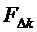 (равно 1, если треугольник направлен одной вершиной вверх):
(равно 1, если треугольник направлен одной вершиной вверх):
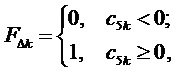 (8)
(8)
где 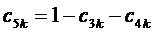 .
.
Здесь использовано условие нахождения конца обобщенного пространственного вектора точно на диагонали ромба, принадлежащей двум смежным треугольникам: для векторов 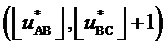 и
и 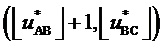 фиг. 3
фиг. 3 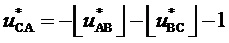 . Поскольку для корневого вектора ромба
. Поскольку для корневого вектора ромба 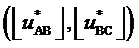 имеем
имеем 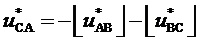 , то принадлежность конца вектора треугольнику, направленному одной вершиной вверх, может быть выражена неравенством
, то принадлежность конца вектора треугольнику, направленному одной вершиной вверх, может быть выражена неравенством 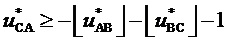 . Отсюда, с учетом равенства
. Отсюда, с учетом равенства 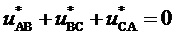 и (7), и следует (8). Причисление диагонали к одному из треугольников является условным, т.к., в любом из треугольников, выбор вблизи общей границы хотя и осуществляется формально из трех векторов, но ближайшими двумя будут именно два вектора вершин диагонали ромба, один из которых в этом случае и будет в результате выбран.
и (7), и следует (8). Причисление диагонали к одному из треугольников является условным, т.к., в любом из треугольников, выбор вблизи общей границы хотя и осуществляется формально из трех векторов, но ближайшими двумя будут именно два вектора вершин диагонали ромба, один из которых в этом случае и будет в результате выбран.
6. Определение для очередного интервала отсчета с номером k по результатам сравнений барицентрических координат отсчета ЗПВ значений (только 0 или 1, т.е. получаемых как логические уровни) величин 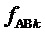 и
и 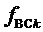 , отвечающих за приращение сигналов двух выполняемых линейных напряжений как выходных координат ВПВ
, отвечающих за приращение сигналов двух выполняемых линейных напряжений как выходных координат ВПВ 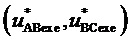 относительно корневого вектора ромба
относительно корневого вектора ромба 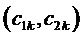 :
:
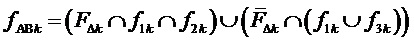 ,
, 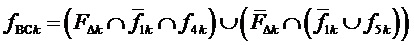 , (9)
, (9)
где 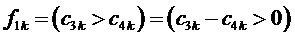 ,
, 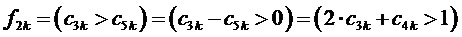 ,
, 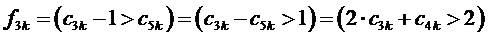 ,
, 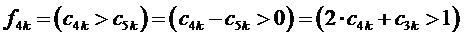 ,
, 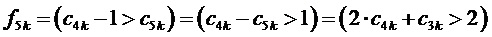 ;
;
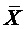 - результат инверсии (логического отрицания) величины
- результат инверсии (логического отрицания) величины 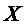 ,
,
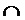 и
и 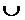 - символы конъюнкции и дизъюнкции, соответственно.
- символы конъюнкции и дизъюнкции, соответственно.
Происхождение (9) и компонентов этой формулы объясняются при помощи фиг. 4. Приращение по координате 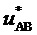 относительно корневого вектора
относительно корневого вектора 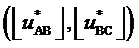 имеет место, когда значение
имеет место, когда значение 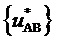 является максимальным из значений трех БК при нахождении отсчета ЗПВ внутри треугольника, направленного одной вершиной вверх, или когда значение
является максимальным из значений трех БК при нахождении отсчета ЗПВ внутри треугольника, направленного одной вершиной вверх, или когда значение 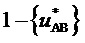 не является максимальным из значений трех БК при нахождении отсчета ЗПВ внутри треугольника, направленного вершиной вниз. Аналогично, приращение по координате
не является максимальным из значений трех БК при нахождении отсчета ЗПВ внутри треугольника, направленного вершиной вниз. Аналогично, приращение по координате 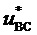 имеет место, когда значение
имеет место, когда значение 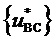 является максимальным из значений трех БК при нахождении отсчета ЗПВ внутри треугольника, направленного вверх, или когда значение
является максимальным из значений трех БК при нахождении отсчета ЗПВ внутри треугольника, направленного вверх, или когда значение 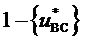 не является максимальным из значений трех БК при нахождении отсчета ЗПВ внутри треугольника, направленного вниз.
не является максимальным из значений трех БК при нахождении отсчета ЗПВ внутри треугольника, направленного вниз.
Как видим, логические функции 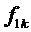 …
…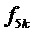 могут быть представлены в максимально простой форме. Кроме исходного варианта, практически непосредственно следующего из выражений для значений БК на фиг. 4, дополнительные варианты представления каждой из логических функций
могут быть представлены в максимально простой форме. Кроме исходного варианта, практически непосредственно следующего из выражений для значений БК на фиг. 4, дополнительные варианты представления каждой из логических функций 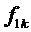 …
…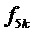 предложены здесь, исходя из предположения о возможности уменьшения погрешности сравнения при сравнении с константой, и для возможной минимизации числа подвергаемых обработке величин.
предложены здесь, исходя из предположения о возможности уменьшения погрешности сравнения при сравнении с константой, и для возможной минимизации числа подвергаемых обработке величин.
7. Определение для очередного интервала отсчета с номером k сигналов относительных значений двух выполняемых линейных напряжений 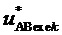 и
и 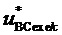 в соответствии с выражением:
в соответствии с выражением:
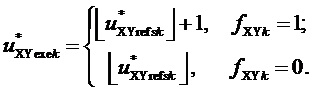 (10)
(10)
Формально, считая 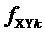 коэффициентом,
коэффициентом, 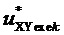 также можно определить следующим образом:
также можно определить следующим образом:
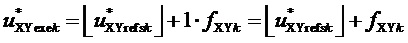 . (11)
. (11)
8. Вычисление сигналов относительных значений трех выполняемых фазных напряжений относительно узла G для очередного интервала отсчета с номером k 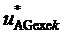 ,
, 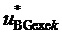 и
и 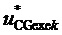 для получения требуемых значений
для получения требуемых значений 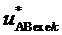 и
и 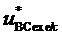 при минимальном возможном значении трехфазного синфазного напряжения МУИН (см. (1))
при минимальном возможном значении трехфазного синфазного напряжения МУИН (см. (1)) 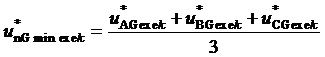 из набора -1/3, 0, 1/3:
из набора -1/3, 0, 1/3:
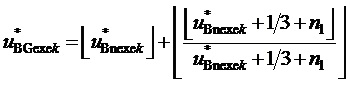 , (12)
, (12)
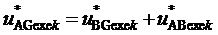 , (13)
, (13)
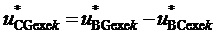 , (14)
, (14)
где 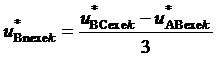 , (15)
, (15)
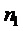 - натуральное число,
- натуральное число,
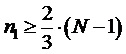 , (16)
, (16)
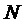 - число уровней МУИН.
- число уровней МУИН.
Для определенности в качестве значения 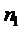 может быть задано как любое заведомо большое натуральное число, так и минимальное значение, удовлетворяющее описанным выше условиям, т.е.
может быть задано как любое заведомо большое натуральное число, так и минимальное значение, удовлетворяющее описанным выше условиям, т.е. 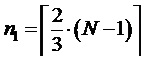 , где
, где 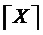 - округление
- округление 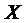 до ближайшего целого в большую сторону (функция «потолок», англ. «ceiling»).
до ближайшего целого в большую сторону (функция «потолок», англ. «ceiling»).
Соответствие минимальных доступных нормированных значений трехфазного синфазного напряжения для пространственных векторов МУИН 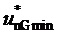 нормированным значениям фазного напряжения нагрузки
нормированным значениям фазного напряжения нагрузки 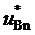 , позволившее получить выражение (12) и условие (16), показано на фиг. 5. Немного более подробное пояснение см. в описании изобретения к патенту № 2818965 «Способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения».
, позволившее получить выражение (12) и условие (16), показано на фиг. 5. Немного более подробное пояснение см. в описании изобретения к патенту № 2818965 «Способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения».
9. Выработка системой управления МУИН в соответствии с топологией МУИН сигналов непосредственно для драйверов полупроводниковых ключей для получения рассчитываемых значений сигналов фазных напряжений 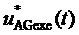 ,
,  и
и  (благодаря (5), при реализации способа мы можем иметь дело с сигналами как мгновенными функциями общего времени
(благодаря (5), при реализации способа мы можем иметь дело с сигналами как мгновенными функциями общего времени 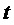 , т.е. с
, т.е. с 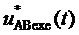 ,
,  ,
, 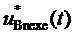 ,
,  ,
, 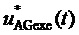 ,
,  и
и 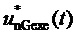 , значения которых могут дискретно изменяться только при изменении значения
, значения которых могут дискретно изменяться только при изменении значения 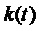 ). При этом сохраняющаяся избыточность ключевых состояний при формировании заданных выходных фазных напряжений внутри каждого из отдельно взятых плеч (фаз) МУИН позволяет для конкретных топологий МУИН оптимизировать распределение токов и напряжений по отдельным элементам (полупроводниковым полностью управляемым ключам) фазных плеч.
). При этом сохраняющаяся избыточность ключевых состояний при формировании заданных выходных фазных напряжений внутри каждого из отдельно взятых плеч (фаз) МУИН позволяет для конкретных топологий МУИН оптимизировать распределение токов и напряжений по отдельным элементам (полупроводниковым полностью управляемым ключам) фазных плеч.
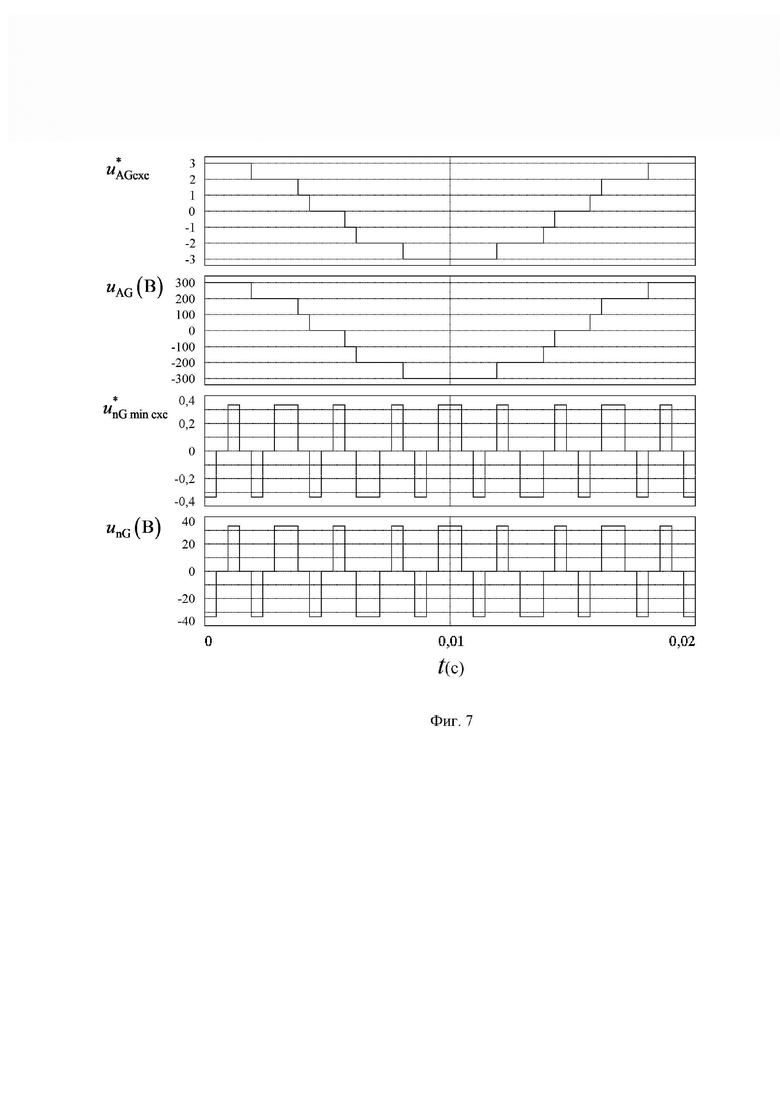
Верификация предложенного способа ПВШИМ выходного напряжения МУИН проведена на модели программного пакета моделирования устройств и систем силовой электроники PSIM (Франция). Осциллограммы сигналов как результат применения способа показаны на фиг. 6 и фиг. 7 для значений 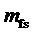 = 42 и
= 42 и 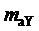 = 3,14 (
= 3,14 (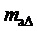
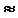 5,44) при
5,44) при 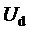 = 100 В. Сигналы системы управления (включая выполняемые сигналы) являются безразмерными, а напряжения силовой схемы выражены в вольтах. На фиг. 6 представлены следующие сигналы: функции номера интервала действующего отсчета
= 100 В. Сигналы системы управления (включая выполняемые сигналы) являются безразмерными, а напряжения силовой схемы выражены в вольтах. На фиг. 6 представлены следующие сигналы: функции номера интервала действующего отсчета 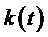 ; функций отсчетов сигналов относительных значений базисных линейных напряжений задания
; функций отсчетов сигналов относительных значений базисных линейных напряжений задания  и
и 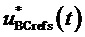 ; функций взятия целой части отсчетов сигнала одного из линейных напряжений задания
; функций взятия целой части отсчетов сигнала одного из линейных напряжений задания  , приращения соответствующего выполняемого линейного напряжения
, приращения соответствующего выполняемого линейного напряжения 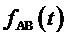 и собственно суммарный (в смысле (11)) сигнал выполняемого относительного линейного напряжения
и собственно суммарный (в смысле (11)) сигнал выполняемого относительного линейного напряжения 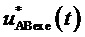 , а также сигналы выходных напряжений силовой части инвертора - линейного
, а также сигналы выходных напряжений силовой части инвертора - линейного 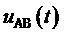 и фазного относительно нейтральной точки нагрузки
и фазного относительно нейтральной точки нагрузки 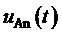 . На фиг. 7 показаны сигналы
. На фиг. 7 показаны сигналы 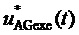 относительного значения выполняемого фазного напряжения относительно узла G и минимального по модулю достижимого значения трехфазного синфазного напряжения МУИН
относительного значения выполняемого фазного напряжения относительно узла G и минимального по модулю достижимого значения трехфазного синфазного напряжения МУИН  , а также сигналы напряжений силовой части инвертора - напряжения фазы A относительно узла G
, а также сигналы напряжений силовой части инвертора - напряжения фазы A относительно узла G 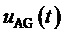 и итогового (как результат примененного подхода) трехфазного синфазного напряжения
и итогового (как результат примененного подхода) трехфазного синфазного напряжения 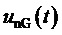 . Как видно из фиг. 6 и фиг. 7, при принятии силовых ключей идеальными формы (зависимости от времени) сигналов напряжений силовой цепи (
. Как видно из фиг. 6 и фиг. 7, при принятии силовых ключей идеальными формы (зависимости от времени) сигналов напряжений силовой цепи (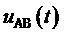 ,
,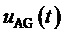 и
и 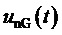 ) в точности повторяют формы соответствующих выполняемых сигналов системы управления (
) в точности повторяют формы соответствующих выполняемых сигналов системы управления (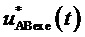 ,
,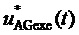 и
и  ).
).
Очевидно, что полученные в результате применения на компьютерной модели предложенного пространственно-векторного способа управления выходным напряжением трехфазного МУИН осциллограммы линейного 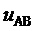 и фазного
и фазного 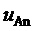 напряжений аналогичны осциллограммам, полученным в результате применения способа-прототипа (см. J. Rodriguez, L. Moran, C. Silva, P. Correa, “A high performance vector control of a 11-level inverter,” IPEMC 2000, 3rd International Power Electronics and Motion Control Conference, Beijing, China, August 15-18, 2000. Proceedings, pp. 1116-1121, а также статьи, упомянутые выше при описании прототипа). Таким образом, тот же результат, т.е. пространственно-векторное управление выходным напряжением с выбором ближайшего вектора, реализован новым способом, использующим выбор наибольших значений барицентрических координат отсчета пространственного вектора задания на треугольниках ближайших векторов. Следует отметить, что указанные барицентрические координаты, изначально определяемые через дробные части относительных значений трех напряжений, в зависимости от типа треугольника, прямой или обратной трехфазных систем линейных напряжений МУИН, в методе пространственно-векторной широтно-импульсной модуляции выражают суммарные коэффициенты заполнения соответствующих векторов на такте ШИМ (отношения длительностей действия векторов к длительности интервала ШИМ).
напряжений аналогичны осциллограммам, полученным в результате применения способа-прототипа (см. J. Rodriguez, L. Moran, C. Silva, P. Correa, “A high performance vector control of a 11-level inverter,” IPEMC 2000, 3rd International Power Electronics and Motion Control Conference, Beijing, China, August 15-18, 2000. Proceedings, pp. 1116-1121, а также статьи, упомянутые выше при описании прототипа). Таким образом, тот же результат, т.е. пространственно-векторное управление выходным напряжением с выбором ближайшего вектора, реализован новым способом, использующим выбор наибольших значений барицентрических координат отсчета пространственного вектора задания на треугольниках ближайших векторов. Следует отметить, что указанные барицентрические координаты, изначально определяемые через дробные части относительных значений трех напряжений, в зависимости от типа треугольника, прямой или обратной трехфазных систем линейных напряжений МУИН, в методе пространственно-векторной широтно-импульсной модуляции выражают суммарные коэффициенты заполнения соответствующих векторов на такте ШИМ (отношения длительностей действия векторов к длительности интервала ШИМ).
Третья и четвертая диаграммы фиг. 7 подтверждают, что значения и сигнала выполняемого минимального достижимого синфазного напряжения 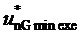 , и самого синфазного напряжения
, и самого синфазного напряжения 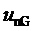 в силовой части трехфазного МУИН ограничены в пределах ожидаемых диапазонов:
в силовой части трехфазного МУИН ограничены в пределах ожидаемых диапазонов: 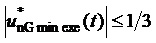 ,
, 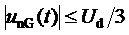 . При этом, как показывают осциллограммы
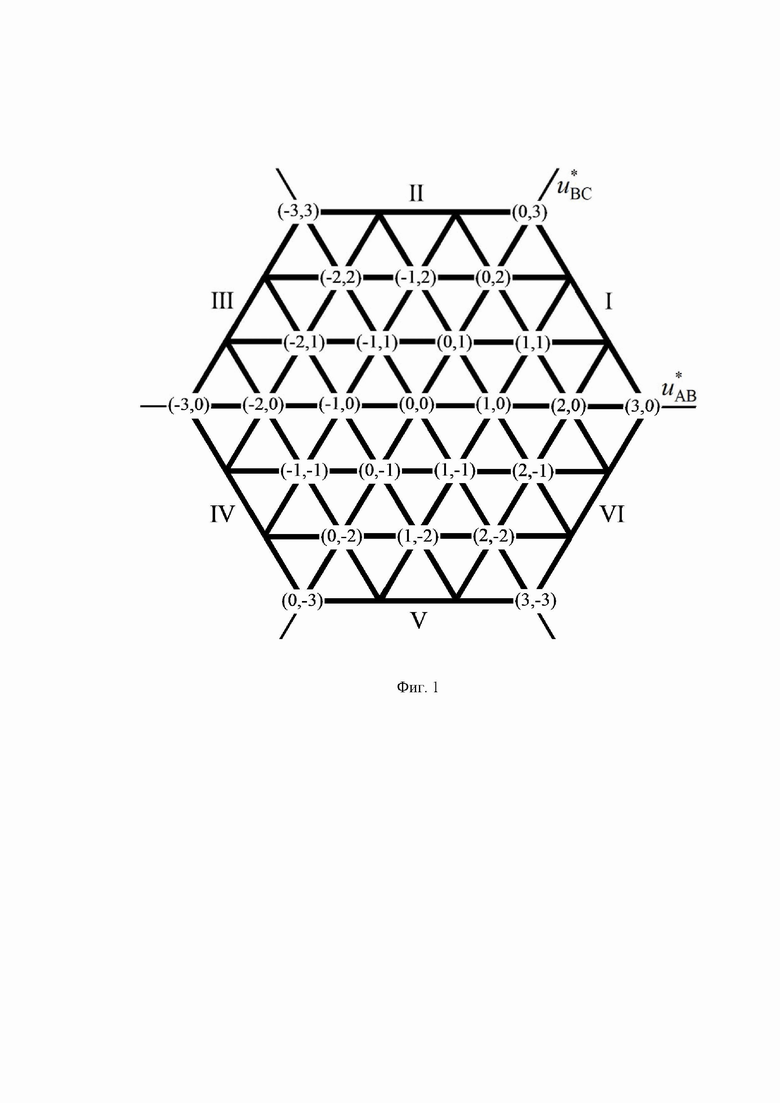
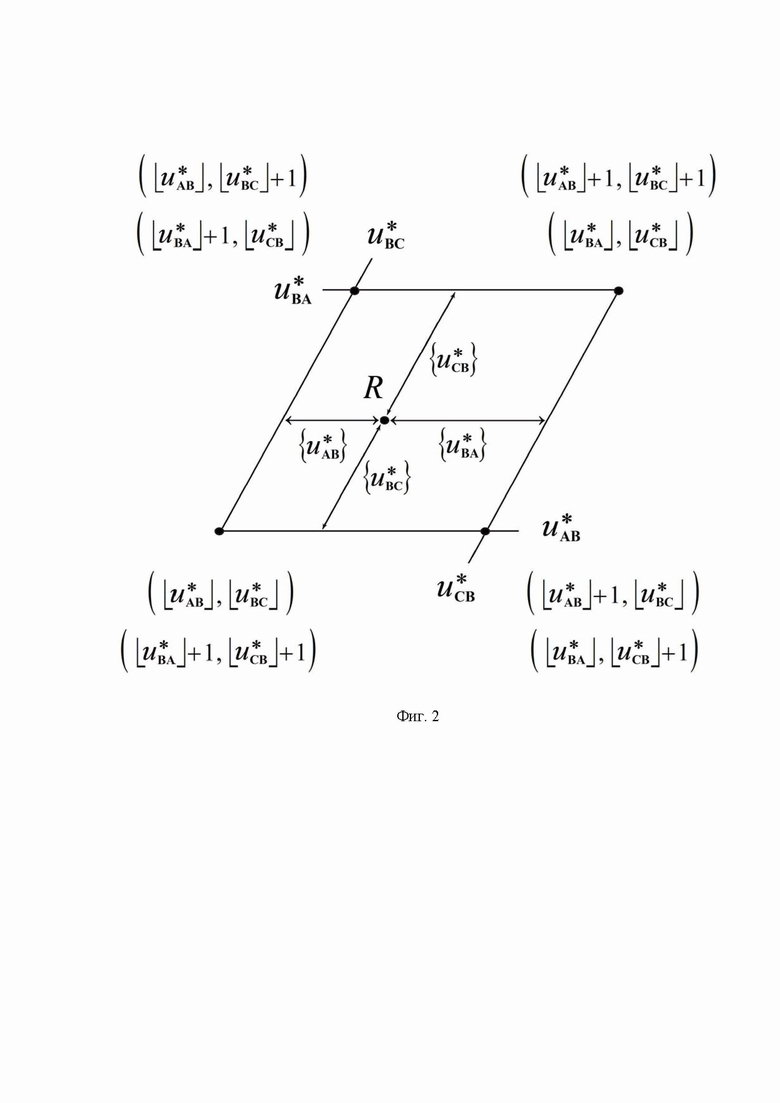
. При этом, как показывают осциллограммы 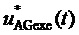 и
и 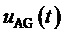 (первая и вторая диаграммы фиг. 7), применение способа не приводит к каким-либо излишним (дополнительным) изменениям фазного напряжения МУИН относительно его заземленного узла, что означает сохранение низкого количества переключений силовых полупроводниковых ключей плеч инвертора за период выходного напряжения и низкого уровня соответствующих (динамических) потерь мощности в них.
(первая и вторая диаграммы фиг. 7), применение способа не приводит к каким-либо излишним (дополнительным) изменениям фазного напряжения МУИН относительно его заземленного узла, что означает сохранение низкого количества переключений силовых полупроводниковых ключей плеч инвертора за период выходного напряжения и низкого уровня соответствующих (динамических) потерь мощности в них.
Таким образом, предлагаемый пространственно-векторный способ управления выходным напряжением многоуровневого трехфазного автономного инвертора напряжения, реализующий выбор ближайшего к заданному вектора, по сравнению с прототипом, при том же качестве выходных напряжений МУИН по гармоническому составу и при том же уровне потерь мощности на переключение силовых полупроводниковых ключей (т.е. при том же значении КПД МУИН), при гарантированном ограничении значений синфазного напряжения позволяет сократить число необходимых операций за счет упрощенной процедуры идентификации трех ближайших векторов и выбора одного из них (использующей целые и дробные части отсчетов нормированных значений линейных напряжений задания как относящиеся к положению пространственного вектора задания наклонные 60-градусные координаты базового вектора ромба ближайших векторов и барицентрические координаты на треугольниках трех ближайших векторов, соответственно), без какого-либо усложнения и без использования таблиц поиска применяется к любой схемной конфигурации МУИН при произвольном числе одинаковых по величине формируемых уровней выходного линейного напряжения, что позволяет понизить требования к используемым в системе управления аппаратным средствам и тем самым расширяет применение метода выбора ближайшего вектора при пространственно-векторном управлении выходным напряжением МУИН.
| название | год | авторы | номер документа |
|---|---|---|---|
| Способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения | 2023 |
|
RU2818965C1 |
| СПОСОБ ВЕКТОРНОГО УПРАВЛЕНИЯ СИНХРОННЫМ ЭЛЕКТРОДВИГАТЕЛЕМ С ПОСТОЯННЫМИ МАГНИТАМИ НА РОТОРЕ И ЭЛЕКТРОПРИВОД ДЛЯ ОСУЩЕСТВЛЕНИЯ ЭТОГО СПОСОБА | 1998 |
|
RU2141719C1 |
| СПОСОБ ВЕКТОРНОГО УПРАВЛЕНИЯ СКОРОСТЬЮ ВРАЩЕНИЯ ТРЕХФАЗНОЙ МАШИНЫ | 2013 |
|
RU2557071C2 |
| ВЫПРЯМИТЕЛЬ ТРЕХФАЗНОГО ТОКА | 2005 |
|
RU2297707C2 |
| СПОСОБ ВЕКТОРНОЙ ОРИЕНТАЦИИ ТОКА ЭЛЕКТРОМЕХАНИЧЕСКОГО ПРЕОБРАЗОВАТЕЛЯ ЭНЕРГИИ И УСТРОЙСТВО ВЕКТОРНОЙ ОРИЕНТАЦИИ ("ВЕКТОРИНГ") ДЛЯ ОСУЩЕСТВЛЕНИЯ СПОСОБА | 1998 |
|
RU2141720C1 |
| СПОСОБ УПРАВЛЕНИЯ ТРЕХФАЗНЫМ ВЕНТИЛЬНЫМ ДВИГАТЕЛЕМ | 2012 |
|
RU2522675C2 |
| ЧАСТОТНО-РЕГУЛИРУЕМЫЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД | 2006 |
|
RU2313894C1 |
| СПОСОБ ЗАДАНИЯ НЕСИММЕТРИИ НАПРЯЖЕНИЙ В ТРЕХФАЗНОЙ СИСТЕМЕ | 1992 |
|
RU2024173C1 |
| Способ задания несимметрии напряжений в трехфазной системе | 1978 |
|
SU750394A1 |
| ЧАСТОТНО-РЕГУЛИРУЕМЫЙ АСИНХРОННЫЙ ЭЛЕКТРОПРИВОД | 2008 |
|
RU2401502C2 |
Изобретение относится к электротехнике, а именно к области силовой электроники, и может быть использовано для управления многоуровневым трехфазным автономным инвертором напряжения (в дальнейшем также называемым «инвертор») с произвольным числом одинаковых по величине уровней выходного линейного напряжения. Техническим результатом является формирование регулируемого трехфазного переменного напряжения инвертора произвольной схемной конфигурации с произвольным числом одинаковых по величине формируемых уровней выходного линейного напряжения (без использования таблиц поиска и без какого-либо усложнения при росте числа уровней инвертора) путем выбора на каждом такте доступного вектора, ближайшего к отсчету пространственного вектора напряжения задания, при упрощенной процедуре идентификации трех ближайших векторов и выбора одного из них, которая позволяет понизить требования к используемым в системе управления аппаратным средствам, что расширяет применение метода выбора ближайшего вектора при пространственно-векторном управлении выходным напряжением инвертора. Технический результат достигается за счет пространственно-векторного способа управления выходным напряжением инвертора, в котором реализуется выбор вектора, ближайшего к заданному вектору, и используется для этого выбора сравнение барицентрических координат вектора задания на треугольнике ближайших векторов. В качестве наклонных 60-градусных координат базового вектора ромба ближайших векторов и барицентрических координат на треугольниках трех ближайших векторов выступают соответственно целые и дробные части нормированных значений линейных напряжений (определяющих положение пространственного вектора напряжения), а непосредственной вычислительной обработке подвергаются отсчеты только двух линейных напряжений задания. Кроме того, за счет выбора ключевых состояний фаз трехфазного инвертора мгновенное значение его синфазного напряжения гарантированно остается в пределах ±1/3 от величины питающего постоянного напряжения единичного (базового) уровня, что смягчает проблему синфазного напряжения и упрощает меры по защите от сопровождающих его нежелательных явлений, в частности облегчает фильтрацию синфазного тока инвертора. 7 ил.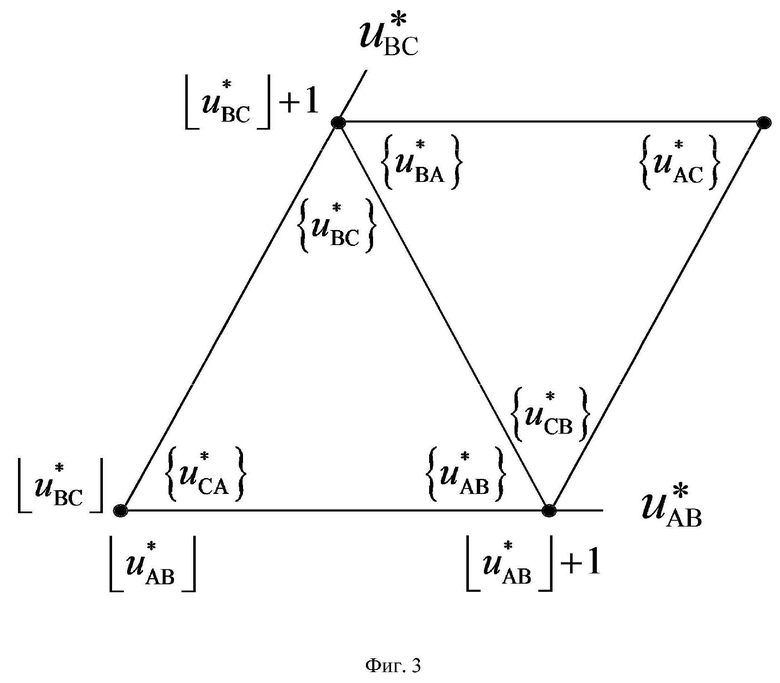
Пространственно-векторный способ управления выходным напряжением многоуровневого трехфазного автономного инвертора напряжения, состоящий в том, что период выходного напряжения разбивается на равные тактовые интервалы, и на каждом таком интервале формируемый меняющийся во времени выполняемый обобщенный пространственный вектор выходного напряжения принимает значение доступного для реализации инвертором пространственного вектора, ближайшего к отсчитанному для данного такта положению на плоскости обобщенного пространственного вектора задания, отличающийся тем, что данный ближайший вектор выбирается как соответствующий той из барицентрических координат отсчета пространственного вектора задания на треугольнике трех ближайших векторов, которая имеет максимальное значение, при этом для обоих видов треугольников ближайших векторов координаты трех ближайших к отсчитанному вектору задания векторов и барицентрические координаты отсчета на идентифицированном треугольнике вычисляются, соответственно, через целые и дробные части отсчетов сигналов относительных величин двух линейных напряжений как косоугольных координат отсчета пространственного вектора задания, для каждого пространственного вектора, являющегося значением меняющегося во времени выполняемого обобщенного пространственного вектора выходного напряжения, вычисляются достижимое для него минимальное по модулю нормированное по постоянному напряжению единичного (базового) уровня значение синфазного напряжения многоуровневого трехфазного автономного инвертора напряжения из набора -1/3, 0, 1/3 и необходимые для его достижения нормированные значения фазных напряжений относительно заземляемого узла инвертора.
| Способ пространственно-векторной широтно-импульсной модуляции выходного напряжения многоуровневого трехфазного автономного инвертора напряжения | 2023 |
|
RU2818965C1 |
| СПОСОБ УПРАВЛЕНИЯ ТРЕХФАЗНЫМ МОСТОВЫМ ПРЕОБРАЗОВАТЕЛЕМ | 2007 |
|
RU2379819C2 |
| US 2011249479 A1, 13.10.2011 | |||
| Способ управления матричным преобразователем частоты | 2016 |
|
RU2641653C1 |
| Способ управления инвертором напряжения в системах бесперебойного питания и системах накопления электрической энергии при резкопеременной нагрузке | 2018 |
|
RU2697262C1 |
| J | |||
| Rodriguez, L | |||
| Moran, J | |||
| Pontt, P | |||
| Correa, C | |||
| Silva, "A high-performance vector control of an 11-level inverter," IEEE Transactions on Industrial Electronics, Vol | |||
| Устройство для выпрямления многофазного тока | 1923 |
|
SU50A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
| Капельная масленка с постоянным уровнем масла | 0 |
|
SU80A1 |
Авторы
Даты
2025-03-28—Публикация
2024-08-28—Подача