Изобретение относится к контрольно-измерительной технике и может быть использовано для измерения частоты гармонического сигнала, несущей частоты.
Важнейшей характеристикой периодических процессов является частота, которая определяется числом полных циклов (периодов) колебаний за единичный интервал времени. Необходимость в измерении частоты возникает во многих областях науки и техники и особенно часто в радиоэлектронике, которая охватывает обширную область электрических колебаний от инфра низких до сверхвысоких частот включительно.
При нарушении равномерности амплитуды колебаний сигнала он становится не гармоническим. Это является одной из причин возникновения погрешности измерения частоты основной гармоники сигнала.
Известен спектральный способ измерения частоты сигнала основанный на выполнении преобразования Фурье. (Харкевич А.А. Спектры и анализ. - М.: Госиздат физико-математической литературы, 1962. 236 с.) (Цифровой спектральный анализ и его приложения. С.Л. Марпл-мл. М.: Мир, 1990, - 584 с.). Идея предлагаемого способа измерения частоты сигнала заключается в том, что значение центра jmax сигнала в частотной области, определенное с помощью преобразования Фурье по принципу положения максимума амплитуды спектра мощности сигнала в частотной области и вычисленного на его основе значения частоты сигнала. Измерение частоты сводится к определению количества периодов К сигнала с помощью быстрого преобразования Фурье (БПФ) на интервале наблюдения N*dt, где N - количество отсчетов, a dt - интервал дискретности измерения, и последующему вычислению частоты сигнала по формуле f=K/(N*dt). Разрешение по частоте df, т.е. абсолютная погрешность результата измерения частоты, равно I/(N*dt) или, что то же, f/K, отсюда относительная погрешность определения частоты δ f=1/K. Таким образом, погрешность определения частоты этим известным способом может быть значительной, если количество периодов сигнала в интервале наблюдения мало (менее 10) (В.И. Тарханов, В.С. Тутыгин. Приборный комплекс для поиска и исследования сигналов ЯМР в магнитоупорядоченных веществах. Журнал «Научное приборостроение», 2003, том 13, №1), поэтому погрешность определения частоты достигает 10% и более. (Патент RU 2478213)
Таким образом, недостаток данного способа определения частоты - низкое быстродействие и высокая погрешность, возрастающая при уменьшении количества периодов в анализируемом сигнале. Поэтому используется способ измерения только в качестве грубой оценки.
Известен способ измерения частоты сигнала, заключающийся в измерении длительности периода Тх следования сигнала и в последующем определении частоты fx как величины, обратной периоду. (Бронштейн И.Н., Семендяев К.А. Справочник по математике. - М.: Наука, 1980. 976 с.). Для измерения периода Тх гармонический сигнал преобразуется в последовательность прямоугольных импульсов, передние и задние фронты которых соответствуют переходам через ноль анализируемого гармонического сигнала. Далее используют двоичный счетчик, в котором в процессе измерения каждого периода Тх в диапазоне от Txmin до Txmax получают соответствующие числа NT, предварительно очищают число nmin младших разрядов этого счетчика, обеспечивающих измерение минимального периода Txmin с погрешностью дискретности, не превышающей δ Т, определяют частоту fсч заполнения счетчика с учетом величины Txmin и числа NTKmin, получаемого в счетчике при измерении Txmin, определяют общее число nmax разрядов счетчика, исходя из величины максимального периода измеряемой частоты, отличается тем, что задают значение частоты fсч, округленное в сторону увеличения до ближайшей величины fсч=2Q*106 Гц, где Q - целое положительное или отрицательное число, подают числа NTK, получаемые после окончания периода Тх в nmin младших разрядах счетчика, на адресные входы постоянного запоминающего устройства (ПЗУ), в ячейках памяти которого хранятся предварительно записанные числа NПЗУ, пропорциональные соответствующим значениям fc частоты сигналов. При выполнении условия nmin<nизм nmax, nизм=nmin+m1 или nmin nизм<nmax, nизм=nmax-m2 производят m1 или m2 сдвиг числа NTK в сторону младших или старших разрядов. Запоминают число m1 или m2 проведенных сдвигов и определяют частоту fx1 или fx2 исследуемых сигналов. (Патент РФ №2008 149062)
Недостаток данного способа определения частоты - возрастающая погрешность при увеличении неравномерности амплитуды анализируемого сигнала и возрастающее время измерения при уменьшении частоты сигнала.
В качестве прототипа предлагаемого изобретения рассматривается способ измерения частоты гармонического сигнала, заключающийся в том, что сигнал, дважды последовательно дифференцируют. Измеряют в заданный момент времени значение амплитуды сигнала и его второй производной в любой точке регистрируемого сигнала, кроме точек, в которых амплитуда сигнала или амплитуда его второй производной равны нулю. Вычисляют отношение значений амплитуды второй производной к амплитуде сигнала в выбранной точке. О значении величины частоты сигнала судят по результату извлечения корня квадратного из частного от деления значений амплитуд второй производной и сигнала. (Учебное пособие / Заездный А.М., Плоткин Е.И., Черкасский Ю.А.; Под редакцией А.М. Заездного; Министерство связи СССР. Ленинградский электротехнический институт связи им. проф. М.А. Бонч-Бруевича. - Ленинград: [б.и.], 1971 г. 123 с.)
В основу данного способа измерения частоты положена зависимость U''(t)/U(t)=const для любой точки гармонического сигнала U(t)=Asinω0(t) заданной частоты ω0, кроме точек, в которых A амплитуда сигнала U (t) или амплитуда его второй производной U''(t) равны нулю.
Недостатком данного способа измерения частоты является зависимость результата измерения от неравномерности амплитуды анализируемого сигнала.
В прототипе использовано представление гармонического колебания в фазовом пространстве. Фазовое пространство - пространство, образованное системой координат Xi, которыми являются величины определяющие состояние сигнала. Термин "фаза" здесь означает момент, стадию анализируемого сигнала. В качестве фазовых координат могут выступать следующие зависимые друг от друга функции независимой текущей переменной (пространственной координаты или времени): сигнал, производные от сигнала любого порядка (интегралы) и любые функциональные преобразования от их совокупности. Для каждого значения независимой текущей переменной состоянию сигнала соответствует изображающая точка в выбранном фазовом пространстве. Перемещение этой точки в фазовом пространстве происходит при изменении состояния (параметров) сигнала. След от перемещения изображающей точки в фазовом пространстве образует фазовое изображение сигнала. Представление сигнала в фазовом пространстве в виде фазовой траектории, по которой перемещается изображающая точка, позволяет получить полное представление о характере анализируемого сигнала, кроме оценки его как функции независимой текущей переменной, поскольку при этом методе анализа независимая текущая переменная из рассмотрения исключается. (Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. М.: Государственное издательство физико-математической литературы, 1959. Юревич Е.И. Теория автоматического управления. Л.: Энергия, 1969. 375 с.)
В прототипе фазовыми координатами служат сигнал и его вторая производная. Гармоническое колебание может быть представлено на фазовых плоскостях различных оснований четных разностей, то есть в качестве фазовых координат могу быть использованы, например, сигнал и его вторая, четвертая, шестая и т.д. четные производные или первая производная сигнала и его третья, пятая, седьмая и т.д. нечетные производные.
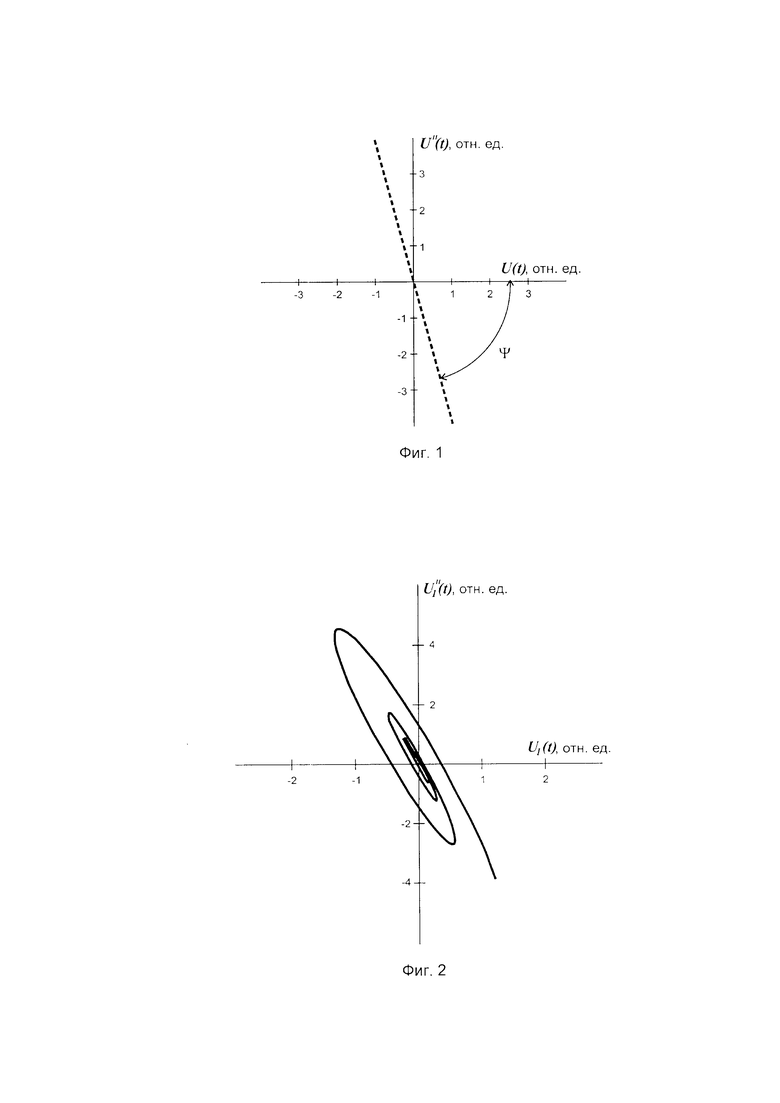
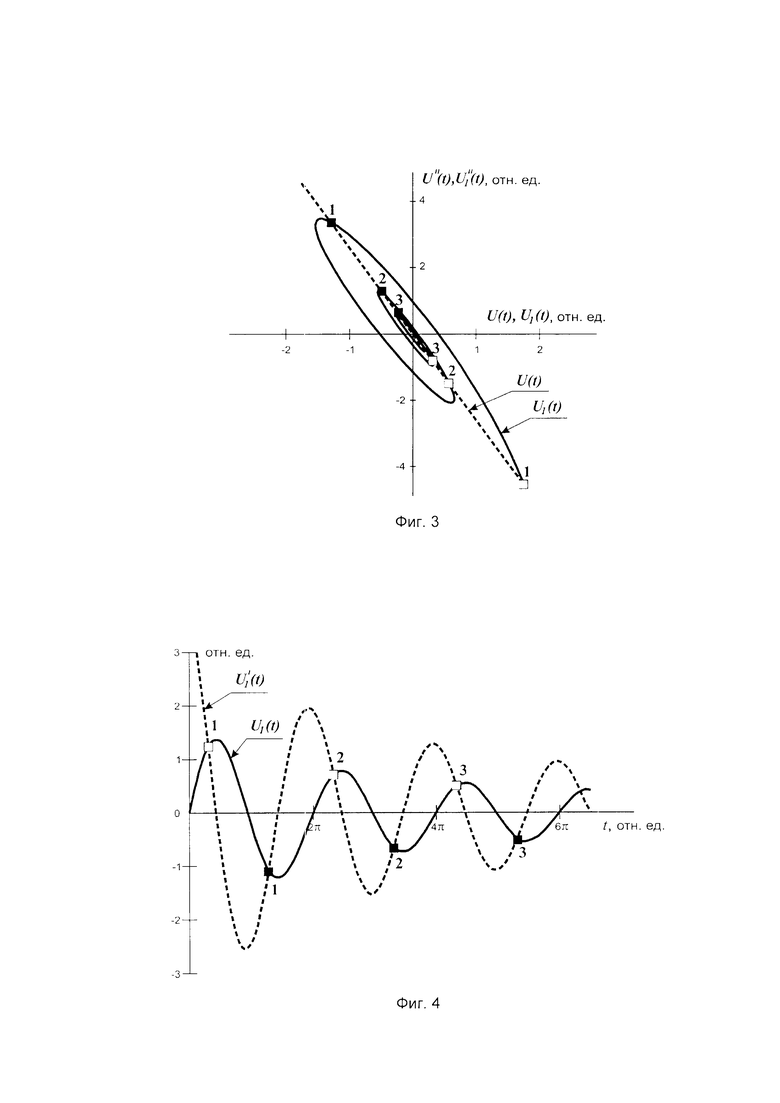
Фазовое изображение гармонического сигнала U(t)=Asinω0(t) на фазовой плоскости, координатами которой являются его вторая производная U''(t) и анализируемый сигнал U(t), представляет собой отрезок прямой линии, проходящей чрез начало координат (Фиг. 1). Длина отрезка прямой линии зависит от амплитуды А сигнала U (t) и его частоты ω0, угол наклона прямой ψ зависит только от частоты со0 сигнала U(t), начальное положение изображающей точки от начальной фазы сигнала.
Фазовые изображения гармонического сигнала любой частоты тождественны и представляют собой отрезки прямых линий проходящих чрез начало координат. При изменении частоты ω0 сигнала меняется угол наклона прямой ψ и, соответственно, меняется величина корня квадратного из частного от деления значений амплитуд второй производной и сигнала, что является информативным параметром в этом способе измерения частоты сигнала.
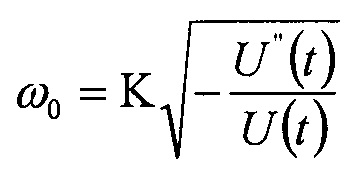
Где К - коэффициент пропорциональности.
Если сигнал представляет собой относительно высокочастотное колебание с плавно меняющейся амплитудой U1(t) (Фиг. 4), его фазовое изображение принимает вид спирали (Фиг. 2). Продольный размах спирали зависит от амплитуды А сигнала U1(t) и его частоты, а поперечный размах спирали зависит от глубины модуляции амплитуды сигнала U1(t). Угол наклона спирали в системе координат зависит от несущей частоты ω0 сигнала U1(t). При увеличении глубины модуляции амплитуды сигнала U1(t) увеличивается поперечный размах спирали. При этом U''(t)/U1(t)≠const для сигнала U1(t). Величина отношения амплитуд второй производной и сигнала при различных значениях независимой текущей переменной не одинакова, что и является причиной возникающей погрешности измерения несущей частоты ω0 сигнала с неравномерной амплитудой U1(t).
Совмещение в единой системе координат фазового изображения гармонического сигнала U(t) (Фиг. 1) и фазового изображения сигнала с неравномерной амплитудой U1(t) (Фиг. 2) одного аргумента, показывает, что прямая линия и спираль имеют точки пересечения (1, 2, 3 и т.д.), показаны на (Фиг. 3). В течение каждого условного периода сигнала с неравномерной амплитудой U1(t) имеются две такие точки.
В точках (1, 2 и 3) спирального фазового изображения сигнала с неравномерной амплитудой U1(t) величина значений амплитуды его второй производной 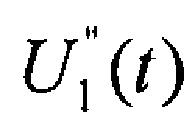 и амплитуды сигнала U1(t), а соответственно и частное от деления их величин такая же, как в гармоническом сигнале U (t).
и амплитуды сигнала U1(t), а соответственно и частное от деления их величин такая же, как в гармоническом сигнале U (t).
Точки (1, 2 и 3) на фазовом изображении сигнала с неравномерной амплитудой U1(t) соответствуют значениям независимой текущей переменной tω, при котором амплитуда сигнала с неравномерной амплитудой U1(t) равна амплитуде его первой производной 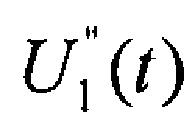 . Показано на (Фиг. 4), соответственно точки (1, 2 и 3).
. Показано на (Фиг. 4), соответственно точки (1, 2 и 3).
Задачей, на решение которой направлено данное изобретение, является обеспечение максимальной точности измерения частоты сигнала, сохраняя постоянное и теоретически бесконечно малое время съема измерительной информации.
Поставленная задача решается за счет достижения технического результата, заключающегося в исключении влияния неравномерности амплитуды сигнала U1(t) на результат измерения частоты ω0.
Данный технический результат достигается тем, что способ измерения частоты сигнала, заключающийся в том, что сигнал дважды последовательно дифференцируют, одновременно измеряют амплитуду сигнала и амплитуду его второй производной, о значении частоты сигнала судят по результату извлечения корня квадратного из частного от деления значений амплитуд второй производной и сигнала, отличающийся тем, что значения амплитуды второй производной и амплитуды сигнала измеряют в момент равенства амплитуд сигнала и его первой производной.
Таким образом, достигнутое исключение влияния неравномерности амплитуды в сигнале обеспечивает по сравнению с прототипом высокую точность измерения частоты сигнала.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТЫ (ВАРИАНТЫ) И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ (ВАРИАНТЫ) | 2008 |
|
RU2402025C2 |
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТЫ СИГНАЛА | 2011 |
|
RU2478213C2 |
| Дифракционный способ измерения линейного размера объекта | 2023 |
|
RU2803823C1 |
| Дифракционный способ измерения линейного размера объекта | 2016 |
|
RU2629895C1 |
| Дифракционный способ измерения линейного размера изделия и устройство для его осуществления | 1987 |
|
SU1469352A1 |
| СПОСОБ АКУСТИЧЕСКОГО ИЗМЕРЕНИЯ РАСХОДА ТЕКУЧИХ СРЕД | 2007 |
|
RU2348904C1 |
| СПОСОБ ФИЛЬТРАЦИИ ИЗМЕРИТЕЛЬНЫХ СИГНАЛОВ | 2010 |
|
RU2462814C2 |
| СПОСОБ ИЗМЕРЕНИЯ ЧАСТОТЫ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2005 |
|
RU2300112C2 |
| ФАЗОМЕТР С ГЕТЕРОДИННЫМ ПРЕОБРАЗОВАНИЕМ ЧАСТОТЫ | 2012 |
|
RU2497136C1 |
| ШИРОКОПОЛОСНАЯ ФАЗОРАЗНОСТНАЯ ЛОКАЛЬНАЯ РАДИОНАВИГАЦИОННАЯ СИСТЕМА | 2015 |
|
RU2602432C1 |
Изобретение относится к контрольно-измерительной технике и может быть использовано для измерения частоты гармонического сигнала, измерения несущей частоты. Техническим результатом при реализации заявленного решения является существенное уменьшение влияния на результат измерения неравномерности амплитуды сигнала. 4 ил.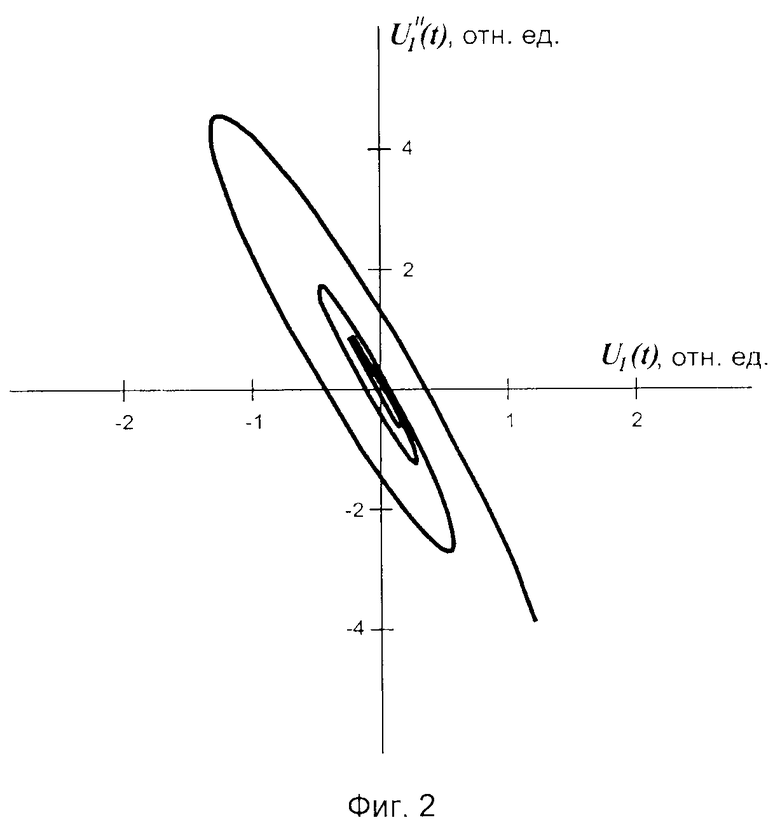
Способ измерения частоты, заключающийся в том, что сигнал дважды последовательно дифференцируют, одновременно измеряют амплитуду сигнала и амплитуду его второй производной, о значении частоты сигнала судят по результату извлечения корня квадратного из частного от деления значений амплитуд второй производной и сигнала, отличающийся тем, что значения амплитуды сигнала и амплитуды второй его производной измеряют в момент равенства амплитуд сигнала и его первой производной.
| Дифракционный способ измерения линейного размера объекта | 2023 |
|
RU2803823C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЧАСТОТЫ СИНУСОИДАЛЬНОГО СИГНАЛА | 1993 |
|
RU2090897C1 |
| DE 4239741 A1, 01.06.1994 | |||
| US 10527659 B2, 07.01.2020 | |||
| CN 102435844 A, 02.05.2012 | |||
| US 11906557 B2, 20.02.2024. | |||
Авторы
Даты
2024-12-18—Публикация
2024-03-14—Подача