следовательно, дает выигршд) в быстродействии по сравнению со сложением в двоичной системе счисления f2.
Недостатком является то, что в результате выполнения операций алгебраического сложения могут возникнуть некомпактные представления числа в 2-ЗРС, переполняющие разрядную сетку устройства, в то время как это же число может быть записано в 2-ЗРС, taK что переполнения не произойдет., Например, десятичное число 16 допускает в 2-ЗРС представление 10000, занимающее 5 разрядов, однако в результате выполнения операций сложения описываемым устройством может получиться, например, и такая запись этого же числа; ИИ110000, занимающая уже 10 разрядов. Это приводит к ложным переполнениям и необходимости контролировать и преобразовы- вать форму представления числа, что связано с увеличением времени выполнения операций и дополнительными аппаратурными затратами.
Известно устройство алгебраического сложения чисел, представленных в 2-ЗРС, -с переносом не более чем на один разряд, состоящее из п однотипных блоков, каждый из которыхсодержит блоки образования положительной и отрицательной сумм, блоки образования положительного и отрицательного переноса и блок образования окончательного результата Sj.
Наиболее близким к изобретению является устройство алгебраического сложения чисел в знакоразрядной системе счисления (ЗРС-) с основанием большим 2, состоящее из п однотипных блоков, i-и из которых содержит полный и неполный одноразрядные полусумматоры в ЭРС, входы полного полусумматора являются входами значений 1-х разрядов операндов, входы неполного полусумматора соединены соответственно с выходами суммы полного полусумматора и переноса полного полусумматора -1-го блока, а выходы неполного полусумматора являются выходами значения i-ro разряда результата 4,
Недостатком устройства является невозможность его применения для сложения чисел, представленных в ЗРС с основанием 2. Необходимость работать с основанием, большим 2, усложняет аппаратурную реализацию устройства. Кроме того, ЗРС с основанием, .больщим 2, значительно более избыточны, чем ЗРС с основанием 2. Так, например, в ЗРС. с основанием 3 используется не менее 5 цифр (2, 1, О, 1,2), а в ЗРС с основанием 2 только 3 (Т, О, 1). Это приводит к дополнительным аппаратурным затратам при реализаций устройства.
Целью изобретения является уменьшение аппаратных затрат для реализации устройства для алгебраического сложения с переносом не более чем на один разряд в знакоразрядной системе счисления.
Для достижения поставленной цели ус ройство для параллельного алгебраического сложения в знакоразрядной системе счисления, состоящее из п вы0 числительных блоков, каждый из которых содержит неполный и полный одноразрядные полусумматоры в знакоразрядной системе счисления, причем первый вход неполного одноразрядно5 го полусумматора в знакоразрядной системе счисления I-го вычислительного блока соединен с первым выходом полного одноразрядного полусуммйтора в знакоразрядной системе
0 счисления i-ro вычислительного блока, второй вход неполного одноразрядного полусумматора в знакоразрядной системе счисления 1-го вычислительного блока соединен с вторым
5 выходом полного одноразрядного полусумматора в знакоразрядной системе счисления (i-1 )-го вычислительного блока, а выход неполного одноразрядного полусумматора в знакоразряд ной системе счисления i-ro вычислительного блока подключен к выходу i-ro разряда результата устройства, содержит два преобразователя знакоразрядного кода в аддитивную форму, причем i-е входы первого и второго
преобразователей знакоразрядного кода в аддитивную форму подключены к входам i-X разрядов первого и второго операндов устройства соответственно, а i-e выходы первого
0 и второго преобразователей знакоразрядного кода в аддитивную форму подключены к первому и второму входам полного одноразрядного полусумматора в знакоразрядной системе
5 счисления i-ro вычислительного блока.
Кроме того, преобразователь знакоразрядного кода в аддитивную форму состоит из п преобразующих блоков , вход и выход каждого из которых представляет собой две шины цифры и знака разряда, каждый из которых содержит два блока сравнения, элемент НЕ, два элемента И, эле5 мент ИЛИ, сумматор по модулю 2 и неполный одноразрядный полусумматор в знакоразрядной системе счисления, причем первые входы цифры блоков сравнения i-ro преобразующего
0 блока подключены к шине цифры входа 1-го преобразующего блока, к первому входу неполного одноразрядного полусумматора s знакоразрядной системе счисления, к входу элемента НЕ (1-1 )-го преобразующего блока и
второму входу цифры первого блок-а сравгнения (I-l)-ro преобразующего блока, первые входы знака блоков сравнения 1-го преобразующего блока подключены к шине знака входа i-ro преобразующего блока, к первому входу сумматора по модулю 2- i-ro преобразукндего блока, к первому входу первого элемента И (i-t )-го преобразующего блока и к вторсяиу входу знака первого блока сравнения (1-1 )-го преобразующего блока, вторые входы цифры и знака второго блока сравнения i-ro преобразующего блока соединены соответственно с вторыми входами цифры и знака первого блока сравнения (i+l)-ro преобразукчаего блока, выходы второго блока сравнения и . Элемента НЕ t-го преобразующего блока подключены к первому и второму входам второго элемента И 1-го преобра зующего блока, а выходы первого блока сравнения и второго элемента И t-го преобразующего блока подключены к первому и второму входам эле.мента ИЛИ, выход которого подключен к второму входу сумматора по модулю 2 -го преобразующего блока, к второму входу первого элемента И (1-1 )-го преобразующего блока и к второму входу неполного одноразрядного полусумматора в знакоразрядной системе счисления (1-1 )-го преобразуюсяего блока, третий и четвертый входы неполного одноразрядного полусумматора в знакоразрядной системе счисления 1-го преобразующего блока подключены к выходам сумматора по модули 2 и первого элемента И -го преобразующего блока, выход неполного одноразрядного полусумматора в энакоразрядной системе счисления 1-го преобразукяяего, блока подключен к шине цифры выхода этого блока, а его
128
64
Веса Е азрядов
второй выход подключен к шине знака выхода i-ro преобразующего блока.
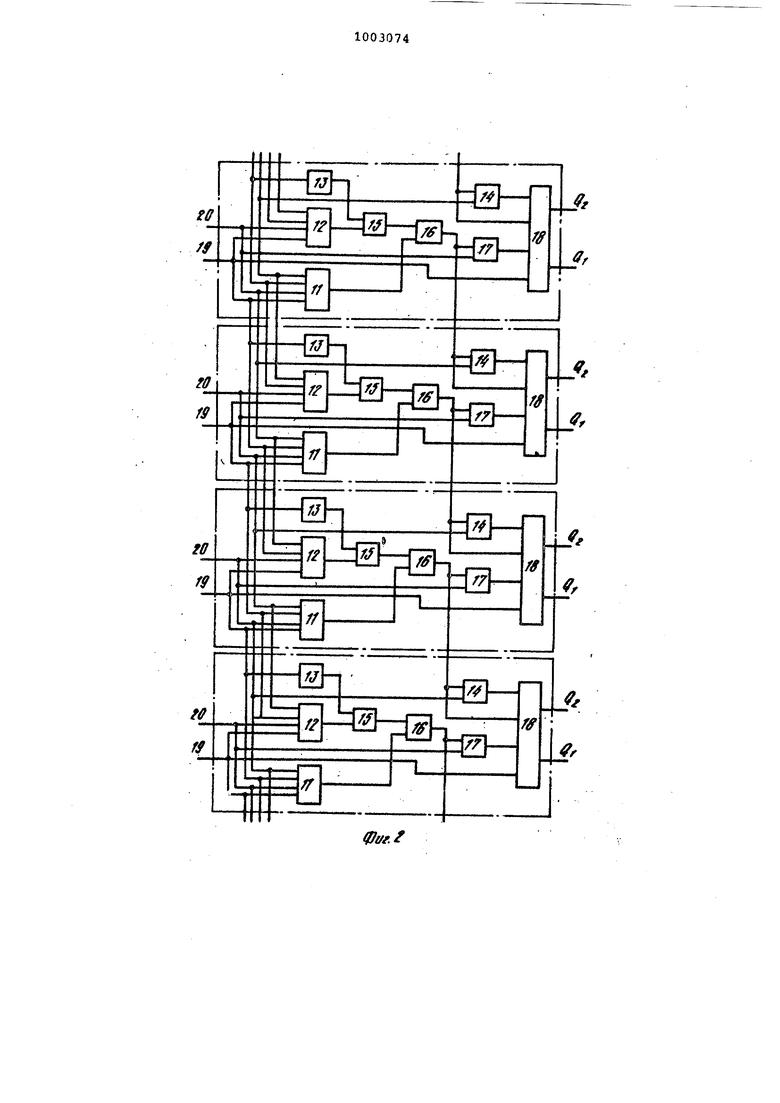
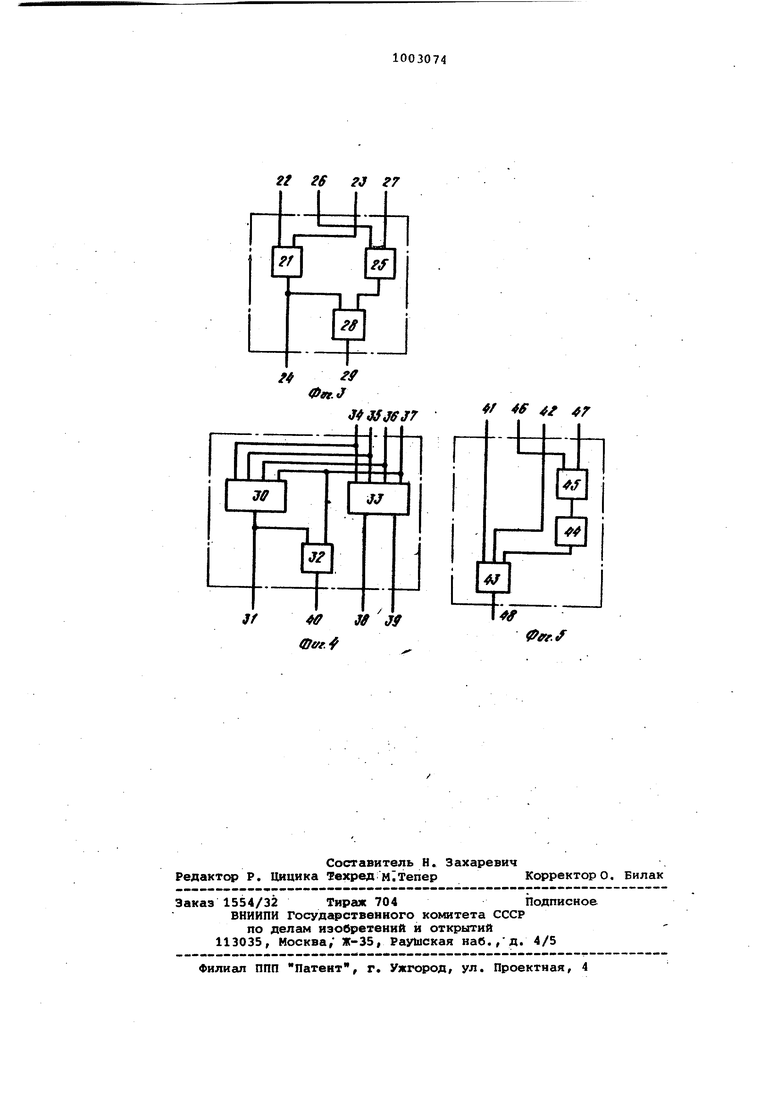
На фиг. 1 показана функциональноот схема устройства (изображены четыре из п вычислительных блоков и соот- . ветствующие им части преобразователей знакоразрядного кода в ддитивную форму), на фиг. 2 - функциональная схема четьфех блоков преобразователя знакоразрядного кода к адди0тивной форме; на фиг. 3 и 4 - функциональные схемы неполного и полного одноразрядных полусумматоров в знакоразрядной системе счисления соответственно} на фиг. 5 - функци5ональная схема входящего в состав перечисленных блоков блока сравнения
На фиг. 1 показаны первый 1 и второй 2 преобразователи знакоразрядного кода в аддитивную форму, входы 3 и 4 которых являются входами 1-х
0 разрядов операндов устройства. Выхо-ды преобразователей 1 и 2 соединены с входами 5 и б полных одноразрядных полусумматоров в знакоразрядной 5 системе счисления 7, выходы 8 и 9 которых соединены с входами неполных одноразрядных полусумматоров 10 в знакоразрядной системе счисления. Выходы неполных одноразрядных полусумматоров 10 являются выходами зна0чений i-X разрядов результата устройства параллельного алгебраического сложения.
Чтобы пояснить работу устройства, введем понятие аддитивной формы пред5ставления числа в двоичной энакоразрядной системе счисления (2-ЗРС). В силу избыточности любое число Ткроме О ) в 2-ЗРС представляется беско- .нечным числом способов. Например, , -1 обозначается через I, нули ле0вее первой значащей цифры опускаютг ся:
16
1 Десятичная запись числа






| название | год | авторы | номер документа |
|---|---|---|---|
| Десятичный сумматор в избыточной системе счисления | 1988 |
|
SU1594524A1 |
| Устройство для параллельного сложения чисел, представленных в двоичной знакоразрядной системе счисления | 1989 |
|
SU1727120A1 |
| Устройство для суммирования | 1978 |
|
SU955036A1 |
| Устройство для вычисления квадратного корня | 1981 |
|
SU1008736A1 |
| Десятичный сумматор в избыточной системе счисления | 1985 |
|
SU1256015A1 |
| Сумматор в знакоразрядной позиционно-остаточной системе счисления | 1986 |
|
SU1383349A1 |
| Сумматор избыточного кода | 1987 |
|
SU1476460A1 |
| Устройство для умножения | 1987 |
|
SU1411733A1 |
| Устройство для умножения | 1991 |
|
SU1803914A1 |
| Устройство для умножения | 1983 |
|
SU1130859A1 |


Аддитивной называют такую форму () представления числа в 2-ЗРС, которая не имеет единиц одного знака в соседних разрядах. Так, в приведенном примере форь«1 записи 2 и 5
аддитивны, а 1, 3, 4 - не аддитивны, так как содержат сочетания 11 или IT
При алгебраическом сложении чисел, представленных в аддитивной 2-ЗРС форме, пepeнoJЫ не могут распространиться далее,/чем на один разряд. Например, 1010101 1 I 1 1. О 1 1 промежуточная сумма ,:0 Т О I 1 1 О перенос 1 О О 00 01 0. 10101100 ркончательная сумма При этом предполагается, что перенос производится только там, где он неизбежен, т.е. , но не . Представленные числа в аддитивной 2-ЗРС форме не однозначны, однако в любом представлении числа х в аддитивной форме число значащих цифр не больше + 3. От любого представления числа в 2-ЗРС можно перейти к аддитивному представлению путем параллельного (одновременного по всем разрядам) преобразования. Устройство, выполняювдее :это преобразование, назовем преобразователем 2-ЗРС кодачисла в аддитивную форму.
Первый вспомогательный код
Второй вспомогаВ этом примере 1 в 3-м разряде исходного кола заменена на 1 в 4-м и 1 в 3-м разрядах второго и первого вспомогательных кодов соответственно, так как имеется комбинация 101. 1 в 5-м разряде исходного кода заменена на 1 в б-м и 1 в 5-м разрядах второго и первого вспомогательных кодов, так как имеется комбинация 11 В силу наличия комбинаций IT и 11 преобразованы аналогичным образом содержимые б-го и 8-го разрядов исходного кода. Содержимые 1-, 2} 47 7-и 9-го разрядов исходного кода пе ренесены в первый вспомогательный код без изменения. Затем вспомогательные коды складываются, необходимость в nepeHf-ice при этом не возникает. В результате получается адди :ивный код исходного числа.
1
Устройство для параллельного алгебраического сложения в знакоразряД ной системесчисления работает следующим образом.
На входы 3 и 4 первого 1 и второго 2 преобразователей 2-ЗРС кода в аддитивн.ую форму подаются сигналы, соответствующие 2-ЗРС кодам первого и второго операндов. На выходах преобразователей 1 и 2 формируются сигналы, соответствующие аддитивным 2-ЗРС кодам операндов, которые подаются на входы 5 и 6 полных одноразрядных полусумматоров в- 2-ЗРС 7. Полусумматоры 7 вырабатывают сигналы переноса rfj на выходах 8 и сигналы пром(ежу.точной суммы выходах 9 в соответствии с табл. 1 (гдей. иЬ.-сигналы на входах 5 и б). Алгоритм параллельного преобразо-вания в аддитивную форму может быть, Например, следующим. По исходноглу коду числа формируются два вспомогательных кода. Значение I-го разряда первого вспомогательного кода равно значению 1-го разряда исходного кода, взятому с обратным знаком, если в I-м и (1-1 )-м разрядах исходного кода стоят единицы одного знака, или если в t-M и (i-2)-M разрядах исходного кода записаны единицы одного знака .и в (i-1 )-м разряде исходного кода записан ноль, при тех же условиях, значение (2i-1 )-го разряда второго вспомогательного кода равно значению i-ro разряда исходного кода. В остальных случаях значение i-го разряда первого вспомогательного кода равно значению 1-го разряда исходного кода, а значение (21-1 )-го разряда второго вспомогательного кода равно нулю. Аддитивный код числа получается путем сложения первого и второго вспомогательных кодов (переносы при этом не возникают). . Рассмотрим пример преобразования -ЗРС кода числа в аддитивную форму . по этому алгоритму.
Таблица
Номер входа блока сравнения
Сигнал на выходе блока сравнения Таким образом, первый блок сравнения 11 выяБляет наличие комбинаций 11 и 11 в исходном 2-ЗРС коде. Второй блок сравнения 12 вместе с элементами НЕ 13 и И 15 выявляет наличие комбинаций 101 и 101. Сумматор по модулю 2 17 служит для определения знака i-го разряда первого вспомогательного кода. Сигналы цифры и i-го разряда первого вспомогательного кода формируются на первом и втором входах неполного одноразряд ного полусумматора в 2-ЗРС 18, на третьем и чет ертом входах которого формируются сигналы цифры и знака i-го разряда второго вспомогательного кода. Неполный одноразрядный полу сумматор в 2-ЗРС 18 работает в соответствии с табл. 2, на его выходах формируются сигналы цифры и знака 1-го разряда аддитивного 2-ЗРС кода На фиг. 3 показан пример конкретной реализации неполного одноразрядного полусумматора в 2-ЗРС. Неполный одноразрядныйполусумматор содержит сумматор по модулю 2 21f входы которого 22 и 23 являются первым и треть им входами неполного одноразрядного полусумматора, а выход 24 соединен с первым выходом неполного одноразрядного полусумматораJ элемент ИЛИ 25, входы которого 26 и 27 являются. вторым и четвертым входами неполного одноразрядного полусумматора; элемент И 28, входы которого соединены с. выходами элемента ИЛИ 25 и суммато ра по модулю 2 21, а выход 29 является вторым выходом неполного однот разрядного полусумматора. Неполный одноразрядный полусумматор 2-ЗРС работает следующим образом На нечетные входы подаются сигналы цифр, а на четные входы сигналы знаков 1-х разрядов слагаемых. На выходах в соответствии с табл. 2 и кодировкой цифр 1, О, f двоичным сигналом формируются сигналы цифры и знака результата. На фиг. 4 приведен пример реализации полного одноразрядного поПусум
Таблица 3
Сигналы на входах матбра в 2-ЗРС. Полный полусумматор содержит блок сравнения 30, выход 31 которого соединен с первым выходом полного одноразрядного полусумматора и первым входом элемента И 32; не- / полный полусумматор в 2-ЗРС 33, первый, второй, третий и четвертый входы которого ,34- 37 соединены соответственно с первыми, вторыми, третьими и четвертыми входами блока сравнения и полного одноразрядного полусумматора, а выходы 38 и 39 являются третьим и четвертым выходами полного одноразрядного полусумматора; элемент И 32, второй вход которого соединен с четвертым входом полного полусумматора, а выход 40 соединен с вторым выходом полногоодноразрядного полусумматора . Работа полного одноразрядного полусумматора в 2-ЗРС аналогична работе неполного одноразрядного полусум матора и отличается от нее формированием сигналов цифры и знака переноса в соответствии с табл. 1. На Фиг. 5 приведен пример реализации блока сравнения. Первый и второй входы 41 и 42 элемента И 43 являются первым и третьим входами блока сравнения, а третий вход элемента И 43 через элемент НЕ 44 соединен с выходом сумматора по модулю 2 45, входы 46 и 47 котЬрого являются вторым и четвертым входами блока сравнения. Выход 48 элемента И 43 является выходом блока сравнения. Работа блока сравнения поясняется табл. 3. Время выполнения устройством операции алгебраического сложения не зависит от разрядности устройства и составляет в приведенной на фиг.2-5 реализации 14С, где tr - условное время задержки сигнала на элементах И, ИЛИ, НЕ И сумматоре по -модулю 2. Оптимизация схемы позволяет на тех же элементах сократить время до 10, а использование элементов трехзначной логики с задержкой Т на элементе - до 5 -V . I Для сравнения отметим, что в сумматорах, работающих в двоичной систе ме счиспения, время сложения возрастает с увеличением числа разрядов п (за исключением параллельно-парал лельных сумматоров, которые не могут быть построены для п -30 из-за больших нагрузок на элементы 5} ). Так, в многоразрядном сумматоресо сквозным переносом время оценивается в Znt, Таким образом, при предлагаемое устройство дает выигры1 в быстродействии более чем в 10 раз В сверхпараллельных сумматорах время Т сложения оценивается в (2 )ос) + 3 )&, где k - коэффициен объединения, характеризующий нагруз ку на элементы При k 3 предлагаемое устройство дает выигрыш в быстродействии по сравнению с сверх параллельным сумматором при п 50. При k 5 и п4150 сверхпараллельный сумматор работает быстрее, чем данное устройство на элементах двухзначной логики, однако при этом нагрузка на элементы в сверхпараллель ном сумматоре оказывается вдвое бол шей , Отсутствие переносов далее, чем на один разряд, а также ограничения на используемые коды чисел и возникающие комбинации сигналов, позволяют контролировать правильность вы полняемых операций и упрощает диагностику неисправностей. Так, на тример, наличие комбинаций 11 или 11 на выходах преобразователя кода к аддитивной форме или на выходах неполных полусумматоров свидетельству ет об ошибке. Операции сложения и вычитания в знакоразрядной системе счисления вы полняются одним устройством, что уп рощает его структуру по сравнению с аналогичными устройствами, работающими в ДВОИЧНО системе счисления. Кроме того, построение процессора на базе 2-ЗРС позволяет дополнительно, ускорить выполнение операции умножения за счет преобразования кода одного из множителей к форме с малым числом единиц 1. По сравнению с первым, вторым и третьим аналогами, описанными выше, усаройство обладает тем преимувдеством, что позволяет эффективно контролировать переполнение. Аддитивный код числа в 2-ЗРС содержит не более loQg, х + 3 значаших цифр (в двоичной системе счисления код числа имеет + 1 значащих цифр), что. позволяет при помоши п разрядного устройства представлять числа из диапазона .; выход за пределы разрядной сетки служит признаком переполнения. Кроме того, по сравнению со вторым аналогом - сумматором работающим е системе СОК, - сумматор в 2-ЗРС обладает тем преимуществом, что преобразование кода числа из 2-ЗРС в обычный двоичный код осутествляется по простым алгоритмам. Устройство параллельного алгебраического сложения в 2-ЗРС состоит из п однотипных блоков с одьотипными связями между блоками,причем пй блок непосредственно связан толь, ко с (i-1 )-м и (21-1 )-м блоками. Это позволяет повысить эффективность использования процессора., построенного на базе данного устройства, за счет изменения разрядности суммирующих устройств в процессе счета задач. При выполнении расчетов .повышенной точности несколько устройств сложения могут быть легко объединены в одно устройство сложения большой разрядности и, обратно, при расчетах мгьлой точности устройство сложения может быть расчленено на части, выполняющие параллельно независимые вычисления (причем это расчленение может выполняться программой системного математического обеспечения). Приведенные характеристики устройства параллельного алгебраического сложения показывают, что оно дает существенный выигрыш в быстродействии по сравнению с сущ ствующими. устройствами при операциях над числами большой разрядности, т.е. при вычислениях повышенной точности. Это позволяет говорить о возможности повышения быстродействия спегщализированных ЭВМ повышенной точности, построенных на элементах с двумя устойчивыми состояниями. Формула изобретения 1. Устройство для параллельного алгебраического сложения в знакоразрядной системе счисления, состоящее из п вычислительных блоков, каждый из которых содержит неполный и полный одноразрядные полусумматоры в знакоразрядной системе счисления, причем первый вход неполного одноразрядного полусумматора в знакоразрядной системе счисления i-го вычислительного блока соединен с первым выходом полного одноразрядного полу умматора в знакоразрядной системе счисления i-ro вычислительного блока второй вход неполного одноразрядного полусумматора в знакоразрядной системе счисления i-го вычислительного блока соединен с вторым выходом полного одноразрядного полусумматора в знакоразрядной системе счисления (i-1 )-го вычислительного блока, а выход неполного одноразрядного полусумматора в знакоразрядной системе счисления i -го вычислительного блока подключен к выходу i-ro разряда результата устройства, о т л ичающееся тем, что; с целью уменьшения-аппаратных затрат, устройство содержит два преобразователя знакоразрядного кода в аддитивную форму, причем i-е входы первого и второго преобразователей знакоразрядного кода в аддитивную форму подключены к входам i-x разрядов первого и второго операндов устройства соответственно, а i-е выходы первого и второго преобразователей знакоразрядного кода в аддитивную форму подключены-, соответственно к первому и второму входам полного одноразрядного полусумматора в знакоразрядной системе счисления i-го вычислительного блока.
Источники информации, принятые во внимание при экспертизе
(4. AvizienisA, Signed-digit number representations for fast paraHel arithmetic. - IRE Trans on Electron. Computer , 1961, № 3, с.. 390, рис. 2 (прототип).
Йи«/
гб j г
4t
Й
i
f
J

Авторы
Даты
1983-03-07—Публикация
1981-09-28—Подача