Предметом изоЬретения является электромеханическое устройство для решения характеристических уравнений систем автоматического регулирования, состоящее из фазовых модуляторов и потенциометров, моделирующих характеристические полиномы структурных звеньев системы автоматического регулирования, следящих систем, с помощью которых отрабатывается напряжение, соответствующее характеристическому полиному всей системы, а также электронно-лучевого индикатора корней полиномов.
Предлагаемое устройство выполняет следующие функции: составляет характеристическое уравнение системы автоматического регулирования по заданным оператором звеньям и структуре системы; определяет корни характеристического уравнения системы; изображает корни на комплексной плоскости.
Предлагаемое устройство отличается от известных тем, что оно дает возможность составлять характеристические полиномы непосредственно по структуре и характеристикам отдельных звеньев системы автоматического регулирования, не прибегая к вычислению коэффициентов характеристического полинома.
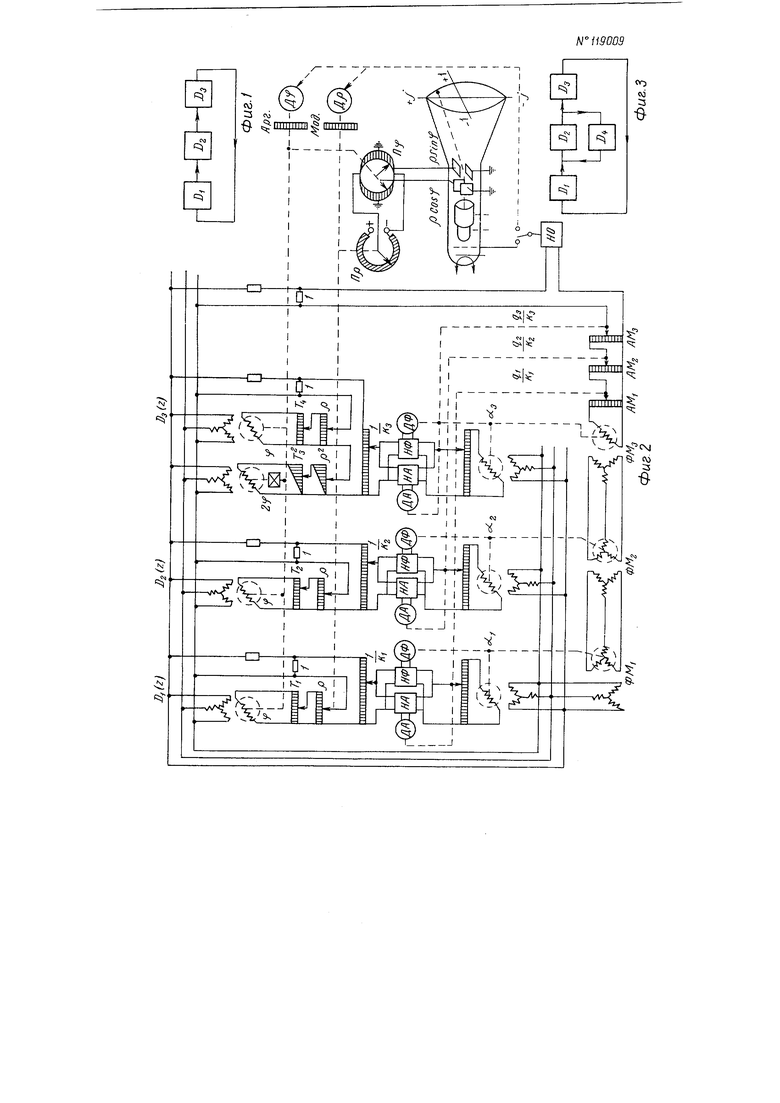
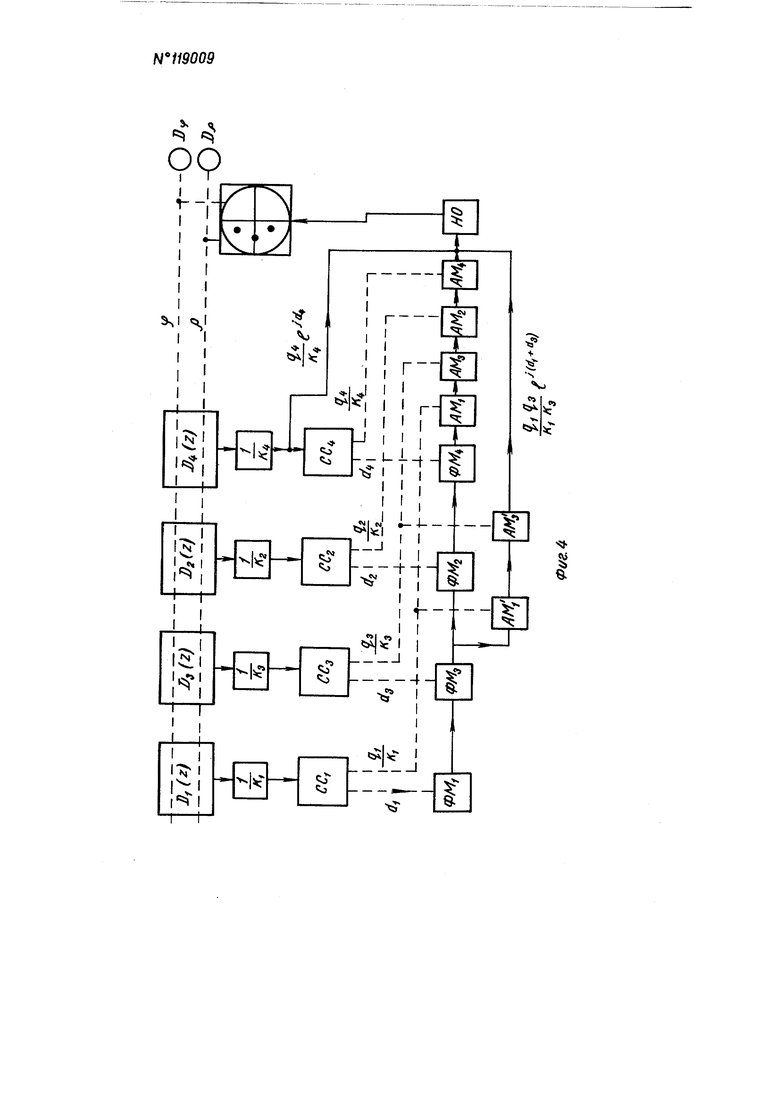
На фиг. 1 представлена структурная схема системы автоматического регулирования без обратной связи из трех звеньев; на фиг. 2 - принципиальная электрическая схема составителя-рещателя характеристического уравнения системы автоматического регулирования без обратной связи; на фиг. 3-схема системы автоматического регулирования с обратной связью; на фиг. 4 - структурная схема составителя-решателя характеристического уравнения системы автоматического регулирования с обратной связью.
Характеристическое уравнение системы автоматического регулирования без обратной связи, состоящей из трех звеньев (фиг. 1), имеет вид:
№ 119009- 2 -
D, (z) A (z) D, (z),
f -KrKy- - -UJ
где: Oi(2.). ), -С)з(2) - характеристические полиномы звеньев,
2, 3. -.коэффициенты усиления.
Величин2 г в общем случае является комплексной и может быть выражена в показательной форме
z p-e- (2)
Поэтому характеристические полиномы звеньев также являются комплексными величинами:
D,(z)
2 (2) 926 (3)
D,(z)q,e Следовательно, характеристичесЕСое уравнение системы приводится к виду:
lllll i . е-/ (1 + «2 + «з) 1 Q,4)
К, -К,-К,
Пусть, например, звенья DI и D системы являются инерционными, а звено DS, - колебательным, тогда:
D, (Z) Т,ое 1 д,е
D, (z) -- T.Z + 1 - + 1 д.,е
01 (Z) Гз 2;2 н- Г, - z н-1 Гз 2 р2е Ь + 7,pe3-f + 1 д.
Моделирование характеристических полиномов звеньев в устройстве (фиг. 2) производится также, как описано в авт. ев- № 98013Аргументы комплексных членов по тиномов 2ф и изображаются фазами переменных напряжений, изменяемых с помощью фазовращателей (сельсинов с трехфазными статорами и однофазными моторами). Фазовращатели приводятся в движение все одновременно от двигателя Дф. Модули комплексных ч.тенов полиномов Tip , TZ р, и T/t р изобрал аются амплитудами переменных напряжений, изменяемых с помощью потенциометров. При этом постоянные времени Т, Т, Гз и Т задаются вручную, а величины р и р изменяются с помощью потенциометров, движки которых перемещаются все одновременно от двигателя Д р . Единица моделируется переменным напряжением постоянной амплитуды.
Рещение уравнения основано на методе обследования комплексной плоскости. Обследование осуществляется путем спиральной или радиальной развертки независимой неременной z р е 5t в комплексной плоскости.
Выходные напряжения схем, моделирующих полиномы, при этом непрерывно изменяются. Эти напряжения необходимо разделить на коэффициенты усиления и перемножить между собой. Коэффициенты
усиления устанавливаются вручную на потенциометрах-v,
Для перемножения предусмотрены следящие системы, отрабатывающие
4iЧ- Я:;
модули-JTP , -,:- , г и аргументы « , я.,, а., полученных величин, ч 1А .V/V 3
Для каждого полинома предусмотрены два нуль-органа НА и НФ. НА реагирует только на амплитуду переменного напряжения, ЯФ - только на фазу этого напряжения. Эти нуль-органы воздействуют на двигатель амплитуды ДА и двигатель фазы ДФ.
AI А.г АЗ
Двигатель ДА ведет движок уравновешивающего потенциометра до равновесия, двигатель ДФ поворачивает ротор уравновешивающего фазовращателя до совпадения фаз. Двигатели ДФ поворачиваЕот также роторы фазовращателей ФМь ФМо, ФМз, из которых ФМ1 и ФМг представляют собой сельсин-дифференциалы, а ФМз-обычный сельсин. Сельсин ФМ1 питается от сети трехфазного тока, в результате фаза выходного напряжения Ф/Из равна ai-fa,,. Двигатели Д/1 перемещают также движки потенциометров амплитудных модуляторов.
В результате выходное напряжение АМз составляет
1 2 3 J( + :)
К, К, R,
Это напряжение складывается с напряжением, равным единице, п подается на Н3ль-орган НО. Те значения р и э , при которых срабатывает пуль-орган, и являются корнями характеристического уравнения системы.
Для отсчета значений корпей в простейшем случае при срабатывании нуль-органа двигатели останавливаются и величины f п а отсчитываются по шкалам Арг. и Мод.
Для автоматического изображения корпей на комплексной плоскости примепяется электронно-лучевая трубка, экран которой изображает комплексную плоскость. С помощью линейного потепциометра Яр, движок которого, вращаемый двигателем Д р, электрически соединег с сипус-косинусным потеппиометром Яф, связанным с двигателем Дт , на отклоняющие пластины трубки подаются напряжения р созф и р sin о, подготавливающие развертку луча по экрану.
В момент срабатывания нуль-органа на сетку трубки подается сигнал, отпирающий луч, и на экране появляется точка, изображающая корень. Путем применепия трубки с длительпым послесвечением можно наблюдать на экране одновременно несколько корней уравнения.
Характеристическое уравнение системы автоматического регулирования с обратной связью (фиг. 3) имеет вид:
D,(( .,(,,(7)
Представляя полиномы звеньев в виде комплексных величин, характеристическое уравнение (7) приводится к виду:
9, (. .. 9. + .) 1 д, (8)
К, Л, /fi к, K
Первый член уравнения в устройстве (фиг. 4) моделируется так, что полиномы при этом располагаются в порядке DI, D, D, D.
Второй член уравнения моделируется путем отбора выходного напряжения с ФМз. Это напряжение пропускается через амплитудные модуляторы ЛМ/и ЛМз, управляемые от осей отработки -р.- и ||- следящих систем СС и ССзТретий член уравнения получается путем отбора напряжения от полинома Di(z) после потенциометра для установки коэффициента уси-ления 1/К4. Напряжения всех трех членов складываются между собой Л подаются на нуль-орган.
- 3 -№ 119009
А JД :(
№ 119009
Предмет изобретения
Составитель-решатель характеристических уравнений систем автоматического регулирования, содержащий фазовые модуляторы и потенциометры для образования и непрерывного изменения аргумента и модуля полиномов от комплексной переменной, значения модуля и аргумента которой, обращающие в нуль характеристический полином, наблюдаются на экране электронно-лучевой трубки или по соответствующим щкалам, отличающийся тем, что, с целью ускорения и упрощения анализа систем автоматического регулирования, фазовые модуляторы и потенциометры соединены между собой соответственно операторным выражениям звеньев исследуемой системы автоматического регулирования в отдельные узлы, на выходе которых включены следящие устройства, производящие умножение модулей и сложение аргументов, относящихся к отдельным структурным звеньям системы..




Авторы
Даты
1959-01-01—Публикация
1953-10-07—Подача