Изв&:тиые электрические устройства для интегрирования дифференциальных уравнений в частных производных, с дискретным пространством и временем, конечно-разностным методом (например уравнения типа теплопроводности) выполняются в Ы1де нескольких пар потенциометров, величины потенциалов на которых имитируют значение функции в выбранных точках области- Счетно-решающий элемент, состоящий из нескольких конденсаторов переменной емкости, поочередно подключает;ся к соответствующим потенциометрам. После осуществления необходимых переключений между конденсаторами счетн о-решающего элемента новое значение потенциала, соответствующее значению функции времени, отличающегося от предыдущего на интервал Л/, переносят с помощью статического нуль-инструмента на один из потенциометров моделирующих задание функции в точках области. Путем последовательного обхода всех пар потенциометров на одной из них появится новое значение функции, соответствующее времени / + ДГ, где t - текущее значение времени. Чтобы продвинуться в решении уравнения еще на один щаг Д/, полученное распределение потенциала используется для получения последующего значения функции, соответстЕл-ющего времени t + 2А/ и т. д.
В отличие от этого в описываемом интеграторе для рещения дифференциальных уравнений в частных лроизводных приращение времени моделируется не емкостями, а омическими сопротивлениями, что позволяет уменьшить ошибку прибора, соответственно повысив точность решения уравнений.
Ло 124653- 2 -
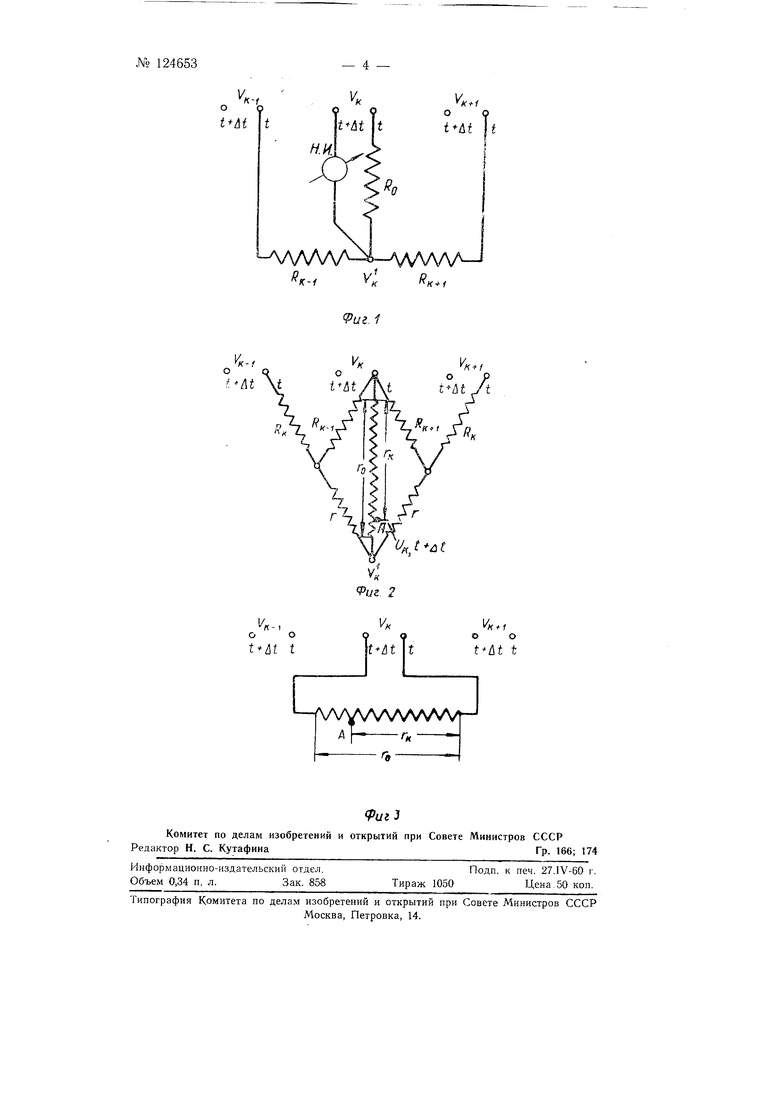
Интег 1атор состоит из набора потенциометров с высокой разрешаюHieii способностью, счетио-решаюпщего элемента (блока омических сопротивлений) я измерительных приборов. С помощью переключающего устройства счетно-решающий элемент поочередно подключается к соответствующим ripj,eH,ojvieTpaM, чем моделируется приращение времени. Простой расчет-показывает, что если к трем точкам К-/, /С, K+J {фиг. 1) подключить три потенциала . V, , имитирующие значение функции 1/ в соответствующих точках области, то в узле V установится соотнон)ение потенциалов, отвечающее уравнению типа теплопроводно;сти, записанное в конечных разностях следующим образом:
V,,,,f , I/. ь --2 I/,.., -f-I/....,, /
л V-2VV
Д х
Действительно, для точки У справедливо равенство:
-1-1/;. I/.-1/;. i/.
/ к- I/XQ К
Полагая ,, найдем
1/ l.-1-ьг К- 4- 1/.-.,
1..
где г RIRf). Падение напряжения на сопротивлении , отнесенное к временному интервалу Д/, составит
llzIl J I,. K.-fl/.,.,
Д г Д 2-г Сравнивая (4) и (1), найдем условия моделирования
(5)
2-f-r
При заданных а, Дх и г определится значение временного интервала Дг. В процессе решения уравнения на потенциометрах каждой пары по иучается два значения функции (потенциала) в данной точке, разделенные временным интервалом Дг.
При рещении нелинейного дифференциального уравнения типа
ди
()-f- -- I (U) dt д X д X
применяется омический элемент (блок сопротивлений), изображенный на фиг. 2. Этот элемент воспроизводит приращение времени для случая зависимости коэффициентов уравнения от функции- Результат решений (значение функции U ,t + Дг) при этом получается на сопротивление Гй в точке А. Условия моделирования будут:
где UK 1 . Сопротивления / постоянны. Одноз-начно устанавливаЬя- рк .
ются также соотнощения между Д, ДА- и а к- Для упрощения схемы счетно-решающего элемента можно значение перенести на один из потенциометров пары /С (фиг. 2), а затем используется схема, приведенная на фиг. 3. Величина потенциала точки Л потенциометра Го, соответ-, ствующая функции . t/« ,,/+Д .переносится на левый цотенцнометр пары А.
0(2)
ди
(6)
- ,«
Преимущества таких интеграторов определяются простотой измерения (в состоянии равновесия) и возможностью активного вмешательства в процесс решения на любой его стадии. Поэтому такие интеграторы особенно удобны для решения уравнений в частных производных с переменными Коэффициентами, зависяш,ими от координат, времени или искомой функции, и задач с источниками и стоками (например задача о диффузии нейтронов и т. п.).
Предмет изобретения
Интегратор для решения дифференциальных ураниений в частных производных по авт. св. № 122341, отличающийся тем, что, с целью уменьшения ошибки интегрирования для моделирования приращения времени, применен блок омических сопротивлений, поочередно соединяемый с потенциометрами, моделирующими пространственпое распределение функции.


| название | год | авторы | номер документа |
|---|---|---|---|
| Интегратор для решения дифференциальных уравнений в частных производных | 1958 |
|
SU122341A1 |
| Интегратор для решения дифференциальных уравнений в частных производных | 1957 |
|
SU118624A1 |
| Аналоговое устройство для реше-Ния диффЕРЕНциАльНыХ уРАВНЕНий | 1979 |
|
SU798895A1 |
| Аналоговое устройство для решения уравнений математической физики | 1980 |
|
SU920768A1 |
| Устройство для решения дифференциальных уравнений | 1980 |
|
SU1339594A1 |
| Устройство для решения диффе-РЕНциАльНыХ уРАВНЕНий B чАСТНыХпРОизВОдНыХ | 1979 |
|
SU842858A1 |
| УСТРОЙСТВО для МОДЕЛИРОВАНИЯ СИСТЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ГИПЕРБОЛИЧЕСКОГО | 1973 |
|
SU408330A1 |
| Оптоэлектронный управляемый элемент сеточного процессора | 1988 |
|
SU1603407A1 |
| Устройство для решения дифференциальных уравнений в частных производных смешанного типа | 1986 |
|
SU1345218A1 |
| Электроинтегратор для решения дифференциальных уравнений в частных производных | 1960 |
|
SU139094A1 |


Авторы
Даты
1959-01-01—Публикация
1959-04-06—Подача