112545052
Изобретение относится к спект- ществления N- последующих N -точеч- ральному анализу методом дискретного ных ПДПФ преобразования Фурье (ДПФ)и может
быть использовано в радиотехнике,
геофизике, вычислительной технике г F (k, k ) ) 6 F (Ц , n)1 1 при построении спектроанализаторов н м °
.
.
различного назначения.-W 2,К 1,Н, .
Цель изобретения - увеличение
точности. .В результате получают
Алгоритм многомерного ПДПФ содер- Q R.-1
жит две п ереиндексации данных дляF (k , k) У F (k , k,).
перехода от одномерного случая к мно- °
гомерному и обратно, а также пос-Переупорядочиванием выходных зналедовальных групп одномерных N -то-ченйй многомерного массива опредечечных устройств ДПФ. ляется F (К) . Это достигается двумя
В соответствии с алгоритмом Гудаспособами:
на первом шаге осуществляется пере-У
индексация одновременного массива1 . k . K,U N/N ,
при N N -N ... N, если общее
число отсчетов N разбито на группыjo где определяется из соотношений
N (все -Ng - вза1шно простые)
J .; N/Ng 1,5 Г,7.
-(N/Npn ,, . .
где - - операция вычета по25 определяется из
группы сравнений В дальнейшем рассматривается днумерный ПДПФ. ТогдаV 6 modN .
5 ij J
n N,n, N,-n,, . (1)30 p -
После переиндексацин вычисляетсяK UK
N N -точечных ПДПФ. Порядок очеред-i i 2 г N,
ности должен выбираться, исходя из ; U 0 modN :
минимальной временной и аппаратурной35 г i
сложности. .и N-1-U
Известно, что i
/IL Л. Разрядность чисел после каждого
k k., - - 1 J 2.Т шага преобразования астет. После
и к N первого преобразования, если R 16 . W W 2 -t .
R R + log R ,
Для первой группы из N N -точеч-
ных поразрядных преобразований R- - разрядность комбинационных
S-TOM разряде.45 слоев, хранящихся в ПЗУ;
, , , Зхс - ближайшее целое, не меньше х.
F Qk , п ) 1.о .IX .(.n , - (J После второго преобразования
h,o
,K,NI s, ,
W . /. , (2) K Hog.RL .
kj 1, N.Ня фиг. 1 представлена схема
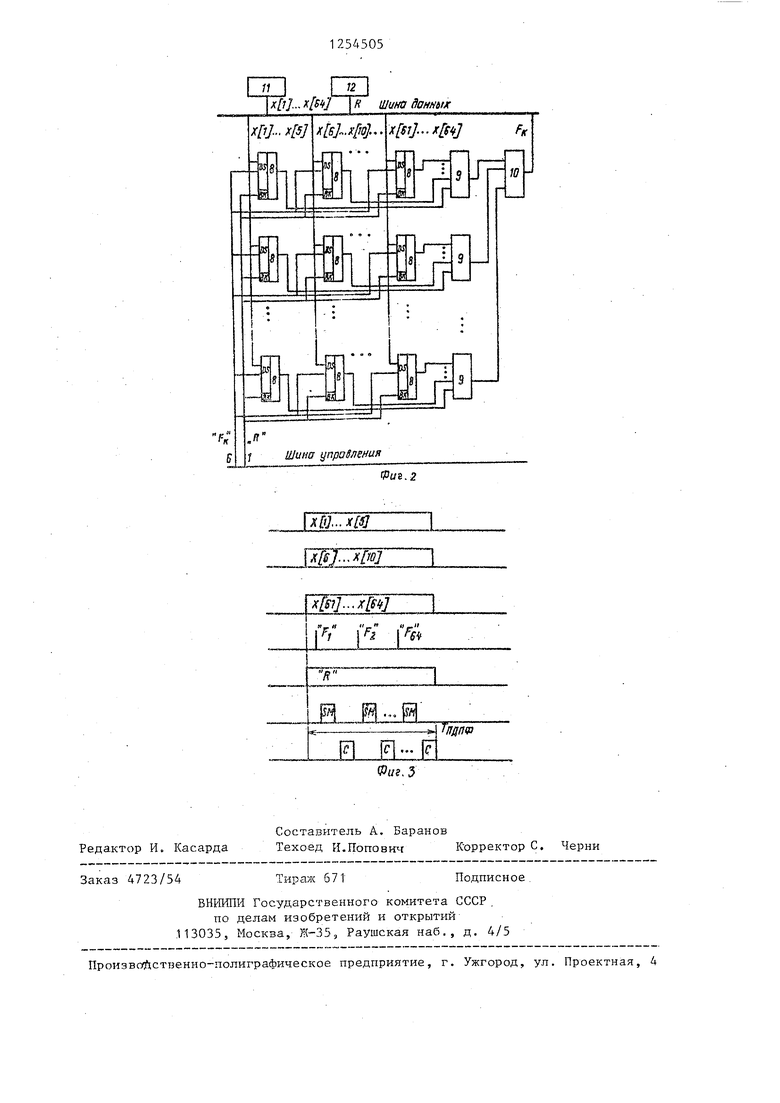
устройства для дискретного двумерно- После поразрядного суммированияVQ преобразования Фурье; на фиг. 2 , - ,блок дискретного преобразо.вания
F (k , Пд) i- s 2 Фурье.-N;, являющийся составной ча °стью многомерного ПДПФ (для примера
Суммирование необходимо в связивыбрано i 64); на фиг. 3 - временс перегруппировкой данных для осу-ные диаграммы работы устройства.
, k ) н м
.
31
Устройство двумерного ПДПФ содер жит блок 1 постоянной памяти 1, труп
пы блоков дискретного преобразования
Фурье 2-2.
3, -3.,
блок 4 постоянной памяти, блоки 5-7 памяти.
Блоки 2 и 3 дискретного преобразования Фурье (фиг. 2) содержат узлы
8постоянной памяти, сумматоры
9и 10 , узел 11 памяти и аналог о - цифровой
12.
(АЦД)
преобразователь
п.
п.. 0,0 1,02,0 0,11,12,1 0,2 1,2 2,2 0,3 1,3 2,30,41,42,4
С выхода блока 1 двумерный массив записывается в блок 5 и из него считывается в блок 2 в порядке, указанном на фиг. 1, в соответствии с алгоритмом: на первый сверху блок 2 подается х , N -1 ; п на второй - X , N -1 ; n 1 и т.д. Из группы блоков 2 считываются числа в, соответствии с (2). Числа FJ (Ц , П-) записыают.ся в блок 6. Числа из блока 6 в порядке, указан- iHOM на схеме, считываются на вторую группу блоков 3, состоящую из N поразрядных блоков ДПФ на N точек каждый. С выхода этих блоков 3 сии- маются сигналы F (k, k.), поступающие в блок 7 и из него через блок 4, преобразуясь в Р(К), - в шину данных
п О336699132165198231364297
п, п,10,011,012,013,014,015,016,017,о 18,019,0
. п3303 633964l94 24935285б15 4бТ7
п, ,0 21,022,023,024,025,026,027,028,029,0
п 660 693 726 759 792 825 858 891 924 957 п, п, 30,0 0,1 1,1 2,1 3,1 4,1 5,1 6,1 7,1 8,1
2545054
Устройство работает следующим
образом.
Числовая R-разрядная последовательность поступает из шины данных на блок 1, работающий по алгоритму (1). Например, при N 3; N 5, в соответствии с
3ri.,V,
где п.
I
п 0,4. Тогда алгоритм пря О,-2;
мой переиндексации можно представить
таблицей 1.
Таблица 1
По шине управления подаются сигналы п ;, п, -к/ , к,, в блоках 5-7 эти сигналы управляют расположением данных. Сигналы К и К в блоках 2 и 3 выбирают соответствующую страницу для всех F (К, п ) и всех F(K , К ), компоненты которых F;(K, п) и F (K, К).
Приведены таблицы прямого и обратного преобразования для практически интересного случая N 1023, N 32, N2 33. Первая ступень такого спектроанализатора осуществляет 33 31-точечных ПДПФ, а вторая - 31 33-точечных ПДПФ. Для такого преобразования +31 П
12- 1023
Тогда прямая перестановка имеет вид, показанный в табл. 2.
Таблица 2
.LA
bJ..
n990316496130 163 196 229 262295
n , ,110,111,112,113,1 14,1 15,1 16,1 17,118,1
n 328361394427460 493 526 559 592625
n, ,120,12J,122,123,1 24,1 25,1 26,1 27,128,1
n658691724757790 823 856 889 922955
n, ,130,1
:..- и.т.д.
n988 1021.
n,, ,32 1,322,323,32......................... 29,32 30,32
n992 23568.,,.,.,.;,......,,..,... 926 959
Обратная пефестановка проводится по алгоритму
К :528 К + 496 К
9 ЧР73
35
Тогда F(0,0)-vF(0) ; F( l ,0) :-F(528)-; F(2,0).-vF(33); F(3 ,0)(561) ; F(4,0)-F(66); F(5,0)- -F(594); « F(6,0)--F(59); ...
Работа схемгл (фиг, 2) одномерного ПДПФ осуществляется по алгоритму Пеледа-Лиу .и представлена на рремен- ных диаграммах (фиг. 3). По одинпад,- цатиразрядным D S-входам узлов подается 6 разрядов кода частоты (команда F 1) , возбуждая во всех узлах 8 страницу F., Затем командой R в
гЧ
ветззь 1 считываются младшие (первые) разряды чисел X 1 , XL2 . . . , X 641 , в ветвь 2 вторые разряды этих чисел, в ветвь R - старЕше R-тые разряды. 64- битовое слово каждой ветви разделено на 13 слов - по числу исполъзуе мых корпусов узлов 8. 5-би55
50
7
Продолжение табл. 2 q
I 10 I 11
товое слово первый разрядов чисел X 1 , X 21,. ;. . ,, X 5 подаются на DS -входы первого узла 8, 5-битовое слово-первых разрядов чисел , , ..., подается на ды 2-го узла 8 первой ветви. 5-б1-гто- вое слово первых разрядов чисел X 60 ., X 61 , . . . , X 64 подается па DS-входы 13-го узла 8 первой ветви . Аналогично и одновременно 5-би- товые слова BTopfiix, третьих. . ., . , R-тых разрядов тех же чисел подаются на В5-входы всех узлов 8 второй, ..., .R-той ветвей о После сложения чисел от каждого узла 8 в с т гматорах 9 и поразряднь х составляющих - в cyt-i- маторе 10 команда F выб1-ф 1ет другую страницу узла 8 и т.д.
Формула изобретения
Устройство для дискретного дву- .мерного преобразования Фурье, содержащее первую группу из N блоков дискретного преобразования Фурье (N вторая размерность преобразования) 5 вторзло группу из N блоков дискретного преобразования Фурье
(N - первая размерность преобразования) , первый и второй блоки посто янной памяти, второй и третий блоки памяти, адресные входы которых явля ются входами задания номеров отсчетов группы устройства, отличающееся тем, что, с целью увеличения точности, выход первого бло ка постоянной памяти подключен к информационному входу первого блока памяти, выход которого подключен к информационным входам блоков дискретного преобразования Фурье, первой группы, выходы которых поключе ны к информационному входу второго блока памяти, выход которого.подклю чен к информационным входам блоков дискретного преобразования Фурье второй группы, выходы которых подШина данных
2545058
ключены к информационному входу третьего блока памяти, выход которого подключен к адресному входу второ го блока постоянной памяти, выход которого является информационным выходом устройства, информационным входом которого является адресный вход первого блока постоянной памяти, входы задания коэффициента блоков
(О дискретного преобразования Фурье ; первой группы соединены между собой и являются входом задания номера первой размерности гармоники устройства, входы задания коэффициентов
15 блоков дискретного преобразования Фурье второй группы соединены между собой и являются входом задания номера второй размерности гармоники устройства.
Шина у продления
Фиг.1
... ir Шина данных
xis..
L
p;
,f
f №//ff дпраШаия
1ЖЖ.
ШИ:
Редактор И, Касарда
Составитель А. Баранов
Техоед И.Поповн г Корректор С. Черни
Заказ 4723/54
Тираж 671
БНРПШИ Государственного комитета СССР.
по делам изобретений и открытий .113035, Москва, Ж-35, Раушская наб, , д. 4/5
Производственно-полиграфическое предприятие, г. Ужгород, ул. Проектная, 4
ф...ф 9
№
FK
W
Ы
Подписное.


| название | год | авторы | номер документа |
|---|---|---|---|
| Субоптимальный нелинейный фильтр | 1990 |
|
SU1714618A1 |
| Устройство для решения дифференциальных уравнений в частных производных | 1987 |
|
SU1525715A1 |
| Устройство для выполнения преобразования Фурье | 1986 |
|
SU1332331A1 |
| АРИФМЕТИЧЕСКОЕ УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ | 1991 |
|
RU2015550C1 |
| Устройство для решения дифференциальных уравнений в частных производных | 1990 |
|
SU1734103A1 |
| СИСТОЛИЧЕСКИЙ ПРОЦЕССОР ДИСКРЕТНОГО ПРЕОБРАЗОВАНИЯ ФУРЬЕ С КОРРЕКЦИЕЙ ОШИБКИ | 1992 |
|
RU2018950C1 |
| Анализатор спектра | 1980 |
|
SU1029182A1 |
| Дискретный согласованный фильтр | 1985 |
|
SU1343548A1 |
| Устройство для измерения фазовых сдвигов | 1984 |
|
SU1226341A1 |
| Устройство для быстрого преобразования Фурье | 1983 |
|
SU1130872A1 |

Изобретение относится к технике спектрального анализа методом дискретного преобразования Фурье (ДПФ) и может быть использовано в радиотехнике , геофизике, вычислительной технике при построении спектроанализато- ров различного назначения. Цель изобретения - повышение точности вычислений. ПсГставленная цель дбстигается тем, что первый блок постоянной памяти подключен к первому блоку памядам блоков ДПФ первой группы, выходы которых подключены к входу второго блока памяти, выход которого подключен к входам блоков ДПФ второй . .группы, выходы которых подключены к входу третьего блока памяти, выход которого подключен к входу второго блока постоянной памяти. Зил, 2 табл.


| Коча В.М., Ланнэ А.А | |||
| Аппаратур ная реализация цифровых фильтров | |||
| - Зарубежная радиотехника, 1981, № 9, с | |||
| Способ смешанной растительной и животной проклейки бумаги | 1922 |
|
SU49A1 |
| Маккелланд Дж., Рейдер Ч.М | |||
| Применение теории чисел в цифровой об- работке сигналов | |||
| М.: Радио и связь, 1983, с | |||
| Железнодорожный снегоочиститель | 1920 |
|
SU264A1 |
Авторы
Даты
1986-08-30—Публикация
1984-12-07—Подача