11332331
Изобретение относится к автомати10
F(kfl) где f(nT)
if - угол ,через который берутся тригонометрические коэффициенты (tf const 90°) ; Т - интервал дискретизации;
п - порядковый номер отсчета входного сигнала; N - количество отсчетов
входного сигнала. В этом алгоритме для получения нового отсчета в частотной области не требуется нового набора тригонометрических коэффициентов, так как значение экспоненциального множителя в формуле (2) не зависит от k. Вследствие этого быстродействие адгорит- ма резко повышается. Кроме того, - последовательность отсче-20 подобрав соответствующим образом знаке и вычислительной технике и может быть использовано в измерительной технике, радиотехнике и электросвязи для выполнения преобразования Фурье непрерывных и дискретных, детерми- рованных и случайных сигналов в реальном масштабе времени.
Цель изобретения - повышение точности вычисления коэффициентов дискретного преобразования Фурье за счет использования модифицированного алгоритма.
В дискретном преобразовании Фурье 15 (ДПФ ) реализуется следующий алгоритм:
N-1
S- .-f -г -j SlTnk , , 2 f(пТ) . е л (1)
тов входного сигнала; k - номер выделяемого отсчета в частотной области;
Ъ 1. NT
- выбранное расстояние
чение угла цг , можно получить набор тригонометрических коэффициентов в виде простых чисел. Так, при if 90 эти числа будут иметь значения 25 1,0,-1, что дополнительно повышает быстродействие за счет исключения операций умножения.
Таким образом, предлагаемый алгоритм ДПФ по сравнению с классичес- Т - интервал дискретизации возо ким имеет на несколько порядков бомежду отсчетами в частотной области;
N - количество отсчетов входного сигнала;
временной области; п - порядковый номер отсчета
входного сигнала. Из формулы (1) видно, что при
изменении k значения экспоненциального множителя также изменяются. Из ЭТОГО следует, что для получения какого-либо HOBcfro отсчета в частотной. области требуется новый набор тригонометрических коэффициентов. Последнее обстоятельство в сильной степени снижает быстродействие алгоритма. Для устранения этого недостатка предлагается алгоритм ДПФ следующего вида:
N-1
F(kn) И f(2T-)
п-О ft .,
де r()
-jnif
(2)
360f
-последовательность отсчетов входного сигналя ;
-любое положительное , число (k+0), например номер выделяемого отсчета в частотной области;
-выбранное расстояние между отсчетами в частотной области;
лее высокое быстродействие, что дает возможность использовать его для выполнения преобразования Фурье в реальном масштабе времени. По сравнению с алгоритмом вычисления коэффициентов Фурье в известном устройстве данный алгоритм является более точным.
Вычисление коэффициентов Фурье в
известном устройстве осуществляется по следующим приближенным формулам:
и
а 27Г
Ilx{n).F sin - ni - e(n), 1
(3)
к 1
nil
, . г 2я Ь; I.X(n).F cos -rjn I
-f(n), (4)
где X(n) 5
последовательность отсчетов входного сигнала; количество отсчетов входного сигнала; порядковый номер отсчета; номер коэффициента Фурье; S(n) - последовательность псевдослучайных чисел с равноN п - i мерным законом распределения .
Как видно, в формулах (3 ) и (4) вместо точных фильтрующих функций
27г. 27
sin П-- ПI, COS ПI
используют2
ся приближенные (sin (n)
2 i и (cos ni- f(n)).
Усредненное значение этих функций при N становится равным точ ным, В остальных случаях они имеют погрешность и тем большую, чем меньше N. Величину погрешности в воспроизведении какого-либо уровня точной фильтрующей функции можно оценить, определив дисперсию усредненного значения приближенных фильтрующих функций для этого уровня. Это величи на находится из соотношения
D L
го м -
-ср
N
где Орр - дисперсия усредненного зна чения приближенной фильтрующей функции;
D - дисперсия последователь- ности случайных чисел f(n); L - количество уровней, с помощью которых воспроизводит ся точная фильтрующая функция.
Дисперсию последовательности (п) можно найти из следующего выражения:
t-V
D ((x)dx
со
(x)dx - 2Л1 Л xf (x)dx
-со.
+ т f(X)dx,
где X - последовательность случайных чисел;
m - математическое ожидание; f(х) - закон распределения случайной величины.
Для с(п), имеющей равномерное распределение в диапазоне чисел от О до 1, величина m 0,5 и f(х) 1. Тогда получаем
f1
0„ - 2-0,5 xdx +
-се 1
1
+ 0,25i dx .
(7)
Таким образом, для дисперсии а следовательно, и для погрешности алгоритма ДПФ, предложенного в известном устройстве, получаем
D ---- V 12 N
(8)
при L 1024 имеем П 85
П .
ч- N
(9)
чи
10
15
-20
; т 25
30
35
40
.
45
50
55
Из (9) видно, что для вычисления коэффициентов Фурье с погрешностью 1% требуется 8500 отсчетов входной последовательности. При меньшем количестве отсчетов величина погрешности будет больше. Кроме того, в известном устройстве точные фильтрующие функции выбираемые из блока постоянной памяти имеют круговые часто2 . ты -гт- I. Это приводит к тому, что
в блоке постоянной памяти могут храниться тригонометрические коэффициенты только для конкретного значения N. В этом случае спектральный анализ можно проводить только по N временным отсчетам. Количество временных отсчетов исследуемой реализации случайного процесса может быть в общем случае не кратно N. Вследствие этого часть временных отсчетов не будет использоваться, что приводит к дополнительной погрешности анализа.
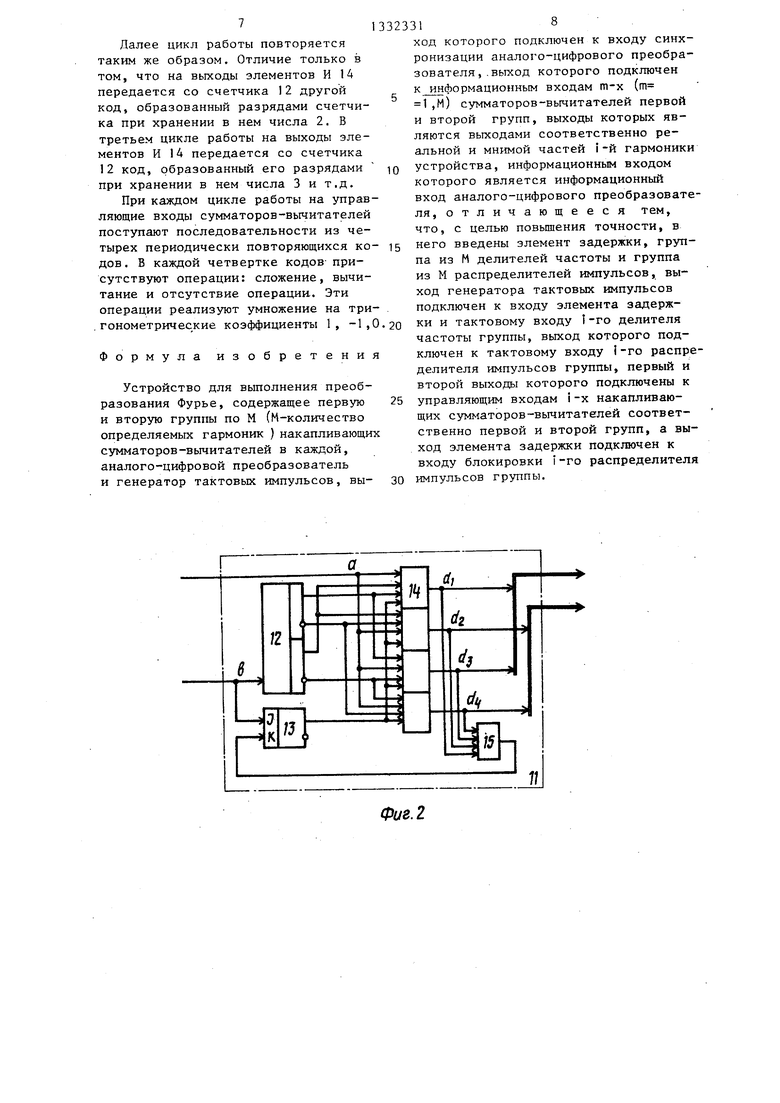
На фиг.1 представлена функциональная схема устройства для выполнения преобразования Фурье; на фиг.2 - принципиальная схема распределителя импульсов; на фиг.3 - временные диаграммы в контрольных точках.
Устройство содержит информационный вход 1, генератор 2 тактовых импульсов, аналого-цифровой преобразователь (АЦП) 3, М накапливающих сумматоров-вычитателей 4 первой и второй групп .5, информационные выходы 6 первой и второй групп, элемент 7 задержки, группу 8 из М блоков 9 делителей частоты и группу 10 из М распределителей 11 импульсов.
Устройство работает следующим образом.
Входной аналоговый сигнал поступает на вход I АЦП 3. Тактовые импульсы с периодом Т с выхода генератора 2 поступают на вход синхронизации АЦП 3, на входы блоков 9 делителей частоты и на вход элемента 7 задержки. Значения исследуемого сигнала в момент, дискретизации в виде цифрового кода с выхода АЦП 3 поступают на информационные входы накапливающих сумматоров-вычитателей 4.
с выходов делителей 9 частоты импульсы поступают на тактовые входы соответствующих распределителей 11 импульсов, на входы блокировки поступают тактовые импульсы с выхода элемента 7 задержки.
Распределитель 11 импульсов (фиг.2) содержит счетчик 12, 1К-триггер 13, узел элементов И 14, элемент ю входы элементов И 14 импульсы от
ИЛИ 15. Каждый распределитель импульсов посылает две последовательности кодов на входы выбора режима двух соответствующих накапливающих сумматоров-вычитателей для вычисления двух коэффициентов Фурье (а,- и Ь.).В каждой последовательности кодов присутствуют только три опе- рации: сложение, вычитание и отсутствие операции. Операция сложения соответствует умножению на тригонометрический коэффициент 1, операция вычитания эквивалентна - умножению на тригонометрический коэффициент -1 и отсутствие операции соответст- 25 время также присутствует низкий по- вует умножению на тригонометрический тенциал, и триггер 13 продолжает
находиться в нулевом состоянии, блокируя элементы И 14.
Блокировка элементов И 14 проискоэффициент 0.
С приходом на управляющий вход сумматора-вычитателя 4 кода на сложение число, поступившее на его инфор- 30 ходит до тек пор, пока на I-вход мационный вход, складывается с накоп- триггера 13 не придет положительный ленной в нем ранее суммой, с прихо- импульс от делителя 9 частоты. С дом кода на вычитание - вычитается приходом этого импульса триггер 13 и при коде, соответствующем отсутст- переходит в единичное состояние, а ВИЮ операции, число с информацио,нно- 5 счетчике 12 срабатывает младший го входа в сумматор-вычитатель не пе- разряд. На выходе триггера 13 появля- редается. Таким образом, в накапли- ется высокий потенциал, который вающих сумматорах-вычитателях 4 первой группы 5 оказываются записанными М значений коэффициентов а, а в накапливающих сумматорах-вычитателях 4 второй группы 5-м значений коэффициентов Ь. :
Мг
уже не блокирует элементы И 14. Первый пришедший импульс с элемента 7
40
пТ
кГ
пТ
sin nif ;
а, Гf(-Si- )
V|-1
. sr.. / n I X
b; (-Q--) COS n Lf 0 14
©0) (11)
задержки передает на выходы элемента И 14 четырехразрядный код, образованный разрядами счетчика 12. Этот код в виде двух двухразрядных кодов поступает на управляюй{ий вход
45 сумматоров-вычитателей, в которых
выполняются соответствующие операции. Четырехразрядный код с выходов элементов И 14, в котором обязательно присутствует единица, поступает на
где K -i ,
P..
P; - коэффициент деления f-го
блока 9 деления, if 90.
Элемент 7 задержки необходим для того, чтобы исключить возможность прихода кодов, поступающих на входы выбора режима накапливающих суммато ров-вычитателей, в моменты, к,огда происходит аналого-цифровое преобра316
зование в АЦП 3, т.е. в переходные моменты.
В исходном состоянии счетчик 12 и I К-триггер 13 сбро1Г1ены (находятся в нулевом состоянии ). Низкий потенциал с выхода IК-триггера 13 поступает на один из входов элемента И 14 и блокирует их. Приходящие на другие
элемента 7 задержки не могут передать на выходы элементов И 14 код, образованный разрядами счетчика 12. На выходах элементов И 14 присутствуют низкие потенциалы, которые передаются на выход в виде двух двухраэ- рядных кодов 00 и 00. Эти коды для сумматоров-вычитателей оз нача- ют отсутствие операции. Кроме того,
низкие потенциалы с выходов элементов И I4 поступают на входы элемента ИЛИ 15, г. выхода которого низкий по- . тенциал поступает на К-вход IК-триггера 13. На I-входе триггера 13 в это
Блокировка элементов И 14 происит до тек пор, пока на I-вход ггера 13 не придет положительный ульс от делителя 9 частоты. С ходом этого импульса триггер 13 еходит в единичное состояние, а четчике 12 срабатывает младший ряд. На выходе триггера 13 появля я высокий потенциал, который
ходит до тек пор, пока на I-вход триггера 13 не придет положительный импульс от делителя 9 частоты. С приходом этого импульса триггер 13 переходит в единичное состояние, а счетчике 12 срабатывает младший разряд. На выходе триггера 13 появля- ется высокий потенциал, который
уже не блокирует элементы И 14. Первый пришедший импульс с элемента 7
ходит до тек пор, пока на I-вход триггера 13 не придет положительный импульс от делителя 9 частоты. С приходом этого импульса триггер 13 переходит в единичное состояние, а счетчике 12 срабатывает младший разряд. На выходе триггера 13 появля- ется высокий потенциал, который
задержки передает на выходы элемента И 14 четырехразрядный код, образованный разрядами счетчика 12. Этот код в виде двух двухразрядных кодов поступает на управляюй{ий вход
сумматоров-вычитателей, в которых
выполняются соответствующие операции. Четырехразрядный код с выходов элементов И 14, в котором обязательно присутствует единица, поступает на
входы элемента ШШ 15. Положительный импульс с вьпсода элемента ШШ 15 сбрасывает IК-триггер в нулевое состояние .
Таким образом, все узлы распределителя импульсов приходят в исходное состояние за исключением того, что в счетчике 12 зафиксирована единица.
Далее цикл работы повторяется таким же образом. Отличие только в том, что на выходы элементов И 14 передается со счетчика 12 другой код, образованный разрядами счетчика при хранении в нем числа 2. В третьем цикле работы на выходы элементов И 14 передается со счетчика 12 код, образованный его разрядами при хранении в нем числа 3 и т.д.
При каждом цикле работы на управляющие входы сумматоров-вычитателей поступают последовательности из четырех периодически повторяющихся кодов. В каждой четвертке кодов присутствуют операции: сложение, вычитание и отсутствие операции. Эти операции реализуют умножение на три- . гонометричес кие коэффициенты 1, -1,0
Формула изобретения
Устройство для выполнения преобразования Фурье, содержащее первую и вторую группы по М (М-количество определяемых гармоник ) накапливающих сумматоров-вычитателей в каждой, аналого-цифровой преобразователь и генератор тактовых импульсов, вы323318
ход которого подключен к входу синхронизации аналого-цифрового преобразователя, .выход которого подключен к информационным входам т-х (т 1,М) сумматоров-вьиитателей первой и второй групп, выходы которых являются выходами соответственно реальной и мнимой частей i-и гармоники
Q устройства, информационным входом которого является информационный вход аналого-цифрового преобразователя, отличающееся тем, что, с целью повышения точности, в
15 него введены элемент задержки, группа из М делителей частоты и группа из М распределителей импульсов, выход генератора тактовых импульсов подключен к входу элемента задерж- 20 ки и тактовому входу I-го делителя частоты группы, выход которого подключен к тактовому входу i-го распределителя импульсов группы, первый и второй выходы которого подключены к
25 управляющим входам i-х накапливающих сумматоров-вычитателей соответственно первой и второй групп, а выход элемента задержки подключен к входу блокировки i-го распределителя
30 импульсов группы.
Фив. 2
U
и и и
и о и и
111111ГМПН1111111111ИГП11111М11П11И1111111111И1Ш1И11Ш1М1ПП1 t
fr
4
Jt J
t
J
i
i
1
d,
d3
di
4
Jt J
t
J
1


| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для выполнения преобразования Фурье | 1987 |
|
SU1418747A1 |
| Цифровой фильтр | 1987 |
|
SU1390784A1 |
| Устройство для выполнения преобразования Фурье | 1987 |
|
SU1424027A1 |
| УСТРОЙСТВО ДЛЯ ВЫПОЛНЕНИЯ ПРЕОБРАЗОВАНИЯ ФУРЬЕ | 2000 |
|
RU2182358C2 |
| Цифровой обнаружитель-измеритель частоты | 1989 |
|
SU1797127A1 |
| Устройство для вычисления коэффициентов Фурье | 1985 |
|
SU1290351A1 |
| Устройство для измерения фазовых сдвигов | 1984 |
|
SU1226341A1 |
| Анализатор спектра Фурье | 1985 |
|
SU1302293A1 |
| Устройство для вычисления коэффициентов Фурье | 1985 |
|
SU1278886A1 |
| Устройство для вычисления коэффициентов Фурье | 1985 |
|
SU1283790A1 |


Изобретение относится к автоматике и вычислительной технике и может быть использовано в измерительной технике, радиотехнике и электросвязи для выполнения преобразования Фурье непрерывных дискретных, детерминированных и случайных сигналов в реальном масштабе времени. Цель изобретения - повышение точности. Поставленная цель достигается за счет того, что в состав устройства входят информационный вход 1, генератор тактовых импульсов 2, аналого-цифровой преобразователь 3, накапливающие сумматоры-вычитатели 4, объединенные в группы 5, выходы реальных и мнимых частей гармоник 6, элемент задержки, группа В из М делителей 9 частоты (М - число вычисляемых гармоник), группа )0 из М распределителей импульсов и соответствующие связи между узлами устройства. 3 ил. 9 сл со оо 1ч5 оо со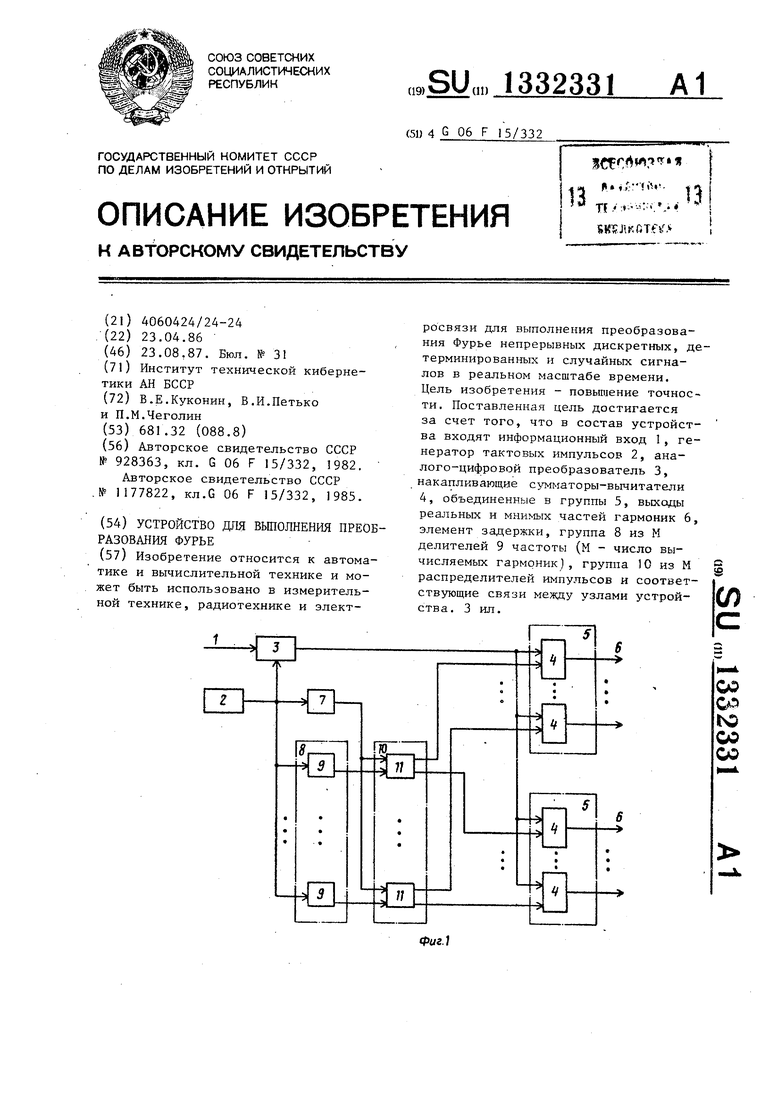
Составитель А.Баранов Редактор В.Петраш Техред Л.Сердюкова Корректор м.Демчик
Заказ 3834/45 Тираж 672Подписное
ВНИИПИ Государственного комитета СССР
по делам изобретений и открытий 113035, Москва, Ж-35, Раушская наб., д.4/5
Производственно-полиграфическое предприятие, г.Ужгород, ул. Проектная, 4
| Устройство для выполнения преобразования Фурье | 1980 |
|
SU928363A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Устройство для выполнения преобразования фурье | 1984 |
|
SU1177822A1 |
Авторы
Даты
1987-08-23—Публикация
1986-04-23—Подача