I
Изобретение относится к вычислительной технике и может быть использовано автономно или в комплексе с многопроцессорными проблемно ориентированными вычислительными системами для оперативного вычисления нелинейных функциональных зависимостей на основе метода Т-преобразова- телей.
Целью изобретения является увеличение точности вычислений.
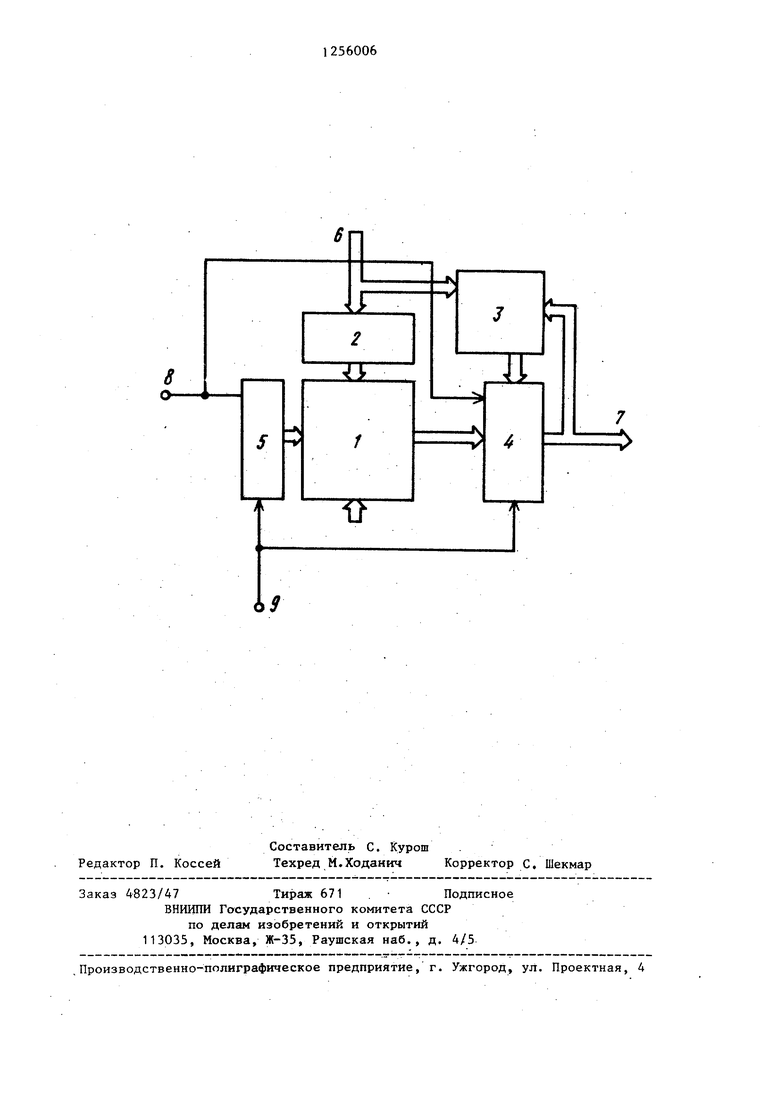
На чертеже приведена схема цифрового Т-генератора функций.
Цифровой Т-генератор функций (фиг, 1) содержит блок 1 памяти, дешифратор 2, умножитель 3, накапливающий сумматор 4, счетчик адреса 5 входную шину 6 5 выходную шину 7, вход сброса 8 и синхровход 9.
Пусть дана произвольная функция X(-t) 5 где t - аргумент изменяется в некотором интервале , до T.e.{t,,t,,} . Значение ординаты функции xCt) в определенном интервале изменения аргумента t,- i , экстраполирование функции
1 m 1 п mttX
x(i) 5 когда аргумент t изменяется за пределами интервала t eftg ,t и интерполирование функции, когда
- о N ) - ;; ..
t )
-J-- .j .- j ,
точками t.j,tj ,...,i: . Будем считать, что значение ординаты функции X(i в этих точках равно соответственно Л(1о) , X(i J,...X(i) .На основании прямого Т-преобразования вида
1256006 .2
для случая, когда Н- 1, и являются основой для организации вычислительного процесса.
Вычисление значения ординаты функции X (t) .
Значение функции X(i:) в интервале
,.} с
hnm
в соответстto
изменения аргумента (t,
заданной точностью
ВИИ с (2) определяется на основании
прямого Т-преобразования (1) как
РР
X(t)C(t-t,) x,(K)Z:At x.(K). (3)
К--0
,
15 где at; t -t; .
Учитывая, что Р Т-дискреты К; (К) в каждой точке tj известны заранее, то выражение (З)может быть записано в более простом виде .соответственно .
20 X(i) ...X(p)ut.-X,(P-1).(P-2)r
at,+...X.(2)At,aj.(1)At.+Xi(.0) Ир
Экстраполирование функции X(t) .
Вычисление значения X(t) , когда , реализуется по выражению (4); когда A tN-t- l- 0, т.е. или Д-t t -1„ О, T.e..
Интерполирование функцииX(t) .
Определение значений реализуется
Представим интервал изме- 30 по выражению функции (4). когда
35
.
Цифровой Т- генератор функций (фиг. 1) в режиме вычисления значений ординат х (t) работает следующим образом
В блок 1 памяти, заносится и хранится в течение всего вычислительно- , го процесса Р Т-дискрета Х;(К) для каждой точки t- интервала изменения аргумента. Аргумент t представляется h двоичными разрядами таким образом, чтобы m старшими разрядами hn :j fog, () представлялось как количество точек (N .+ 1), дискретизация интервала изменения аргумента
К .
Э x(t) у
/t t.,i--0,1,...,N
д t
Ч)
где
Н. некоторая масштабная по- стоянная, равная H-:t- -t| ,, XJ{K) - функция целочисленного аргумента К 05152э3...5
в каждой точке аргумента t:, ( i - 0,15, .. , N ) -вычисляется Р дискрет Х,-{о),Х,(1),Х(2),...Д(Р)где Р выбирается- из условия Р
Х,(К)
$
(1)
где
- заданная точность вычисления функции X(t).
Далее, полученные в каждой точке. t.-jP Т-дискреты Х ,(к) пересчитываются
Значение функции X(i:) в интервале
,.} с
hnm
в соответст
изменения аргумента (t,
заданной точностью
ВИИ с (2) определяется на основании
прямого Т-преобразования (1) как
РР
X(t)C(t-t,) x,(K)Z:At x.(K). (3)
К--0
где at; t -t; .
Учитывая, что Р Т-дискреты К; (К) в каждой точке tj известны заранее, то выражение (З)может быть записано в более простом виде .соответственно .
X(i) ...X(p)ut.-X,(P-1).(P-2)r
at,+...X.(2)At,aj.(1)At.+Xi(.0) Ир
Экстраполирование функции X(t) .
Вычисление значения X(t) , когда , реализуется по выражению (4); когда A tN-t- l- 0, т.е. или Д-t t -1„ О, T.e..
Интерполирование функцииX(t) .
Определение значений реализуется
по выражению функции (4). когда
по выражению функции (4). когда
.
Цифровой Т- генератор функций (фиг. 1) в режиме вычисления значений ординат х (t) работает следующим образом
В блок 1 памяти, заносится и хранится в течение всего вычислительно- го процесса Р Т-дискрета Х;(К) для каждой точки t- интервала изменения аргумента. Аргумент t представляется h двоичными разрядами таким образом, чтобы m старшими разрядами hn :j fog, () представлялось как количество точек (N .+ 1), дискретизация интервала изменения аргумента t гп;п.-.сллЬ младшими разрядами представлялась разность д-Ь- - 1 . Тогда при подаче на входную шину 6 значения аргумента , старших разрядов подаются на вход дешифратора 2, а (к -т) младших разрядов соответствующие л1 .-1-tj .подаются на первый вход умножителя 3, В зависимости от входного кода на соответствующем выходе дешифратора 2 появляется единичный сигнал, который выбирает строку блока 1 памяти , где хранятся/Т-дискреты ХДк),
соответствующие точке t . Счетчик адреса находится в нулевом состоянии благодаря чему по нулевому адресу f -й строки блока памяти считывается Т-дискрета X|(PJ, которая подается на второй вход накапливающего сумматора 4. После этого на синхровход 9 подается импульс, по переднему фронт которого значение К-(.Р) записывается в накапливающий сумматор 4, а по заднему фронту в счетчик адреса 5 записывается единица. Значение X.(PJ подается из выхода накапливающего сумматора 4 на второй вход умножителя 3, на первый вход которого пода ется значение 4tj из входной шины 6, В умножителе 3 и в соответствии с (4) реализуется произведение Х (Р)д{ . которое подается на первый вход накапливающего сумматора 4. На второй вход накапливающего сумматора подается .значение (Р- 1), которое считывается из первого адреса i-и строки блока 1 памяти. После этого на синхровход 9 подается второй им- пульс, по переднему фронту которого в накапливающий сумматор 4 в соответствии с (4) записывается сумма X(P)Ati+X,{P- 1), а в счетчик 5 адреса добавляется вторая единица. В блоке 1 памяти по второму адресу
1-1 строки считывается значение, которое поступает на второй вход накапливающего.сумматора 4. В умножителе 3 реализуется по выражению (4 произведение
X.(P)&t, + X,(p-1)&t, ; которое подается на первый вход накапливающего сумматора 4. Далее на управляющую шину подается снова им- пульс, по переднему фронту которого значение С X ( Р)ut; (P-l) д1 записывается в накапливающий сумматор 4 и подается на второй вход умножителя 3. По заднему фронту им- пульса в счетчик 5 адреса добавляется третья единица и значение Х(Р-2} считанное из третьей строки блока памяти 1, подается на второй вход накапливающего сумматора 4. Так вы- числительный процесс повторяется (Р +1) раз. По переднему фронту (Р + 1)-го импульса, подаваемого на синхровход 9, значение ...К;СР)л1, Х,(Р+1)
atj+..X,. (ullut,/: .
поступающее из выхода умножителя 3, суммируется по вы- - ражению (4) со значением Х(о) , поступающим из блока 1 памяти, а результат вычисления X (t) подается на выходную шину 7. Таким образом, при подаче на синхровход 9 (Р + 1) импульсов, период следования которых равен длительности операции умножения в умножителе 3, мы получаем значения ординаты произвольной функции X(t) с заданной точностью вычислени & , представленной выражением (2), Т-дискреты ) которой записаны в блоке 1 памяти. При реализации операции экстраполирования вычислительный процесс будет аналогичен описанному с -ТОЙ лишь разницей, что на (h -hi ) младших разрядов входной шины 6 будет подаваться значение At t-t О или ut . В режиме интерполирования функций цифровой Т- генератор функций работает аналогично режиму вычисления значения орди- наты функции, т.е. на входную шину 6 подается N -разрядное значение ар- тумента t , причем t., ь t 6 f
N
Формула изобретения
Цифровой Т генератор функций, со держа.1ий блок памяти, умножитель, накапливающий сумматор, причем выход умножителя подключен к первому информационному входу накапливающего сумматора, о т л и ч а ю щ и и с я тем, что, с целью увеличения точности вычислений, в него введены дешифратор ч счетчик адреса, причем синхровход генератора подключен к счетному входу счетчика адреса и входу разрешения записи накапливающего сумматора, второй информационный вход которого подключен к выходу блока памяти, группа разрядов выбора адресного входа которого подключена к выходу счетчика адреса, вход сброса которого подключен к входу сброса накапливающего сумматора и является входом сброса генератора, вход дещи- фратора является входом старших разрядов аргумента генератора, вход младших разрядов аргумента которого подключен к.первому информационному входу умножителя,второй информационный вход которого подключен к выходу накапливающего сумматора и является выходом функции генератора, выход дешифратора подключен к группе разрядов выбора интервала изменения аргумента адресного входа блока па- мяти.
Редактор П. Коссей
Составитель С. Курош Техред М.Ходанич Корректор С, Шекмар
Заказ 4823/47Тираж 671 . Подписное
ВНИИПИ Государственного комитета СССР
по делам изобретений и открытий 113035, Москва, Ж-35, Раушская наб., д. 4/5
.Производственно-полиграфическое предприятие, г. Ужгород, ул. Проектная, 4

| название | год | авторы | номер документа |
|---|---|---|---|
| Цифровой Т-генератор функций комплексного переменного | 1987 |
|
SU1483445A1 |
| Цифровой Т-генератор функций | 1987 |
|
SU1423999A1 |
| Устройство для вычисления функций | 1985 |
|
SU1280391A1 |
| Устройство для воспроизведения функций | 1986 |
|
SU1348828A1 |
| Устройство для вычисления элементарных функций | 1981 |
|
SU983707A1 |
| Генератор функций | 1984 |
|
SU1241219A1 |
| Аппроксимирующий функциональный преобразователь | 1984 |
|
SU1205153A1 |
| Генератор функций | 1984 |
|
SU1275411A1 |
| Цифровой функциональный преобразователь | 1980 |
|
SU955082A1 |
| Устройство для цифровой фильтрации | 1985 |
|
SU1381541A1 |
Изобретение относится к вычислительной технике и может быть использовано автономно или в комплексе с цифровой вычислительной машиной для оперативного вычисления широкого класса функций с задпнной точностью. Генератор содержит блок памяти, умножитель, дешифратор, счетчик адреса, накапливающий сумматор. Целью изобретения является увеличение точности, что достигается благодаря введению дешифратора и счетчика адреса. 1 ил. 1C ел О5

| Очаг для массовой варки пищи, выпечки хлеба и кипячения воды | 1921 |
|
SU4A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Цифровой генератор функций | 1976 |
|
SU736079A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1986-09-07—Публикация
1985-01-21—Подача