Изобретение относится к вычислительной технике и может быть использовано для параллельного суммирования многоразрядных двоичных чисел.
Цель изобретения - расширение функциональных возможностей за счет суммирования чисел, представленных в двоичной избыточной минимальной и оптимальной системах счисления, при сохранении суммирования чисел, пред ставленных в коде Фибоначчи и традиционной двоичной системе счисления.
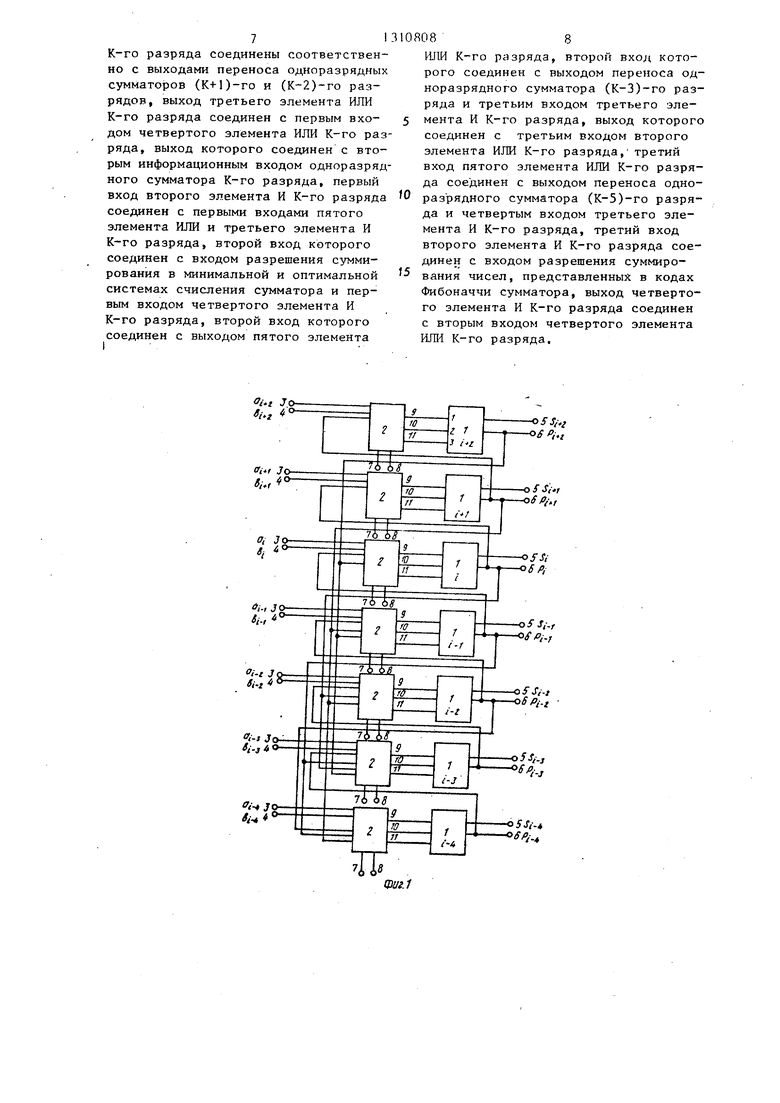
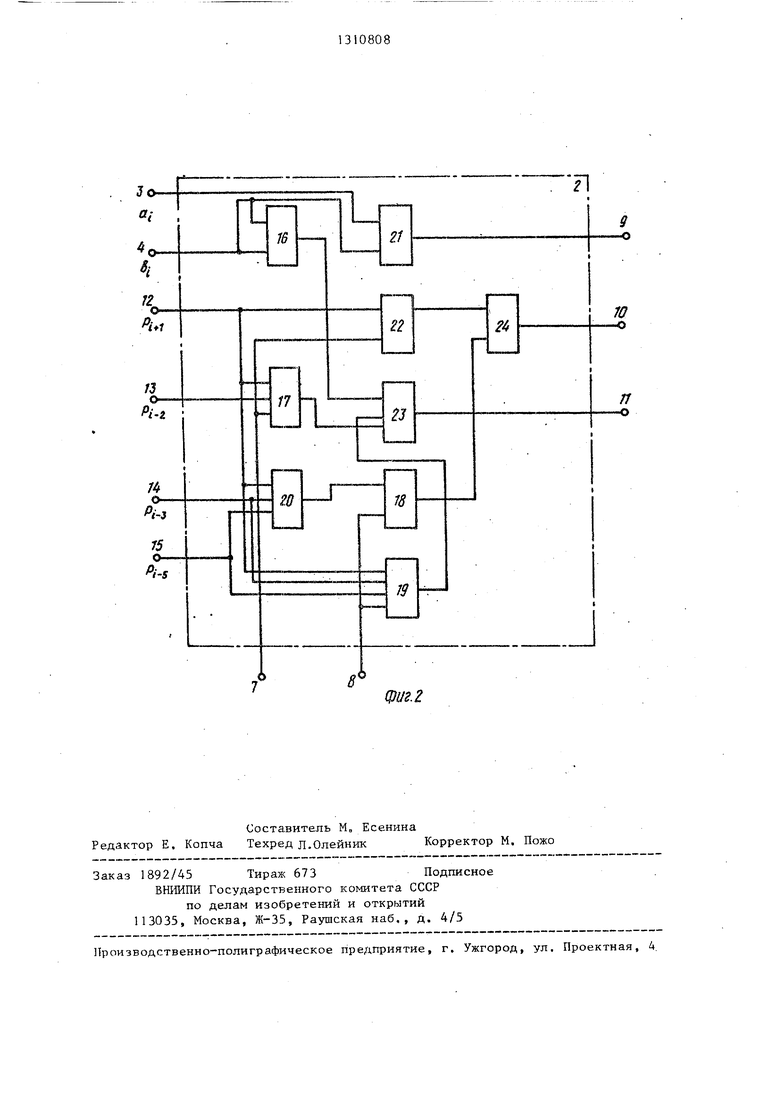
На фиг. 1 изображена функциональная схема комбинационного сумматора; на фиг, 2 - функциональная схема ло- гического узла.
Комбинационный сумматор содержит (фиг. 1) в каждом разряде одноразрядный сумматор 1, логический узел 2, вход 3 соответствующего разряда one- ранда, вход 4 соответствующего разряда второго операнда, выход 5 суммы соответствующего разряда, выход 6 переноса соответствующего разряда, вход 7 разрешения суммирования чисел представленных в кодах Фибоначчи сумматора, вход 8 разрешения суммирования в минимальной и оптимальной системах счисления сумматора.
Логический узел (фиг. 2) содержит входы 9-11 логического узла, входы 12 - 15 соответственно переноса из (К+1)-го, (К-2)-го, ()-го, (К-5)- го разрядов, четыре элемента И 16 - 19, и пять элементов ИЛИ 20 - 24.
I Любое натуральное число А в двоичной минимальной системе счисления представляется в виде многочлена
(О
(2)
А- 11об , 1 1
где ,l ;
О, при i О, Cf (i) I, при ,
V(i-2)+ (i-3), при i 1.
Значение (| (i+l) является мощностью п-разрядного минимального и (п+1)-разрядного кода Фибоначчи.
Минимальная система счисления предполагает наличие не менее 4-х нулей после 1, (это вытекает из выражения (2)), что определяет обна- ружающие и корректирующие свойства информации, представленной в этой системе счисления.
Предлагаемый способ сложения основан на соотношении
(3 g;(i)+V(i) tt ((i-3)(i-5).
5
0
0 5
5
(4)
0
Правило сложения следовательно имеет вид
0+0 0;
0+1 -- 1;
1+0 1;
1+1 1000101.
Анализ выражения (3) позволяет предположить, что операция сложения будет протекать с появлением промежуточных сумм в ряде случаев.
Учитывая, что в минимальной системе счисления минимальная форма представления чисел предполагает наличие после каждой единитды не ме- нее четырех нулей, видно, что сигналы переносов в (1+1)-й (1-3)-й разряды осуществляются беспрепятственно, возможное наличие единицы в (i-5)-M разряде приводит к необходимости появления промежуточных сумм в ряде случаев.
Следовательно, алгоритм сложения чисел, представленных в минимальной системе счисления, имеет следующий вид.
1.Образование промежуточной суммы и сигнала переноса.
2.Суммирование промежуточной суммы и сигнала переноса.
3.Повторение пунктов 1 и 2 до тех пор, пока промежуточная сумма не станет эквивалентна окончательной,
о чем свидетельствует нулевой сигнал переноса.
Представление чисел в двоичной оптимальной системе счисления производится также в виде многочлена, но для этой цели, кроме выражения (2), используется и выражение
Го при ii 0; (5) (i) (i-2)+(i-3) + l, при . Особенностью представления в двоичной оптимальной системе счисления является строго определенное число нулей между логическими единицами
1
Z 2,
(6)
50
55
где Z - количество нулей.
В силу того, что основную информационную нагрузку несут веса, ((i), () используются для построения чисел, то операции сложения аналогичны минимальной системе счисления.
Одноразрядный сумматор 1 предназначен для суммирования разрядов слагаемых и сигнала переноса, поступающих на его вход и выдачи значения суммы данного разряда на выходную
шину 5 и сигнала переноса из данного разряда в соседние по выходной ши- не 6.
Логический узел 2 предназначен для формирования из сигналов слагае- мых и нескольких сигналов переноса (для чисел Фибоначчи имеем 2 сигнала переноса из (i-l)-ro и (i+2)-ro разрядов, для минимальной и оптимальной систем счисления - 3 сигнала переноса из (i-l)-ro, ()-ro и (i+5)-ro разрядов) входных сигналов для одноразрядного сумматора 1 в соответствии с выражениями (8) и (9).
Первая шина 7 управления предназ- начена для разрешения функционирования комбинационного сумматора с числами, представленными в кодах Фибоначчи, вторая шина 8 управления - для работы комбинационного сумматора в двоичных минимальной и оптимальной системах счисления.
Элементы И 16 и ИЛИ 21 предназна- чеш;1 для организации функционирования узла при работе в традиционной системе счисления, передачи входных значений слагаемых и сигнала переноса на выход.
Элементы ИЛИ 22 и И 17 служат для формирования выходных сигналов при функционировании в кодах Фибоначчи.
Элементы ИЛИ 24 и 20, И 18 и 19 организуют выходные сигналы при работе в двоичной минимальной и оптимальной системах счисления.
Логический узел имеет шесть входных шин 3,4,12 - 15 (обозначим их соответственно а Д,с,а,е ,ж) и три выходных 9 - 11 - соответственно I, II и III.
Входные шины 3,4,12 - 15 подключены соответственно к первому, второму, третьему, четвертому, пятому, шестому входам логического узла (фиг. 1), выходные шины 16 - 18 - к первому, второму, третьему выходам. Количество выходных шин определено схемной особенностью одноразрядного сумматора, а количество входных шин арифметическими операциями сложения в рассматриваемых системах счисления
Для традиционной системы счисления на выходных шинах будут следующие логические функции:
I а V S ;
;(7)
,
o
0
5
5
для кодов Фибоначчи:
I а V 5 ;
II су ;(8)
III а5V СП ,
для двоичных ганимальной и оптимальной систем счисления:
I а V 5 ;
II с ve V )к;(9)
III а5 V се . Устройство работает следующим
образом.
При функционировании в традиционной двоичной системе счисления на входы 7 и 8 устройства подан О. Это приводит к тому, что логический узел 2 реагирует на сигналы на входах слагаемых и входе переноса из младшего разряда. На входы одноразрядного сумматора 1 поступают сигналы в соответствии с выражением (7).
Сигналы разрядов слагаемых поступают в логическом узле 2 на входы элемента И 16 и ИЛИ 21,- с выхода последнего - на вход одноразрядного сумматора 1. Элемент И 16 в зависимости от значений разрядов слагаемых формирует сигнал на третий вход одноразрядного сумматора. Сигнал переноса из младшего разряда беспрепят- 0 ственно проходит на вход одноразрядного устройства.
Элементы И 17 - 19 заперты О на входах 7 и 8 устройства.
Следовательно, сигнал переноса, . 5 распространяясь с выхода однораз-- рядного сумматора i-ro разряда в (1+1)-й, (1-2)-й, (1-3)-й (1-5)-й разряды, на входе логического узла оказывает влияние только в (i+I)-M 0 разряде. Алгоритм функционирования зависит от выражения, описывающего операцию сложения в традиционной двоичной системе счисления: V(i)+()j(i) V(i+).
5 При функционировании устройства с числами в коде Фибоначчи 1 подается на вход 7, это приводит к следующей перенастройке архитектуры логического узла 2 каждого разряда.
Алгоритм функционирования узла виден из выражения (8), вытекающего из следующего соотношения, описывающего операцию сложения единичных разрядов двух слагаемых
Q(i) + (fj(i) ф(1+1)+9(1-2).
Сигналы, приходящие на входы логического узла, проходят на его выходы.
0
5
В данном случае на выходной шине сигнал аналогичен предыдущему случаю Формирование сигналов на остальных выходах следующее,
Сигналы переноса из (i-l)-ro и (i+2)-ro разрядов поступают соответственно на третий и четвертый входы логического узла.
Элемент И I7 учитывает одновременный приход единичных сигналов переноса и подает его через элемент ИЛИ 23 на третий вход одноразрядного сумматора 1, предварительно учитывая сигнал с выхода элемента И 16.
Элементы ИЛИ 22 и 23 формируют сигнал на второй вход одноразрядного сумматора I,
Элементы И 17, ИЛИ 23 и 22 учи- тывают особенность формирования сигнала суммы и переноса в коде Фибоначчи, заключающегося в том, что из сигналов переноса формируется самостоятельный сигнал S, участвующий в получении суммы, и сигнал переноса Р
Значение сигналов S Р переноса
00
01
10
1 1
О
В двоичной оптимальной и минимальной системах счисления процесс сложения осуществляется следующим образом.
На вход 8,устройства подается единичный сигнал, на вход 7 - нулевой сигнал. Это приводит к тому, что элемент И 17 запирается, а элементы И 18 и 19 открываются и участвуют в процессе формирования сигнала на второй вход одноразрядного сумматора из сигналов переноса из СК-1)-го, (К+3)-го, (К+5)-го разрядов. Зависимость выходных сигналов от входных определена соотношением (9), Это определяет и работу логического узла.
Рассмотрим особенности алгоритма сложения в двоичной минимальной и двоичной оптимальной системах счисления. Они обусловлены наличием сигналов в К-й разряд из старших и младшего разряда. Следовательно, из этих
сигналов могут быть выделены сигналы сумм и сигналы переноса:
Значение сигналов S Р переноса
000О О
00
ОП
11
,
й8,
f5 Формула изобретения
Комбинационный сумматор, содержащий в каждом разряде одноразрядный сумматор, два элемента И и три эле20 мента ИЛИ, причем вход К-го разряда первого операнда сумматора (, п, где п - разрядность операндов) соединен с первыми входами первого элемента И данного разряда и первого
25 элемента ИЛИ данного разряда, вход К-го разряда второго операнда сумматора соединен с вторыми входами первого элемента И данного разряда и первого элемента ШЖ данного разряда, выход первого элемента И К-го т разряда соеданен с первым входом второго элемента ИЛИ К-го разряда, второй вход которого соединен с выходом второго элемента И К-го разряда, первый вход которого соединен с первым входом третьего элемента ИЛИ К-го разряда), второй вход которого соединен с вторым входом второго элемента И К-го разряда, выходы первого и второго элементов ИЛИ К-го разряда соединены соответственно с первым информационным входом и входом переноса одноразрядного сумматора К-го разряда, выход суммы и выход переноса которого соединены соответственно с выходом суммы и переноса К-го разряда сумматора, ю т л и - чающийся тем, что, с целью расширения функциональных возможностей за счет суммирования чисел, представленных в двоичной избыточной минимальной и оптимальной системах счисления, при сохранении суммирования чисел, представленных в коде. j Фибоначчи и традиционной двоичной системе счисления, в каждый разряд сумматора введены два элемента ИЛИ и два элемента И, причем первый и второй входы третьего элемента ИЛИ
30
35
40
45
50
7
К-го разряда соединены соответственно с выходами переноса одноразрядных сумматоров (К+1)-го и (К-2)-го разрядов, выход третьего элемента ИЛИ К-го разряда соединен с первым входом четвертого элемента ИЛИ К-го разряда, выход которого соединен с вторым информационным входом одноразрядного сумматора К-го разряда, первый вход второго элемента И К-го разряда соединен с первыми входами пятого элемента ИЛИ и третьего элемента И К-го разряда, второй вход которого соединен с входом разрешения суммирования в минимальной и оптимальной системах счисления сумматора и первым входом четвертого элемента И К-го разряда, второй вход которого соединен с выходом пятого элемента I
10808В
Ш1И К-го разряда, второй вход которого соединен с выходом переноса одноразрядного сумматора (К-З)-го разряда и третьим входом третьего эле5 мента И К-го разряда, выход которого соединен с третьим входом второго элемента ИЛИ К-го разряда,- третий вход пятого элемента ИЖ К-го разряда соединен с выходом переноса одно10 разрядного сумматора (К-5)-го разряда и четвертым входом третьего элемента И К-го разряда, третий вход второго элемента И К-го разряда соединен с входом разрешения суммиро 5 вания чисел, представленных в кодах Фибоначчи сумматора, выход четвертого элемента И К-го разряда соединен с вторым входом четвертого элемента ИЛИ К-го разряда.
41
.


| название | год | авторы | номер документа |
|---|---|---|---|
| Комбинационный сумматор | 1987 |
|
SU1442988A1 |
| Последовательный сумматор | 1977 |
|
SU696452A1 |
| Накапливающий сумматор | 1986 |
|
SU1401453A1 |
| Комбинационный сумматор | 1975 |
|
SU570896A1 |
| Накапливающий сумматор | 1985 |
|
SU1278835A1 |
| Устройство для сложения п-разрядных десятичных чисел | 1980 |
|
SU900282A1 |
| Сумматор кодов Фибоначчи | 1981 |
|
SU981993A1 |
| КОМБИНАЦИОННЫЙ СУММАТОР СТРУКТУРНЫХ КОДОВ | 1991 |
|
RU2023288C1 |
| Устройство для сложения в избыточной двоичной системе счисления | 1977 |
|
SU696450A1 |
| Последовательный сумматор | 1988 |
|
SU1571573A1 |
Изобретение относится к вычислительной технике и может быть использовано для параллельного суммирова- .ния многоразрядных двоичных чисел. Цель изобретения - расширение функциональных возможнЬстей за счет способности суммировать числа, представленные в двоичных избыточных минимальной и оптимальной системах счисления при сохранении работоспособности с числами, представленными в кодб Фибоначчи и традиционной системе счисления. Комбинационный сумматор в каждом разряде содержит одноразрядный сумматор, четыре элемента И, пять элементов ИЛИ. 2 ил 00 о 00


| Сумматор кодов Фибоначчи | 1981 |
|
SU981993A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Комбинационный сумматор | 1975 |
|
SU570896A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Сплав для отливки колец для сальниковых набивок | 1922 |
|
SU1975A1 |
| I | |||
Авторы
Даты
1987-05-15—Публикация
1985-12-03—Подача