Изобретение относится к вычислительной технике, в маетности к гибридным вычислительным машинам, и предназначено для решения задач теории переноса, описываемых интегродиф- ференциальными уравнениями.
Цель изобретения - расширение функциональных возможностей устройства за счет решения интегродифферен- циальных уравнений переноса.
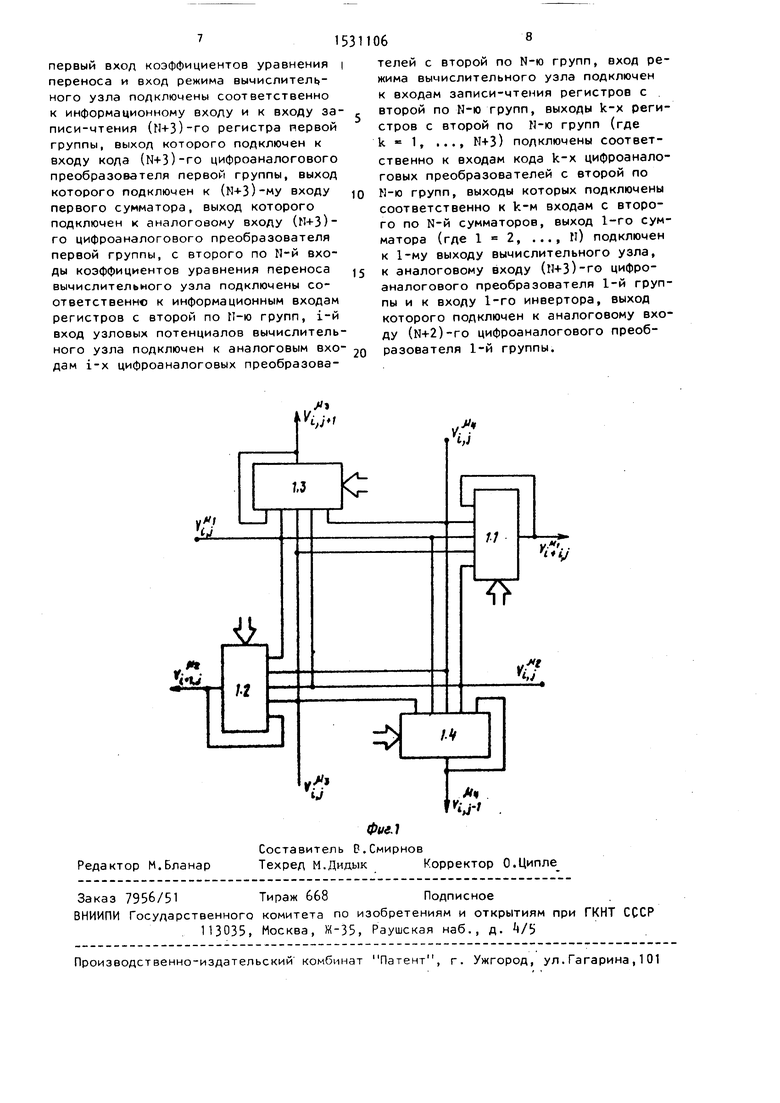
На фиг.1 представлена схема вычислительного узла для случая N « , на фиг.2 - схема вычислительного элемента узла.
Зм
10
15
Вычислительный узел соде числительных элементов 1.1N - число угловых направлен носа. Вычислительный элемен жит (N+3) регистров 2.1-2.N цифроаналоговых преобразова 3.1-3.N+3, сумматор , инве
Рассмотрим работу вычисл узла цифроаналогового проце примере решения простейшей ории переноса в плоскопарал геометрии, описываемой след тегродифференциальным кинет уравнением:
(U д +,4 (x,(u )W(x,p fu ) + S(x,(U), (1)
Вычислительный узел содержит N вычислительных элементов 1.11.N, где N - число угловых направлений переноса. Вычислительный элемент 1 содержит (N+3) регистров 2.1-2.N+3, N+3 цифроаналоговых преобразователей 3.1-3.N+3, сумматор , инвертор 5.
Рассмотрим работу вычислительного узла цифроаналогового процессора на примере решения простейшей задачи теории переноса в плоскопараллельной геометрии, описываемой следующим ин- тегродифференциальным кинетическим уравнением:

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для решения нелинейных задач теории поля | 1984 |
|
SU1229781A1 |
| Вычислительный узел для решения уравнений теплопроводности | 1983 |
|
SU1112379A1 |
| Аналого-цифровое устройство для решения системы дифференциальных уравнений | 1987 |
|
SU1462378A1 |
| Устройство для решения задач теории переноса | 1986 |
|
SU1420604A1 |
| Вычислительный узел сеточной модели для решения нелинейных уравнений теплопроводности | 1986 |
|
SU1388912A1 |
| Устройство для решения нелинейных дифференциальных уравнений теплопроводности | 1983 |
|
SU1151985A1 |
| Аналого-цифровая вычислительная система | 1987 |
|
SU1509955A1 |
| Аналого-цифровая вычислительная система и аналоговая вычислительная машина (ее варианты) | 1983 |
|
SU1259300A1 |
| Нелинейный интерполятор | 1985 |
|
SU1267446A1 |
| Устройство для решения нелинейных задач теории поля | 1983 |
|
SU1149282A1 |
Изобретение относится к вычислительной технике, в частности к гибридным вычислительным устройствам, и предназначено для решения задач теории переноса, описываемых интегродифференциальными уравнениями в частных производных. Цель изобретения - расширение функциональных возможностей за счет решения интегродифференциальных уравнений переноса. Вычислительный узел содержит N вычислительных элементов, каждый из которых имеет группу из (N+3)-х регистров 2, группу из (N+3)-х цифроаналоговых преобразователей 3, сумматор 4 и инвертор 5. 2 ил.
/ К
,и) - плотность частиц в точке X, летящих под углом
5 к оси ОХ, |U CDS }; W(x,() - плотность вероятности перехода частиц, дви- жу1чихся в направлении fu , в направлении |ii в точке х;
S(x,(U) - источник частиц в точке х с направлением движения по fU ,
21, , SJ- кусочно-непрерывные
(М,
CplY , м) Ч ui, ij
((
(Un
&х
д...- ;-2. (
+ л; ( (« )
де С| ij
S .. м
значение моделируемой функции в точк е ij дискретного пространства в углопом направлении переноса III ;
функция дискретного источника частиц в точке ij с напрар лением движения по
орту |u,;
телесный угол, по которому производится интегрирование числа частиц, попавших в этот угол и рассеянных в направлении Л, .
чГ:,„ -чГ, ZK,,,-f,),s,(3)
функции поглощения и рассеяния в точке х.
Кусочно-разностная аппроксимация уравнения (1) по одному из направлений переноса |Цу, например в направлении fU,, переводит исходную задачу в дискретное пространство, образованное ортами направления переноса в соответствии со схемой переноса.
Получаемое при этом разностное уравнение для одной узловой точки и для одного /III -го направления переноса имеет вид
(Un
(
м
Уравнение (2) записано для узловой точки дискретного пространства при моделировании переноса в направлении орта М, с учетом поглощения и рассеяния в этой узловой точке.
При решении уравнения (2) на вычислительном элементе предполагается, что выходной величиной являются функции плотности частиц, вылетающих в направлении орта /К, из узловой точки ij с учетом процессов поглощения и рассеяния а этой точке, а также с учетом дополнительного источника частиц в этой точке:
коэффициенты этого уравнения имеют следующий вид:
К . - ,
к - .
К1 - г, ,
(М
в уравнеUX
,
Функцию источника S ,НИИ (3) можно представить для некоторых задач теории переноса как суперпозицию плотности генерации частиц, зависящую от внешних условий S и плотности генерации частиц, обусловленную внутренними факторами моделируемой среды f, для последней в случае линейной зависимости от моделируемой функции имеют f ;
тогда последний член уравнения (З) может быть представлен следующим образом:
(Ui (U, (Ui
K,S;J K.cs jj Z,4,,.). Перед решением уравнения
(5) (3) с
учетом (k) и () в регистры 2.1- . 2.N+3 заносятся коды коэффициентов
V V - V V
1 7.1 2,N э
При решении эти коды поступают на цифровые входы цифроаналоговых преобразователей 3..N-i-3. На аналоговые входы цифроаналоговых преобразователей 3.1-З.М подаются значения узловых потенциалов V ;. с выходов сумматоров k, включенных в другие узлы матричного процессора .. Величины этих узловых потенциалов V; связаны с моделируемыми переменными (J j через масштабные коэффициенты тЛ(( muiV) Произведения этих пот енциалов и кодов коэффициентов поступают в соответствии с решаемым уравнением (З) с выходов цифроаналоговых преобразователей 3.1-З.М на вход сумматора k. На вход последнего также поступают аналоговые значения произведения
опорного потенциала V
7
на соответствующий код, произведения отрицательной величины выходного потенциала V на код коэффициента поглощения и произведения величины выходного потенциала на код коэффициента внутреннего источника.
На выходе сумматора 4 формируется потенциал V ,,| , являющийся решением уравнения (3) и соответствующий моделируемой плотности частиц, вылетающих из точки ij в направлении луча К, .
53П06
Таким образом, каждый вычислитель- ный элемент моделирует перенос частиц в направлении fU| с учетом поглощения и рассеяния в этой точке дискретного пространства, в которую включен данный вычислительный элемент, а вычислительный узел является совокупностью таких элементов и на нем осуществляется взаимный переход при рассеянии из одного направления в другое.
10
5
0
5
0
5
0
5
0
5
Формула изобретения
Вычислительный узел цифроаналого- вого матричного процессора для решения задач теории переноса, содержащий первую группу из (М+2)-х регистров, где N - число моделируемых угловых направлений, первую группу из (Ы+2)-х цифроаналоговых преобразователей, первый сумматор и первый инвертор, причем первый вход коэффициентов уравнения переноса вычислительного узла подключен к информационным входам регистров первой группы, i-й вход узловых потенциалов вычислительного узла (где i 1, ..., N+l) подключен к аналоговому входу i-ro циф- роаналогового преобразователя, первой группы, вход режима вычислительного узла подключен к входам записи- чтения регистров первой группы, выход j-ro регистра первой группы (где j 1, ..., N+2) подключен к входу кода j-ro цифроаналогового преобразователя, выходы цифроаналоговых преобразователей с первого по (N+2)-M первой группы подключены соответственно к входам с первого по (Н+2)-й первого сумматора, выход которого подключен к первому выходу вычислительного узла и к входу первого инвертора, выход которого подключен к аналоговому входу (N+2)-ro цифроаналогового преобразователя, отличающийся тем, что, с целью расширения функциональных возможностей за счет решения интегродифференциальных уравнений переноса, вычислительный узел содержит ()й регистр первой группы, (ы+3)-й цифроаналоговый преобразователь первой группы, с второй по N-ю группы из (N+3)-x регистров в каждой, с второй по 11-ю группы из (N+3)-x цифроаналоговых преобразователей в ка,„дой, с второго по П-й сумматоры, с второго по N-й инверторы, пои этом
первый вход коэффициентов уравнения переноса и вход режима вычислитель - ного узла подключены соответственно к информационному входу и к входу записи-чтения (П+3)-го регистра первой группы, выход которого подключен к входу кода {Ы+3)-го цифроаналогового преобразователя первой группы, выход которого подключен к (М-|-3)му входу первого сумматора, выход которого подключен к аналоговому входу (И+З)- го цифроаналогового преобразователя первой группы, с второго по Н-й входы коэффициентов уравнения переноса вычислительного узла подключены соответственно к информационным входам регистров с второй по П-ю групп, i-й вход узловых потенциалов вычислитель ного узла подключен к аналоговым вхо дам i-x цифроаналоговых преобразователей с второй по N-ю групп, вход режима вычислительного узла подключен к входам записи-чтения регистров с
, второй по N-Ю трупп, выходы k-x регистров с второй по N-ю групп (где k 1, ... N+3) подключены соответственно к входам кода k-x цифроаналоговых преобразователей с второй по 10 N-ю групп, выходы которых подключены соответственно к k-м входам с второго по N-й сумматоров, выход 1-го сумматора (где 1 2, ..., N) подключен к 1-му выходу вычислительного узла, 15 к аналоговому входу (N+3)-ro цифро- аналогового преобразователя 1-й группы и к входу 1-го инвертора, выход которого подключен к аналоговому входу (N+2)-ro цифроаналогового преоб20 разователя 1-й группы.

| Вычислительный узел для решения уравнений теплопроводности | 1983 |
|
SU1112379A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Устройство для решения нелинейных дифференциальных уравнений теплопроводности | 1983 |
|
SU1151985A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
Авторы
Даты
1989-12-23—Публикация
1988-03-31—Подача