СЛ
эо ю го W
3158
Изобретение относится к радиотехнике и может быть использовано для фильтрации сигналов в системах измерения, управления, связи, обработки данных, в радиолокации и вычислительной технике,,
Цель изобретения - повышение точности фильтрации путем уменьшения шума квантования.
На фиг. 1 приведена топологическая схема, иллюстрирующая принцип работы рекурсивного цифрового фильтра; на фиг. электрическая схема рекурсивного цифрового фильтра; на фиг. 3 - диаграмма расположения зон Y(n) в диапазоне возможных значений выходной последовательности Y(.n) .
Рекурсивный цифровой фильтр содержит сумматор 1, первый и второй умножители 2 и 3, первый 4, второй 5, третий 6 и четвертый 7 регистры, первый и второй блоки 8 и 9 памяти, первый 10, второй 11, третий 12 и четвертый 13 компараторы, первый и второй эпементы И 14 и 15, первый и второй счетчики 16 и 17.
В ходе фильтрации в петле обратной связи раздельно обрабатывают КОДОВУЮ последовательность Y(n), являющуюся ближайшей в сторону уменьшения от выходной последовательности Y(n), удовлетворяющей условию |Y4n)V integer Y4n)b,+0,5j| 1/1; п)
UY(n)b,- integer Y4n)VO, 1/1,
где b, и b г - коэффициенты ветвей
обратной связи;
1-lbJ и кодовую последовательность AY(n)
Y(n)-Y(n), причем в ветвях обработки $(п) квантуют путем округления каждое произведение, а в ветвях обработки кодовой последовательности
dY(n) - сумму о В ветвях обработки кордовой последовательности Y(.n) знали- зируют состояние узлов разветвления в случае достижения последними в ходе фильтрации нулевого состояния квантование суммы посредством округления заменяют квантованием суммы посредством усечения.
На топологической схеме (фиг« 1)
ветвь Y(n)/Y(n) означает получение
кодовой последовательности Y(n) из
Y(n), узел®- квантование путем ок10
15
20
25
30
35
40
и 45
50
55
ругления, а узел( квантование либо путем округления, либо путем усечения.
Разностное уравнение для выходного напряжения такой структуры с учетом квантования путем округления получается в виде
Y(n)X(nJ+integer Y(n-1) -b + 1/l integer YtU-2)bl+1/l + + unteger /lY(n-1)b1+ZlY(n-2) S+0,5,
где 1/1 - предельное значение ошибки округления для нижних ветвей петли обратной связи согласно условию (1); 0,5 - предельное значение ошибки округления в верхних ветвях„
В результате этих ошибок при незагруженном фильтре, т.е. при Х(п)0, в каждой из этих ветвей могут возникнуть собственные колебания предельных циклов„
Условием отсутствия колебаний предельных циклов согласно формуле Джексона для нижних ветвей является неравенство
.....ca.
Таким образом, достаточным условием отсутствия колебаний предельных циклов в нижних ветвях является выбор 1, удовлетворяющего неравенству (3), что обеспечивается условием (1).
Подавление колебаний предельных циклов в верхних ветвях обеспечивается путем замены квантования суммы посредством округления на квантование суммы посредством усечения в тот момент, когда фильтр находится в состоянии предельных циклов или в их непосредственной близости,, Критерий того, что фильтр находится в состоянии предельных циклов или в их непосредственной близости, - это достижение узлами разветвления нижних ветвей нулевого состояния, которое выявляется при помощи анализатора нулей„
В этом случае для любого незагруженного идеального фильтра должно выполняться неравенство
|Y(n)UIY(n-1)| ,
где равенство наступает только при Y(n) Y(n-1) 0.
Для верхних ветвей неравенство (4) записывается как
|/JY(n-1)b,+dYU-2)-b2 U UYCn-1)|,
15)
но поскольку в верхних ветвях в этом случае имеет место квантование путем усечения, для которого
unteger UY(n-1)b1+/JY(n-2)bl I -f )bt+dY(, то в результате
integer f|d Y(;ii-1)b,+dY(n-2)b2|;U (4Ytn-2)f.(6)
Таким образом, фильтр ведет себя как идеальный и колебания предельных циклов в верхних ветвях, а следовательно, и во всем фильтре не возникают „
При нагруженном фильтре, т„е0 когда Х(п)0, в результате квантования в верхних и нижних ветвях генерируется шум, который прикладывается к узлу суммирования о Средняя мощность шума, приложенного к узлу суммирования от каждого квантователя (предполагая, что закон распределения ошибки округления в диапазоне от -1/1 до 1/1 для нижних ветвей, т.е. второго и третьего слагаемых уравнения (2), и от -1/2 до 1/2 для верхних ветвей, т.е„ четвертого слагаемого уравне-- ния (2), равновероятный), определяется как
2yjft +
31
4uk
313
2ule
+ Hii.
12
1
А U кй
12
15823346
(1) оказывается, что 4Y(n) сильно ограничено по амплитуде некоторым 4Y(n)McWf, что хорошо видно из диаграмм, изображающих расположение зон
Y(n) в диапазоне возможных значений Y(n) согласно условию (1) (фиг. 3, а-b).
На фиг. 3,а изображена диаграмма
расположения зон Y(n) в диапазоне
возможных значении Y(n) согласно первому неравенству условия (1). Зоны
Y(n) заштрихованы. Здесь jY(n)
1 MOtKC
5 при любом Y(n) равно расстоянию между двумя соседними зонами Y(n), или
4Y(n).
1
(пН) 1Ь7
0
nl+J lb
1-2
Гь/
(8)
На фиг. 3, б изображена диаграмма
расположения зон Y(n) в диапазоне
возможных значений Y(n) согласно второму неравенству условия (1), Здесь
4Y(n) 4Y(n)
2максаналогкчно (8) будет равна:
ll llllll -
2MUKC Ц, Ibi
Ч
1-2 IbV
(9)
На фиг. 3, b изображена диаграмма
-х 35 результирующего расположения зон Y(n)
в диапазоне Y(n) согласно условию (1),
f- где зоны Y(n) появляются: в местах
пересечения зон Y(,n) от первых двух 40 диаграмм, а результирующее 4Y(n) здесь определяется как
dY(n)(n),Meicc+4Y(i04Me|KC


| название | год | авторы | номер документа |
|---|---|---|---|
| Рекурсивный цифровой фильтр | 1988 |
|
SU1656672A1 |
| ПРОГРАММИРУЕМЫЙ ЦИФРОВОЙ ФИЛЬТР | 1991 |
|
RU2006936C1 |
| Цифровой фильтр с многоуровневой дельта-модуляцией | 1988 |
|
SU1587624A1 |
| Цифровой рекурсивный фильтр | 1988 |
|
SU1578720A1 |
| Цифровой фильтр | 1988 |
|
SU1569957A1 |
| Цифровой нерекурсивный фильтр | 1990 |
|
SU1786638A1 |
| Устройство для вычисления скользящего спектра | 1987 |
|
SU1427386A1 |
| Цифровой фильтр с дельта-модуляцией | 1987 |
|
SU1418908A1 |
| ЦИФРОВОЙ ЧАСТОТОМЕР | 1996 |
|
RU2097774C1 |
| СПОСОБ ПРЕОБРАЗОВАНИЯ ЦИФРОВОГО СИГНАЛА ИЗОБРАЖЕНИЯ И УСТРОЙСТВО ДЛЯ ЕГО РЕАЛИЗАЦИИ | 2004 |
|
RU2287909C2 |
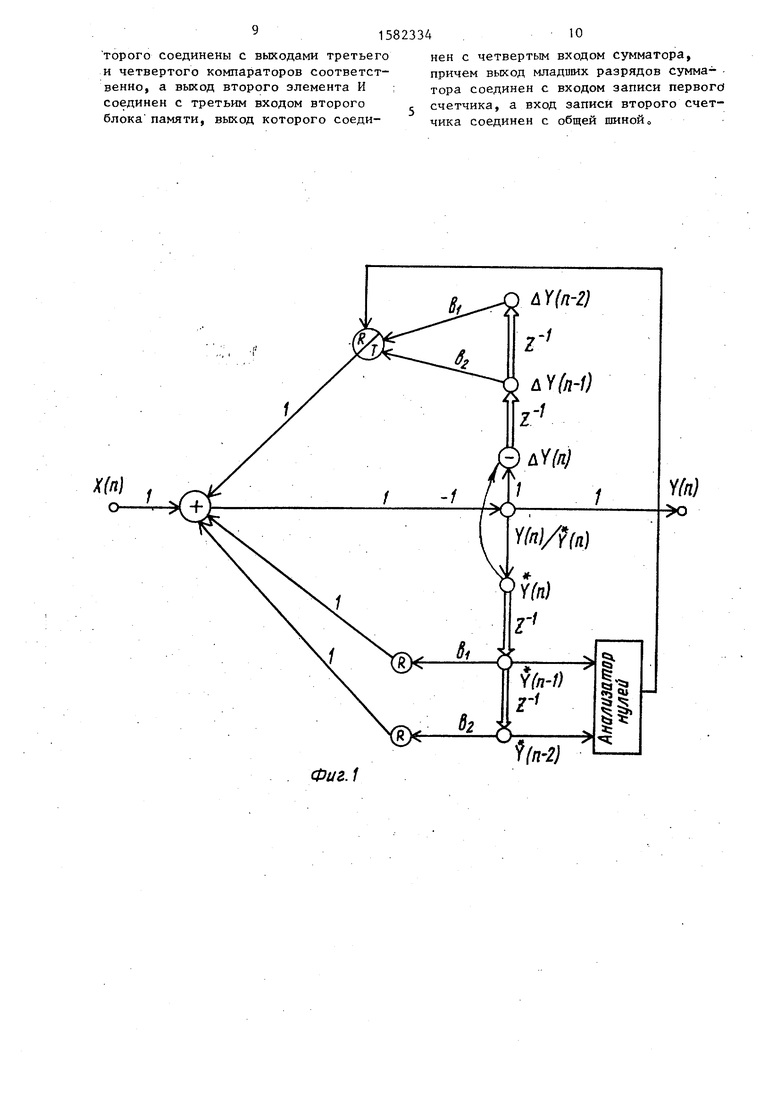

Изобретение относится к радиотехнике и может быть использовано в системах измерения, управления, связи, радиолокации и вычислительной техники. Целью изобретения является повышение точности фильтрации путем уменьшения шумов квантования. Рекурсивный цифровой фильтр содержит сумматор 1, умножители 2 и 3, регистры 4 - 7, блоки памяти 8 и 9, компараторы 10 - 13, элементы И 14 и 15, счетчики 16 и 17. В устройстве в ходе фильтрации в петле обратной связи раздельно обрабатывают кодовую последовательность Y (п), являющуюся ближайшей в сторону уменьшения от выходной последовательности Y (п). В ветвях обработки кодовой последовательности Y (п) анализируют состояние узлов разветвления и в случае достижения последним в ходе фильтрации нулевого состояния квантование суммы посредством округления заменяют квантованием суммы посредством усечения. 3 ил.
где U - величина шага квантования входного напряжения.
Для обычного фильтра второго порядка с квантованием после каждого умножения средняя мощность шума округления, прикладываемого к узлу суммирования,- равна: иЈа/6„ При сравнении его с правой частью уравнения (7) видно, что при достаточно большом 1 (5-Ю) предлагаемый фильт имеет величину шума округления в 2 раза меньше, чем у обычного фильтра второго порядка„
В результате осуществления раздельной обработки кодовых последовательностей Y(n) и 4Y(n) по условию
+
1Ь.
1Ь
(10)
Таким образом, общее количество возможных значений четвертого слагаемого (2) для /3Y(n), находящихся в диапазоне амплитуд от 0 до dY(n)MO(KC, определяется как комбинация возможных 4Y(n) по 2 или
1
N (n)MeUtt
(11)
Для большинства реальных рекурсив- ных цифровых фильтров второго порядка при 1 (4 - 10) колеблется в пределах 6-20 единиц младшего разряда, а N согласно (11) в пределах 49 - 441, что позволяет рассчитать зара-
нее все возможные значения четвертого слагаемого, а верхние ветви петли обратной связи реализовать на основе блока памяти.
В результате .входная последовательность Х(п) поступает на один из входов сумматора 1, где складывается с вторым и третьим слагаемыми (2), поступающими с выходов умножителей 2 и 3, и четвертым слагаемым с второго яблока 9 памятно Результирующая кодо- вая последовательность Y(n) поступает на выход фильтра, старшие разряды этой последовательности - на адресный вход первого блока 8 памяти и вход старших разрядов первого регистра 4, а младшие разряды - на вход записи первого счетчика 16. Таким образом, диапазон возможных значений Y(n) разбивается на поддиапазоны (фиг„3,с) на выходах второго блока 8 памяти формируются граничные значения зоны - Y(n) данного поддиапазона, которые
подаются на первые входы первого и второго, компараторов 10 и 11, а на вторые их входы подаются младшие разряды У(п) с выхода первого счет- чика 16. Первый счетчик 16 считает в сторону уменьшения до тех пор, по- ка код на его выходе не окажется в границах зоны Y(n). В этом случае первый и второй компараторы 10 и 11 вырабатывают сигналы, которые, объ - единяясь на первом элементе И 14, создают сигнал, который останавливает счет первого и второго счетчиков,
16и 17. Второй счетчик 17 считает от нуля в сторону увеличения, формируя йХ(п)а После этого код с выхода первого счетчика 16 вместе со старшими разрядами с выхода сумматора 1,
.образуя Y(n) , записывается в первый
регистр 4, а код с второго счетчика
17записывается в третий регистр 6, причем перед этим коды, находящиеся первом и третьем регистрах 4 и 6, переписываются во второй и четвертый регистры 5 и 7 соответственно. После этого коды на выходах третьего и четвертого регистров 6 и 7 поступают
на первый и второй входы второго блока 9 памяти, на выходе которого формируется новое .значение четвертого слагаемого (2), а коды с выходов пер (вого и второго регистров 4 и 5 поступают на входы первого и второго умножителей 2 и 3 соответственно,
5
Q 0
0 35
40
55
45
50
где они умножаются на коэффициенты Ъ, и bji и квантуются, образуя новые вторые и третьи слагаемые (2)0 Кроме того, коды с выхода первого и второго регистров 4 и 5 поступают на входы третьего и четвертого компараторов 12 и 13 и в случае их равенства нулю эти компараторы вырабатывают сигналы, которые объединяются на вто ром элементе И 15 и создают сигнал, который подается на третий вход второго блока 9 памяти, и в этом случае с выхода второго блока 9 памяти выбираются значения четвертого слагаемого (2), взятые с усечением.
Формула изобретения
Рекурсивный цифровой фильтр, содержащий первый и второй умножители и последовательно соединенные сумматор, первый и второй регистры, выходы которых соединены через первый и второй умножители соответственно с первым и вторым входами сумматора соответственно, третий вход которого является входом рекурсивного цифрового фильтра, выходом которого является выход сумматора, отличаю-, щ и и с я тем, что, с целью повышения точности фильтрации путем уменьшения шума квантования, введены первый и второй счетчики, первый блок памяти, вход которого соединен с выходом старших разрядов сумматора, первый и второй компараторы, первые входы которых соединены с первым и вторым вы- ходами первого блока памяти, а вторые входы компараторов подключены к выходу первого счетчика и второму входу первого регистра, первый элемент И, первый и второй входы которого соединены с выходами первого и второго компараторов соответственно, а выход первого элемента И соединен с управляющими входами первого и второго счетчиков, третий к четвертый компараторы, первые входы которых соединены с общей шиной, а их вторые входы соединены с выходами первого и второго регистров соответственно, последовательно соединенные третий регистр, вход которого соединен с выходом второго счетчика, четвертый регистр и второй блок памяти, второй вход которого соединен с выходом третьего регистра, а также второй элемент И, первьй и второй входы которого соединены с выходами третьего и четвертого компараторов соответственно, а выход второго элемента И соединен с третьим входом второго блока памяти, выход которого соедиФиг.1
нен с четвертым входом сумматора, причем выход младпмх разрядов сумматора соединен с входом записи первого1 счетчика, а вход записи второго счетчика соединен с общей шиной
Э А УМ
V
«
&
«
3Ъ
i
й
«
r
§
4j
4
V, cfhS1
V «
I
fvi ui
в
I
i i
us.

| Kieburtz R0 Control of Limit Cycles Recursive Digital Filters by Randomized Quanta | |||
| IEEE Circuits and systems, CAS-24, fP 6, 1977, p | |||
| ДЖИНО-ПРЯДИЛЬНАЯ МАШИНА | 1920 |
|
SU296A1 |
Авторы
Даты
1990-07-30—Публикация
1987-12-28—Подача