Фиг. 1
Изобретение относится к машиностроению и может быть использовано, например, в робототехнике.
Цель изобретения - повышение быстродействия механизма.
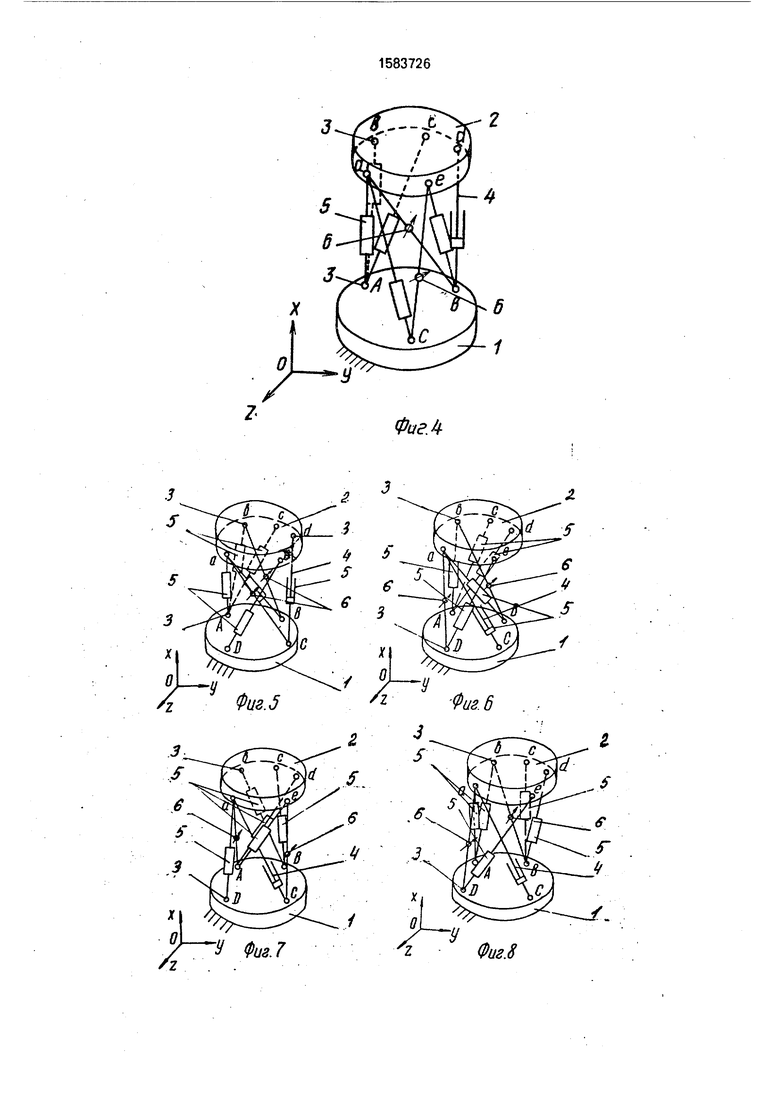
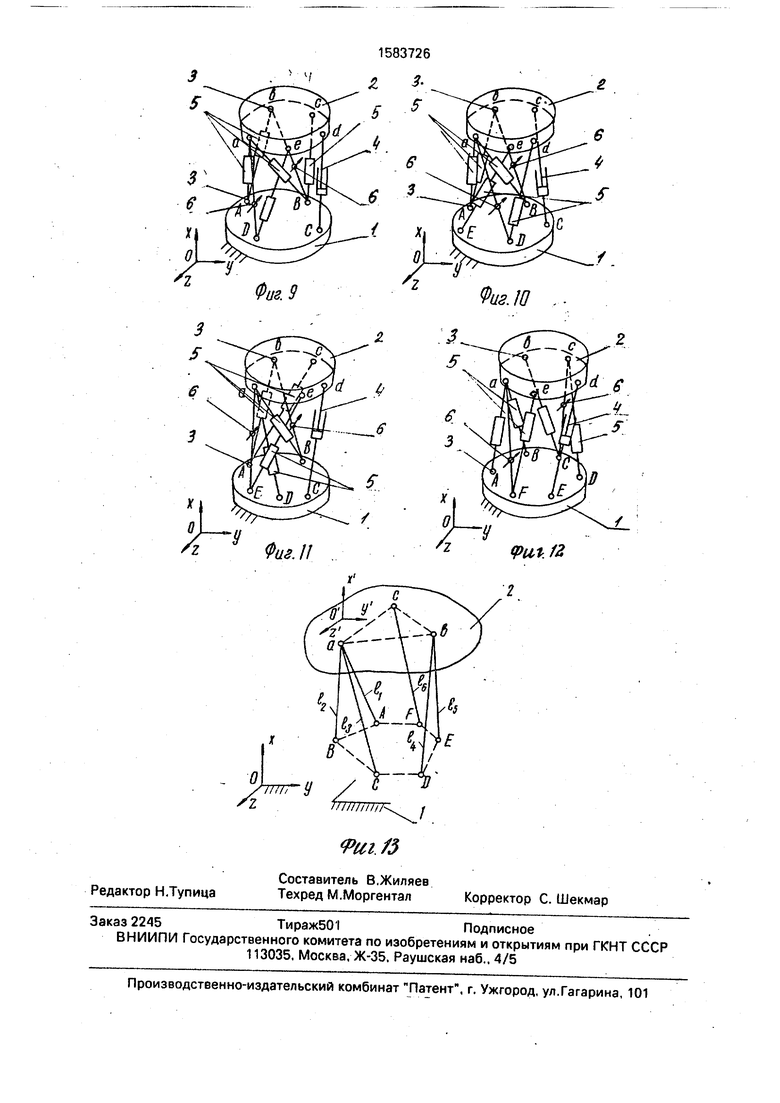
На фиг. 1-12 показаны различные схемы предлагаемых -координзтных механизмов; на фиг. 13 - структура 1-координатного механизма, для которой определение координат точек подвижного звена осуществляется в явном виде.
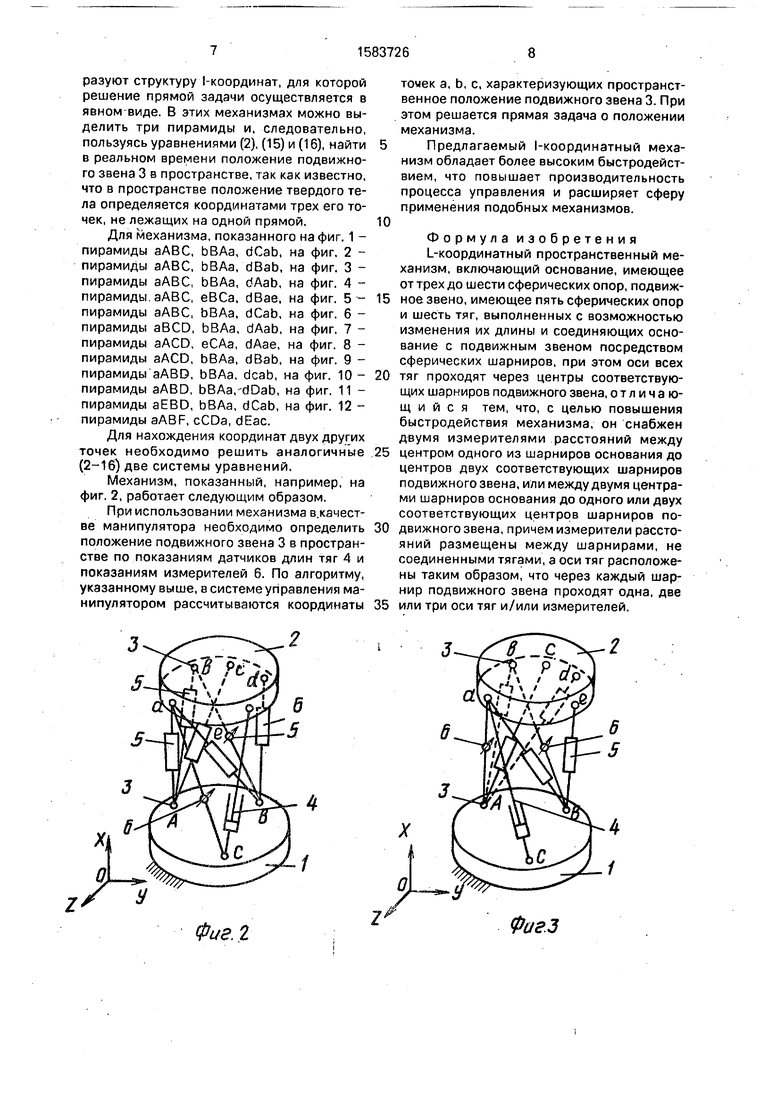
Все схемы 1-координатных пространственных механизмов содержат основание 1, имеющее от трех до шести сферических опор 2, подвижное звено 3, имеющее пять сферических опор 2 и шесть тяг 4, выполненных с эозможностью изменения их длин ы и соединяющих основание 1 с подвижным звеном 3 посредством сферических шарниров 5, а также измеритель 6 расстояний между центрами сферических опор 2 основания 1 и центрами сферических опор 2 подвижного звена 3.
Механизмы, представленные на фиг. 1- 12, отличаются количеством точек основания 1, в которых размещаются центры сферических опор 2. Количество точек на основании 1 в этих механизмах изменяется от трех до шести. Эти механизмы реализуют свою, отличную от других, структуру 1-коор- динат.
При управлении движением 1-координатных пространственных механизмов необходимо решать прямую и обратную задачу о положениях. Прямая задача сводится к определению положения подвижного звена 3 по заданным значениям обобщенных координат. В 1-координатных механизмах обобщенными координатами являются длины И, 12,...,б шести тяг 4.
Обратная задача предполагает определение обойденных координат И, механизма по заданному пространственному положению подвижного звена 3,
Общий метод решения прямой задачи строится на анализе системы уравнений, каждая из которых устанавливает зависимость расстояний между двумя точками от их координат. Причем в общем случае число уравнений системы равно числу точек подвижного звена 3, в которых расположены сферические опоры 2, умноженному на три, так как каждая точка на подвижном звене 3 характеризуется тремя значениями координат - х, у, 2, Если число точек на подвижном звене 3 равно пяти, то количество уравнений связи равно пятнадцати.
Для механизма, показанного, например, на фиг. 12, такая система имеет вид:
(Ха - ХА)2 + (Уа - УА)2 + (za - 2д)2 Н2,
(ха (хь (Хс (Xd
(Хе (ха (Ха (Хс (Хс
0 (Хе (ха (ХЬ (Хс
(хь 5 ,
-ХВ)2 + (Уа - УВ)2 + (Za - ZB)2 I22.
-хсГ + (уь - усг + (zb - zcr з,.
-XD), + (Ус - УО)2 + (2с - ZD)2 - .
-ХЕ)2 + (yd - УЕ), + ( Zd -ZE)2 I 52 XF)2 + (Уе VFj 2-4ze - 2F/ I 6 -Хь12+(Уа-уьГ„+ (Za-Zb)2 (аЬ)2. -ХеГ + (Уа-хьГ + (ус- -xdf+ (Ус- -Xd),+ (Ус-Xdf + (Уа
-Хе)2 + (УЬ -Хе)2 + (Ус
-Xd)2 + (yb
уе)2+ (za-ze)2 (ае)2
/„ /„uv
уь)+ (zc-zbf- (cb/, yd)2 + ( (Cd)2 yd)2 + (ze-zd)2(ed)2 -yd)2 + (za-zd)2 (ad)2
-Уе)2 + (Zb-Ze)2 (be)2, Уе + (Zc -ze)2- (Ce)2
(1)
- УеГ + -Vdf +
()2 (
Решение такой системы уравнений возможно лишь численными методами, что занимает много времени.
Но существует ряд структур, для которых прямая задача решается в явном виде и 0 сводится к последовательному решению трех систем уравнений, каждая из которых содержит по три уравнения. На фиг. 13 показана структура, для которой прямая задача решается в явном виде и координаты 5 точек а, Ь, с определяются последовательным решением следующих систем:
1. Для определения координат точки а система уравнений имеет вид:
(ха - хд)2 + (Уа - уд)2 + (za - 2д)2 I 12, (Ха - ХВ)2 + (Уэ- УВ)2 + (Za- ZB)2 I 22, (2) (ха - ХС)2 + (Уа- УС)2 + (z а - ZC)2 I З2Эта система, состоящая из трех уравнений с тремя неизвестными, решается следующим образом: из второго и третьего уравнения вычтем первое, получим:
(хв2 + у в2 + ZB2) - (хд2 + уд2 + ZA2) - 2ха(хв -ХД) - 2уа(у В - УА) -2Za(ZB - ZA) V -I Г, (3)
(ХС + УС + ZC ) - (ХД + УА + ZA ) - 2ха(хс-ХА) - 2уа(ус - уд) - 2za(zc - ZA) з - h Введем следующие обозначения:
ХАВ ХА - хв, удв уд - ув, ZAB ZA - ZB, (4)
ХСА ХГ - ХА, VCA УС - УА, ZCA ZC - ZA
В XR + VR + ZFT: С2 хг + vr +
В KB + ув + ZB ; С
А2 ХА2 + УА2 + ZA2.
Подставим (4) в (3)
хс + ус + zc :
В2-А2 + 2ха ХАВ + 2уа yAB + 2Za ZAB 2
-И2,(5)
С -А - 2ха ХСА - 2уа усд - 2za ZCA з - -If
Выразим ха через za. Для этого оба уравнения (5) решим относительно уа и приравняем правые части
В2 -А2+2ха-хАВ -f 2za-ZAB-l22+li2 XCA-ZAB - хдв-ZCA к Уа -2 удв ХСА -улв - ХАВ -усд
Г2 А2 9х .Хгд 97 ,7г. ,, 2 , , 2 Подставим (9} в (7) и (8), получим ХСА 2Za ZCA1з + Иха «1-Кзга,(10)
УСА5ya- K2-K4Za
Подставим (10) в одно из уравнений (2), пол- В2 -A2-l22 +li2 + 2ха-Хдв + 2za ZABучим:
2УВА(Kl-K3Za-XA)2 + (K2-K4Za-yA)2 + (Za-ZA)ll
(11)
С - А2 - 2ха -Ход - 2za-.ZcA - 1з 2 + li 2 W. Преобразуя (11), получим квадратное урав- 2усА нение относительно Za
Z aW + К42 - У - 2Z(K1 Kg + К2 К4 - КЗ ХА - К4УА
откуда+ZA).t (Кг + К27+ ХА + УА + ZA2-2Ki ХА - 2fe уд(В2-А2)уСА-(122-112)уСА + 2хаХАВУСА+ l) ° ,..
+ 2Za ZAB УСА - ЧС2 - А2) УАВ + (32 - ) УАВ +15 ( , г„ ,„ ,, „ ,„
2ха ХСА УАВ -Ь 2 ZCA УАВ, , (6) W |ДК24 Г Г $ Z
2Ха(хСА - УАВ - ХАВ УСА) (В2 - А2) УСА -2Za + А 1 2ХА) + К2((2
022-112)УСА + (С2-А2)УАВ-032-112)УАВ-20
-2zA(zcA УАВ - ZAB УСА),Обозначим:
Кз2 + К42 + 1 mi Увс(А2 - И 2) + усд(В2 - I2 2) + УАВ (С2 - 1з 2) .
ЗСХСА-УАВ-ХАВ-УЬА) jfKi- ХА) + К(К2 - уд) + ZA т2 , (13)
25 А2-112 + К1(К1-2хА)+К2(К2-2уА)тз
, 12СА УАВ - АВ УСА .
ХСА-УАВ -хдв-усА Тогда решение уравнения (12) с учетом (13)
имеет вид:
где увс ув-ус.(7)
Аналогично выразим уа через Za. Для 30 тз ± Vm2 2 - 4пцтз/14
этого оба уравнения (5) решим относительноа2mi
ха и приравняем правые части
В2 -А2 +2уа-уАВ +2za-2AB -l22 + li 2Подставив (14) в (10), найдем значения
ха-2хдв ха и уа- Таким образом, координаты точки а
35 определены. 2 Д2 9- о . | 2 . | 22. Для определения координат точки b
Xg ;r:.S 22Уа УСА- Za ZcA-|з-Zlll, необходимо решить систему уравнений
2хсА(хь - ха)2 + (хь - уа)2 +(zb - za)2 (аЬ)2,
.2 А2,/, 2 . 2чо (Xb-XD)2 + (yb-yD)2 + (zb-ZD) (15)
(В2 - А2)хсд - (122 - ЮХСА +2У| удв ХСА +40 (хь - хЕ)2 + (уь - ye)2 + (zb - zE)2 Is2 2za ZAB XCA - ЧС4 - А )хдв + (з - И ) ХАВ + 2уа аналогичную системе (2). ХАВ УСА + 2гэ хдв ZCA.3. Для определения координат точки с
откуда 2 22 .. ,j. 2необходимо решить систему уравнений
Уа ХВС(АЧ12 ( Э (Xc-xa)2 + (yc-ya(zc-yjf (caf.
хсД.гдВ-хДв(У 45(хс-хь) +(yc-yb(zc-zb)2 (cbf, (16)
I ХСА-УАВ-ХАВ-УСА w(хс - хгГ + (ус - угГ + (zc - zpf le ,
где хвс хв - хс.также аналогичную системе (2). Решение
Обозначимэтих систем осуществляется в явном виде и увс(А2 - И V усдСВ -ьУуАвССУ-Ь2)требует гораздо меньшего времени, чем рё- 2(хсА-уАВ-ХАВ-усд fe° шенГ системы (1}
у Увеличение быстродействия механизмов, показанных на фиг. 1-12, можно обебгд2 2х , 2ч , 2ч печить путем оснащения их двумя хвс(А и ) + ХСА(Р 2 J т хдв(. 1з ) измерителями 6 расстояний от центров сфе- 2(хсА Удв ХАВ УСА55 рических опор 2 основания 1 до центров
2-сферических опор 2 подвижного звена 3.
Измерители 6 расстояний в каждом из
ZCA Удв ZAB УСА .. . этих механизмов располагаются так. что оси
хсА Удв - хдв Усдf . измерителей 6 совместно с осями тяг 4 образуют структуру l-координат, для которой решение прямой задачи осуществляется в явном виде. В этих механизмах можно выделить три пирамиды и, следовательно, пользуясь уравнениями (2), (15) и (16), найти в реальном времени положение подвижного звена 3 в пространстве, так как известно, что в пространстве положение твердого тела определяется координатами трех его точек, не лежащих на одной прямой.
Для механизма, показанного на фиг. 1 - пирамиды аАВС, ЬВАа, dCab, на фиг. 2 - пирамиды аАВС, ЬВАа, dBab, на фиг. 3 - пирамиды аАВС, ЬВАа, dAab, на фиг. 4 - пирамиды аАВС, еВСа, dBae, на фиг. 5 - пирамиды аАВС, ЬВАа, dCab, на фиг. 6 ЬВАа, dAab, на фиг.
еСАа,
7
dAae, на фиг. 8 ЬВАа, dBab, на фиг. 9 ЬВАа, dcab, на фиг. 10 - bBAa.-dDab, ЬВАа, dCab,
на фиг. 11 - на фиг. 12 пирамиды aBCD, пирамиды aACD, пирамиды aACD, пирамиды aABD, пирамиды aABD, пирамиды aEBD, пирамиды aABF, cCDa, dEac.
Для нахождения координат двух других точек необходимо решить аналогичные (2-16) две системы уравнений.
Механизм, показанный, например, на фиг. 2, работает следующим образом.
При использовании механизма в качестве манипулятора необходимо определить положение подвижного звена 3 в пространстве по показаниям датчиков длин тяг 4 и показаниям измерителей 6. По алгоритму, указанному выше, в системе управления манипулятором рассчитываются координаты
точек а, Ь, с, характеризующих пространственное положение подвижного звена 3. При этом решается прямая задача о положении механизма.
Предлагаемый 1-координатный механизм обладает более высоким быстродействием, что повышает производительность процесса управления и расширяет сферу применения подобных механизмов.
Формула изобретения L-координатный пространственный механизм, включающий основание, имеющее от трех до шести сферических опор, подвижнов звено, имеющее пять сферических опор и шесть тяг, выполненных с возможностью изменения их длины и соединяющих основание с подвижным звеном посредством сферических шарниров, при этом оси всех
тяг проходят через центры соответствующих шарниров подвижного звена, отличающийся тем, что, с целью повышения быстродействия механизма, он снабжен двумя измерителями расстояний между
центром одного из шарниров основания до центров двух соответствующих шарниров подвижного звена, или между двумя центрами шарниров основания до одного или двух соответствующих центров шарниров подвижного звена, причем измерители рассто- яний размещены между шарнирами, не соединенными тягами, а оси тяг расположены таким образом, что через каждый шарнир подвижного звена проходят одна, две
или три оси тяг и/или измерителей.

| название | год | авторы | номер документа |
|---|---|---|---|
| Промышленный робот | 1985 |
|
SU1301685A1 |
| КОМПЛЕКСНАЯ СИСТЕМА НАВИГАЦИОННОГО ОБЕСПЕЧЕНИЯ ЗАХОДА НА ПОСАДКУ | 1992 |
|
RU2042923C1 |
| Способ определения параметров изоляции фаз сети с изолированной нейтралью | 1990 |
|
SU1780044A1 |
| Устройство для автоматического измерения геометрических параметров крупногабаритных изделий | 1988 |
|
SU1497449A1 |
| Устройство для управления @ -фазным вентильным электродвигателем | 1987 |
|
SU1522354A2 |
| Способ и система швартовки судна | 2020 |
|
RU2747521C1 |
| Стенд для испытания промышленных роботов-манипуляторов | 1987 |
|
SU1495114A1 |
| СТЕНД ДЛЯ ИЗМЕРЕНИЯ МАССЫ, КООРДИНАТ ЦЕНТРА МАСС И МОМЕНТОВ ИНЕРЦИИ ИЗДЕЛИЯ | 2012 |
|
RU2506551C2 |
| Оптическая система формирования и наведения лазерного излучения | 2018 |
|
RU2699944C1 |
| Устройство для управления манипулятором по вектору скорости | 1989 |
|
SU1705803A1 |

Изобретение относится к машиностроению и может быть использовано, например, в робототехнике. Целью изобретения является повышение быстродействия механизма. Координатный пространственный механизм содержит основание 1, имеющее от трех до шести сферических опор 2, подвижное звено 3, имеющее пять сферических опор 2 и шесть тяг 4, выполненных с возможностью изменения их длины и соединяющих основание 1 с подвижным звеном 3 посредством сферических шарниров 5, а также измеритель 5 расстояний между центрами сферических опор 2 основание 1 и центрами сферических опор 2 подвижного звена 3. Количество точек на основании 1 в механизме изменяется от трех до шести. 13 ил.
Фиг. г
ФиеЗ
Фиг Л
Фиг.8
Фиг. 9
Фаз. И
О
/77777-У XZ
Редактор Н.Тупица
Составитель В.Жиляев Техред М.Моргентал
Физ.Ш .Фиг. 12
Фиг. /5
Корректор С. Шекмар
| @ -Координатный пространственный механизм (его варианты) | 1984 |
|
SU1222538A1 |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1990-08-07—Публикация
1988-04-12—Подача