Изобретение относится к машиностроению, а именно к методам и средствам контроля зубчатых колес.
Цель изобретения - повышение точности измерения путем обеспечения возможности базирования устройства непосредственно на контролируемые поверхности зубьев и упрощение процесса контроля за счет исключения переналадки устройства на каждый контролируемый параметр.
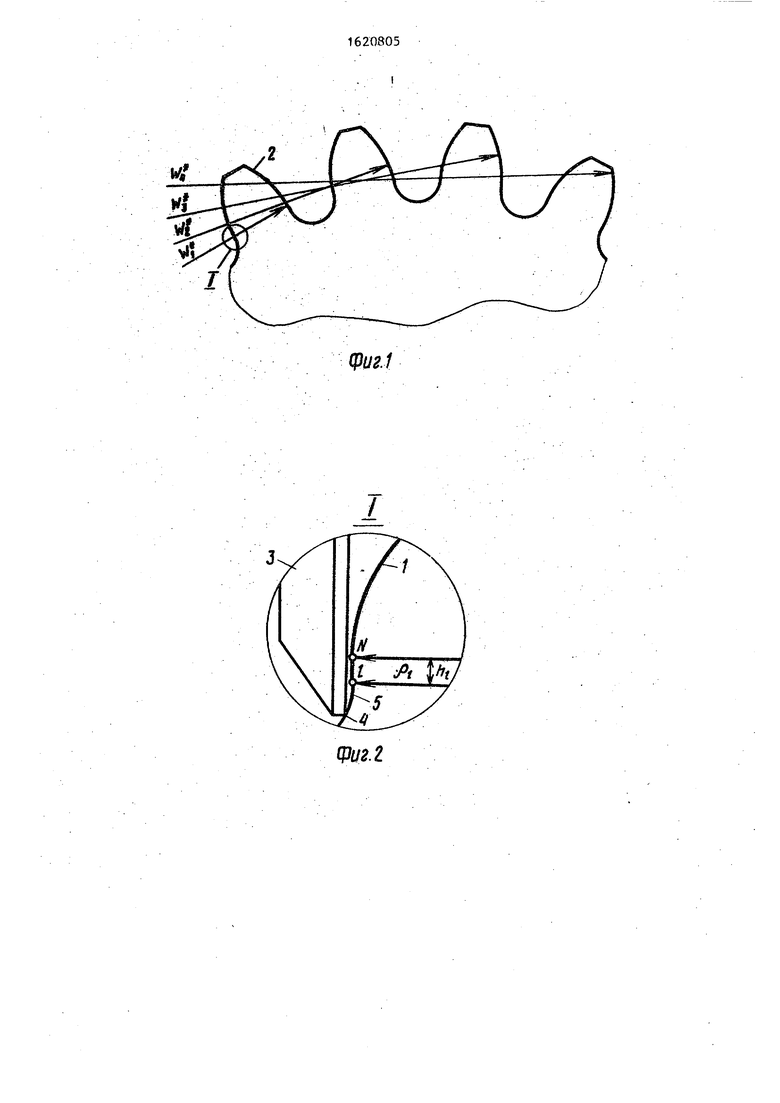
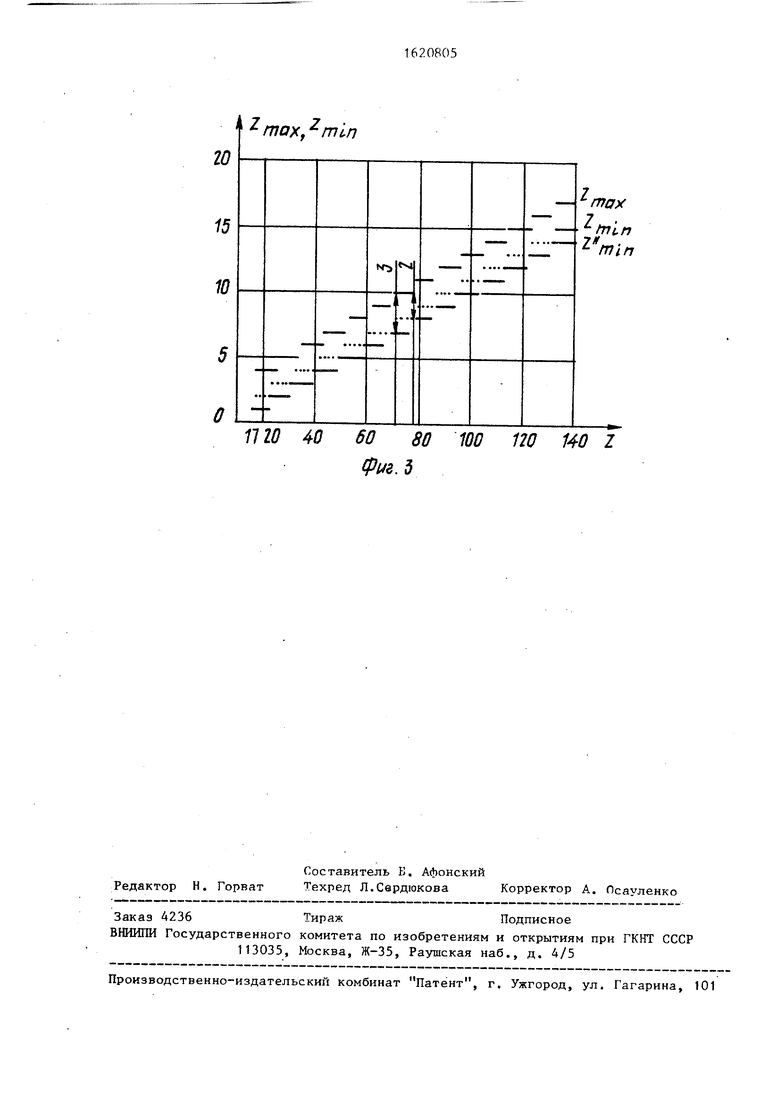
На фиг. 1 показан участок контролируемого колеса с расположением общих нормалей; на фиг. 2 - узел I на фиг. 1 (с ножкой нормалемера); на фиг.З - график для определения величин XhMH
и ZAIOKCКонтролируемое зубчатое колесо имеет выпуклый эвольвентный профиль 1 зуба 2. Ножка нормалемера является касательной к профилю 1 в точке N. На ножке 3 нормалемера имеется кромка 4. Выпуклый эвольвектный профиль
1 зуба 2 в граничной точке 1 сопря,жен с вогнутой переходной кривой 5„
Контроль профиля 1 зуба 2 по предлагаемому способу осуществляется путем последовательного измерения HOJV- малемером величин общих нормалей Wt к левому профилю 1 зуба 2 и к правым профилям зубьев „ Общие нормали Wt- являются одновременно и хордами, так как точки профилей зубьев, находящиеся на концах общей нормали, принадлежат одной окружности с центром на оси зубчатого колеса. Измеренную величину нормали W, сравнивают с номинальной величиной
W- (№(й; - 0,5) + Zxtp,«Ј +
+ Z inVtfOtncostfcospb,(О
где Z - чигло зубьев, заключаемых в общую нормаль.
о
00
о ел
При таком способе левая ножка 3 нормалемера последовательно касается левого профиля 1 зуба 2 в различных точках (фиг. 1). Для того, чтобы рабочая поверхность ножки нормалемера всегда была касательной к эвольвент- ному участку профиля зуба Тт.е. всегда имелась общая нормаль), необходимо соблюдение двух условий, ограничивающих максимальное и минимальное число зубьев в общей нормали. Во-первых точка N контакта ножки нормалеме- ра с профилем зуба не должна совпадать с точкой проЛиля зуба на окружности вершин. Во-вторых, точка N не должна опускаться ниже граничной точки 1 профиля, т.е. нижней точки эволь- вентного участка профиля.
Учитывая рост радиуса кривизны профиля зуба эвольвентного зубчатого колеса от граничной точки к точке на окружности верпин, в математической форме записи эти условия можно записать:
Ра,
(2) (3)
Де ршл РаЯиУс кривизны профилей
WMCIKC
зубьев в точках касания ножек нормалемера с профилем зубьев при заключении в нормаль W цла, максимального числа зубьев ZWQKt;
PWMHH кривизны профилей зубьев в точках касания ножек нормалемера с профилями зубьев при заклю- чении в нормаль WJAHH минимального числа зубьf-в 7-MHH
Од - радиус кривизны профилей зубьев в точках на окружности вершин; 9о - радиус, кривизны профилей зубьев в граничных точках профилей I.
Из геометрии эвольвентных зубчаых передач известно:
) 0,5W«aicc(MnH)cos рь (4)
Dq 0,5da sin(a
р 0,5d (ho + с P (1 -sinef) -х)я,
d - делительный диаметр зубчатого колеса;
hg- коэффициент высоты головки; с - коэффициент радиального
зазора;
- коэффициент радиуса кривизны переходной кривой.
Pf
В соответствии с ГОСТ 13755-81 1; с 0,25; Q 0,38; о( 20.
В (2) подставим .4) и (5) с учетом (1) и индекса макс.
Получим
7{ s / dpsini/Qft „ ,
(nc7SЈcos|bB+ 2 in V«y,(6)
/
В выражении (6) величина Z.xg получается дробной, но так как в общую нормаль нельзя заключить дробное число зубьев, то эта величина округляется до ближайшего меньшего целого числа Z, С учетом этого (6) примет вид:
71 /dflsinf/q . 1 „ . ,
2 ТГ Wos6kos{3b+ 2 2xt6
-Z in Vo4).
8t3) подставим (4) с учетом (1) и индекса мин. Получим:
1/2Р,
( Z in VO.)
(7)
Л
В выражении (7) величина получается дробной, но так как в общую нормаль нельзя заключить дробное число зубьев, то эта величина округ- ляется до ближайшего большего целого числа ). С учетом этого (7) примет вид:
5
мин
1 (2 Pi г
IT Wos cospg, - Z in Wt).
i
2
- 2xtgO - (8)
Для эвольвентных зубчатых передач с исходным контуром проведены теоретические исследования в общеприменя- емом диапазоне чисел зубьев кблес Z 12-500 и коэффициентов смещений исходного контура х -1,0-2,0 с целью определения величин 7, /макс и 2МИН. Полученные результаты свидетельствуют о том, что у эвольвентных зубчатых колес можно измерить
3-4 нормали с различным числом зубьев в них и тем самым обеспечить контроль профиля 1 зуба 2 в трех-четырех точках. Часть результатов этих иссле- дований представлена на фиг. 3, где видно, что для зубчатых колес с Z 17-140 при х 0 имеет место выражение Х.щаче- 7-мин (2...3), т.е. можно осуществить контроль трех-четырех точек профиля 1. Так на зубчатом колесе с / 20 и х 0 теорети
чески можно измерить четыре общих
U, rf. ЛЛ.
т - . т т . т.т . т,т
нормали W, ; WЈ; w г заключением в них Z, 1, /а 2, /а 3; 7,4 4 зубьев соответственно.
Проведенные экспериментальные замеры на таком зубчатом колесе с m 5 мм показали, что измерение общей нормали W с заключением в нее Z( зуба затруднено. Так, при установке ножек микрометрического нормалемера во впадины между зубьями и вращении микрометрического винта ножка 3, как правило, своей кромкой 4 упиралась в вогнутую переходную кривую 5 (фиг. 2), и величин-а W оказывалась завышенной. Это вызвано тем, что номинальная точка касания N находится на малом расстоянии h от граничной точки 1 (в зависимости от числа зубьев колеса и коэффициента смещения исходного контура hi может колебаться в пределах (0,03-0,23)гч), а установить ножку 3 нормалемера, избежав при этом кромочного контакта, так, чтобы расстояние от кромки 4 ноки 3 нормалемера до точки касания N с профилем 1 зуба 2 было не более hi затруднительно.
Учитывая сложность измерения величины нормали при заключении в нее мкч числа зубьев, определенного по формуле (8), в случае теоретической возможности контроля четырех точек профиля 1 необходимо уменьшить ZI)V1V,H на единицу. При этом hi увеличиваетс до (0,48-0,59)т, а минимальное число
зубьев / ниц, заключаемых в общую нормаль, определяется из выражений:
хмии 2М4кс 2.
На Лиг. 3 значение мцц показано штриховой линией.
Формула изобретения
Способ дискретного контроля профилей зубьев зубчатых колес, заключающийся в том, что измеряют на разных высотах зубьев величины хорд между разноименными профилями зубьев и
сравнивают их с соответствующими номинальными величинами хорд, отличающийся тем, что, с целью повышения точности и упрощения процесса измерения, хорды измеряют как
обррте нормали к разноименным профилям зубьев, последовательно увеличивают количество зубьев 7., охватываемых общей нормалью от Х.мн до 7, макг зубьев, а и У. цлд (ее определяют математическими выражениями
У- млн Z|wavc
1 dqsino q Т m «cose cosfJe
- Z in VO),
макс
42-x-tgtif
где d - диаметр окружности вериин зубьев колеса;
о( Q - угол профиля зуба в точке на окружности вершин;
п - нормальный модуль зубчатого колеса;
С - у.гол профиля зуба исходного контура;
Bg - основной угол наклона зубьев;
х - коэффициентtсмещения исходного контура; in V. tgrft- /t ,
(/f- угол профиля (для непрямозубых колес).


| название | год | авторы | номер документа |
|---|---|---|---|
| Способ контроля профилей зубьев зубчатых колес | 1990 |
|
SU1739179A1 |
| Способ контроля параметров цилиндрических зубчатых колес | 1978 |
|
SU868309A1 |
| Способ контроля профилей зубьев зубчатых колес | 1991 |
|
SU1772588A1 |
| ТРОХОИДАЛЬНОЕ ЗУБЧАТОЕ ЗАЦЕПЛЕНИЕ | 2017 |
|
RU2673574C1 |
| Способ обработки зубьев зубчатых колес дисковым лезвийным инструментом | 2021 |
|
RU2763831C1 |
| Зубчатая передача | 1983 |
|
SU1116245A1 |
| ПРЯМОЗУБАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 1999 |
|
RU2160403C1 |
| КОСОЗУБАЯ ЗУБЧАТАЯ ПЕРЕДАЧА | 1995 |
|
RU2116532C1 |
| ЗУБЧАТАЯ ПАРА | 1944 |
|
SU67425A1 |
| СПОСОБ ЧИСТОВОЙ ОБРАБОТКИ ЦИЛИНДРИЧЕСКИХ ЗУБЧАТЫХ КОЛЕС | 1989 |
|
RU2029663C1 |
Изобретение относится к машиностроению, а именно к методам и средствам контроля зубчатых колес. Цель изобретения - повышение точности измерения путем обеспечения возможности базирования устройства непосредственно на контролируемые поверхности зубьев и упрощение процесса контроля за счет исключения переналадки устройства на каждый контролируемый параметр. Это достигается тем, что хорды измеряют как общие нормали на нескольких зубьях последовательно, а количество замеров (т.е. количество зубьев) определяют математическим выражением. 3 ил.
.1
Фиг. 2
7720 40 60 80 100 120 140 I фм. 5
| Цилиндрические зубчатые передачи внешнего зацепления | |||
| Расчет геометрии | |||
| М.: Машиностроение,t974, с | |||
| Нефтяной конвертер | 1922 |
|
SU64A1 |
Авторы
Даты
1991-01-15—Публикация
1988-04-15—Подача