Изобретение относится к области магнитного курсоуказания и навигации, может быть использовано для курсовых систем подвижных объектов, например, летательных аппаратов (ЛА).
Целью изобретения является повышение точности определения девиации, обеспечивающее повышение точности определения магнитного курса ЛА.
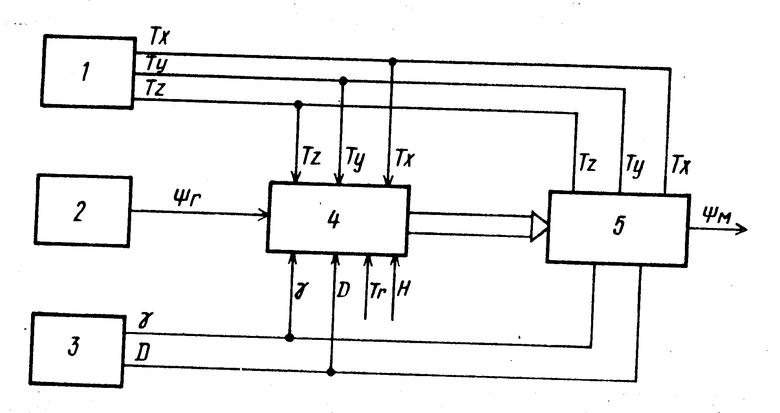
На чертеже приведена структурная схема устройства для осуществления способа.
Устройство содержит блок из трех ортогональных жестко закрепленных на корпусе объекта магнитометров 1 для измерения проекции продольной Тх, поперечной TΣ и нормальной Ту составляющих вектора напряженности результирующего магнитного поля объекта на оси связанной системы координат OXYZ, гироскоп 2 направления для определения гироскопического курса Ψг подвижного объекта, гировертикаль 3 для определения углов крена γ и тангажа V подвижного объекта, первый вычислитель 4 для определения в процессе предстартовой подготовки коэффициентов Пуассона и компонент постоянного магнитного поля подвижного объекта, второй вычислитель 5 для определения угла магнитного курса подвижного объекта Ψм. Выходы блока 1 соединены с входом первого вычислителя 4 и второго вычислителя 5, выход блока 2 соединен с входом первого вычислителя 4, выход блока 3 соединен с входом первого вычислителя 4 и второго вычислителя 5, на вход первого вычислителя подаются, кроме того, с потенциометра ручной выставки стартовые значения горизонтальной составляющей вектора напряженности геомагнитного поля Тг и угла магнитного наклонения Н измеренные, например, с помощью дефлектора и инклинатора, выход первого вычислителя 4 соединен с входом второго вычислителя 5.
Магнитный курс Ψм определяют из выражения
Ψм=Ψк+δ, (1) где Ψк компасный курс;
δ- девиационная поправка.
Магнитные девиации магниточувствительных датчиков обусловлены наличием собственного магнитного поля носителя, на котором они установлены, а геометрические девиации обусловлены изменением ориентации подвижного объекта относительно геомагнитного поля, причем, структура собственного магнитного поля объекта такова, что оно содержит постоянную и переменную составляющие. Постоянное магнитное поле носителя определяется наличием на носителе элементов из магнитомягких и магнитотвердых материалов, характеризуемых магнитной восприимчивостью к внешнему магнитному полю (намагничиваемостью в технологических и эксплуатационных условиях). Эта составляющая напряженности магнитного поля носителя 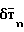 colon (P,Q,R) фиксирована относительно корпуса носителя и не изменяет своего направления относительно корпуса основания при изменении ориентации объекта. Переменное магнитное поле носителя
colon (P,Q,R) фиксирована относительно корпуса носителя и не изменяет своего направления относительно корпуса основания при изменении ориентации объекта. Переменное магнитное поле носителя 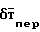 складывается из четырех составляющих: индуктивного поля магнитных масс
складывается из четырех составляющих: индуктивного поля магнитных масс 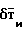 , магнитного поля электронагрузок δТ, магнитного поля вихревых токов
, магнитного поля электронагрузок δТ, магнитного поля вихревых токов 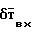 , магнитного поля реактивных двигателей
, магнитного поля реактивных двигателей  .
.
Напряженность результирующего магнитного поля носителя 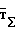 определяется векторной суммой составляющих
определяется векторной суммой составляющих
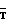 +δTн=
+δTн= 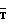 +
+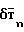 +
+ 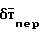 =
= 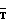 +δTи+(
+δTи+(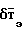 +
+ +
+ +δTдв),
+δTдв),
(2) где 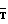 напряженность геомагнитного поля.
напряженность геомагнитного поля.
Превалирующую роль в формировании магнитного поля носителя играют три первые составляющие (причем 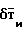 и
и 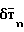 образуют в сумме магнитные помехи от ферромагнитных масс
образуют в сумме магнитные помехи от ферромагнитных масс 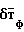 ) и определяемые в проекциях на связанные оси объекта XYZ векторноматричным уравнением Пуассона
) и определяемые в проекциях на связанные оси объекта XYZ векторноматричным уравнением Пуассона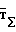
 +
+ +
+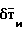 = A
= A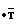 +
+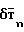 +S·A
+S·A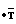 ;
;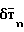 colon (P, Q, R), (3) где S матрица коэффициента Пуассона;
colon (P, Q, R), (3) где S матрица коэффициента Пуассона;
S 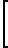
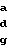

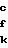
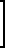 ;
;
(4)
А матрица ориентации системы координат, связанной с объектом XYZ относительно горизонтальной геомагнитной системы координат.
Пусть имеется не менее четырех результатов экспериментов, проведенных при четырех различных стояночных курсах Ψi объекта, на каждом из которых при соответствующих значениях стояночных углов тангажа V и крена γi измеряют продольную Тхi поперечную Тzi и нормальную Tyiкомпоненты результирующего магнитного поля объекта, формируют три разностных уравнения Пуассона (3), которые запишутся в матричном виде следующим образом
(S+E)(Ai-Aj)
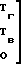
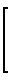
 (i,j
(i,j 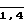 )
)
(5)
Разностные уравнения (5) должны удовлетворять непременному условию i≠j и каждый результат эксперимента (i или j) не должен повторяться в системе более чем два раза.
Системе трех разностных уравнений вида (5) соответствует система девяти скалярных разностных уравнений Пуассона следующего вида
(a + 1)˙(ai aj) + b(bi bj)+c(ci cj)Txi-Txj
d(ai aj) + (e + 1)(bi bj) +f(ci cj)Tyi Tyj (i,j 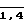 )
)
g(ai aj) + h(bi bj) + (k+1)(ci cj)Tzi Tzj (6) где ai; aj; bi; bj; ci; cj
функции, определяемые зависимостями от составляющих Тг Тв вектора 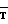 и углов ориентации подвижного объекта Ψi; vi; γi; Ψj; vj; γj.
и углов ориентации подвижного объекта Ψi; vi; γi; Ψj; vj; γj.
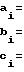
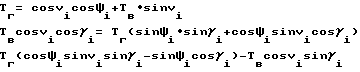
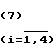
выражения для aj; bj; cj имеет аналогичный вид.
Систему девяти скалярных уравнений вида (6) можно привести к матричной форме: N
N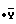 , где
, где 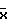 ,
,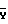 матрицы-столбцы размером (9х1);
матрицы-столбцы размером (9х1);
N квадратная матрица размером (9х9) с элементами
aij (ai aj); bij (bi bj);
cij (ci cj); (i, j 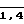 )
)
Причем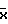 colon(a+1;b;c;d;e+1;f;g;h;k+1);
colon(a+1;b;c;d;e+1;f;g;h;k+1);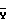 colon(Tx12;Ty12;Tz12;Tx13;Ty13;Tx24;Ty24;Tz24),
colon(Tx12;Ty12;Tz12;Tx13;Ty13;Tx24;Ty24;Tz24),
(9) где Тх12 Тх-Тх2; Ту12 Ту1-Ту2;Тz24 Тzz-Тz4
Матрица N для системы девяти уравнений вида (6), соответствующая варианту трех экспериментов типа (1-2)->(1-3)->(2-4) имеет следующий вид
N 

(10)
Матрица N является неособенной, так как не содержит линейно зависимые строки и столбцы. Для нахождения обратной матрицы N-1детерминант матрицы N может быть определен по стандартной программе, например, приведением матрицы N к форме Фробениуса (диагонализация матрицы) с последующим определением произведения элементов главной диагонали.
Окончательно детерминат Д матрицы имеет вид
D det [N] (a a2)2 (a2 a3) (b4 b2) x
x(b2 b3)2 (c1 -c2) (c2 c3) (c3 c4) a122˙a23˙b12˙b232˙c12˙c34 (11)
Решая далее уравнение (8) относительно 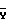 , получим
, получим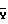 N
N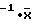 (12)
(12)
Раскрывая решение (12), используя формулы Крамера, находим выражения для определения коэффициентов Пуассона и составляющих вектора постоянного магнитного поля носителя
a 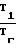 ·F1-1;b
·F1-1;b 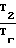 · F2; c
· F2; c 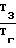 · F3; d=
· F3; d= 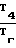 · F4; l
· F4; l 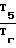 · F5-1
· F5-1
f 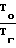 · F6; g
· F6; g  · F7; h
· F7; h 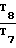 · F8; k
· F8; k 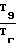 · F9-1;
· F9-1;
(13) где Fi(i=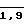 ) вспомогательные функции, зависящие от углов ориентации носителя (Ψi; Vi; γi) и угла магнитного наклонения
) вспомогательные функции, зависящие от углов ориентации носителя (Ψi; Vi; γi) и угла магнитного наклонения 
F1= [cv1cΨ1-cv2cΨ2+tg (sv1-sv2)]-1
(sv1-sv2)]-1
F2= [tg cv2cγ2-cv1cγ1)+sΨ1sγ1-sΨ2sγ2+sv1cΨ1c1-sv2cΨ2cγ2]-1 F3= [sv1cΨ1sγ1-sv2cγ2-sΨ1cγ1+sΨccγ2-tg
cv2cγ2-cv1cγ1)+sΨ1sγ1-sΨ2sγ2+sv1cΨ1c1-sv2cΨ2cγ2]-1 F3= [sv1cΨ1sγ1-sv2cγ2-sΨ1cγ1+sΨccγ2-tg (cv1sγ1-cv2sγ2)]-1
(cv1sγ1-cv2sγ2)]-1
F4= [cv1cΨ1-cv2cΨ2+tg (sv1-sv2)]-1 F1
(sv1-sv2)]-1 F1
F5= [tg (cv2cγ2-cv3cγ3)+sΨ3sγ3-sΨ2sγ2+sv3cΨ3cγ3-sv2cΨ2cγ2] -1
(cv2cγ2-cv3cγ3)+sΨ3sγ3-sΨ2sγ2+sv3cΨ3cγ3-sv2cΨ2cγ2] -1
F6= [sv3cΨ3sγ3-sv2cΨ2sγ2-sΨ3cγ3+sΨ2cγ2-tg (cv3sγ3-cv2sγ)] -1
(cv3sγ3-cv2sγ)] -1
F7= [cv3cΨ3-cv2cΨ2+tg (sv3-sv2)]-1
(sv3-sv2)]-1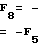 [tg
[tg (cb2cγ2-cb3cγ3] +sΨ3cγ3-sΨ2sγ2+sv3cΨ3cγ3-sv2cΨ2cγ2] -1
(cb2cγ2-cb3cγ3] +sΨ3cγ3-sΨ2sγ2+sv3cΨ3cγ3-sv2cΨ2cγ2] -1
F9= [sv3cΨ3sγ3-sv4cΨ4sγ4-sΨ3cγ3+sΨ4cγ4-tg (cv3cγ3-cv4sγ4)] -1
(cv3cγ3-cv4sγ4)] -1
(14)
где Т1 (Тх1 Тх2); Т2 (Ту1 Ту2) Т1; Т3 (Тz1- Tz2) T2; Т4= (Тх1 Тх3) Т3; Т5 (Ту1 Ту3)- Т4; Т6 (Tz1 Tz3)-T5; Т7 (Тх2 Тх4) Т6;
Т8(Ту2 -Ту4)-Т7; Т9=(Тz2-Tz4)-Т8 (15)
После определения коэффициентов Пуассона составляющие вектора постоянного магнитного поля носителя определяются следующим образом. Запишем матричное уравнение Пуассона (3) в виде
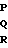
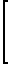
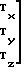 (S+E)·A
(S+E)·A
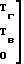
(16) отсюда в скалярном виде алгоритмы определения составляющих вектора постоянного магнитного поля носителя принимают вид
P Txi (a + 1)˙ai b˙bi c˙ci;
Q Tyi a˙ai (e + 1)˙bi f˙ci; (17)
R Tzi g˙ai h˙bi (k + 1)˙ci где функции ai; bi; ci определяются выражениями (7).
Напряженность магнитных помех оси ферромагнитных масс объекта может превышать по модулю вектор Т напряженности геомагнитного поля. При этом магнитные девиации магниточувствительных датчиков курсовых систем могут достигать нескольких десятков градусов.
Преобразуем матричное уравнение Пуассона (3) к следующему виду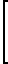
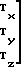 (E+S)·A
(E+S)·A
 +
+ 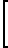
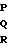
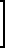
(18) где Тx, Ту, Тz проекция вектора 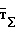 - результирующего магнитного поля объекта на его оси XYZ, Е единичная матрица размером (3х3) г;
- результирующего магнитного поля объекта на его оси XYZ, Е единичная матрица размером (3х3) г;
Тг Тв горизонтальная и вертикальная составляющие геомагнитного поля, Тв= z˙T˙sin
Tn HT˙cos (19)
(19) угол магнитного наклонения вектора Т напряженности геомагнитного поля.
угол магнитного наклонения вектора Т напряженности геомагнитного поля.
А [a˙j]33 матрица направляющих косинусов, где
a11 cosv˙cosΨ a21= -sinΨsinγ-sinvcosΨcosγ a31= sinvcosΨsinγ-sinΨcosγ
a12 sinv a22= cosvcosγ a32 -sinγ cosv
a13 cosvsinΨ a23= cosΨsinγ-sinvsinΨcosγ a33= sinvsinΨsinγ+cosΨcosγ (20)
обозначим s sin; c cos; Ψ; v; γ- углы магнитного курса, тангажа, крена соответственно.
Из теории и практики измерения магнитных девиаций известно, что коэффициент Пуансона (a, b.k) и составляющие постоянного магнитного поля объекта δTn= colon (P, Q, R) можно считать постоянными величинами для конкретного фиксированного распределения ферромагнитных масс объекта.
Матричное уравнение (18) имеет вид [c˙cγ + b˙sγ˙Tг˙s Ψ+ [(a + 1) cv b˙s˙vcγ + csvsγ] ˙Tг˙cΨ+ [(a + 1) x x sv + bcv˙cγ c cvsγT8 Tx P sx; [(e + 1)sγ + fcγ˙TгsΨ + [d˙cv (e + 1) x x svcγ + fsvsγ˙Tг˙cΨ+[dsv + + (e + 1) cvcγ fcvsγ ˙Tв Ty Q sy. -[h˙sγ + (k + 1) cγ˙T1 s Ψ+ [g˙cv hsv1 (k + 1) svsγ]Tг˙c Ψ+ [g sv + + h ˙cvc γ- (k + 1)cvsγ]˙Tв Tz R sz
Вводят следующие обозначения Tг˙sΨx; Tг˙c Ψ J элементы матрицы М
m11 (e˙cγ-bsγ); m21 [(e + 1) sγ + f˙cγ] m31=-[hsγ+(k+1)cγ]
m12 [(a + 1)cv- bsvcγ+csvsγ] m22[dcv(e+1)svcγ+fsvsγ] m32 [gcv-hsvcγ+(k +1) svsγ]
m13=[(a+1)sv+bcvcγ-ccvsγ] m23=[dsv+(e+1)cvcγ-fcvcγ] m33= [gsv+hcvcγ-(k+1)cvcγ]
(22)
Систему уравнений (21) сведем к матричному виду
M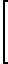

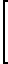
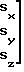
(23)
М квадратная матрица размером (3х3),
Sx Tx P; Sy Ty Q; Sz Tz R (24)
Решая уравнение (11), получается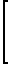
 M
M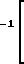
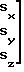
(25)
М-1 обратная матpица
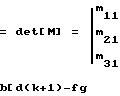
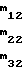
 (a+1)[hf-(e+1)k+1)]+c[g(e+1)-dh]+
(a+1)[hf-(e+1)k+1)]+c[g(e+1)-dh]+
(26)
По формулам Крамера
Tг·cΨ x 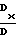 Tг·sΨ
Tг·sΨ 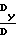
(27)
L1=dh-g(e+1);
L2=gf-d(k+1);
L3=bg-h(a+1);
L4=cg-(a+1)(k+1);
L5=bg-g(a-1)(e+1);
Px=L1cγ+L2sγ;
Py=L3cγ-L4sγ;
Pz=L5cγ-L6sγ;
Введем вспомогательные функции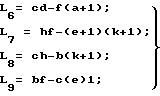
(28)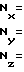
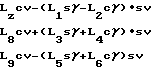
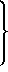
(29)
В итоге соотношение для нахождения магнитного курса запишется в следующем виде
Ψм=arctg(A1/B1)+π˙k1, (30) где
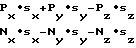
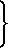 (31)
(31)
k1= 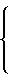
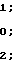
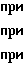
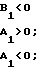
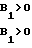
(32)
Практически при осуществлении способа в процессе предстартовой подготовки объекта последовательно устанавливают не менее чем в четырех различных курсовых положениях, в каждом из положений в первый вычислитель 4 поступают значения продольной Тхi нормальной Тyi и поперечной Tzi составляющих вектора напряженности результирующего поля объекта с блока 1, угла курса Ψгi с блока 2, углов крена γi и тангажа v объекта с блока 3 (i 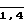 ). На основании поступивших значений указанных величин первый вычислитель 4 определяет коэффициенты Пуассона и компоненты постоянного магнитного поля подвижного объекта, по соотношениям (13-17) которые поступают на вход второго вычислителя 5 и запоминаются в нем, вычислитель 4 задействован только в процессе предстартовой подготовки. Во время движения подвижного объекта по поступающим на входы второго вычислителя 5 с блока 1 и блока 3 значения продольной Тх, поперечной Тz и нормальной Ту составляющих вектора напряженности результирующего магнитного поля, значениям углов крена γ и тангажа v и коэффициентам Пуассона и компонентам постоянного магнитного поля подвижного объекта (a, b, c, d, e, f, g, h, k, p, Q, R), запомненным в вычислителе 5, формируется по соотношениям (28-32) сигнал магнитного курса подвижного объекта Ψм который в дальнейшем может использоваться, например, корректирующий в курсовом канале системы ориентации объекта.
). На основании поступивших значений указанных величин первый вычислитель 4 определяет коэффициенты Пуассона и компоненты постоянного магнитного поля подвижного объекта, по соотношениям (13-17) которые поступают на вход второго вычислителя 5 и запоминаются в нем, вычислитель 4 задействован только в процессе предстартовой подготовки. Во время движения подвижного объекта по поступающим на входы второго вычислителя 5 с блока 1 и блока 3 значения продольной Тх, поперечной Тz и нормальной Ту составляющих вектора напряженности результирующего магнитного поля, значениям углов крена γ и тангажа v и коэффициентам Пуассона и компонентам постоянного магнитного поля подвижного объекта (a, b, c, d, e, f, g, h, k, p, Q, R), запомненным в вычислителе 5, формируется по соотношениям (28-32) сигнал магнитного курса подвижного объекта Ψм который в дальнейшем может использоваться, например, корректирующий в курсовом канале системы ориентации объекта.
В качестве датчиков блока 1 могут быть использованы, например, феррозондовые датчики в качестве блока 2 и блока 3 могут быть использованы, например, гироагрегат ГА-8 и гировертикаль МГВ-2.
Первый вычислитель 4 и второй вычислитель 5 могут быть реализованы например, на стандартных элементах вычислительной техники.
| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ КООРДИНАТЫ МЕСТОПОЛОЖЕНИЯ ПОДВИЖНОГО ОБЪЕКТА | 1991 |
|
RU1829578C |
| СПОСОБ ОПРЕДЕЛЕНИЯ МАГНИТНОЙ ДЕВИАЦИИ НА ПОДВИЖНОМ ОБЪЕКТЕ | 2022 |
|
RU2796372C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ И КОМПЕНСАЦИИ ДЕВИАЦИИ МАГНИТОМЕТРИЧЕСКИХ ДАТЧИКОВ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2013 |
|
RU2550774C1 |
| СПОСОБ ВЫПОЛНЕНИЯ ДЕВИАЦИОННЫХ РАБОТ НА ПОДВИЖНЫХ ОБЪЕКТАХ | 1998 |
|
RU2156440C2 |
| СПОСОБ ВЫПОЛНЕНИЯ ДЕВИАЦИОННЫХ РАБОТ НА ПОДВИЖНЫХ ОБЪЕКТАХ | 1996 |
|
RU2108546C1 |
| СПОСОБ ЦИФРОВОЙ КОМПЕНСАЦИИ ЭЛЕКТРОМАГНИТНОЙ ДЕВИАЦИИ ДЛЯ МАГНИТНОГО ЭЛЕКТРОННОГО КОМПАСА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 2001 |
|
RU2210060C2 |
| СПОСОБ ОПРЕДЕЛЕНИЯ МАГНИТНОЙ ДЕВИАЦИИ НА ПОДВИЖНОМ ОБЪЕКТЕ | 2008 |
|
RU2365877C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ПУАССОНА ПОДВИЖНОГО ОБЪЕКТА И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ | 1995 |
|
RU2096818C1 |
| СПОСОБ ОПРЕДЕЛЕНИЯ КОЭФФИЦИЕНТОВ ПУАССОНА ПОДВИЖНОГО ОБЪЕКТА | 1998 |
|
RU2134426C1 |
| НАВИГАЦИОННО-ПИЛОТАЖНЫЙ КОМПЛЕКС | 2016 |
|
RU2634083C1 |
Изобретение предназначено для магнитного курсоуказания и навигации, может быть использовано для курсовых систем подвижных объектов, например, летательных аппаратов. Цель изобретения повышение точности определения девиации и магнитного курса подвижного объекта. Способ основан на предстартовом нахождении коэффициентов Пуассона и компонент постоянного магнитного поля подвижного объекта и использовании разработанных зависимостей определения магнитного курса в процессе движения объекта. 1 ил.
СПОСОБ ОПРЕДЕЛЕНИЯ ДЕВИАЦИИ КУРСОУКАЗАТЕЛЯ ПОДВИЖНОГО ОБЪЕКТА, при котором последовательно устанавливают объект в фиксированные курсовые положения, регистрируют показания курсоуказателя и обрабатывают результаты измерений, отличающийся тем, что, с целью повышения точности, дополнительно не менее чем в четырех курсовых положениях объекта измеряют нормальную составляющую напряженности магнитного поля объекта, углы крена и тангажа, а при обработке результатов измерений находят через коэффициенты Пуассона продольную, нормальную и поперечную составляющие магнитного поля объекта.
| 0 |
|
SU94599A1 | |
| Печь для непрерывного получения сернистого натрия | 1921 |
|
SU1A1 |
Авторы
Даты
1995-12-10—Публикация
1989-07-24—Подача