Изобретение относится к способам исследования материалов с помощью оптических средств, а именно к способам количеовенно 0 микроструктурного анализа материалов с шаровидными частицами и их плоскими круговыми контактами, и может быть использовано для определения числа неравновеликих контактов частиц в единице объема, их среднего диаметра и дисперсии.
Наиболее близким к предлагаемому по технической сущности и достигаемому результату является способ микроструктурного анализа материалов с шаровидными частицами одинакового диаметра, контакты между которыми плоские и имеют форму круга одинакового диаметра.
Сущность способа заключается в том, что измеряют площадь S шлифа, подсчитывают число п контактов частиц на плоскости шлифа и определяют число NKa контактов
на единицу п лощади шлифа NKa - n/S, подсчитывают число Рк точек пересечения с контактами на единицу длины случайной секущей, определяют число NK контактов между частицами в единице объема материала
NKV 2NKa2/(,TPK|).(1)
При этом полагают, что диаметр DK всех контактов одинаков и может быть определен по формуле (в описании эта формула не приводится, однако она может быть получена из известных взаимосвязей между параметрами структуры и с учетом тождества D л 5к
Пк
где SK и Пк - соответственно плоN3
сл
Ю
щадь ч периметр равновеликих контактов в единице объема материала)
п о PKL N
(2)
Способ имеет ограниченное применение. Он предназначен только для анализа
материалов с равновеликими как частицами, так и их контактами. Его использование для, анализа материалов, содержащих неравновеликие шаровидные частицы и неравновеликие их контакты возможно лишь в качестве оценочного анализа.
Цель изобретения - расширение возможностей способа путем применения для анализа материалов с неравновеликими частицами и их контактами.
Поставленная цель достигается тем, чго в известном способе микроструктурного анализа материалов с шаровидными частицами и их плоскими круговыми контактами, включающем измерение площади шлифа, подсчет «исла следов контактов частиц на плоскости шлифа, определение их числа на единице площади шлифа и определение числа контактов в единице объема, дополнительно измеряют длину следа каждого контакта на плоскости шлифа, определяют средний диаметр контактов и дисперсию, а число контактов в единице обьема, их средний диаметр и дисперсию определяют по формулам
л hi
(3) (4)
Li - DK ),
(5)
где Li - длина следа 1-контакта на плоскости
шлифа;
п - число измеренных следов контактов;
S - площадь шлифа;
No число следов контактов на единице площади шлифа, n/S;
NKV число контактов в единице объема;
DK - средний диаметр контактов;
а2 - дисперсия.
Формулу (3) для определения числа контактов получим следующим путем. 1/1з формул (1) и (2) следует, что при одинаковых диаметрах контактов
Мка Jr/4NKVDK
Видоизменим уравнение (6) применительно к системе неравновеликих контактов. Для этого рассмотрим систему контактов частиц, в единице объема которой находятся контакты следующих диаметров
NKI контактов диаметра DKI ;
1 к2то жеDK
Для контактов каждого диаметра в отдельности соблюдается условие (6)
NKA -ц NKI DKI ,
где ,2гл.
Просуммируем по отдельности левые и правые части этих равенств
2 NKA, f % (NK.DKI).(7)
1 14| 1
Левая часть полученного равенства равна общему числу NKa следов неравновеликих контактов на единице площади шлифа, а
правая деленная на -т NKV , - среднему
арифметическому диаметру D контактов,
т.е.
,с,
20 (7Э)
откуда следует формула (3).
Для установления зависимостей (4) и (5) рассмотрим систему равновеликих контактов равномерно (по положению и направлению) расположенных в объеме материала и пересекаемых плоскостью микрошлифа. Длина L следа отдельного контакта на площади шлифа (хорда окружности) обусловлена расстоянием F хорды до центра контакта
.(8)
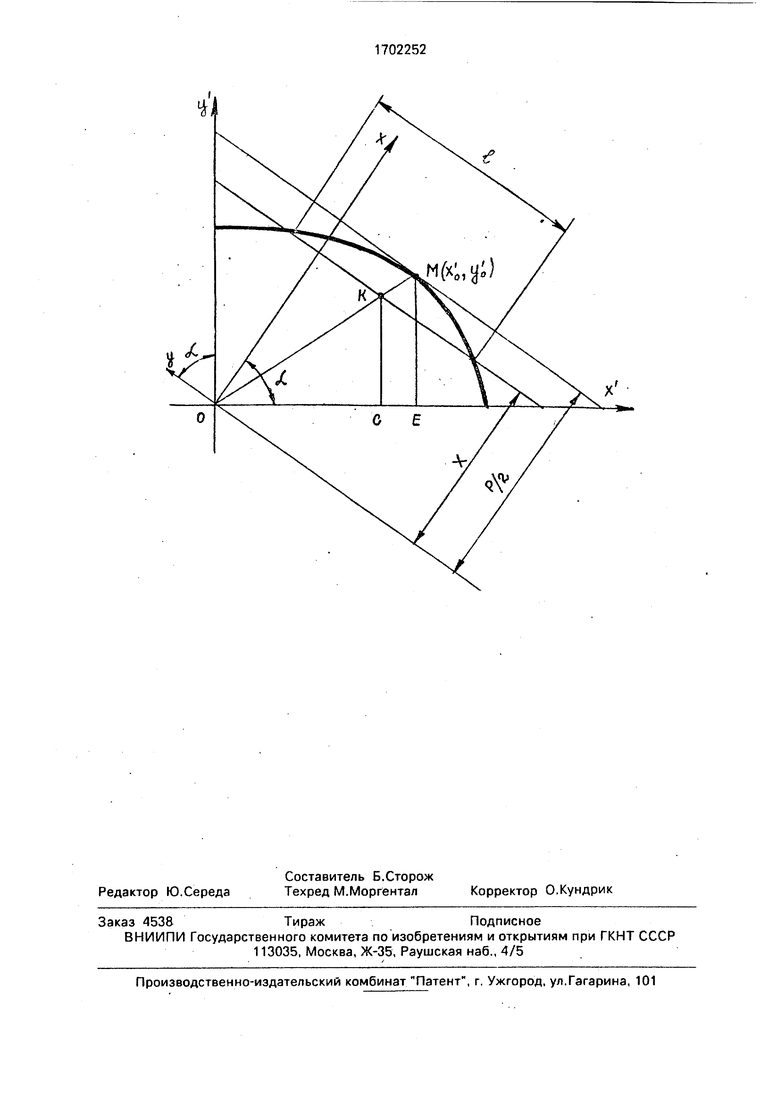
Для учета влияния относительного расположения контакта и секущей (плоскости шлифа) на величину L рассмотрим в декартовой системе координат Oxyz пересечение единичного произвольно расположенного контакта диаметра DK секущей плоскостью, перпендикулярной плоскости хОу. Отметим, что пересечение единичного контакта системой параллельных плоскостей в данном рассмотрении равнозначно пересечению плоскостью шлифа равномерно расположенных равновеликих контактов.
На чертеже показана 1/4 часть проекции окружности на плоскость хОу - эллипса.
Большая ось эллипса (Ох1) равна DK, малая (Оу ) - Dncos p. Углы аи определяют взаимное расположение контакта и секущей: а - острый угол между проекцией перпендикуляра к контакту на плоскость хОу и осью Оу; р- острый угол между перпендикуляром к контакту и осью Oz.
Кроме того, I - проекция L; OK - проекция F; ОЕ хо ; ЕМ у0 ; Р/2 - расстояние от центра О до касательной (роловина расстояния между касательными к эллипсу); х - расстояние произвольной секущей плоскости (ее следа на плоскости хОу) до центра контакта; ось Оу, секущая и касательная к окружности (эллипсу) параллельны.
25
30
35
40
45
50



| название | год | авторы | номер документа |
|---|---|---|---|
| СПОСОБ ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПАРАМЕТРОВ СТРУКТУРЫ МЕТАЛЛА | 2005 |
|
RU2317539C2 |
| СПОСОБ ДИСТАНЦИОННОГО КОНТРОЛЯ РАЗМЕРОВ ТОНКОДИСПЕРСНЫХ АЭРОЗОЛЕЙ СТОЙКИХ ТОКСИЧНЫХ ХИМИКАТОВ ПРИ ВОЗНИКНОВЕНИИ ЗАПРОЕКТНЫХ АВАРИЙ НА ХИМИЧЕСКИ ОПАСНЫХ ОБЪЕКТАХ | 2014 |
|
RU2578105C1 |
| Способ количественной оценки неоднородности зёренной структуры листовых металлических материалов | 2016 |
|
RU2628815C1 |
| Способ количественной оценки распределения дисперсных фаз листовых алюминиевых сплавов | 2018 |
|
RU2694212C1 |
| Способ определения интегральных значений параметров напряженно-деформированного состояния тел при циклическом нагружении | 1989 |
|
SU1753352A1 |
| СПОСОБ СТЕРЕОЛОГИЧЕСКОГО ИССЛЕДОВАНИЯ СТРУКТУРНОЙ ОРГАНИЗАЦИИ ОБЪЕКТОВ | 2002 |
|
RU2291488C9 |
| СПОСОБ ОПРЕДЕЛЕНИЯ ЭНЕРГИИ АКТИВАЦИИ ФАЗОВЫХ ПРЕВРАЩЕНИЙ ПРИ РАСПАДЕ МАРТЕНСИТА В СТАЛИ | 2014 |
|
RU2574950C1 |
| АБРАЗИВНЫЙ МАТЕРИАЛ И СПОСОБ ЕГО ПОЛУЧЕНИЯ | 1996 |
|
RU2142976C1 |
| СПОСОБ ПОЛУЧЕНИЯ МОДИФИЦИРУЮЩИХ МАТЕРИАЛОВ ДЛЯ АЛЮМИНИЯ И ЕГО СПЛАВОВ | 2004 |
|
RU2257419C1 |
| КАМЕРА ДЛЯ ВАКУУМНОЙ СУШКИ (ВАРИАНТЫ), ИХ ПРИМЕНЕНИЕ И ТЕПЛООБМЕННИК | 2006 |
|
RU2341166C2 |
Изобретение относится к способам количественного микроструктурного анализа материалов с шаровидными частицами, образующими плоские круговые контакты.,С целью повышения достоверности при анализе материалов с неравновеликими частицами, дополнительно измеряют длину следа каждого контакта на плоскости шлифа и определяют средний диаметр контактов и дисперсию. Число контактов в единице объема, их средний диаметр и дисперсию определяют по формулам: NKV (4/я X KA/DK); DK Г(я /2Хп/Ј 1)(4/гг„)Ј U-DK) 1 1 1 1 где U - длина следа 1-контакта на плоскости шлифа; п - число измеренных следов контактов; NK, число следов контактов на единице площади шлифа; NKA n/S; S - площадь шлифа; fxkv - число контактов в единице объема; DK - средний диаметр контактов; а2 - дисперсия 1 ил , 1 табл (Л
Мкп
Окп
Используя аналитическую геометрию можно показать, что в рассматриваемом случае уравнение эллипса примет вид
,2л f ,.1
4(x V
DK
+
4(У ) D 2 cos 2 p
(9)
а уравнение касательной в произвольной точке М(х0, УО )
+
4У
- 1
D cos 2 #
При этом расстояние Р зависит от аи рм определяется по формуле
Р DK Vi -slr aslfV.Ol) Величину F определим как длину гипотенузы прямоугольного треугольника, проекция которого на плоскость хОу показана как ОСК,
F ( КС/cos pf (12)
Из уравнений (9) и (10) следует ,/Р. х()
l2 cos a;
ОС 2 ххо/р х(,(13)
Подставим выражения (13) и (12) в (8) и после некоторых преобразований получим
(14)
(p/2)2-xT и
((р/2)2-х2)-г/2.(15)
Уравнения (14) и (15) выражают зависимость величины следа контакта на произвольной секущей плоскости и ее обратной величины от расстояния секущей до центра контакта и посредством р. от их взаимного углового расположения.
Любое расстояние секущей от центра эллипса равновероятно. Поэтому средние значения L и 1/L при изменении х от 0 до Р/2 находимы как средние значения функций (14) и (15), интегрируемых в этих преде
L 2
И2
/L
JLJx.|Dr)
,
Уравнения (16) и (17) выражают зависимость между средними значениями L следов равновеликих контактов (и их обратными величинами 1/L) на плоскости шлифа и диаметром контакта,
Можно показать, что только 1/L является параметром, пригодным для надежной оценки среднего диаметра контакта при неравновеликих контактах. Применив подход, ранее использованный при выводе уравнения (7а), получим
hi
S
d w
i -- Т1
5
10
или с учетом (17)
WQ W
ZX;42(. 09)
Левая часть равенства (19) равна общему числу Мст неравновеликих контактов в единице объема, а прааая, поделенная на
8 М
2 ка
Jt
- среднему арифметическому об
0
ратных величин следов всех контактов на плоскости шлифа, т.е.
NKV - NKai7L.(20)
ni
Решая совместно уравнения (20) и (3), получим уравнение (4)
1 -ЯП(Л
.(4)
гГ -п
2 п
I
1/Li
на N
Используя этот же подход и умножив левую и правую часть выражения (16)
25 на N
ка| , получим
m
30
35
40
Ј(Мк.1мк;ад. (21)
Левая часть равенства (21) равна сумме длин следов контактов на единице площади
Мкэi j п
шяифа(У Мили -- У LI), а правая, 1n i 1
умноженная на тг/4, -суммарной площади Sg контактов в единице объема, т.е. равенство (21) превращается в
N A-5T|. ч п7 (22) -:г-
i
Нетрудно доказать, используя тождество OKI DK - (Ок - DKI), что правую часть выражения (22) можно представить в виде
22
NKV(DK + о ). В связи с этим, после преобразования выражения (22), получим
NKA
45
б2:.
мК
Kv
ft Ј / 4 к
Sbi K Dj-Z k- .
( п -,;
0
5
Предлагаемый способ микроструктурного анализа основан на строгих математических соотношениях и открывает возможность определять число контактов частиц в единице объема материалов с неравновеликими контактами и частицами, т.е. расширяет возможности анализа. Полученные этим способом значения можно использовать для определения связности (среднего числа контактов на одну частицу) в материалах с неравновеликими частицами и их контактами - весьма важного структурного параметра материала, позволяющего устанавливать структурные корреляции
свойств материала, типа проводимости и прочности.
Предлагаемый способ использован для микроструктурного анализа образцов, полученных спеканием свободно насыпанного порошка бронзы со сферической формой частиц и следующим гранулометрическим составом: 85 мас.% порошка имели диаметр от 50 до 400 мкм. Измерение следов контактов частиц выполняли на микрофотографии шлифа с площадью S, равной после приведения к плоскости шлифа 9 мм . Измерены 358 следов контактов частиц. Сумма длин измеренных следов составила 5,460 мм, сумма обратных длин - 35248 (приведены к плоскости шлифа), Параметры трехмерной структуры, расчитанные по исходным данным предлагаемым способом и известным (предполагая равенство диаметров контактов), приведены в таблице.
Как следует из данных таблицы точность оценки числа контактов и их среднего диаметра известным способом в предположении равенства диаметров низкая: погрешность составляет соответственно 21 и 18%.
Использование предлагаемого способа расширяет возможности известного микроструктурного анализа(принятого также в качестве базового) и позволяет определять
число контактов сферических частиц, образующих неравновеликие плоские круговые контакты, а также их средний диаметр и дисперсию.
Формула изобретения
Способ микроструктурного анализа материалов, включающий измерение площади шлифа, подсчет числа следов контактов частиц на плоскости шлифа, определение их
числа на единице площади шлифа и опре- числа контактов в единице обьема, отличающийся тем, что, с целью повышения достоверности при анализе м,а- термалов с неравновеликими частицами,
дополнительно измеряют длину следа каждого контакта на плоскости шлифа, определяют средний диаметр контактов и дисперсию, а число контактов в единице объема N«v, их средний диаметр D и дисперсию о определяют по формулам
NW
D
DK- 2
п
- ,ь
zif/i.;
;-
-letA LrD)
где Li - длина следа l-контакта на плоскости
шлифа;
п - число измеренных следов контактов;
N«a - число следок контактов на единице площади шлифа, N; а n/S;
S - площадь шлифа.
| Салтыков Л.А | |||
| Стереометрическая металлография | |||
| М.: Металлургия, 1976, с.266 | |||
| Чернявский К.С | |||
| Стереология в металловедении | |||
| М : Металлургия, 1977, с.214-216 |
Авторы
Даты
1991-12-30—Публикация
1987-09-29—Подача