00
сл
Устройство относится к области вычислительной техники и может быть использовано для согласования с вычислительными устройствами, функционирующими в СОК, а также в технике связи при передаче информации кодами СОК.
Известно устройство для преобразования чисел из десятичной системы счисления в Ьйстёму остаточных классов, содержащее блоки умножения по модулю и блок суммирования по тому же модулю. Вход каждого блока умножения соединен с. шиной подачи соответствующего разряда числа, представленного в позиционной системе счисления, а выходы блоков умножения по модулю соединены со входами блока по тому же модулю, а также преобразователи степеней основания в систему остаточных классов, а каждый выход соединен со входом блока умножения по модулю. .
Недостатком известного устройства является большой объем оборудования.
Наиболее близким по технической сущности к заявляемому устройству является устройство, содержащее группу табличных преобразователей позиционного кода в код индекса, группу сумматоров по модулю и группу табличных преобразователей кода индекса в код остатка.
Недостатком данного устройства является невозможность преобразования числа из позиционной системы в систему остаточных классов.
Цель изобретения - расширение области применения за счет выполнения преобразователя из позиционной системы счисления в систему остаточных классов.
Поставленная цель достигается тем, что устройство содержит группу преобразователей позиционного кода в код индекса, группу сумматоров по модулю, группу табличных преобразователей кода индекса в код остатка и группу накапливающих сумматоров.
Введение накапливающих сумматоров позволяет расширить область применения за счет получения возможности преобразования из позиционной системы счисления в систему остаточных классов, следовательно, предлагаемое решение обладает существенными отличиями.
На чертеже приведена структурная схема устройства
Устройство для преобразования чисел из позиционной системы счисления в систему остаточных классов содержит информационные зходы 1, группу 2 табличных преобразователей позиционного кода в код индекса, входами подключенные к информационным входам, группу 3 сумматоров по
модулю, первые входы которых подключены к выходам группы 2, а вторые - к шине 4 подачи константы, группу 5 табличных преобразователей кода индекса в код остатка,
входом подключенной к выходам группы 3, группу 6 накапливающих сумматоров, входом подключенную к выходам группы 5, выходы группы 6 являются выходами устройства.
Предложенное устройство реализуют перевод чисел из позиционной системы счисления в систему остаточных классов следующим образом.
Любое .число в позиционной системе
счисления может быть представлено следующим образом:
+ an-iNn 1 + ... + aiN + а0 или
А У aiN
Перевод числа из позиционной системы счисления в систему остаточных классов может быт.ь осуществлен с помощью наборов, констант, являющихся эквивалентами степеней N, где N - основание позиционной системы счисления.
Пусть А задано в позиционной системе счисления с основанием N в виде
+ an-iNn 1 + ... + aiN + а0
или
А У aiN1
Здесь а - одно из чисел 0, 1, 2....N-1.
Пусть N1- 01 0)# 0) ()) для ,2...п - есть представления степеней N в системе остаточных классов, а величины aj
(«1 0), ai 0)ап 0)) для ,2...n представления коэффициентов полинома (1). И пусть дан полином г
Q(x)
aix1
О)
где at («1 0). о (0«n (0) j 1,2n,
х (х1(1),х2®xn(0
Коэффициенты и степени основания представлены в системе остаточных классов по основаниям Pi,P2Рп. Тогда в
соответствии с правилами сложения и умножения в системе остаточных классов получим:
Q(x)(bi0)xi(i)
РЛ
ап
55 Используя свойства полинома Q(x), запишем выражение (1) с коэффициентами и степенями N, выраженными в СОК в виде
Qj У a/OflO) ,.,n
Получим
A(Joai(i)(i);|)an(l)(0
Таким образом, для образования числа N в СОК необходимо значение г констант, являющихся степенями N и N-1 констант, соответствующих возможным значениям а.
Рассмотрим перевод числа 102 из десятичной системы в СОК с основаниями , P 5, Рз 7. Основание системы N 10 (1,1,1); .0,3); N2 100 (1,0.2) (2,2,2); ai - 0 (0,0.0); 32 - 1 0-1.1) 102(21+01+11, 21+ 00 + 01, 21+ 03 + 12); 10240,2,4).
При рассмотрении данного примера видно, что для нахождения остатка по данному модулю, необходимо использовать операцию умножения, Ее можно заменить простым сложением, если от сомножителей перейти к их индексам.
Пусть у нас имеется сравнение
axs 1(mod P)
в общем случае сравнение
а т. B(mod P)
может иметь бесконечное множество решений. В частном случае, если число а не кратно Р и Р простое, то в этом случае справедливо сравнение s 1(mod P)
Если это тождество.имеет место, то число а называется первообразным корнем числа Р.
Если а- первообразный корень числа р, то сравнение
ах A(moa P),
где А не кратно Р. имеет единственное решение. Число I, являющееся решением сравнения (2) называется индексом числа А. Если А и В - целые положительные числа, индексы которых по модулю р соответственно равны И и 2 при первообразном корне а и, если через индекс I обозначить произведение А на В,то индекс произведения будет равен сумме индексов сомножителей И и ia, взятой по модулю р-1. Обратимся к рассмотренному выше примеру. Заменим сомножители их индексами, а произведение - суммой индексов сомножителей
, р-1 2, , р-1 4 , р-1 6
indO ind1 0 ind
ind 2 1 ind 2 1 ind ind 3 1
обозначим действие нахождения числа по его индексу i знаком . Тогда
Для р 3,Для р 5
1/
(0+1)2
)2 (f-)eO 1 (0+0)10 l nd V+OH)
-v
(-+0)0
Q 5
0
5
0
5
о 5
0
е
Для
(2+0)2
0-3 ind 1(2+1)0
1 (0+2)2
Для нуля индекс отсутствует. Обозначим его знаком - и будем считать, что сумма индекса нуля и индекса любого числа есть -. Сложим полученные значения в соответствии с правилами сложения в СОК и получим число (0, 2, 4). Таким образом, заменив умножение простым сложением индексов степеней N и индексов соответствующих коэффициентов полинома (1): представлен- но в СОК мы получили такой же резул гат, как и при суммировании произведений arNi
Устройство работает следующим образом. Коэффициенты числа А, представление которого необходимо получить, подаются на информационный вход устройства, группа 2 преобразуется коэффициенты ai в коды индексов. В группе 3 осуществляется сложение индексов коэффициентов с индексами соответствующих степеней N , в группе 5 находится антииндекс суммы, в группе Б осуществляется последовательное суммирование произведений asN1. В первом такте суммируются индексы коэффициентов N1 с индексами степеней ai, полученные для модуля PI, во втором также для модуля Р2. в п-м - для модуля Рп.
Таким образом, за счет введения новых элементов и связей, устройство решает поставленную задачу.
Достоверность поставленной цели подтверждается изложенным в описании принципа действия.
Формула изобретения Устройство для преобразования чисел в системе СОК, содержащее группу табличных преобразователей позиционного кода в код индекса, группу сумматоров по модулю и группу табличных преобразователей кода индекса в код остатка, причем выходы табличных преобразователей позиционного кода в код индекса группы соединены с входами первых слагаемых соответствующих сумматоров по модулю группы, выходы которых соединены с входами соответствующих табличных преобразователей кода индекса в код остатка группы, отличающееся тем, что, с целью расширения области применения за счет выполнения преобразования из позиционной системы счисления в систему остаточных классов, оно содержит группу накапливающих сумматоров по модулю, причем информационный вход устройства соединен с входами табличных преобразователей позиционного кода в код индекса группы, входы вторых
слагаемых сумматоров по модулю группыкод остатка группы соединены с входами
соединены с соответствующими входамисоответствующих накапливающих сумматоконстант группы устройства, выходы таб-ров по модулю группы, выходы которых явличных преобразователей кода индекса вляются выходами группы устройства.

Изобретение относится к области вычислительной техники и может быть использовано для согласования с вычислительными устройствами, функционирующими в СОК, Цель изобретения - расширение области применения за счет выполнения преобразования из позиционной системы счисления в систему остаточных классов Поставленная цель достигается тем, что устройство содержит группу табличных преобразователей 2 позиционного кода в код индекса, группу сумматоров 3 по модулю, группу табличных преобразователей 5 кода индекса в код остатка, группу накапливающих сумматоров 6 по модулю. 1 ил.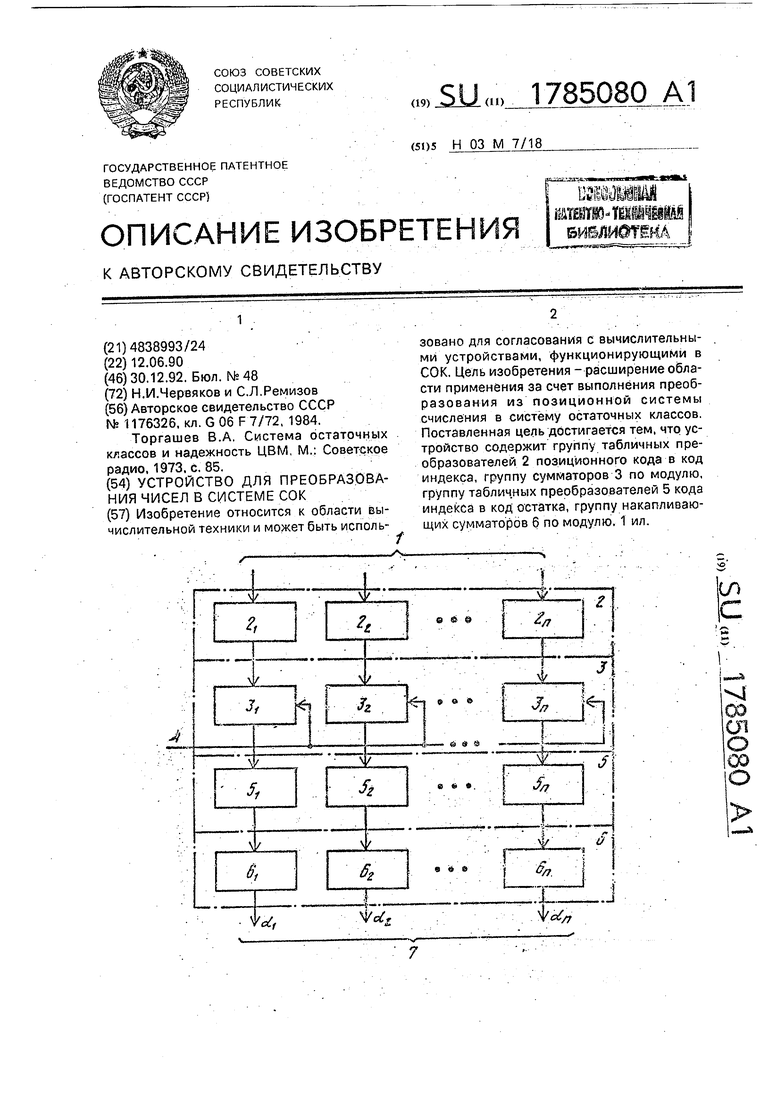


| Арифметическое устройство в системе остаточных классов | 1984 |
|
SU1176326A1 |
| Приспособление для точного наложения листов бумаги при снятии оттисков | 1922 |
|
SU6A1 |
| Торгашев В.А, Система остаточных классов и надежность ЦВМ М. | |||
| Советское радио, 1973, с | |||
| Устройство для выпрямления опрокинувшихся на бок и затонувших у берега судов | 1922 |
|
SU85A1 |
Авторы
Даты
1992-12-30—Публикация
1990-06-12—Подача