Предлагаемое изобретение относится к области авиационного приборостроения и предназначено для повышения точности решения задачи навигации летательных аппаратов (ЛА), типа самолета.
Поскольку инерциальным навигационным системам (ИНС) присущи принципиально неустранимые недостатки: растущие во времени погрешности определения координат и скорости, то для повышения точности ИНС применяют коррекцию от дополнительных источников навигационной информации.
При наличии гравиметра в 2-x компонентной ИНС появляется возможность коррекции ошибок по аномалиям гравитационного поля Земли. В технической литературе (см. Красовский Л.А., Белоглазов И.Н., Чигин Г.П. Теория корреляционно-экстремальных систем Наука, 1979, стр.225-231 - прототип) описан аналогичный способ формирования корректирующих поправок по аномальной составляющей напряженности гравитационного потенциала Земли, заключающийся в выработке оптимальных оценок выходных параметров ИНС путем обработки корреляционно-экстремальным алгоритмом измеренного значения аномалий ускорения силы тяжести Земли и эталонного (картированного) значения в координатах, определяемых ИНС, пересчитанного на высоту полета. Условиями коррекции по указанному способу является стационарный горизонтальный полет ЛА и точный контроль высоты, осуществляемый измерителями неинерциальной структуры. Однако даже при соблюдении указанных условий полета, выделение полезного сигнала при гравитационных аномалиях на фоне инерциальных шумов, порождаемых траекторным движением ЛА, представляет собой трудную задачу.
Поступающий на вход оптимального фильтра зашумленный неучтенными инерционными ускорениями сигнал снижает точность и увеличивает время (дальность) оценивания фазовых координат ЛА. В указанной выше книге приводятся следующие данные:
при использовании гравитационного поля с градиентом ˜10 этвеш получены оценки фазовых координат (среднеквадратическое отклонение)
по координатам σx=223 м
по скорости σv=1 м/с
при времени наблюдения ˜2000 с., в то время как для многих задач навигации ЛА требуется иметь погрешность по координатам σx≤50 м, по скорости σv≤0,2 м/с при времени наблюдения не более 300 с. Целью предлагаемого изобретения является повышение точности оценивания и сокращение времени получения осредненной сценки фазовых координат ЛА.
Поставленная цель достигается тем, что в известном способе формирования корректирующего ИНС сигнала по аномальной части напряженности гравитационного потенциала Земли, включающем формирование оптимальных сценок выходных параметров ИНС по сигналам наблюдения, формируемым как разность измеренного сигнала ускорения аномалии силы тяжести и расчетного сигнала аномалии, причем расчетный сигнал формируют в виде суммы двух сигналов - сигнала, соответствующего картированному значению аномалии для измеряемых ИНС координат ЛА, пересчитанному на измеряемую высоту полета, и сигнала, соответствующего вертикальной составляющей траекторного ускорения, формируемого по текущим показаниям ИНС об абсолютных угловой и линейной скоростях ЛА, производят формирование сигналов, соответствующих 1 производной высоты и 2 производной высоты путем выделения этих сигналов из сигналов измерителя высоты неинерциальной структуры, формируют прогнозируемый сигнал аномалии силы тяжести как сумму сигнала, соответствующего расчетному значению аномалии и сигнала, соответствующего 2 производной высоты, и формируют сигнал наблюдения в оптимальном фильтре как разность измеренного сигнала аномалии и сигнала, соответствующего прогнозируемому значению аномалии.
Сущность способа заключается в следующем. Корректирующий сигнал - суть оптимальные оценки ошибок ИНС, вырабатываемые калмановской процедурой фильтрации, сигналы наблюдения в которой формируют как разность сигнала, соответствующего измеренному значению аномалии ускорения силы тяжести, и адекватного ему картированного сигнала аномалии; пересчитанного с учетом искажающих значение аномалии, замеряемой на подвижном объекте, факторов: высоты полета и ускорений, вызванных движением объекта.
Способ осуществляют следующим образом. Получают с помощью ИНС сигналы, соответствующие географическим координатам ЛА: долготе λ и широте ϕ, и сигналы, соответствующие горизонтальным проекциям на оси сопровождающего трехгранника абсолютных угловой ωx, ωy и линейной Vx, Vy скоростей ЛА.
Получают сигнал, соответствующий текущей высоте полета Н с помощью измерителя высоты неинерциальной структуры. Получают сигнал, соответствующий текущей аномалии ускорения силы тяжести ΔGизм. Формируют сигнал, соответствующий картированному значению аномалии как известную функцию координат ЛА ΔGкар (λ, ϕ).
Формируют сигнал картированной аномалии с учетом высоты полета ЛА согласно соотношению
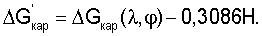
Формируют сигнал расчетной аномалии ускорения силы тяжести как сумму сигнала 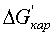 сигнала, соответствующего вертикальной составляющей траекторного ускорения согласно соотношению:
сигнала, соответствующего вертикальной составляющей траекторного ускорения согласно соотношению:
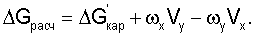
Выделяют из сигнала текущей высоты сигналы, соответствующие 1-ой производной высоты 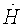 и 2-ой производной высоты
и 2-ой производной высоты 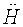 путем применения процедуры скользящей регрессии.
путем применения процедуры скользящей регрессии.
Мгновенное значение высоты во время измерения представляют уравнением регрессии вида:
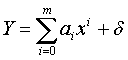
коэффициенты ai(i=0...m) суть:
a0=Н сглаженное значение высоты;
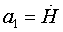 сглаженное значение вертикальной скорости;
сглаженное значение вертикальной скорости;
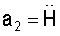 сглаженное значение вертикального ускорения a3...am высшие производные от Н;
сглаженное значение вертикального ускорения a3...am высшие производные от Н;
x=T-t, где T - период, на котором производится аппроксимация значения измерения высоты,
t - текущее время на периоде измерения.
Условие минимума для метода наименьших квадратов, записанное в виде
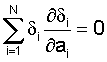
где i=0,1...5,
N - количество измерений.
В матричной форме будет иметь вид
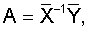
где А - матрица искомых коэффициентов
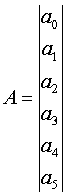
Матрица А определяет на конец периода наблюдений показаний высотомера параметры вертикального движения
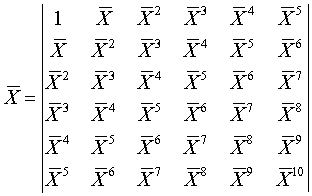
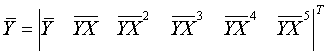
(Черта над элементами означает их средние значения.)
Элементы матрицы определяется соотношениями
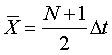
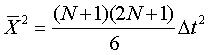
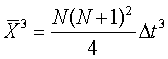
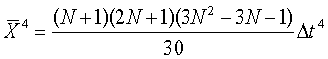
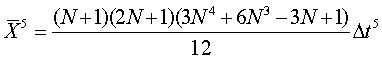
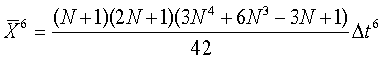
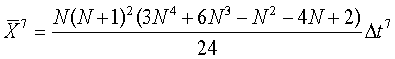
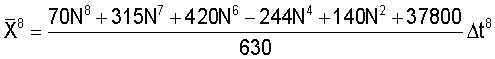
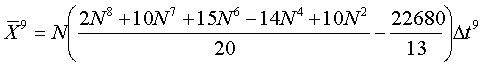
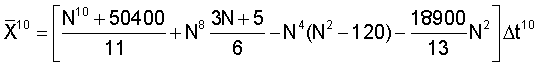
При N≫1 матрица 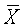 переплетается в виде
переплетается в виде

Обратная матрица записывается следующим образом
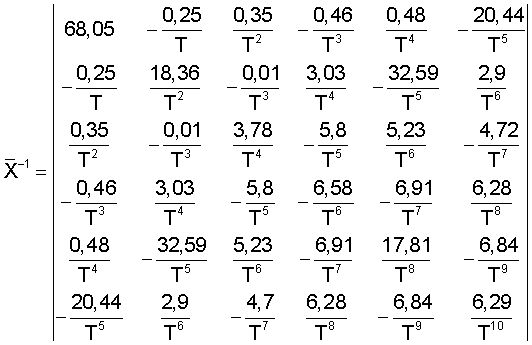
Искомые коэффициенты определяют из следующих зависимостей
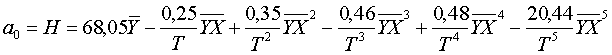
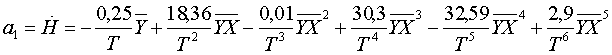
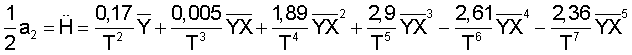
Средние значения элементов матрицы определяют по мере измерений в соответствии со следующими рекуррентными выражениями.
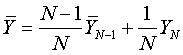
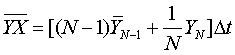
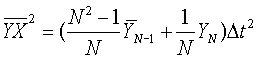
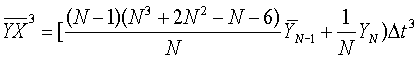
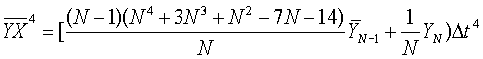
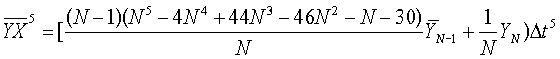
где 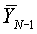 - априорное среднее значение измерения;
- априорное среднее значение измерения;
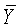 - апостериорное среднее значение измерения;
- апостериорное среднее значение измерения;
YN - текущее измерение.
Дополнительно формируют сигнал, соответствующий прогнозируемому значению аномалии как сумму сигнала расчетной аномалии и сигнала, соответствующего 2-ой производной высоты
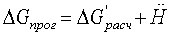
Формируют сигнал наблюдения как разность сигнала, соответствующего измеренному значению аномалии и сигнала, соответствующего прогнозированному значению аномалии
Z=ΔGизм-ΔGпрог.
Формируют сигналы коррекции как оценки ошибок ИНС по координатам, скорости и вертикали путем обработки сигнала наблюдения оптимальной калмановской процедурой фильтрации.
Рекуррентная калмановская процедура фильтрации представляется в виде дискретного прогнозирования и коррекции по поступающему сигналу наблюдения, согласно уравнениям:
Прогноз:
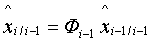
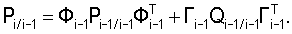
Коррекция:
Ki=Pi/i-1HT(HPi/i-1HT+Ri)-1,
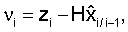
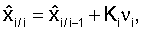
Pi/i=Pi/i-1-KiHPi/i-1,
где Pi/i - ковариационная матрица ошибок оценивания вектора xi на i шаге по i наблюдения zi,
Фi-1=Ф(ti,ti-1) - переходная матрица для вектора xi ошибок ИНС,
Гi-1=Г(ti,ti-1) - переходная матрица распределения неучитываемых в векторе xi шумов ИНС,
Qi/i - ковариационная матрица с неучитываемых в векторе шумов ИНС
(Т - знак транспонирования).
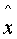 - вектор сценок
- вектор сценок 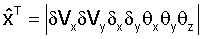
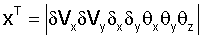 вектор состояния системы с компонентами,
вектор состояния системы с компонентами,
δVx, δVy - ошибки ИНС по скорости,
δx, δy - ошибки ИНС по координатам,
θx, θy, θz - ошибки углов ориентации приборного трехгранника, относительно расчетного
A - матрица системы уравнений ошибок ИНС
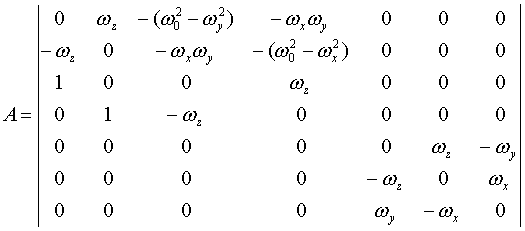
z - одномерный вектор наблюдения;
H - матрица связи вектора наблюдения с вектором состояния, получаемая варьированием вектора наблюдения по фазовым координатам вектора состояния
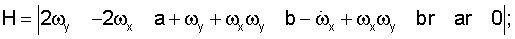
a, b - заданные коэффициенты-градиенты аномалии ускорения силы тяжести
Вектор шумов системы 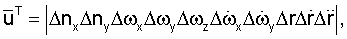
Δnx, Δny - инструментальные ошибки акселерометров;
Δωx, Δωy, Δωz, 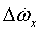 ,
, 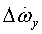 - инструментальные ошибки гироскопов;
- инструментальные ошибки гироскопов;
Δr, 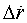 ,
, 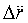 - ошибки измерения параметров вертикального движения;
- ошибки измерения параметров вертикального движения;
Q - ковариационная матрица шумов системы;
R - ковариационная матрица шумов измерения.
Были проведены исследования в виде моделирования на ЭВМ ЕС-1033, реализующего предлагаемый способ формирования корректирующего ИНС сигнала по аномальной составляющей ускорения силы тяжести Земли.
В качестве исходных данных для моделирования было принято (среднеквадратическое отклонение):
ошибки по координатам σx(0)=0,1 км;
-"- по скорости σv(0)=1 м/с;
уход гироскопов σω(0)=0,1 град/ч;
дрейф акселерометров σa(0)=5·10-5 g.
Погрешности измерительных средств составляли:
высотомера σн=0,5 м;
гравиметра σгр=1 мгл=10-6 g.
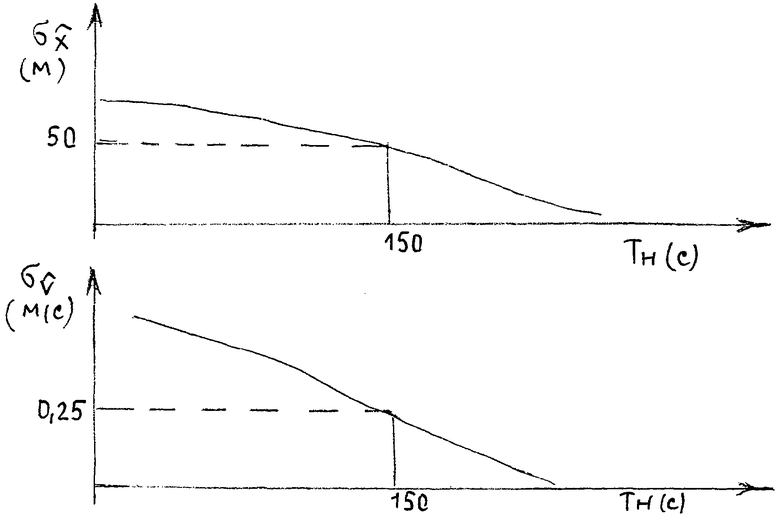
Моделирование выполнялось для режима полета на постоянной высоте Н=10 000 м и с постоянной скоростью V=250 м/с. По результатам моделирования построены зависимости точности оценивания координат и скорости от времени наблюдения.
Из чертежа видно, что к концу цикла наблюдения происходит увеличение точности оценивания координат, скорости и вертикали. Точность определения координат 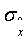 равна 50 м и точность определения составляющих скорости
равна 50 м и точность определения составляющих скорости 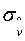 равна 0,25 м/с к концу интервала фильтрации 150 с. Полученные положительные результаты обусловлены тем, чти подавление инерционных шумов, вызванных траекторным движением ЛА в векторе наблюдения, создает благоприятные предпосылки для работы оптимального фильтра, подавляющего в свою очередь помеху измерения.
равна 0,25 м/с к концу интервала фильтрации 150 с. Полученные положительные результаты обусловлены тем, чти подавление инерционных шумов, вызванных траекторным движением ЛА в векторе наблюдения, создает благоприятные предпосылки для работы оптимального фильтра, подавляющего в свою очередь помеху измерения.
Полученные результаты позволяют сделать вывод, что предлагаемый способ формирования корректирующего ИНС сигнала по аномальной составляющей ускорения силы тяжести Земли обеспечивает в сравнении с прототипом лучшую точность оценивания при сокращении времени фильтрации.
| название | год | авторы | номер документа |
|---|---|---|---|
| АВТОНОМНАЯ КОРРЕКТИРУЕМАЯ ИНЕРЦИАЛЬНАЯ НАВИГАЦИОННАЯ СИСТЕМА | 2015 |
|
RU2629658C2 |
| СПОСОБ ФОРМИРОВАНИЯ БАРОИНЕРЦИАЛЬНОЙ ВЫСОТЫ И ВЕРТИКАЛЬНОЙ СКОРОСТИ | 2019 |
|
RU2713583C1 |
| УСТРОЙСТВО АВТОНОМНОЙ КОРРЕКЦИИ | 2001 |
|
RU2219496C2 |
| Способ коррекции бесплатформенной инерциальной навигационной системы | 2016 |
|
RU2646954C2 |
| ИНЕРЦИАЛЬНО-РАДИОНАВИГАЦИОННАЯ СИСТЕМА | 2013 |
|
RU2539846C1 |
| Способ коррекции углов ориентации ЛА по сигналам от одноантенной СНС | 2022 |
|
RU2790081C1 |
| СПОСОБ ОПТИМАЛЬНОГО ОЦЕНИВАНИЯ ОШИБОК ИНЕРЦИАЛЬНОЙ НАВИГАЦИОННОЙ СИСТЕМЫ И ЕЁ КОРРЕКЦИИ ПО НЕПОДВИЖНОМУ НАЗЕМНОМУ ОРИЕНТИРУ С ИЗВЕСТНЫМИ ГЕОГРАФИЧЕСКИМИ КООРДИНАТАМИ | 2019 |
|
RU2713582C1 |
| АСТРОНАВИГАЦИОННАЯ СИСТЕМА | 2014 |
|
RU2607197C2 |
| Астроинерциальная навигационная система с коррекцией по гравитационному полю Земли | 2023 |
|
RU2820600C1 |
| СПОСОБ ФОРМИРОВАНИЯ ВОЗДУШНО-СКОРОСТНЫХ ПАРАМЕТРОВ МАНЕВРЕННОГО ОБЪЕКТА | 2019 |
|
RU2713585C1 |
Изобретение относится к области авиационного приборостроения и предназначено для повышения точности решения задачи навигации летательных аппаратов, типа самолетов. Сущность: для осуществления коррекции формируют сигнал позиционной, скоростной и угловой коррекции комплексной ИНС методом калмановской фильтрации разности сигналов измеренной и расчетной аномалии гравитационного поля Земли, формируемого в виде суммы - запомненного сигнала аномалии гравитационного поля, который соответствует текущему местоположению объекта, и сигнала вертикального ускорения объекта. При этом измеряют текущее значение высоты с помощью измерителя высоты неинерциальной структуры. Формируют по нему сигналы вертикальной скорости и ускорения. Затем формируют сигнал суммы расчетной гравитационной аномалии и сформированных сигналов. Полученный сигнал используют при формировании сигнала позиционной скоростной и угловой коррекции. Технический результат: повышение точности. 1 ил.
Способ коррекции комплексной ИНС, включающий формирование сигнала позиционной, скоростной и угловой коррекции комплексной ИНС методом калмановской фильтрации разности сигнала измеренной и сигнала расчетной аномалии гравитационного поля Земли, формируемого в виде суммы - запомненного сигнала аномалии гравитационного поля, соответствующего текущему местоположению объекта, и сигнала вертикального ускорения объекта, отличающийся тем, что с целью увеличения точности и сокращения времени коррекции, измеряют текущее значение высоты с помощью измерителя высоты неинерциальной структуры, формируют по нему сигналы вертикальной скорости и ускорения, формируют сигнал суммы расчетной гравитационной аномалии и сформированных сигналов, используют полученный сигнал при формировании сигнала позиционной скоростной и угловой коррекции.
| А.А.Красовский, И.Н.Белоглазов, Г.П.Чигин | |||
| Теория корреляционно-экстремальных систем | |||
| М.: Наука, 1979, стр.225-231. |
Авторы
Даты
2006-09-27—Публикация
1985-10-08—Подача