Известны способы кодирования чисел, основанные на представлении числа в виде совокупности наименьших положительных вычетов числа по системе взаимно простых модулей.
Предлагаемый способ отличается тем, что, с целью упрощения реализации операций, требующих определения величины числа, код числа дополняют линейной комбинацией цифр представления остаточных классов с постоянными коэффициентами, однозначно определяемыми систе.мой линейных полиномов, равных модулям системы остаточных классов при некотором фиксированном значении аргумента, фиксируют переполнения при алгебраическом суммировании цифр системы остаточных классов, формируют на выходе дешифратора величину, зависящую от комбинаций возможных переполнений, и при переполнении сумматора с фиксированной разрядной сеткой при сложении дополнительных цифр с величиной на выходе дешифратора формируют сигнал выхода результата за диапазон взанмно однозначного соответствия системы остаточных классов. При переполнении сумматора с фиксированной разрядной сеткой при суммировании дополнительной цифры положительного числа, дополнительной цифры суммы диапазона взаимно однозначного соответствия с отрицательным числом и величины на выходе дешифратора формируют сигнал положительного
знака результата, а при отсутствии переполнения фор.мируют сигнал отрицательного знака результата.
Чтобы упростить деление числа на два при отсутствии четных оснований, осуществляют поразрядное деление, суммируют результаты с фиксированием переполнений при сложении разрядов, суммируют на отдельном сумматоре дополнительную цифру результата саму с собой и с величиной на выходе дешифратора, определяемой комбинацией переполнений, сравнивают pe3yvTbTaT с дополнительной цифрой делимого и при их равенстве выводят результат поразрядного деления на выход, при отсутствии равенства вычитают единицы из разрядов делимого и снова осуществляют поразрядное деление.
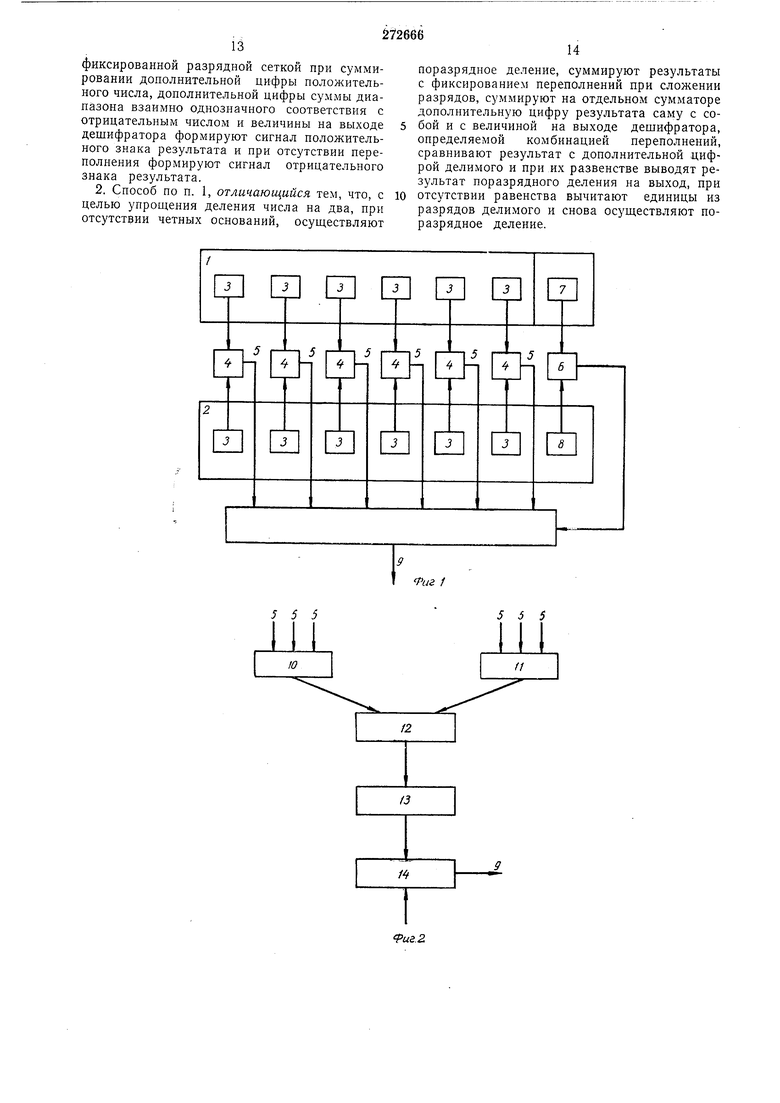
На фиг. 1 представлена блок-схема предлагаемого устройства; на фиг. 2 - первый вариант функциональной схемы блока анализа; на фиг. 3 - второй вариант функциональной схемы блока анализа.
Рассмотрим целое число N как значение полинома с целочисленными коэффициентами
V (х) а„Х + а„-1 ... -f + а, Выберем систему линейных цолиномов вида )х-I; -целое число; ,2 ..., n + i, называемых в дальнейшем основаниями системы. Разделив полином N (х) на каждое Pi(x); i,2,... ,п+, получаем N(x) () q,(x)+,,(1) где Yi-не зависящие от х целые числа, называемые в дальнейшем компонентами. Очевидно, (li) ,2,... ,п+1. Совокупность-компонент Yi (t 1,2,... ,ra-f 1) единственным образом определяет полином Л (л ) на основании формулы Лагранжа: (..4,p- тд,& P(x)-(x-li) (x-lz)... (). Проиллюстрируем сказанное примером. Выберем li 7, |2 5, Ь 3. Пример: N(x)3x + 8x+l2. Определить компоненты (х): j A/-(|,).yV(7) .3-72 + 8-7 +12 215 7V(|2)A(5) 3-5-2+8-5+12 127 Л(|з)Л(3) 3-32+8-3+12 63 Восстановим полином -N (х) по его компонентам:Р{х) (х-7) (х-5) (х-3)л;з-15x2 + + 71х-105 Р1(л:)3л:г-30x + 71 Pi(|,)Pi(7)&; pi(|2)P45) 4; Р1()63. Подставив в формулу (1) вычисленные значения входящих в нее величин для данного примера, получим N(x) -(xs-8x+ 5) -J X 84 X ( + 2l) + X () Зл;2+8х-+12. Пусть даны два полинома Л1(л;) и N2(x) и пусть Yf и f| , (i 1,2 ... д+1) соответственно их компоненты. Пусть далее компоненты полиномов N±{x) и NX(X), являющихся суммой и произведением исходных полиномов, соответственно Y- и Y.r- Тогда имеют место соотнощениях - „1. „2() - Ti Tf (последнее соотнощение справедливо при условии, что степень полинома (х) не превышает л). Фиксируя х-Хо, мы получаем числа NI{XO) и N2(XQ}, и соотношения (2) определяют правила выполнения операций над представляющими эти числа компонентами. Эти правила определяют возможность замены рациональых операций над числами независимым пааллельным выполнением операций над кол онентами этих чисел. При фиксированном формула (1) приимает следующий вид: (яо) 2 АТ, (-УО) (5;)Р1(;) Возможность параллельной и независимой работы с компонентами числа является существенным отличием от работы с числами в позиционной системе счисления. Наличие же точной формулы (3) для восстановления числа N по его компонентам отличает данную систему от системы счисления в остаточных классах. Это позволяет простым способом, на основе конечных соотношений (линейных форм с постоянными коэффициентами), преодолевать трудности, возникающие при реализации в системе остаточных классов операций, для которых необходима информация в той или иной форме о полном значении числа. Приведем пример, иллюстрирующий правила выполнения операций над числами. Система оснований PI(X)X-7; Р2(х) х-5; Р(х). Выберем X(, IQ. Это приводит к числовым основаниям системы Pi 3, Р2 5 и Рз 7. В этих условиях Я(;со)Я(10)3-5-7 105. С учетом вычислений, приведенных в предыдущем примере, мы написать в соответствии с выражением (4): 21 . 4 . 105 35 . . 105 -;- . s - lill « ff3-88 5-4 И, следовательно, формулу (3) восстановления числа в виде Л -- (35Y1-42Y2 + 15Y3).(6) Пусть даны два числа: Ai 48 и //2 53. Вычислим их компоненты: Ai(x)4x+8; (7)36; Y2 Ai(5) 28; Y3 (3)20; N2(x)5x + 3; Yi2 (7) 38; Y22 (5)28; (3) 18. Па основании (2) напишем для суммы f+ +364-38 74, Y 28 + 28 56; Y3+ 20 + +18 38. Восстановим по (5) число Ni + N2 по его компонентам: N, + NZ -i- (35-74 - 42,56+15-38) - 88 101. Аналогично получим произведение Восстановим по (5) чнсло Ni-Nz по его компонентам:N. (35-1368 - 42-784 +15-360) 8 В приведенном примере компоненты были величинами того же порядка, что и сами числа. Хотя это и вытекает из самой особенности примера, предназначавшегося лишь для иллюстрации правил выполнения операций, и в представлениях больших многозначных чисел можно надлежащим выбором оснований и хо получить компоненты на много порядков меньшие, чем сами числа, тем не менее в процессе выполнения операций ввиду немодульного их характера могут накапливаться величины компонент. Чтобы придать операциям в системе компонент модульный характер, установим связь компонент с остатками. Если а;(,2..., п+1) являются остатками числа N по основаниям соответственно PI, то ввиду соотношения (1), /V ; Р;-{- 7( остатки Л по основанию PI совпадают с остатками у по этому основанию, и поэтому справедливо равенство 11 1 + К,Р,,(7) где KI - целое, положительное или отрицательное число. Введя -в (3) у1, выраженным через а по (6), напишем л 24т;-2Л,., + лЛгЛ1 1 11 1 -- LSC.a. . L J Здесь GI и ; - целые числа, определившиеся в результате приведения всех элементов суммы к общему знаменателю D. Входящая в формулу (7) величина 2 л(9) называется весом числа N. Вес числа является важной интегральной характеристикой числа. Он играет фундаментальную роль в слабопозиционной системе счисления. Дело в том, что каждое число Л может быть представлено при данном значении в форме полинома различными способами. Эти способы приводят к различным величинам компонент, хотя остатки числа, как зависяшие только от его величины, а не от формы представления, сохранят свои значения для различных представлений. Иначе говоря, для различных представлений числа N-yVj N компоненты Y/ Т; запишутся в виде -;;:zza,-f/c;-p;; т; л Л-rln+lП + 1 l,K,-Z,K, ... .,K, W. I11 Рассмотрим пример, иллюстрирующий понятие веса, сохраняя систему оснований предыдущего примера. Ai ai + /Ci3; .2 сс2 + 5Я2; Аз аз+7/Сз {35ai-42a2 + 15a3+105/Ci-210(2 + +105/Сз) -(35ai-42а2+15аз4-105(/ 1-2/C2-f 8 Здесь Ki-2K2 + N - вес числа. Определим вес числа 48: Y, 36 0+12-3; Y2 28 3 + 5.5; 6-f2-7. Здесь , /С2 5 и /Сз 2, л- 12-10 + + 2 4. Число 48 можно представить полиномом различным образом, например 48 2-5х-2 (). В этом случае Yi 49-35-2 12 0 + 4-3; у2 25-25-2 2 + 3+(-1)5; 7з 9-15-2 -8 6+(-2)-7 Wjv 4-2(-1) + (-2) 4 + 2-2 4. Как видим, изменение формы представления числа не влияет на его вес. Значение веса состоит в том, что он позволяет перекинуть мост между остатками числа и его компонентами. Хотя вес определяется через KI , его можно вычислить -ИНЫМ путем. Из теории остаточных классов известно, что число через остатки выражается формулой п + 1 .B.-rA Р,(10) где BI - ортогональные базисы системы, ГА - целое число. Приравнивая правые части (7) и (9), после преобразований получим .D., и, обозначив ii, окончательно - N (mod D), I Так, в условиях предыдущего примера Si 70, , , D 8, . Вычцсляем Ц; ; 120-15 H-s я 17Для Wjv получаем формулу + 2a2 + a.3 (mod 8). Вычислим по этой формуле вес числа 48, остатки которого по принятым основаниям «1 0, а2 3: аз 61 уу 6+6-12 (mod 8) 4. Анализ весов операндов позволяет установить переполнение при сложении, определитью знак результата при вычитании, сравнить числа по величине, провести деление на различные константы, включая основание системы, и т. п. Так, для WM +Л2 веса суммы числа NI +N2, где остаточное представление чиселi Л и имеет вид NI. («; а .., а ,), jV, - (af а,..., « ), 1 V 1 2 п+у а V I 2 и+у можно получить формулу П + 1 1,+. lF;v.+W, + S / (12) 1 Здесь е 1, еслиа +а Р; , еслиа}+«КЛ Если N-L + , то имеет место переполнение. Аналогично строится и определение знака и сравнение чисел. Разность заменяется суммой + (P-Nz), и условие переполнения превращается в правило знаков: + , +Wр-Л2+ Если Wjv,, то , если Wff, , то 7Vi-WV2 0. Деление числа Л на константу, например на 2 (при отсутствии четных оснований в принятой системе), осуществляется на основании условия: «+I Гл./2+1Гл.. 03) I где JV/2 - результат формального поразрядного деления Л на 2. Если условие (12) соблюдено, то Ы1ч и является истинным частным, в противном случае истинным частным будет число ЛГ-1 Приведем иллюстрирующий пример в уелоВИЯХ принятой ранее системы: N 7, 46. Определить наличие переполнения при сложении. -, „ , .7 .г В остаточнои форме и имеют вид: , I.V % I O/. . 4-А/2-(1.1,4); lFyv,5+3 + 4(mod 8) 4 yVi-fAf2 (2,4,0); 8i 0, 62 0, . 8 Определим знак разности Л( 1,3,3); ТГл., 6 -jV 2(2,4,3); Wp-Ni Q + 8+3(mod8)5 (026) е 1 е 1 е 0 Ь i 2 , з м + 6 + 5+1-2 10 8. Следовательно, . NI (1, 3, 5) Разделим NI на 2: (2, 4, 5) (. ) -(2,45)- 10 + 8 + 5(nod8) 7 / .2 /пдг 2 ( д 2 (1,3,3); ei i, 62, 63 1 Истинное частное равно: (1, 3, 3)-(1, 1, 1) (О, 2, 2) (9 9 99 94 (.-lU/ п 1 4) Разделим N на 2: (2,3,2) д, у-(2,3,2); - 10 + 6+2(mod8) 2 Yi(2,3,2) 2 (1, 1, 4) 2 л i о i i о i n Q / Q 2 I 2 + +-/ + U NZ Истинное частное составляет , Как уже указывалось, вес числа не зависит от формы его полиномиального представления и различные представления отличаются друг от друга величинами KIПусть К; и К - величины /С; для раз « ix представлений N N одного и того числа N. Пусть далее К С, +/,. Вычислим вес числа для представления N и ль1 л + 1 пг1 r.v. У К. W;r У ч К , У №+г) - i г 2 i I 2 1-г 1} . Пг1 Лг1 - у } Д V ) / 2 -i гИз равенства WN WA вытекает уравнение «и 2 ) названное уравнением инвариантности. Оно позволяет широко маневрировать величинами KI (являющимися связями между непозиционным и позиционным представлениями числа). Когда для проведения операций надо иметь представление о полном значении числа для использования формул восстановления в виде (1) или (3), необходимо знать компоненты Тг , в то время как нам известны лищь величины остатков а. Переход от «г к г прово(8) нужную величину WN, и по этим Л; вычисляют У1. В большинстве случаев оказывается возможным сосредоточить вес в компоненте но одному из оснований, а остальные комноненты отождествить с остатками числа. Рассмотрим одну из задач, где такой переход должен осуществляться. Пусть требуется расширить диапазон представления числа .V в системе, т. е. определить ко.мпоненты п+2 Yn+a,.. - числа Л по ряду дополнительно введенных оснований Рл + , Рn+Z -S O-ЬП+ЗПолагая последовательно в формуле (1) : |n-t2, X n+z, получим формулы для дополнительных компонент в виде линейных форм: Л--2n-1-I я-(-3 9i ТР Р Тг. -.(15) 11 где -постоянные величины, определяемые выбранной системой дополнительных оснований. В формулу (14) входят величины Yi, которые и нужно в этом случае определить указанным выше путем. Рассмотрим для иллюстрации расширение системы, применявшейся в предыдущих примерах 2 3, Рз 5, 4 7 еше одним основанием хо-(--). Здесь . Подставив в (1) вместо X значение -1, получим: ,;. .. -192-192 -:) + + 3т1-8т. + 6т,. Применим формулу (15) для определения удля числа N 73. В остаточной форме Л (1,3,3) W/v, 6. Так как в формуле для веса /Ci входит с коэффициентом 1, формула будет удовлетворена, если нримем K ,, К 0, /Сз 0. Тогда получим у1 l-f-3-6 19; Y2 3, Y3 3a. Вычислим Y4 3- 19-8 3-f 6 51. Так как в представление числа входит не Y4, а 04 то Y4 можно вычислить по модулю 11. Это дает а4 7. Число 73 имеет по основанию 11 в остатке 7. Рассмотрим блок-схему арифметического устройства, реализующего операции сложения и вычитания над числами, представленными в слабопозиционной системе счисления. Для работы в диапазоне достаточно использовать основания Р, 17; Л 23: Рз 29; Яб 31. Блок-схема арифметического устройства представлена на фиг. 1. Здесь в двух регистрах 1 VL 2 хранятся два операнда А и В: Л (ai,a2, -. - ссб), 5 (р1, рд, . . . . Ре) с весами WA и WB , хранящимися на тех же регистрах. Как видно из фиг. 1, регистры / и 2 представляют собой набор шести пятиразрядных регистров 3. пятиразрядные сумматоры, работающие по заданному модулю, могут быть табличные сумматоры, выполненные на диодах, прошивкой оксиферов или любым другим способом. Каждая из схем суммирования Г; имеет выход 5 е,;, сигнализирующий о переходе через модуль PI в процессе суммирования, т. е. ( 1, если , где Х: число в данном разряде, модуль системы. 1,2,3,4,5,6. В остальных случаях Е; 0. Соответственно схема 6 суммирует веса WA и WB, хранимые в регистрах 7 и 8. Блок анализа вырабатывает сигнал ср по выходу 9, определяемый следующим образом. При сложении признак свидетельствует о переполнении, т. е. о ситуации, когда иначе говоря, о выходе суммы за принятый диапазон представления чисел Р. При вычитании нрнзнак q; l свидетельствует о положительном знаке разультата, а ф 0-об отрицательном знаке результата. Блок-схема блока анализа представлена на фиг. 2. Схемы 10 и // представляют собой дешиф раторные схе.мы, в которых закоммутированк значения всевозможных комибнаций /.;. Это возможно, поскольку величины /. определяются только выбранными основаниями системы, то есть после выбора системы оснований л г являются константами системы. Схема 10 должна реализовывать следующую таблицу в зависимости от значений ei 2 5, подаваемых на ее вход. простой дещифраторчто легко реализуется ной схемой, в которой закоммутированы знаAI + AO, AI+АЗ, .2 + A3. чения AI, 2, Лз, Аналогично работает и схема 11. Результаты поступают на схему 12 формирования суммы величин ч. Сумматор 13 получает окончательную сумму, которая сравнивается с константной Д схемой 14. Довольно просто можно реализовать одноступенчатую схему 75, ра бота которой поясняется табл. 2.
11
Таблица 2
272666
12 продолжение табл. 2





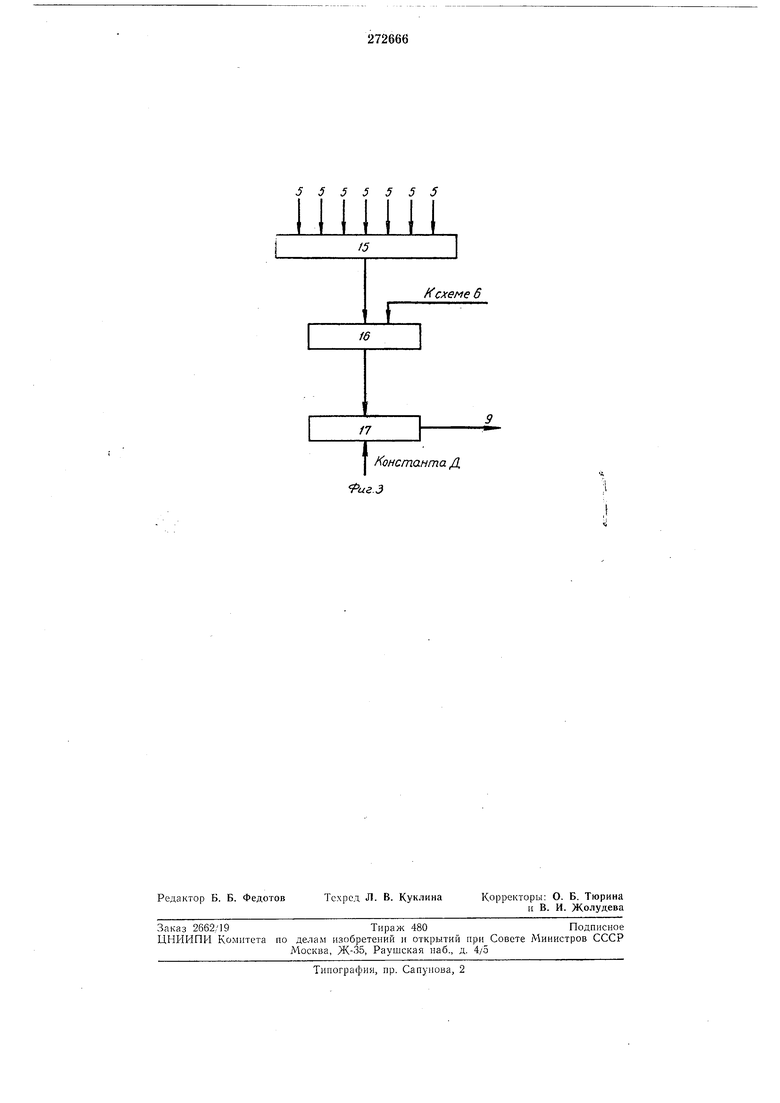

При этом В схеме дешифратора коммутируются 63 значения выходных величин. Общая схема блока анализа в этом случае представлена на фиг. 3.
Таким образом, схема 15 реализует как функции дешифраторов 10 и 11, так и функции схемы суммирования 12.
Выход схемы 15, цредставляющий собой
сумму 2 1 -i поступает на схему 16, где
суммируется с суммой весов операндов, получаемых со схемы 6.
Результат сравнивается с величиной Д, схемой 17, постоянной для выбранной системы оснований, и, если он не меньше Д, вырабатывается сигнал ф.
Поскольку схемы 15, 16 и 17 являются схемами дешифраторного типа, то для выработки признака ф требуется суммарное время нарастания фронта входного сигнала на трех дешифраторных узлах последовательно.
Предмет изобретения
фиксированной разрядной сеткой при суммировании дополнительной цифры положительиого числа, дополнительной цифры суммы диапазона взаимно однозначного соответствия с отрицательным числом и величины на выходе дешифратора формируют сигнал положительного знака результата и нри отсутствии переполнения формируют сигнал отрицательного знака результата.
поразрядное деление, суммируют результаты с фиксированием переполнений при слол ;ении разрядов, суммируют на отдельном сумматоре дополнительную цифру результата саму с собой и с величиной на выходе дешифратора, определяемой комбинацией переполнений, сравнивают результат с дополнительной цифрой делимого и при их развенстве выводят результат поразрядного деления на выход, при
отсутствии равенства вычитают единицы из разрядов делимого и снова осуществляют поразрядное деление.
555
555
555553
К схеме 6
I ЛЬяс/па/у/ла Д .З

Даты
1970-01-01—Публикация