1
Изобретение относится к области вычислительной техники и предназначено для преобразования десятичного кода в код системы остаточных классов (СОК).
Известны устройства для преобразования чисел из десятичной системы счисления в систему остаточных классов, заданных в позиционной системе счисления (в частности, в десятичной) в коды СОК, в которых осуществляется суммирование констант десятичных разрядов AiN (где Л - значение i-ro десятичного разряда. Л - основание системы счисления), выраженных в СОК, для чего необходимо осуществлять преобразование в СОК и значения Ai, и значения N (для получения констант степеней основания р и констант коэффициентов а,).
Предлагаемое устройство отличается от известного тем, что вход каждого блока умножения по модулю соединен с выходом преобразователя соответствующей степени основания в систему остаточных классов и с шиной подачи соответствующего разряда десятичного числа, а выходы блоков умножения по модулю соединены со входами блока суммирования по тому же модулю, что позволяет упростить устройство за счет исключения преобразователей величин Аг в СОК.
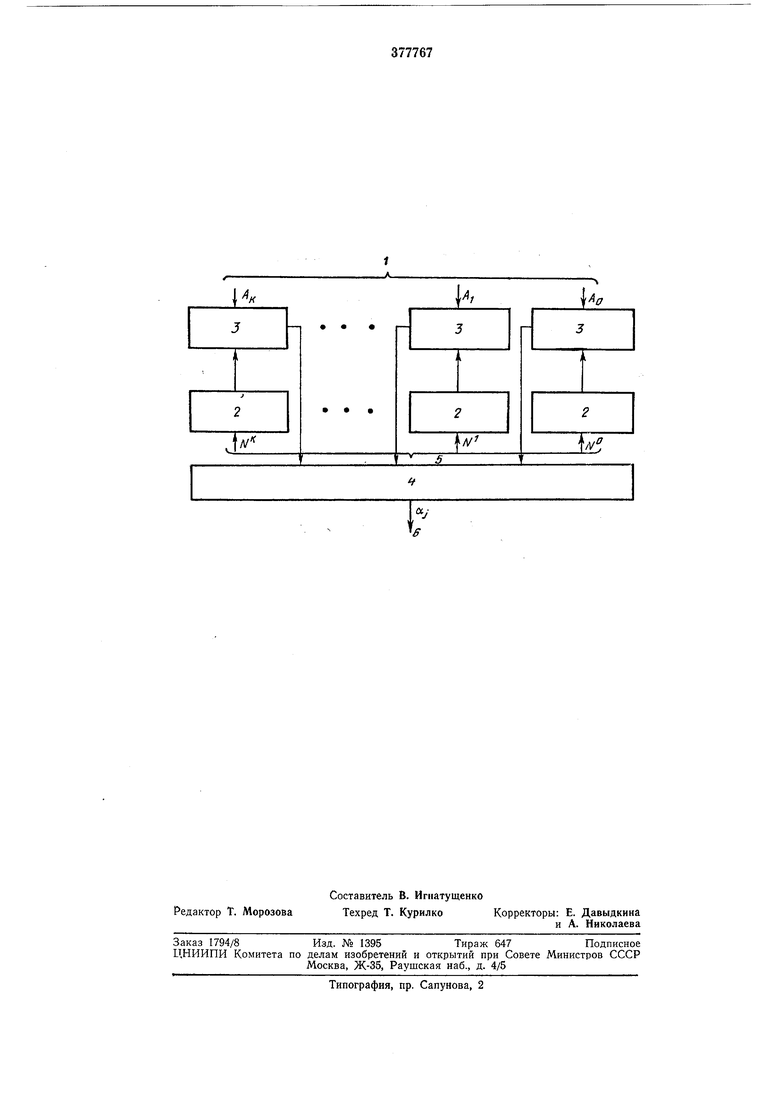
На чертеже дана схема предлагаемого устройства (для преобразования по одному модулю PJ) .
Устройство содержит шины / подачи значений разрядов Ai преобразуемого десятичного числа, преобразователи 2 степеней основания (Л ) в СОК, блоки 3 умножения по модулю PJ, блок 4 суммирования по модулю PJ, шины 5 подачи значений степеней основания Л/ и выход 6.
Устройство использует следующий принцип преобразования чисел.
Число в позиционной системе счисления (в том числе и в десятичной) может быть представлено в виде
Х + +... ...+
+ A,NI + A,№,(i)
где Q. - 1, .
Используя аппарат теории сравнений, выразим степени основания следующими выражениями:С,1, С, N,(mod PJ), ...,С, A(mod Pj}. (2)
С учетом свойств сравнений получим Х A,N + Ak-iN - +...+ А,№ Е А,С, + +Лй-1Сй-1 + ... + A,C,-i-A,C,(mod Pj) Х,. (3)
Для применения указанного принципа в системе счисления с основанием необходимо знать остатки от деления на все модули системы степеней основания , которые дадут набор постоянных чисел С, для каждого модуля. Полученные остатки С{ после умножения на соответствующие цифры любого исходного десятичного числа и составляют суммы, по которым можно определить наименьшие положительные вычеты по всем модулям системы. Полученные наименьшие положительные вычеты и представляют разряды числа, представленного в системе остаточных классов. Из выражения (3) следует, что X, X,(4) X.AfCtGI определяется выражением (2). Разряды числа X в системе остаточных классов образуются путем суммирования значений Ai и Ci по выбранным модулям, т. е. - (AQ)modP.(5) Если в выражении (4) количество разрядов числа Xi больше, чем количество разрядов выбранного модуля, то для этого числа преобразование можно повторить. При переводе десятичного числа X в систему остаточных классов это число вначале преобразуется в другое десятичное число Х, которое сравнимо с исходным, но имеет количество разрядов меньше, а затем число Xi переводится в СОК. Пусть, например, необходимо перевести десятичное число 2556854 в СОК по mod 7. Коэффициенты Ci по mod 7 соответственно равны С, 1, С, Е 10 Е (mod 7) - 3(mod7), С, Е 10(mod 7) Е 2(mod 7), С, Е 10(mod 7) Е - l(mod 7), €4 Е 10(mod 7) Е - 3(mod 7), Ct Е loomed 7) Е - 2(mod 7), С, ElO(mod7)E I(mod7), C,ElO(mod7)E3(mod7), CgE 10(mod 7)E2(mod 7). Значения С; периодически повторяются. Найдем X с учетом коэффициентов Cj. X Е Л,С„ + А,С, + А,С, + Л,С, -f А,С, + + А,С, + А,С, + A,C,(mod 7) Е Е4-1 + 5.3 -f 9-2 + 8(- 1) -f 6(-3) + 5(-2)-f +5-1 +2-3(mod7)E 12(mod7) ;s,. Количество разрядов в числе Xi l2 (два десятичных разряда) больше, чем количество разрядов mod 7 (один разряд), поэтому преобразование можно повторить АГ Е 2 1 + 1 3(mod 7) Е 5(mod 7). Таким образом, наименьший положительный вычет числа J 25568954 по mod 7 равен 5, т. е. разряд числа X в системе остаточныхклассов по модулю 7 равен 5. Устройство работает следуюш;им образом. Число X, Подлежащее преобразованию, в десятичном или двоично-десятичном коде подается по шинам / и 5. При считывании информации разряды десятичного числа поступают на блоки 8, где происходит умножение каждого разряда (Аг) на коэффициенты Сг. Затем полученные произведения ЛгС,- поступают в блок суммирования 4, где происходит суммирование величин по mod PJ, и на выходе 6 образуются значения aj. Предмет изобретения Устройство для преобразования чисел и; десятичной системы счисления в систему остаточных классов, содержащее преобразователи степеней основания в систему остаточных классов, блоки умножения по модулю и блок суммирования по тому же модулю, отличающееся тем, что, с целью упрощения устройства, вход каждого блока умножения по модулю соединен с выходом преобразователя соответствующей степени основания в систему остаточных классов и с шиной подачи соответствующего разряда десятичного числа, а выходы блоков умножения по модулю соединены со входами блока суммирования по тому же модулю.
jK
u
ff

| название | год | авторы | номер документа |
|---|---|---|---|
| Устройство для преобразования чисел из порционной системы счисления в систему остаточных классов | 1981 |
|
SU1008729A1 |
| ВСЕСОЮЗН/лЯ I ПАТЕНТКО-ИКьл-- HA": | 1973 |
|
SU374595A1 |
| Преобразователь двоичного кода в код системы остаточных классов | 1980 |
|
SU959062A1 |
| Устройство для преобразования чисел в системе СОК | 1990 |
|
SU1785080A1 |
| НЕЙРОННАЯ СЕТЬ УСКОРЕННОГО МАСШТАБИРОВАНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2007 |
|
RU2359325C2 |
| НЕЙРОННАЯ СЕТЬ ДЛЯ ПРЕОБРАЗОВАНИЯ ОСТАТОЧНОГО КОДА В ДВОИЧНЫЙ ПОЗИЦИОННЫЙ КОД | 2006 |
|
RU2318238C1 |
| «РЕОБР'АЗОВАТеЛЬ ДВОИЧНОГО КОДА - | 1973 |
|
SU374596A1 |
| УСТРОЙСТВО ДЛЯ ОСНОВНОГО ДЕЛЕНИЯ МОДУЛЯРНЫХ ЧИСЕЛ | 2013 |
|
RU2559771C2 |
| ПРЕОБРАЗОВАТЕЛЬ ЧИСЕЛ ИЗ ПОЗИЦИОННЫХ ОДНОРОДНЫХ СИСТЕМ СЧИСЛЕНИЯ В СИСТЕМЫ ОСТАТОЧНЫХ КЛАССОВ | 1968 |
|
SU211154A1 |
| Устройство для вычисления позиционных характеристик модулярного кода | 1984 |
|
SU1244797A1 |

75
J./V
X
s
Авторы
Даты
1973-01-01—Публикация